Reinforce-Ada
Collection
Training & test sets and finetuned models
•
17 items
•
Updated
•
2
problem
stringlengths 18
2.25k
| gt
stringlengths 1
173
|
|---|---|
2. Variant 1.
Given the set $A=\{1,2,3, \ldots, 1002\}$. Petya and Vasya are playing a game. Petya names a number $n$, and Vasya selects a subset from $A$ consisting of $n$ elements. Vasya wins if there are no two coprime numbers in the chosen subset; otherwise, Petya wins. What is the smallest $n$ that Petya should name to guarantee a win?
|
502
|
Michael picks three different digits from the set $\{1,2,3,4,5\}$ and forms a mixed number by placing the digits in the spaces of $\square$. The fractional part of the mixed number must be less than 1. (For example, $4 \frac{2}{3}$ ). What is the difference between the largest and smallest possible mixed number that can be formed?
(A) $4 \frac{3}{5}$
(B) $4 \frac{9}{20}$
(C) $4 \frac{3}{10}$
(D) $4 \frac{4}{15}$
(E) $4 \frac{7}{20}$
|
4\frac{7}{20}
|
Simplify the expression
$$
\frac{x \sqrt[3]{\frac{1}{y}}-y \sqrt[3]{\frac{1}{x}}}{\sqrt[3]{\frac{x}{y}}-\sqrt[3]{\frac{y}{x}}}
$$
|
\sqrt[3]{x^{2}}+\sqrt[3]{y^{2}}
|
One, (40 points) Find the smallest integer $c$, such that there exists a positive integer sequence $\left\{a_{n}\right\}(n \geqslant 1)$ satisfying:
$$
a_{1}+a_{2}+\cdots+a_{n+1}<c a_{n}
$$
for all $n \geqslant 1$.
|
4
|
Test $B-5$. Let $T$ be the inscribed trapezoid $ABCD$ (counterclockwise) in the unit circle $O$, $ABCDI, AB=s_{1}$, $CD=s_{2}, OE=d, E$ is the intersection point of the heights. When $d \neq 0$, determine the minimum upper bound of $\frac{s_{1}-s_{2}}{d}$. If the minimum upper bound can be achieved, determine all such cases.
|
2
|
## Task A-4.2.
A Gaussian integer is a complex number whose real and imaginary parts are integers. Determine the largest natural number $n$ for which there exists a set of $n$ Gaussian integers such that the squares of their absolute values are consecutive natural numbers.
|
3
|
Three, (This question is worth 20 points)
Find the real number pairs $(p, q)$ such that the inequality $\left|x^{2}+p x+q\right| \leqslant 2$ holds for all $1 \leqslant x \leqslant 5$.
untranslated part:
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
---
Three, (This question is worth 20 points)
Find the real number pairs $(p, q)$ such that the inequality $\left|x^{2}+p x+q\right| \leqslant 2$ holds for all $1 \leqslant x \leqslant 5$.
|
(-6,7)
|
## Task 1 - 030931
We are looking for all three-digit numbers consisting of different digits, where the sum of all two-digit numbers that can be formed from any two of its digits is equal to twice the number.
|
198
|
7. Given the function $f(x)=x+\frac{9}{x}$ on the interval $[1,4]$, the maximum value is $M$, and the minimum value is $m$. Then the value of $M-m$ is $\qquad$ .
|
4
|
Example 5: A and B take turns picking distinct numbers from $0,1, \cdots, 81$, with A starting first, and each person picks one number from the remaining numbers each time. After all 82 numbers are picked, let $A$ and $B$ be the sums of all numbers chosen by A and B, respectively. During the process of picking numbers, A hopes that the greatest common divisor (GCD) of $A$ and $B$ is as large as possible, while B hopes that the GCD of $A$ and $B$ is as small as possible. Under the best strategies for both A and B, find the GCD of $A$ and $B$ after all numbers are picked. ${ }^{[4]}$
|
41
|
XXIV OM - I - Problem 12
In a class of n students, a Secret Santa event was organized. Each student draws the name of the person for whom they are to buy a gift, so student $ A_1 $ buys a gift for student $ A_2 $, $ A_2 $ buys a gift for $ A_3 $, ..., $ A_k $ buys a gift for $ A_1 $, where $ 1 \leq k \leq n $. Assuming that all drawing outcomes are equally probable, calculate the probability that $ k = n $.
|
\frac{1}{n}
|
# Problem 6. (3 points)
Three runners are moving along a circular track at constant equal speeds. When two runners meet, they instantly turn around and start running in opposite directions.
At some point, the first runner meets the second. After 15 minutes, the second runner meets the third for the first time. Another 25 minutes later, the third runner meets the first for the first time.
How many minutes does it take for one runner to complete the entire track?
|
80
|
Consider a square $ABCD$ with center $O$. Let $E, F, G$, and $H$ be points on the interiors of sides $AB, BC, CD$, and $DA$, respectively, such that $AE = BF = CG = DH$. It is known that $OA$ intersects $HE$ at point $X$, $OB$ intersects $EF$ at point $Y$, $OC$ intersects $FG$ at point $Z$, and $OD$ intersects $GH$ at point $W$. Let $x$ and $y$ be the lengths of $AE$ and $AH$, respectively.
a) Given that Area $(EFGH) = 1 \text{ cm}^2$, calculate the value of $x^2 + y^2$.
b) Verify that $HX = \frac{y}{x+y}$. Then, conclude that $X, Y, Z$, and $W$ are vertices of a square.
c) Calculate
Area $(ABCD) \cdot$ Area $(XYZW)$.
|
1
|
2. Positive numbers $a, b, c$ satisfy $\left\{\begin{array}{l}a+b+c=10, \\ a^{2}+b^{2}=c^{2} .\end{array}\right.$ Then the maximum value of $ab$ is $\qquad$
|
50(3-2 \sqrt{2})
|
4A. Two squares with side 1 are given, such that one vertex of one square is the center of the other square. What is the smallest possible value of the area of the intersecting part?
|
\frac{1}{4}
|
On a circle of radius 1, a point $O$ is marked, and from it, a notch is made to the right with a radius of $l$. From the resulting point $O_{1}$, another notch is made in the same direction with the same radius, and this is repeated 1968 times. After this, the circle is cut at all 1968 notches, resulting in 1968 arcs. How many different lengths of arcs can be obtained in this way?
|
3
|
8. The speed of the yacht in still water is $x$ km/h, and the speed of the current is $y$ km/h. Pleasant Goat drives the yacht from downstream location $\mathrm{A}$ to upstream location $\mathrm{B}$, and then immediately returns to downstream $\mathrm{A}$. The time it takes for the yacht to travel from $\mathrm{A}$ to $\mathrm{B}$ is twice the time it takes to travel from $\mathrm{B}$ to $\mathrm{A}$. Therefore, $\frac{x}{y}=$ $\qquad$ .
|
3
|
6. There are two docks, $\mathrm{A}$ and $\mathrm{B}$, on a river, with $\mathrm{A}$ upstream and $\mathrm{B}$ downstream. Two people, Jia and Yi, start from $\mathrm{A}$ and $\mathrm{B}$ respectively at the same time, rowing towards each other, and meet after 4 hours. If Jia and Yi start from $\mathrm{A}$ and $\mathrm{B}$ respectively at the same time, rowing in the same direction, Yi catches up with Jia after 16 hours. It is known that Jia's rowing speed in still water is 6 kilometers per hour, then Yi's rowing speed in still water is $\qquad$ kilometers per hour.
|
10
|
6.52. $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}$.
|
0
|
7.6. Along the shore of a round lake, apple trees grow. Petya and Vasya start walking from point $A$ on the shore in opposite directions along the shore and count all the apple trees they encounter, as well as all the apples growing on the trees. Meeting at some point $B$, they compared their results. It turned out that Petya counted twice as many apple trees as Vasya, and seven times as many apples as Vasya. They were surprised by this result and decided to repeat the experiment. They set off from point $B$ in the same directions as initially, and met again at point $C$. It turned out that on the way from $B$ to $C$, Petya again counted twice as many apple trees as Vasya, and seven times as many apples as Vasya. Their surprise grew even more, and they decided to repeat the experiment again. Setting off from $C$ in the same directions, they met at point $D$. It turned out that Petya again counted twice as many apple trees as Vasya. Who counted more apples on the way from $C$ to $D$ and by how many times?
Answer. On the way from $C$ to $D$, Vasya counted 3 times more apples than Petya.
|
3
|
4. In $\triangle A B C$, if $(\sin A+\sin B)(\cos A+\cos B)=2 \sin C$, then $\triangle A B C(\quad)$.
A. is an isosceles triangle but not necessarily a right triangle
B. is a right triangle but not necessarily an isosceles triangle
C. is neither an isosceles triangle nor a right triangle
D. is both an isosceles triangle and a right triangle
|
A
|
11. The Youth Palace is recruiting for spring calligraphy, art, and music instrument classes. The calligraphy class has enrolled 29 students, the art class has enrolled 28 students, and the music instrument class has enrolled 27 students. Among these students, 13 are enrolled in both calligraphy and art, 12 are enrolled in both calligraphy and music instruments, 11 are enrolled in both art and music instruments, and 5 are enrolled in all three subjects. Therefore, the number of students who are only enrolled in one subject is $\qquad$.
|
27
|
Example 5 Find the largest positive integer $x$, such that for every positive integer $y$, we have $x \mid\left(7^{y}+12 y-1\right)$.
|
18
|
12. Calculate:
\[
\begin{array}{l}
\sqrt{2005 \times 2006 \times 2007 \times 2008+1}-2006^{2} \\
=
\end{array}
\]
|
2005
|
1. Function
$$
f(x)=\sin ^{4} x+\sin x \cdot \cos x+\cos ^{4} x
$$
The maximum value is $\qquad$.
|
\frac{9}{8}
|
In a six-page homework assignment, we need to place four figures. The order of the figures is fixed, and a maximum of two figures can be on one page. In how many ways can this be done? (We do not consider the position of the figures on a page.)
|
90
|
Example 1. Find $\lim _{x \rightarrow 0} \frac{\sin x e^{x}-5 x}{4 x^{2}+7 x}$.
|
-\frac{4}{7}
|
3. [4] Let $p$ be a monic cubic polynomial such that $p(0)=1$ and such that all the zeros of $p^{\prime}(x)$ are also zeros of $p(x)$. Find $p$. Note: monic means that the leading coefficient is 1 .
|
(x+1)^{3}
|
Example 11 (1994 Sichuan Province High School Competition Question) Given that point $P$ moves on the circle $x^{2}+(y-4)^{2}=1$, and point $Q$ moves on the ellipse $\frac{x^{2}}{9}+y^{2}=1$, find the maximum value of $|P Q|$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
3\sqrt{3}+1
|
$37 \cdot 6$ points $(x, y)$ where both $x, y$ are rational numbers are called rational points. In a circle with radius $r$ and center $(a, b)$, if $a$ is a rational number and $b$ is an irrational number, the number of rational points on this circle is
(A) at most one.
(B) at most two.
(C) at most three.
(D) infinitely many.
(1st "Hope Cup" National Mathematics Invitational Competition, 1990)
|
B
|
12.4. Let $I_{n}=\int_{1}^{n} \frac{[x]}{x^{2}+1} d x, n \in \mathbb{N}, n \geq 2$. Calculate: $\lim _{n \rightarrow \infty} \frac{I_{n}}{\ln n}$.
|
1
|
Example 3 Let $a b c \neq 0, a+b+c=a^{2}+b^{2}+c^{2}=2$. Find the value of the algebraic expression $\frac{(1-a)^{2}}{b c}+\frac{(1-b)^{2}}{c a}+\frac{(1-c)^{2}}{a b}$.
|
3
|
5. Two people toss a coin: one tossed it 10 times, and the other 11 times. Find the probability that the second person gets more heads than the first.
|
\frac{1}{2}
|
7.6 On a horizontal line, points $A$ and $B$ are marked, the distance between which is 4. Above the line, two semicircles with a radius of 2 are constructed, centered at points
A and B. Additionally, one circle, also with a radius of 2, is constructed, for which the point of intersection of these semicircles is the lowest point - see the figure. Find the area of the figure obtained by subtracting from the area of the circle the parts common to it and the two semicircles (the shaded area in the figure). Justify your answer.
|
8
|
## 5. Soba
Ana can paint the room in 15 hours, Barbara in 10 hours, and Cvijeta twice as fast as Ana. Ana starts painting and paints alone for one and a half hours, then Barbara joins her and they paint together until half the room is painted. After that, Cvijeta joins them and all three paint until the entire room is painted. How many minutes in total did it take to paint the room?
Result: $\quad 334$
|
334
|
2255 $\underset{\star}{\star \star}$ Find the value of $10 \cot (\operatorname{arccot} 3+\operatorname{arccot} 7+\operatorname{arccot} 13+\operatorname{arccot} 21)$.
|
15
|
16. As shown in Figure 14,
$\odot \mathrm{O}_{1}$ and $\odot \mathrm{O}_{2}$ intersect
at points $A$ and $B$, $\bigcirc \mathrm{O}_{2}$
passes through $\odot O_{1}$, and $A C$ and $A D$
are diameters of $\odot \mathrm{O}_{1}$ and $\odot \mathrm{O}_{2}$
respectively. Then the following conclusions:
(1) $C, B, D$ are collinear;
(2) $A D = C D$;
(3) $A C^{2} - C B^{2} = A D^{2} - B D^{2}$
which of the following is correct?
(A) Only (1);
(B) (1) and (3);
(C) (2) and (3);
(D) (1) and (2);
(E) All correct.
|
E
|
8. The function $f(x)$ is defined on $\mathbf{R}$, and for any real number $x$, it holds that $f(1+x)=f(3-x)$, and $f(2+x)=$ $-f(4-x)$, find the value of $f(1)+f(2)+\cdots+f(100)$.
|
0
|
Let $f(x) = 2^x + 3^x$. For how many integers $1 \leq n \leq 2020$ is $f(n)$ relatively prime to all of $f(0), f(1), \dots, f(n-1)$?
|
11
|
16. 2. $47 \star \star$ For some natural numbers $n$, the first digit of the numbers $2^{n}$ and $5^{n}$ is the same. What are these first digits?
Will keep the format and line breaks as requested.
|
3
|
11. Let $a, b, c$ be distinct positive integers. Then the minimum value of $\frac{a b c}{a+b+c}$ is . $\qquad$
|
1
|
364. Find all natural numbers $a$ for which the number $a^{2}-10 a+21$ is prime.
|
8,2
|
2. Given $f(x)=\lg (x+1)-\frac{1}{2} \log _{3} x$. Then the set
$$
M=\left\{n \mid f\left(n^{2}-8 n-2018\right) \geqslant 0, n \in \mathbf{Z}\right\}
$$
the number of subsets of $M$ is $\qquad$.
|
1
|
Example 3 The function $f$ is defined on the set of positive integers, and satisfies
$$
f(x)=\left\{\begin{array}{l}
n-3, \quad n \geqslant 1000 \\
f(f(n+5)), 1 \leqslant n<1000 .
\end{array}\right.
$$
Find $f(84)$.
|
997
|
Determine the greatest positive integer \(n\) for which there exists a sequence of distinct positive integers \(s_1\), \(s_2\), \(\ldots\), \(s_n\) satisfying \[s_1^{s_2}=s_2^{s_3}=\cdots=s_{n-1}^{s_n}.\]
[i]Proposed by Holden Mui[/i]
|
n = 5
|
Example 3. Factorize: $x^{5}+x^{4}+1$.
|
(x^{2}+x+1)(x^{3}-x+1)
|
6. Given two quadratic equations
$$
a x^{2}+b x+c=0, u x^{2}+v x+w=0(a \neq u)
$$
both have real roots. If the coefficients of the quadratic terms of these two equations are swapped, then $w c>0$ is the ( ) condition for at least one of the two quadratic equations obtained after the swap to have real roots.
(A) Sufficient but not necessary
(B) Necessary but not sufficient
(C) Sufficient and necessary
(D) Neither sufficient nor necessary
|
A
|
72. Given three integers $x, y, z$ satisfying $x+y+z=100$, and $x<y<2z$, then the minimum value of $z$ is
|
21
|
If $x+y+z=25$ and $y+z=14$, then $x$ is
(A) 8
(B) 11
(C) 6
(D) -6
(E) 31
Part B: Each question is worth 6 credits.
|
11
|
2. In a dark room on the warehouse, 24 slippers are scattered, which originally formed 12 pairs: 3 different colors and 4 different styles (there were no identical pairs). What is the smallest number of slippers the seller must take out of the room to definitely present the customer with 3 pairs of slippers of 3 different colors and simultaneously 3 different styles?
(S. B. Gashkov)
## Answer: 21.
|
21
|
10.2 Find the number conjugate to the number $z=\frac{2 \sqrt{3}-i}{\sqrt{3}+i}+3$.
|
4.25+0.75\sqrt{3}i
|
3. From a right prism with a square base of side length $L_{1}$ and height $H$, we extract a frustum of a pyramid, not necessarily a right one, with square bases of side lengths $L_{1}$ (for the lower base) and $L_{2}$ (for the upper base), and height $H$. The two resulting pieces are shown in the following image.
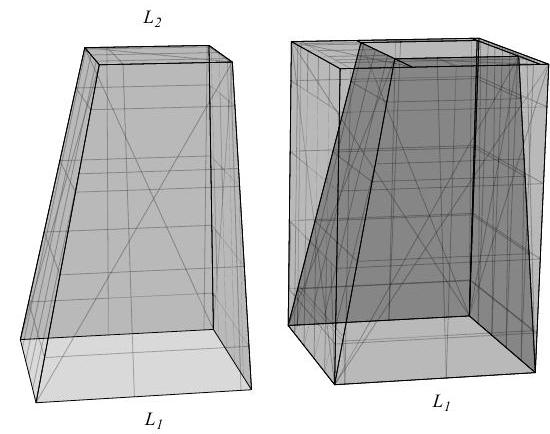
If the volume of the frustum of the pyramid is 2/3 of the total volume of the prism, what is the value of $L_{1} / L_{2}$?
|
\frac{1+\sqrt{5}}{2}
|
7.229. $27 \cdot 2^{-3 x}+9 \cdot 2^{x}-2^{3 x}-27 \cdot 2^{-x}=8$.
|
0
|
4. "24 Points" is a familiar math game to many people, the game process is as follows: arbitrarily draw 4 cards from 52 cards (excluding the jokers). Use the numbers on these 4 cards (from 1 to 13, where $A=1, J=11, Q=12, K=13$) to derive 24 using the four basic arithmetic operations. The person who finds the algorithm first wins. The game rules state that all 4 cards must be used, and each card can only be used once. For example, with $2,3,4, Q$, the algorithm $2 \times Q \times(4-3)$ can be used to get 24.
If in one game, you happen to draw $2,5, \mathrm{~J}, \mathrm{Q}$, then your algorithm is: $\qquad$
|
2\times(11-5)+12
|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?
Fig. 13: to the solution of problem 11.2
#
|
34
|
10.285. In a circle of radius $R$, two parallel chords are drawn on opposite sides of the center, one of which subtends an arc of $60^{\circ}$, the other $120^{\circ}$. Find the area of the part of the circle enclosed between the chords.
|
\frac{R^{2}(\pi+\sqrt{3})}{2}
|
10. (20 points) The sequence $\left\{a_{n}\right\}$ has the sum of the first $n$ terms $S_{n}$ satisfying
$$
a_{n}=\frac{1}{2}+\frac{1}{2} \sqrt{1+8 S_{n-1}} \quad (n \geqslant 2) \text {. }
$$
Also, $a_{1}=1$, find the general term formula of the sequence.
|
a_{n}=n
|
1) Calculate:
$$
\frac{2008+2007 \times 2009}{2008 \times 2009-1}+\frac{2009+2008 \times 2010}{2009 \times 2010-1}=
$$
$\qquad$
|
2
|
3. (10 points) As shown in the figure, given that $A B C D E F G H I$ is a regular nonagon, then $\angle D I G=$ $\qquad$ degrees.
|
60
|
In triangle $A B C$, the altitudes $A A_{1}$ and $C C_{1}$ intersect at point $H$, which lies inside the triangle. It is known that $H$ is the midpoint of $A A_{1}$, and $C H: H C_{1}=2: 1$. Find the measure of angle $B$.
|
45
|
*6. From $1,2, \cdots, 1996$, select $k$ numbers such that the sum of any two numbers cannot be divisible by their difference. Then the maximum possible value of $k$ is $\qquad$ .
|
666
|
52. The median line of a trapezoid divides it into two quadrilaterals. The difference in the perimeters of these two quadrilaterals is 24, and the ratio of their areas is $\frac{20}{17}$. If the height of the trapezoid is 2, then the area of this trapezoid is $\qquad$ _.
|
148
|
7.2. The sum of three positive integers (not necessarily distinct) is 100. By subtracting them pairwise (the larger minus the smaller), three difference numbers can be obtained. What is the maximum possible value of the sum of these three difference numbers?
|
194
|
(16) Find the maximum value of the function $y=\left[\sin \left(\frac{\pi}{4}+x\right)-\sin \left(\frac{\pi}{4}-x\right)\right] \sin \left(\frac{\pi}{3}+x\right)$, and determine the set of $x$ values for which the maximum value is achieved.
|
\frac{3\sqrt{2}}{4}
|
2. A box contains 9 good items and 3 defective items. Each time an item is taken, it is not replaced. What is the probability that 3 defective items have been taken before 2 good items are taken? $\qquad$
|
\frac{1}{55}
|
## Task Condition
Find the $n$-th order derivative.
$$
y=\lg (5 x+2)
$$
|
y^{(n)}=\frac{(-1)^{n-1}\cdot(n-1)!\cdot5^{n}}{\ln10\cdot(5x+2)^{n}}
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
43
|
3. The curve represented by the equation $|x|-1=\sqrt{1-(y-1)^{2}}$ is
A. a circle
B. two circles
C. half a circle
D. two semicircles
|
D
|
3. Given $\arcsin (\sin \alpha+\sin \beta)+\arcsin (\sin \alpha-\sin \beta)=\frac{\pi}{2}, \sin ^{2} \alpha+\sin ^{2} \beta=$
|
\frac{1}{2}
|
B3. Solve the exponential equation $\frac{2^{x}+2^{-x}}{2}=2\left(2^{x}-2^{-x}\right)$. The solution should be exact.
19th Knowledge Competition
in mathematics for students of secondary technical and vocational schools
National Competition, April 13, 2019
Attach the sticker with the code
## Tasks for 4th year
Time for solving: 120 minutes. In section A, we will award three points for each correct answer, and deduct one point for each incorrect answer. Enter the answers for section A in the left table, leave the right table blank.
| B1 | B2 | B3 |
| :--- | :--- | :--- |
| | | |
|
\log_{2}(\frac{\sqrt{15}}{3})
|
5. The sum of four consecutive primes is itself prime.
What is the largest of the four primes?
A 37
B 29
C 19
D 13
E 7
|
7
|
2. $x \in[0, \pi], y=\sin (\cos x)$ minimum value is $a$, $y=\cos (\sin x)$ minimum value is $b, y=\tan(\sin x)$ minimum value is $c$, $y=\cot(\cos x)$ minimum value is $d$. Then the relationship of $a, b, c, d$ is ( ).
(A) $d<a<c<b$
(B) $c<a<b<d$
(C) $a<d<c<b$
(D) $b<a<d<c$
|
C
|
Find all values of the real parameter $a$, for which the system
$(|x| + |y| - 2)^2 = 1$
$y = ax + 5$
has exactly three solutions
|
a = \pm \frac{5}{3}, \pm 5
|
## Task 6 - 050936
A mother places a bowl of cherries on the table for her three children, Jürgen, Renate, and Christine, with the note that each should take a third of the cherries upon their return.
Jürgen, who comes home first, takes one cherry first because the number of cherries is not divisible by three, and then takes a third of the remaining cherries.
When Renate comes home, she thinks she is the first. She takes two cherries first because the number of cherries is not divisible by three, and then takes a third of the remaining cherries.
Christine also believes she is the first when she returns, and takes a third of the cherries in the bowl.
The mother then notices that a total of 42 cherries have been eaten.
How many cherries were in the bowl initially?
|
58
|
$16 \cdot 11$ Let $P$ be a point inside circle $K$ but not coinciding with the center. Draw all chords of circle $K$ passing through $P$ and determine their midpoints. The locus of these midpoints is
(A) a circle with one point removed.
(B) if the distance from point $P$ to the center of circle $K$ is less than half the radius of circle $K$, it is a circle; otherwise, it is a circular arc less than $360^{\circ}$.
(C) a semicircle with one point removed.
(D) a semicircle.
(E) a circle.
(26th American High School Mathematics Examination, 1975)
|
E
|
17. If $a, b$ and $c$ are positive real numbers such that
$$
a b+a+b=b c+b+c=c a+c+a=35 \text {, }
$$
find the value of $(a+1)(b+1)(c+1)$.
|
216
|
Example 3 Let $a$ and $b$ be positive real numbers, and
$$
\begin{array}{l}
\frac{1}{a}-\frac{1}{b}-\frac{1}{a+b}=0 . \\
\text { Then }\left(\frac{b}{a}\right)^{3}+\left(\frac{a}{b}\right)^{3}=
\end{array}
$$
|
2 \sqrt{5}
|
11) Carlo ha sei mele e sei pere: in quanti modi può mettere in fila 6 frutti, in modo tale che tra due mele non ci sia mai nessuna pera?
(A) 16
(B) 22
(C) 32
(D) 35
(E) 39
|
22
|
19. [11] Find the smallest positive integer $n$ such that the polynomial $(x+1)^{n}-1$ is "divisible by $x^{2}+1$ modulo 3 ", or more precisely, either of the following equivalent conditions holds:
- there exist polynomials $P, Q$ with integer coefficients such that $(x+1)^{n}-1=\left(x^{2}+1\right) P(x)+3 Q(x)$;
- or more conceptually, the remainder when (the polynomial) $(x+1)^{n}-1$ is divided by (the polynomial) $x^{2}+1$ is a polynomial with (integer) coefficients all divisible by 3 .
|
8
|
3. (5 points) If “*” represents an operation, and satisfies the following relationships:
(1) $1 * 1=1$;
(2) $(n+1) * 1=3 \times(n * 1)$
then $5 * 1-2 * 1=$ $\qquad$
|
78
|
98. Let positive numbers $a, b, c$ satisfy $a+b+c \leqslant \frac{3}{2}$, find the minimum value of $S=abc+\frac{1}{abc}$. (2008 Moldova Mathematical Olympiad Problem)
|
\frac{65}{8}
|
5. Among the teachers of a certain middle school, the total number of people who can speak English and Russian is 110. According to statistics, 75 people can speak English, and 55 people can speak Russian. The number of teachers in the school who can speak English but not Russian is . $\qquad$
|
55
|
3. Find all natural solutions to the inequality
$$
\frac{4}{5}+\frac{4}{45}+\frac{4}{117}+\cdots+\frac{4}{16 n^{2}-8 n-3}>n-5
$$
In your answer, write the sum of all found solutions.
|
15
|
## Task 3 - 240813
We are looking for a decomposition of the number 500 into four summands, with the following conditions required:
(1) All four summands are natural numbers.
(2) If you add 4 to the first summand, the result is the same as if you subtract 4 from the second summand. The same result also occurs if you multiply the third summand by 4, and also if you divide the fourth summand by 4.
Investigate whether there is only one such decomposition! If this is the case, determine it and confirm that it has the properties (1), (2)!
|
76,84,20,320
|
14. Let \( f(x) = \frac{a^x}{1 + a^x} \) where \( a > 0, a \neq 1 \), and \([m]\) denotes the greatest integer not exceeding the real number \( m \). Find the range of the function \(\left[f(x) - \frac{1}{2}\right] + \left[f(-x) - \frac{1}{2}\right]\).
|
-1or0
|
Example 1 Find the units digit of $3^{406}$ when it is written in decimal form.
|
9
|
5. (40th IMO Problem) $n$ is a given integer, $n \geqslant 2$, determine the smallest constant $c$, such that the inequality $\sum_{1 \leqslant i<j \leqslant n} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right) \leqslant c\left(\sum_{i=1}^{n} x_{i}\right)^{4}$ holds for all non-negative real numbers $x_{1}, x_{2}, \cdots, x_{n}$.
|
\frac{1}{8}
|
13.5 It is known that a set of 6 weights can be used to measure 63 objects of consecutive natural number weights using a balance scale. Find this set of weights.
|
1,2,4,8,16,32
|
Given a positive integer $n \geq 2$, determine the largest positive integer $N$ for which there exist $N+1$ real numbers $a_{0}, a_{1}, \ldots, a_{N}$ such that
(1) $a_{0}+a_{1}=-\frac{1}{n}$, and
(2) $\left(a_{k}+a_{k-1}\right)\left(a_{k}+a_{k+1}\right)=a_{k-1}-a_{k+1}$ for $1 \leq k \leq N-1$.
Proposed by: Romania
|
n
|
## 1. Smaller Number
The sum of two three-digit numbers, all six of whose digits are mutually distinct, is 1000. What is the maximum value that the smaller of these two numbers can have?
Result: $\quad 498$
|
498
|
How many experiments do we need to perform at least so that the probability of rolling with 3 dice
a) once a 15,
b) once at least a 15,
is greater than $1 / 2$
|
15
|
2. Given the curve $y=x^{3}-x$, draw a tangent line to this curve from a point $A(t, 0)$ on the $x$-axis. The maximum number of tangent lines that can be drawn is $(\quad$.
(A) 1
(B) 2
(C) 3
(D) 4
|
C
|
3. The number of positive integers $m$ that make $m^{2}+m+7$ a perfect square is $\qquad$ .
|
2
|
## Task 32/77
For a right-angled triangle, let the perimeter $U$ and the circumradius $r$ be known. Calculate the area $A$ from these!
|
u(\frac{1}{4}u-r)
|
Example 2.54. Calculate the area of one petal of the curve $\rho=\sin ^{2} \varphi$.
|
\frac{3\pi}{16}
|
5. (16th "Hope Cup" Grade 1 High School 2nd Test) The even function $f(x) (x \in \mathbf{R})$ satisfies: $f(-4)=$ $f(1)=0$, and is decreasing on the intervals $[0,3]$ and increasing on $[3,+\infty)$, then the solution set of the inequality $x^{3} f(x)<0$ is ( )
A. $(-\infty,-4) \cup(4,+\infty)$
B. $(-4,-1) \cup(1,4)$
C. $(-\infty,-4) \cup(-1,0)$
D. $(-\infty,-4) \cup(-1,0) \cup(1,4)$
|
D
|
## Task A-2.7.
In a basketball tournament, each team plays exactly twice against each of the other teams. A win brings 2 points, a loss 0 points, and there are no draws. Determine all natural numbers $n$ for which there exists a basketball tournament with $n$ teams where one team, the tournament winner, has 26 points, and exactly two teams have the lowest number of points, which is 20 points.
|
12
|
On a board, there are $n$ equations in the form $*x^2+*x+*$. Two people play a game where they take turns. During a turn, you are aloud to change a star into a number not equal to zero. After $3n$ moves, there will be $n$ quadratic equations. The first player is trying to make more of the equations not have real roots, while the second player is trying to do the opposite. What is the maximum number of equations that the first player can create without real roots no matter how the second player acts?
|
0
|
Exercise 5. A player has four black cards and three red cards, all distinct. In how many ways can he order them so that two successive cards are not both red?
|
1440
|
11.4. Vasya has three cans of paint of different colors. In how many different ways can he paint a fence consisting of 10 boards so that any two adjacent boards are of different colors, and he uses all three colors of paint?
|
1530
|
Selected easy prompts used to train Qwen2.5-Math-7B.