problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \neq X$. Prove that points $A, X$, and $Y$ are collinear.
|
Consider the (direct) homothety that takes triangle $A D E$ to triangle $A B C$, and let $Y^{\prime}$ be the image of $Y$ under this homothety; in other words, let $Y^{\prime}$ be the intersection of the line parallel to $B Y$ through $D$ and the line parallel to $C Y$ through $E$.
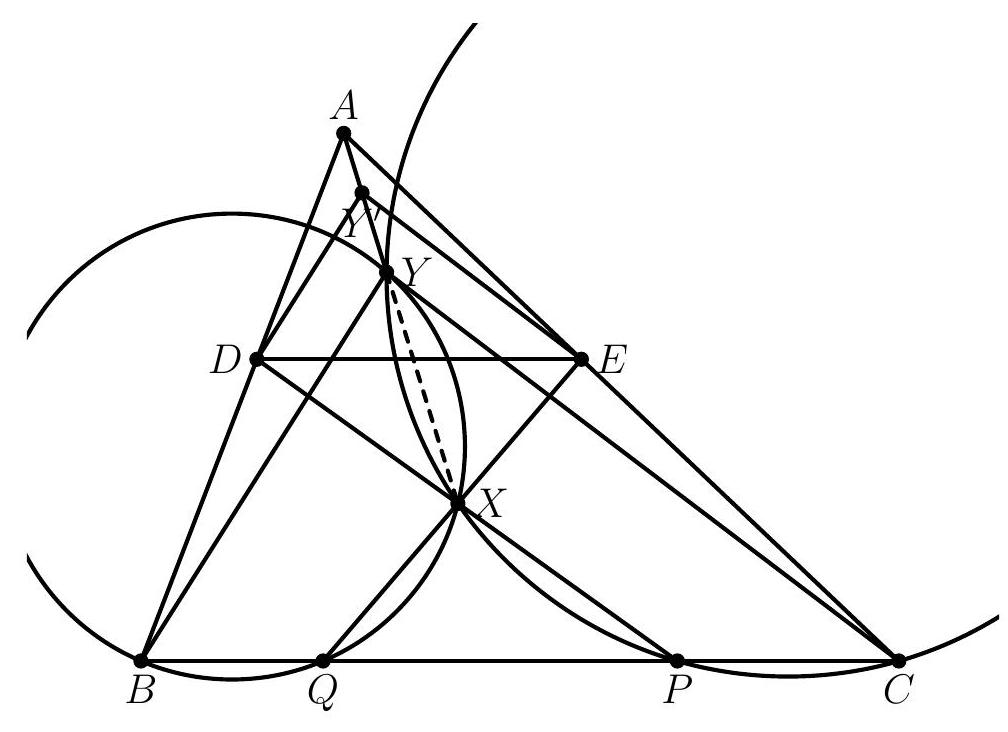
The homothety implies that $A, Y$, and $Y^{\prime}$ are collinear, and that $\angle D Y^{\prime} E=\angle B Y C$. Since $B Q X Y$ and $C P X Y$ are cyclic,
$\angle D Y^{\prime} E=\angle B Y C=\angle B Y X+\angle X Y C=\angle X Q P+\angle X P Q=180^{\circ}-\angle P X Q=180^{\circ}-\angle D X E$,
which implies that $D Y^{\prime} E X$ is cyclic. Therefore
$$
\angle D Y^{\prime} X=\angle D E X=\angle P Q X=\angle B Y X
$$
which, combined with $D Y^{\prime} \| B Y$, implies $Y^{\prime} X \| Y X$. This proves that $X, Y$, and $Y^{\prime}$ are collinear, which in turn shows that $A, X$, and $Y$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \neq X$. Prove that points $A, X$, and $Y$ are collinear.
|
Consider the (direct) homothety that takes triangle $A D E$ to triangle $A B C$, and let $Y^{\prime}$ be the image of $Y$ under this homothety; in other words, let $Y^{\prime}$ be the intersection of the line parallel to $B Y$ through $D$ and the line parallel to $C Y$ through $E$.

The homothety implies that $A, Y$, and $Y^{\prime}$ are collinear, and that $\angle D Y^{\prime} E=\angle B Y C$. Since $B Q X Y$ and $C P X Y$ are cyclic,
$\angle D Y^{\prime} E=\angle B Y C=\angle B Y X+\angle X Y C=\angle X Q P+\angle X P Q=180^{\circ}-\angle P X Q=180^{\circ}-\angle D X E$,
which implies that $D Y^{\prime} E X$ is cyclic. Therefore
$$
\angle D Y^{\prime} X=\angle D E X=\angle P Q X=\angle B Y X
$$
which, combined with $D Y^{\prime} \| B Y$, implies $Y^{\prime} X \| Y X$. This proves that $X, Y$, and $Y^{\prime}$ are collinear, which in turn shows that $A, X$, and $Y$ are collinear.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 3"
}
|
c2662896-d3ab-5e68-bb60-20bb487f6879
| 606,331
|
Let $n$ be a positive integer and $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers. Prove that
$$
\sum_{i=1}^{n} \frac{1}{2^{i}}\left(\frac{2}{1+a_{i}}\right)^{2^{i}} \geq \frac{2}{1+a_{1} a_{2} \ldots a_{n}}-\frac{1}{2^{n}}
$$
|
We first prove the following lemma:
Lemma 1. For $k$ positive integer and $x, y>0$,
$$
\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}} \geq 2\left(\frac{2}{1+x y}\right)^{2^{k-1}}
$$
The proof goes by induction. For $k=1$, we have
$$
\left(\frac{2}{1+x}\right)^{2}+\left(\frac{2}{1+y}\right)^{2} \geq 2\left(\frac{2}{1+x y}\right)
$$
which reduces to
$$
x y(x-y)^{2}+(x y-1)^{2} \geq 0 .
$$
For $k>1$, by the inequality $2\left(A^{2}+B^{2}\right) \geq(A+B)^{2}$ applied at $A=\left(\frac{2}{1+x}\right)^{2^{k-1}}$ and $B=\left(\frac{2}{1+y}\right)^{2^{k-1}}$ followed by the induction hypothesis
$$
\begin{aligned}
2\left(\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}}\right) & \geq\left(\left(\frac{2}{1+x}\right)^{2^{k-1}}+\left(\frac{2}{1+y}\right)^{2^{k-1}}\right)^{2} \\
& \geq\left(2\left(\frac{2}{1+x y}\right)^{2^{k-2}}\right)^{2}=4\left(\frac{2}{1+x y}\right)^{2^{k-1}}
\end{aligned}
$$
from which the lemma follows.
The problem now can be deduced from summing the following applications of the lemma, multiplied by the appropriate factor:
$$
\begin{aligned}
\frac{1}{2^{n}}\left(\frac{2}{1+a_{n}}\right)^{2^{n}}+\frac{1}{2^{n}}\left(\frac{2}{1+1}\right)^{2^{n}} & \geq \frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n} \cdot 1}\right)^{2^{n-1}} \\
\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n-1}}\right)^{2^{n-1}}+\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n}}\right)^{2^{n-1}} & \geq \frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-1} a_{n}}\right)^{2^{n-2}} \\
\frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-2}}\right)^{2^{n-2}}+\frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-1} a_{n}}\right)^{2^{n-2}} & \geq \frac{1}{2^{n-3}}\left(\frac{2}{1+a_{n-2} a_{n-1} a_{n}}\right)^{2^{n-3}} \\
\ldots & )^{2^{k}} \\
\frac{1}{2^{k}}\left(\frac{2}{1+a_{k}}\right)^{2^{k}}+\frac{1}{2^{k}}\left(\frac{2}{1+a_{k+1} \ldots a_{n-1} a_{n}}\right)^{2^{k-1}} & \geq \frac{1}{2^{k-1}}\left(\frac{2}{1+a_{k} \ldots a_{n-2} a_{n-1} a_{n}}\right)^{2} \\
\frac{1}{2}\left(\frac{2}{1+a_{1}}\right)^{2}+\frac{1}{2}\left(\frac{2}{1+a_{2} \ldots a_{n-1} a_{n}}\right)^{2} & \geq \frac{2}{1+a_{1} \ldots a_{n-2} a_{n-1} a_{n}}
\end{aligned}
$$
Comment: Equality occurs if and only if $a_{1}=a_{2}=\cdots=a_{n}=1$.
Comment: The main motivation for the lemma is trying to "telescope" the sum
$$
\frac{1}{2^{n}}+\sum_{i=1}^{n} \frac{1}{2^{i}}\left(\frac{2}{1+a_{i}}\right)^{2^{i}}
$$
that is,
$$
\frac{1}{2}\left(\frac{2}{1+a_{1}}\right)^{2}+\cdots+\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n-1}}\right)^{2^{n-1}}+\frac{1}{2^{n}}\left(\frac{2}{1+a_{n}}\right)^{2^{n}}+\frac{1}{2^{n}}\left(\frac{2}{1+1}\right)^{2^{n}}
$$
to obtain an expression larger than or equal to
$$
\frac{2}{1+a_{1} a_{2} \ldots a_{n}}
$$
It seems reasonable to obtain a inequality that can be applied from right to left, decreases the exponent of the factor $1 / 2^{k}$ by 1 , and multiplies the variables in the denominator. Given that, the lemma is quite natural:
$$
\frac{1}{2^{k}}\left(\frac{2}{1+x}\right)^{2^{k}}+\frac{1}{2^{k}}\left(\frac{2}{1+y}\right)^{2^{k}} \geq \frac{1}{2^{k-1}}\left(\frac{2}{1+x y}\right)^{2^{i-1}}
$$
or
$$
\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}} \geq 2\left(\frac{2}{1+x y}\right)^{2^{k-1}}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer and $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers. Prove that
$$
\sum_{i=1}^{n} \frac{1}{2^{i}}\left(\frac{2}{1+a_{i}}\right)^{2^{i}} \geq \frac{2}{1+a_{1} a_{2} \ldots a_{n}}-\frac{1}{2^{n}}
$$
|
We first prove the following lemma:
Lemma 1. For $k$ positive integer and $x, y>0$,
$$
\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}} \geq 2\left(\frac{2}{1+x y}\right)^{2^{k-1}}
$$
The proof goes by induction. For $k=1$, we have
$$
\left(\frac{2}{1+x}\right)^{2}+\left(\frac{2}{1+y}\right)^{2} \geq 2\left(\frac{2}{1+x y}\right)
$$
which reduces to
$$
x y(x-y)^{2}+(x y-1)^{2} \geq 0 .
$$
For $k>1$, by the inequality $2\left(A^{2}+B^{2}\right) \geq(A+B)^{2}$ applied at $A=\left(\frac{2}{1+x}\right)^{2^{k-1}}$ and $B=\left(\frac{2}{1+y}\right)^{2^{k-1}}$ followed by the induction hypothesis
$$
\begin{aligned}
2\left(\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}}\right) & \geq\left(\left(\frac{2}{1+x}\right)^{2^{k-1}}+\left(\frac{2}{1+y}\right)^{2^{k-1}}\right)^{2} \\
& \geq\left(2\left(\frac{2}{1+x y}\right)^{2^{k-2}}\right)^{2}=4\left(\frac{2}{1+x y}\right)^{2^{k-1}}
\end{aligned}
$$
from which the lemma follows.
The problem now can be deduced from summing the following applications of the lemma, multiplied by the appropriate factor:
$$
\begin{aligned}
\frac{1}{2^{n}}\left(\frac{2}{1+a_{n}}\right)^{2^{n}}+\frac{1}{2^{n}}\left(\frac{2}{1+1}\right)^{2^{n}} & \geq \frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n} \cdot 1}\right)^{2^{n-1}} \\
\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n-1}}\right)^{2^{n-1}}+\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n}}\right)^{2^{n-1}} & \geq \frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-1} a_{n}}\right)^{2^{n-2}} \\
\frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-2}}\right)^{2^{n-2}}+\frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-1} a_{n}}\right)^{2^{n-2}} & \geq \frac{1}{2^{n-3}}\left(\frac{2}{1+a_{n-2} a_{n-1} a_{n}}\right)^{2^{n-3}} \\
\ldots & )^{2^{k}} \\
\frac{1}{2^{k}}\left(\frac{2}{1+a_{k}}\right)^{2^{k}}+\frac{1}{2^{k}}\left(\frac{2}{1+a_{k+1} \ldots a_{n-1} a_{n}}\right)^{2^{k-1}} & \geq \frac{1}{2^{k-1}}\left(\frac{2}{1+a_{k} \ldots a_{n-2} a_{n-1} a_{n}}\right)^{2} \\
\frac{1}{2}\left(\frac{2}{1+a_{1}}\right)^{2}+\frac{1}{2}\left(\frac{2}{1+a_{2} \ldots a_{n-1} a_{n}}\right)^{2} & \geq \frac{2}{1+a_{1} \ldots a_{n-2} a_{n-1} a_{n}}
\end{aligned}
$$
Comment: Equality occurs if and only if $a_{1}=a_{2}=\cdots=a_{n}=1$.
Comment: The main motivation for the lemma is trying to "telescope" the sum
$$
\frac{1}{2^{n}}+\sum_{i=1}^{n} \frac{1}{2^{i}}\left(\frac{2}{1+a_{i}}\right)^{2^{i}}
$$
that is,
$$
\frac{1}{2}\left(\frac{2}{1+a_{1}}\right)^{2}+\cdots+\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n-1}}\right)^{2^{n-1}}+\frac{1}{2^{n}}\left(\frac{2}{1+a_{n}}\right)^{2^{n}}+\frac{1}{2^{n}}\left(\frac{2}{1+1}\right)^{2^{n}}
$$
to obtain an expression larger than or equal to
$$
\frac{2}{1+a_{1} a_{2} \ldots a_{n}}
$$
It seems reasonable to obtain a inequality that can be applied from right to left, decreases the exponent of the factor $1 / 2^{k}$ by 1 , and multiplies the variables in the denominator. Given that, the lemma is quite natural:
$$
\frac{1}{2^{k}}\left(\frac{2}{1+x}\right)^{2^{k}}+\frac{1}{2^{k}}\left(\frac{2}{1+y}\right)^{2^{k}} \geq \frac{1}{2^{k-1}}\left(\frac{2}{1+x y}\right)^{2^{i-1}}
$$
or
$$
\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}} \geq 2\left(\frac{2}{1+x y}\right)^{2^{k-1}}
$$
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution\n\n"
}
|
633aac9c-db10-5818-8461-399e1809ac3d
| 606,346
|
Line $\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.
|
We start with the following lemma.
Lemma 1. Points $M, N, P, Q$ are concyclic.
Point $M$ is the Miquel point of lines $A P=A B, P S=\ell, A S=A D$, and $B R=B C$, and point $N$ is the Miquel point of lines $C Q=C D, R C=B C, Q R=\ell$, and $D S=A D$. Both points $M$ and $N$ are on the circumcircle of the triangle determined by the common lines $A D, \ell$, and $B C$, which is $L R S$.
Then, since quadrilaterals $Q N R C, P M A S$, and $A B C D$ are all cyclic, using directed angles (modulo $180^{\circ}$ )
$$
\begin{aligned}
\measuredangle N M P & =\measuredangle N M S+\measuredangle S M P=\measuredangle N R S+\measuredangle S A P=\measuredangle N R Q+\measuredangle D A B=\measuredangle N R Q+\measuredangle D C B \\
& =\measuredangle N R Q+\measuredangle Q C R=\measuredangle N R Q+\measuredangle Q N R=\measuredangle N Q R=\measuredangle N Q P,
\end{aligned}
$$
which implies that $M N Q P$ is a cyclic quadrilateral.
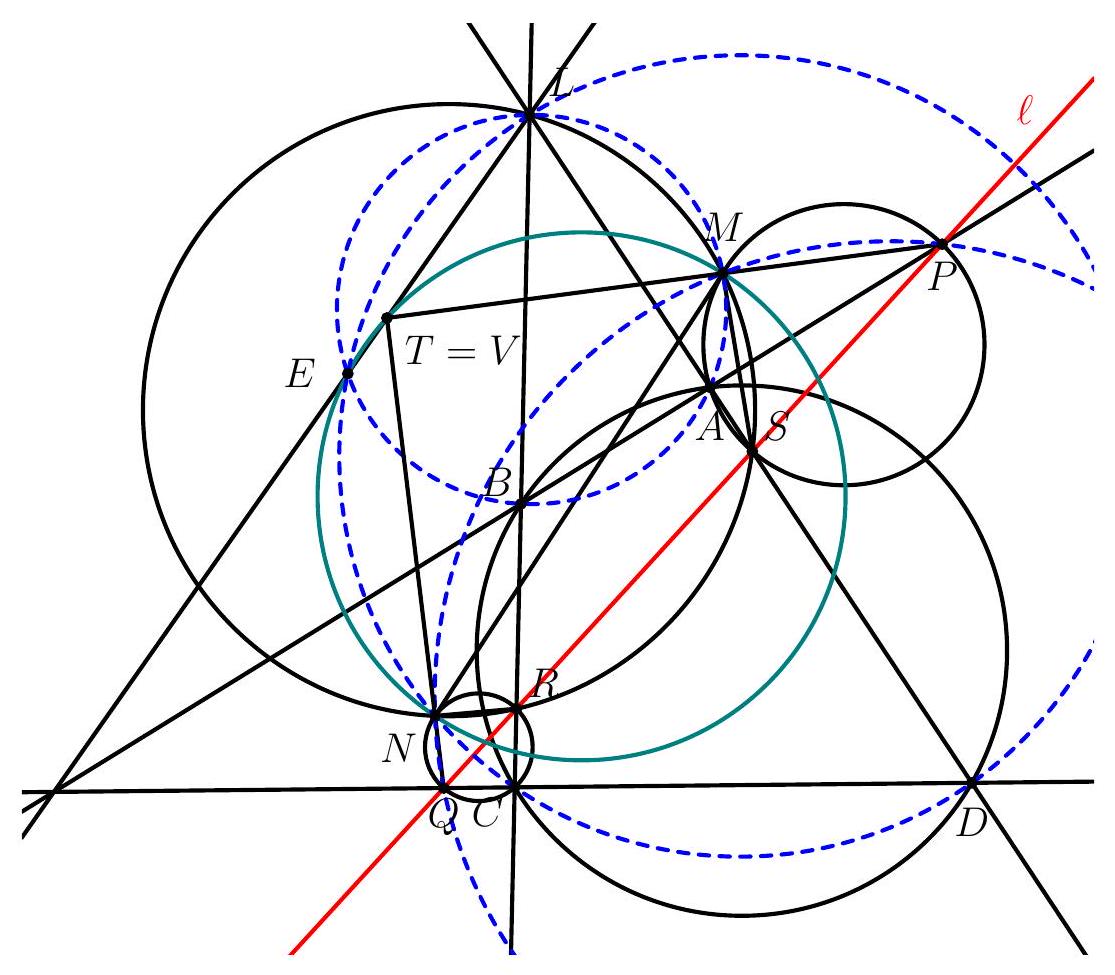
Let $E$ be the Miquel point of $A B C D$ (that is, of lines $A B, B C, C D, D A$ ). It is well known that $E$ lies in the line $t$ connecting the intersections of the opposite lines of $A B C D$. Let lines $N Q$ and $t$ meet at $T$. If $T \neq E$, using directed angles, looking at the circumcircles of $L A B$ (which contains, by definition, $E$ and $M$ ), $A P S$ (which also contains $M$ ), and $M N Q P$,
$$
\measuredangle T E M=\measuredangle L E M=\measuredangle L A M=\measuredangle S A M=\measuredangle S P M=\measuredangle Q P M=\measuredangle Q N M=\measuredangle T N M,
$$
that is, $T$ lies in the circumcircle $\omega$ of $E M N$. If $T=E$, the same computation shows that $\measuredangle L E M=\measuredangle E N M$, which means that $t$ is tangent to $\omega$.
Now let lines $M P$ and $t$ meet at $V$. An analogous computation shows, by looking at the circumcircles of $L C D$ (which contains $E$ and $N$ ), $C Q R$, and $M N Q P$, that $V$ lies in $\omega$ as well, and that if $V=E$ then $t$ is tangent to $\omega$.
Therefore, since $\omega$ meet $t$ at $T, V$, and $E$, either $T=V$ if both $T \neq E$ and $V \neq E$ or $T=V=E$. At any rate, the intersection of lines $M P$ and $N Q$ lies in $t$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Line $\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.
|
We start with the following lemma.
Lemma 1. Points $M, N, P, Q$ are concyclic.
Point $M$ is the Miquel point of lines $A P=A B, P S=\ell, A S=A D$, and $B R=B C$, and point $N$ is the Miquel point of lines $C Q=C D, R C=B C, Q R=\ell$, and $D S=A D$. Both points $M$ and $N$ are on the circumcircle of the triangle determined by the common lines $A D, \ell$, and $B C$, which is $L R S$.
Then, since quadrilaterals $Q N R C, P M A S$, and $A B C D$ are all cyclic, using directed angles (modulo $180^{\circ}$ )
$$
\begin{aligned}
\measuredangle N M P & =\measuredangle N M S+\measuredangle S M P=\measuredangle N R S+\measuredangle S A P=\measuredangle N R Q+\measuredangle D A B=\measuredangle N R Q+\measuredangle D C B \\
& =\measuredangle N R Q+\measuredangle Q C R=\measuredangle N R Q+\measuredangle Q N R=\measuredangle N Q R=\measuredangle N Q P,
\end{aligned}
$$
which implies that $M N Q P$ is a cyclic quadrilateral.

Let $E$ be the Miquel point of $A B C D$ (that is, of lines $A B, B C, C D, D A$ ). It is well known that $E$ lies in the line $t$ connecting the intersections of the opposite lines of $A B C D$. Let lines $N Q$ and $t$ meet at $T$. If $T \neq E$, using directed angles, looking at the circumcircles of $L A B$ (which contains, by definition, $E$ and $M$ ), $A P S$ (which also contains $M$ ), and $M N Q P$,
$$
\measuredangle T E M=\measuredangle L E M=\measuredangle L A M=\measuredangle S A M=\measuredangle S P M=\measuredangle Q P M=\measuredangle Q N M=\measuredangle T N M,
$$
that is, $T$ lies in the circumcircle $\omega$ of $E M N$. If $T=E$, the same computation shows that $\measuredangle L E M=\measuredangle E N M$, which means that $t$ is tangent to $\omega$.
Now let lines $M P$ and $t$ meet at $V$. An analogous computation shows, by looking at the circumcircles of $L C D$ (which contains $E$ and $N$ ), $C Q R$, and $M N Q P$, that $V$ lies in $\omega$ as well, and that if $V=E$ then $t$ is tangent to $\omega$.
Therefore, since $\omega$ meet $t$ at $T, V$, and $E$, either $T=V$ if both $T \neq E$ and $V \neq E$ or $T=V=E$. At any rate, the intersection of lines $M P$ and $N Q$ lies in $t$.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 1"
}
|
848a0115-7f58-5c49-91e2-d109890bfbd5
| 606,351
|
Line $\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.
|
Barycentric coordinates are a viable way to solve the problem, but even the solution we have found had some clever computations. Here is an outline of this solution.
Lemma 2. Denote by $\operatorname{pow}_{\omega} X$ the power of point $X$ with respect to circle $\omega$. Let $\Gamma_{1}$ and $\Gamma_{2}$ be circles with different centers. Considering $A B C$ as the reference triangle in barycentric coordinates, the radical axis of $\Gamma_{1}$ and $\Gamma_{2}$ is given by
$$
\left(\operatorname{pow}_{\Gamma_{1}} A-\operatorname{pow}_{\Gamma_{2}} A\right) x+\left(\operatorname{pow}_{\Gamma_{1}} B-\operatorname{pow}_{\Gamma_{2}} B\right) y+\left(\operatorname{pow}_{\Gamma_{1}} C-\operatorname{pow}_{\Gamma_{2}} C\right) z=0
$$
Proof: Let $\Gamma_{i}$ have the equation $\Gamma_{i}(x, y, z)=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z)\left(r_{i} x+s_{i} y+t_{i} z\right)$. Then $\operatorname{pow}_{\Gamma_{i}} P=\Gamma_{i}(P)$. In particular, $\operatorname{pow}_{\Gamma_{i}} A=\Gamma_{i}(1,0,0)=r_{i}$ and, similarly, $\operatorname{pow}_{\Gamma_{i}} B=s_{i}$ and $\operatorname{pow}_{\Gamma_{i}} C=t_{i}$.
Finally, the radical axis is
$$
\begin{aligned}
& \operatorname{pow}_{\Gamma_{1}} P=\operatorname{pow}_{\Gamma_{2}} P \\
\Longleftrightarrow & \Gamma_{1}(x, y, z)=\Gamma_{2}(x, y, z) \\
\Longleftrightarrow & r_{1} x+s_{1} y+t_{1} z=r_{2} x+s_{2} y+t_{2} z \\
\Longleftrightarrow & \left(\operatorname{pow}_{\Gamma_{1}} A-\operatorname{pow}_{\Gamma_{2}} A\right) x+\left(\operatorname{pow}_{\Gamma_{1}} B-\operatorname{pow}_{\Gamma_{2}} B\right) y+\left(\operatorname{pow}_{\Gamma_{1}} C-\operatorname{pow}_{\Gamma_{2}} C\right) z=0 .
\end{aligned}
$$
We still use the Miquel point $E$ of $A B C D$. Notice that the problem is equivalent to proving that lines $M P, N Q$, and $E K$ are concurrent. The main idea is writing these three lines as radical axes. In fact, by definition of points $M, N$, and $E$ :
- $M P$ is the radical axis of the circumcircles of $P A S$ and $P B R$;
- $N Q$ is the radical axis of the circumcircles of $Q C R$ and $Q D S$;
- $E K$ is the radical axis of the circumcircles of $K B C$ and $K A D$.
Looking at these facts and the diagram, it makes sense to take triangle $K Q P$ the reference triangle. Because of that, we do not really need to draw circles nor even points $M$ and $N$, as all powers can be computed directly from points in lines $K P, K Q$, and $P Q$.
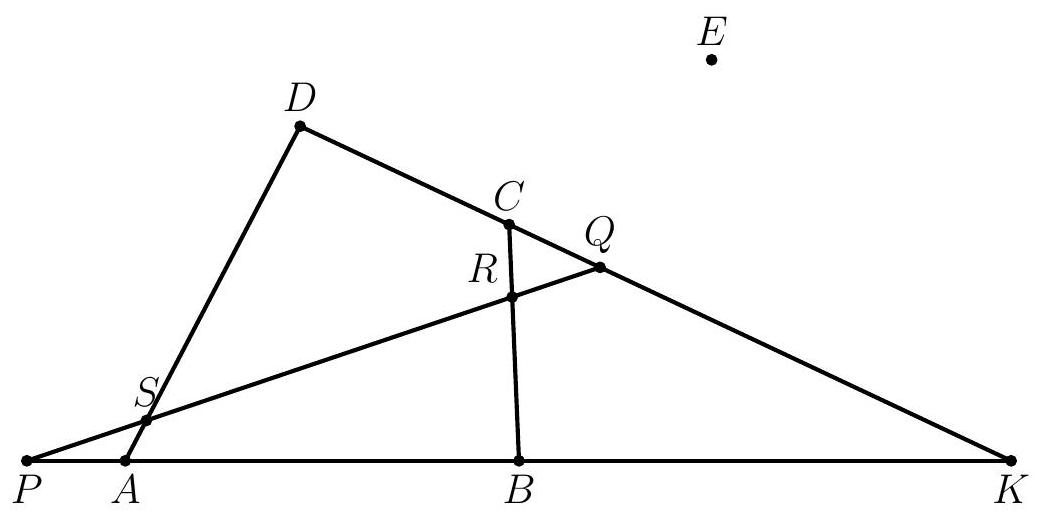
Associate $P$ with the $x$-coordinate, $Q$ with the $y$-coordinate, and $K$ with the $z$-coordinate. Applying the lemma, the equations of lines $P M, Q N$, and $E K$ are
- MP: $(K A \cdot K P-K B \cdot K P) x+(Q S \cdot Q P-Q R \cdot Q P) y=0$
- $N Q:(K C \cdot K Q-K D \cdot K Q) x+(P R \cdot P Q-P S \cdot P Q) z=0$
- MP: $(-Q C \cdot Q K+Q D \cdot Q K) y+(P B \cdot P K-P A \cdot P K) z=0$
These equations simplify to
- $M P:(A B \cdot K P) x+(P Q \cdot R S) y=0$
- $N Q:(-C D \cdot K Q) x+(P Q \cdot R S) z=0$
- $M P:(C D \cdot K Q) y+(A B \cdot K P) z=0$
Now, if $u=A B \cdot K P, v=P Q \cdot R S$, and $w=C D \cdot K Q$, it suffices to show that
$$
\left|\begin{array}{ccc}
u & v & 0 \\
-w & 0 & v \\
0 & w & u
\end{array}\right|=0
$$
which is a straightforward computation.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Line $\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.
|
Barycentric coordinates are a viable way to solve the problem, but even the solution we have found had some clever computations. Here is an outline of this solution.
Lemma 2. Denote by $\operatorname{pow}_{\omega} X$ the power of point $X$ with respect to circle $\omega$. Let $\Gamma_{1}$ and $\Gamma_{2}$ be circles with different centers. Considering $A B C$ as the reference triangle in barycentric coordinates, the radical axis of $\Gamma_{1}$ and $\Gamma_{2}$ is given by
$$
\left(\operatorname{pow}_{\Gamma_{1}} A-\operatorname{pow}_{\Gamma_{2}} A\right) x+\left(\operatorname{pow}_{\Gamma_{1}} B-\operatorname{pow}_{\Gamma_{2}} B\right) y+\left(\operatorname{pow}_{\Gamma_{1}} C-\operatorname{pow}_{\Gamma_{2}} C\right) z=0
$$
Proof: Let $\Gamma_{i}$ have the equation $\Gamma_{i}(x, y, z)=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z)\left(r_{i} x+s_{i} y+t_{i} z\right)$. Then $\operatorname{pow}_{\Gamma_{i}} P=\Gamma_{i}(P)$. In particular, $\operatorname{pow}_{\Gamma_{i}} A=\Gamma_{i}(1,0,0)=r_{i}$ and, similarly, $\operatorname{pow}_{\Gamma_{i}} B=s_{i}$ and $\operatorname{pow}_{\Gamma_{i}} C=t_{i}$.
Finally, the radical axis is
$$
\begin{aligned}
& \operatorname{pow}_{\Gamma_{1}} P=\operatorname{pow}_{\Gamma_{2}} P \\
\Longleftrightarrow & \Gamma_{1}(x, y, z)=\Gamma_{2}(x, y, z) \\
\Longleftrightarrow & r_{1} x+s_{1} y+t_{1} z=r_{2} x+s_{2} y+t_{2} z \\
\Longleftrightarrow & \left(\operatorname{pow}_{\Gamma_{1}} A-\operatorname{pow}_{\Gamma_{2}} A\right) x+\left(\operatorname{pow}_{\Gamma_{1}} B-\operatorname{pow}_{\Gamma_{2}} B\right) y+\left(\operatorname{pow}_{\Gamma_{1}} C-\operatorname{pow}_{\Gamma_{2}} C\right) z=0 .
\end{aligned}
$$
We still use the Miquel point $E$ of $A B C D$. Notice that the problem is equivalent to proving that lines $M P, N Q$, and $E K$ are concurrent. The main idea is writing these three lines as radical axes. In fact, by definition of points $M, N$, and $E$ :
- $M P$ is the radical axis of the circumcircles of $P A S$ and $P B R$;
- $N Q$ is the radical axis of the circumcircles of $Q C R$ and $Q D S$;
- $E K$ is the radical axis of the circumcircles of $K B C$ and $K A D$.
Looking at these facts and the diagram, it makes sense to take triangle $K Q P$ the reference triangle. Because of that, we do not really need to draw circles nor even points $M$ and $N$, as all powers can be computed directly from points in lines $K P, K Q$, and $P Q$.

Associate $P$ with the $x$-coordinate, $Q$ with the $y$-coordinate, and $K$ with the $z$-coordinate. Applying the lemma, the equations of lines $P M, Q N$, and $E K$ are
- MP: $(K A \cdot K P-K B \cdot K P) x+(Q S \cdot Q P-Q R \cdot Q P) y=0$
- $N Q:(K C \cdot K Q-K D \cdot K Q) x+(P R \cdot P Q-P S \cdot P Q) z=0$
- MP: $(-Q C \cdot Q K+Q D \cdot Q K) y+(P B \cdot P K-P A \cdot P K) z=0$
These equations simplify to
- $M P:(A B \cdot K P) x+(P Q \cdot R S) y=0$
- $N Q:(-C D \cdot K Q) x+(P Q \cdot R S) z=0$
- $M P:(C D \cdot K Q) y+(A B \cdot K P) z=0$
Now, if $u=A B \cdot K P, v=P Q \cdot R S$, and $w=C D \cdot K Q$, it suffices to show that
$$
\left|\begin{array}{ccc}
u & v & 0 \\
-w & 0 & v \\
0 & w & u
\end{array}\right|=0
$$
which is a straightforward computation.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 2"
}
|
848a0115-7f58-5c49-91e2-d109890bfbd5
| 606,351
|
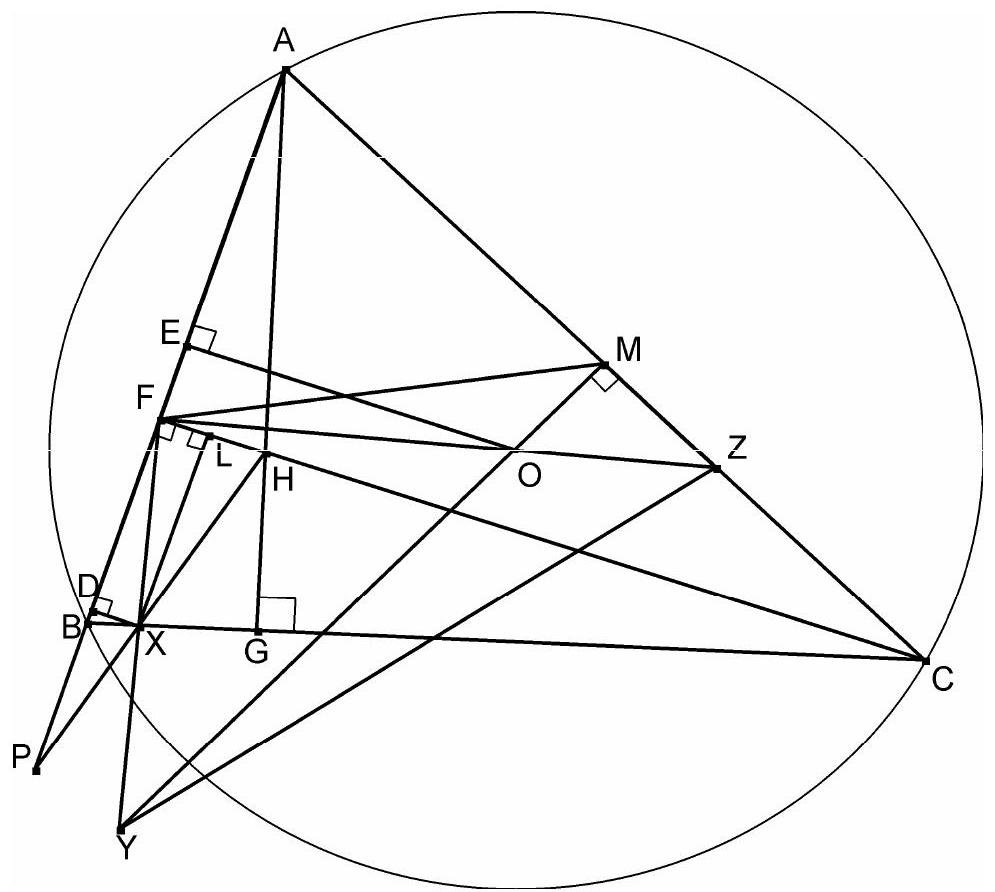
An acute-angled scalene triangle $A B C$ is given, with $A C>B C$. Let $O$ be its circumcentre, $H$ its orthocentre, and $F$ the foot of the altitude from $C$. Let $P$ be the point (other than $A$ ) on the line $A B$ such that $A F=P F$, and $M$ be the midpoint of $A C$. We denote the intersection of $P H$ and $B C$ by $X$, the intersection of $O M$ and $F X$ by $Y$, and the intersection of $O F$ and $A C$ by $Z$. Prove that the points $F, M, Y$ and $Z$ are concyclic.
|
It is enough to show that $\mathrm{O} F \perp F X$.
Let $\mathrm{OE} \perp \mathrm{AB}$, then it is trivial that :
$$
C \mathrm{H}=2 \mathrm{OE} .
$$
Since from the hypothesis we have $\mathrm{P} F=\mathrm{A} F$ then we take $\mathrm{PB}=\mathrm{P} F-\mathrm{B} F$ or
$$
\mathrm{PB}=\mathrm{A} F-\mathrm{B} F
$$
Also, $\angle X P B=\angle H A P$ and $\angle H A P=\angle H C X$ since AFGC in inscribable (where G is the foot of the altidude from A),
so $\angle X P B=\angle H C X$ and since $\angle B X P=\angle H X C$, the triangles XHC and XBP are similar.
If XL and XD are respectively the heights of the triangles XHC and XBP we have:
$$
\frac{X D}{X L}=\frac{P B}{C H},
$$
and from (1) and (2) we get:
$$
\frac{X D}{X L}=\frac{A F-B F}{2 O E}=\frac{F E}{O E} \Rightarrow \frac{X D}{F D}=\frac{F E}{O E}
$$
Therefore the triangles XFD, OEF are similar and we get:
$\angle O F X=\angle O F C+\angle L F X=\angle F O E+\angle F X D=\angle X F D+\angle F X D=90^{\circ}$, so $\mathrm{O} F \perp F X$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
An acute-angled scalene triangle $A B C$ is given, with $A C>B C$. Let $O$ be its circumcentre, $H$ its orthocentre, and $F$ the foot of the altitude from $C$. Let $P$ be the point (other than $A$ ) on the line $A B$ such that $A F=P F$, and $M$ be the midpoint of $A C$. We denote the intersection of $P H$ and $B C$ by $X$, the intersection of $O M$ and $F X$ by $Y$, and the intersection of $O F$ and $A C$ by $Z$. Prove that the points $F, M, Y$ and $Z$ are concyclic.
|
It is enough to show that $\mathrm{O} F \perp F X$.
Let $\mathrm{OE} \perp \mathrm{AB}$, then it is trivial that :
$$
C \mathrm{H}=2 \mathrm{OE} .
$$
Since from the hypothesis we have $\mathrm{P} F=\mathrm{A} F$ then we take $\mathrm{PB}=\mathrm{P} F-\mathrm{B} F$ or
$$
\mathrm{PB}=\mathrm{A} F-\mathrm{B} F
$$
Also, $\angle X P B=\angle H A P$ and $\angle H A P=\angle H C X$ since AFGC in inscribable (where G is the foot of the altidude from A),
so $\angle X P B=\angle H C X$ and since $\angle B X P=\angle H X C$, the triangles XHC and XBP are similar.
If XL and XD are respectively the heights of the triangles XHC and XBP we have:
$$
\frac{X D}{X L}=\frac{P B}{C H},
$$
and from (1) and (2) we get:
$$
\frac{X D}{X L}=\frac{A F-B F}{2 O E}=\frac{F E}{O E} \Rightarrow \frac{X D}{F D}=\frac{F E}{O E}
$$
Therefore the triangles XFD, OEF are similar and we get:
$\angle O F X=\angle O F C+\angle L F X=\angle F O E+\angle F X D=\angle X F D+\angle F X D=90^{\circ}$, so $\mathrm{O} F \perp F X$.

|
{
"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution:"
}
|
35af2f2a-6f2d-5324-93f3-2afadcad0676
| 606,353
|
Does there exist a sequence $a_{1}, a_{2}, \ldots, a_{n}, \ldots$ of positive real numbers satisfying both of the following conditions:
(i) $\sum_{i=1}^{n} a_{i} \leq n^{2}$, for every positive integer $n$;
(ii) $\sum_{i=1}^{n} \frac{1}{a_{i}} \leq 2008$, for every positive integer $n$ ?
|
The answer is no.
It is enough to show that
if $\sum_{i=1}^{n} a_{i} \leq n^{2}$ for any $n$, then $\sum_{i=2}^{2^{n}} \frac{1}{a_{i}}>\frac{n}{4}$. (or any other precise estimate)
For this, we use that $\sum_{i=2^{k}+1}^{2^{k+1}} a_{i} \sum_{i=2^{k}+1}^{2^{k+1}} \frac{1}{a_{i}} \geq 2^{2 k}$ for any $k \geq 0$ by the arithmetic-harmonic mean inequality.
Since $\sum_{i=2^{k}+1}^{2^{k+1}} a_{i}<\sum_{i=1}^{2^{k+1}} a_{i} \leq 2^{2 k+2}$, it follows that $\sum_{i=2^{k}+1}^{2^{k+1}} \frac{1}{a_{i}}>\frac{1}{4}$ and hence $\sum_{i=2}^{2^{n}} \frac{1}{a^{i}}>\sum_{k=0}^{n-1} \sum_{i=2^{k}+1}^{2^{k+1}} \frac{1}{a_{i}}>\frac{n}{4}$. (it can be stated in words)
## Remark: no points for using some inequality, that doesn't lead to solution
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Does there exist a sequence $a_{1}, a_{2}, \ldots, a_{n}, \ldots$ of positive real numbers satisfying both of the following conditions:
(i) $\sum_{i=1}^{n} a_{i} \leq n^{2}$, for every positive integer $n$;
(ii) $\sum_{i=1}^{n} \frac{1}{a_{i}} \leq 2008$, for every positive integer $n$ ?
|
The answer is no.
It is enough to show that
if $\sum_{i=1}^{n} a_{i} \leq n^{2}$ for any $n$, then $\sum_{i=2}^{2^{n}} \frac{1}{a_{i}}>\frac{n}{4}$. (or any other precise estimate)
For this, we use that $\sum_{i=2^{k}+1}^{2^{k+1}} a_{i} \sum_{i=2^{k}+1}^{2^{k+1}} \frac{1}{a_{i}} \geq 2^{2 k}$ for any $k \geq 0$ by the arithmetic-harmonic mean inequality.
Since $\sum_{i=2^{k}+1}^{2^{k+1}} a_{i}<\sum_{i=1}^{2^{k+1}} a_{i} \leq 2^{2 k+2}$, it follows that $\sum_{i=2^{k}+1}^{2^{k+1}} \frac{1}{a_{i}}>\frac{1}{4}$ and hence $\sum_{i=2}^{2^{n}} \frac{1}{a^{i}}>\sum_{k=0}^{n-1} \sum_{i=2^{k}+1}^{2^{k+1}} \frac{1}{a_{i}}>\frac{n}{4}$. (it can be stated in words)
## Remark: no points for using some inequality, that doesn't lead to solution
|
{
"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution."
}
|
00c532a9-9fbd-577e-9a17-29c6128a4942
| 606,356
|
Let $n$ be a positive integer. The rectangle $A B C D$ with side lengths $A B=90 n+1$ and $B C=90 n+5$ is partitioned into unit squares with sides parallel to the sides of $A B C D$. Let $S$ be the set of all points which are vertices of these unit squares. Prove that the number of lines which pass through at least two points from $S$ is divisible by 4.
|
Denote $90 n+1=m$. We investigate the number of the lines modulo 4 consecutively reducing different types of lines.
The vertical and horizontal lines are
$(m+5)+(m+1)=2(m+3)$ which is divisible to 4.
Moreover, every line which makes an acute angle to the axe $O x$ (i.e. that line has a positive angular coefficient) corresponds to unique line with an obtuse angle (consider the symmetry with respect to the line through the midpoints of $A B$ and $C D$ ). Therefore it is enough to prove that the lines with acute angles are an even number.
Every line which does not pass through the center $O$ of the rectangle corresponds to another line with the same angular coefficent(consider the symmetry with respect to $O$ ). Therefore it is enough to consider the lines through $O$.
Every line through $O$ has an angular coefficient $\frac{p}{q}$, where $(p, q)=1, p$ and $q$ are odd positive integers. (To see this, consider the two nearest, from the two sides, to $O$ points of the line).
If $p \neq 1, q \neq 1, \quad p \leq m$ and $q \leq m$, the line with angular coefficient $\frac{p}{q}$, uniquely corresponds to the line with angular coefficient $\frac{q}{p}$. It remains to prove that the number of the remaining lines is even.
The last number is
$$
1+\frac{\varphi(m+2)}{2}+\frac{\varphi(m+4)}{2}-1=\frac{\varphi(m+2)+\varphi(m+4)}{2}
$$
because we have:
1) one line with $p=q=1$;
2) $\frac{\varphi(m+2)}{2}$ lines with angular coefficient $\frac{p}{m+2}, p \leq m$ is odd and $(p, m+2)=1$;
3) $\frac{\varphi(m+4)}{2}-1$ lines with angular coefficient $\frac{p}{m+4}, p \leq m$ is odd and $(p, m+4)=1$.
Now the assertion follows from the fact that the number $\varphi(m+2)+\varphi(m+4)=\varphi(90 n+3)+\varphi(90 n+5)$ is divisible to 4.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. The rectangle $A B C D$ with side lengths $A B=90 n+1$ and $B C=90 n+5$ is partitioned into unit squares with sides parallel to the sides of $A B C D$. Let $S$ be the set of all points which are vertices of these unit squares. Prove that the number of lines which pass through at least two points from $S$ is divisible by 4.
|
Denote $90 n+1=m$. We investigate the number of the lines modulo 4 consecutively reducing different types of lines.
The vertical and horizontal lines are
$(m+5)+(m+1)=2(m+3)$ which is divisible to 4.
Moreover, every line which makes an acute angle to the axe $O x$ (i.e. that line has a positive angular coefficient) corresponds to unique line with an obtuse angle (consider the symmetry with respect to the line through the midpoints of $A B$ and $C D$ ). Therefore it is enough to prove that the lines with acute angles are an even number.
Every line which does not pass through the center $O$ of the rectangle corresponds to another line with the same angular coefficent(consider the symmetry with respect to $O$ ). Therefore it is enough to consider the lines through $O$.
Every line through $O$ has an angular coefficient $\frac{p}{q}$, where $(p, q)=1, p$ and $q$ are odd positive integers. (To see this, consider the two nearest, from the two sides, to $O$ points of the line).
If $p \neq 1, q \neq 1, \quad p \leq m$ and $q \leq m$, the line with angular coefficient $\frac{p}{q}$, uniquely corresponds to the line with angular coefficient $\frac{q}{p}$. It remains to prove that the number of the remaining lines is even.
The last number is
$$
1+\frac{\varphi(m+2)}{2}+\frac{\varphi(m+4)}{2}-1=\frac{\varphi(m+2)+\varphi(m+4)}{2}
$$
because we have:
1) one line with $p=q=1$;
2) $\frac{\varphi(m+2)}{2}$ lines with angular coefficient $\frac{p}{m+2}, p \leq m$ is odd and $(p, m+2)=1$;
3) $\frac{\varphi(m+4)}{2}-1$ lines with angular coefficient $\frac{p}{m+4}, p \leq m$ is odd and $(p, m+4)=1$.
Now the assertion follows from the fact that the number $\varphi(m+2)+\varphi(m+4)=\varphi(90 n+3)+\varphi(90 n+5)$ is divisible to 4.
|
{
"resource_path": "Balkan_MO/segmented/en-2008-BMO-type1.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution."
}
|
186884e0-6654-547b-9767-01bd3ec6c6ef
| 606,358
|
In a triangle $A B C$, points $M$ and $N$ on the sides $A B$ and $A C$ respectively are such that $M N \| B C$. Let $B N$ and $C M$ intersect at point $P$. The circumcircles of triangles $B M P$ and $C N P$ intersect at two distinct points $P$ and $Q$. Prove that $\angle B A Q=\angle C A P$.
(Moldova)
|
Since the quadrilaterals $B M P Q$ and $C N P Q$ are cyclic, we have $\angle B Q N=\angle B Q P+$ $\angle P Q N=\angle A M C+\angle M C A=180^{\circ}-$ $\angle C A B$, so $A B Q N$ is cyclic as well. Hence $\frac{\sin \angle B A Q}{\sin \angle N A Q}=\frac{B Q}{N Q}$. Moreover, triangles $M B Q$ and $C N Q$ are similar, so
$$
\frac{\sin \angle B A Q}{\sin \angle C A Q}=\frac{B Q}{N Q}=\frac{B M}{C N}=\frac{A B}{A C}
$$
On the other hand, if $A P$ meets $B C$ at $A_{1}$, then by the Cheva theorem $\frac{B A_{1}}{A_{1} C}=$
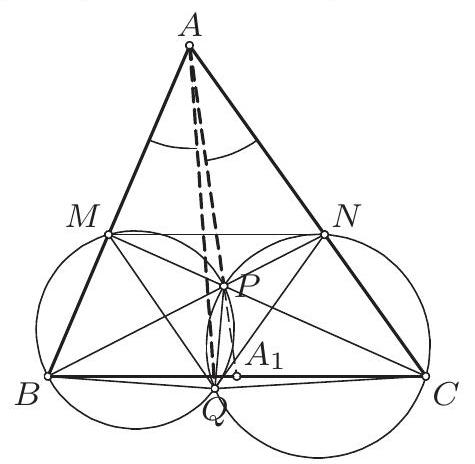
$\frac{B M}{M A} \cdot \frac{A N}{N C}=1$, so $A_{1}$ is the midpoint of $B C$ and
$$
\frac{\sin \angle C A P}{\sin \angle B A P}=\frac{A B}{A C} \cdot \frac{A C \cdot A A_{1} \sin \angle C A P}{A B \cdot A A_{1} \sin \angle B A P}=\frac{A B}{A C} \cdot \frac{S_{\triangle C A A_{1}}}{S_{\triangle B A A_{1}}}=\frac{A B}{A C}
$$
Therefore, if we denote $\angle C A P=\varphi, \angle B A Q=\psi$ and $\angle B A C=\alpha$, we have $\frac{\sin \psi}{\sin (\alpha-\psi)}=\frac{\sin \varphi}{\sin (\alpha-\varphi)}$, which is equivalent to $\sin \psi \sin (\alpha-\varphi)=\sin \varphi \sin (\alpha-\psi)$. The addition formulas reduce the last equality to $0=\sin \alpha(\sin \varphi \cos \psi-\sin \psi \cos \varphi)=$ $\sin \alpha \sin (\varphi-\psi)$, from which we conclude that $\psi=\varphi$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C$, points $M$ and $N$ on the sides $A B$ and $A C$ respectively are such that $M N \| B C$. Let $B N$ and $C M$ intersect at point $P$. The circumcircles of triangles $B M P$ and $C N P$ intersect at two distinct points $P$ and $Q$. Prove that $\angle B A Q=\angle C A P$.
(Moldova)
|
Since the quadrilaterals $B M P Q$ and $C N P Q$ are cyclic, we have $\angle B Q N=\angle B Q P+$ $\angle P Q N=\angle A M C+\angle M C A=180^{\circ}-$ $\angle C A B$, so $A B Q N$ is cyclic as well. Hence $\frac{\sin \angle B A Q}{\sin \angle N A Q}=\frac{B Q}{N Q}$. Moreover, triangles $M B Q$ and $C N Q$ are similar, so
$$
\frac{\sin \angle B A Q}{\sin \angle C A Q}=\frac{B Q}{N Q}=\frac{B M}{C N}=\frac{A B}{A C}
$$
On the other hand, if $A P$ meets $B C$ at $A_{1}$, then by the Cheva theorem $\frac{B A_{1}}{A_{1} C}=$

$\frac{B M}{M A} \cdot \frac{A N}{N C}=1$, so $A_{1}$ is the midpoint of $B C$ and
$$
\frac{\sin \angle C A P}{\sin \angle B A P}=\frac{A B}{A C} \cdot \frac{A C \cdot A A_{1} \sin \angle C A P}{A B \cdot A A_{1} \sin \angle B A P}=\frac{A B}{A C} \cdot \frac{S_{\triangle C A A_{1}}}{S_{\triangle B A A_{1}}}=\frac{A B}{A C}
$$
Therefore, if we denote $\angle C A P=\varphi, \angle B A Q=\psi$ and $\angle B A C=\alpha$, we have $\frac{\sin \psi}{\sin (\alpha-\psi)}=\frac{\sin \varphi}{\sin (\alpha-\varphi)}$, which is equivalent to $\sin \psi \sin (\alpha-\varphi)=\sin \varphi \sin (\alpha-\psi)$. The addition formulas reduce the last equality to $0=\sin \alpha(\sin \varphi \cos \psi-\sin \psi \cos \varphi)=$ $\sin \alpha \sin (\varphi-\psi)$, from which we conclude that $\psi=\varphi$, as desired.
|
{
"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl",
"problem_match": "\n2.",
"solution_match": "\n2."
}
|
8fabb8e6-48c6-5fce-8b91-cdbd07e436bc
| 606,363
|
A $9 \times 12$ rectangle is divided into unit squares. The centers of all the unit squares, except the four corner squares and the eight squares adjacent (by side) to them, are colored red. Is it possible to numerate the red centers by $C_{1}, C_{2}, \ldots, C_{96}$ so that the following two conditions are fulfilled:
$1^{\circ}$ All segments $C_{1} C_{2}, C_{2} C_{3}, \ldots C_{95} C_{96}, C_{96} C_{1}$ have the length $\sqrt{13}$;
$2^{\circ}$ The poligonal line $C_{1} C_{2} \ldots C_{96} C_{1}$ is centrally symmetric?
(Bulgaria)
|
Place the given rectangle into the coordinate plane so that the center of the square at the intersection of $i$-th column and $j$-th row has the coordinates $(i, j)$. Suppose that a desired numeration of the red points exists; it corresponds to a path, i.e. a closed poligonal line consisting of 96 segments of length $\sqrt{13}$, passing through each red point exactly once. Note that points $(i, j)$ and $(k, l)$ are adjacent in the path if and only if $\{|i-k|,|j-l|\}=\{2,3\}$.
The center of symmetry must be at point $C\left(5 \frac{1}{2}, 5\right)$. Consider the points $A(2,2)$, $B(11,8)$. These two points are symmetric with respect to $C$ and divide the path into two parts $\gamma_{1}$ and $\gamma_{2}$. Note that, if the rectangular board is colored alternately white and black (like a chessboard), $A$ and $B$ are of different colors, and each segment connects two squares of different colors. It follows that each of $\gamma_{1}, \gamma_{2}$ consists of an odd number of segments. Thus these two parts are of different lengths and cannot be symmetric to each other. Therefore each
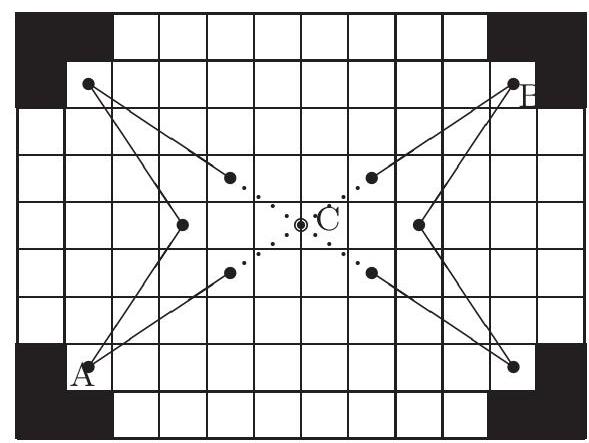
of $\gamma_{1}, \gamma_{2}$ is centrally symmetric itself.
Being of an odd length, each of the parts $\gamma_{1}, \gamma_{2}$ must contain a segment which is centrally symmetric with respect to $C$. There are only two such segments one connecting $(5,4)$ and $(8,6)$, and one connecting $(5,6)$ and $(8,4)$, so these two segments must be parts of our path. Moreover, point $(2,2)$ is connected with only two points, namely $(4,5)$ and $(5,4)$, so these three points are directly connected. Analogous conclusions can be made about points $(2,8),(11,2)$ and $(11,8)$, so the closed path $(5,4)-(2,2)-(4,5)-(2,8)-(5,6)-(8,4)-(11,2)-(9,5)-(11,8)-$ $(8,6)-(5,4)$ is entirely contained in our path, which is clearly a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A $9 \times 12$ rectangle is divided into unit squares. The centers of all the unit squares, except the four corner squares and the eight squares adjacent (by side) to them, are colored red. Is it possible to numerate the red centers by $C_{1}, C_{2}, \ldots, C_{96}$ so that the following two conditions are fulfilled:
$1^{\circ}$ All segments $C_{1} C_{2}, C_{2} C_{3}, \ldots C_{95} C_{96}, C_{96} C_{1}$ have the length $\sqrt{13}$;
$2^{\circ}$ The poligonal line $C_{1} C_{2} \ldots C_{96} C_{1}$ is centrally symmetric?
(Bulgaria)
|
Place the given rectangle into the coordinate plane so that the center of the square at the intersection of $i$-th column and $j$-th row has the coordinates $(i, j)$. Suppose that a desired numeration of the red points exists; it corresponds to a path, i.e. a closed poligonal line consisting of 96 segments of length $\sqrt{13}$, passing through each red point exactly once. Note that points $(i, j)$ and $(k, l)$ are adjacent in the path if and only if $\{|i-k|,|j-l|\}=\{2,3\}$.
The center of symmetry must be at point $C\left(5 \frac{1}{2}, 5\right)$. Consider the points $A(2,2)$, $B(11,8)$. These two points are symmetric with respect to $C$ and divide the path into two parts $\gamma_{1}$ and $\gamma_{2}$. Note that, if the rectangular board is colored alternately white and black (like a chessboard), $A$ and $B$ are of different colors, and each segment connects two squares of different colors. It follows that each of $\gamma_{1}, \gamma_{2}$ consists of an odd number of segments. Thus these two parts are of different lengths and cannot be symmetric to each other. Therefore each

of $\gamma_{1}, \gamma_{2}$ is centrally symmetric itself.
Being of an odd length, each of the parts $\gamma_{1}, \gamma_{2}$ must contain a segment which is centrally symmetric with respect to $C$. There are only two such segments one connecting $(5,4)$ and $(8,6)$, and one connecting $(5,6)$ and $(8,4)$, so these two segments must be parts of our path. Moreover, point $(2,2)$ is connected with only two points, namely $(4,5)$ and $(5,4)$, so these three points are directly connected. Analogous conclusions can be made about points $(2,8),(11,2)$ and $(11,8)$, so the closed path $(5,4)-(2,2)-(4,5)-(2,8)-(5,6)-(8,4)-(11,2)-(9,5)-(11,8)-$ $(8,6)-(5,4)$ is entirely contained in our path, which is clearly a contradiction.
|
{
"resource_path": "Balkan_MO/segmented/en-2009-BMO-type2.jsonl",
"problem_match": "\n3.",
"solution_match": "\n3."
}
|
bf7ce674-0b20-5b87-bdfd-859a0056894f
| 606,367
|
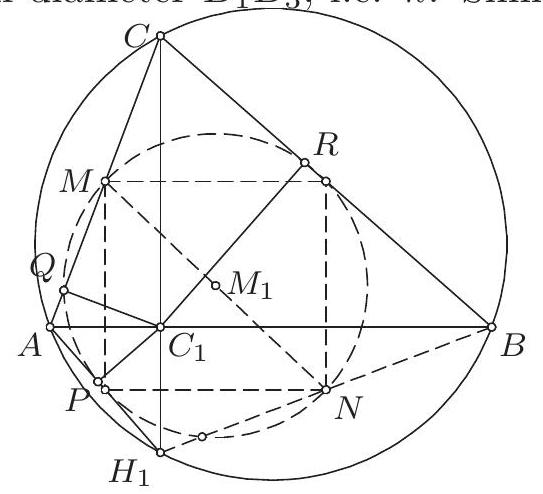
Let $A B C$ be an acute-angled triangle with orthocenter $H$ and let $M$ be the midpoint of $A C$. The foot of the altitude from $C$ is $C_{1}$. Point $H_{1}$ is symmetric to $H$ in $A B$. The projections of $C_{1}$ on lines $A H_{1}, A C$ and $B C$ are $P, Q$ and $R$ respectively. If $M_{1}$ is the circumcenter of triangle $P Q R$, prove that the point symmetric to $M$ with respect to $M_{1}$ lies on line $B H_{1}$.
(Serbia)
|
We shall use the following simple statement.
Lemma. Let $A_{1} A_{2} A_{3} A_{4}$ be a convex cyclic quadrilateral whose diagonals are orthogonal and meet at $X$. If $B_{i}$ is the midpoint of side $A_{i} A_{i+1}$ and $X_{i}$ the projection of $X$ on this side $\left(A_{5}=A_{1}\right)$, then the eight points $B_{i}, X_{i}$ $(i=1,2,3,4)$ lie on a circle.
Proof. Quadrilateral $B_{1} B_{2} B_{3} B_{4}$ is a rectangle because $B_{1} B_{2}\left\|B_{3} B_{4}\right\| A_{1} A_{3}$ and $B_{2} B_{3}\left\|B_{4} B_{1}\right\| A_{2} A_{4}$. Denote by $k$ the circumcircle of $B_{1} B_{2} B_{3} B_{4}$. Since $\angle B_{3} X A_{3}=\angle A_{4} A_{3} A_{1}=\angle A_{4} A_{2} A_{1}=\angle A_{1} X X_{1}$, points $B_{3}, X, X_{1}$ are collinear, so $X_{1}$ lies on the circle with diameter $B_{1} B_{3}$, i.e. $k$. Similarly, $X_{2}, X_{3}, X_{4}$ lie on $k$.
It is known that $H_{1}$ lies on the circumcircle of $A B C$. By the lemma, points $P, Q, R$ all lie on the circle with diameter $M N$, where $N$ is the midpoint of $B H_{1}$. Therefore $N$ is symmetric to $M$ with respect to $M_{1}$ and lies on $B H_{1}$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with orthocenter $H$ and let $M$ be the midpoint of $A C$. The foot of the altitude from $C$ is $C_{1}$. Point $H_{1}$ is symmetric to $H$ in $A B$. The projections of $C_{1}$ on lines $A H_{1}, A C$ and $B C$ are $P, Q$ and $R$ respectively. If $M_{1}$ is the circumcenter of triangle $P Q R$, prove that the point symmetric to $M$ with respect to $M_{1}$ lies on line $B H_{1}$.
(Serbia)
|
We shall use the following simple statement.
Lemma. Let $A_{1} A_{2} A_{3} A_{4}$ be a convex cyclic quadrilateral whose diagonals are orthogonal and meet at $X$. If $B_{i}$ is the midpoint of side $A_{i} A_{i+1}$ and $X_{i}$ the projection of $X$ on this side $\left(A_{5}=A_{1}\right)$, then the eight points $B_{i}, X_{i}$ $(i=1,2,3,4)$ lie on a circle.
Proof. Quadrilateral $B_{1} B_{2} B_{3} B_{4}$ is a rectangle because $B_{1} B_{2}\left\|B_{3} B_{4}\right\| A_{1} A_{3}$ and $B_{2} B_{3}\left\|B_{4} B_{1}\right\| A_{2} A_{4}$. Denote by $k$ the circumcircle of $B_{1} B_{2} B_{3} B_{4}$. Since $\angle B_{3} X A_{3}=\angle A_{4} A_{3} A_{1}=\angle A_{4} A_{2} A_{1}=\angle A_{1} X X_{1}$, points $B_{3}, X, X_{1}$ are collinear, so $X_{1}$ lies on the circle with diameter $B_{1} B_{3}$, i.e. $k$. Similarly, $X_{2}, X_{3}, X_{4}$ lie on $k$.
It is known that $H_{1}$ lies on the circumcircle of $A B C$. By the lemma, points $P, Q, R$ all lie on the circle with diameter $M N$, where $N$ is the midpoint of $B H_{1}$. Therefore $N$ is symmetric to $M$ with respect to $M_{1}$ and lies on $B H_{1}$ as desired.

|
{
"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl",
"problem_match": "\n2.",
"solution_match": "\n2."
}
|
358e2bc6-d7e2-5225-8247-19b941730f1b
| 606,377
|
We define a $w$-strip as the set of all points in the plane that are between or on two parallel lines on a mutual distance $w$. Let $S$ be a set of $n$ points in the plane such that any three points from $S$ can be covered by a 1 -strip. Show that the entire set $S$ can be covered by a 2 -strip.
(Romania)
|
Of all triangles with the vertices in $S$, consider one with a maximum area, say $\triangle A B C$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points symmetric to $A, B, C$ with respect to the midpoints of $B C, C A, A B$, respectively. We claim that all points from $S$ must lie inside or on the boundary of $\triangle A^{\prime} B^{\prime} C^{\prime}$. Indeed, if $X \in S$ is outside $\triangle A^{\prime} B^{\prime} C^{\prime}$, we can assume without loss of generality that $X$ and $B C$ are on different sides of $B^{\prime} C^{\prime}$, and then $\triangle B C X$ has an area greater than $\triangle A B C$, a contradiction.
The triangle $A B C$ can be covered by a 1-strip, so the triangle $A^{\prime} B^{\prime} C^{\prime}$, being similar to $A B C$ with ratio 2 , can be covered by a 2 -strip, also covering all of $S$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We define a $w$-strip as the set of all points in the plane that are between or on two parallel lines on a mutual distance $w$. Let $S$ be a set of $n$ points in the plane such that any three points from $S$ can be covered by a 1 -strip. Show that the entire set $S$ can be covered by a 2 -strip.
(Romania)
|
Of all triangles with the vertices in $S$, consider one with a maximum area, say $\triangle A B C$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points symmetric to $A, B, C$ with respect to the midpoints of $B C, C A, A B$, respectively. We claim that all points from $S$ must lie inside or on the boundary of $\triangle A^{\prime} B^{\prime} C^{\prime}$. Indeed, if $X \in S$ is outside $\triangle A^{\prime} B^{\prime} C^{\prime}$, we can assume without loss of generality that $X$ and $B C$ are on different sides of $B^{\prime} C^{\prime}$, and then $\triangle B C X$ has an area greater than $\triangle A B C$, a contradiction.
The triangle $A B C$ can be covered by a 1-strip, so the triangle $A^{\prime} B^{\prime} C^{\prime}$, being similar to $A B C$ with ratio 2 , can be covered by a 2 -strip, also covering all of $S$.
|
{
"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl",
"problem_match": "\n3.",
"solution_match": "\n3."
}
|
f382c2f9-bdfe-5942-a009-da357933120f
| 606,380
|
For every integer $n \geq 2$, denote by $f(n)$ the sum of positive integers not exceeding $n$ that are not coprime to $n$. Prove that $f(n+p) \neq f(n)$ for any such $n$ and any prime number $p$.
(Turkey)
Time allowed: 270 minutes.
Each problem is worth 10 points.
## SOLUTIONS
|
There are $n+1-\varphi(n)$ nonnegative integers not coprime with $n$, and whenever $r$ is among them, so is $n-r$. This gives us the formula $f(n)=\frac{1}{2} n(n+1-\varphi(n))$. Suppose that $f(n)=f(n+p)$. We observe first that $n$ and $n+p$ divide $2 f(n)<n(n+p)$, so $n$ and $n+p$ are not coprime, which implies that $n=k p$ for some $k \in \mathbb{N}$. Then the equality $f(n)=f(n+p)$ is equivalent to $k(k p+1-\varphi(k p))=(k+1)(k p+p+$ $1-\varphi(k p+p)$ ), so
$$
k p+1-\varphi(k p)=(k+1) x \quad \text { and } \quad k p+p+1-\varphi(k p+p)=k x
$$
for some $x \in \mathbb{N}, x<p$. Subtraction gives us $x=\varphi(k p+p)-\varphi(k p)-p$. Since $\varphi(k p)$ and $\varphi(k p+p)$ are both divisible by $p-1$ (by the formula for $\varphi(n)$ ), we obtain $x \equiv-1(\bmod p-1)$.
If $p=2$ then $x=1$ and $\varphi(2 k+2)=k+3$, which is impossible because $\varphi(2 k+2) \leq$ $k+1$. If $p=3$ then $x=1$ and $\varphi(3 k+3)=2 k+4$, again impossible because $\varphi(3 k+3) \leq 2 k+2$. Therefore $p \geq 5$, so $x \equiv-1(\bmod p-1)$ implies $x=p-2$. Plugging this value in (1) leads to
$$
\varphi(k p)=2 k+3-p \quad \text { and } \quad \varphi(k p+p)=2 k+1+p
$$
If $k$ is divisible by $p$, then $\varphi(k p)$ is also divisible by $p$, so $p \mid 2 k+3$ and hence $p \mid 3$, a contradiction. Similarly, $p \nmid k+1$. It follows that $\varphi(k p)=(p-1) \varphi(k)$ and $\varphi(k p+p)=(p-1) \varphi(k+1)$ which together with (1) yields
$$
\varphi(k)=\frac{2 k+2}{p-1}-1 \quad \text { and } \quad \varphi(k+1)=\frac{2 k+2}{p-1}+1
$$
From here we see that $\varphi(t)$ is not divisible by 4 either for $t=k$ or for $t=k+1$, which is only possible if $t=q^{i}$ or $t=2 q^{i}$ for some odd prime $q$ and $i \in \mathbb{N}$, or $t \in\{1,2,4\}$. The cases $t=1,2,4$ are easily ruled out, so either $k$ or $k+1$ is of the form $q^{i}$ or $2 q^{i}$. For $t=k=q^{i}, \varphi\left(q^{i}\right)+1=q^{i-1}(q-1)+1$ divides $2 q^{i}+2$ which is impossible because $q^{i}+1>q^{i-1}(q-1)+1>\frac{2}{3}\left(2 q^{i}+2\right)$. The other three cases are similarly shown to be impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For every integer $n \geq 2$, denote by $f(n)$ the sum of positive integers not exceeding $n$ that are not coprime to $n$. Prove that $f(n+p) \neq f(n)$ for any such $n$ and any prime number $p$.
(Turkey)
Time allowed: 270 minutes.
Each problem is worth 10 points.
## SOLUTIONS
|
There are $n+1-\varphi(n)$ nonnegative integers not coprime with $n$, and whenever $r$ is among them, so is $n-r$. This gives us the formula $f(n)=\frac{1}{2} n(n+1-\varphi(n))$. Suppose that $f(n)=f(n+p)$. We observe first that $n$ and $n+p$ divide $2 f(n)<n(n+p)$, so $n$ and $n+p$ are not coprime, which implies that $n=k p$ for some $k \in \mathbb{N}$. Then the equality $f(n)=f(n+p)$ is equivalent to $k(k p+1-\varphi(k p))=(k+1)(k p+p+$ $1-\varphi(k p+p)$ ), so
$$
k p+1-\varphi(k p)=(k+1) x \quad \text { and } \quad k p+p+1-\varphi(k p+p)=k x
$$
for some $x \in \mathbb{N}, x<p$. Subtraction gives us $x=\varphi(k p+p)-\varphi(k p)-p$. Since $\varphi(k p)$ and $\varphi(k p+p)$ are both divisible by $p-1$ (by the formula for $\varphi(n)$ ), we obtain $x \equiv-1(\bmod p-1)$.
If $p=2$ then $x=1$ and $\varphi(2 k+2)=k+3$, which is impossible because $\varphi(2 k+2) \leq$ $k+1$. If $p=3$ then $x=1$ and $\varphi(3 k+3)=2 k+4$, again impossible because $\varphi(3 k+3) \leq 2 k+2$. Therefore $p \geq 5$, so $x \equiv-1(\bmod p-1)$ implies $x=p-2$. Plugging this value in (1) leads to
$$
\varphi(k p)=2 k+3-p \quad \text { and } \quad \varphi(k p+p)=2 k+1+p
$$
If $k$ is divisible by $p$, then $\varphi(k p)$ is also divisible by $p$, so $p \mid 2 k+3$ and hence $p \mid 3$, a contradiction. Similarly, $p \nmid k+1$. It follows that $\varphi(k p)=(p-1) \varphi(k)$ and $\varphi(k p+p)=(p-1) \varphi(k+1)$ which together with (1) yields
$$
\varphi(k)=\frac{2 k+2}{p-1}-1 \quad \text { and } \quad \varphi(k+1)=\frac{2 k+2}{p-1}+1
$$
From here we see that $\varphi(t)$ is not divisible by 4 either for $t=k$ or for $t=k+1$, which is only possible if $t=q^{i}$ or $t=2 q^{i}$ for some odd prime $q$ and $i \in \mathbb{N}$, or $t \in\{1,2,4\}$. The cases $t=1,2,4$ are easily ruled out, so either $k$ or $k+1$ is of the form $q^{i}$ or $2 q^{i}$. For $t=k=q^{i}, \varphi\left(q^{i}\right)+1=q^{i-1}(q-1)+1$ divides $2 q^{i}+2$ which is impossible because $q^{i}+1>q^{i-1}(q-1)+1>\frac{2}{3}\left(2 q^{i}+2\right)$. The other three cases are similarly shown to be impossible.
|
{
"resource_path": "Balkan_MO/segmented/en-2010-BMO-type2.jsonl",
"problem_match": "\n4.",
"solution_match": "\n4."
}
|
7f330dd6-2174-5725-85a5-49570da9e6c3
| 606,383
|
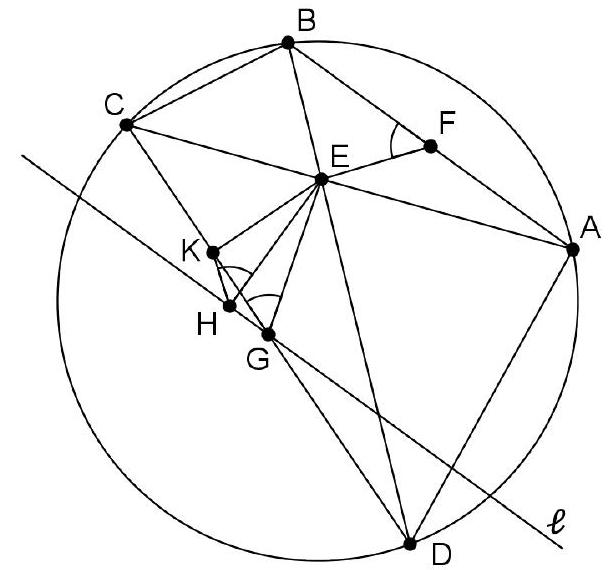
Let $A B C D$ be a cyclic quadrilateral which is not a trapezoid and whose diagonals meet at $E$. The midpoints of $A B$ and $C D$ are $F$ and $G$ respectively, and $\ell$ is the line through $G$ parallel to $A B$. The feet of the perpendiculars from $E$ onto the lines $\ell$ and $C D$ are $H$ and $K$, respectively. Prove that the lines $E F$ and $H K$ are perpendicular.
|
The points $E, K, H, G$ are on the circle of diameter $G E$, so
$$
\angle E H K=\angle E G K
$$
Also, from $\angle D C A=\angle D B A$ and $\frac{C E}{C D}=\frac{B E}{B A}$ it follows
$$
\frac{C E}{C G}=\frac{2 C E}{C D}=\frac{2 B E}{B A}=\frac{B E}{B F},
$$
therefore $\triangle C G E \sim \triangle B F E$. In particular, $\angle E G C=\angle B F E$, so by $(\dagger)$
$$
\angle E H K=\angle B F E .
$$
But $H E \perp F B$ and so, since $F E$ and $H K$ are obtained by rotations of these lines by the same (directed) angle, $F E \perp H K$.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral which is not a trapezoid and whose diagonals meet at $E$. The midpoints of $A B$ and $C D$ are $F$ and $G$ respectively, and $\ell$ is the line through $G$ parallel to $A B$. The feet of the perpendiculars from $E$ onto the lines $\ell$ and $C D$ are $H$ and $K$, respectively. Prove that the lines $E F$ and $H K$ are perpendicular.
|
The points $E, K, H, G$ are on the circle of diameter $G E$, so
$$
\angle E H K=\angle E G K
$$
Also, from $\angle D C A=\angle D B A$ and $\frac{C E}{C D}=\frac{B E}{B A}$ it follows
$$
\frac{C E}{C G}=\frac{2 C E}{C D}=\frac{2 B E}{B A}=\frac{B E}{B F},
$$
therefore $\triangle C G E \sim \triangle B F E$. In particular, $\angle E G C=\angle B F E$, so by $(\dagger)$
$$
\angle E H K=\angle B F E .
$$
But $H E \perp F B$ and so, since $F E$ and $H K$ are obtained by rotations of these lines by the same (directed) angle, $F E \perp H K$.


|
{
"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl",
"problem_match": "# PROBLEM 1",
"solution_match": "\nSolution."
}
|
f89c0e6d-4465-5955-b8ae-be529bb4869b
| 604,161
|
Given real numbers $x, y, z$ such that $x+y+z=0$, show that
$$
\frac{x(x+2)}{2 x^{2}+1}+\frac{y(y+2)}{2 y^{2}+1}+\frac{z(z+2)}{2 z^{2}+1} \geq 0 .
$$
When does equality hold?
|
The inequality is clear if $x y z=0$, in which case equality holds if and only if $x=y=z=0$.
Henceforth assume $x y z \neq 0$ and rewrite the inequality as
$$
\frac{(2 x+1)^{2}}{2 x^{2}+1}+\frac{(2 y+1)^{2}}{2 y^{2}+1}+\frac{(2 z+1)^{2}}{2 z^{2}+1} \geq 3 .
$$
Notice that (exactly) one of the products $x y, y z, z x$ is positive, say $y z>0$, to get
$$
\begin{array}{rlr}
\frac{(2 y+1)^{2}}{2 y^{2}+1}+\frac{(2 z+1)^{2}}{2 z^{2}+1} & \geq \frac{2(y+z+1)^{2}}{y^{2}+z^{2}+1} & \text { (by Jensen) } \\
& =\frac{2(x-1)^{2}}{x^{2}-2 y z+1} & (\text { for } x+y+z=0) \\
& \geq \frac{2(x-1)^{2}}{x^{2}+1} . & (\text { for } y z>0)
\end{array}
$$
Here equality holds if and only if $x=1$ and $y=z=-1 / 2$. Finally, since
$$
\frac{(2 x+1)^{2}}{2 x^{2}+1}+\frac{2(x-1)^{2}}{x^{2}+1}-3=\frac{2 x^{2}(x-1)^{2}}{\left(2 x^{2}+1\right)\left(x^{2}+1\right)} \geq 0, \quad x \in \mathbb{R},
$$
the conclusion follows. Clearly, equality holds if and only if $x=1$, so $y=z=-1 / 2$. Therefore, if $x y z \neq 0$, equality holds if and only if one of the numbers is 1 , and the other two are $-1 / 2$.
Marking Scheme. Proving the inequality and identifying the equality case when one of the variables vanishes
Applying Jensen or Cauchy-Schwarz inequality to the fractions involving the pair of numbers of the same sign 3p
Producing the corresponding lower bound in the third variable ................... 3p

Remark. Any partial or equivalent approach should be marked accordingly.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given real numbers $x, y, z$ such that $x+y+z=0$, show that
$$
\frac{x(x+2)}{2 x^{2}+1}+\frac{y(y+2)}{2 y^{2}+1}+\frac{z(z+2)}{2 z^{2}+1} \geq 0 .
$$
When does equality hold?
|
The inequality is clear if $x y z=0$, in which case equality holds if and only if $x=y=z=0$.
Henceforth assume $x y z \neq 0$ and rewrite the inequality as
$$
\frac{(2 x+1)^{2}}{2 x^{2}+1}+\frac{(2 y+1)^{2}}{2 y^{2}+1}+\frac{(2 z+1)^{2}}{2 z^{2}+1} \geq 3 .
$$
Notice that (exactly) one of the products $x y, y z, z x$ is positive, say $y z>0$, to get
$$
\begin{array}{rlr}
\frac{(2 y+1)^{2}}{2 y^{2}+1}+\frac{(2 z+1)^{2}}{2 z^{2}+1} & \geq \frac{2(y+z+1)^{2}}{y^{2}+z^{2}+1} & \text { (by Jensen) } \\
& =\frac{2(x-1)^{2}}{x^{2}-2 y z+1} & (\text { for } x+y+z=0) \\
& \geq \frac{2(x-1)^{2}}{x^{2}+1} . & (\text { for } y z>0)
\end{array}
$$
Here equality holds if and only if $x=1$ and $y=z=-1 / 2$. Finally, since
$$
\frac{(2 x+1)^{2}}{2 x^{2}+1}+\frac{2(x-1)^{2}}{x^{2}+1}-3=\frac{2 x^{2}(x-1)^{2}}{\left(2 x^{2}+1\right)\left(x^{2}+1\right)} \geq 0, \quad x \in \mathbb{R},
$$
the conclusion follows. Clearly, equality holds if and only if $x=1$, so $y=z=-1 / 2$. Therefore, if $x y z \neq 0$, equality holds if and only if one of the numbers is 1 , and the other two are $-1 / 2$.
Marking Scheme. Proving the inequality and identifying the equality case when one of the variables vanishes
Applying Jensen or Cauchy-Schwarz inequality to the fractions involving the pair of numbers of the same sign 3p
Producing the corresponding lower bound in the third variable ................... 3p

Remark. Any partial or equivalent approach should be marked accordingly.
|
{
"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl",
"problem_match": "# PROBLEM 2",
"solution_match": "\nSolution."
}
|
4cd97ab9-6970-5d06-9ffb-c65f1d1a2670
| 604,175
|
Let $S$ be a finite set of positive integers which has the following property: if $x$ is a member of $S$, then so are all positive divisors of $x$. A non-empty subset $T$ of $S$ is good if whenever $x, y \in T$ and $x<y$, the ratio $y / x$ is a power of a prime number. A non-empty subset $T$ of $S$ is bad if whenever $x, y \in T$ and $x<y$, the ratio $y / x$ is not a power of a prime number. We agree that a singleton subset of $S$ is both good and bad. Let $k$ be the largest possible size of a good subset of $S$. Prove that $k$ is also the smallest number of pairwise-disjoint bad subsets whose union is $S$.
|
Notice first that a bad subset of $S$ contains at most one element from a good one, to deduce that a partition of $S$ into bad subsets has at least as many members as a maximal good subset.
Notice further that the elements of a good subset of $S$ must be among the terms of a geometric sequence whose ratio is a prime: if $x<y<z$ are elements of a good subset of $S$, then $y=x p^{\alpha}$ and $z=y q^{\beta}=x p^{\alpha} q^{\beta}$ for some primes $p$ and $q$ and some positive integers $\alpha$ and $\beta$, so $p=q$ for $z / x$ to be a power of a prime.
Next, let $P=\{2,3,5,7,11, \cdots\}$ denote the set of all primes, let
$$
m=\max \left\{\exp _{p} x: x \in S \text { and } p \in P\right\}
$$
where $\exp _{p} x$ is the exponent of the prime $p$ in the canonical decomposition of $x$, and notice that a maximal good subset of $S$ must be of the form $\left\{a, a p, \cdots, a p^{m}\right\}$ for some prime $p$ and some positive integer $a$ which is not divisible by $p$. Consequently, a maximal good subset of $S$ has $m+1$ elements, so a partition of $S$ into bad subsets has at least $m+1$ members.
Finally, notice by maximality of $m$ that the sets
$$
S_{k}=\left\{x: x \in S \text { and } \sum_{p \in P} \exp _{p} x \equiv k(\bmod m+1)\right\}, \quad k=0,1, \cdots, m
$$
form a partition of $S$ into $m+1$ bad subsets. The conclusion follows.
 Considering the maximal exponent $m$ of a prime and deriving $k=m+1 \ldots \ldots \mathbf{1 p}$ Noticing that the intersection of a bad set and a good set contains at most one element and infering that a partition of $S$ into bad sets has at least $k$ members.....2p
Producing a partition of $S$ into $k$ bad subsets . . . . . . . . . . . . . . . . . . . . . . .
Remark. Any partial or equivalent approach should be marked accordingly.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a finite set of positive integers which has the following property: if $x$ is a member of $S$, then so are all positive divisors of $x$. A non-empty subset $T$ of $S$ is good if whenever $x, y \in T$ and $x<y$, the ratio $y / x$ is a power of a prime number. A non-empty subset $T$ of $S$ is bad if whenever $x, y \in T$ and $x<y$, the ratio $y / x$ is not a power of a prime number. We agree that a singleton subset of $S$ is both good and bad. Let $k$ be the largest possible size of a good subset of $S$. Prove that $k$ is also the smallest number of pairwise-disjoint bad subsets whose union is $S$.
|
Notice first that a bad subset of $S$ contains at most one element from a good one, to deduce that a partition of $S$ into bad subsets has at least as many members as a maximal good subset.
Notice further that the elements of a good subset of $S$ must be among the terms of a geometric sequence whose ratio is a prime: if $x<y<z$ are elements of a good subset of $S$, then $y=x p^{\alpha}$ and $z=y q^{\beta}=x p^{\alpha} q^{\beta}$ for some primes $p$ and $q$ and some positive integers $\alpha$ and $\beta$, so $p=q$ for $z / x$ to be a power of a prime.
Next, let $P=\{2,3,5,7,11, \cdots\}$ denote the set of all primes, let
$$
m=\max \left\{\exp _{p} x: x \in S \text { and } p \in P\right\}
$$
where $\exp _{p} x$ is the exponent of the prime $p$ in the canonical decomposition of $x$, and notice that a maximal good subset of $S$ must be of the form $\left\{a, a p, \cdots, a p^{m}\right\}$ for some prime $p$ and some positive integer $a$ which is not divisible by $p$. Consequently, a maximal good subset of $S$ has $m+1$ elements, so a partition of $S$ into bad subsets has at least $m+1$ members.
Finally, notice by maximality of $m$ that the sets
$$
S_{k}=\left\{x: x \in S \text { and } \sum_{p \in P} \exp _{p} x \equiv k(\bmod m+1)\right\}, \quad k=0,1, \cdots, m
$$
form a partition of $S$ into $m+1$ bad subsets. The conclusion follows.
 Considering the maximal exponent $m$ of a prime and deriving $k=m+1 \ldots \ldots \mathbf{1 p}$ Noticing that the intersection of a bad set and a good set contains at most one element and infering that a partition of $S$ into bad sets has at least $k$ members.....2p
Producing a partition of $S$ into $k$ bad subsets . . . . . . . . . . . . . . . . . . . . . . .
Remark. Any partial or equivalent approach should be marked accordingly.
|
{
"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl",
"problem_match": "# PROBLEM 3",
"solution_match": "\nSolution."
}
|
7e22dae2-c48e-5c68-a7b6-a13101d8f996
| 604,187
|
Let $A B C D E F$ be a convex hexagon of area 1 , whose opposite sides are parallel. The lines $A B, C D$ and $E F$ meet in pairs to determine the vertices of a triangle. Similarly, the lines $B C, D E$ and $F A$ meet in pairs to determine the vertices of another triangle. Show that the area of at least one of these two triangles is at least $3 / 2$.
|
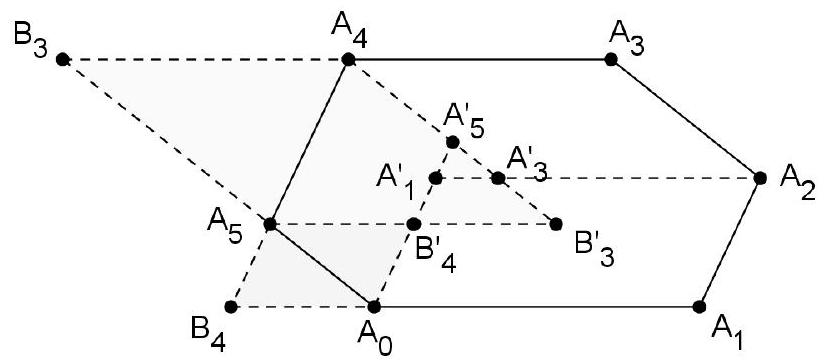
Unless otherwise stated, throughout the proof indices take on values from 0 to 5 and are reduced modulo 6 . Label the vertices of the hexagon in circular order, $A_{0}, A_{1}, \cdots, A_{5}$, and let the lines of support of the alternate sides $A_{i} A_{i+1}$ and $A_{i+2} A_{i+3}$ meet at $B_{i}$. To show that the area of at least one of the triangles $B_{0} B_{2} B_{4}, B_{1} B_{3} B_{5}$ is greater than or equal to $3 / 2$, it is sufficient to prove that the total area of the six triangles $A_{i+1} B_{i} A_{i+2}$ is at least 1:
$$
\sum_{i=0}^{5} \operatorname{area} A_{i+1} B_{i} A_{i+2} \geq 1
$$
To begin with, reflect each $B_{i}$ through the midpoint of the segment $A_{i+1} A_{i+2}$ to get the points $B_{i}^{\prime}$. We shall prove that the six triangles $A_{i+1} B_{i}^{\prime} A_{i+2}$ cover the hexagon. To this end, reflect $A_{2 i+1}$ through the midpoint of the segment $A_{2 i} A_{2 i+2}$ to get the points $A_{2 i+1}^{\prime}$, $i=0,1,2$. The hexagon splits into three parallelograms, $A_{2 i} A_{2 i+1} A_{2 i+2} A_{2 i+1}^{\prime}, i=0,1,2$, and a (possibly degenerate) triangle, $A_{1}^{\prime} A_{3}^{\prime} A_{5}^{\prime}$. Notice first that each parallelogram $A_{2 i} A_{2 i+1} A_{2 i+2} A_{2 i+1}^{\prime}$ is covered by the pair of triangles $\left(A_{2 i} B_{2 i+5}^{\prime} A_{2 i+1}, A_{2 i+1} B_{2 i}^{\prime} A_{2 i+2}\right)$, $i=0,1,2$. The proof is completed by showing that at least one of these pairs contains a triangle that covers the triangle $A_{1}^{\prime} A_{3}^{\prime} A_{5}^{\prime}$. To this end, it is sufficient to prove that $A_{2 i} B_{2 i+5}^{\prime} \geq A_{2 i} A_{2 i+5}^{\prime}$ and $A_{2 j+2} B_{2 j}^{\prime} \geq A_{2 j+2} A_{2 j+3}^{\prime}$ for some indices $i, j \in\{0,1,2\}$. To establish the first inequality, notice that
$$
\begin{gathered}
A_{2 i} B_{2 i+5}^{\prime}=A_{2 i+1} B_{2 i+5}, \quad A_{2 i} A_{2 i+5}^{\prime}=A_{2 i+4} A_{2 i+5}, \quad i=0,1,2, \\
\\
\frac{A_{1} B_{5}}{A_{4} A_{5}}=\frac{A_{0} B_{5}}{A_{5} B_{3}} \quad \text { and } \quad \frac{A_{3} B_{1}}{A_{0} A_{1}}=\frac{A_{2} A_{3}}{A_{0} B_{5}},
\end{gathered}
$$
to get
$$
\prod_{i=0}^{2} \frac{A_{2 i} B_{2 i+5}^{\prime}}{A_{2 i} A_{2 i+5}^{\prime}}=1
$$
Similarly,
$$
\prod_{j=0}^{2} \frac{A_{2 j+2} B_{2 j}^{\prime}}{A_{2 j+2} A_{2 j+3}^{\prime}}=1
$$
whence the conclusion.
Marking Scheme. Stating that the total area of the small triangles $\geq 1 \ldots \ldots . . \mathbf{1 p}$
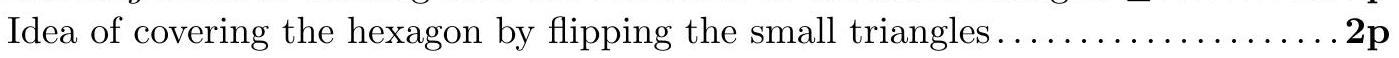
Decomposition of the hexagon into three adequate parallelograms and a triangle $\mathbf{1 p}$
Proving that each pair of triangles adjacent to a parallelogram covers that parallelogram
Proving the central triangle also covered 5p
Remark. Any partial or equivalent approach should be marked accordingly.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon of area 1 , whose opposite sides are parallel. The lines $A B, C D$ and $E F$ meet in pairs to determine the vertices of a triangle. Similarly, the lines $B C, D E$ and $F A$ meet in pairs to determine the vertices of another triangle. Show that the area of at least one of these two triangles is at least $3 / 2$.
|
Unless otherwise stated, throughout the proof indices take on values from 0 to 5 and are reduced modulo 6 . Label the vertices of the hexagon in circular order, $A_{0}, A_{1}, \cdots, A_{5}$, and let the lines of support of the alternate sides $A_{i} A_{i+1}$ and $A_{i+2} A_{i+3}$ meet at $B_{i}$. To show that the area of at least one of the triangles $B_{0} B_{2} B_{4}, B_{1} B_{3} B_{5}$ is greater than or equal to $3 / 2$, it is sufficient to prove that the total area of the six triangles $A_{i+1} B_{i} A_{i+2}$ is at least 1:
$$
\sum_{i=0}^{5} \operatorname{area} A_{i+1} B_{i} A_{i+2} \geq 1
$$
To begin with, reflect each $B_{i}$ through the midpoint of the segment $A_{i+1} A_{i+2}$ to get the points $B_{i}^{\prime}$. We shall prove that the six triangles $A_{i+1} B_{i}^{\prime} A_{i+2}$ cover the hexagon. To this end, reflect $A_{2 i+1}$ through the midpoint of the segment $A_{2 i} A_{2 i+2}$ to get the points $A_{2 i+1}^{\prime}$, $i=0,1,2$. The hexagon splits into three parallelograms, $A_{2 i} A_{2 i+1} A_{2 i+2} A_{2 i+1}^{\prime}, i=0,1,2$, and a (possibly degenerate) triangle, $A_{1}^{\prime} A_{3}^{\prime} A_{5}^{\prime}$. Notice first that each parallelogram $A_{2 i} A_{2 i+1} A_{2 i+2} A_{2 i+1}^{\prime}$ is covered by the pair of triangles $\left(A_{2 i} B_{2 i+5}^{\prime} A_{2 i+1}, A_{2 i+1} B_{2 i}^{\prime} A_{2 i+2}\right)$, $i=0,1,2$. The proof is completed by showing that at least one of these pairs contains a triangle that covers the triangle $A_{1}^{\prime} A_{3}^{\prime} A_{5}^{\prime}$. To this end, it is sufficient to prove that $A_{2 i} B_{2 i+5}^{\prime} \geq A_{2 i} A_{2 i+5}^{\prime}$ and $A_{2 j+2} B_{2 j}^{\prime} \geq A_{2 j+2} A_{2 j+3}^{\prime}$ for some indices $i, j \in\{0,1,2\}$. To establish the first inequality, notice that
$$
\begin{gathered}
A_{2 i} B_{2 i+5}^{\prime}=A_{2 i+1} B_{2 i+5}, \quad A_{2 i} A_{2 i+5}^{\prime}=A_{2 i+4} A_{2 i+5}, \quad i=0,1,2, \\
\\
\frac{A_{1} B_{5}}{A_{4} A_{5}}=\frac{A_{0} B_{5}}{A_{5} B_{3}} \quad \text { and } \quad \frac{A_{3} B_{1}}{A_{0} A_{1}}=\frac{A_{2} A_{3}}{A_{0} B_{5}},
\end{gathered}
$$
to get
$$
\prod_{i=0}^{2} \frac{A_{2 i} B_{2 i+5}^{\prime}}{A_{2 i} A_{2 i+5}^{\prime}}=1
$$
Similarly,
$$
\prod_{j=0}^{2} \frac{A_{2 j+2} B_{2 j}^{\prime}}{A_{2 j+2} A_{2 j+3}^{\prime}}=1
$$
whence the conclusion.

Marking Scheme. Stating that the total area of the small triangles $\geq 1 \ldots \ldots . . \mathbf{1 p}$
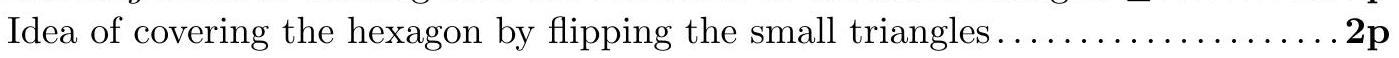
Decomposition of the hexagon into three adequate parallelograms and a triangle $\mathbf{1 p}$
Proving that each pair of triangles adjacent to a parallelogram covers that parallelogram
Proving the central triangle also covered 5p
Remark. Any partial or equivalent approach should be marked accordingly.
|
{
"resource_path": "Balkan_MO/segmented/en-2011-BMO-type1.jsonl",
"problem_match": "# PROBLEM 4",
"solution_match": "\nSolution."
}
|
a9756494-36d3-5f6c-86db-46a9b48f012d
| 604,201
|
\quad$ Let $A, B$ and $C$ be points lying on a circle $\Gamma$ with centre $O$. Assume that $\angle A B C>90$. Let $D$ be the point of intersection of the line $A B$ with the line perpendicular to $A C$ at $C$. Let $l$ be the line through $D$ which is perpendicular to $A O$. Let $E$ be the point of intersection of $l$ with the line $A C$, and let $F$ be the point of intersection of $\Gamma$ with $l$ that lies between $D$ and $E$.
Prove that the circumcircles of triangles $B F E$ and $C F D$ are tangent at $F$.
|
Let $\ell \cap A O=\{K\}$ and $G$ be the other end point of the diameter of $\Gamma$ through $A$. Then $D, C, G$ are collinear. Moreover, $E$ is the orthocenter of triangle $A D G$. Therefore $G E \perp A D$ and $G, E, B$ are collinear.
As $\angle C D F=\angle G D K=\angle G A C=\angle G F C, F G$ is tangent to the circumcircle of triangle $C F D$ at $F$. As $\angle F B E=\angle F B G=\angle F A G=\angle G F K=\angle G F E, F G$ is also tangent to the circumcircle of $B F E$ at $F$. Hence the circumcircles of the triangles $C F D$ and $B F E$ are tangent at $F$.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
\quad$ Let $A, B$ and $C$ be points lying on a circle $\Gamma$ with centre $O$. Assume that $\angle A B C>90$. Let $D$ be the point of intersection of the line $A B$ with the line perpendicular to $A C$ at $C$. Let $l$ be the line through $D$ which is perpendicular to $A O$. Let $E$ be the point of intersection of $l$ with the line $A C$, and let $F$ be the point of intersection of $\Gamma$ with $l$ that lies between $D$ and $E$.
Prove that the circumcircles of triangles $B F E$ and $C F D$ are tangent at $F$.
|
Let $\ell \cap A O=\{K\}$ and $G$ be the other end point of the diameter of $\Gamma$ through $A$. Then $D, C, G$ are collinear. Moreover, $E$ is the orthocenter of triangle $A D G$. Therefore $G E \perp A D$ and $G, E, B$ are collinear.

As $\angle C D F=\angle G D K=\angle G A C=\angle G F C, F G$ is tangent to the circumcircle of triangle $C F D$ at $F$. As $\angle F B E=\angle F B G=\angle F A G=\angle G F K=\angle G F E, F G$ is also tangent to the circumcircle of $B F E$ at $F$. Hence the circumcircles of the triangles $C F D$ and $B F E$ are tangent at $F$.

|
{
"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution."
}
|
8ad74077-a892-5b78-8b16-c68a5f491b10
| 604,215
|
Prove that
$$
\sum_{c y c}(x+y) \sqrt{(z+x)(z+y)} \geq 4(x y+y z+z x),
$$
for all positive real numbers $x, y$ and $z$.
|
We will obtain the inequality by adding the inequalities
$$
(x+y) \sqrt{(z+x)(z+y)} \geq 2 x y+y z+z x
$$
for cyclic permutation of $x, y, z$.
Squaring both sides of this inequality we obtain
$$
(x+y)^{2}(z+x)(z+y) \geq 4 x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}+4 x y^{2} z+4 x^{2} y z+2 x y z^{2}
$$
which is equivalent to
$$
x^{3} y+x y^{3}+z\left(x^{3}+y^{3}\right) \geq 2 x^{2} y^{2}+x y z(x+y)
$$
which can be rearranged to
$$
(x y+y z+z x)(x-y)^{2} \geq 0
$$
which is clearly true.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that
$$
\sum_{c y c}(x+y) \sqrt{(z+x)(z+y)} \geq 4(x y+y z+z x),
$$
for all positive real numbers $x, y$ and $z$.
|
We will obtain the inequality by adding the inequalities
$$
(x+y) \sqrt{(z+x)(z+y)} \geq 2 x y+y z+z x
$$
for cyclic permutation of $x, y, z$.
Squaring both sides of this inequality we obtain
$$
(x+y)^{2}(z+x)(z+y) \geq 4 x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}+4 x y^{2} z+4 x^{2} y z+2 x y z^{2}
$$
which is equivalent to
$$
x^{3} y+x y^{3}+z\left(x^{3}+y^{3}\right) \geq 2 x^{2} y^{2}+x y z(x+y)
$$
which can be rearranged to
$$
(x y+y z+z x)(x-y)^{2} \geq 0
$$
which is clearly true.
|
{
"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution 1."
}
|
36d8b6b0-4757-56f8-81f8-55a19f290550
| 604,232
|
Prove that
$$
\sum_{c y c}(x+y) \sqrt{(z+x)(z+y)} \geq 4(x y+y z+z x),
$$
for all positive real numbers $x, y$ and $z$.
|
For positive real numbers $x, y, z$ there exists a triangle with the side lengths $\sqrt{x+y}, \sqrt{y+z}, \sqrt{z+x}$ and the area $K=\sqrt{x y+y z+z x} / 2$.
The existence of the triangle is clear by simple checking of the triangle inequality. To prove the area formula, we have
$$
K=\frac{1}{2} \sqrt{x+y} \sqrt{z+x} \sin \alpha
$$
where $\alpha$ is the angle between the sides of length $\sqrt{x+y}$ and $\sqrt{z+x}$. On the other hand, from the law of cosines we have
$$
\cos \alpha=\frac{x+y+z+x-y-z}{2 \sqrt{(x+y)(z+x)}}=\frac{x}{\sqrt{(x+y)(z+x)}}
$$
and
$$
\sin \alpha=\sqrt{1-\cos ^{2} \alpha}=\frac{\sqrt{x y+y z+z x}}{\sqrt{(x+y)(z+x)}}
$$
Now the inequality is equivalent to
$$
\sqrt{x+y} \sqrt{y+z} \sqrt{z+x} \sum_{c y c} \sqrt{x+y} \geq 16 K^{2}
$$
This can be rewritten as
$$
\frac{\sqrt{x+y} \sqrt{y+z} \sqrt{z+x}}{4 K} \geq 2 \frac{K}{\sum_{c y c} \sqrt{x+y} / 2}
$$
to become the Euler inequality $R \geq 2 r$.

|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that
$$
\sum_{c y c}(x+y) \sqrt{(z+x)(z+y)} \geq 4(x y+y z+z x),
$$
for all positive real numbers $x, y$ and $z$.
|
For positive real numbers $x, y, z$ there exists a triangle with the side lengths $\sqrt{x+y}, \sqrt{y+z}, \sqrt{z+x}$ and the area $K=\sqrt{x y+y z+z x} / 2$.
The existence of the triangle is clear by simple checking of the triangle inequality. To prove the area formula, we have
$$
K=\frac{1}{2} \sqrt{x+y} \sqrt{z+x} \sin \alpha
$$
where $\alpha$ is the angle between the sides of length $\sqrt{x+y}$ and $\sqrt{z+x}$. On the other hand, from the law of cosines we have
$$
\cos \alpha=\frac{x+y+z+x-y-z}{2 \sqrt{(x+y)(z+x)}}=\frac{x}{\sqrt{(x+y)(z+x)}}
$$
and
$$
\sin \alpha=\sqrt{1-\cos ^{2} \alpha}=\frac{\sqrt{x y+y z+z x}}{\sqrt{(x+y)(z+x)}}
$$
Now the inequality is equivalent to
$$
\sqrt{x+y} \sqrt{y+z} \sqrt{z+x} \sum_{c y c} \sqrt{x+y} \geq 16 K^{2}
$$
This can be rewritten as
$$
\frac{\sqrt{x+y} \sqrt{y+z} \sqrt{z+x}}{4 K} \geq 2 \frac{K}{\sum_{c y c} \sqrt{x+y} / 2}
$$
to become the Euler inequality $R \geq 2 r$.

|
{
"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution 2."
}
|
36d8b6b0-4757-56f8-81f8-55a19f290550
| 604,232
|
Let $n$ be a positive integer. Let $P_{n}=\left\{2^{n}, 2^{n-1} \cdot 3,2^{n-2} \cdot 3^{2}, \ldots, 3^{n}\right\}$. For each subset $X$ of $P_{n}$, we write $S_{X}$ for the sum of all elements of $X$, with the convention that $S_{\emptyset}=0$ where $\emptyset$ is the empty set. Suppose that $y$ is a real number with $0 \leq y \leq 3^{n+1}-2^{n+1}$. Prove that there is a subset $Y$ of $P_{n}$ such that $0 \leq y-S_{Y}<2^{n}$
|
Let $\alpha=3 / 2$ so $1+\alpha>\alpha^{2}$.
Given $y$, we construct $Y$ algorithmically. Let $Y=\varnothing$ and of course $S_{\varnothing}=0$. For $i=0$ to $m$, perform the following operation:
$$
\text { If } S_{Y}+2^{i} 3^{m-i} \leq y \text {, then replace } Y \text { by } Y \cup\left\{2^{i} 3^{m-i}\right\}
$$
When this process is finished, we have a subset $Y$ of $P_{m}$ such that $S_{Y} \leq y$.
Notice that the elements of $P_{m}$ are in ascending order of size as given, and may alternatively be described as $2^{m}, 2^{m} \alpha, 2^{m} \alpha^{2}, \ldots, 2^{m} \alpha^{m}$. If any member of this list is not in $Y$, then no two consecutive members of the list to the left of the omitted member can both be in $Y$. This is because $1+\alpha>\alpha^{2}$, and the greedy nature of the process used to construct $Y$.
Therefore either $Y=P_{m}$, in which case $y=3^{m+1}-2^{m+1}$ and all is well, or at least one of the two leftmost elements of the list is omitted from $Y$.
If $2^{m}$ is not omitted from $Y$, then the algorithmic process ensures that $\left(S_{Y}-2^{m}\right)+2^{m-1} 3>y$, and so $y-S_{Y}<2^{m}$. On the other hand, if $2^{m}$ is omitted from $Y$, then $y-S_{Y}<2^{m}$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Let $P_{n}=\left\{2^{n}, 2^{n-1} \cdot 3,2^{n-2} \cdot 3^{2}, \ldots, 3^{n}\right\}$. For each subset $X$ of $P_{n}$, we write $S_{X}$ for the sum of all elements of $X$, with the convention that $S_{\emptyset}=0$ where $\emptyset$ is the empty set. Suppose that $y$ is a real number with $0 \leq y \leq 3^{n+1}-2^{n+1}$. Prove that there is a subset $Y$ of $P_{n}$ such that $0 \leq y-S_{Y}<2^{n}$
|
Let $\alpha=3 / 2$ so $1+\alpha>\alpha^{2}$.
Given $y$, we construct $Y$ algorithmically. Let $Y=\varnothing$ and of course $S_{\varnothing}=0$. For $i=0$ to $m$, perform the following operation:
$$
\text { If } S_{Y}+2^{i} 3^{m-i} \leq y \text {, then replace } Y \text { by } Y \cup\left\{2^{i} 3^{m-i}\right\}
$$
When this process is finished, we have a subset $Y$ of $P_{m}$ such that $S_{Y} \leq y$.
Notice that the elements of $P_{m}$ are in ascending order of size as given, and may alternatively be described as $2^{m}, 2^{m} \alpha, 2^{m} \alpha^{2}, \ldots, 2^{m} \alpha^{m}$. If any member of this list is not in $Y$, then no two consecutive members of the list to the left of the omitted member can both be in $Y$. This is because $1+\alpha>\alpha^{2}$, and the greedy nature of the process used to construct $Y$.
Therefore either $Y=P_{m}$, in which case $y=3^{m+1}-2^{m+1}$ and all is well, or at least one of the two leftmost elements of the list is omitted from $Y$.
If $2^{m}$ is not omitted from $Y$, then the algorithmic process ensures that $\left(S_{Y}-2^{m}\right)+2^{m-1} 3>y$, and so $y-S_{Y}<2^{m}$. On the other hand, if $2^{m}$ is omitted from $Y$, then $y-S_{Y}<2^{m}$ ).
|
{
"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution 1."
}
|
c43dfea6-df01-5761-9e08-5cb6650d2b24
| 604,248
|
Let $n$ be a positive integer. Let $P_{n}=\left\{2^{n}, 2^{n-1} \cdot 3,2^{n-2} \cdot 3^{2}, \ldots, 3^{n}\right\}$. For each subset $X$ of $P_{n}$, we write $S_{X}$ for the sum of all elements of $X$, with the convention that $S_{\emptyset}=0$ where $\emptyset$ is the empty set. Suppose that $y$ is a real number with $0 \leq y \leq 3^{n+1}-2^{n+1}$. Prove that there is a subset $Y$ of $P_{n}$ such that $0 \leq y-S_{Y}<2^{n}$
|
Note that $3^{m+1}-2^{m+1}=(3-2)\left(3^{m}+3^{m-1} \cdot 2+\cdots+3 \cdot 2^{m-1}+2^{m}\right)=S_{P_{m}}$. Dividing every element of $P_{m}$ by $2^{m}$ gives us the following equivalent problem:
Let $m$ be a positive integer, $a=3 / 2$, and $Q_{m}=\left\{1, a, a^{2}, \ldots, a^{m}\right\}$. Show that for any real number $x$ satisfying $0 \leq x \leq 1+a+a^{2}+\cdots+a^{m}$, there exists a subset $X$ of $Q_{m}$ such that $0 \leq x-S_{X}<1$.
We will prove this problem by induction on $m$. When $m=1, S_{\varnothing}=0, S_{\{1\}}=1, S_{\{a\}}=3 / 2$, $S_{\{1, a\}}=5 / 2$. Since the difference between any two consecutive of them is at most 1, the claim is true.
Suppose that the statement is true for positive integer $m$. Let $x$ be a real number with $0 \leq$ $x \leq 1+a+a^{2}+\cdots+a^{m+1}$. If $0 \leq x \leq 1+a+a^{2}+\cdots+a^{m}$, then by the induction hypothesis there exists a subset $X$ of $Q_{m} \subset Q_{m+1}$ such that $0 \leq x-S_{X}<1$.
If $\frac{a^{m+1}-1}{a-1}=1+a+a^{2}+\cdots+a^{m}<x$, then $x>a^{m+1}$ as
$$
\frac{a^{m+1}-1}{a-1}=2\left(a^{m+1}-1\right)=a^{m+1}+\left(a^{m+1}-2\right) \geq a^{m+1}+a^{2}-2=a^{m+1}+\frac{1}{4} .
$$
Therefore $0<\left(x-a^{m+1}\right) \leq 1+a+a^{2}+\cdots+a^{m}$. Again by the induction hypothesis, there exists a subset $X$ of $Q_{m}$ satisfying $0 \leq\left(x-a^{m+1}\right)-S_{X}<1$. Hence $0 \leq x-S_{X^{\prime}}<1$ where $X^{\prime}=X \cup\left\{a^{m+1}\right\} \subset Q_{m+1}$.

|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Let $P_{n}=\left\{2^{n}, 2^{n-1} \cdot 3,2^{n-2} \cdot 3^{2}, \ldots, 3^{n}\right\}$. For each subset $X$ of $P_{n}$, we write $S_{X}$ for the sum of all elements of $X$, with the convention that $S_{\emptyset}=0$ where $\emptyset$ is the empty set. Suppose that $y$ is a real number with $0 \leq y \leq 3^{n+1}-2^{n+1}$. Prove that there is a subset $Y$ of $P_{n}$ such that $0 \leq y-S_{Y}<2^{n}$
|
Note that $3^{m+1}-2^{m+1}=(3-2)\left(3^{m}+3^{m-1} \cdot 2+\cdots+3 \cdot 2^{m-1}+2^{m}\right)=S_{P_{m}}$. Dividing every element of $P_{m}$ by $2^{m}$ gives us the following equivalent problem:
Let $m$ be a positive integer, $a=3 / 2$, and $Q_{m}=\left\{1, a, a^{2}, \ldots, a^{m}\right\}$. Show that for any real number $x$ satisfying $0 \leq x \leq 1+a+a^{2}+\cdots+a^{m}$, there exists a subset $X$ of $Q_{m}$ such that $0 \leq x-S_{X}<1$.
We will prove this problem by induction on $m$. When $m=1, S_{\varnothing}=0, S_{\{1\}}=1, S_{\{a\}}=3 / 2$, $S_{\{1, a\}}=5 / 2$. Since the difference between any two consecutive of them is at most 1, the claim is true.
Suppose that the statement is true for positive integer $m$. Let $x$ be a real number with $0 \leq$ $x \leq 1+a+a^{2}+\cdots+a^{m+1}$. If $0 \leq x \leq 1+a+a^{2}+\cdots+a^{m}$, then by the induction hypothesis there exists a subset $X$ of $Q_{m} \subset Q_{m+1}$ such that $0 \leq x-S_{X}<1$.
If $\frac{a^{m+1}-1}{a-1}=1+a+a^{2}+\cdots+a^{m}<x$, then $x>a^{m+1}$ as
$$
\frac{a^{m+1}-1}{a-1}=2\left(a^{m+1}-1\right)=a^{m+1}+\left(a^{m+1}-2\right) \geq a^{m+1}+a^{2}-2=a^{m+1}+\frac{1}{4} .
$$
Therefore $0<\left(x-a^{m+1}\right) \leq 1+a+a^{2}+\cdots+a^{m}$. Again by the induction hypothesis, there exists a subset $X$ of $Q_{m}$ satisfying $0 \leq\left(x-a^{m+1}\right)-S_{X}<1$. Hence $0 \leq x-S_{X^{\prime}}<1$ where $X^{\prime}=X \cup\left\{a^{m+1}\right\} \subset Q_{m+1}$.

|
{
"resource_path": "Balkan_MO/segmented/en-2012-BMO-type3.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution 2."
}
|
c43dfea6-df01-5761-9e08-5cb6650d2b24
| 604,248
|
In a mathematical competition some competitors are friends; friendship is always mutual, that is to say that when $A$ is a friend of $B$, then also $B$ is a friend of $A$. We say that $n \geq 3$ different competitors $A_{1}, A_{2}, \ldots, A_{n}$ form a weakly-friendly cycle if $A_{i}$ is not a friend of $A_{i+1}$ for $1 \leq i \leq n\left(A_{n+1}=A_{1}\right)$, and there are no other pairs of non-friends among the components of this cycle.
The following property is satisfied:
for every competitor $C$, and every weakly-friendly cycle $\mathscr{S}$ of competitors not including $C$, the set of competitors $D$ in $\mathscr{S}$ which are not friends of $C$ has at most one element.
Prove that all competitors of this mathematical competition can be arranged into three rooms, such that every two competitors that are in the same room are friends.
(Serbia)
Time allowed: 270 minutes.
Each problem is worth 10 points.
## SOLUTIONS
|
Consider the graph $\mathcal{G}$ whose vertices are the contestants, where there is an edge between two contestants if and only if they are not friends.
Lemma. There is a vertex in graph $\mathcal{G}$ with degree at most 2 .
Proof. Suppose that each vertex has a degree at least three. Consider the longest induced path $P=u_{0} u_{1} u_{2} \ldots u_{k}$ in the graph (that is, the path in which no two nonadjacent vertices are connected by an edge). The vertex $u_{0}$ is connected to another two vertices $v$ and $w$, which must be outside the path $P$. Since $P$ is the longest induced path, $v$ and $w$ have neighbors in it. Let $u_{i}$ and $u_{j}$ be the neighbors of $v$ and $w$ respectively with the smallest $i$ and $j$; assume without loss of generality that $i \geq j$. Then $u_{0}, u_{1}, \ldots, u_{i}, v$ form a weakly friendly cycle, but $w$ has two neighbors in it ( $u_{0}$ and $u_{j}$ ), a contradiction.
We now prove the problem statement by induction on the number $n$ of vertices in $\mathcal{G}$. For $n \leq 3$ the statement is trivial; assume that it holds for $n-1$. By the Lemma, there is a vertex $v$ in $\mathcal{G}$ of degree at most two. Graph $\mathcal{G}^{\prime}$, obtained by removing vertex $v$ (and all edges incident to it), clearly satisfies the problem conditions, so its vertices can be partitioned into three rooms in a desired way. Since $v$ has no neighbors in at least one of the rooms, we can place $v$ in that room, finishing the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a mathematical competition some competitors are friends; friendship is always mutual, that is to say that when $A$ is a friend of $B$, then also $B$ is a friend of $A$. We say that $n \geq 3$ different competitors $A_{1}, A_{2}, \ldots, A_{n}$ form a weakly-friendly cycle if $A_{i}$ is not a friend of $A_{i+1}$ for $1 \leq i \leq n\left(A_{n+1}=A_{1}\right)$, and there are no other pairs of non-friends among the components of this cycle.
The following property is satisfied:
for every competitor $C$, and every weakly-friendly cycle $\mathscr{S}$ of competitors not including $C$, the set of competitors $D$ in $\mathscr{S}$ which are not friends of $C$ has at most one element.
Prove that all competitors of this mathematical competition can be arranged into three rooms, such that every two competitors that are in the same room are friends.
(Serbia)
Time allowed: 270 minutes.
Each problem is worth 10 points.
## SOLUTIONS
|
Consider the graph $\mathcal{G}$ whose vertices are the contestants, where there is an edge between two contestants if and only if they are not friends.
Lemma. There is a vertex in graph $\mathcal{G}$ with degree at most 2 .
Proof. Suppose that each vertex has a degree at least three. Consider the longest induced path $P=u_{0} u_{1} u_{2} \ldots u_{k}$ in the graph (that is, the path in which no two nonadjacent vertices are connected by an edge). The vertex $u_{0}$ is connected to another two vertices $v$ and $w$, which must be outside the path $P$. Since $P$ is the longest induced path, $v$ and $w$ have neighbors in it. Let $u_{i}$ and $u_{j}$ be the neighbors of $v$ and $w$ respectively with the smallest $i$ and $j$; assume without loss of generality that $i \geq j$. Then $u_{0}, u_{1}, \ldots, u_{i}, v$ form a weakly friendly cycle, but $w$ has two neighbors in it ( $u_{0}$ and $u_{j}$ ), a contradiction.
We now prove the problem statement by induction on the number $n$ of vertices in $\mathcal{G}$. For $n \leq 3$ the statement is trivial; assume that it holds for $n-1$. By the Lemma, there is a vertex $v$ in $\mathcal{G}$ of degree at most two. Graph $\mathcal{G}^{\prime}$, obtained by removing vertex $v$ (and all edges incident to it), clearly satisfies the problem conditions, so its vertices can be partitioned into three rooms in a desired way. Since $v$ has no neighbors in at least one of the rooms, we can place $v$ in that room, finishing the proof.
|
{
"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl",
"problem_match": "\n4.",
"solution_match": "\n4."
}
|
2dd7b8ff-3346-5ccf-8ce1-adb515f40080
| 604,325
|
Let $x, y$ and $z$ be positive real numbers such that $x y+y z+z x=3 x y z$. Prove that
$$
x^{2} y+y^{2} z+z^{2} x \geq 2(x+y+z)-3
$$
and determine when equality holds.
|
The given condition can be rearranged to $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=3$. Using this, we obtain:
$$
\begin{aligned}
x^{2} y+y^{2} z+z^{2} x-2(x+y+z)+3 & =x^{2} y-2 x+\frac{1}{y}+y^{2} z-2 y+\frac{1}{z}+z^{2} x-2 x+\frac{1}{x}= \\
& =y\left(x-\frac{1}{y}\right)^{2}+z\left(y-\frac{1}{z}\right)^{2}+x\left(z-\frac{1}{z}\right)^{2} \geq 0
\end{aligned}
$$
Equality holds if and only if we have $x y=y z=z x=1$, or, in other words, $x=y=z=1$.
Alternative solution. It follows from $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=3$ and Cauchy-Schwarz inequality that
$$
\begin{aligned}
3\left(x^{2} y+y^{2} z+z^{2} x\right) & =\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\left(x^{2} y+y^{2} z+z^{2} x\right) \\
& \left.=\left(\left(\frac{1}{\sqrt{y}}\right)^{2}+\left(\frac{1}{\sqrt{z}}\right)^{2}+\left(\frac{1}{\sqrt{x}}\right)^{2}\right)\left((x \sqrt{y})^{2}\right)+(y \sqrt{z})^{2}+(z \sqrt{x})^{2}\right) \\
& \geq(x+y+z)^{2}
\end{aligned}
$$
Therefore, $x^{2} y+y^{2} z+z^{2} x \geq \frac{(x+y+z)^{2}}{3}$ and if $x+y+z=t$ it suffices to show that $\frac{t^{2}}{3} \geq 2 t-3$. The latter is equivalent to $(t-3)^{2} \geq 0$. Equality holds when
$$
x \sqrt{y} \sqrt{y}=y \sqrt{z} \sqrt{z}=z \sqrt{x} \sqrt{x},
$$
i.e. $x y=y z=z x$ and $t=x+y+z=3$. Hence, $x=y=z=1$.
Comment. The inequality is true with the condition $x y+y z+z x \leq 3 x y z$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $x y+y z+z x=3 x y z$. Prove that
$$
x^{2} y+y^{2} z+z^{2} x \geq 2(x+y+z)-3
$$
and determine when equality holds.
|
The given condition can be rearranged to $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=3$. Using this, we obtain:
$$
\begin{aligned}
x^{2} y+y^{2} z+z^{2} x-2(x+y+z)+3 & =x^{2} y-2 x+\frac{1}{y}+y^{2} z-2 y+\frac{1}{z}+z^{2} x-2 x+\frac{1}{x}= \\
& =y\left(x-\frac{1}{y}\right)^{2}+z\left(y-\frac{1}{z}\right)^{2}+x\left(z-\frac{1}{z}\right)^{2} \geq 0
\end{aligned}
$$
Equality holds if and only if we have $x y=y z=z x=1$, or, in other words, $x=y=z=1$.
Alternative solution. It follows from $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=3$ and Cauchy-Schwarz inequality that
$$
\begin{aligned}
3\left(x^{2} y+y^{2} z+z^{2} x\right) & =\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\left(x^{2} y+y^{2} z+z^{2} x\right) \\
& \left.=\left(\left(\frac{1}{\sqrt{y}}\right)^{2}+\left(\frac{1}{\sqrt{z}}\right)^{2}+\left(\frac{1}{\sqrt{x}}\right)^{2}\right)\left((x \sqrt{y})^{2}\right)+(y \sqrt{z})^{2}+(z \sqrt{x})^{2}\right) \\
& \geq(x+y+z)^{2}
\end{aligned}
$$
Therefore, $x^{2} y+y^{2} z+z^{2} x \geq \frac{(x+y+z)^{2}}{3}$ and if $x+y+z=t$ it suffices to show that $\frac{t^{2}}{3} \geq 2 t-3$. The latter is equivalent to $(t-3)^{2} \geq 0$. Equality holds when
$$
x \sqrt{y} \sqrt{y}=y \sqrt{z} \sqrt{z}=z \sqrt{x} \sqrt{x},
$$
i.e. $x y=y z=z x$ and $t=x+y+z=3$. Hence, $x=y=z=1$.
Comment. The inequality is true with the condition $x y+y z+z x \leq 3 x y z$.
|
{
"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
eb0844f2-1223-523a-9ddd-c2697944cf95
| 604,335
|
A special number is a positive integer $n$ for which there exist positive integers $a, b, c$ and $d$ with
$$
n=\frac{a^{3}+2 b^{3}}{c^{3}+2 d^{3}}
$$
Prove that:
(a) there are infinitely many special numbers;
(b) 2014 is not a special number.
|
(a) Every perfect cube $k^{3}$ of a positive integer is special because we can write
$$
k^{3}=k^{3} \frac{a^{3}+2 b^{3}}{a^{3}+2 b^{3}}=\frac{(k a)^{3}+2(k b)^{3}}{a^{3}+2 b^{3}}
$$
for some positive integers $a, b$.
(b) Observe that $2014=2.19 .53$. If 2014 is special, then we have,
$$
x^{3}+2 y^{3}=2014\left(u^{3}+2 v^{3}\right)
$$
for some positive integers $x, y, u, v$. We may assume that $x^{3}+2 y^{3}$ is minimal with this property. Now, we will use the fact that if 19 divides $x^{3}+2 y^{3}$, then it divides both $x$ and $y$. Indeed, if 19 does not divide $x$, then it does not divide $y$ too. The relation $x^{3} \equiv-2 y^{3}(\bmod 19)$ implies $\left(x^{3}\right)^{6} \equiv\left(-2 y^{3}\right)^{6}(\bmod 19)$. The latter congruence is equivalent to $x^{18} \equiv 2^{6} y^{18}(\bmod 19)$. Now, according to the Fermat's Little Theorem, we obtain $1 \equiv 2^{6}(\bmod 19)$, that is 19 divides 63 , not possible.
It follows $x=19 x_{1}, y=19 y_{1}$, for some positive integers $x_{1}$ and $y_{1}$. Replacing in (1) we get
$$
19^{2}\left(x_{1}^{3}+2 y_{1}^{3}\right)=2.53\left(u^{3}+2 v^{3}\right)
$$
i.e. $19 \mid u^{3}+2 v^{3}$. It follows $u=19 u_{1}$ and $v=19 v_{1}$, and replacing in (2) we get
$$
x_{1}^{3}+2 y_{1}^{3}=2014\left(u_{1}^{3}+2 v_{1}^{3}\right) .
$$
Clearly, $x_{1}^{3}+2 y_{1}^{3}<x^{3}+2 y^{3}$, contradicting the minimality of $x^{3}+2 y^{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A special number is a positive integer $n$ for which there exist positive integers $a, b, c$ and $d$ with
$$
n=\frac{a^{3}+2 b^{3}}{c^{3}+2 d^{3}}
$$
Prove that:
(a) there are infinitely many special numbers;
(b) 2014 is not a special number.
|
(a) Every perfect cube $k^{3}$ of a positive integer is special because we can write
$$
k^{3}=k^{3} \frac{a^{3}+2 b^{3}}{a^{3}+2 b^{3}}=\frac{(k a)^{3}+2(k b)^{3}}{a^{3}+2 b^{3}}
$$
for some positive integers $a, b$.
(b) Observe that $2014=2.19 .53$. If 2014 is special, then we have,
$$
x^{3}+2 y^{3}=2014\left(u^{3}+2 v^{3}\right)
$$
for some positive integers $x, y, u, v$. We may assume that $x^{3}+2 y^{3}$ is minimal with this property. Now, we will use the fact that if 19 divides $x^{3}+2 y^{3}$, then it divides both $x$ and $y$. Indeed, if 19 does not divide $x$, then it does not divide $y$ too. The relation $x^{3} \equiv-2 y^{3}(\bmod 19)$ implies $\left(x^{3}\right)^{6} \equiv\left(-2 y^{3}\right)^{6}(\bmod 19)$. The latter congruence is equivalent to $x^{18} \equiv 2^{6} y^{18}(\bmod 19)$. Now, according to the Fermat's Little Theorem, we obtain $1 \equiv 2^{6}(\bmod 19)$, that is 19 divides 63 , not possible.
It follows $x=19 x_{1}, y=19 y_{1}$, for some positive integers $x_{1}$ and $y_{1}$. Replacing in (1) we get
$$
19^{2}\left(x_{1}^{3}+2 y_{1}^{3}\right)=2.53\left(u^{3}+2 v^{3}\right)
$$
i.e. $19 \mid u^{3}+2 v^{3}$. It follows $u=19 u_{1}$ and $v=19 v_{1}$, and replacing in (2) we get
$$
x_{1}^{3}+2 y_{1}^{3}=2014\left(u_{1}^{3}+2 v_{1}^{3}\right) .
$$
Clearly, $x_{1}^{3}+2 y_{1}^{3}<x^{3}+2 y^{3}$, contradicting the minimality of $x^{3}+2 y^{3}$.
|
{
"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
9173244f-9b99-5fbe-af3d-a1f1a809e70c
| 604,346
|
Let $A B C D$ be a trapezium inscribed in a circle $\Gamma$ with diameter $A B$. Let $E$ be the intersection point of the diagonals $A C$ and $B D$. The circle with center $B$ and radius $B E$ meets $\Gamma$ at the points $K$ and $L$, where $K$ is on the same side of $A B$ as $C$. The line perpendicular to $B D$ at $E$ intersects $C D$ at $M$.
Prove that $K M$ is perpendicular to $D L$.
|
Since $A B \| C D$, we have that $A B C D$ is isosceles trapezium. Let $O$ be the center of $k$ and $E M$ meets $A B$ at point $Q$. Then, from the right angled triangle $B E Q$, we have $B E^{2}=B O \cdot B Q$. Since $B E=B K$, we get $B K^{2}=B O \cdot B Q$ (1). Suppose that $K L$ meets $A B$ at $P$. Then, from the right angled triangle $B A K$, we have $B K^{2}=B P . B A$ (2)
From (1) and (2) we get $\frac{B P}{B Q}=\frac{B O}{B A}=\frac{1}{2}$, and therefore $P$ is the midpoint of $B Q$ (3). However, $D M \| A Q$ and $M Q \| A D$ (both are perpendicular to $D B$ ). Hence, $A Q M D$ is parallelogram and thus $M Q=A D=B C$. We conclude that $Q B C M$ is isosceles trapezium. It follows from (3) that $K L$ is the perpendicular bisector of $B Q$ and $C M$, that is, $M$ is symmetric to $C$ with respect to $K L$. Finally, we get that $M$ is the orthocenter
of the triangle $D L K$ by using the well-known result that the reflection of the orthocenter of a triangle to every side belongs to the circumcircle of the triangle and vise versa.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a trapezium inscribed in a circle $\Gamma$ with diameter $A B$. Let $E$ be the intersection point of the diagonals $A C$ and $B D$. The circle with center $B$ and radius $B E$ meets $\Gamma$ at the points $K$ and $L$, where $K$ is on the same side of $A B$ as $C$. The line perpendicular to $B D$ at $E$ intersects $C D$ at $M$.
Prove that $K M$ is perpendicular to $D L$.
|
Since $A B \| C D$, we have that $A B C D$ is isosceles trapezium. Let $O$ be the center of $k$ and $E M$ meets $A B$ at point $Q$. Then, from the right angled triangle $B E Q$, we have $B E^{2}=B O \cdot B Q$. Since $B E=B K$, we get $B K^{2}=B O \cdot B Q$ (1). Suppose that $K L$ meets $A B$ at $P$. Then, from the right angled triangle $B A K$, we have $B K^{2}=B P . B A$ (2)

From (1) and (2) we get $\frac{B P}{B Q}=\frac{B O}{B A}=\frac{1}{2}$, and therefore $P$ is the midpoint of $B Q$ (3). However, $D M \| A Q$ and $M Q \| A D$ (both are perpendicular to $D B$ ). Hence, $A Q M D$ is parallelogram and thus $M Q=A D=B C$. We conclude that $Q B C M$ is isosceles trapezium. It follows from (3) that $K L$ is the perpendicular bisector of $B Q$ and $C M$, that is, $M$ is symmetric to $C$ with respect to $K L$. Finally, we get that $M$ is the orthocenter
of the triangle $D L K$ by using the well-known result that the reflection of the orthocenter of a triangle to every side belongs to the circumcircle of the triangle and vise versa.
|
{
"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
714c3ebf-74fa-576e-9d75-b265371566b3
| 604,360
|
Let $a, b$ and $c$ be positive real numbers. Prove that
$$
a^{3} b^{6}+b^{3} c^{6}+c^{3} a^{6}+3 a^{3} b^{3} c^{3} \geq a b c\left(a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3}\right)+a^{2} b^{2} c^{2}\left(a^{3}+b^{3}+c^{3}\right)
$$
|
After dividing both sides of the given inequality by $a^{3} b^{3} c^{3}$ it becomes
$$
\left(\frac{b}{c}\right)^{3}+\left(\frac{c}{a}\right)^{3}+\left(\frac{a}{b}\right)^{3}+3 \geq\left(\frac{a}{c} \cdot \frac{b}{c}+\frac{b}{a} \cdot \frac{c}{a}+\frac{c}{b} \cdot \frac{a}{b}\right)+\left(\frac{a}{b} \cdot \frac{a}{c}+\frac{b}{a} \cdot \frac{b}{c}+\frac{c}{a} \cdot \frac{c}{b}\right) .
$$
Set
$$
\frac{b}{a}=\frac{1}{x}, \quad \frac{c}{b}=\frac{1}{y}, \quad \frac{a}{c}=\frac{1}{z} .
$$
Then we have that $x y z=1$ and by substituting (2) into (1), we find that
$$
x^{3}+y^{3}+z^{3}+3 \geq\left(\frac{y}{z}+\frac{z}{x}+\frac{x}{y}\right)+\left(\frac{x}{z}+\frac{y}{x}+\frac{z}{y}\right) .
$$
Multiplying the inequality (3) by $x y z$, and using the fact that $x y z=1$, the inequality is equivalent to
$$
x^{3}+y^{3}+z^{3}+3 x y z-x y^{2}-y z^{2}-z x^{2}-y x^{2}-z y^{2}-x z^{2} \geq 0 .
$$
Finally, notice that by the special case of Schur's inequality
$$
x^{r}(x-y)(x-z)+y^{r}(y-x)(y-z)+z^{r}(z-y)(z-x) \geq 0, \quad x, y, z \geq 0, r>0,
$$
with $r=1$ there holds
$$
x(x-y)(x-z)+y(y-x)(y-z)+z(z-y)(z-x) \geq 0
$$
which after expansion actually coincides with the congruence (4).
Remark 1. The inequality (5) immediately follows by supposing (without loss of generality) that $x \geq y \geq z$, and then writing the left hand side of the inequality (5) in the form
$$
(x-y)(x(x-z)-y(y-z))+z(y-z)(x-z)
$$
which is obviously $\geq 0$.
Remark 2. One can obtain the relation (4) using also the substitution $x=a b^{2}, y=b c^{2}$ and $z=c a^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$ and $c$ be positive real numbers. Prove that
$$
a^{3} b^{6}+b^{3} c^{6}+c^{3} a^{6}+3 a^{3} b^{3} c^{3} \geq a b c\left(a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3}\right)+a^{2} b^{2} c^{2}\left(a^{3}+b^{3}+c^{3}\right)
$$
|
After dividing both sides of the given inequality by $a^{3} b^{3} c^{3}$ it becomes
$$
\left(\frac{b}{c}\right)^{3}+\left(\frac{c}{a}\right)^{3}+\left(\frac{a}{b}\right)^{3}+3 \geq\left(\frac{a}{c} \cdot \frac{b}{c}+\frac{b}{a} \cdot \frac{c}{a}+\frac{c}{b} \cdot \frac{a}{b}\right)+\left(\frac{a}{b} \cdot \frac{a}{c}+\frac{b}{a} \cdot \frac{b}{c}+\frac{c}{a} \cdot \frac{c}{b}\right) .
$$
Set
$$
\frac{b}{a}=\frac{1}{x}, \quad \frac{c}{b}=\frac{1}{y}, \quad \frac{a}{c}=\frac{1}{z} .
$$
Then we have that $x y z=1$ and by substituting (2) into (1), we find that
$$
x^{3}+y^{3}+z^{3}+3 \geq\left(\frac{y}{z}+\frac{z}{x}+\frac{x}{y}\right)+\left(\frac{x}{z}+\frac{y}{x}+\frac{z}{y}\right) .
$$
Multiplying the inequality (3) by $x y z$, and using the fact that $x y z=1$, the inequality is equivalent to
$$
x^{3}+y^{3}+z^{3}+3 x y z-x y^{2}-y z^{2}-z x^{2}-y x^{2}-z y^{2}-x z^{2} \geq 0 .
$$
Finally, notice that by the special case of Schur's inequality
$$
x^{r}(x-y)(x-z)+y^{r}(y-x)(y-z)+z^{r}(z-y)(z-x) \geq 0, \quad x, y, z \geq 0, r>0,
$$
with $r=1$ there holds
$$
x(x-y)(x-z)+y(y-x)(y-z)+z(z-y)(z-x) \geq 0
$$
which after expansion actually coincides with the congruence (4).
Remark 1. The inequality (5) immediately follows by supposing (without loss of generality) that $x \geq y \geq z$, and then writing the left hand side of the inequality (5) in the form
$$
(x-y)(x(x-z)-y(y-z))+z(y-z)(x-z)
$$
which is obviously $\geq 0$.
Remark 2. One can obtain the relation (4) using also the substitution $x=a b^{2}, y=b c^{2}$ and $z=c a^{2}$.
|
{
"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
0bedad70-1390-5602-9f96-118630d84815
| 604,388
|
Let $A B C$ be a scalene triangle with incentre $I$ and circumcircle ( $\omega$ ). The lines $A I, B I, C I$ intersect $(\omega)$ for the second time at the points $D, E, F$, respectively. The lines through $I$ parallel to the sides $B C, A C, A B$ intersect the lines $E F, D F, D E$ at the points $K, L, M$, respectively. Prove that the points $K, L, M$ are collinear.
|
First we will prove that $K A$ is tangent to $(\omega)$.
Indeed, it is a well-known fact that $F A=F B=F I$ and $E A=E C=E I$, so $F E$ is the perpendicular bisector of $A I$. It follows that $K A=K I$ and
$$
\angle K A F=\angle K I F=\angle F C B=\angle F E B=\angle F E A,
$$
so $K A$ is tangent to $(\omega)$. Similarly we can prove that $L B, M C$ are tangent to $(\omega)$ as well.
Let $A^{\prime}, B^{\prime}, C^{\prime}$ the intersections of $A I, B I, C I$ with $B C, C A, A B$ respectively. From Pascal's Theorem on the cyclic hexagon $A A C D E B$ we get $K, C^{\prime}, B^{\prime}$ collinear. Similarly $L, C^{\prime}, A^{\prime}$ collinear and $M, B^{\prime}, A^{\prime}$ collinear.
Then from Desargues' Theorem for $\triangle D E F, \triangle A^{\prime} B^{\prime} C^{\prime}$ which are perspective from the point $I$, we get that points $K, L, M$ of the intersection of their corresponding sides are collinear as wanted.
Remark (P.S.C.). After proving that $K A, L B, M C$ are tangent to ( $\omega$ ), we can argue as follows:
It readily follows that $\triangle K A F \sim \triangle K A E$ and so $\frac{K A}{K E}=\frac{K F}{K A}=\frac{A F}{A E}$, thus $\frac{K F}{K E}=\left(\frac{A F}{A E}\right)^{2}$. In a similar way we can find that $\frac{M E}{M D}=\left(\frac{C E}{C D}\right)^{2}$ and $\frac{L D}{L F}=\left(\frac{B D}{B F}\right)^{2}$. Multiplying we obtain $\frac{K F}{K E} \cdot \frac{M E}{M D} \cdot \frac{L D}{L F}=1$, so by the converse of Menelaus theorem applied in the triangle $D E F$ we get that the points $K, L, M$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with incentre $I$ and circumcircle ( $\omega$ ). The lines $A I, B I, C I$ intersect $(\omega)$ for the second time at the points $D, E, F$, respectively. The lines through $I$ parallel to the sides $B C, A C, A B$ intersect the lines $E F, D F, D E$ at the points $K, L, M$, respectively. Prove that the points $K, L, M$ are collinear.
|
First we will prove that $K A$ is tangent to $(\omega)$.
Indeed, it is a well-known fact that $F A=F B=F I$ and $E A=E C=E I$, so $F E$ is the perpendicular bisector of $A I$. It follows that $K A=K I$ and
$$
\angle K A F=\angle K I F=\angle F C B=\angle F E B=\angle F E A,
$$
so $K A$ is tangent to $(\omega)$. Similarly we can prove that $L B, M C$ are tangent to $(\omega)$ as well.

Let $A^{\prime}, B^{\prime}, C^{\prime}$ the intersections of $A I, B I, C I$ with $B C, C A, A B$ respectively. From Pascal's Theorem on the cyclic hexagon $A A C D E B$ we get $K, C^{\prime}, B^{\prime}$ collinear. Similarly $L, C^{\prime}, A^{\prime}$ collinear and $M, B^{\prime}, A^{\prime}$ collinear.
Then from Desargues' Theorem for $\triangle D E F, \triangle A^{\prime} B^{\prime} C^{\prime}$ which are perspective from the point $I$, we get that points $K, L, M$ of the intersection of their corresponding sides are collinear as wanted.
Remark (P.S.C.). After proving that $K A, L B, M C$ are tangent to ( $\omega$ ), we can argue as follows:
It readily follows that $\triangle K A F \sim \triangle K A E$ and so $\frac{K A}{K E}=\frac{K F}{K A}=\frac{A F}{A E}$, thus $\frac{K F}{K E}=\left(\frac{A F}{A E}\right)^{2}$. In a similar way we can find that $\frac{M E}{M D}=\left(\frac{C E}{C D}\right)^{2}$ and $\frac{L D}{L F}=\left(\frac{B D}{B F}\right)^{2}$. Multiplying we obtain $\frac{K F}{K E} \cdot \frac{M E}{M D} \cdot \frac{L D}{L F}=1$, so by the converse of Menelaus theorem applied in the triangle $D E F$ we get that the points $K, L, M$ are collinear.
|
{
"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
3c83929b-30fa-5c9f-9884-62502da37077
| 604,399
|
A jury of 3366 film critics are judging the Oscars. Each critic makes a single vote for his favourite actor, and a single vote for his favourite actress. It turns out that for every integer $n \in\{1,2, \ldots, 100\}$ there is an actor or actress who has been voted for exactly $n$ times. Show that there are two critics who voted for the same actor and for the same actress.
|
Let us assume that every critic votes for a different pair of actor and actress. We'll arrive at a contradiction proving the required result. Indeed:
Call the vote of each critic, i.e his choice for the pair of an actor and an actress, as a double-vote, and call as a single-vote each one of the two choices he makes, i.e. the one for an actor and the other one for an actress. In this terminology, a double-vote corresponds to two single-votes.
For each $n=34,35, \ldots, 100$ let us pick out one actor or one actress who has been voted by exactly $n$ critics (i.e. appears in exactly $n$ single-votes) and call $S$ the set of these movie stars. Calling $a, b$ the number of men and women in $S$, we have $a+b=67$.
Now let $S_{1}$ be the set of double-votes, each having exactly one of its two corresponding singlevotes in $S$, and let $S_{2}$ be the set of double-votes with both its single-votes in $S$. If $s_{1}, s_{2}$ are the number of elements in $S_{1}, S_{2}$ respectively, we have that the number of all double-votes with at least one single-vote in $S$ is $s_{1}+s_{2}$, whereas the number of all double-votes with both single-votes in $S$ is $s_{2} \leq a b$.
Since all double-votes are distinct, there must exist at least $s_{1}+s_{2}$ critics. But the number of all single-votes in $S$ is $s_{1}+2 s_{2}=34+35+\cdots+100=4489$, and moreover $s \leq a b$. So there exist at least $s_{1}+s_{2}=s_{1}+2 s_{2}-s_{2} \geq 4489-a b$ critics.
Now notice that as $a+b=67$, the maximum value of $a b$ with $a, b$ integers is obtained for $\{a, b\}=$ $\{33,34\}$, so $a b \leq 33 \cdot 34=1122$. A quick proof of this is the following: $a b=\frac{(a+b)^{2}-(a-b)^{2}}{4}=$ $\frac{67^{2}-(a-b)^{2}}{4}$ which is maximized (for not equal integers $a, b$ as $a+b=67$ ) whenever $|a-b|=1$, thus for $\{a, b\}=\{33,34\}$.
Thus there exist at least $4489-1122=3367$ critics which is a contradiction and we are done.
Remark. We are going here to give some motivation about the choice of number 34, used in the above solution.
Let us assume that every critic votes for a different pair of actor and actress. One can again start by picking out one actor or one actress who has been voted by exactly $n$ critics for $n=k, k+1, \ldots, 100$. Then $a+b=100-k+1=101-k$ and the number of all single-votes is $s_{1}+2 s_{2}=k+k+1+\cdots+100=$ $5050-\frac{k(k-1)}{2}$, so there exist at least $s_{1}+s_{2}=s_{1}+2 s_{2}-s_{2} \geq 5050-\frac{k(k-1)}{2}-a b$ and
$$
a b=\frac{(a+b)^{2}-(a-b)^{2}}{4}=\frac{(101-k)^{2}-(a-b)^{2}}{4} \leq \frac{(101-k)^{2}-1}{4} .
$$
After all, the number of critics is at least
$$
5050-\frac{k(k-1)}{2}-\frac{(101-k)^{2}-1}{4}
$$
In order to arrive at a contradiction we have to choose $k$ such that
$$
5050-\frac{k(k-1)}{2}-\frac{(101-k)^{2}-1}{4} \geq 3367
$$
and solving the inequality with respect to $k$, the only value that makes the last one true is $k=34$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A jury of 3366 film critics are judging the Oscars. Each critic makes a single vote for his favourite actor, and a single vote for his favourite actress. It turns out that for every integer $n \in\{1,2, \ldots, 100\}$ there is an actor or actress who has been voted for exactly $n$ times. Show that there are two critics who voted for the same actor and for the same actress.
|
Let us assume that every critic votes for a different pair of actor and actress. We'll arrive at a contradiction proving the required result. Indeed:
Call the vote of each critic, i.e his choice for the pair of an actor and an actress, as a double-vote, and call as a single-vote each one of the two choices he makes, i.e. the one for an actor and the other one for an actress. In this terminology, a double-vote corresponds to two single-votes.
For each $n=34,35, \ldots, 100$ let us pick out one actor or one actress who has been voted by exactly $n$ critics (i.e. appears in exactly $n$ single-votes) and call $S$ the set of these movie stars. Calling $a, b$ the number of men and women in $S$, we have $a+b=67$.
Now let $S_{1}$ be the set of double-votes, each having exactly one of its two corresponding singlevotes in $S$, and let $S_{2}$ be the set of double-votes with both its single-votes in $S$. If $s_{1}, s_{2}$ are the number of elements in $S_{1}, S_{2}$ respectively, we have that the number of all double-votes with at least one single-vote in $S$ is $s_{1}+s_{2}$, whereas the number of all double-votes with both single-votes in $S$ is $s_{2} \leq a b$.
Since all double-votes are distinct, there must exist at least $s_{1}+s_{2}$ critics. But the number of all single-votes in $S$ is $s_{1}+2 s_{2}=34+35+\cdots+100=4489$, and moreover $s \leq a b$. So there exist at least $s_{1}+s_{2}=s_{1}+2 s_{2}-s_{2} \geq 4489-a b$ critics.
Now notice that as $a+b=67$, the maximum value of $a b$ with $a, b$ integers is obtained for $\{a, b\}=$ $\{33,34\}$, so $a b \leq 33 \cdot 34=1122$. A quick proof of this is the following: $a b=\frac{(a+b)^{2}-(a-b)^{2}}{4}=$ $\frac{67^{2}-(a-b)^{2}}{4}$ which is maximized (for not equal integers $a, b$ as $a+b=67$ ) whenever $|a-b|=1$, thus for $\{a, b\}=\{33,34\}$.
Thus there exist at least $4489-1122=3367$ critics which is a contradiction and we are done.
Remark. We are going here to give some motivation about the choice of number 34, used in the above solution.
Let us assume that every critic votes for a different pair of actor and actress. One can again start by picking out one actor or one actress who has been voted by exactly $n$ critics for $n=k, k+1, \ldots, 100$. Then $a+b=100-k+1=101-k$ and the number of all single-votes is $s_{1}+2 s_{2}=k+k+1+\cdots+100=$ $5050-\frac{k(k-1)}{2}$, so there exist at least $s_{1}+s_{2}=s_{1}+2 s_{2}-s_{2} \geq 5050-\frac{k(k-1)}{2}-a b$ and
$$
a b=\frac{(a+b)^{2}-(a-b)^{2}}{4}=\frac{(101-k)^{2}-(a-b)^{2}}{4} \leq \frac{(101-k)^{2}-1}{4} .
$$
After all, the number of critics is at least
$$
5050-\frac{k(k-1)}{2}-\frac{(101-k)^{2}-1}{4}
$$
In order to arrive at a contradiction we have to choose $k$ such that
$$
5050-\frac{k(k-1)}{2}-\frac{(101-k)^{2}-1}{4} \geq 3367
$$
and solving the inequality with respect to $k$, the only value that makes the last one true is $k=34$.
|
{
"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
9de7f38a-3a1d-5f43-ac45-ccdb1b909d08
| 604,408
|
Prove that among any 20 consecutive positive integers there exists an integer $d$ such that for each positive integer $n$ we have the inequality
$$
n \sqrt{d}\{n \sqrt{d}\}>\frac{5}{2}
$$
where $\{x\}$ denotes the fractional part of the real number $x$. The fractional part of a real number $x$ is $x$ minus the greatest integer less than or equal to $x$.
|
Among the given numbers there is a number of the form $20 k+15=5(4 k+3)$. We shall prove that $d=5(4 k+3)$ satisfies the statement's condition. Since $d \equiv-1(\bmod 4)$, it follows that $d$ is not a perfect square, and thus for any $n \in \mathbb{N}$ there exists $a \in \mathbb{N}$ such that $a+1>n \sqrt{d}>a$, that is, $(a+1)^{2}>n^{2} d>a^{2}$. Actually, we are going to prove that $n^{2} d \geq a^{2}+5$. Indeed:
It is known that each positive integer of the form $4 s+3$ has a prime divisor of the same form. Let $p \mid 4 k+3$ and $p \equiv-1(\bmod 4)$. Because of the form of $p$, the numbers $a^{2}+1^{2}$ and $a^{2}+2^{2}$ are not divisible by $p$, and since $p \mid n^{2} d$, it follows that $n^{2} d \neq a^{2}+1, a^{2}+4$. On the other hand, $5 \mid n^{2} d$, and since $5 \nmid a^{2}+2, a^{2}+3$, we conclude $n^{2} d \neq a^{2}+2, a^{2}+3$. Since $n^{2} d>a^{2}$ we must have $n^{2} d \geq a^{2}+5$ as claimed. Therefore,
$$
n \sqrt{d}\{n \sqrt{d}\}=n \sqrt{d}(n \sqrt{d}-a) \geq a^{2}+5-a \sqrt{a^{2}+5}>a^{2}+5-\frac{a^{2}+\left(a^{2}+5\right)}{2}=\frac{5}{2},
$$
which was to be proved.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that among any 20 consecutive positive integers there exists an integer $d$ such that for each positive integer $n$ we have the inequality
$$
n \sqrt{d}\{n \sqrt{d}\}>\frac{5}{2}
$$
where $\{x\}$ denotes the fractional part of the real number $x$. The fractional part of a real number $x$ is $x$ minus the greatest integer less than or equal to $x$.
|
Among the given numbers there is a number of the form $20 k+15=5(4 k+3)$. We shall prove that $d=5(4 k+3)$ satisfies the statement's condition. Since $d \equiv-1(\bmod 4)$, it follows that $d$ is not a perfect square, and thus for any $n \in \mathbb{N}$ there exists $a \in \mathbb{N}$ such that $a+1>n \sqrt{d}>a$, that is, $(a+1)^{2}>n^{2} d>a^{2}$. Actually, we are going to prove that $n^{2} d \geq a^{2}+5$. Indeed:
It is known that each positive integer of the form $4 s+3$ has a prime divisor of the same form. Let $p \mid 4 k+3$ and $p \equiv-1(\bmod 4)$. Because of the form of $p$, the numbers $a^{2}+1^{2}$ and $a^{2}+2^{2}$ are not divisible by $p$, and since $p \mid n^{2} d$, it follows that $n^{2} d \neq a^{2}+1, a^{2}+4$. On the other hand, $5 \mid n^{2} d$, and since $5 \nmid a^{2}+2, a^{2}+3$, we conclude $n^{2} d \neq a^{2}+2, a^{2}+3$. Since $n^{2} d>a^{2}$ we must have $n^{2} d \geq a^{2}+5$ as claimed. Therefore,
$$
n \sqrt{d}\{n \sqrt{d}\}=n \sqrt{d}(n \sqrt{d}-a) \geq a^{2}+5-a \sqrt{a^{2}+5}>a^{2}+5-\frac{a^{2}+\left(a^{2}+5\right)}{2}=\frac{5}{2},
$$
which was to be proved.
|
{
"resource_path": "Balkan_MO/segmented/en-2015-BMO-type1.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
de1b3225-0afc-5bd8-a794-6020065dae9a
| 604,421
|
Let $A B C D$ be a cyclic quadrilateral with $A B<C D$. The diagonals intersect at the point $F$ and lines $A D$ and $B C$ intersect at the point $E$. Let $K$ and $L$ be the orthogonal projections of $F$ onto lines $A D$ and $B C$ respectively, and let $M, S$ and $T$ be the midpoints of $E F, C F$ and $D F$ respectively. Prove that the second intersection point of the circumcircles of triangles $M K T$ and $M L S$ lies on the segment $C D$.
|
Let $N$ be the midpoint of $C D$. We will prove that the circumcircles of the triangles $M K T$ and $M L S$ pass through $N$. (1)
First will prove that the circumcircle of $M L S$ passes through $N$.
Let $Q$ be the midpoint of $E C$. Note that the circumcircle of $M L S$ is the Euler circle (2) of the triangle $E F C$, so it passes also through $Q .\left({ }^{*}\right)(3)$
We will prove that
$$
\angle S L Q=\angle Q N S \quad \text { or } \quad \angle S L Q+\angle Q N S=180^{\circ}
$$
Indeed, since $F L C$ is right-angled and $L S$ is its median, we have that $S L=S C$ and
$$
\angle S L C=\angle S C L=\angle A C B
$$
In addition, since $N$ and $S$ are the midpoints of $D C$ and $F C$ we have that $S N \| F D$ and similarly, since $Q$ and $N$ are the midpoints of $E C$ and $C D$, so $Q N \| E D$.
It follows that the angles $\angle E D B$ and $\angle Q N S$ have parallel sides, and since $A B<C D$, they are acute, and as a result we have that
$$
\angle E D B=\angle Q N S \quad \text { or } \quad \angle E D B+\angle Q N S=180^{\circ}
$$
But, from the cyclic quadrilateral $A B C D$, we get that
$$
\angle E D B=\angle A C B
$$
Now, from (2),(3) and (4) we obtain immediately (1), so the quadrilateral $L N S Q$ is cyclic. Since from $\left(^{*}\right)$, its circumcircle passes also through $M$, we get that the points $M, L, Q, S, N$ are cocylic and this means that the circumcircle of $M L S$ passes through $N$.
Similarly, the circumcircle of $M K T$ passes also through $N$ and we have the desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral with $A B<C D$. The diagonals intersect at the point $F$ and lines $A D$ and $B C$ intersect at the point $E$. Let $K$ and $L$ be the orthogonal projections of $F$ onto lines $A D$ and $B C$ respectively, and let $M, S$ and $T$ be the midpoints of $E F, C F$ and $D F$ respectively. Prove that the second intersection point of the circumcircles of triangles $M K T$ and $M L S$ lies on the segment $C D$.
|
Let $N$ be the midpoint of $C D$. We will prove that the circumcircles of the triangles $M K T$ and $M L S$ pass through $N$. (1)
First will prove that the circumcircle of $M L S$ passes through $N$.
Let $Q$ be the midpoint of $E C$. Note that the circumcircle of $M L S$ is the Euler circle (2) of the triangle $E F C$, so it passes also through $Q .\left({ }^{*}\right)(3)$

We will prove that
$$
\angle S L Q=\angle Q N S \quad \text { or } \quad \angle S L Q+\angle Q N S=180^{\circ}
$$
Indeed, since $F L C$ is right-angled and $L S$ is its median, we have that $S L=S C$ and
$$
\angle S L C=\angle S C L=\angle A C B
$$
In addition, since $N$ and $S$ are the midpoints of $D C$ and $F C$ we have that $S N \| F D$ and similarly, since $Q$ and $N$ are the midpoints of $E C$ and $C D$, so $Q N \| E D$.
It follows that the angles $\angle E D B$ and $\angle Q N S$ have parallel sides, and since $A B<C D$, they are acute, and as a result we have that
$$
\angle E D B=\angle Q N S \quad \text { or } \quad \angle E D B+\angle Q N S=180^{\circ}
$$
But, from the cyclic quadrilateral $A B C D$, we get that
$$
\angle E D B=\angle A C B
$$
Now, from (2),(3) and (4) we obtain immediately (1), so the quadrilateral $L N S Q$ is cyclic. Since from $\left(^{*}\right)$, its circumcircle passes also through $M$, we get that the points $M, L, Q, S, N$ are cocylic and this means that the circumcircle of $M L S$ passes through $N$.
Similarly, the circumcircle of $M K T$ passes also through $N$ and we have the desired.
|
{
"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl",
"problem_match": "# Problem 2.",
"solution_match": "\nSolution."
}
|
2562b049-0197-5221-a500-54b38da1d2a4
| 604,449
|
The plane is divided into unit squares by two sets of parallel lines, forming an infinite grid. Each unit square is coloured with one of 1201 colours so that no rectangle with perimeter 100 contains two squares of the same colour. Show that no rectangle of size $1 \times 1201$ or $1201 \times 1$ contains two squares of the same colour.
Note: Any rectangle is assumed here to have sides contained in the lines of the grid.
|
Let the centers of the unit squares be the integer points in the plane, and denote each unit square by the coordinates of its center.
Consider the set $D$ of all unit squares $(x, y)$ such that $|x|+|y| \leq 24$. Any integer translate of $D$ is called a diamond.
Since any two unit squares that belong to the same diamond also belong to some rectangle of perimeter 100 , a diamond cannot contain two unit squares of the same colour. Since a diamond contains exactly $24^{2}+25^{2}=1201$ unit squares, a diamond must contain every colour exactly once.
Choose one colour, say, green, and let $a_{1}, a_{2}, \ldots$ be all green unit squares. Let $P_{i}$ be the diamond of center $a_{i}$. We will show that no unit square is covered by two $P$ 's and that every unit square is covered by some $P_{i}$.
Indeed, suppose first that $P_{i}$ and $P_{j}$ contain the same unit square $b$. Then their centers lie within the same rectangle of perimeter 100, a contradiction.
Let, on the other hand, $b$ be an arbitrary unit square. The diamond of center $b$ must contain some green unit square $a_{i}$. The diamond $P_{i}$ of center $a_{i}$ will then contain $b$.
Therefore, $P_{1}, P_{2}, \ldots$ form a covering of the plane in exactly one layer. It is easy to see, though, that, up to translation and reflection, there exists a unique such covering. (Indeed, consider two neighbouring diamonds. Unless they fit neatly, uncoverable spaces of two unit squares are created near the corners: see Fig. 1.)
Figure 1:
Without loss of generality, then, this covering is given by the diamonds of centers $(x, y)$ such that $24 x+25 y$ is divisible by 1201. (See Fig. 2 for an analogous covering with smaller diamonds.) It follows from this that no rectangle of size $1 \times 1201$ can contain two green unit squares, and analogous reasoning works for the remaining colours.

Figure 2:
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The plane is divided into unit squares by two sets of parallel lines, forming an infinite grid. Each unit square is coloured with one of 1201 colours so that no rectangle with perimeter 100 contains two squares of the same colour. Show that no rectangle of size $1 \times 1201$ or $1201 \times 1$ contains two squares of the same colour.
Note: Any rectangle is assumed here to have sides contained in the lines of the grid.
|
Let the centers of the unit squares be the integer points in the plane, and denote each unit square by the coordinates of its center.
Consider the set $D$ of all unit squares $(x, y)$ such that $|x|+|y| \leq 24$. Any integer translate of $D$ is called a diamond.
Since any two unit squares that belong to the same diamond also belong to some rectangle of perimeter 100 , a diamond cannot contain two unit squares of the same colour. Since a diamond contains exactly $24^{2}+25^{2}=1201$ unit squares, a diamond must contain every colour exactly once.
Choose one colour, say, green, and let $a_{1}, a_{2}, \ldots$ be all green unit squares. Let $P_{i}$ be the diamond of center $a_{i}$. We will show that no unit square is covered by two $P$ 's and that every unit square is covered by some $P_{i}$.
Indeed, suppose first that $P_{i}$ and $P_{j}$ contain the same unit square $b$. Then their centers lie within the same rectangle of perimeter 100, a contradiction.
Let, on the other hand, $b$ be an arbitrary unit square. The diamond of center $b$ must contain some green unit square $a_{i}$. The diamond $P_{i}$ of center $a_{i}$ will then contain $b$.
Therefore, $P_{1}, P_{2}, \ldots$ form a covering of the plane in exactly one layer. It is easy to see, though, that, up to translation and reflection, there exists a unique such covering. (Indeed, consider two neighbouring diamonds. Unless they fit neatly, uncoverable spaces of two unit squares are created near the corners: see Fig. 1.)

Figure 1:
Without loss of generality, then, this covering is given by the diamonds of centers $(x, y)$ such that $24 x+25 y$ is divisible by 1201. (See Fig. 2 for an analogous covering with smaller diamonds.) It follows from this that no rectangle of size $1 \times 1201$ can contain two green unit squares, and analogous reasoning works for the remaining colours.

Figure 2:
|
{
"resource_path": "Balkan_MO/segmented/en-2016-BMO-type1.jsonl",
"problem_match": "# Problem 4.",
"solution_match": "\nSolution."
}
|
613e8d76-170e-5d70-9737-a5092f74af9d
| 604,474
|
Let $A B C$ be an acute triangle with with $A B<A C$ and let $\Gamma$ be its circumcircle. Let the tangents to $\Gamma$ at $B$ and $C$ be $t_{B}$ and $t_{C}$ respectively and let their point of intersection be $L$. The line through $B$ parallel to $A C$ intersects $t_{C}$ at $D$. The line through $C$ parallel to $A B$ intersects $t_{B}$ at $E$. The circumcircle of triangle $B D C$ meets the side $A C$ at $T$ where $T$ lies between $A$ and $C$. The circumcircle of triangle $B E C$ meets the line $A B$ at $S$ where $B$ lies between $A$ and $S$.
Prove that the lines $S T, B C$ and $A L$ are concurrent.
|
How we attack this problem depends on how much triangle geometry we can effortlessly recall - a good knowledge of some standard results helps a great deal.
We might instantly note that $A L$ is a symmedian of $A B C$, and so divides the line $B C$ in the ratio $c^{2}: b^{2}$. Now the plan is to show that $S T$ also divides $B C$ in this ratio.
Since we are working with ratios of distances, Menelaus' theorem may prove useful.
A key step is to notice (based on a careful diagram) that $A C$ is tangent to circle $C B S$. Once spotted this is easy to prove. The parallels give us $\angle B=\angle B C E$, and, since $B E$ is tangent to circle $A B C$, we have $\angle E B C=\angle A$ by the alternate segment theorem. Now angles in a triangle give $\angle C=\angle C E B$, and we have the converse to the alternate segment theorem. We obtain $A B$ is tangent to circle $C B D$ in the same way.
Now we have some tangencies and want some ratios.
Tangent-secant yields $A T . b=c^{2}$ and $c . A S=b^{2}$ or, equivalently, $b . C T=b^{2}-c^{2}$ and $c . B S=b^{2}-c^{2}$.
By Menelaus we know that $S T$ divides $B C$ in the ratio $A T . B S: A S . C T$ and it's all over bar the shouting.
If we are not lucky enough to have the stuff about the symmedian at our fingertips, we can still get essentially the same solution with a bit more work. We begin with the second half of the proof above, and establish that $S T$ divides $B C$ in the ratio $c^{2}: b^{2}$. Now we need to prove that $A L$ divides $B C$ in the same ratio.
The next (non-obvious!) step is to draw a parallel to $B C$ through $A$ as shown.
Now $\triangle A B C \sim \triangle B^{\prime} A B \sim \triangle C C^{\prime} A$ and the ratio $B^{\prime} A: A C^{\prime}$ which equals $B X: X C$ drops out as $c^{2}: b^{2}$ as required.
Clearly knowing the standard symmedian configuration and corresponding ratio is an enormous advantage.
Finally it is worth noting that, to the right sort of mind, the problem screams out for areal coordinates. These turn out to kill it fairly easily, not least because all three circles pass through at least two vertices of $\triangle A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with with $A B<A C$ and let $\Gamma$ be its circumcircle. Let the tangents to $\Gamma$ at $B$ and $C$ be $t_{B}$ and $t_{C}$ respectively and let their point of intersection be $L$. The line through $B$ parallel to $A C$ intersects $t_{C}$ at $D$. The line through $C$ parallel to $A B$ intersects $t_{B}$ at $E$. The circumcircle of triangle $B D C$ meets the side $A C$ at $T$ where $T$ lies between $A$ and $C$. The circumcircle of triangle $B E C$ meets the line $A B$ at $S$ where $B$ lies between $A$ and $S$.
Prove that the lines $S T, B C$ and $A L$ are concurrent.
|
How we attack this problem depends on how much triangle geometry we can effortlessly recall - a good knowledge of some standard results helps a great deal.
We might instantly note that $A L$ is a symmedian of $A B C$, and so divides the line $B C$ in the ratio $c^{2}: b^{2}$. Now the plan is to show that $S T$ also divides $B C$ in this ratio.
Since we are working with ratios of distances, Menelaus' theorem may prove useful.

A key step is to notice (based on a careful diagram) that $A C$ is tangent to circle $C B S$. Once spotted this is easy to prove. The parallels give us $\angle B=\angle B C E$, and, since $B E$ is tangent to circle $A B C$, we have $\angle E B C=\angle A$ by the alternate segment theorem. Now angles in a triangle give $\angle C=\angle C E B$, and we have the converse to the alternate segment theorem. We obtain $A B$ is tangent to circle $C B D$ in the same way.
Now we have some tangencies and want some ratios.
Tangent-secant yields $A T . b=c^{2}$ and $c . A S=b^{2}$ or, equivalently, $b . C T=b^{2}-c^{2}$ and $c . B S=b^{2}-c^{2}$.
By Menelaus we know that $S T$ divides $B C$ in the ratio $A T . B S: A S . C T$ and it's all over bar the shouting.
If we are not lucky enough to have the stuff about the symmedian at our fingertips, we can still get essentially the same solution with a bit more work. We begin with the second half of the proof above, and establish that $S T$ divides $B C$ in the ratio $c^{2}: b^{2}$. Now we need to prove that $A L$ divides $B C$ in the same ratio.
The next (non-obvious!) step is to draw a parallel to $B C$ through $A$ as shown.

Now $\triangle A B C \sim \triangle B^{\prime} A B \sim \triangle C C^{\prime} A$ and the ratio $B^{\prime} A: A C^{\prime}$ which equals $B X: X C$ drops out as $c^{2}: b^{2}$ as required.
Clearly knowing the standard symmedian configuration and corresponding ratio is an enormous advantage.
Finally it is worth noting that, to the right sort of mind, the problem screams out for areal coordinates. These turn out to kill it fairly easily, not least because all three circles pass through at least two vertices of $\triangle A B C$.
|
{
"resource_path": "Balkan_MO/segmented/en-2017-BMO-type3.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution."
}
|
9c7cba3a-a820-596a-9776-75f0f389b914
| 604,502
|
A quadrilateral $A B C D$ is inscribed in a circle $k$, where $A B>C D$ and $A B$ is not parallel to $C D$. Point $M$ is the intersection of the diagonals $A C$ and $B D$ and the perpendicular from $M$ to $A B$ intersects the segment $A B$ at the point $E$. If $E M$ bisects the angle $C E D$, prove that $A B$ is a diameter of the circle $k$.
|
Let the line through $M$ parallel to $A B$ meet the segments $A D, D H, B C, C H$ at points $K, P, L, Q$, respectively. Triangle $H P Q$ is isosceles, so $M P=M Q$. Now from
$$
\frac{M P}{B H}=\frac{D M}{D B}=\frac{K M}{A B} \quad \text { and } \quad \frac{M Q}{A H}=\frac{C M}{C A}=\frac{M L}{A B}
$$
we obtain $A H / H B=K M / M L$.
Let the lines $A D$ and $B C$ meet at point $S$ and let the line $S M$ meet $A B$ at $H^{\prime}$. Then $A H^{\prime} / H^{\prime} B=K M / M L=A H / H B$, so $H^{\prime} \equiv H$, i.e. $S$ lies on the line $M H$.
The quadrilateral $A B C D$ is not a trapezoid, so $A H \neq B H$. Consider the point $A^{\prime}$ on the ray $H B$ such that $H A^{\prime}=H A$. Since $\varangle S A^{\prime} M=\varangle S A M=\varangle S B M$, quadrilateral $A^{\prime} B S M$ is cyclic and therefore $\varangle A B C=\varangle A^{\prime} B S=\varangle A^{\prime} M H=\varangle A M H=90^{\circ}-\varangle B A C$, which implies that $\varangle A C B=90^{\circ}$.
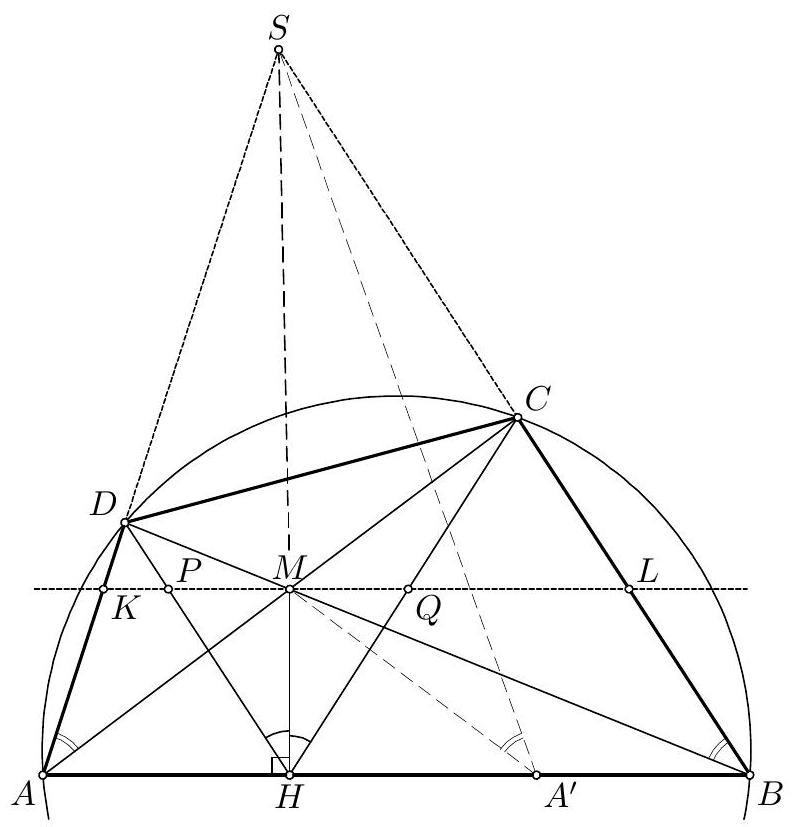
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A quadrilateral $A B C D$ is inscribed in a circle $k$, where $A B>C D$ and $A B$ is not parallel to $C D$. Point $M$ is the intersection of the diagonals $A C$ and $B D$ and the perpendicular from $M$ to $A B$ intersects the segment $A B$ at the point $E$. If $E M$ bisects the angle $C E D$, prove that $A B$ is a diameter of the circle $k$.
|
Let the line through $M$ parallel to $A B$ meet the segments $A D, D H, B C, C H$ at points $K, P, L, Q$, respectively. Triangle $H P Q$ is isosceles, so $M P=M Q$. Now from
$$
\frac{M P}{B H}=\frac{D M}{D B}=\frac{K M}{A B} \quad \text { and } \quad \frac{M Q}{A H}=\frac{C M}{C A}=\frac{M L}{A B}
$$
we obtain $A H / H B=K M / M L$.
Let the lines $A D$ and $B C$ meet at point $S$ and let the line $S M$ meet $A B$ at $H^{\prime}$. Then $A H^{\prime} / H^{\prime} B=K M / M L=A H / H B$, so $H^{\prime} \equiv H$, i.e. $S$ lies on the line $M H$.
The quadrilateral $A B C D$ is not a trapezoid, so $A H \neq B H$. Consider the point $A^{\prime}$ on the ray $H B$ such that $H A^{\prime}=H A$. Since $\varangle S A^{\prime} M=\varangle S A M=\varangle S B M$, quadrilateral $A^{\prime} B S M$ is cyclic and therefore $\varangle A B C=\varangle A^{\prime} B S=\varangle A^{\prime} M H=\varangle A M H=90^{\circ}-\varangle B A C$, which implies that $\varangle A C B=90^{\circ}$.

|
{
"resource_path": "Balkan_MO/segmented/en-2018-BMO-type3.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution."
}
|
d890d45a-f52e-578b-98f3-207b038a0650
| 604,537
|
Let $a, b, c$ be real numbers, such that $0 \leq a \leq b \leq c$ and $a+b+c=a b+b c+c a>0$. Prove that $\sqrt{b c}(a+1) \geq 2$. Find all triples $(a, b, c)$ for which equality holds.
## Proposed by Romania
|
Let $a+b+c=a b+b c+c a=k$. Since $(a+b+c)^{2} \geq 3(a b+b c+c a)$, we get that $k^{2} \geq 3 k$. Since $k>0$, we obtain that $k \geq 3$.
We have $b c \geq c a \geq a b$, so from the above relation we deduce that $b c \geq 1$.
By AM-GM, $b+c \geq 2 \sqrt{b c}$ and consequently $b+c \geq 2$. The equality holds iff $b=c$.
The constraint gives us
$$
a=\frac{b+c-b c}{b+c-1}=1-\frac{b c-1}{b+c-1} \geq 1-\frac{b c-1}{2 \sqrt{b c}-1}=\frac{\sqrt{b c}(2-\sqrt{b c})}{2 \sqrt{b c}-1}
$$
For $\sqrt{b c}=2$ condition $a \geq 0$ gives $\sqrt{b c}(a+1) \geq 2$ with equality iff $a=0$ and $b=c=2$. For $\sqrt{b c}<2$, taking into account the estimation for $a$, we get
$$
a \sqrt{b c} \geq \frac{b c(2-\sqrt{b c})}{2 \sqrt{b c}-1}=\frac{b c}{2 \sqrt{b c}-1}(2-\sqrt{b c}) .
$$
Since $\frac{b c}{2 \sqrt{b c}-1} \geq 1$, with equality for $b c=1$, we get $\sqrt{b c}(a+1) \geq 2$ with equality iff $a=b=c=1$.
For $\sqrt{b c}>2$ we have $\sqrt{b c}(a+1)>2(a+1) \geq 2$.
The proof is complete.
The equality holds iff $a=b=c=1$ or $a=0$ and $b=c=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers, such that $0 \leq a \leq b \leq c$ and $a+b+c=a b+b c+c a>0$. Prove that $\sqrt{b c}(a+1) \geq 2$. Find all triples $(a, b, c)$ for which equality holds.
## Proposed by Romania
|
Let $a+b+c=a b+b c+c a=k$. Since $(a+b+c)^{2} \geq 3(a b+b c+c a)$, we get that $k^{2} \geq 3 k$. Since $k>0$, we obtain that $k \geq 3$.
We have $b c \geq c a \geq a b$, so from the above relation we deduce that $b c \geq 1$.
By AM-GM, $b+c \geq 2 \sqrt{b c}$ and consequently $b+c \geq 2$. The equality holds iff $b=c$.
The constraint gives us
$$
a=\frac{b+c-b c}{b+c-1}=1-\frac{b c-1}{b+c-1} \geq 1-\frac{b c-1}{2 \sqrt{b c}-1}=\frac{\sqrt{b c}(2-\sqrt{b c})}{2 \sqrt{b c}-1}
$$
For $\sqrt{b c}=2$ condition $a \geq 0$ gives $\sqrt{b c}(a+1) \geq 2$ with equality iff $a=0$ and $b=c=2$. For $\sqrt{b c}<2$, taking into account the estimation for $a$, we get
$$
a \sqrt{b c} \geq \frac{b c(2-\sqrt{b c})}{2 \sqrt{b c}-1}=\frac{b c}{2 \sqrt{b c}-1}(2-\sqrt{b c}) .
$$
Since $\frac{b c}{2 \sqrt{b c}-1} \geq 1$, with equality for $b c=1$, we get $\sqrt{b c}(a+1) \geq 2$ with equality iff $a=b=c=1$.
For $\sqrt{b c}>2$ we have $\sqrt{b c}(a+1)>2(a+1) \geq 2$.
The proof is complete.
The equality holds iff $a=b=c=1$ or $a=0$ and $b=c=2$.
|
{
"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl",
"problem_match": "# Problem 2.",
"solution_match": "\nSolution."
}
|
1b5e20f6-1fa4-5adc-b5cd-0ffc39682953
| 604,617
|
Let $A B C$ be an acute scalene triangle. Let $X$ and $Y$ be two distinct interior points of the segment $B C$ such that $\angle C A X=\angle Y A B$. Suppose that:
1) $K$ and $S$ are the feet of perpendiculars from $B$ to the lines $A X$ and $A Y$ respectively;
2) $T$ and $L$ are the feet of perpendiculars from $C$ to the lines $A X$ and $A Y$ respectively. Prove that $K L$ and $S T$ intersect on the line $B C$.
## Proposed by Greece
|
Denote $\phi=\widehat{X A B}=\widehat{Y A C}, \alpha=\widehat{C A X}=\widehat{B A Y}$. Then, because the quadrilaterals ABSK and ACTL are cyclic, we have
$$
\widehat{B S K}+\widehat{B A K}=180^{\circ}=\widehat{B S K}+\phi=\widehat{L A C}+\widehat{L T C}=\widehat{L T C}+\phi
$$
so, due to the 90-degree angles formed, we have $\widehat{K S L}=\widehat{K T L}$. Thus, KLST is cyclic.
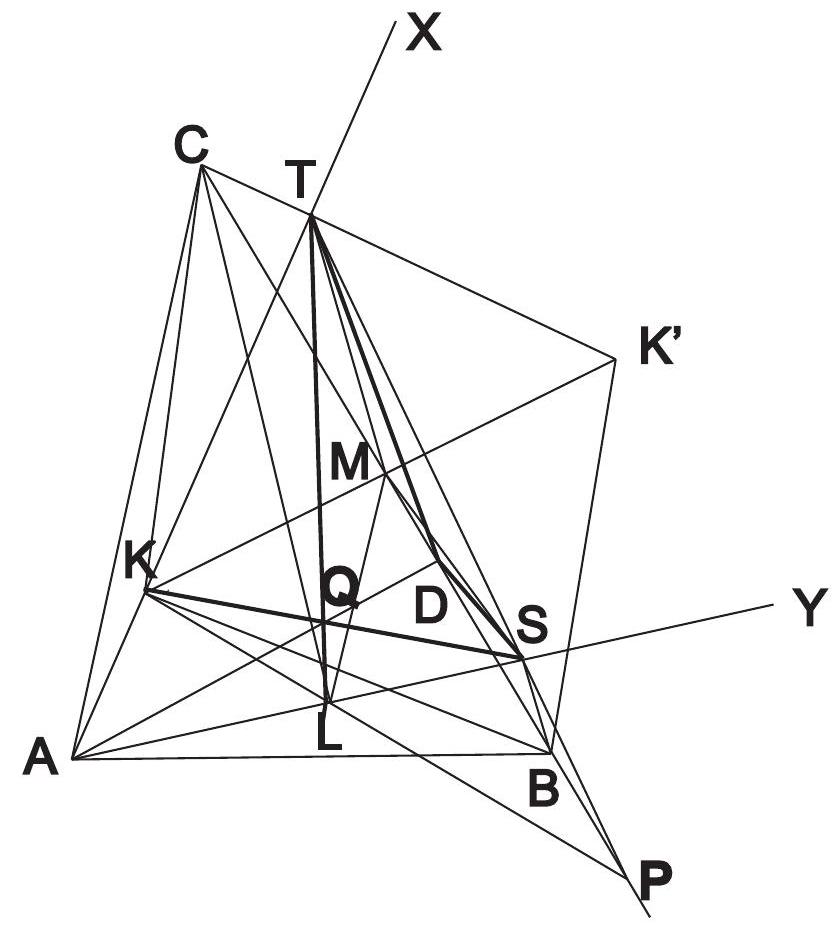
Figure 1: G6
Consider $M$ to be the midpoint of $B C$ and $K^{\prime}$ to be the symmetric point of $K$ with respect to $M$. Then, $B K C K^{\prime}$ is a parallelogram, and so $B K \| C K^{\prime}$. But $B K \| C T$, because they are both perpendicular to $A X$. So, $K^{\prime}$ lies on $C T$ and, as $\widehat{K T K^{\prime}}=90$ and $M$ is the midpoint of $K K^{\prime}, M K=M T$. In a similar way, we have that $M S=M L$. Thus, the center of $(K L S T)$ is $M$.
Consider $D$ to be the foot of altitude from $A$ to $B C$. Then, $D$ belongs in both $(A B K S)$ and $(A C L T)$. So,
$$
\widehat{A D T}+\widehat{A C T}=180^{\circ}=\widehat{A B S}+\widehat{A D S}=\widehat{A D T}+90^{\circ}-\alpha=\widehat{A D S}+90^{\circ}-\alpha
$$
and $A D$ is the bisector of $\widehat{S D T}$.
Because $D M$ is perpendicular to $A D, D M$ is the external bisector of this angle, and, as $M S=M T$, it follows that $D M S T$ is cyclic. In a similar way, we have that $D M L K$ is also cyclic.
So, we have that $S T, K L$ and $D M$ are the radical axes of these three circles, $(K L S T)$, $(D M S T),(D M K L)$. These lines are, therefore, concurrent, and we have proved the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute scalene triangle. Let $X$ and $Y$ be two distinct interior points of the segment $B C$ such that $\angle C A X=\angle Y A B$. Suppose that:
1) $K$ and $S$ are the feet of perpendiculars from $B$ to the lines $A X$ and $A Y$ respectively;
2) $T$ and $L$ are the feet of perpendiculars from $C$ to the lines $A X$ and $A Y$ respectively. Prove that $K L$ and $S T$ intersect on the line $B C$.
## Proposed by Greece
|
Denote $\phi=\widehat{X A B}=\widehat{Y A C}, \alpha=\widehat{C A X}=\widehat{B A Y}$. Then, because the quadrilaterals ABSK and ACTL are cyclic, we have
$$
\widehat{B S K}+\widehat{B A K}=180^{\circ}=\widehat{B S K}+\phi=\widehat{L A C}+\widehat{L T C}=\widehat{L T C}+\phi
$$
so, due to the 90-degree angles formed, we have $\widehat{K S L}=\widehat{K T L}$. Thus, KLST is cyclic.

Figure 1: G6
Consider $M$ to be the midpoint of $B C$ and $K^{\prime}$ to be the symmetric point of $K$ with respect to $M$. Then, $B K C K^{\prime}$ is a parallelogram, and so $B K \| C K^{\prime}$. But $B K \| C T$, because they are both perpendicular to $A X$. So, $K^{\prime}$ lies on $C T$ and, as $\widehat{K T K^{\prime}}=90$ and $M$ is the midpoint of $K K^{\prime}, M K=M T$. In a similar way, we have that $M S=M L$. Thus, the center of $(K L S T)$ is $M$.
Consider $D$ to be the foot of altitude from $A$ to $B C$. Then, $D$ belongs in both $(A B K S)$ and $(A C L T)$. So,
$$
\widehat{A D T}+\widehat{A C T}=180^{\circ}=\widehat{A B S}+\widehat{A D S}=\widehat{A D T}+90^{\circ}-\alpha=\widehat{A D S}+90^{\circ}-\alpha
$$
and $A D$ is the bisector of $\widehat{S D T}$.
Because $D M$ is perpendicular to $A D, D M$ is the external bisector of this angle, and, as $M S=M T$, it follows that $D M S T$ is cyclic. In a similar way, we have that $D M L K$ is also cyclic.
So, we have that $S T, K L$ and $D M$ are the radical axes of these three circles, $(K L S T)$, $(D M S T),(D M K L)$. These lines are, therefore, concurrent, and we have proved the desired result.
|
{
"resource_path": "Balkan_MO/segmented/en-2019-BMO-type1.jsonl",
"problem_match": "# Problem 3.",
"solution_match": "\nSolution."
}
|
2c00dbbb-d31f-5fc0-a1eb-f5b20853f219
| 604,628
|
Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\gamma$.
|
. We will first prove that $C$ is the midpoint of the segment $B E$. From the angle equalities
- $\angle B C D=\angle A C B=\angle C B A=\angle E B A$
- $\angle B D C=\angle B A D+\angle D B A=\angle B A D+\angle D A E=\angle B A E$
we can conclude that the triangles $\triangle A B E$ and $\triangle D C B$ are similar.
Thus, $B E / B C=A B / C D=2$, which implies that $C$ is indeed the midpoint of the segment $B E$.
We will now prove that $A E$ is tangent to the circle $A C O$. From the angle equalities
- $\angle O A E=90^{\circ}-\angle E B A$
- $\angle O C A=\angle O C B-\angle A C B=90^{\circ}-\angle C B A=90^{\circ}-\angle E B A$
we can conclude that $\angle O A E=\angle O C A$, which implies that $A E$ is indeed tangent to the circle $A C O$.
Finally, let $\Gamma$ be the image of $\gamma$ under the homothethy of center $A$ and factor 2 . Clearly, $\Gamma$ is also tangent to $A E$ at $A$ and passes through $C$, so $\Gamma$ must coincide with the circle $A C O$, which obviously passes through $O$. Thus, $\gamma$ passes through the midpoint of the segment $A O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\gamma$.

|
. We will first prove that $C$ is the midpoint of the segment $B E$. From the angle equalities
- $\angle B C D=\angle A C B=\angle C B A=\angle E B A$
- $\angle B D C=\angle B A D+\angle D B A=\angle B A D+\angle D A E=\angle B A E$
we can conclude that the triangles $\triangle A B E$ and $\triangle D C B$ are similar.
Thus, $B E / B C=A B / C D=2$, which implies that $C$ is indeed the midpoint of the segment $B E$.
We will now prove that $A E$ is tangent to the circle $A C O$. From the angle equalities
- $\angle O A E=90^{\circ}-\angle E B A$
- $\angle O C A=\angle O C B-\angle A C B=90^{\circ}-\angle C B A=90^{\circ}-\angle E B A$
we can conclude that $\angle O A E=\angle O C A$, which implies that $A E$ is indeed tangent to the circle $A C O$.
Finally, let $\Gamma$ be the image of $\gamma$ under the homothethy of center $A$ and factor 2 . Clearly, $\Gamma$ is also tangent to $A E$ at $A$ and passes through $C$, so $\Gamma$ must coincide with the circle $A C O$, which obviously passes through $O$. Thus, $\gamma$ passes through the midpoint of the segment $A O$.

|
{
"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 1"
}
|
b44d9ca9-d550-5c53-9bd3-466717b20c72
| 604,656
|
Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\gamma$.

|
. Like in the previous solution, we will first prove that $C$ is the midpoint of the segment $B E$. Let $F$ be the midpoint of the segment $A B$. Because $\angle E A C=\angle A B D=\angle F C D$, we have that $C F \| A E$. This implies that $C F$ is a midline in triangle $\triangle B A E$, so $C$ is indeed the midpoint of the segment $B E$.
Let $L$ be the midpoint of the segment $A O$. Because $L D$ is a midline in triangle $\triangle A O C$, so $L D \| O C$, which means that $\angle A L D=\angle A O C$. From the angle equalities
- $\angle A L D=\angle A O C=\angle B O C+\angle A O B=\angle B A E+2 \angle B E A$
- $\angle A B D=\angle C E A=\angle B C A-\angle B E A=\angle A B E-\angle B E A$
- $\angle A L D+\angle A B D=\angle B A E+2 \angle B E A+\angle A B E-\angle B E A=180^{\circ}$
we obtain that the quadrilateral $A B D L$ is cyclic, thus $L$ lies on $\gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\gamma$.

|
. Like in the previous solution, we will first prove that $C$ is the midpoint of the segment $B E$. Let $F$ be the midpoint of the segment $A B$. Because $\angle E A C=\angle A B D=\angle F C D$, we have that $C F \| A E$. This implies that $C F$ is a midline in triangle $\triangle B A E$, so $C$ is indeed the midpoint of the segment $B E$.
Let $L$ be the midpoint of the segment $A O$. Because $L D$ is a midline in triangle $\triangle A O C$, so $L D \| O C$, which means that $\angle A L D=\angle A O C$. From the angle equalities
- $\angle A L D=\angle A O C=\angle B O C+\angle A O B=\angle B A E+2 \angle B E A$
- $\angle A B D=\angle C E A=\angle B C A-\angle B E A=\angle A B E-\angle B E A$
- $\angle A L D+\angle A B D=\angle B A E+2 \angle B E A+\angle A B E-\angle B E A=180^{\circ}$
we obtain that the quadrilateral $A B D L$ is cyclic, thus $L$ lies on $\gamma$.

|
{
"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 2"
}
|
b44d9ca9-d550-5c53-9bd3-466717b20c72
| 604,656
|
Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\gamma$.

|
. Like in the previous solutions, establish that $C$ is the midpoint of the segment $B E$.
Let $S$ be the intersection between $B D$ and $A E$. We will first show that $S$ also lies on $C O$. Because
$$
\angle B D C=\angle B A D+\angle D B A=\angle B A D+\angle D A E=\angle B A E
$$
(just like in solution 1), we obtain that the triangle $\triangle S B E$ is isosceles, so $C O$ passes through $S$, because it is the perpendicular bisector of the segment $B E$.
Because $\angle B O C=\angle B A S$, we obtain that the quadrilateral $A S O B$ is cyclic, so $\angle B A L=\angle B S O$. Denote by $L$ the intersection between $A O$ and $\gamma$, then $\angle L D S=\angle B A L$. Combining these two equalities leads to $\angle B S O=\angle L D S$, so $L D \| S O$.
This means that $L D$ is midline in triangle $\triangle A O C$, so $L$, which lies on $\gamma$, is the midpoint of the segment $A O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\gamma$.

|
. Like in the previous solutions, establish that $C$ is the midpoint of the segment $B E$.
Let $S$ be the intersection between $B D$ and $A E$. We will first show that $S$ also lies on $C O$. Because
$$
\angle B D C=\angle B A D+\angle D B A=\angle B A D+\angle D A E=\angle B A E
$$
(just like in solution 1), we obtain that the triangle $\triangle S B E$ is isosceles, so $C O$ passes through $S$, because it is the perpendicular bisector of the segment $B E$.
Because $\angle B O C=\angle B A S$, we obtain that the quadrilateral $A S O B$ is cyclic, so $\angle B A L=\angle B S O$. Denote by $L$ the intersection between $A O$ and $\gamma$, then $\angle L D S=\angle B A L$. Combining these two equalities leads to $\angle B S O=\angle L D S$, so $L D \| S O$.
This means that $L D$ is midline in triangle $\triangle A O C$, so $L$, which lies on $\gamma$, is the midpoint of the segment $A O$.

|
{
"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 3"
}
|
b44d9ca9-d550-5c53-9bd3-466717b20c72
| 604,656
|
Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\gamma$.

|
. Like in the previous solutions, establish that $C$ is the midpoint of the segment $B E$.
Let $F$ be the midpoint of the segment $A B$. Then both $F$ and $C$ lie on the circle of diameter $B O$. Because the quadrilateral $B F D C$ is cyclic, it means that $D$ also lies on that circle.
Let $K$ be the midpoint of $B O$. Then, $A K$ must be the perpendicular bisector of the segment $B C$, so $A K \| O C$, which implies that $\angle K A D=\angle D C O$. However, $\angle D C O=\angle K B D$, because $D B C O$ is cyclic. From the two equalities we obtain that $\angle K A D=\angle K B D$, so $K$ lies on $\gamma$. Furthermore, $A K$ is the bisector of $\angle B A D$, so $K$ is in fact the midpoint of the $\operatorname{arc} B D$.
Now consider a reflection across $O F$. Clearly, $B$ maps to $A$. Because $O F$ is the perpendicular bisector of the segment $A B, \gamma$ maps to itself through this reflection. Thus, $K$, the intersection between $O B$ and $\gamma$, will map to $L$, the intersection between $O A$ and $\gamma$. This implies that $L$ is the midpoint of the segment $A O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A B=A C$, let $D$ be the midpoint of the side $A C$, and let $\gamma$ be the circumcircle of the triangle $A B D$. The tangent of $\gamma$ at $A$ crosses the line $B C$ at $E$. Let $O$ be the circumcentre of the triangle $A B E$. Prove that the midpoint of the segment $A O$ lies on $\gamma$.

|
. Like in the previous solutions, establish that $C$ is the midpoint of the segment $B E$.
Let $F$ be the midpoint of the segment $A B$. Then both $F$ and $C$ lie on the circle of diameter $B O$. Because the quadrilateral $B F D C$ is cyclic, it means that $D$ also lies on that circle.
Let $K$ be the midpoint of $B O$. Then, $A K$ must be the perpendicular bisector of the segment $B C$, so $A K \| O C$, which implies that $\angle K A D=\angle D C O$. However, $\angle D C O=\angle K B D$, because $D B C O$ is cyclic. From the two equalities we obtain that $\angle K A D=\angle K B D$, so $K$ lies on $\gamma$. Furthermore, $A K$ is the bisector of $\angle B A D$, so $K$ is in fact the midpoint of the $\operatorname{arc} B D$.
Now consider a reflection across $O F$. Clearly, $B$ maps to $A$. Because $O F$ is the perpendicular bisector of the segment $A B, \gamma$ maps to itself through this reflection. Thus, $K$, the intersection between $O B$ and $\gamma$, will map to $L$, the intersection between $O A$ and $\gamma$. This implies that $L$ is the midpoint of the segment $A O$.
|
{
"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 4"
}
|
b44d9ca9-d550-5c53-9bd3-466717b20c72
| 604,656
|
Let $a_{1}=2$ and, for every positive integer $n$, let $a_{n+1}$ be the smallest integer strictly greater than $a_{n}$ that has more positive divisors than $a_{n}$. Prove that $2 a_{n+1}=3 a_{n}$ only for finitely many indices $n$.
|
Begin with a mere remark on the terms of the sequence under consideration.
Lemma 1. Each $a_{n}$ is minimal amongst all positive integers having the same number of positive divisors as $a_{n}$.
Proof. Suppose, if possible, that for some $n$, some positive integer $b<a_{n}$ has as many positive divisors as $a_{n}$. Then $a_{m}<b \leqslant a_{m+1}$ for some $m<n$, and the definition of the sequence forces $b=a_{m+1}$. Since $b<a_{n}$, it follows that $m+1<n$, which is a contradiction, as $a_{m+1}$ should have less positive divisors than $a_{n}$.
Let $p_{1}<p_{2}<\cdots<p_{n}<\cdots$ be the strictly increasing sequence of prime numbers, and write canonical factorisations into primes in the form $N=\prod_{i \geqslant 1} p_{i}^{e_{i}}$, where $e_{i} \geqslant 0$ for all $i$, and $e_{i}=0$ for all but finitely many indices $i$; in this notation, the number of positive divisors of $N$ is $\tau(N)=$ $\prod_{i \geqslant 1}\left(e_{i}+1\right)$.
Lemma 2. The exponents in the canonical factorisation of each $a_{n}$ into primes form a non-strictly decreasing sequence.
Proof. Indeed, if $e_{i}<e_{j}$ for some $i<j$ in the canonical decomposition of $a_{n}$ into primes, then swapping the two exponents yields a smaller integer with the same number of positive divisors, contradicting Lemma 1.
We are now in a position to prove the required result. For convenience, a term $a_{n}$ satisfying $3 a_{n}=2 a_{n+1}$ will be referred to as a special term of the sequence.
Suppose now, if possible, that the sequence has infinitely many special terms, so the latter form a strictly increasing, and hence unbounded, subsequence. To reach a contradiction, it is sufficient to show that:
(1) The exponents of the primes in the factorisation of special terms have a common upper bound $e$; and
(2) For all large enough primes $p$, no special term is divisible by $p$.
Refer to Lemma 2 to write $a_{n}=\prod_{i \geqslant 1} p_{i}^{e_{i}(n)}$, where $e_{i}(n) \geqslant e_{i+1}(n)$ for all $i$.
Statement (2) is a straightforward consequence of (1) and Lemma 1. Suppose, if possible, that some special term $a_{n}$ is divisible by a prime $p_{i}>2^{e+1}$, where $e$ is the integer provided by (1). Then $e \geqslant e_{i}(n)>0$, so $2^{e_{1}(n) e_{i}(n)+e_{i}(n)} a_{n} / p_{i}^{e_{i}(n)}$ is a positive integer with the same number of positive divisors as $a_{n}$, but smaller than $a_{n}$. This contradicts Lemma 1. Consequently, no special term is divisible by a prime exceeding $2^{e+1}$.
To prove (1), it is sufficient to show that, as $a_{n}$ runs through the special terms, the exponents $e_{1}(n)$ are bounded from above. Then, Lemma 2 shows that such an upper bound $e$ suits all primes.
Consider a large enough special $a_{n}$. The condition $\tau\left(a_{n}\right)<\tau\left(a_{n+1}\right)$ is then equivalent to $\left(e_{1}(n)+1\right)\left(e_{2}(n)+1\right)<e_{1}(n)\left(e_{2}(n)+2\right)$. Alternatively, but equivalently, $e_{1}(n) \geqslant e_{2}(n)+2$. The latter implies that $a_{n}$ is divisible by 8 , for either $e_{1}(n) \geqslant 3$ or $a_{n}$ is a large enough power of 2 .
Next, note that $9 a_{n} / 8$ is an integer strictly between $a_{n}$ and $a_{n+1}$, so $\tau\left(9 a_{n} / 8\right) \leqslant \tau\left(a_{n}\right)$, which is equivalent to
$$
\left(e_{1}(n)-2\right)\left(e_{2}(n)+3\right) \leqslant\left(e_{1}(n)+1\right)\left(e_{2}(n)+1\right),
$$
so $2 e_{1}(n) \leqslant 3 e_{2}(n)+7$. This shows that $a_{n}$ is divisible by 3 , for otherwise, letting $a_{n}$ run through the special terms, 3 would be an upper bound for all but finitely many $e_{1}(n)$, and the special terms would therefore form a bounded sequence.
Thus, $4 a_{n} / 3$ is another integer strictly between $a_{n}$ and $a_{n+1}$. As before, $\tau\left(4 a_{n} / 3\right) \leqslant \tau\left(a_{n}\right)$. Alternatively, but equivalently,
$$
\left(e_{1}(n)+3\right) e_{2}(n) \leqslant\left(e_{1}(n)+1\right)\left(e_{2}(n)+1\right),
$$
so $2 e_{2}(n)-1 \leqslant e_{1}(n)$. Combine this with the inequality in the previous paragraph to write $4 e_{2}(n)-2 \leqslant 2 e_{1}(n) \leqslant 3 e_{2}(n)+7$ and infer that $e_{2}(n) \leqslant 9$. Consequently, $2 e_{1}(n) \leqslant 3 e_{2}(n)+7 \leqslant 34$, showing that $e=17$ is suitable for (1) to hold. This establishes (1) and completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}=2$ and, for every positive integer $n$, let $a_{n+1}$ be the smallest integer strictly greater than $a_{n}$ that has more positive divisors than $a_{n}$. Prove that $2 a_{n+1}=3 a_{n}$ only for finitely many indices $n$.
|
Begin with a mere remark on the terms of the sequence under consideration.
Lemma 1. Each $a_{n}$ is minimal amongst all positive integers having the same number of positive divisors as $a_{n}$.
Proof. Suppose, if possible, that for some $n$, some positive integer $b<a_{n}$ has as many positive divisors as $a_{n}$. Then $a_{m}<b \leqslant a_{m+1}$ for some $m<n$, and the definition of the sequence forces $b=a_{m+1}$. Since $b<a_{n}$, it follows that $m+1<n$, which is a contradiction, as $a_{m+1}$ should have less positive divisors than $a_{n}$.
Let $p_{1}<p_{2}<\cdots<p_{n}<\cdots$ be the strictly increasing sequence of prime numbers, and write canonical factorisations into primes in the form $N=\prod_{i \geqslant 1} p_{i}^{e_{i}}$, where $e_{i} \geqslant 0$ for all $i$, and $e_{i}=0$ for all but finitely many indices $i$; in this notation, the number of positive divisors of $N$ is $\tau(N)=$ $\prod_{i \geqslant 1}\left(e_{i}+1\right)$.
Lemma 2. The exponents in the canonical factorisation of each $a_{n}$ into primes form a non-strictly decreasing sequence.
Proof. Indeed, if $e_{i}<e_{j}$ for some $i<j$ in the canonical decomposition of $a_{n}$ into primes, then swapping the two exponents yields a smaller integer with the same number of positive divisors, contradicting Lemma 1.
We are now in a position to prove the required result. For convenience, a term $a_{n}$ satisfying $3 a_{n}=2 a_{n+1}$ will be referred to as a special term of the sequence.
Suppose now, if possible, that the sequence has infinitely many special terms, so the latter form a strictly increasing, and hence unbounded, subsequence. To reach a contradiction, it is sufficient to show that:
(1) The exponents of the primes in the factorisation of special terms have a common upper bound $e$; and
(2) For all large enough primes $p$, no special term is divisible by $p$.
Refer to Lemma 2 to write $a_{n}=\prod_{i \geqslant 1} p_{i}^{e_{i}(n)}$, where $e_{i}(n) \geqslant e_{i+1}(n)$ for all $i$.
Statement (2) is a straightforward consequence of (1) and Lemma 1. Suppose, if possible, that some special term $a_{n}$ is divisible by a prime $p_{i}>2^{e+1}$, where $e$ is the integer provided by (1). Then $e \geqslant e_{i}(n)>0$, so $2^{e_{1}(n) e_{i}(n)+e_{i}(n)} a_{n} / p_{i}^{e_{i}(n)}$ is a positive integer with the same number of positive divisors as $a_{n}$, but smaller than $a_{n}$. This contradicts Lemma 1. Consequently, no special term is divisible by a prime exceeding $2^{e+1}$.
To prove (1), it is sufficient to show that, as $a_{n}$ runs through the special terms, the exponents $e_{1}(n)$ are bounded from above. Then, Lemma 2 shows that such an upper bound $e$ suits all primes.
Consider a large enough special $a_{n}$. The condition $\tau\left(a_{n}\right)<\tau\left(a_{n+1}\right)$ is then equivalent to $\left(e_{1}(n)+1\right)\left(e_{2}(n)+1\right)<e_{1}(n)\left(e_{2}(n)+2\right)$. Alternatively, but equivalently, $e_{1}(n) \geqslant e_{2}(n)+2$. The latter implies that $a_{n}$ is divisible by 8 , for either $e_{1}(n) \geqslant 3$ or $a_{n}$ is a large enough power of 2 .
Next, note that $9 a_{n} / 8$ is an integer strictly between $a_{n}$ and $a_{n+1}$, so $\tau\left(9 a_{n} / 8\right) \leqslant \tau\left(a_{n}\right)$, which is equivalent to
$$
\left(e_{1}(n)-2\right)\left(e_{2}(n)+3\right) \leqslant\left(e_{1}(n)+1\right)\left(e_{2}(n)+1\right),
$$
so $2 e_{1}(n) \leqslant 3 e_{2}(n)+7$. This shows that $a_{n}$ is divisible by 3 , for otherwise, letting $a_{n}$ run through the special terms, 3 would be an upper bound for all but finitely many $e_{1}(n)$, and the special terms would therefore form a bounded sequence.
Thus, $4 a_{n} / 3$ is another integer strictly between $a_{n}$ and $a_{n+1}$. As before, $\tau\left(4 a_{n} / 3\right) \leqslant \tau\left(a_{n}\right)$. Alternatively, but equivalently,
$$
\left(e_{1}(n)+3\right) e_{2}(n) \leqslant\left(e_{1}(n)+1\right)\left(e_{2}(n)+1\right),
$$
so $2 e_{2}(n)-1 \leqslant e_{1}(n)$. Combine this with the inequality in the previous paragraph to write $4 e_{2}(n)-2 \leqslant 2 e_{1}(n) \leqslant 3 e_{2}(n)+7$ and infer that $e_{2}(n) \leqslant 9$. Consequently, $2 e_{1}(n) \leqslant 3 e_{2}(n)+7 \leqslant 34$, showing that $e=17$ is suitable for (1) to hold. This establishes (1) and completes the solution.
|
{
"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl",
"problem_match": "## 2020 BMO, Problem 4",
"solution_match": "\nSolution."
}
|
17f3c23d-30bf-5bf4-add0-149a7077a44b
| 604,740
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$. Suppose also that $X$ and $C$ lie on opposite sides of the line $A B$ and that $Y$ and $B$ lie on opposite sides of the line $A C$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
|
. Extend $X A$ and $Y A$ to meet $\omega$ again at $X^{\prime}$ and $Y^{\prime}$ respectively. We then have that:
$$
\angle Y^{\prime} Y C=\angle A Y C=\angle B X A=\angle B X X^{\prime} .
$$
so $B C X^{\prime} Y^{\prime}$ is an isosceles trapezium and hence $X^{\prime} Y^{\prime} \| B C$.
Let $\ell$ be the line through $A$ parallel to $B C$ and let $\ell$ intersect $\omega$ at $P, Q$ with $P$ on the opposite side of $A B$ to $C$. As $X^{\prime} Y^{\prime}\|B C\| P Q$ then
$$
\angle X A P=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A
$$
which shows that $\ell$ is tangent to the circumcircle of triangle $A X Y$. Let $X Y$ intersect $P Q$ at $Z$. By power of a point we have that
$$
Z A^{2}=Z X \cdot Z Y=Z P \cdot Z Q
$$
As $P, Q$ are independent of the positions of $X, Y$, this shows that $Z$ is fixed and hence $X Y$ passes through a fixed point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$. Suppose also that $X$ and $C$ lie on opposite sides of the line $A B$ and that $Y$ and $B$ lie on opposite sides of the line $A C$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
|
. Extend $X A$ and $Y A$ to meet $\omega$ again at $X^{\prime}$ and $Y^{\prime}$ respectively. We then have that:
$$
\angle Y^{\prime} Y C=\angle A Y C=\angle B X A=\angle B X X^{\prime} .
$$
so $B C X^{\prime} Y^{\prime}$ is an isosceles trapezium and hence $X^{\prime} Y^{\prime} \| B C$.

Let $\ell$ be the line through $A$ parallel to $B C$ and let $\ell$ intersect $\omega$ at $P, Q$ with $P$ on the opposite side of $A B$ to $C$. As $X^{\prime} Y^{\prime}\|B C\| P Q$ then
$$
\angle X A P=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A
$$
which shows that $\ell$ is tangent to the circumcircle of triangle $A X Y$. Let $X Y$ intersect $P Q$ at $Z$. By power of a point we have that
$$
Z A^{2}=Z X \cdot Z Y=Z P \cdot Z Q
$$
As $P, Q$ are independent of the positions of $X, Y$, this shows that $Z$ is fixed and hence $X Y$ passes through a fixed point.
|
{
"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl",
"problem_match": "## BMO 2021 - Problem 1",
"solution_match": "\nSolution 1"
}
|
323e6cc8-3aa0-5b14-96d5-52936f05b76d
| 604,756
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$. Suppose also that $X$ and $C$ lie on opposite sides of the line $A B$ and that $Y$ and $B$ lie on opposite sides of the line $A C$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
|
. Let $B^{\prime}$ and $C^{\prime}$ be the points of intersection of the lines $A B$ and $A C$ with $\omega$ respectively and let $\omega_{1}$ be the circumcircle of the triangle $A B^{\prime} C^{\prime}$. Let $\varepsilon$ be the tangent to $\omega_{1}$ at the point $A$. Because $A B<A C$ the lines $B^{\prime} C^{\prime}$ and $\varepsilon$ intersects at a point $Z$ which is fixed and independent of $X$ and $Y$.
We have
$$
\angle Z A C^{\prime}=\angle C^{\prime} B^{\prime} A=\angle C^{\prime} B^{\prime} B=\angle C^{\prime} C B .
$$
Therefore, $\varepsilon \| B C$.
Let $X^{\prime}, Y^{\prime}$ be the points of intersection of the lines $X A, Y A$ with $\omega$ respecively. From the hypothesis we have $\angle B X X^{\prime}=\angle Y^{\prime} Y C$. Therefore
$$
\widehat{B X^{\prime}}=\widehat{Y^{\prime} C} \Longrightarrow \widehat{B C}+\widehat{C X^{\prime}}=\widehat{Y^{\prime} B}+\widehat{B C} \Longrightarrow \widehat{C X^{\prime}}=\widehat{Y^{\prime} B}
$$
and so $X^{\prime} Y^{\prime}\|B C\| \varepsilon$. Thus
$$
\angle X A Z=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A .
$$
From the last equality we have that $\varepsilon$ is also tangent to the circmucircle $\omega_{2}$ of the triangle $X A Y$.
Consider now the radical centre of the circles $\omega, \omega_{1}, \omega_{2}$. This is the point of intersection of the radical axes $B^{\prime} C^{\prime}\left(\right.$ of $\omega$ and $\left.\omega_{1}\right), \varepsilon\left(\right.$ of $\omega_{1}$ and $\left.\omega_{2}\right)$ and $X Y$ (of $\omega$ and $\omega_{2}$ ).
This must be point $Z$ and therefore the variable line $X Y$ passes through the fixed point $Z$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$. Suppose also that $X$ and $C$ lie on opposite sides of the line $A B$ and that $Y$ and $B$ lie on opposite sides of the line $A C$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
|
. Let $B^{\prime}$ and $C^{\prime}$ be the points of intersection of the lines $A B$ and $A C$ with $\omega$ respectively and let $\omega_{1}$ be the circumcircle of the triangle $A B^{\prime} C^{\prime}$. Let $\varepsilon$ be the tangent to $\omega_{1}$ at the point $A$. Because $A B<A C$ the lines $B^{\prime} C^{\prime}$ and $\varepsilon$ intersects at a point $Z$ which is fixed and independent of $X$ and $Y$.

We have
$$
\angle Z A C^{\prime}=\angle C^{\prime} B^{\prime} A=\angle C^{\prime} B^{\prime} B=\angle C^{\prime} C B .
$$
Therefore, $\varepsilon \| B C$.
Let $X^{\prime}, Y^{\prime}$ be the points of intersection of the lines $X A, Y A$ with $\omega$ respecively. From the hypothesis we have $\angle B X X^{\prime}=\angle Y^{\prime} Y C$. Therefore
$$
\widehat{B X^{\prime}}=\widehat{Y^{\prime} C} \Longrightarrow \widehat{B C}+\widehat{C X^{\prime}}=\widehat{Y^{\prime} B}+\widehat{B C} \Longrightarrow \widehat{C X^{\prime}}=\widehat{Y^{\prime} B}
$$
and so $X^{\prime} Y^{\prime}\|B C\| \varepsilon$. Thus
$$
\angle X A Z=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A .
$$
From the last equality we have that $\varepsilon$ is also tangent to the circmucircle $\omega_{2}$ of the triangle $X A Y$.
Consider now the radical centre of the circles $\omega, \omega_{1}, \omega_{2}$. This is the point of intersection of the radical axes $B^{\prime} C^{\prime}\left(\right.$ of $\omega$ and $\left.\omega_{1}\right), \varepsilon\left(\right.$ of $\omega_{1}$ and $\left.\omega_{2}\right)$ and $X Y$ (of $\omega$ and $\omega_{2}$ ).
This must be point $Z$ and therefore the variable line $X Y$ passes through the fixed point $Z$.
|
{
"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl",
"problem_match": "## BMO 2021 - Problem 1",
"solution_match": "\nSolution 2"
}
|
323e6cc8-3aa0-5b14-96d5-52936f05b76d
| 604,756
|
Let $a, b$ and $c$ be positive integers satisfying the equation
$$
(a, b)+[a, b]=2021^{c} .
$$
If $|a-b|$ is a prime number, prove that the number $(a+b)^{2}+4$ is composite.
Here, $(a, b)$ denotes the greatest common divisor of $a$ and $b$, and $[a, b]$ denotes the least common multiple of $a$ and $b$.
|
We write $p=|a-b|$ and assume for contradiction that $q=(a+b)^{2}+4$ is a prime number.
Since $(a, b) \mid[a, b]$, we have that $(a, b) \mid 2021^{c}$. As $(a, b)$ also divides $p=|a-b|$, it follows that $(a, b) \in\{1,43,47\}$. We will consider all 3 cases separately:
(1) If $(a, b)=1$, then $1+a b=2021^{c}$, and therefore
$$
q=(a+b)^{2}+4=(a-b)^{2}+4(1+a b)=p^{2}+4 \cdot 2021^{c} .
$$
(a) Suppose $c$ is even. Since $q \equiv 1 \bmod 4$, it can be represented uniquely (up to order) as a sum of two (non-negative) squares. But (1) gives potentially two such representations so in order to have uniqueness we must have $p=2$. But then $4 \mid q$ a contradiction.
(b) If $c$ is odd then $a b=2021^{c}-1 \equiv 1 \bmod 3$. Thus $a \equiv b \bmod 3$ implying that $p=|a-b| \equiv 0 \bmod 3$. Therefore $p=3$. Without loss of generality $b=a+3$. Then $2021^{c}=a b+1=a^{2}+3 a+1$ and so
$$
(2 a+3)^{2}=4 a^{2}+12 a+9=4 \cdot 2021^{c}+5
$$
So 5 is a quadratic residue modulo 47, a contradiction as
$$
\left(\frac{5}{47}\right)=\left(\frac{47}{5}\right)=\left(\frac{2}{5}\right)=-1 .
$$
(2) If $(a, b)=43$, then $p=|a-b|=43$ and we may assume that $a=43 k$ and $b=43(k+1)$, for some $k \in \mathbb{N}$. Then $2021^{c}=43+43 k(k+1)$ giving that
$$
(2 k+1)^{2}=4 k^{2}+4 k+4-3=4 \cdot 43^{c-1} \cdot 47-3 .
$$
So -3 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{-3}{47}\right)=\left(\frac{-1}{47}\right)\left(\frac{3}{47}\right)=\left(\frac{47}{3}\right)=\left(\frac{2}{3}\right)=-1
$$
(3) If $(a, b)=47$ then analogously there is a $k \in \mathbb{N}$ such that
$$
(2 k+1)^{2}=4 \cdot 43^{c} \cdot 47^{c-1}-3 .
$$
If $c>1$ then we get a contradiction in exactly the same way as in (2). If $c=1$ then $(2 k+1)^{2}=169$ giving $k=6$. This implies that $a+b=47 \cdot 6+47 \cdot 7=47 \cdot 13 \equiv 1 \bmod 5$. Thus $q=(a+b)^{2}+4 \equiv 0 \bmod 5$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b$ and $c$ be positive integers satisfying the equation
$$
(a, b)+[a, b]=2021^{c} .
$$
If $|a-b|$ is a prime number, prove that the number $(a+b)^{2}+4$ is composite.
Here, $(a, b)$ denotes the greatest common divisor of $a$ and $b$, and $[a, b]$ denotes the least common multiple of $a$ and $b$.
|
We write $p=|a-b|$ and assume for contradiction that $q=(a+b)^{2}+4$ is a prime number.
Since $(a, b) \mid[a, b]$, we have that $(a, b) \mid 2021^{c}$. As $(a, b)$ also divides $p=|a-b|$, it follows that $(a, b) \in\{1,43,47\}$. We will consider all 3 cases separately:
(1) If $(a, b)=1$, then $1+a b=2021^{c}$, and therefore
$$
q=(a+b)^{2}+4=(a-b)^{2}+4(1+a b)=p^{2}+4 \cdot 2021^{c} .
$$
(a) Suppose $c$ is even. Since $q \equiv 1 \bmod 4$, it can be represented uniquely (up to order) as a sum of two (non-negative) squares. But (1) gives potentially two such representations so in order to have uniqueness we must have $p=2$. But then $4 \mid q$ a contradiction.
(b) If $c$ is odd then $a b=2021^{c}-1 \equiv 1 \bmod 3$. Thus $a \equiv b \bmod 3$ implying that $p=|a-b| \equiv 0 \bmod 3$. Therefore $p=3$. Without loss of generality $b=a+3$. Then $2021^{c}=a b+1=a^{2}+3 a+1$ and so
$$
(2 a+3)^{2}=4 a^{2}+12 a+9=4 \cdot 2021^{c}+5
$$
So 5 is a quadratic residue modulo 47, a contradiction as
$$
\left(\frac{5}{47}\right)=\left(\frac{47}{5}\right)=\left(\frac{2}{5}\right)=-1 .
$$
(2) If $(a, b)=43$, then $p=|a-b|=43$ and we may assume that $a=43 k$ and $b=43(k+1)$, for some $k \in \mathbb{N}$. Then $2021^{c}=43+43 k(k+1)$ giving that
$$
(2 k+1)^{2}=4 k^{2}+4 k+4-3=4 \cdot 43^{c-1} \cdot 47-3 .
$$
So -3 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{-3}{47}\right)=\left(\frac{-1}{47}\right)\left(\frac{3}{47}\right)=\left(\frac{47}{3}\right)=\left(\frac{2}{3}\right)=-1
$$
(3) If $(a, b)=47$ then analogously there is a $k \in \mathbb{N}$ such that
$$
(2 k+1)^{2}=4 \cdot 43^{c} \cdot 47^{c-1}-3 .
$$
If $c>1$ then we get a contradiction in exactly the same way as in (2). If $c=1$ then $(2 k+1)^{2}=169$ giving $k=6$. This implies that $a+b=47 \cdot 6+47 \cdot 7=47 \cdot 13 \equiv 1 \bmod 5$. Thus $q=(a+b)^{2}+4 \equiv 0 \bmod 5$, a contradiction.
|
{
"resource_path": "Balkan_MO/segmented/en-2021-BMO-type1.jsonl",
"problem_match": "## BMO 2021 - Problem 3",
"solution_match": "\nSolution."
}
|
c9b8ab81-62f4-5c71-83bc-a5084935c369
| 604,804
|
Problem. Let $A B C$ be an acute triangle such that $C A \neq C B$ with circumcircle $\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.
|
. Firstly observe that $O A X B$ is cyclic, with diameter $O X$, and $Y$ also lies on this circle since $O Y \perp X C$. Hence:
$$
\angle A Z C=\angle X A B=\angle A B X=\angle A Y X
$$
and so $C Y A Z$ is cyclic.
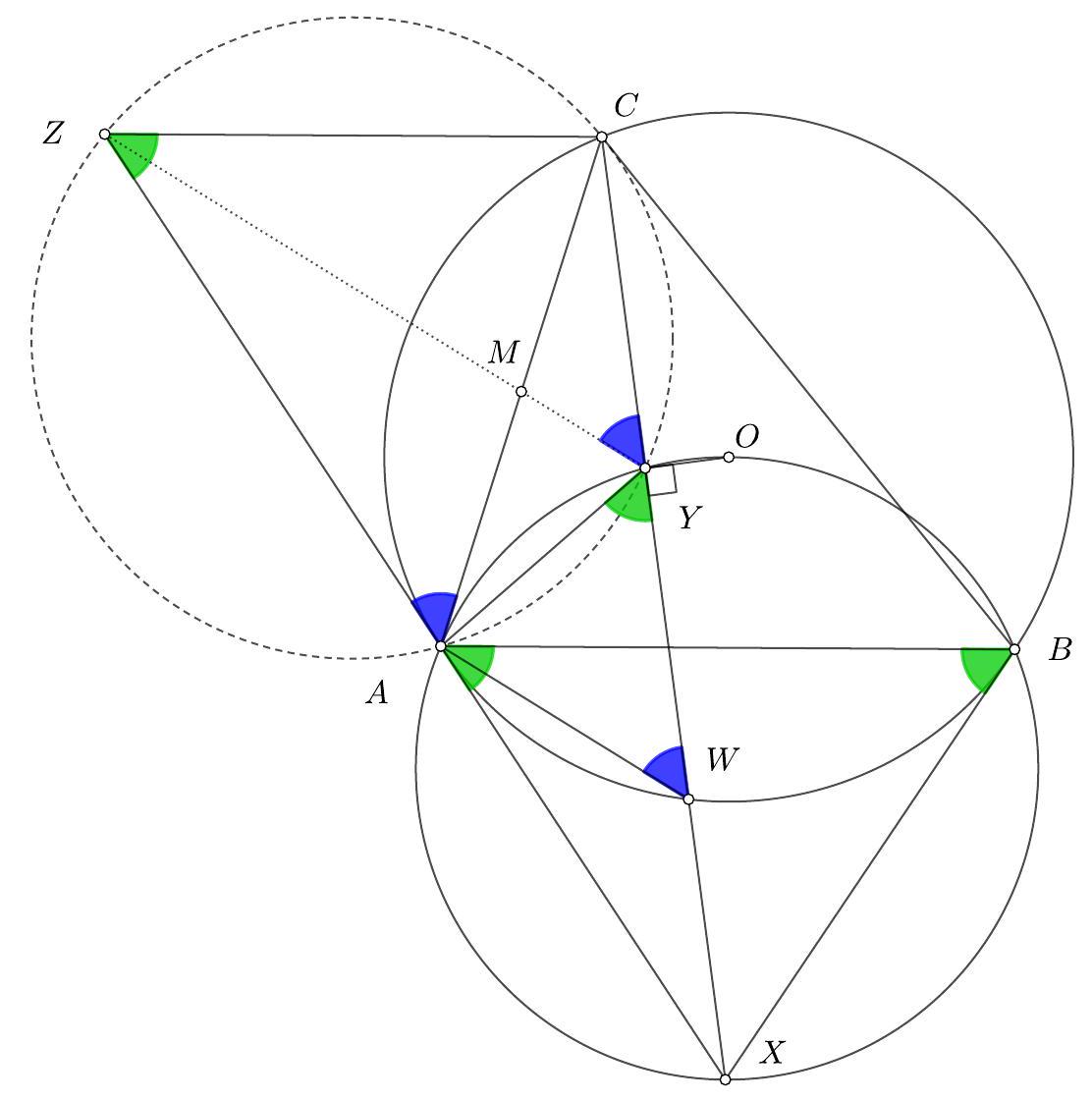
Let $M$ be the intersection of $Y Z$ and $A C$ and let $C Y$ intersect $\omega$ again at $W$. Using the new cyclic relation we get $\angle C Y Z=\angle C A Z$ and then using that $Z A$ is tangent to $\omega$ we get $\angle C A Z=\angle C W A$, so $\angle C Y M=\angle C W A$. Therefore the triangles $C W A$ and $C Y M$ are similar. But $C W$ is a chord of $\omega$, and $Y$ is the foot of the perpendicular from $O$, hence $Y$ is the midpoint of $C W$. It follows from the similarity relation that $M$ is the midpoint of $A C$, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be an acute triangle such that $C A \neq C B$ with circumcircle $\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.
|
. Firstly observe that $O A X B$ is cyclic, with diameter $O X$, and $Y$ also lies on this circle since $O Y \perp X C$. Hence:
$$
\angle A Z C=\angle X A B=\angle A B X=\angle A Y X
$$
and so $C Y A Z$ is cyclic.

Let $M$ be the intersection of $Y Z$ and $A C$ and let $C Y$ intersect $\omega$ again at $W$. Using the new cyclic relation we get $\angle C Y Z=\angle C A Z$ and then using that $Z A$ is tangent to $\omega$ we get $\angle C A Z=\angle C W A$, so $\angle C Y M=\angle C W A$. Therefore the triangles $C W A$ and $C Y M$ are similar. But $C W$ is a chord of $\omega$, and $Y$ is the foot of the perpendicular from $O$, hence $Y$ is the midpoint of $C W$. It follows from the similarity relation that $M$ is the midpoint of $A C$, as required.
|
{
"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl",
"problem_match": "# Problem 1",
"solution_match": "\nSolution 1"
}
|
d0d1dab7-85d9-56ab-aa41-17a423c90108
| 604,845
|
Problem. Let $A B C$ be an acute triangle such that $C A \neq C B$ with circumcircle $\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.
|
. Let $M$ be the midpoint of $A C$. We have $\angle C A Z=\angle C B A$ and $\angle Z C A=$ $\angle B A C$ so the triangles $C A Z$ and $A B C$ are similar. The line $C Y X$ is the $C$-symmedian of triangle $A B C$, and $Z M$ is the corresponding median in triangle $C A Z$, hence by isogonality $\angle A Z M=\angle A C Y$. So
$$
\angle Z M A=180^{\circ}-\angle A Z M-\angle M A Z=180^{\circ}-\angle A C Y-\angle C B A
$$
Now observe $\angle O M C=\angle O Y C=90^{\circ}$, so $C M Y O$ is cyclic. Thus:
$$
\angle C Y M=\angle C O M=\frac{1}{2} \angle C O A=\angle C B A
$$
This shows that
$$
\angle Y M C=180^{\circ}-\angle M C Y-\angle C Y M=180^{\circ}-\angle A C Y-\angle C B A
$$
Combining this with (1) we get that $\angle Y M C=\angle Z M A$ and as $A, C, M$ are collinear, it follows that $Z, M, Y$ are collinear as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be an acute triangle such that $C A \neq C B$ with circumcircle $\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.
|
. Let $M$ be the midpoint of $A C$. We have $\angle C A Z=\angle C B A$ and $\angle Z C A=$ $\angle B A C$ so the triangles $C A Z$ and $A B C$ are similar. The line $C Y X$ is the $C$-symmedian of triangle $A B C$, and $Z M$ is the corresponding median in triangle $C A Z$, hence by isogonality $\angle A Z M=\angle A C Y$. So
$$
\angle Z M A=180^{\circ}-\angle A Z M-\angle M A Z=180^{\circ}-\angle A C Y-\angle C B A
$$
Now observe $\angle O M C=\angle O Y C=90^{\circ}$, so $C M Y O$ is cyclic. Thus:
$$
\angle C Y M=\angle C O M=\frac{1}{2} \angle C O A=\angle C B A
$$
This shows that
$$
\angle Y M C=180^{\circ}-\angle M C Y-\angle C Y M=180^{\circ}-\angle A C Y-\angle C B A
$$
Combining this with (1) we get that $\angle Y M C=\angle Z M A$ and as $A, C, M$ are collinear, it follows that $Z, M, Y$ are collinear as required.
|
{
"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl",
"problem_match": "# Problem 1",
"solution_match": "\nSolution 2"
}
|
d0d1dab7-85d9-56ab-aa41-17a423c90108
| 604,845
|
Problem. Let $A B C$ be an acute triangle such that $C A \neq C B$ with circumcircle $\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.
|
. As in Solution 2 we have that $C X$ is the $A$-symmedian of triangle $A B C$ and that triangle $A B C$ is similar to triangle $C A Z$.
Let $f$ be the spiral similarity which maps $A C$ onto $A B$ and let $g$ be the reflection on the perpendicular bisector of $A B$. Note that $f$ is a rotation about $A$ by an angle of $\angle C A B$ (clockwise in our figure) followed by a homothety centered at $A$ by a factor of $A B / A C$. By the similarity of triangles $A B C$ and $C A Z$ we have that $g(f(Z))=C$, so actually $f(Z)$ is the other point of intersection, say $C^{\prime}$, of $C Z$ with $\omega$.
As in Solution 1 we have that $C Y A Z$ is cyclic. Therefore, letting $W$ be the other point of intersection of $C Y$ with $\omega$, we have $\angle W A B=\angle W C B=\angle C A Y$. We also have $\angle A C Y=$ $\angle A B W$. It follows that $f(Y)=W$.
Let $W^{\prime}=g(W)$. Then $W^{\prime} \in \omega$ and since $C W$ is the $A$-symmedian, then $C W^{\prime}$ passes through the midpoint $N$ of $A B$. Now $C W^{\prime}$ and $C^{\prime} W$ intersect on the perpendicular bisector of $A B$ and therefore they intersect on $N$. It follows that $N=A B \cap C^{\prime} W=A f(C) \cap f(Z) f(Y)$ is the image of $M=A C \cap Z Y$ under $f$. Since $N$ is the midpoint of $A B$, then $M$ is the midpoint of $A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be an acute triangle such that $C A \neq C B$ with circumcircle $\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.
|
. As in Solution 2 we have that $C X$ is the $A$-symmedian of triangle $A B C$ and that triangle $A B C$ is similar to triangle $C A Z$.
Let $f$ be the spiral similarity which maps $A C$ onto $A B$ and let $g$ be the reflection on the perpendicular bisector of $A B$. Note that $f$ is a rotation about $A$ by an angle of $\angle C A B$ (clockwise in our figure) followed by a homothety centered at $A$ by a factor of $A B / A C$. By the similarity of triangles $A B C$ and $C A Z$ we have that $g(f(Z))=C$, so actually $f(Z)$ is the other point of intersection, say $C^{\prime}$, of $C Z$ with $\omega$.
As in Solution 1 we have that $C Y A Z$ is cyclic. Therefore, letting $W$ be the other point of intersection of $C Y$ with $\omega$, we have $\angle W A B=\angle W C B=\angle C A Y$. We also have $\angle A C Y=$ $\angle A B W$. It follows that $f(Y)=W$.
Let $W^{\prime}=g(W)$. Then $W^{\prime} \in \omega$ and since $C W$ is the $A$-symmedian, then $C W^{\prime}$ passes through the midpoint $N$ of $A B$. Now $C W^{\prime}$ and $C^{\prime} W$ intersect on the perpendicular bisector of $A B$ and therefore they intersect on $N$. It follows that $N=A B \cap C^{\prime} W=A f(C) \cap f(Z) f(Y)$ is the image of $M=A C \cap Z Y$ under $f$. Since $N$ is the midpoint of $A B$, then $M$ is the midpoint of $A C$.
|
{
"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl",
"problem_match": "# Problem 1",
"solution_match": "\nSolution 3"
}
|
d0d1dab7-85d9-56ab-aa41-17a423c90108
| 604,845
|
Problem. Let $A B C$ be an acute triangle such that $C A \neq C B$ with circumcircle $\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.
|
. Let $E=A B \cap C X$ and $F=A W \cap C Z$. We have $(C, W ; X, E)=-1$. Projecting from the line $C X$ onto the line $C Z$ from $A$ we get that $(C, F ; Z, \infty)=-1$. Thus $Z$ is the midpoint of $C F$. Since also $Y$ is the midpoint of $C W$, we get that $Z Y$ bisects $C A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be an acute triangle such that $C A \neq C B$ with circumcircle $\omega$ and circumcentre $O$. Let $t_{A}$ and $t_{B}$ be the tangents to $\omega$ at $A$ and $B$ respectively, which meet at $X$. Let $Y$ be the foot of the perpendicular from $O$ onto the line segment $C X$. The line through $C$ parallel to line $A B$ meets $t_{A}$ at $Z$. Prove that the line $Y Z$ passes through the midpoint of the line segment $A C$.
|
. Let $E=A B \cap C X$ and $F=A W \cap C Z$. We have $(C, W ; X, E)=-1$. Projecting from the line $C X$ onto the line $C Z$ from $A$ we get that $(C, F ; Z, \infty)=-1$. Thus $Z$ is the midpoint of $C F$. Since also $Y$ is the midpoint of $C W$, we get that $Z Y$ bisects $C A$.
|
{
"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl",
"problem_match": "# Problem 1",
"solution_match": "\nSolution 4"
}
|
d0d1dab7-85d9-56ab-aa41-17a423c90108
| 604,845
|
Problem. Let $a, b$ and $n$ be positive integers with $a>b$ such that all of the following hold:
(i) $a^{2021}$ divides $n$,
(ii) $b^{2021}$ divides $n$,
(iii) 2022 divides $a-b$.
Prove that there is a subset $T$ of the set of positive divisors of the number $n$ such that the sum of the elements of $T$ is divisible by 2022 but not divisible by $2022^{2}$.
|
If $1011 \mid a$, then $1011^{2021} \mid n$ and we can take $T=\left\{1011,1011^{2}\right\}$. So we can assume that $3 \nmid a$ or $337 \nmid a$.
We continue with the following claim:
Claim. If $k$ is a positive integer, then $a^{k} b^{2021-k} \mid n$.
Proof of the Claim. We have that $n^{2021}=n^{k} \cdot n^{2021-k}$ is divisible by $a^{2021 k} \cdot b^{2021(2021-k)}$ and taking the 2021-root we get the desired result.
Back to the problem, we will prove that the set $T=\left\{a^{k} b^{2021-k}: k \geqslant 0\right\}$ consisting of 2022 divisors of $n$, has the desired property. The sum of its elements is equal to
$$
S=\sum_{k=0}^{2021} a^{k} b^{2021-k} \equiv \sum_{k=0}^{2021} a^{2021} \equiv 0 \bmod 2022
$$
On the other hand, the last sum is equal to $\frac{a^{2022}-b^{2022}}{a-b}$.
If $3 \nmid a$, we will prove that $S$ is not divisible by 9 . Indeed if $3 \nmid a$ then we also have $3 \nmid b$. So if $3^{t} \| a-b$ then, since $3^{1} \| 2022$, by the Lifting the Exponent Lemma, we have that $3^{t+1} \| a^{2022}-b^{2022}$. This implies that $S$ is not divisible by 9 , therefore, $2022^{2}$ doesn't divide $S$.
If $3 \mid a$, then we have $337 \nmid a$ and a similar argument shows that $337^{2} \nmid S$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Problem. Let $a, b$ and $n$ be positive integers with $a>b$ such that all of the following hold:
(i) $a^{2021}$ divides $n$,
(ii) $b^{2021}$ divides $n$,
(iii) 2022 divides $a-b$.
Prove that there is a subset $T$ of the set of positive divisors of the number $n$ such that the sum of the elements of $T$ is divisible by 2022 but not divisible by $2022^{2}$.
|
If $1011 \mid a$, then $1011^{2021} \mid n$ and we can take $T=\left\{1011,1011^{2}\right\}$. So we can assume that $3 \nmid a$ or $337 \nmid a$.
We continue with the following claim:
Claim. If $k$ is a positive integer, then $a^{k} b^{2021-k} \mid n$.
Proof of the Claim. We have that $n^{2021}=n^{k} \cdot n^{2021-k}$ is divisible by $a^{2021 k} \cdot b^{2021(2021-k)}$ and taking the 2021-root we get the desired result.
Back to the problem, we will prove that the set $T=\left\{a^{k} b^{2021-k}: k \geqslant 0\right\}$ consisting of 2022 divisors of $n$, has the desired property. The sum of its elements is equal to
$$
S=\sum_{k=0}^{2021} a^{k} b^{2021-k} \equiv \sum_{k=0}^{2021} a^{2021} \equiv 0 \bmod 2022
$$
On the other hand, the last sum is equal to $\frac{a^{2022}-b^{2022}}{a-b}$.
If $3 \nmid a$, we will prove that $S$ is not divisible by 9 . Indeed if $3 \nmid a$ then we also have $3 \nmid b$. So if $3^{t} \| a-b$ then, since $3^{1} \| 2022$, by the Lifting the Exponent Lemma, we have that $3^{t+1} \| a^{2022}-b^{2022}$. This implies that $S$ is not divisible by 9 , therefore, $2022^{2}$ doesn't divide $S$.
If $3 \mid a$, then we have $337 \nmid a$ and a similar argument shows that $337^{2} \nmid S$.
|
{
"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl",
"problem_match": "# Problem 2",
"solution_match": "\nSolution."
}
|
e8749cc7-f2ad-5639-a45e-ab0c82e60044
| 604,887
|
In triangle $A B C$, the incircle touches sides $B C, C A, A B$ at $D, E, F$ respectively. Assume there exists a point $X$ on the line $E F$ such that
$$
\angle X B C=\angle X C B=45^{\circ} .
$$
Let $M$ be the midpoint of the arc $B C$ on the circumcircle of $A B C$ not containing $A$. Prove that the line $M D$ passes through $E$ or $F$.
|
. We first state a well-known lemma.
Lemma: In triangle $A B C$, let $D, E, F$ be the points of tangency of the incircle to the sides $B C, C A, A B$ and let $I$ be the incenter. Then the intersection of $E F$ and $B I$ lies on the circle of diameter $B C$.
Proof: Let $S$ be the intersection of $E F$ and $B I . \angle B I C=\angle E F C$, hence $S$ lies on the circumcircle of $F I C$ in which $I C$ is a diameter. Thus $\angle I S C=90^{\circ}$, hence $\angle B S C=90^{\circ}$.
Returning to the problem, let $I$ be the incenter. The lemma implies that the two intersection points of $E F$ with the circle of diameter $B C$ are precisely the intersection points of $E F$ with $B I$ and $C I$. We have $\angle B X C=90^{\circ}$, therefore either $B X$ or $C X$ is an internal angle bisector, which means either $\angle B=90^{\circ}$ or $\angle C=90^{\circ}$.
Assume, without loss of generality, that $\angle B=90^{\circ}$. Then we have $\angle A M C=90^{\circ}$, so $M$ is the second intersection point of $A I$ with the circle of diameter $A C$, thus the lemma implies that $M$ lies on $D F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the incircle touches sides $B C, C A, A B$ at $D, E, F$ respectively. Assume there exists a point $X$ on the line $E F$ such that
$$
\angle X B C=\angle X C B=45^{\circ} .
$$
Let $M$ be the midpoint of the arc $B C$ on the circumcircle of $A B C$ not containing $A$. Prove that the line $M D$ passes through $E$ or $F$.
|
. We first state a well-known lemma.
Lemma: In triangle $A B C$, let $D, E, F$ be the points of tangency of the incircle to the sides $B C, C A, A B$ and let $I$ be the incenter. Then the intersection of $E F$ and $B I$ lies on the circle of diameter $B C$.
Proof: Let $S$ be the intersection of $E F$ and $B I . \angle B I C=\angle E F C$, hence $S$ lies on the circumcircle of $F I C$ in which $I C$ is a diameter. Thus $\angle I S C=90^{\circ}$, hence $\angle B S C=90^{\circ}$.
Returning to the problem, let $I$ be the incenter. The lemma implies that the two intersection points of $E F$ with the circle of diameter $B C$ are precisely the intersection points of $E F$ with $B I$ and $C I$. We have $\angle B X C=90^{\circ}$, therefore either $B X$ or $C X$ is an internal angle bisector, which means either $\angle B=90^{\circ}$ or $\angle C=90^{\circ}$.
Assume, without loss of generality, that $\angle B=90^{\circ}$. Then we have $\angle A M C=90^{\circ}$, so $M$ is the second intersection point of $A I$ with the circle of diameter $A C$, thus the lemma implies that $M$ lies on $D F$.
|
{
"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
22bb783e-be47-5aaa-9760-57cffe9db953
| 604,953
|
In triangle $A B C$, the incircle touches sides $B C, C A, A B$ at $D, E, F$ respectively. Assume there exists a point $X$ on the line $E F$ such that
$$
\angle X B C=\angle X C B=45^{\circ} .
$$
Let $M$ be the midpoint of the arc $B C$ on the circumcircle of $A B C$ not containing $A$. Prove that the line $M D$ passes through $E$ or $F$.
|
.
Let $I$ be the incenter of $\triangle A B C$ and let $K$ be the foot of the perpendicular from $D$ to $E F$. We begin by proving that $B K X C$ is cyclic, which can be done in two ways:
First Way. Note that $\angle K F D=90^{\circ}-\frac{\angle C}{2}$ and $\angle K E D=90^{\circ}-\frac{\angle B}{2}$, so by using $K D \perp E F$, we have $\frac{F K}{E D}=\frac{\tan \frac{\angle C}{2}}{\tan \frac{\angle B}{2}}$. Similarly, since $\angle I B D=\frac{\angle B}{2}$ and $\angle I C D=\frac{\angle C}{2}$, by using $I D \perp B C$, we have $\frac{B F}{E C}=\frac{B D}{D C}=\frac{\tan \frac{\angle C}{2}}{\tan \frac{\angle B}{2}}$. Then, since $\angle B F K=90^{\circ}+\frac{\angle A}{2}=$ $\angle K E C$, we conclude that $\triangle B F K$ and $\triangle C E K$ are similar, so $\angle F K B=\angle C K E$ which shows line $E F$ is the external-angle bisector of $\angle B K C$. Therefore, $X$ lies on both the perpendicular bisector of the segment $B C$ and the external angle bisector of $\angle B K C$ (and these lines are distinct) thus it lies on the circumcirle of $\triangle B K C$ (in particular the midpoint of arc $B K C$ ).
Second Way. Let $T$ be the intersection of $E F$ and $B C$, and $N$ be the midpoint of the segment $B C$. It is well-known that $(T, D ; B, C)$ is harmonic and $T B \cdot T C=T D \cdot T N$. On the other hand, since $X B=X C$, we have $\angle X N D=90^{\circ}=\angle X K D$, so $X K D N$ is cyclic and $T D \cdot T N=T K \cdot T X$. Therefore, we have $T K \cdot T X=T B \cdot T C$, which implies $B K X C$ is cyclic.
Now we will show that either $\angle B=90^{\circ}$ or $\angle C=90^{\circ}$. Note that $\angle B K C=\angle B X C=$ $90^{\circ}=\angle F K D=\angle E K D$ and $\angle F K B=\angle E K C$. Then we have
$$
\angle F K B=\angle B K D=\angle D K C=\angle C K E=45^{\circ} .
$$
Hence $B K$ bisects $\angle F K D$, but $B$ also lies on the perpendicular bisector of $D F$. Therefore, either $F K D B$ is cyclic or $K F=K D$ while the former implies that $\angle B=180^{\circ}-\angle F K D=$ $90^{\circ}$. In the latter case, we have $K B \perp F D$, which gives $90^{\circ}-\frac{\angle C}{2}=\angle K F D=90^{\circ}-$ $\angle F K B=45^{\circ}$ and so $\angle C=90^{\circ}$ as desired.
We consider, without loss of generality, the case where $\angle B=90^{\circ}$. Observing that $A, I, M$ are collinear we get:
$$
\angle C D I=90^{\circ}=\angle C B A=\angle C M A=\angle C M I
$$
Hence $M D I C$ is cyclic so:
$$
\angle M D C=\angle M I C=180^{\circ}-\angle C I A=180^{\circ}-\left(90^{\circ}+\frac{\angle B}{2}\right)=45^{\circ}
$$
We also have $\angle F D B=90^{\circ}-\frac{\angle B}{2}=45^{\circ}$ so $\angle F D B=\angle M D C$ and thus $M, D, F$ are collinear as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the incircle touches sides $B C, C A, A B$ at $D, E, F$ respectively. Assume there exists a point $X$ on the line $E F$ such that
$$
\angle X B C=\angle X C B=45^{\circ} .
$$
Let $M$ be the midpoint of the arc $B C$ on the circumcircle of $A B C$ not containing $A$. Prove that the line $M D$ passes through $E$ or $F$.
|
.
Let $I$ be the incenter of $\triangle A B C$ and let $K$ be the foot of the perpendicular from $D$ to $E F$. We begin by proving that $B K X C$ is cyclic, which can be done in two ways:
First Way. Note that $\angle K F D=90^{\circ}-\frac{\angle C}{2}$ and $\angle K E D=90^{\circ}-\frac{\angle B}{2}$, so by using $K D \perp E F$, we have $\frac{F K}{E D}=\frac{\tan \frac{\angle C}{2}}{\tan \frac{\angle B}{2}}$. Similarly, since $\angle I B D=\frac{\angle B}{2}$ and $\angle I C D=\frac{\angle C}{2}$, by using $I D \perp B C$, we have $\frac{B F}{E C}=\frac{B D}{D C}=\frac{\tan \frac{\angle C}{2}}{\tan \frac{\angle B}{2}}$. Then, since $\angle B F K=90^{\circ}+\frac{\angle A}{2}=$ $\angle K E C$, we conclude that $\triangle B F K$ and $\triangle C E K$ are similar, so $\angle F K B=\angle C K E$ which shows line $E F$ is the external-angle bisector of $\angle B K C$. Therefore, $X$ lies on both the perpendicular bisector of the segment $B C$ and the external angle bisector of $\angle B K C$ (and these lines are distinct) thus it lies on the circumcirle of $\triangle B K C$ (in particular the midpoint of arc $B K C$ ).
Second Way. Let $T$ be the intersection of $E F$ and $B C$, and $N$ be the midpoint of the segment $B C$. It is well-known that $(T, D ; B, C)$ is harmonic and $T B \cdot T C=T D \cdot T N$. On the other hand, since $X B=X C$, we have $\angle X N D=90^{\circ}=\angle X K D$, so $X K D N$ is cyclic and $T D \cdot T N=T K \cdot T X$. Therefore, we have $T K \cdot T X=T B \cdot T C$, which implies $B K X C$ is cyclic.
Now we will show that either $\angle B=90^{\circ}$ or $\angle C=90^{\circ}$. Note that $\angle B K C=\angle B X C=$ $90^{\circ}=\angle F K D=\angle E K D$ and $\angle F K B=\angle E K C$. Then we have
$$
\angle F K B=\angle B K D=\angle D K C=\angle C K E=45^{\circ} .
$$
Hence $B K$ bisects $\angle F K D$, but $B$ also lies on the perpendicular bisector of $D F$. Therefore, either $F K D B$ is cyclic or $K F=K D$ while the former implies that $\angle B=180^{\circ}-\angle F K D=$ $90^{\circ}$. In the latter case, we have $K B \perp F D$, which gives $90^{\circ}-\frac{\angle C}{2}=\angle K F D=90^{\circ}-$ $\angle F K B=45^{\circ}$ and so $\angle C=90^{\circ}$ as desired.
We consider, without loss of generality, the case where $\angle B=90^{\circ}$. Observing that $A, I, M$ are collinear we get:
$$
\angle C D I=90^{\circ}=\angle C B A=\angle C M A=\angle C M I
$$
Hence $M D I C$ is cyclic so:
$$
\angle M D C=\angle M I C=180^{\circ}-\angle C I A=180^{\circ}-\left(90^{\circ}+\frac{\angle B}{2}\right)=45^{\circ}
$$
We also have $\angle F D B=90^{\circ}-\frac{\angle B}{2}=45^{\circ}$ so $\angle F D B=\angle M D C$ and thus $M, D, F$ are collinear as required.
|
{
"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution 2"
}
|
22bb783e-be47-5aaa-9760-57cffe9db953
| 604,953
|
Let $A B C$ be an acute-angled triangle with $A C>A B$ and let $D$ be the foot of the $A$-angle bisector on $B C$. The reflections of lines $A B$ and $A C$ in line $B C$ meet $A C$ and $A B$ at points $E$ and $F$ respectively. A line through $D$ meets $A C$ and $A B$ at $G$ and $H$ respectively such that $G$ lies strictly between $A$ and $C$ while $H$ lies strictly between $B$ and $F$. Prove that the circumcircles of $\triangle E D G$ and $\triangle F D H$ are tangent to each other.
|
. Let $X$ and $Y$ lie on the tangent to the circumcircle of $\triangle E D G$ on the opposite side to $D$ as shown in the figure below. Regarding diagram dependency, the acute condition with $A C>A B$ ensures $E$ lies on extension of $C A$ beyond $A$, and $F$ lies on extension of $A B$ beyond $B$. The condition on $\ell$ means the points lie in the orders $E, A, G, C$ and $A, B, H, F$.
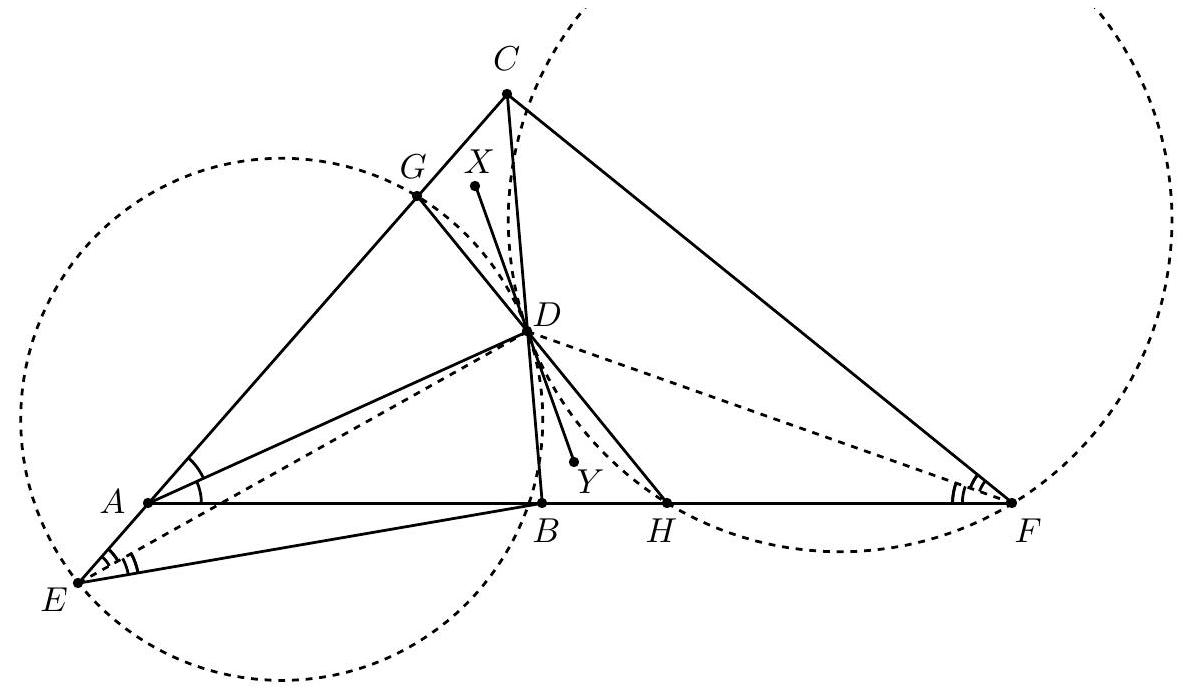
Using the alternate segment theorem, the condition that $\odot E D G$ and $\odot F D H$ are tangent at $D$ can be rewritten as
$$
\Varangle H F D=\Varangle Y D H .
$$
But using the same theorem, we get $\Varangle Y D H=\Varangle X D G=\Varangle D E G$. So we can remove $G, H$ from the figure, and it is sufficient to prove that $\Varangle D E A=\Varangle D F B$.
The reflection property means that $A D$ and $B D$ are external angle bisectors in $\triangle E A B$ and hence $D$
is the $E$-excentre of this triangle. Thus $D E$ (internally) bisects $\Varangle B E A$, giving
$$
\Varangle D E A=\Varangle D E B .
$$
Now observe that the pairs of lines $(B E, C E)$ and $(B F, C F)$ are reflections in $B C$ thus $E, F$ are reflections in $B C$. Also $D$ is its own reflection in $B C$. Hence $\Varangle D E B=\Varangle D F B$ and so
$$
\Varangle D E A=\Varangle D E B=\Varangle D F B,
$$
as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with $A C>A B$ and let $D$ be the foot of the $A$-angle bisector on $B C$. The reflections of lines $A B$ and $A C$ in line $B C$ meet $A C$ and $A B$ at points $E$ and $F$ respectively. A line through $D$ meets $A C$ and $A B$ at $G$ and $H$ respectively such that $G$ lies strictly between $A$ and $C$ while $H$ lies strictly between $B$ and $F$. Prove that the circumcircles of $\triangle E D G$ and $\triangle F D H$ are tangent to each other.
|
. Let $X$ and $Y$ lie on the tangent to the circumcircle of $\triangle E D G$ on the opposite side to $D$ as shown in the figure below. Regarding diagram dependency, the acute condition with $A C>A B$ ensures $E$ lies on extension of $C A$ beyond $A$, and $F$ lies on extension of $A B$ beyond $B$. The condition on $\ell$ means the points lie in the orders $E, A, G, C$ and $A, B, H, F$.

Using the alternate segment theorem, the condition that $\odot E D G$ and $\odot F D H$ are tangent at $D$ can be rewritten as
$$
\Varangle H F D=\Varangle Y D H .
$$
But using the same theorem, we get $\Varangle Y D H=\Varangle X D G=\Varangle D E G$. So we can remove $G, H$ from the figure, and it is sufficient to prove that $\Varangle D E A=\Varangle D F B$.
The reflection property means that $A D$ and $B D$ are external angle bisectors in $\triangle E A B$ and hence $D$
is the $E$-excentre of this triangle. Thus $D E$ (internally) bisects $\Varangle B E A$, giving
$$
\Varangle D E A=\Varangle D E B .
$$
Now observe that the pairs of lines $(B E, C E)$ and $(B F, C F)$ are reflections in $B C$ thus $E, F$ are reflections in $B C$. Also $D$ is its own reflection in $B C$. Hence $\Varangle D E B=\Varangle D F B$ and so
$$
\Varangle D E A=\Varangle D E B=\Varangle D F B,
$$
as required.
|
{
"resource_path": "Balkan_MO/segmented/en-2024-BMO-type1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 1"
}
|
d70b96ff-607b-5cca-9e18-9bcb23679048
| 604,993
|
Let $n \geq k \geq 3$ be integers. Show that for every integer sequence $1 \leq a_{1}<a_{2}<\ldots<$ $a_{k} \leq n$ one can choose non-negative integers $b_{1}, b_{2}, \ldots, b_{k}$, satisfying the following conditions:
(i) $0 \leq b_{i} \leq n$ for each $1 \leq i \leq k$,
(ii) all the positive $b_{i}$ are distinct,
(iii) the sums $a_{i}+b_{i}, 1 \leq i \leq k$, form a permutation of the first $k$ terms of a non-constant arithmetic progression.
|
. Let the resulting progression be $A n s:=\left\{a_{k}-(k-1), a_{k}-(k-2), \ldots, a_{k}\right\}$ and $a_{t}$ be the largest number not belonging to $A n s$. Clearly the set $A n s \backslash\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ has cardinality $t$; let its members be $c_{1}>c_{2}>\cdots>c_{t}$. Define $b_{j}:=c_{j}-a_{j}$ for $1 \leq j \leq t$ or zero otherwise. Since $\left\{c_{j}\right\}$ is decreasing and $\left\{a_{j}\right\}$ is increasing, all $b_{j}$ are distinct and clearly $b_{1}<n$. After we add $b_{j}$ to $a_{j}$ we get a permutation of Ans as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq k \geq 3$ be integers. Show that for every integer sequence $1 \leq a_{1}<a_{2}<\ldots<$ $a_{k} \leq n$ one can choose non-negative integers $b_{1}, b_{2}, \ldots, b_{k}$, satisfying the following conditions:
(i) $0 \leq b_{i} \leq n$ for each $1 \leq i \leq k$,
(ii) all the positive $b_{i}$ are distinct,
(iii) the sums $a_{i}+b_{i}, 1 \leq i \leq k$, form a permutation of the first $k$ terms of a non-constant arithmetic progression.
|
. Let the resulting progression be $A n s:=\left\{a_{k}-(k-1), a_{k}-(k-2), \ldots, a_{k}\right\}$ and $a_{t}$ be the largest number not belonging to $A n s$. Clearly the set $A n s \backslash\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ has cardinality $t$; let its members be $c_{1}>c_{2}>\cdots>c_{t}$. Define $b_{j}:=c_{j}-a_{j}$ for $1 \leq j \leq t$ or zero otherwise. Since $\left\{c_{j}\right\}$ is decreasing and $\left\{a_{j}\right\}$ is increasing, all $b_{j}$ are distinct and clearly $b_{1}<n$. After we add $b_{j}$ to $a_{j}$ we get a permutation of Ans as desired.
|
{
"resource_path": "Balkan_MO/segmented/en-2024-BMO-type1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
8820a8f3-b899-5a15-9bb2-0e08ec9d94eb
| 605,005
|
Let $n \geq k \geq 3$ be integers. Show that for every integer sequence $1 \leq a_{1}<a_{2}<\ldots<$ $a_{k} \leq n$ one can choose non-negative integers $b_{1}, b_{2}, \ldots, b_{k}$, satisfying the following conditions:
(i) $0 \leq b_{i} \leq n$ for each $1 \leq i \leq k$,
(ii) all the positive $b_{i}$ are distinct,
(iii) the sums $a_{i}+b_{i}, 1 \leq i \leq k$, form a permutation of the first $k$ terms of a non-constant arithmetic progression.
|
. Let the resulting progression be $A n s:=\left\{a_{k}-(k-1), a_{k}-(k-2), \ldots, a_{k}\right\}$.
We proceed with the following reduction. Let $\delta$ be the smallest $b$ we used before (in the beginning it is $n$ ). While $a_{1} \notin A n s$ we map $a_{1}$ to the largest element $q$ of $A n s \backslash\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ and put $\delta_{\text {new }}:=b_{1}:=q-a_{1}$. Now we rearrange the sequence of $a$-s. We do not touch $\operatorname{Ans} \cap\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ so every $b$ is defined at most once (in the end undefined $b$-s become zeros). Also $b<\delta$ and $\delta$ decreases at each step, because $q$ decreases and $a_{1}$ grows, and hence all nonzero $b$-s are distinct.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq k \geq 3$ be integers. Show that for every integer sequence $1 \leq a_{1}<a_{2}<\ldots<$ $a_{k} \leq n$ one can choose non-negative integers $b_{1}, b_{2}, \ldots, b_{k}$, satisfying the following conditions:
(i) $0 \leq b_{i} \leq n$ for each $1 \leq i \leq k$,
(ii) all the positive $b_{i}$ are distinct,
(iii) the sums $a_{i}+b_{i}, 1 \leq i \leq k$, form a permutation of the first $k$ terms of a non-constant arithmetic progression.
|
. Let the resulting progression be $A n s:=\left\{a_{k}-(k-1), a_{k}-(k-2), \ldots, a_{k}\right\}$.
We proceed with the following reduction. Let $\delta$ be the smallest $b$ we used before (in the beginning it is $n$ ). While $a_{1} \notin A n s$ we map $a_{1}$ to the largest element $q$ of $A n s \backslash\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ and put $\delta_{\text {new }}:=b_{1}:=q-a_{1}$. Now we rearrange the sequence of $a$-s. We do not touch $\operatorname{Ans} \cap\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ so every $b$ is defined at most once (in the end undefined $b$-s become zeros). Also $b<\delta$ and $\delta$ decreases at each step, because $q$ decreases and $a_{1}$ grows, and hence all nonzero $b$-s are distinct.
|
{
"resource_path": "Balkan_MO/segmented/en-2024-BMO-type1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2"
}
|
8820a8f3-b899-5a15-9bb2-0e08ec9d94eb
| 605,005
|
Let $a$ and $b$ be distinct positive integers such that $3^{a}+2$ is divisible by $3^{b}+2$. Prove that $a>b^{2}$ 。
|
. Obviously we have $a>b$. Let $a=b q+r$, where $0 \leq r<b$. Then
$$
3^{a} \equiv 3^{b q+r} \equiv(-2)^{q} \cdot 3^{r} \equiv-2 \quad\left(\bmod 3^{b}+2\right)
$$
So $3^{b}+2$ divides $A=(-2)^{q} .3^{r}+2$ and it follows that
$$
\left|(-2)^{q} \cdot 3^{r}+2\right| \geq 3^{b}+2 \text { or }(-2)^{q} \cdot 3^{r}+2=0
$$
We make case distinction:
1. $(-2)^{q} .3^{r}+2=0$. Then $q=1$ and $r=0$ or $a=b$, a contradiction.
2. $q$ is even. Then
$$
A=2^{q} \cdot 3^{r}+2=\left(3^{b}+2\right) \cdot k
$$
Consider both sides of the last equation modulo $3^{r}$. Since $b>r$ :
$$
2 \equiv 2^{q} \cdot 3^{r}+2=\left(3^{b}+2\right) k \equiv 2 k \quad\left(\bmod 3^{r}\right)
$$
so it follows that $3^{r} \mid k-1$. If $k=1$ then $2^{q} .3^{r}=3^{b}$, a contradiction. So $k \geq 3^{r}+1$, and therefore:
$$
A=2^{q} .3^{r}+2=\left(3^{b}+2\right) k \geq\left(3^{b}+2\right)\left(3^{r}+1\right)>3^{b} .3^{r}+2
$$
It follows that
$$
2^{q} .3^{r}>3^{b} .3^{r} \text {, i.e. } 2^{q}>3^{b} \text {, which implies } 3^{b^{2}}<2^{b q}<3^{b q} \leq 3^{b q+r}=3^{a} \text {. }
$$
Consequently $a>b^{2}$.
3. If $q$ is odd. Then
$$
2^{q} \cdot 3^{r}-2=\left(3^{b}+2\right) k
$$
Considering both sides of the last equation modulo $3^{r}$, and since $b>r$, we get: $k+1$ is divisible by $3^{r}$ and therefore $k \geq 3^{r}-1$. Thus $r>0$ because $k>0$, and:
$$
\begin{array}{r}
2^{q} .3^{r}-2=\left(3^{b}+2\right) k \geq\left(3^{b}+2\right)\left(3^{r}-1\right), \text { and therefore } \\
2^{q} .3^{r}>\left(3^{b}+2\right)\left(3^{r}-1\right)>3^{b}\left(3^{r}-1\right)>3^{b} \frac{3^{r}}{2}, \text { which shows } \\
2^{q+1}>3^{b} .
\end{array}
$$
But for $q>1$ we have $2^{q+1}<3^{q}$, which combined with the above inequality, implies that $3^{b^{2}}<2^{(q+1) b}<3^{q b} \leq 3^{a}$, q.e.d. Finally, If $q=1$ then $2^{q} .3^{r}-2=\left(3^{b}+2\right) k$ and consequently $2.3^{r}-2 \geq 3^{b}+2 \geq 3^{r+1}+2>2.3^{r}-2$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be distinct positive integers such that $3^{a}+2$ is divisible by $3^{b}+2$. Prove that $a>b^{2}$ 。
|
. Obviously we have $a>b$. Let $a=b q+r$, where $0 \leq r<b$. Then
$$
3^{a} \equiv 3^{b q+r} \equiv(-2)^{q} \cdot 3^{r} \equiv-2 \quad\left(\bmod 3^{b}+2\right)
$$
So $3^{b}+2$ divides $A=(-2)^{q} .3^{r}+2$ and it follows that
$$
\left|(-2)^{q} \cdot 3^{r}+2\right| \geq 3^{b}+2 \text { or }(-2)^{q} \cdot 3^{r}+2=0
$$
We make case distinction:
1. $(-2)^{q} .3^{r}+2=0$. Then $q=1$ and $r=0$ or $a=b$, a contradiction.
2. $q$ is even. Then
$$
A=2^{q} \cdot 3^{r}+2=\left(3^{b}+2\right) \cdot k
$$
Consider both sides of the last equation modulo $3^{r}$. Since $b>r$ :
$$
2 \equiv 2^{q} \cdot 3^{r}+2=\left(3^{b}+2\right) k \equiv 2 k \quad\left(\bmod 3^{r}\right)
$$
so it follows that $3^{r} \mid k-1$. If $k=1$ then $2^{q} .3^{r}=3^{b}$, a contradiction. So $k \geq 3^{r}+1$, and therefore:
$$
A=2^{q} .3^{r}+2=\left(3^{b}+2\right) k \geq\left(3^{b}+2\right)\left(3^{r}+1\right)>3^{b} .3^{r}+2
$$
It follows that
$$
2^{q} .3^{r}>3^{b} .3^{r} \text {, i.e. } 2^{q}>3^{b} \text {, which implies } 3^{b^{2}}<2^{b q}<3^{b q} \leq 3^{b q+r}=3^{a} \text {. }
$$
Consequently $a>b^{2}$.
3. If $q$ is odd. Then
$$
2^{q} \cdot 3^{r}-2=\left(3^{b}+2\right) k
$$
Considering both sides of the last equation modulo $3^{r}$, and since $b>r$, we get: $k+1$ is divisible by $3^{r}$ and therefore $k \geq 3^{r}-1$. Thus $r>0$ because $k>0$, and:
$$
\begin{array}{r}
2^{q} .3^{r}-2=\left(3^{b}+2\right) k \geq\left(3^{b}+2\right)\left(3^{r}-1\right), \text { and therefore } \\
2^{q} .3^{r}>\left(3^{b}+2\right)\left(3^{r}-1\right)>3^{b}\left(3^{r}-1\right)>3^{b} \frac{3^{r}}{2}, \text { which shows } \\
2^{q+1}>3^{b} .
\end{array}
$$
But for $q>1$ we have $2^{q+1}<3^{q}$, which combined with the above inequality, implies that $3^{b^{2}}<2^{(q+1) b}<3^{q b} \leq 3^{a}$, q.e.d. Finally, If $q=1$ then $2^{q} .3^{r}-2=\left(3^{b}+2\right) k$ and consequently $2.3^{r}-2 \geq 3^{b}+2 \geq 3^{r+1}+2>2.3^{r}-2$, a contradiction.
|
{
"resource_path": "Balkan_MO/segmented/en-2024-BMO-type1.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution 1"
}
|
72a043a3-5f0e-5dc8-9a80-40bb5d686c27
| 605,025
|
Let $a$ and $b$ be distinct positive integers such that $3^{a}+2$ is divisible by $3^{b}+2$. Prove that $a>b^{2}$ 。
|
. $D=a-b$, and we shall show $D>b^{2}-b$. We have $3^{b}+2 \mid 3^{a}+2$, so $3^{b}+2 \mid 3^{D}-1$. Let $D=b q+r$ where $r<b$. First suppose that $r \neq 0$. We have
$$
1 \equiv 3^{D} \equiv 3^{b q+r} \equiv(-2)^{q+1} 3^{r-b} \quad\left(\bmod 3^{b}+2\right) \Longrightarrow 3^{b-r} \equiv(-2)^{q+1} \quad\left(\bmod 3^{b}+2\right)
$$
Therefore
$$
3^{b}+2 \leq\left|(-2)^{q+1}-3^{b-r}\right| \leq 2^{q+1}+3^{b-r} \leq 2^{q+1}+3^{b-1}
$$
Hence
$$
2 \times 3^{b-1}+2 \leq 2^{q+1} \Longrightarrow 3^{b-1}<2^{q} \Longrightarrow \frac{\log 3}{\log 2}(b-1)<q
$$
Which yields $D=b q+r>b q>\frac{\log 3}{\log 2} b(b-1) \geq b^{2}-b$ as desired. Now for the case $r=0,(-2)^{q} \equiv 1$ $\left(\bmod 3^{b}+2\right)$ and so
$$
3^{b}+2 \leq\left|(-2)^{q}-1\right| \leq 2^{q}+1 \Longrightarrow 3^{b-1}<3^{b}<2^{q} \Longrightarrow \frac{\log 3}{\log 2}(b-1)<q
$$
and analogous to the previous case, $D=b q+r=b q>\frac{\log 3}{\log 2} b(b-1) \geq b^{2}-b$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be distinct positive integers such that $3^{a}+2$ is divisible by $3^{b}+2$. Prove that $a>b^{2}$ 。
|
. $D=a-b$, and we shall show $D>b^{2}-b$. We have $3^{b}+2 \mid 3^{a}+2$, so $3^{b}+2 \mid 3^{D}-1$. Let $D=b q+r$ where $r<b$. First suppose that $r \neq 0$. We have
$$
1 \equiv 3^{D} \equiv 3^{b q+r} \equiv(-2)^{q+1} 3^{r-b} \quad\left(\bmod 3^{b}+2\right) \Longrightarrow 3^{b-r} \equiv(-2)^{q+1} \quad\left(\bmod 3^{b}+2\right)
$$
Therefore
$$
3^{b}+2 \leq\left|(-2)^{q+1}-3^{b-r}\right| \leq 2^{q+1}+3^{b-r} \leq 2^{q+1}+3^{b-1}
$$
Hence
$$
2 \times 3^{b-1}+2 \leq 2^{q+1} \Longrightarrow 3^{b-1}<2^{q} \Longrightarrow \frac{\log 3}{\log 2}(b-1)<q
$$
Which yields $D=b q+r>b q>\frac{\log 3}{\log 2} b(b-1) \geq b^{2}-b$ as desired. Now for the case $r=0,(-2)^{q} \equiv 1$ $\left(\bmod 3^{b}+2\right)$ and so
$$
3^{b}+2 \leq\left|(-2)^{q}-1\right| \leq 2^{q}+1 \Longrightarrow 3^{b-1}<3^{b}<2^{q} \Longrightarrow \frac{\log 3}{\log 2}(b-1)<q
$$
and analogous to the previous case, $D=b q+r=b q>\frac{\log 3}{\log 2} b(b-1) \geq b^{2}-b$.
|
{
"resource_path": "Balkan_MO/segmented/en-2024-BMO-type1.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution 2"
}
|
72a043a3-5f0e-5dc8-9a80-40bb5d686c27
| 605,025
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\sqrt{a^{3} b+a^{3} c}+\sqrt{b^{3} c+b^{3} a}+\sqrt{c^{3} a+c^{3} b} \geq \frac{4}{3}(a b+b c+c a)
$$
|
W.L.O.G. $a \geq b \geq c$.
$$
\begin{gathered}
a \geq b \geq c \Rightarrow a b \geq a c \geq b c \Rightarrow a b+a c \geq a b+b c \geq a c+b c \Rightarrow \sqrt{a b+a c} \geq \sqrt{b c+b a} \geq \sqrt{a c+b c} \\
\sqrt{a^{3} b+a^{3} c}+\sqrt{b^{3} c+b^{3} a}+\sqrt{c^{3} a+c^{3} b}=a \sqrt{a b+a c}+b \sqrt{b c+b a}+c \sqrt{c a+c b} \geq \\
\frac{(a+b+c)}{3}(\sqrt{a b+a c}+\sqrt{b c+b a}+\sqrt{c a+c b})=\frac{(a+b+c)}{3}(\sqrt{a(b+c)}+\sqrt{b(c+a)}+\sqrt{c(a+b)}) \geq \\
\frac{(a+b+c)}{3}\left(\frac{2 a(b+c)}{a+b+c}+\frac{2 b(c+a)}{b+c+a}+\frac{c(a+b)}{c+a+b}\right)=\frac{(a+b+c)}{3} \frac{4(a b+b c+c a)}{a+b+c}=\frac{4}{3}(a b+b c+c a)
\end{gathered}
$$
(1) Chebyshev's inequality
(2) $\mathrm{GM} \geq \mathrm{HM}$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\sqrt{a^{3} b+a^{3} c}+\sqrt{b^{3} c+b^{3} a}+\sqrt{c^{3} a+c^{3} b} \geq \frac{4}{3}(a b+b c+c a)
$$
|
W.L.O.G. $a \geq b \geq c$.
$$
\begin{gathered}
a \geq b \geq c \Rightarrow a b \geq a c \geq b c \Rightarrow a b+a c \geq a b+b c \geq a c+b c \Rightarrow \sqrt{a b+a c} \geq \sqrt{b c+b a} \geq \sqrt{a c+b c} \\
\sqrt{a^{3} b+a^{3} c}+\sqrt{b^{3} c+b^{3} a}+\sqrt{c^{3} a+c^{3} b}=a \sqrt{a b+a c}+b \sqrt{b c+b a}+c \sqrt{c a+c b} \geq \\
\frac{(a+b+c)}{3}(\sqrt{a b+a c}+\sqrt{b c+b a}+\sqrt{c a+c b})=\frac{(a+b+c)}{3}(\sqrt{a(b+c)}+\sqrt{b(c+a)}+\sqrt{c(a+b)}) \geq \\
\frac{(a+b+c)}{3}\left(\frac{2 a(b+c)}{a+b+c}+\frac{2 b(c+a)}{b+c+a}+\frac{c(a+b)}{c+a+b}\right)=\frac{(a+b+c)}{3} \frac{4(a b+b c+c a)}{a+b+c}=\frac{4}{3}(a b+b c+c a)
\end{gathered}
$$
(1) Chebyshev's inequality
(2) $\mathrm{GM} \geq \mathrm{HM}$
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\nA1.",
"solution_match": "\nSolution."
}
|
8a6cfa24-98e9-5786-838e-4d000734ec8f
| 605,069
|
For all $x, y, z>0$ satisfying $\frac{x}{y z}+\frac{y}{z x}+\frac{z}{x y} \leq x+y+z$, prove that
$$
\frac{1}{x^{2}+y+z}+\frac{1}{y^{2}+z+x}+\frac{1}{z^{2}+x+y} \leq 1
$$
|
By Cauchy-Schwarz inequality, we have
$$
\left(x^{2}+y+z\right)\left(y^{2}+y z^{2}+z x^{2}\right) \geq(x y+y z+z x)^{2}
$$
and hence we obtain that
$$
\frac{1}{x^{2}+y+z}+\frac{1}{y^{2}+z+x}+\frac{1}{z^{2}+x+y} \leq \frac{2\left(x y^{2}+y z^{2}+z x^{2}\right)+x^{2}+y^{2}+z^{2}}{(x y+y z+z x)^{2}}
$$
Using the condition $\frac{x}{y z}+\frac{y}{z x}+\frac{z}{x y} \leq x+y+z$, we also have
$$
x^{2}+y^{2}+z^{2} \leq x y z(x+y+z)
$$
and hence
$$
2\left(x^{2}+y^{2}+z^{2}\right)+x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2} \leq(x y+y z+z x)^{2} .
$$
Finally, by AM-GM
$$
x^{2}+z^{2} x^{2} \geq 2 z x^{2}
$$
which yields that
$$
2\left(x^{2}+y^{2}+z^{2}\right)+x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2} \geq 2\left(x y^{2}+y z^{2}+z x^{2}\right)+x^{2}+y^{2}+z^{2}
$$
Using (1), (2) and (3), we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
For all $x, y, z>0$ satisfying $\frac{x}{y z}+\frac{y}{z x}+\frac{z}{x y} \leq x+y+z$, prove that
$$
\frac{1}{x^{2}+y+z}+\frac{1}{y^{2}+z+x}+\frac{1}{z^{2}+x+y} \leq 1
$$
|
By Cauchy-Schwarz inequality, we have
$$
\left(x^{2}+y+z\right)\left(y^{2}+y z^{2}+z x^{2}\right) \geq(x y+y z+z x)^{2}
$$
and hence we obtain that
$$
\frac{1}{x^{2}+y+z}+\frac{1}{y^{2}+z+x}+\frac{1}{z^{2}+x+y} \leq \frac{2\left(x y^{2}+y z^{2}+z x^{2}\right)+x^{2}+y^{2}+z^{2}}{(x y+y z+z x)^{2}}
$$
Using the condition $\frac{x}{y z}+\frac{y}{z x}+\frac{z}{x y} \leq x+y+z$, we also have
$$
x^{2}+y^{2}+z^{2} \leq x y z(x+y+z)
$$
and hence
$$
2\left(x^{2}+y^{2}+z^{2}\right)+x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2} \leq(x y+y z+z x)^{2} .
$$
Finally, by AM-GM
$$
x^{2}+z^{2} x^{2} \geq 2 z x^{2}
$$
which yields that
$$
2\left(x^{2}+y^{2}+z^{2}\right)+x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2} \geq 2\left(x y^{2}+y z^{2}+z x^{2}\right)+x^{2}+y^{2}+z^{2}
$$
Using (1), (2) and (3), we are done.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\nA2.",
"solution_match": "\n## Solution."
}
|
f7bd6a9c-8c53-5cce-a307-3e67c842e84d
| 605,082
|
Prove that there is no function from positive real numbers to itself, $f:(0,+\infty) \rightarrow(0,+\infty)$ such that:
$$
f(f(x)+y)=f(x)+3 x+y f(y) \quad \text {,for every } \quad x, y \in(0,+\infty)
$$
|
First we prove that $f(x) \geq x$ for all $x>0$.
Indeed, if there is an $a>0$ with $f(a)<a$ then from the initial for $x=a$ and $y=a-f(a)>0$ we get that $3 a+(a-f(a)) f(a-f(a))=0$. This is absurd since $3 a+(a-f(a)) f(a-f(a))>0$.
So we have that
$$
f(x) \geq x \quad \text {,for all } \quad x>0
$$
Then using (1) we have that $f(x)+3 x+y f(x)=f(f(x)+y) \geq f(x)+y$, so
$$
3 x+y f(y) \geq y \quad, \text { all } \quad x, y>0
$$
Suppose that $y f(y)<y$ for a $y>0$ and let $-y f(y)=b>0$ then for $x=\frac{b}{4}$ we get $\frac{3 b}{4}-b \geq 0$ so $b \leq 0$, absurd. So we have that $y f(y) \geq y$, for all $y>0$, and so
$$
f(y) \geq 1 \quad \text {,for all } \quad y>0
$$
Substituting $y$ with $f(y)$ at the initial we have that
$$
f(x)+3 x+f(y) f(f(y))=f(f(x)+f(y))
$$
and changing the roles of $x, y$ we have that:
$$
f(y)+3 y+f(x) f(f(x))=f(f(x)+f(x))
$$
So we have $f(x) f(f(x))-f(x)-3 x=f(y) f(f(y))-f(y)-3 y$, which means that the function $f(x) f(f(x))-$ $f(x)-3 x$ is constant. That means that there exist a constant $c$ such that
$$
f(x) f(f(x))=f(x)+3 x+c \quad \text {,for all } \quad x>0
$$
So we can write (6) in the form $f(x)(f(f(x))-1)=3 x+c$ and since $f(f(x))>1$ we have that $3 x+c \geq 0$, for all $x>0$. if $c<0$ then for $x=-\frac{c}{4}>0$ we get that $c>0$ which is absurd. So $c \geq 0$.
We write (6) in the form
$$
f(f(x))=1+\frac{3 x}{f(x)}+\frac{c}{f(x)}
$$
Since $c \geq 0$ then from (7) with the help of (1) and (3) we have that $f(f(x)) \leq 4+c$.
But from (1) we have that $f(f(x)) \geq f(x) \geq x$, for all $x \geq 0$, and so
$$
4+c \geq f(f(x)) \geq x \quad \text {,for all } \quad x>0
$$
Taking $x=5+c$ we get that the last one cannot hold. So there is no such a function.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that there is no function from positive real numbers to itself, $f:(0,+\infty) \rightarrow(0,+\infty)$ such that:
$$
f(f(x)+y)=f(x)+3 x+y f(y) \quad \text {,for every } \quad x, y \in(0,+\infty)
$$
|
First we prove that $f(x) \geq x$ for all $x>0$.
Indeed, if there is an $a>0$ with $f(a)<a$ then from the initial for $x=a$ and $y=a-f(a)>0$ we get that $3 a+(a-f(a)) f(a-f(a))=0$. This is absurd since $3 a+(a-f(a)) f(a-f(a))>0$.
So we have that
$$
f(x) \geq x \quad \text {,for all } \quad x>0
$$
Then using (1) we have that $f(x)+3 x+y f(x)=f(f(x)+y) \geq f(x)+y$, so
$$
3 x+y f(y) \geq y \quad, \text { all } \quad x, y>0
$$
Suppose that $y f(y)<y$ for a $y>0$ and let $-y f(y)=b>0$ then for $x=\frac{b}{4}$ we get $\frac{3 b}{4}-b \geq 0$ so $b \leq 0$, absurd. So we have that $y f(y) \geq y$, for all $y>0$, and so
$$
f(y) \geq 1 \quad \text {,for all } \quad y>0
$$
Substituting $y$ with $f(y)$ at the initial we have that
$$
f(x)+3 x+f(y) f(f(y))=f(f(x)+f(y))
$$
and changing the roles of $x, y$ we have that:
$$
f(y)+3 y+f(x) f(f(x))=f(f(x)+f(x))
$$
So we have $f(x) f(f(x))-f(x)-3 x=f(y) f(f(y))-f(y)-3 y$, which means that the function $f(x) f(f(x))-$ $f(x)-3 x$ is constant. That means that there exist a constant $c$ such that
$$
f(x) f(f(x))=f(x)+3 x+c \quad \text {,for all } \quad x>0
$$
So we can write (6) in the form $f(x)(f(f(x))-1)=3 x+c$ and since $f(f(x))>1$ we have that $3 x+c \geq 0$, for all $x>0$. if $c<0$ then for $x=-\frac{c}{4}>0$ we get that $c>0$ which is absurd. So $c \geq 0$.
We write (6) in the form
$$
f(f(x))=1+\frac{3 x}{f(x)}+\frac{c}{f(x)}
$$
Since $c \geq 0$ then from (7) with the help of (1) and (3) we have that $f(f(x)) \leq 4+c$.
But from (1) we have that $f(f(x)) \geq f(x) \geq x$, for all $x \geq 0$, and so
$$
4+c \geq f(f(x)) \geq x \quad \text {,for all } \quad x>0
$$
Taking $x=5+c$ we get that the last one cannot hold. So there is no such a function.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\n## A6.",
"solution_match": "\nSolution."
}
|
7ad1058b-b125-578d-bbf2-c05bbf15e5a0
| 605,128
|
Let positive integers $K$ and $d$ be given. Prove that there exists a positive integer $n$ and a sequence of $K$ positive integers $b_{1}, b_{2}, \ldots, b_{K}$ such that the number $n$ is a $d$-digit palindrome in all number bases $b_{1}, b_{2}, \ldots, b_{K}$.
|
Let a positive integer $d$ be given. We shall prove that, for each large enough $n$, the number $(n!)^{d-1}$ is a $d$-digit palindrome in all number bases $\frac{n!}{i}-1$ for $1 \leqslant i \leqslant n$. In particular, we shall prove that the digit expansion of $(n!)^{d-1}$ in the base $\frac{n!}{i}-1$ is
$$
\left\langle i^{d-1}\binom{d-1}{d-1}, i^{d-1}\binom{d-1}{d-2}, i^{d-1}\binom{d-1}{d-3}, \ldots, i^{d-1}\binom{d-1}{1}, i^{d-1}\binom{d-1}{0}\right\rangle_{\frac{n!}{i}-1}
$$
We first show that, for each large enough $n$, all these digits are smaller than the considered base, that is, they are indeed digits in that base. It is enough to check this assertion for $i=n$, that is, to show the inequality $n^{d-1}\binom{d-1}{j}<(n-1)$ ! -1 . However, since for a fixed $d$ the right-hand side clearly grows faster than the left-hand side, this is indeed true for all large enough $n$.
Everything that is left is to evaluate:
$$
\begin{aligned}
\sum_{j=0}^{d-1} i^{d-1}\binom{d-1}{j}\left(\frac{n!}{i}-1\right)^{j} & =i^{d-1} \sum_{j=0}^{d-1}\binom{d-1}{j}\left(\frac{n!}{i}-1\right)^{j}=i^{d-1} \sum_{j=0}^{d-1}\binom{d-1}{j}\left(\frac{n!}{i}-1\right)^{j} \\
& =i^{d-1}\left(\frac{n!}{i}-1+1\right)^{d-1}=(n!)^{d-1}
\end{aligned}
$$
which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let positive integers $K$ and $d$ be given. Prove that there exists a positive integer $n$ and a sequence of $K$ positive integers $b_{1}, b_{2}, \ldots, b_{K}$ such that the number $n$ is a $d$-digit palindrome in all number bases $b_{1}, b_{2}, \ldots, b_{K}$.
|
Let a positive integer $d$ be given. We shall prove that, for each large enough $n$, the number $(n!)^{d-1}$ is a $d$-digit palindrome in all number bases $\frac{n!}{i}-1$ for $1 \leqslant i \leqslant n$. In particular, we shall prove that the digit expansion of $(n!)^{d-1}$ in the base $\frac{n!}{i}-1$ is
$$
\left\langle i^{d-1}\binom{d-1}{d-1}, i^{d-1}\binom{d-1}{d-2}, i^{d-1}\binom{d-1}{d-3}, \ldots, i^{d-1}\binom{d-1}{1}, i^{d-1}\binom{d-1}{0}\right\rangle_{\frac{n!}{i}-1}
$$
We first show that, for each large enough $n$, all these digits are smaller than the considered base, that is, they are indeed digits in that base. It is enough to check this assertion for $i=n$, that is, to show the inequality $n^{d-1}\binom{d-1}{j}<(n-1)$ ! -1 . However, since for a fixed $d$ the right-hand side clearly grows faster than the left-hand side, this is indeed true for all large enough $n$.
Everything that is left is to evaluate:
$$
\begin{aligned}
\sum_{j=0}^{d-1} i^{d-1}\binom{d-1}{j}\left(\frac{n!}{i}-1\right)^{j} & =i^{d-1} \sum_{j=0}^{d-1}\binom{d-1}{j}\left(\frac{n!}{i}-1\right)^{j}=i^{d-1} \sum_{j=0}^{d-1}\binom{d-1}{j}\left(\frac{n!}{i}-1\right)^{j} \\
& =i^{d-1}\left(\frac{n!}{i}-1+1\right)^{d-1}=(n!)^{d-1}
\end{aligned}
$$
which completes the proof.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\n## C1.",
"solution_match": "\nSolution."
}
|
bf3a52f1-a449-58dd-a3d4-06030b8d8e51
| 605,155
|
The plane is divided into unit squares by means of two sets of parallel lines. The unit squares are coloured in 1201 colours so that no rectangle of perimeter 100 contains two squares of the same colour. Show that no rectangle of size $1 \times 1201$ contains two squares of the same colour.
|
Let the centers of the unit squares be the integer points in the plane, and denote each unit square by the coordinates of its center.
Consider the set $D$ of all unit squares $(x, y)$ such that $|x|+|y| \leq 24$. Any translate of $D$ is called a diamond.
Since any two unit squares that belong to the same diamond also belong to some rectangle of perimeter 100, a diamond cannot contain two unit squares of the same colour. Since a diamond contains exactly $24^{2}+25^{2}=1201$ unit squares, a diamond must contain every colour exactly once.
Choose one colour, say, green, and let $a_{1}, a_{2}, \ldots$ be all green unit squares. Let $P_{i}$ be the diamond of center $a_{i}$. We will show that no unit square is covered by two $P$ 's and that every unit square is covered by some $P_{i}$.
Indeed, suppose first that $P_{i}$ and $P_{j}$ contain the same unit square $b$. Then their centers lie within the same rectangle of perimeter 100, a contradiction.
Let, on the other hand, $b$ be an arbitrary unit square. The diamond of center $b$ must contain some green unit square $a_{i}$. The diamond $P_{i}$ of center $a_{i}$ will then contain $b$.
Therefore, $P_{1}, P_{2}, \ldots$ form a covering of the plane in exactly one layer. It is easy to see, though, that, up to translation and reflection, there exists a unique such covering. (Indeed, consider two neighbouring diamonds. Unless they fit neatly, uncoverable spaces of two unit squares are created near the corners: see Fig. 1.)

Figure 1:
Without loss of generality, then, this covering is given by the diamonds of centers $(x, y)$ such that $24 x+25 y$ is divisible by 1201. (See Fig. 2 for an analogous covering with smaller diamonds.) It follows from this that no rectangle of size $1 \times 1201$ can contain two green unit squares, and analogous reasoning works for the remaining colours.

Figure 2:
Remark(PSC): The number of the unit squares in a diamond can be evaluated alternatively with the formula
$$
2 \times(1+3+5+\ldots+47)+49=2 \times 24^{2}+49=1201
$$
## Geometry
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The plane is divided into unit squares by means of two sets of parallel lines. The unit squares are coloured in 1201 colours so that no rectangle of perimeter 100 contains two squares of the same colour. Show that no rectangle of size $1 \times 1201$ contains two squares of the same colour.
|
Let the centers of the unit squares be the integer points in the plane, and denote each unit square by the coordinates of its center.
Consider the set $D$ of all unit squares $(x, y)$ such that $|x|+|y| \leq 24$. Any translate of $D$ is called a diamond.
Since any two unit squares that belong to the same diamond also belong to some rectangle of perimeter 100, a diamond cannot contain two unit squares of the same colour. Since a diamond contains exactly $24^{2}+25^{2}=1201$ unit squares, a diamond must contain every colour exactly once.
Choose one colour, say, green, and let $a_{1}, a_{2}, \ldots$ be all green unit squares. Let $P_{i}$ be the diamond of center $a_{i}$. We will show that no unit square is covered by two $P$ 's and that every unit square is covered by some $P_{i}$.
Indeed, suppose first that $P_{i}$ and $P_{j}$ contain the same unit square $b$. Then their centers lie within the same rectangle of perimeter 100, a contradiction.
Let, on the other hand, $b$ be an arbitrary unit square. The diamond of center $b$ must contain some green unit square $a_{i}$. The diamond $P_{i}$ of center $a_{i}$ will then contain $b$.
Therefore, $P_{1}, P_{2}, \ldots$ form a covering of the plane in exactly one layer. It is easy to see, though, that, up to translation and reflection, there exists a unique such covering. (Indeed, consider two neighbouring diamonds. Unless they fit neatly, uncoverable spaces of two unit squares are created near the corners: see Fig. 1.)

Figure 1:
Without loss of generality, then, this covering is given by the diamonds of centers $(x, y)$ such that $24 x+25 y$ is divisible by 1201. (See Fig. 2 for an analogous covering with smaller diamonds.) It follows from this that no rectangle of size $1 \times 1201$ can contain two green unit squares, and analogous reasoning works for the remaining colours.

Figure 2:
Remark(PSC): The number of the unit squares in a diamond can be evaluated alternatively with the formula
$$
2 \times(1+3+5+\ldots+47)+49=2 \times 24^{2}+49=1201
$$
## Geometry
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\n## C3.",
"solution_match": "\nSolution."
}
|
9f26cf5c-1725-5fe2-83be-052e2ef811ea
| 605,178
|
The point $M$ lies on the side $A B$ of the circumscribed quadrilateral $A B C D$. The points $I_{1}, I_{2}$, and $I_{3}$ are the incenters of $\triangle M B C, \triangle M C D$, and $\triangle M D A$. Show that the points $M, I_{1}, I_{2}$, and $I_{3}$ lie on a circle.
|
Lemma. Let $I$ be the incenter of $\triangle A B C$ and let the points $P$ and $Q$ lie on the lines $A B$ and $A C$. Then the points $A, I, P$, and $Q$ lie on a circle if and only if
$$
\overline{B P}+\overline{C Q}=B C
$$
where $\overline{B P}$ equals $|B P|$ if $P$ lies in the ray $B A \rightarrow$ and $-|B P|$ if it does not, and similarly for $\overline{C Q}$.
Proof of the lemma. We shall only consider the case when $P$ and $Q$ lie in the segments $A B$ and $A C$. All other cases are treated analogously.
Suppose that $A, I, P$, and $Q$ lie on a circle. Let $D$ and $E$ be the contact points of the incircle of $\triangle A B C$ with $A B$ and $A C$. We have that $\angle P I Q=180^{\circ}-\alpha$, so $\angle D I P=\angle E I Q$ and, therefore, $\triangle D I P \simeq \triangle E I Q$. This gives us $D P=E Q$ and $B P+C Q=B D+C E=B C$, as needed.
The converse is established by following the foregoing chain of inequalities in reverse.
Let the circumcircle of $\triangle M I_{1} I_{3}$ meet the lines $A B, C M$, and $D M$ for the second time at $P, Q$, and $R$. By the lemma, $\overline{B P}+\overline{C Q}=B C$ and $\overline{D R}+\overline{A P}=D A$. Therefore, $\overline{C Q}+\overline{D R}=B C+D A-\overline{B P}-\overline{A P}=$ $B C+D A-A B$. Since $A B C D$ is circumscribed, this is equal to $C D$, and, by the lemma, the proof is complete.
Second solution. Let $\omega_{1}, \omega_{2}$, and $\omega_{3}$ be the incircles of $\triangle M B C, \triangle M C D$, and $\triangle M D A$.
The common internal tangent $t_{1}$ of $\omega_{1}$ and $\omega_{2}$ equals
$\left[\right.$ tangent from $M$ to $\left.\omega_{2}\right]-\left[\right.$ tangent from $M$ to $\left.\omega_{1}\right]=\frac{1}{2}(M C+M D-C D-M B-M C+B C)$.
Analogously, the common internal tangent $t_{2}$ of $\omega_{2}$ and $\omega_{3}$ equals
$\left[\right.$ tangent from $M$ to $\left.\omega_{2}\right]-\left[\right.$ tangent from $M$ to $\left.\omega_{3}\right]=\frac{1}{2}(M C+M D-C D-M D-M A+D A)$.
Finally, the common external tangent $t_{3}$ of $\omega_{1}$ and $\omega_{3}$ equals
$\left[\right.$ tangent from $M$ to $\left.\omega_{1}\right]-\left[\right.$ tangent from $M$ to $\left.\omega_{3}\right]=\frac{1}{2}(M B+M C-B C+M D+M A-D A)$.
Since $A B C D$ is circumscribed, we have $A B+C D=B C+D A$, and, therefore, $t_{1}+t_{2}=t_{3}$. It follows from this that $\omega_{1}, \omega_{2}$, and $\omega_{3}$ have a common tangent $s$ (which separates $\omega_{2}$ from $\omega_{1}$ and $\omega_{3}$ ).
Let $\triangle M K L$ be the triangle formed by the lines $M C, M D$, and $s$. Then, since $I_{1} I_{2}$ and $I_{2} I_{3}$ are external angle bisectors in it, we have $\angle I_{1} I_{2} I_{3}=90^{\circ}-\frac{1}{2} \angle K M L=180^{\circ}-\angle I_{1} M I_{3}$ and, therefore, $M I_{1} I_{2} I_{3}$ is cyclic.
$\operatorname{Remark}(\mathbf{P S C}):$ In the first solution, the angle $\alpha$ refers to the angle $\angle B A C$.
$\operatorname{Remark}(\mathbf{P S C})$ : Referring to solution 1 , the inequality $t_{3} \leq t_{1}+t_{2}$ holds, the equality is possible if and only if the circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ have a common tangent.
Remark(PSC): This problem was selected as G1 relative to the other Geometry problems proposed. PSC thinks the difficulty level of this problem is medium.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The point $M$ lies on the side $A B$ of the circumscribed quadrilateral $A B C D$. The points $I_{1}, I_{2}$, and $I_{3}$ are the incenters of $\triangle M B C, \triangle M C D$, and $\triangle M D A$. Show that the points $M, I_{1}, I_{2}$, and $I_{3}$ lie on a circle.

|
Lemma. Let $I$ be the incenter of $\triangle A B C$ and let the points $P$ and $Q$ lie on the lines $A B$ and $A C$. Then the points $A, I, P$, and $Q$ lie on a circle if and only if
$$
\overline{B P}+\overline{C Q}=B C
$$
where $\overline{B P}$ equals $|B P|$ if $P$ lies in the ray $B A \rightarrow$ and $-|B P|$ if it does not, and similarly for $\overline{C Q}$.
Proof of the lemma. We shall only consider the case when $P$ and $Q$ lie in the segments $A B$ and $A C$. All other cases are treated analogously.

Suppose that $A, I, P$, and $Q$ lie on a circle. Let $D$ and $E$ be the contact points of the incircle of $\triangle A B C$ with $A B$ and $A C$. We have that $\angle P I Q=180^{\circ}-\alpha$, so $\angle D I P=\angle E I Q$ and, therefore, $\triangle D I P \simeq \triangle E I Q$. This gives us $D P=E Q$ and $B P+C Q=B D+C E=B C$, as needed.
The converse is established by following the foregoing chain of inequalities in reverse.
Let the circumcircle of $\triangle M I_{1} I_{3}$ meet the lines $A B, C M$, and $D M$ for the second time at $P, Q$, and $R$. By the lemma, $\overline{B P}+\overline{C Q}=B C$ and $\overline{D R}+\overline{A P}=D A$. Therefore, $\overline{C Q}+\overline{D R}=B C+D A-\overline{B P}-\overline{A P}=$ $B C+D A-A B$. Since $A B C D$ is circumscribed, this is equal to $C D$, and, by the lemma, the proof is complete.

Second solution. Let $\omega_{1}, \omega_{2}$, and $\omega_{3}$ be the incircles of $\triangle M B C, \triangle M C D$, and $\triangle M D A$.
The common internal tangent $t_{1}$ of $\omega_{1}$ and $\omega_{2}$ equals
$\left[\right.$ tangent from $M$ to $\left.\omega_{2}\right]-\left[\right.$ tangent from $M$ to $\left.\omega_{1}\right]=\frac{1}{2}(M C+M D-C D-M B-M C+B C)$.
Analogously, the common internal tangent $t_{2}$ of $\omega_{2}$ and $\omega_{3}$ equals
$\left[\right.$ tangent from $M$ to $\left.\omega_{2}\right]-\left[\right.$ tangent from $M$ to $\left.\omega_{3}\right]=\frac{1}{2}(M C+M D-C D-M D-M A+D A)$.
Finally, the common external tangent $t_{3}$ of $\omega_{1}$ and $\omega_{3}$ equals
$\left[\right.$ tangent from $M$ to $\left.\omega_{1}\right]-\left[\right.$ tangent from $M$ to $\left.\omega_{3}\right]=\frac{1}{2}(M B+M C-B C+M D+M A-D A)$.
Since $A B C D$ is circumscribed, we have $A B+C D=B C+D A$, and, therefore, $t_{1}+t_{2}=t_{3}$. It follows from this that $\omega_{1}, \omega_{2}$, and $\omega_{3}$ have a common tangent $s$ (which separates $\omega_{2}$ from $\omega_{1}$ and $\omega_{3}$ ).

Let $\triangle M K L$ be the triangle formed by the lines $M C, M D$, and $s$. Then, since $I_{1} I_{2}$ and $I_{2} I_{3}$ are external angle bisectors in it, we have $\angle I_{1} I_{2} I_{3}=90^{\circ}-\frac{1}{2} \angle K M L=180^{\circ}-\angle I_{1} M I_{3}$ and, therefore, $M I_{1} I_{2} I_{3}$ is cyclic.
$\operatorname{Remark}(\mathbf{P S C}):$ In the first solution, the angle $\alpha$ refers to the angle $\angle B A C$.
$\operatorname{Remark}(\mathbf{P S C})$ : Referring to solution 1 , the inequality $t_{3} \leq t_{1}+t_{2}$ holds, the equality is possible if and only if the circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ have a common tangent.
Remark(PSC): This problem was selected as G1 relative to the other Geometry problems proposed. PSC thinks the difficulty level of this problem is medium.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\n## G1.",
"solution_match": "\nSolution."
}
|
83353965-80b6-5f53-853d-2abbb5188686
| 605,190
|
Let $A B C D$ be a cyclic quadrilateral, with $A B<C D$, whose diagonals intersect at the point $F$ and $A D, B C$ intersect at the point $E$. Let also $K, L$ be the projections of $F$ onto the sides $A D, B C$ respectively, and $M, S, T$ be the midpoints of $E F, C F, D F$. Prove that the second intersection point of the circumcircles of the triangles $M K T, M L S$ lies on the side $C D$.
|
Let $N$ be the midpoint of $C D$. We will prove that the circumcircles of the triangles $M K T, M L S$ pass through $N$.
We will prove first that the circumcircle of $M L S$ passes through $N$.
Let $Q$ be the midpoint of $E C$. Note that the circumcircle of $M L S$ is the Euler circle of the triangle $E F C$, so it passes also through $Q .\left(^{*}\right)$
We will prove that
$$
\angle S L Q=\angle Q N S
$$
Indeed, since $F L C$ is right-angled and $L S$ is its median, we have that $S L=S C$ and
$$
\angle S L C=\angle S C L=\angle A B C
$$
In addition, since $N, S$ are the midpoints of $D C, F C$ we have that $S N / / F D$.
And finally, $Q, S$ are the midpoints of $E C, C D$, so $Q N / / E D$.
It follows that the angles $\angle E D B$ and $\angle Q N S$ have parallel sides, and since $A B<C D$, they are acute, and as a result we have that
$$
\angle E D B=\angle Q N S
$$
But, from the cyclic quadrilateral $A B C D$, we get that
$$
\angle E D B=\angle A C B
$$
Now, from (2),(3) and (4) we obtain immediately (1), so $\angle S L Q=\angle Q N S$ and the quadrilateral $L N S Q$ is cyclic. Since from $\left(^{*}\right)$ this circle passes also through $M$, we get that the points $M, L, Q, S, N$ are co-cylic and this means that the circumcircle of $M L S$ passes through $N$.
Similarly, that the circumcircle of $M K T$ passes also through $N$ and we have the desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral, with $A B<C D$, whose diagonals intersect at the point $F$ and $A D, B C$ intersect at the point $E$. Let also $K, L$ be the projections of $F$ onto the sides $A D, B C$ respectively, and $M, S, T$ be the midpoints of $E F, C F, D F$. Prove that the second intersection point of the circumcircles of the triangles $M K T, M L S$ lies on the side $C D$.
|
Let $N$ be the midpoint of $C D$. We will prove that the circumcircles of the triangles $M K T, M L S$ pass through $N$.
We will prove first that the circumcircle of $M L S$ passes through $N$.
Let $Q$ be the midpoint of $E C$. Note that the circumcircle of $M L S$ is the Euler circle of the triangle $E F C$, so it passes also through $Q .\left(^{*}\right)$

We will prove that
$$
\angle S L Q=\angle Q N S
$$
Indeed, since $F L C$ is right-angled and $L S$ is its median, we have that $S L=S C$ and
$$
\angle S L C=\angle S C L=\angle A B C
$$
In addition, since $N, S$ are the midpoints of $D C, F C$ we have that $S N / / F D$.
And finally, $Q, S$ are the midpoints of $E C, C D$, so $Q N / / E D$.
It follows that the angles $\angle E D B$ and $\angle Q N S$ have parallel sides, and since $A B<C D$, they are acute, and as a result we have that
$$
\angle E D B=\angle Q N S
$$
But, from the cyclic quadrilateral $A B C D$, we get that
$$
\angle E D B=\angle A C B
$$
Now, from (2),(3) and (4) we obtain immediately (1), so $\angle S L Q=\angle Q N S$ and the quadrilateral $L N S Q$ is cyclic. Since from $\left(^{*}\right)$ this circle passes also through $M$, we get that the points $M, L, Q, S, N$ are co-cylic and this means that the circumcircle of $M L S$ passes through $N$.
Similarly, that the circumcircle of $M K T$ passes also through $N$ and we have the desired.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\nG2.",
"solution_match": "\nSolution."
}
|
0a5ea54e-a0db-5f48-a82a-cd54145524d3
| 605,202
|
Given that $A B C$ is a triangle where $A B<A C$. On the half-lines $B A$ and $C A$ we take points $F$ and $E$ respectively such that $B F=C E=B C$. Let $M, N$ and $H$ be the mid-points of the segments $B F, C E$ and $B C$ respectively and $K$ and $O$ be the circumcircles of the triangles $A B C$ and $M N H$ respectively. We assume that $O K$ cuts $B E$ and $H N$ at the points $A_{1}$ and $B_{1}$ respectively and that $C_{1}$ is the point of intersection of $H N$ and $F E$. If the parallel line from $A_{1}$ to $O C_{1}$ cuts the line $F E$ at $D$ and the perpendicular from $A_{1}$ to the line $D B_{1}$ cuts $F E$ at the point $M_{1}$, prove that $E$ is the orthocenter of the triangle $A_{1} O M_{1}$.
|
The circumcenter of the triangle $\triangle M N H$ coincides with the incentre of the triangle $\triangle A B C$ because the triangles $\triangle B M H$ and $\triangle N H C$ are isosceles and therefore the perpendiculars of the $M H, H N$ are also the bisectors of the angles $\angle A B C, \angle A C B$, respectively.
Let $G, I$ be the points of tangents of the incircle $(O, r)$ of the triangle $\triangle A B C$ with the sides $A B$ and $A C$ respectively. Now if $a, b, c$ are the sides of the triangle $\triangle A B C$ and $s$ the semiperimeter of the triangle , we have
$$
O F^{2}=O G^{2}+F G^{2}=r^{2}+(a-s+b)^{2}
$$
and
$$
O E^{2}=O I^{2}+E I^{2}=r^{2}+(a-s+c)^{2}
$$
Then
$$
O F^{2}-O E^{2}=\alpha(b-c)
$$
Applying two times the theorem of Stewarts at the triangles $\triangle K F B$ and $\triangle K A C$ we get
$$
F A \cdot K A^{2}+c \cdot K F^{2}=a \cdot K A^{2}+a c \cdot F A \quad \text { or } \quad K F^{2}=K A^{2}+a(a-c)
$$
and
$$
E A \cdot K E^{2}+\alpha \cdot K A^{2}=b \cdot K E^{2}+a b \cdot E A \quad \text { or } \quad K E^{2}=K A^{2}+a(b-a)
$$
From (2) and (3) we have
$$
K F^{2}-K E^{2}=a(a-c)-a(b-a)=\alpha(b-c)
$$
From (1),(4), because $O F^{2}-O E^{2}=K F^{2}-K E^{2}$ we have that $F E \perp O K$.
Let $J$ the point of intersection of $F E, O K$.
Because $A_{1} D / / O C_{1}$ we have
$$
\frac{J O}{J A_{1}}=\frac{J C_{1}}{J D}
$$
And since $A_{1} E / / H N$ we get
$$
\frac{J E}{J A_{1}}=\frac{J C_{1}}{J B_{1}}
$$
Therefore, we have
$$
\frac{J O}{J E}=\frac{J B_{1}}{J D}
$$
Thus, from the inverse of Thales theorem we have that $E O / / D B_{1}$, So
$$
A M_{1} \perp E O
$$
Consequently, the point $E$ is the orthocenter of the triangle $\triangle A_{1} O M_{1}$
Remark(PSC): Here in the solution the side $B C$ has been referred as $\alpha$ and $a$, which are equivalent.
## Number theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given that $A B C$ is a triangle where $A B<A C$. On the half-lines $B A$ and $C A$ we take points $F$ and $E$ respectively such that $B F=C E=B C$. Let $M, N$ and $H$ be the mid-points of the segments $B F, C E$ and $B C$ respectively and $K$ and $O$ be the circumcircles of the triangles $A B C$ and $M N H$ respectively. We assume that $O K$ cuts $B E$ and $H N$ at the points $A_{1}$ and $B_{1}$ respectively and that $C_{1}$ is the point of intersection of $H N$ and $F E$. If the parallel line from $A_{1}$ to $O C_{1}$ cuts the line $F E$ at $D$ and the perpendicular from $A_{1}$ to the line $D B_{1}$ cuts $F E$ at the point $M_{1}$, prove that $E$ is the orthocenter of the triangle $A_{1} O M_{1}$.
|
The circumcenter of the triangle $\triangle M N H$ coincides with the incentre of the triangle $\triangle A B C$ because the triangles $\triangle B M H$ and $\triangle N H C$ are isosceles and therefore the perpendiculars of the $M H, H N$ are also the bisectors of the angles $\angle A B C, \angle A C B$, respectively.

Let $G, I$ be the points of tangents of the incircle $(O, r)$ of the triangle $\triangle A B C$ with the sides $A B$ and $A C$ respectively. Now if $a, b, c$ are the sides of the triangle $\triangle A B C$ and $s$ the semiperimeter of the triangle , we have
$$
O F^{2}=O G^{2}+F G^{2}=r^{2}+(a-s+b)^{2}
$$
and
$$
O E^{2}=O I^{2}+E I^{2}=r^{2}+(a-s+c)^{2}
$$
Then
$$
O F^{2}-O E^{2}=\alpha(b-c)
$$
Applying two times the theorem of Stewarts at the triangles $\triangle K F B$ and $\triangle K A C$ we get
$$
F A \cdot K A^{2}+c \cdot K F^{2}=a \cdot K A^{2}+a c \cdot F A \quad \text { or } \quad K F^{2}=K A^{2}+a(a-c)
$$
and
$$
E A \cdot K E^{2}+\alpha \cdot K A^{2}=b \cdot K E^{2}+a b \cdot E A \quad \text { or } \quad K E^{2}=K A^{2}+a(b-a)
$$
From (2) and (3) we have
$$
K F^{2}-K E^{2}=a(a-c)-a(b-a)=\alpha(b-c)
$$
From (1),(4), because $O F^{2}-O E^{2}=K F^{2}-K E^{2}$ we have that $F E \perp O K$.
Let $J$ the point of intersection of $F E, O K$.
Because $A_{1} D / / O C_{1}$ we have
$$
\frac{J O}{J A_{1}}=\frac{J C_{1}}{J D}
$$
And since $A_{1} E / / H N$ we get
$$
\frac{J E}{J A_{1}}=\frac{J C_{1}}{J B_{1}}
$$
Therefore, we have
$$
\frac{J O}{J E}=\frac{J B_{1}}{J D}
$$
Thus, from the inverse of Thales theorem we have that $E O / / D B_{1}$, So
$$
A M_{1} \perp E O
$$
Consequently, the point $E$ is the orthocenter of the triangle $\triangle A_{1} O M_{1}$
Remark(PSC): Here in the solution the side $B C$ has been referred as $\alpha$ and $a$, which are equivalent.
## Number theory
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution."
}
|
7135c64f-2c2f-58ab-a09c-732a84292627
| 605,215
|
A positive integer $n$ is downhill if its decimal representation $\overline{a_{k} a_{k-1} \ldots a_{0}}$ satisfies $a_{k} \geq a_{k-1} \geq \ldots \geq a_{0}$. A real-coefficient polynomial $P$ is integer-valued if $P(n)$ is an integer for all integer $n$, and downhill-integervalued if $P(n)$ is an integer for all downhill positive integers $n$. Is it true that every downhill-integer-valued polynomial is also integer-valued?
|
No, it is not.
A downhill number can always be written as $a-b_{1}-b_{2}-\ldots-b_{9}$, where $a$ is of the form $99 \ldots 99$ and each $b_{i}$ either equals 0 or is of the form $\overline{11 \ldots 11}$.
Let $n$ be a positive integer. The numbers of the form $99 \ldots 99$ yield at most $n$ different remainders upon division by $2^{n}$, as do the numbers of the form $11 \ldots 11$. Therefore, downhill numbers yield at most $n(n+1)^{9}$ different remainders upon division by $2^{n}$.
Let $n$ be so large that $n(n+1)^{9}<2^{n}$. ( $n=63$ works: $63 \times 64^{9}<64^{10}=2^{60}<2^{63}$.) Let $0 \leq r<2^{n}$ be such that no downhill number is congruent to $r$ modulo $2^{n}$.
Consider the polynomial
$$
P(x)=\frac{1}{2 \times\left(2^{n}-1\right)!} \prod_{1 \leq i<2^{n}}(x-r+i) .
$$
We have that $P(r)=\frac{1}{2}$ is not an integer.
Let, then, $x$ be a downhill number. The number $(x-r+1) \ldots\left(x-r+2^{n}-1\right)$ is a multiple of $\left(2^{n}-1\right)$ ! (as a product of $2^{n}-1$ consecutive integers); therefore, $2 P(x)$ is an integer. On the other hand, the number $(x-r)(x-r+1) \ldots\left(x-r+2^{n}-1\right)$ ia a multiple of $2^{n}$ ! (as a product of $2^{n}$ consecutive integers); therefore, $2(x-r) P(x)$ is an integer multiple of $2^{n}$. Since $x$ is downhill, $x-r$ is not divisible by $2^{n}$. Therefore, $2 P(x)$ is even and $P(x)$ is an integer.
Alternative version. A positive integer $n$ is uphill if its decimal representation $\overline{a_{k} a_{k-1} \ldots a_{0}}$ satisfies $a_{k} \leq a_{k-1} \leq \ldots \leq a_{0}$. A real-coefficient polynomial $P$ is integer-valued if $P(n)$ is an integer for all integer $n$, and uphill-integer-valued if $P(n)$ is an integer for all uphill positive integers $n$. Is it true that every uphill-integer-valued polynomial is also integer-valued?
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A positive integer $n$ is downhill if its decimal representation $\overline{a_{k} a_{k-1} \ldots a_{0}}$ satisfies $a_{k} \geq a_{k-1} \geq \ldots \geq a_{0}$. A real-coefficient polynomial $P$ is integer-valued if $P(n)$ is an integer for all integer $n$, and downhill-integervalued if $P(n)$ is an integer for all downhill positive integers $n$. Is it true that every downhill-integer-valued polynomial is also integer-valued?
|
No, it is not.
A downhill number can always be written as $a-b_{1}-b_{2}-\ldots-b_{9}$, where $a$ is of the form $99 \ldots 99$ and each $b_{i}$ either equals 0 or is of the form $\overline{11 \ldots 11}$.
Let $n$ be a positive integer. The numbers of the form $99 \ldots 99$ yield at most $n$ different remainders upon division by $2^{n}$, as do the numbers of the form $11 \ldots 11$. Therefore, downhill numbers yield at most $n(n+1)^{9}$ different remainders upon division by $2^{n}$.
Let $n$ be so large that $n(n+1)^{9}<2^{n}$. ( $n=63$ works: $63 \times 64^{9}<64^{10}=2^{60}<2^{63}$.) Let $0 \leq r<2^{n}$ be such that no downhill number is congruent to $r$ modulo $2^{n}$.
Consider the polynomial
$$
P(x)=\frac{1}{2 \times\left(2^{n}-1\right)!} \prod_{1 \leq i<2^{n}}(x-r+i) .
$$
We have that $P(r)=\frac{1}{2}$ is not an integer.
Let, then, $x$ be a downhill number. The number $(x-r+1) \ldots\left(x-r+2^{n}-1\right)$ is a multiple of $\left(2^{n}-1\right)$ ! (as a product of $2^{n}-1$ consecutive integers); therefore, $2 P(x)$ is an integer. On the other hand, the number $(x-r)(x-r+1) \ldots\left(x-r+2^{n}-1\right)$ ia a multiple of $2^{n}$ ! (as a product of $2^{n}$ consecutive integers); therefore, $2(x-r) P(x)$ is an integer multiple of $2^{n}$. Since $x$ is downhill, $x-r$ is not divisible by $2^{n}$. Therefore, $2 P(x)$ is even and $P(x)$ is an integer.
Alternative version. A positive integer $n$ is uphill if its decimal representation $\overline{a_{k} a_{k-1} \ldots a_{0}}$ satisfies $a_{k} \leq a_{k-1} \leq \ldots \leq a_{0}$. A real-coefficient polynomial $P$ is integer-valued if $P(n)$ is an integer for all integer $n$, and uphill-integer-valued if $P(n)$ is an integer for all uphill positive integers $n$. Is it true that every uphill-integer-valued polynomial is also integer-valued?
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\nN5.",
"solution_match": "\nSolution."
}
|
a8680e2a-02f7-5c7b-a09e-76b02c03c907
| 605,272
|
A positive integer $n$ is downhill if its decimal representation $\overline{a_{k} a_{k-1} \ldots a_{0}}$ satisfies $a_{k} \geq a_{k-1} \geq \ldots \geq a_{0}$. A real-coefficient polynomial $P$ is integer-valued if $P(n)$ is an integer for all integer $n$, and downhill-integervalued if $P(n)$ is an integer for all downhill positive integers $n$. Is it true that every downhill-integer-valued polynomial is also integer-valued?
|
First we show that no uphill number is congruent to 10 modulo 11.
To this end, notice that an uphill number can always be written as $b_{1}+b_{2}+\ldots+b_{m}$, where $m \leq 9$, $b_{1} \leq b_{2} \leq \ldots \leq b_{m}$, and each $b_{i}$ is of the form $11 \ldots 11$. Since the remainder of each $b_{i}$ modulo 11 is either 0 or 1 , the remainder of $b_{1}+b_{2}+\ldots+b_{m}$ modulo 11 is at most 9 , as required.
Consider, then, the polynomial
$$
P(x)=\frac{1}{11} x(x-1) \cdots(x-9)
$$
It value is an integer at every uphill number; however, $P(10)$ is not an integer.
Remark(PSC): PSC believes the alternative version of this problem has medium as level of difficulty.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A positive integer $n$ is downhill if its decimal representation $\overline{a_{k} a_{k-1} \ldots a_{0}}$ satisfies $a_{k} \geq a_{k-1} \geq \ldots \geq a_{0}$. A real-coefficient polynomial $P$ is integer-valued if $P(n)$ is an integer for all integer $n$, and downhill-integervalued if $P(n)$ is an integer for all downhill positive integers $n$. Is it true that every downhill-integer-valued polynomial is also integer-valued?
|
First we show that no uphill number is congruent to 10 modulo 11.
To this end, notice that an uphill number can always be written as $b_{1}+b_{2}+\ldots+b_{m}$, where $m \leq 9$, $b_{1} \leq b_{2} \leq \ldots \leq b_{m}$, and each $b_{i}$ is of the form $11 \ldots 11$. Since the remainder of each $b_{i}$ modulo 11 is either 0 or 1 , the remainder of $b_{1}+b_{2}+\ldots+b_{m}$ modulo 11 is at most 9 , as required.
Consider, then, the polynomial
$$
P(x)=\frac{1}{11} x(x-1) \cdots(x-9)
$$
It value is an integer at every uphill number; however, $P(10)$ is not an integer.
Remark(PSC): PSC believes the alternative version of this problem has medium as level of difficulty.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\nN5.",
"solution_match": "\nSolution."
}
|
a8680e2a-02f7-5c7b-a09e-76b02c03c907
| 605,272
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\frac{1}{a^{5}+b^{5}+c^{2}}+\frac{1}{b^{5}+c^{5}+a^{2}}+\frac{1}{c^{5}+a^{5}+b^{2}} \leq 1 .
$$
|
First we remark that
$$
a^{5}+b^{5} \geq a b\left(a^{3}+b^{3}\right)
$$
Indeed
$$
\begin{aligned}
a^{5}+b^{5} \geq a b\left(a^{3}+b^{3}\right) & \Leftrightarrow a^{5}-a^{4} b-a b^{4}+b^{5} \geq 0 \\
& \Leftrightarrow a^{4}(a-b)-b^{4}(a-b) \geq 0 \\
(a-b)\left(a^{4}-b^{4}\right) \geq 0 & \Leftrightarrow(a-b)^{2}\left(a^{2}+b^{2}\right)(a+b) \geq 0
\end{aligned}
$$
We rewrite the inequality as
$$
\frac{1}{a^{5}+b^{5}+a b c^{3}}+\frac{1}{b^{5}+c^{5}+b c a^{3}}+\frac{1}{c^{5}+a^{5}+c a b^{3}} \leq 1 .
$$
On the other hand the following inequality is true
$$
a^{5}+b^{5}+a b c^{3} \geq a b\left(a^{3}+b^{3}+c^{3}\right)
$$
and similar for the other two.
Finally, using AM-GM we get:
$$
\begin{aligned}
\frac{1}{a^{5}+b^{5}+c^{2}}+\frac{1}{b^{5}+c^{5}+a^{2}}+\frac{1}{c^{5}+a^{5}+b^{2}} & \leq \frac{1}{a^{3}+b^{3}+c^{3}}\left(\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}\right)=\frac{a+b+c}{a^{3}+b^{3}+c^{3}} \\
& \leq \frac{a+b+c}{\frac{(a+b+c)^{3}}{9}}=\frac{9}{(a+b+c)^{2}} \leq \frac{9}{(3 \sqrt[3]{a b c})^{2}}=1
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\frac{1}{a^{5}+b^{5}+c^{2}}+\frac{1}{b^{5}+c^{5}+a^{2}}+\frac{1}{c^{5}+a^{5}+b^{2}} \leq 1 .
$$
|
First we remark that
$$
a^{5}+b^{5} \geq a b\left(a^{3}+b^{3}\right)
$$
Indeed
$$
\begin{aligned}
a^{5}+b^{5} \geq a b\left(a^{3}+b^{3}\right) & \Leftrightarrow a^{5}-a^{4} b-a b^{4}+b^{5} \geq 0 \\
& \Leftrightarrow a^{4}(a-b)-b^{4}(a-b) \geq 0 \\
(a-b)\left(a^{4}-b^{4}\right) \geq 0 & \Leftrightarrow(a-b)^{2}\left(a^{2}+b^{2}\right)(a+b) \geq 0
\end{aligned}
$$
We rewrite the inequality as
$$
\frac{1}{a^{5}+b^{5}+a b c^{3}}+\frac{1}{b^{5}+c^{5}+b c a^{3}}+\frac{1}{c^{5}+a^{5}+c a b^{3}} \leq 1 .
$$
On the other hand the following inequality is true
$$
a^{5}+b^{5}+a b c^{3} \geq a b\left(a^{3}+b^{3}+c^{3}\right)
$$
and similar for the other two.
Finally, using AM-GM we get:
$$
\begin{aligned}
\frac{1}{a^{5}+b^{5}+c^{2}}+\frac{1}{b^{5}+c^{5}+a^{2}}+\frac{1}{c^{5}+a^{5}+b^{2}} & \leq \frac{1}{a^{3}+b^{3}+c^{3}}\left(\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}\right)=\frac{a+b+c}{a^{3}+b^{3}+c^{3}} \\
& \leq \frac{a+b+c}{\frac{(a+b+c)^{3}}{9}}=\frac{9}{(a+b+c)^{2}} \leq \frac{9}{(3 \sqrt[3]{a b c})^{2}}=1
\end{aligned}
$$
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## A1",
"solution_match": "\n## Solution"
}
|
50339cb5-0842-59e3-9edc-0283a5c3e00c
| 605,291
|
Consider the sequence of rational numbers defned by $x_{1}=\frac{4}{3}$ and $x_{n+1}=\frac{x_{n}^{2}}{x_{n}^{2}-x_{n}+1}, n \geq 1$.
Show that the numerator of the lowest term expression of each sum $\sum_{k=1}^{n} x_{k}$ is a perfect square.
|
It is easily seen that the $x_{n}$ are all rational numbers greater than 1 . Rewrite the recurrence formula in the form $x_{n}=\frac{1}{x_{n+1}-1}-\frac{1}{x_{n}-1}, n \geq 1$, to get
$$
\sum_{k=1}^{n} x_{k}=\frac{1}{x_{n+1}-1}-\frac{1}{x_{1}-1}=\frac{x_{n}^{2}-x_{n}+1}{x_{n}-1}-3=\frac{\left(x_{n}-2\right)^{2}}{x_{n}-1}
$$
Finally, express the positive rational number $x_{n}-1$ in lowest terms, $x_{n}-1=\frac{a}{b}$, to deduce that $\frac{(a-b)^{2}}{a b}$ expresses $\sum_{k=1}^{n} x_{k}$ the lowest terms.
Since $\operatorname{gcd}(a, b)=1 \Rightarrow \operatorname{gcd}(a-b, b)=1 \Rightarrow \operatorname{gcd}\left((a-b)^{2}, b\right)=1$. Similarly we can prove that $\operatorname{gcd}\left((a-b)^{2}, a\right)=1$, which implies that $\operatorname{gcd}\left((a-b)^{2}, a b\right)=1$.
The conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Consider the sequence of rational numbers defned by $x_{1}=\frac{4}{3}$ and $x_{n+1}=\frac{x_{n}^{2}}{x_{n}^{2}-x_{n}+1}, n \geq 1$.
Show that the numerator of the lowest term expression of each sum $\sum_{k=1}^{n} x_{k}$ is a perfect square.
|
It is easily seen that the $x_{n}$ are all rational numbers greater than 1 . Rewrite the recurrence formula in the form $x_{n}=\frac{1}{x_{n+1}-1}-\frac{1}{x_{n}-1}, n \geq 1$, to get
$$
\sum_{k=1}^{n} x_{k}=\frac{1}{x_{n+1}-1}-\frac{1}{x_{1}-1}=\frac{x_{n}^{2}-x_{n}+1}{x_{n}-1}-3=\frac{\left(x_{n}-2\right)^{2}}{x_{n}-1}
$$
Finally, express the positive rational number $x_{n}-1$ in lowest terms, $x_{n}-1=\frac{a}{b}$, to deduce that $\frac{(a-b)^{2}}{a b}$ expresses $\sum_{k=1}^{n} x_{k}$ the lowest terms.
Since $\operatorname{gcd}(a, b)=1 \Rightarrow \operatorname{gcd}(a-b, b)=1 \Rightarrow \operatorname{gcd}\left((a-b)^{2}, b\right)=1$. Similarly we can prove that $\operatorname{gcd}\left((a-b)^{2}, a\right)=1$, which implies that $\operatorname{gcd}\left((a-b)^{2}, a b\right)=1$.
The conclusion follows.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## A2",
"solution_match": "\n## Solution"
}
|
afcd1472-bc80-5fba-9715-09d63df8d2c6
| 605,301
|
Consider integers $m \geq 2$ and $n \geq 1$. Show that there is a polynomial $P(x)$ of degree equal to $n$ with integer coefficients such that $P(0), P(1), \ldots, P(n)$ are all perfect powers of $m$.
|
Let $a_{0}, a_{1}, \ldots, a_{n}$ be integers to be chosen later, and consider the polynomial $P(x)=\frac{1}{n!} Q(x)$ where
$$
Q(x)=\sum_{k=0}^{n}(-1)^{n-k}\binom{n}{k} a_{k} \prod_{\substack{0 \leq i \leq n \\ i \neq k}}(x-i) .
$$
Observe that for $l \in\{0,1, \ldots, n\}$ we have
$$
\begin{aligned}
P(l) & =\frac{1}{n!}(-1)^{n!}(\stackrel{n}{l}) a_{l} \prod_{\substack{0 \leq i \leq n \\
i \neq 1}}(l-i) \\
& =\frac{1}{n!}(-1)^{n-1}\binom{n}{l} a_{l} l!(-1)^{n-l}(n-l)! \\
& =a_{l}
\end{aligned}
$$
So $P(x)$ is the unique polynomial of degree at most $n$ such that $P(l)=a_{l}$. (Any two polynomials of degree at most $n$ agreeing on $n+1$ distinct values are equal.) Note in particular that
$$
\sum_{k=0}^{n}(-1)^{n-k}\binom{n}{k} \prod_{\substack{0 \leq i \leq n \\ i \neq k}}(x-i)=n!
$$
If $p$ is a prime dividing $n$ !, we let $r_{p}$ be maximal such that $p^{r_{p}}$ divides $\boldsymbol{n}$ !. If $p$ divides $\boldsymbol{m}$, then there is an integer $d_{p}$ such that $m^{d_{p}} \approx 0\left(\bmod p^{r_{p}}\right)$, for example $d_{p}=r_{p}$ will do. If $p$ does not divide $m$, then there is an integer $d_{p}$ such that $m^{d_{p}} \equiv 1\left(\bmod p^{r_{p}}\right)$, for example, by Euler's theorem, $d_{p}=\varphi\left(p^{r_{p}}\right)$ will do. Let $d=d_{1} d_{2} \ldots d_{p}$ and observe that for every positive integer $t$ we have $m^{\prime d} \equiv 0\left(\bmod p^{r_{p}}\right)$ if $p \mid m$ and $m^{t d} \equiv 1\left(\bmod p^{r_{p}}\right)$ if $p \nmid m$.
Now let $t_{0}, \ldots, t_{n}$ be positive integers to be chosen later and define $a_{k}=m^{t_{k} d}$. We will show that the polynomial $P(x)$ has integer coefficients. We will also show that there is an appropriate choice of $t_{0}, \ldots, t_{n}$ such that $P(x)$ has degree exactly equal to $n$.
To show that $P(x)$ has integer coefficients it is enough to show that for every $\boldsymbol{p}$ dividing $\boldsymbol{n !}$, all coefficients of $Q(x)$ are multiples of $p^{r_{p}}$. This is immediate if $p$ divides $m$ as all $a_{k}$ 's are multiples of $p^{r_{p}}$. If $p$ does not divide $m$ then we have $a_{k} \equiv 1\left(\bmod p^{r_{p}}\right)$ for every $0 \leq k \leq n$ and so by (*)
$$
Q(x) \equiv \sum_{k=0}^{n}(-1)^{n-k}\binom{n}{k} \prod_{\substack{0 \leq i \leq n \\ i \neq k}}(x-i) \equiv n!\equiv 0\left(\bmod p^{r_{p}}\right)
$$
This shows that all coefficients of $Q(x)$ are indeed multiples of $p^{r_{p}}$. It remains to show that there is a choice of $t_{0}, \ldots, t_{n}$ guarantecing that the degree of $P(x)$ is exactly equal to $n$. One such choice is $t_{0}=2$ and $t_{1}=\ldots=t_{n}=1$. This works because if $P(x)$ had degree less than $n$, then looking at the values $P(1), \ldots, P(n)$ we would get that $P(x)$ is constant. But this is impossible as $P(0) \neq P(1)$.
Note. Looking at the coefficient of $x^{n}$ in the definition of $P(x)$ it is not difficult to see that if we fix any $t_{1}, \ldots, t_{n}$ and pick $t_{0}$ large enough we will get that this coefficient is non-zero. In particular, we can additionally guarantee that $P(0), P(1), \ldots, P(n)$ are distinct perfect powers of $m$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider integers $m \geq 2$ and $n \geq 1$. Show that there is a polynomial $P(x)$ of degree equal to $n$ with integer coefficients such that $P(0), P(1), \ldots, P(n)$ are all perfect powers of $m$.
|
Let $a_{0}, a_{1}, \ldots, a_{n}$ be integers to be chosen later, and consider the polynomial $P(x)=\frac{1}{n!} Q(x)$ where
$$
Q(x)=\sum_{k=0}^{n}(-1)^{n-k}\binom{n}{k} a_{k} \prod_{\substack{0 \leq i \leq n \\ i \neq k}}(x-i) .
$$
Observe that for $l \in\{0,1, \ldots, n\}$ we have
$$
\begin{aligned}
P(l) & =\frac{1}{n!}(-1)^{n!}(\stackrel{n}{l}) a_{l} \prod_{\substack{0 \leq i \leq n \\
i \neq 1}}(l-i) \\
& =\frac{1}{n!}(-1)^{n-1}\binom{n}{l} a_{l} l!(-1)^{n-l}(n-l)! \\
& =a_{l}
\end{aligned}
$$
So $P(x)$ is the unique polynomial of degree at most $n$ such that $P(l)=a_{l}$. (Any two polynomials of degree at most $n$ agreeing on $n+1$ distinct values are equal.) Note in particular that
$$
\sum_{k=0}^{n}(-1)^{n-k}\binom{n}{k} \prod_{\substack{0 \leq i \leq n \\ i \neq k}}(x-i)=n!
$$
If $p$ is a prime dividing $n$ !, we let $r_{p}$ be maximal such that $p^{r_{p}}$ divides $\boldsymbol{n}$ !. If $p$ divides $\boldsymbol{m}$, then there is an integer $d_{p}$ such that $m^{d_{p}} \approx 0\left(\bmod p^{r_{p}}\right)$, for example $d_{p}=r_{p}$ will do. If $p$ does not divide $m$, then there is an integer $d_{p}$ such that $m^{d_{p}} \equiv 1\left(\bmod p^{r_{p}}\right)$, for example, by Euler's theorem, $d_{p}=\varphi\left(p^{r_{p}}\right)$ will do. Let $d=d_{1} d_{2} \ldots d_{p}$ and observe that for every positive integer $t$ we have $m^{\prime d} \equiv 0\left(\bmod p^{r_{p}}\right)$ if $p \mid m$ and $m^{t d} \equiv 1\left(\bmod p^{r_{p}}\right)$ if $p \nmid m$.
Now let $t_{0}, \ldots, t_{n}$ be positive integers to be chosen later and define $a_{k}=m^{t_{k} d}$. We will show that the polynomial $P(x)$ has integer coefficients. We will also show that there is an appropriate choice of $t_{0}, \ldots, t_{n}$ such that $P(x)$ has degree exactly equal to $n$.
To show that $P(x)$ has integer coefficients it is enough to show that for every $\boldsymbol{p}$ dividing $\boldsymbol{n !}$, all coefficients of $Q(x)$ are multiples of $p^{r_{p}}$. This is immediate if $p$ divides $m$ as all $a_{k}$ 's are multiples of $p^{r_{p}}$. If $p$ does not divide $m$ then we have $a_{k} \equiv 1\left(\bmod p^{r_{p}}\right)$ for every $0 \leq k \leq n$ and so by (*)
$$
Q(x) \equiv \sum_{k=0}^{n}(-1)^{n-k}\binom{n}{k} \prod_{\substack{0 \leq i \leq n \\ i \neq k}}(x-i) \equiv n!\equiv 0\left(\bmod p^{r_{p}}\right)
$$
This shows that all coefficients of $Q(x)$ are indeed multiples of $p^{r_{p}}$. It remains to show that there is a choice of $t_{0}, \ldots, t_{n}$ guarantecing that the degree of $P(x)$ is exactly equal to $n$. One such choice is $t_{0}=2$ and $t_{1}=\ldots=t_{n}=1$. This works because if $P(x)$ had degree less than $n$, then looking at the values $P(1), \ldots, P(n)$ we would get that $P(x)$ is constant. But this is impossible as $P(0) \neq P(1)$.
Note. Looking at the coefficient of $x^{n}$ in the definition of $P(x)$ it is not difficult to see that if we fix any $t_{1}, \ldots, t_{n}$ and pick $t_{0}$ large enough we will get that this coefficient is non-zero. In particular, we can additionally guarantee that $P(0), P(1), \ldots, P(n)$ are distinct perfect powers of $m$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## A5",
"solution_match": "\n## Solution"
}
|
b5e45747-4398-5c22-bb27-3a5e9d5ae41d
| 605,330
|
Prove that for all positive integer $n$, there is a positive integer $m$, that $7^{n} \mid 3^{m}+5^{m}-1$.
|
We prove this by induction on $\boldsymbol{n}$. The case $\boldsymbol{n}=1$ is indeed trivial for $\boldsymbol{m}=1$. Assume that the statement of the problem holds true for $n$, and we have $3^{m}+5^{m}-1=7^{n} l$ for some positive integer $l$ which is not divisible by 7 (if not we are done). Since $3^{6} \equiv 1(\bmod 7)$ and $5^{6} \equiv 1(\bmod 7)$ we conclude that,
$$
3^{6 \cdot 7^{n-1}} \equiv 1\left(\bmod 7^{n}\right), 5^{6 \cdot 7^{n-1}} \equiv 1\left(\bmod 7^{n}\right) .
$$
Since
$$
v_{7}\left(3^{6.7^{n-1}}-1\right)=v_{7}\left(3^{6}-1\right)+v_{7}\left(7^{n-1}\right)=n \text { and } v_{7}\left(5^{6.7^{n-1}}-1\right)=v_{7}\left(5^{6}-1\right)+v_{7}\left(7^{n-1}\right)=n
$$
Thus we can say that: $3^{6.7^{n-1}}=1+7^{n} r, 5^{6.7^{n-1}}=1+7^{n} s$ for some positive integers $r, s$. We find the reminder of $r, s$ module 7 . Note that:
$$
\frac{y^{7^{k}}-1}{7^{k+1}}=\frac{y-1}{7} \cdot \frac{1+y+\ldots+y^{6}}{7} \cdot \ldots \cdot \frac{1+y^{7^{x-1}}+\ldots+y^{67^{k-1}}}{7}
$$
We use the above identity for $y=3^{6}, 5^{6}$. Note that in both cases $y=1(\bmod 7)$. Now we use the following lemma
Lemma. Let $p$ be an odd prime such that $p \mid a-1$ then $\frac{a^{p}-1}{a-1} \equiv p\left(\bmod p^{2}\right)$.
Proof. Take $a-1=b$, then $p \mid b$ now
$$
\frac{a^{p}-1}{a-1}=\frac{(b+1)^{p}-1}{b}=b^{p-1}+\ldots+\binom{p}{2} b+p \equiv p\left(\bmod p^{2}\right)
$$
since all the binomial coefficients is divisible by $p$. So our proof is complete.
Then by use of the lemma repeatedly we find that all the terms of the above identity ( ${ }^{*}$ ) except the first term is congruent to 1 modulo 7 . Thus we can find that :
$$
\frac{y^{7^{k}}-1}{7^{k+1}} \equiv \frac{y-1}{7}(\bmod 7)
$$
Since
$$
\frac{3^{6}-1}{7}=104 \equiv-1, \frac{5^{6}-1}{7} \equiv 2232 \equiv-1(\bmod 7)
$$
we find that $r \equiv s \equiv-I(\bmod 7)$, and by use of binomial theorem, we can easily find that
$$
3^{6 l \cdot 7^{n-1}}=1+7^{n} r t\left(\bmod 7^{n+1}\right), \quad 5^{6 i \cdot 7^{n-1}}=1+7^{n} s t\left(\bmod 7^{n+1}\right)
$$
for all positive integers $t$.
Now take $\boldsymbol{m}+\boldsymbol{t r} \cdot 7^{\boldsymbol{n - 1}}$ instead of $\boldsymbol{m}$,(while we will specify the number $t$ later) we can find that:
$$
3^{m+6 t \cdot 7^{n-1}}+5^{m+6 r \cdot 7^{n-1}}-1=3^{m} \cdot 3^{6 r} \cdot 7^{n-1}+5^{m} \cdot 5^{61 \cdot 7^{n-1}}-1
$$
Taking modulo $7^{n+1}$ we can find that, the above expression is reduced to
$$
\begin{aligned}
3^{m}\left(1+7^{n} r t\right)+5^{m}\left(1+7^{n} s t\right)-1 & \equiv 3^{m}+5^{m}-1+5^{m} \cdot 7^{n} s t+3^{m} \cdot 7^{n} r t \\
& \equiv 7^{n}\left(l+\left(5^{m} s+3^{m} r\right) t\right)\left(\bmod 7^{n+1}\right)
\end{aligned}
$$
Now, the problem reduced to finding a positive integer $t$ such that
$$
l+\left(5^{m} s+3^{m} \cdot r\right) t \equiv 0(\bmod 7)
$$
since
$$
5^{m} s+3^{m} r \equiv-5^{m}-3^{m} \equiv 1(\bmod 7) .
$$
Since $3^{m}+5^{m}-1 \equiv 0(\bmod 7)$ whence, we find that $\operatorname{gcd}\left(5^{m} s+3^{m} r, 7\right)=1$. Thus such integer $t$ exists, so we are done!
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for all positive integer $n$, there is a positive integer $m$, that $7^{n} \mid 3^{m}+5^{m}-1$.
|
We prove this by induction on $\boldsymbol{n}$. The case $\boldsymbol{n}=1$ is indeed trivial for $\boldsymbol{m}=1$. Assume that the statement of the problem holds true for $n$, and we have $3^{m}+5^{m}-1=7^{n} l$ for some positive integer $l$ which is not divisible by 7 (if not we are done). Since $3^{6} \equiv 1(\bmod 7)$ and $5^{6} \equiv 1(\bmod 7)$ we conclude that,
$$
3^{6 \cdot 7^{n-1}} \equiv 1\left(\bmod 7^{n}\right), 5^{6 \cdot 7^{n-1}} \equiv 1\left(\bmod 7^{n}\right) .
$$
Since
$$
v_{7}\left(3^{6.7^{n-1}}-1\right)=v_{7}\left(3^{6}-1\right)+v_{7}\left(7^{n-1}\right)=n \text { and } v_{7}\left(5^{6.7^{n-1}}-1\right)=v_{7}\left(5^{6}-1\right)+v_{7}\left(7^{n-1}\right)=n
$$
Thus we can say that: $3^{6.7^{n-1}}=1+7^{n} r, 5^{6.7^{n-1}}=1+7^{n} s$ for some positive integers $r, s$. We find the reminder of $r, s$ module 7 . Note that:
$$
\frac{y^{7^{k}}-1}{7^{k+1}}=\frac{y-1}{7} \cdot \frac{1+y+\ldots+y^{6}}{7} \cdot \ldots \cdot \frac{1+y^{7^{x-1}}+\ldots+y^{67^{k-1}}}{7}
$$
We use the above identity for $y=3^{6}, 5^{6}$. Note that in both cases $y=1(\bmod 7)$. Now we use the following lemma
Lemma. Let $p$ be an odd prime such that $p \mid a-1$ then $\frac{a^{p}-1}{a-1} \equiv p\left(\bmod p^{2}\right)$.
Proof. Take $a-1=b$, then $p \mid b$ now
$$
\frac{a^{p}-1}{a-1}=\frac{(b+1)^{p}-1}{b}=b^{p-1}+\ldots+\binom{p}{2} b+p \equiv p\left(\bmod p^{2}\right)
$$
since all the binomial coefficients is divisible by $p$. So our proof is complete.
Then by use of the lemma repeatedly we find that all the terms of the above identity ( ${ }^{*}$ ) except the first term is congruent to 1 modulo 7 . Thus we can find that :
$$
\frac{y^{7^{k}}-1}{7^{k+1}} \equiv \frac{y-1}{7}(\bmod 7)
$$
Since
$$
\frac{3^{6}-1}{7}=104 \equiv-1, \frac{5^{6}-1}{7} \equiv 2232 \equiv-1(\bmod 7)
$$
we find that $r \equiv s \equiv-I(\bmod 7)$, and by use of binomial theorem, we can easily find that
$$
3^{6 l \cdot 7^{n-1}}=1+7^{n} r t\left(\bmod 7^{n+1}\right), \quad 5^{6 i \cdot 7^{n-1}}=1+7^{n} s t\left(\bmod 7^{n+1}\right)
$$
for all positive integers $t$.
Now take $\boldsymbol{m}+\boldsymbol{t r} \cdot 7^{\boldsymbol{n - 1}}$ instead of $\boldsymbol{m}$,(while we will specify the number $t$ later) we can find that:
$$
3^{m+6 t \cdot 7^{n-1}}+5^{m+6 r \cdot 7^{n-1}}-1=3^{m} \cdot 3^{6 r} \cdot 7^{n-1}+5^{m} \cdot 5^{61 \cdot 7^{n-1}}-1
$$
Taking modulo $7^{n+1}$ we can find that, the above expression is reduced to
$$
\begin{aligned}
3^{m}\left(1+7^{n} r t\right)+5^{m}\left(1+7^{n} s t\right)-1 & \equiv 3^{m}+5^{m}-1+5^{m} \cdot 7^{n} s t+3^{m} \cdot 7^{n} r t \\
& \equiv 7^{n}\left(l+\left(5^{m} s+3^{m} r\right) t\right)\left(\bmod 7^{n+1}\right)
\end{aligned}
$$
Now, the problem reduced to finding a positive integer $t$ such that
$$
l+\left(5^{m} s+3^{m} \cdot r\right) t \equiv 0(\bmod 7)
$$
since
$$
5^{m} s+3^{m} r \equiv-5^{m}-3^{m} \equiv 1(\bmod 7) .
$$
Since $3^{m}+5^{m}-1 \equiv 0(\bmod 7)$ whence, we find that $\operatorname{gcd}\left(5^{m} s+3^{m} r, 7\right)=1$. Thus such integer $t$ exists, so we are done!
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## NT3",
"solution_match": "\n## Solution"
}
|
beb64582-ba15-5e9c-a31f-9e9ec3cf168f
| 605,371
|
Given a positive odd integer $n$, show that the arithmetic mean of fractional parts $\left\{\frac{k^{2 n}}{p}\right\}$, $k=1, \ldots, \frac{p-1}{2}$, is the same for infinitely many primes $p$.
|
We show that the arithmetic mean in question is $\frac{1}{2}$ for infinitely many primes congruent to 1 modulo 4.
Notice that $\left\{\frac{k^{2 n}}{p}\right\}=\frac{r_{k}}{p}$, where $r_{k}$ is the remainder $k^{2 n}$ leaves upon division by $p$. Clearly, the $r_{k}$ are quadratic residues modulo $p$.
If $p$ is prime, and $p-1$ and $n$ are relatively prime, then the $r_{k}, k=1, \ldots, \frac{p-1}{2}$, are pairwise distinct, since the $k^{2 n}, k=1, \ldots, \frac{p-1}{2}$, are pairwise distinct modulo $p$, by Fermat's little theorem. In this case, the $r_{k}, k=1, \ldots, \frac{p-1}{2}$, form the set $R$ of all $\frac{p-1}{2}$ quadratic residues modulo $p$ in the range 1 through $p-1$.
If, in addition, $p$ is congruent to 1 modulo 4 , then -1 is a quadratic residue modulo $p$, and the assignment $r \mapsto p-r, r \in R$, defines a permutation of $R$. In this case,
$$
\sum_{r \in R} r=\sum_{r \in R}(p-r)=\frac{p(p-1)}{2}-\sum_{r \in R} r
$$
so
$$
\sum_{r \in R} r=\frac{p(p-1)}{4},
$$
and the arithmetic mean in question is $\frac{1}{2}$.
Finally, since $n$ is odd, infinitely many primes congruent to 1 modulo 4 are also congruent to 2 modulo $n$, by Dirichlet's theorem on arithmetic sequences of integers; for such a prime $p$, the numbers $p-1$ and $n$ are clearly relatively prime. This completes the proof.
## GEOMETRY
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Given a positive odd integer $n$, show that the arithmetic mean of fractional parts $\left\{\frac{k^{2 n}}{p}\right\}$, $k=1, \ldots, \frac{p-1}{2}$, is the same for infinitely many primes $p$.
|
We show that the arithmetic mean in question is $\frac{1}{2}$ for infinitely many primes congruent to 1 modulo 4.
Notice that $\left\{\frac{k^{2 n}}{p}\right\}=\frac{r_{k}}{p}$, where $r_{k}$ is the remainder $k^{2 n}$ leaves upon division by $p$. Clearly, the $r_{k}$ are quadratic residues modulo $p$.
If $p$ is prime, and $p-1$ and $n$ are relatively prime, then the $r_{k}, k=1, \ldots, \frac{p-1}{2}$, are pairwise distinct, since the $k^{2 n}, k=1, \ldots, \frac{p-1}{2}$, are pairwise distinct modulo $p$, by Fermat's little theorem. In this case, the $r_{k}, k=1, \ldots, \frac{p-1}{2}$, form the set $R$ of all $\frac{p-1}{2}$ quadratic residues modulo $p$ in the range 1 through $p-1$.
If, in addition, $p$ is congruent to 1 modulo 4 , then -1 is a quadratic residue modulo $p$, and the assignment $r \mapsto p-r, r \in R$, defines a permutation of $R$. In this case,
$$
\sum_{r \in R} r=\sum_{r \in R}(p-r)=\frac{p(p-1)}{2}-\sum_{r \in R} r
$$
so
$$
\sum_{r \in R} r=\frac{p(p-1)}{4},
$$
and the arithmetic mean in question is $\frac{1}{2}$.
Finally, since $n$ is odd, infinitely many primes congruent to 1 modulo 4 are also congruent to 2 modulo $n$, by Dirichlet's theorem on arithmetic sequences of integers; for such a prime $p$, the numbers $p-1$ and $n$ are clearly relatively prime. This completes the proof.
## GEOMETRY
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## NT5",
"solution_match": "\n## Solution"
}
|
84bded69-459c-51e8-921c-c8c4953b6d5a
| 605,393
|
Let $A B C$ be an acute triangle. Variable points $E$ and $F$ are on sides $A C$ and $A B$ respectively such that $B C^{2}=B A \cdot B F+C E \cdot C A$. As $E$ and $F$ vary prove that the circumcircle of $A E F$ passes through a fixed point other than $A$.
|
1
Let $H$ be the ortocenter of $A B C$ and $K, L, M$ be the feet of perpendiculars respectively from $A, B, C$ to their opposite sides of $A B C$. Also let $D$ be the intersection point of lines $B E$ and $C F$. From power of point we have
$$
B A \cdot B M=B C \cdot B K
$$
and
$$
C A \cdot C L=C B \cdot C K
$$
Adding (1) and (2) we have:
$$
C A \cdot C L+B A \cdot B M=B C \cdot B K+C B \cdot C K=B C(B K+C K)=B C^{2}
$$
Combining (3) with the problem statement $B C^{2}=B A \cdot B F+C E \cdot C A$ we have:
$$
\begin{aligned}
& B A \cdot B F-B A \cdot B M=C A \cdot C L-C E \cdot C A \\
& B A(B F-B M)=C A(C L-C E) \\
& B A \cdot F M=C A \cdot L E \\
& \quad \frac{L E}{F M}=\frac{A B}{A C}=\frac{B L}{C M}
\end{aligned}
$$
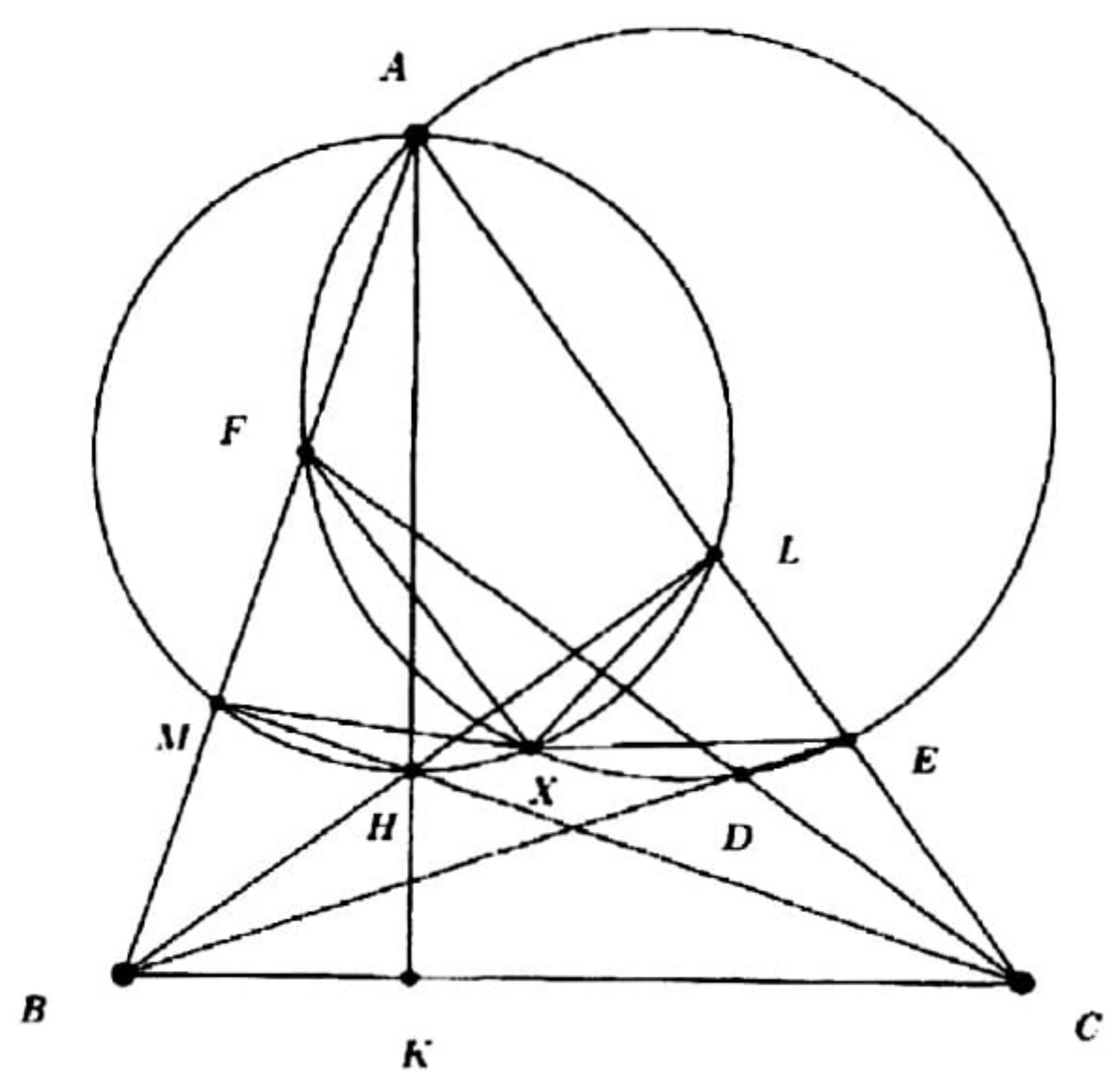
Where the last equality follows from $\triangle A M C \sim \triangle A L B$. Now since $\frac{L E}{F M}=\frac{B L}{C M}$ and $\angle F M C=\angle E L B=90^{\circ}$ we get that triangles $\triangle F M C \sim \triangle E L B$. From this similarity we get
$$
\measuredangle A E D=\measuredangle A E B=\angle L E B=\measuredangle M F C=180^{\circ}-\angle A F C=180-\angle A F D,
$$
meaning points $A, D, E, F$ are concylic.
Since both pairs $\{E, F\}$ and $\{M, L\}$ satisfy the problem condition, we must have this fixed point we are looking for is the second intersection of the circumcircles around $A F D E$ and AMHL. Let this point be $X$. We now prove that $X$ is fixed on the circumcircle of $A M H L$ (which would imply $X$ is fixed).
From the concylicity we have
$$
\angle X L E=180^{\circ}-\measuredangle X L A=\measuredangle X M A=\angle X M F \text { and } \measuredangle X E L=\measuredangle X E A=180-\measuredangle X F A=\measuredangle X F M
$$
and from here we get $\triangle X L E \sim \triangle X M F$. This similarity gives us
$$
\frac{X L}{X M}=\frac{L E}{M F} .
$$
Now combining (4) and (5) we get $\frac{X L}{X M}=\frac{A B}{A C}$ which is a fixed quantity. Since points $M, L$, the circumcircle of $A M L$, and ratio $\frac{X L}{X M}$ are fixed, this implies that point $X$ is fixed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Variable points $E$ and $F$ are on sides $A C$ and $A B$ respectively such that $B C^{2}=B A \cdot B F+C E \cdot C A$. As $E$ and $F$ vary prove that the circumcircle of $A E F$ passes through a fixed point other than $A$.
|
1
Let $H$ be the ortocenter of $A B C$ and $K, L, M$ be the feet of perpendiculars respectively from $A, B, C$ to their opposite sides of $A B C$. Also let $D$ be the intersection point of lines $B E$ and $C F$. From power of point we have
$$
B A \cdot B M=B C \cdot B K
$$
and
$$
C A \cdot C L=C B \cdot C K
$$
Adding (1) and (2) we have:
$$
C A \cdot C L+B A \cdot B M=B C \cdot B K+C B \cdot C K=B C(B K+C K)=B C^{2}
$$
Combining (3) with the problem statement $B C^{2}=B A \cdot B F+C E \cdot C A$ we have:
$$
\begin{aligned}
& B A \cdot B F-B A \cdot B M=C A \cdot C L-C E \cdot C A \\
& B A(B F-B M)=C A(C L-C E) \\
& B A \cdot F M=C A \cdot L E \\
& \quad \frac{L E}{F M}=\frac{A B}{A C}=\frac{B L}{C M}
\end{aligned}
$$

Where the last equality follows from $\triangle A M C \sim \triangle A L B$. Now since $\frac{L E}{F M}=\frac{B L}{C M}$ and $\angle F M C=\angle E L B=90^{\circ}$ we get that triangles $\triangle F M C \sim \triangle E L B$. From this similarity we get
$$
\measuredangle A E D=\measuredangle A E B=\angle L E B=\measuredangle M F C=180^{\circ}-\angle A F C=180-\angle A F D,
$$
meaning points $A, D, E, F$ are concylic.
Since both pairs $\{E, F\}$ and $\{M, L\}$ satisfy the problem condition, we must have this fixed point we are looking for is the second intersection of the circumcircles around $A F D E$ and AMHL. Let this point be $X$. We now prove that $X$ is fixed on the circumcircle of $A M H L$ (which would imply $X$ is fixed).
From the concylicity we have
$$
\angle X L E=180^{\circ}-\measuredangle X L A=\measuredangle X M A=\angle X M F \text { and } \measuredangle X E L=\measuredangle X E A=180-\measuredangle X F A=\measuredangle X F M
$$
and from here we get $\triangle X L E \sim \triangle X M F$. This similarity gives us
$$
\frac{X L}{X M}=\frac{L E}{M F} .
$$
Now combining (4) and (5) we get $\frac{X L}{X M}=\frac{A B}{A C}$ which is a fixed quantity. Since points $M, L$, the circumcircle of $A M L$, and ratio $\frac{X L}{X M}$ are fixed, this implies that point $X$ is fixed.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## G1",
"solution_match": "\n## Solution"
}
|
3aa178da-fdfa-5e63-8f0d-7fe30dd8a643
| 605,400
|
Let $A B C$ be an acute triangle. Variable points $E$ and $F$ are on sides $A C$ and $A B$ respectively such that $B C^{2}=B A \cdot B F+C E \cdot C A$. As $E$ and $F$ vary prove that the circumcircle of $A E F$ passes through a fixed point other than $A$.
|
2
Let the $D$ be the intersection of $B E$ and $C F$ and let circumcircle of triangle $C F A$ intersect $B C$ at point $G$. From power of point we have
$$
B G \cdot B C=B F \cdot B A
$$
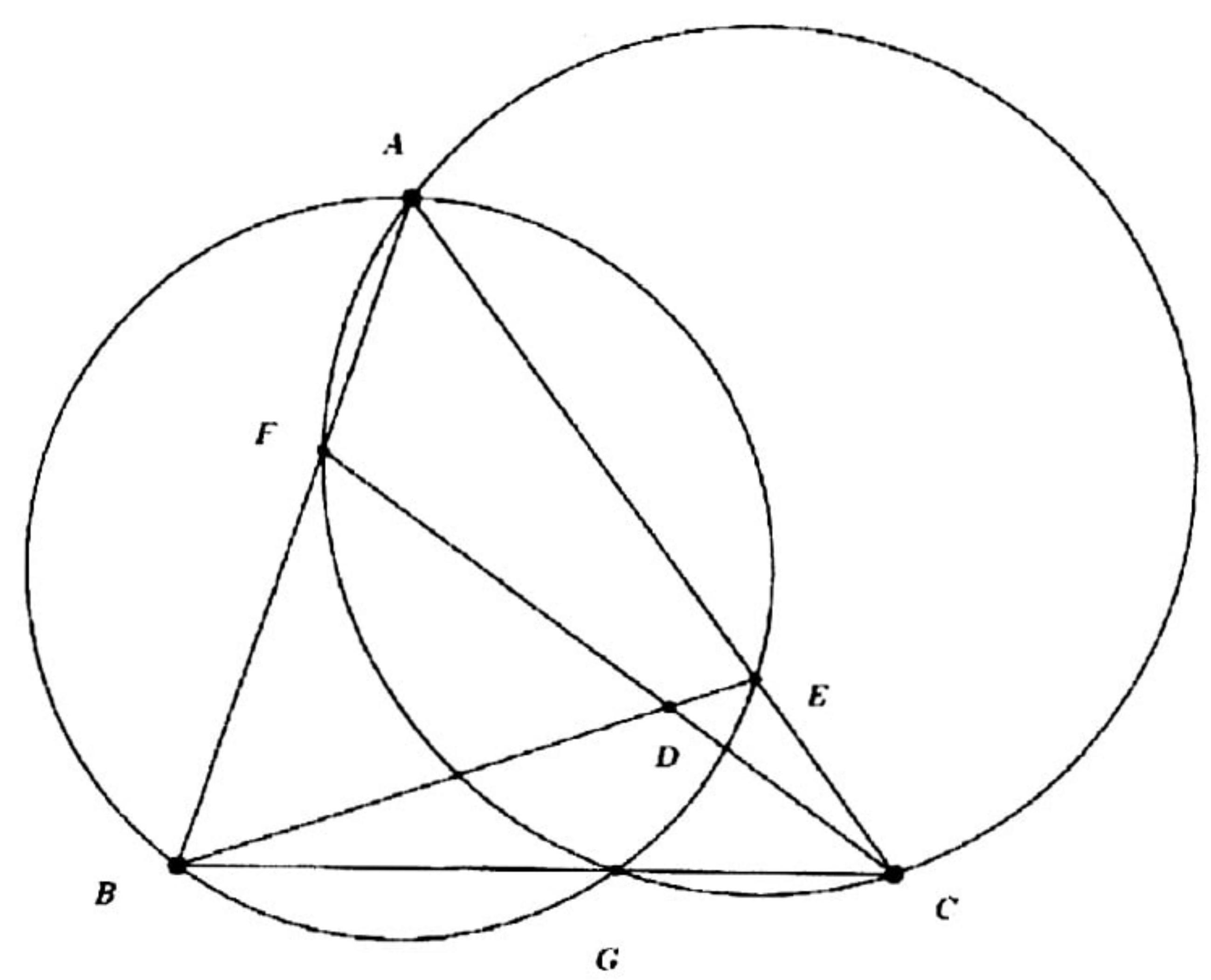
Combining (6) with the problem statement we get
$$
B C^{2}=B A \cdot B F+C E \cdot C A=B G \cdot B C+C E \cdot C A
$$
and from here we get
$$
C E \cdot C A=B C(B C-B G)=B C \cdot C G
$$
(7) implies that $E, A, B, G$ are concyclic as well.
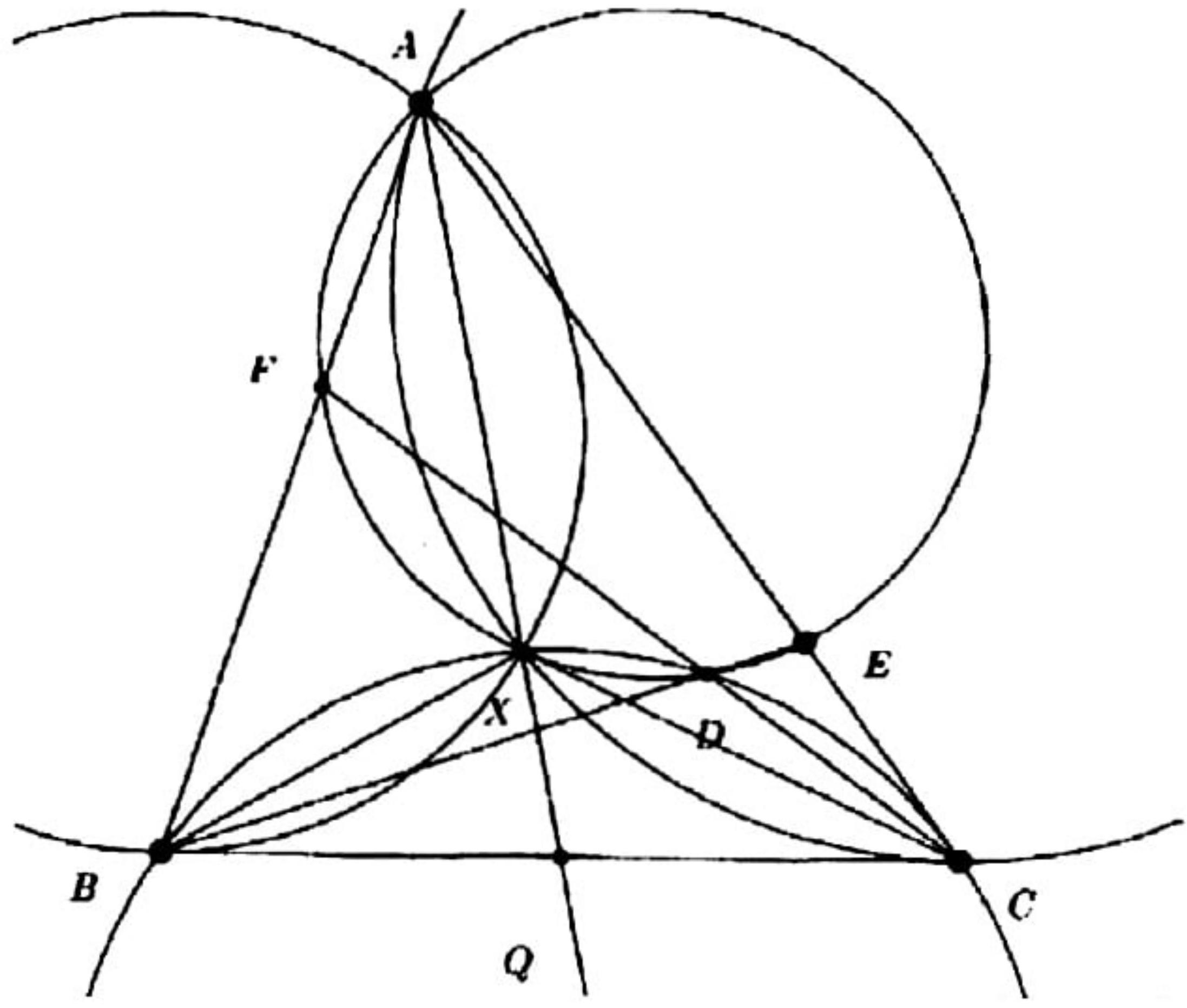
This gives us
$$
\measuredangle G A C=\measuredangle G A E=\measuredangle G B E=\measuredangle C B D
$$
and
$$
\measuredangle B A C-\measuredangle G A C=\measuredangle G A B=\measuredangle G A F=\measuredangle G C F=\measuredangle B C D .
$$
Adding these two equalities gives us
$$
\measuredangle B A C=\measuredangle C B D+\measuredangle B C D=180^{\circ}-\measuredangle B D C .
$$
This implies that $A, E, D, F$ are concyclic. Now let the second intersection of the circumcircles of $B D C$ and $A F D E$ be $X$. We have
$$
\angle X A B=\angle X A F=\angle X D F=180^{\circ}-\angle X D C=\angle X B C
$$
and
$$
\measuredangle X A C=\angle X A E=180^{\circ}-\measuredangle X D E=\angle X D B=\measuredangle X C B
$$
(8) and (9) imply that $B C$ is tangent to the circumcircles of $\triangle X A B$ and $\triangle X A C$ respectively. Let $A X$, the radical axis of the two circumcircles, intersect $B C$ at $Q$. Now we have by power of point
$$
Q B^{2}=Q X \cdot Q A=Q C^{2}
$$
giving up that $A X$ bisects $B C$. So $X$ is the point on the median from $A$ to side $B C$ such that $\measuredangle B X C=180-\measuredangle B A C$. This point is unique and we have proven that it is always on the circumcircle of $A E D F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Variable points $E$ and $F$ are on sides $A C$ and $A B$ respectively such that $B C^{2}=B A \cdot B F+C E \cdot C A$. As $E$ and $F$ vary prove that the circumcircle of $A E F$ passes through a fixed point other than $A$.
|
2
Let the $D$ be the intersection of $B E$ and $C F$ and let circumcircle of triangle $C F A$ intersect $B C$ at point $G$. From power of point we have
$$
B G \cdot B C=B F \cdot B A
$$

Combining (6) with the problem statement we get
$$
B C^{2}=B A \cdot B F+C E \cdot C A=B G \cdot B C+C E \cdot C A
$$
and from here we get
$$
C E \cdot C A=B C(B C-B G)=B C \cdot C G
$$
(7) implies that $E, A, B, G$ are concyclic as well.

This gives us
$$
\measuredangle G A C=\measuredangle G A E=\measuredangle G B E=\measuredangle C B D
$$
and
$$
\measuredangle B A C-\measuredangle G A C=\measuredangle G A B=\measuredangle G A F=\measuredangle G C F=\measuredangle B C D .
$$
Adding these two equalities gives us
$$
\measuredangle B A C=\measuredangle C B D+\measuredangle B C D=180^{\circ}-\measuredangle B D C .
$$
This implies that $A, E, D, F$ are concyclic. Now let the second intersection of the circumcircles of $B D C$ and $A F D E$ be $X$. We have
$$
\angle X A B=\angle X A F=\angle X D F=180^{\circ}-\angle X D C=\angle X B C
$$
and
$$
\measuredangle X A C=\angle X A E=180^{\circ}-\measuredangle X D E=\angle X D B=\measuredangle X C B
$$
(8) and (9) imply that $B C$ is tangent to the circumcircles of $\triangle X A B$ and $\triangle X A C$ respectively. Let $A X$, the radical axis of the two circumcircles, intersect $B C$ at $Q$. Now we have by power of point
$$
Q B^{2}=Q X \cdot Q A=Q C^{2}
$$
giving up that $A X$ bisects $B C$. So $X$ is the point on the median from $A$ to side $B C$ such that $\measuredangle B X C=180-\measuredangle B A C$. This point is unique and we have proven that it is always on the circumcircle of $A E D F$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## G1",
"solution_match": "\n## Solution"
}
|
3aa178da-fdfa-5e63-8f0d-7fe30dd8a643
| 605,400
|
Let $A B C$ be an acute triangle and $D$ a variable point on side $A C$. Point $E$ is on $B D$ such that $B E=\frac{B C^{2}-C D \cdot C A}{B D}$. As $D$ varies on side $A C$ prove that the circumcircle of $A D E$ passes through a fixed point other than $A$.
|
Let the circumcircle of triangle $C E D$ intersect $B C$ at point $G$. From power of point we have
$$
B G \cdot B C=B E \cdot B D .
$$
Combining (1) with the problem statement we get
$$
\frac{B C \cdot B C}{B D}=B E=\frac{B C^{2}-C D \cdot C A}{B D}
$$
and from here we get
$$
C D \cdot C A=B C(B C-B G)=B C \cdot C G .
$$
(2) implies that $D, A, B, G$ are concyclic as well. This gives us
$$
\angle B E C=\measuredangle B G D=180^{\circ}-\measuredangle B A D=180-\measuredangle C A B .
$$
Now let the circumcircle of $A D E$ and $B E C$ intersect again at $X$. Since
$$
\angle X C B=\angle X E B=180^{\circ}-\measuredangle X E D=\angle X A D=\angle X A C
$$
and
$$
\angle B X C=\angle B E C=180^{\circ}-\angle B A C
$$
we have that $X$ is on the unique circle through $A$ and $C$ tangent to side $B C$ at point $C$ and circumcircle of $B H C$ where $H$ is the ortocenter of triangle $A B C$. This intersection is unique and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle and $D$ a variable point on side $A C$. Point $E$ is on $B D$ such that $B E=\frac{B C^{2}-C D \cdot C A}{B D}$. As $D$ varies on side $A C$ prove that the circumcircle of $A D E$ passes through a fixed point other than $A$.
|
Let the circumcircle of triangle $C E D$ intersect $B C$ at point $G$. From power of point we have
$$
B G \cdot B C=B E \cdot B D .
$$
Combining (1) with the problem statement we get
$$
\frac{B C \cdot B C}{B D}=B E=\frac{B C^{2}-C D \cdot C A}{B D}
$$
and from here we get
$$
C D \cdot C A=B C(B C-B G)=B C \cdot C G .
$$
(2) implies that $D, A, B, G$ are concyclic as well. This gives us
$$
\angle B E C=\measuredangle B G D=180^{\circ}-\measuredangle B A D=180-\measuredangle C A B .
$$
Now let the circumcircle of $A D E$ and $B E C$ intersect again at $X$. Since
$$
\angle X C B=\angle X E B=180^{\circ}-\measuredangle X E D=\angle X A D=\angle X A C
$$
and
$$
\angle B X C=\angle B E C=180^{\circ}-\angle B A C
$$
we have that $X$ is on the unique circle through $A$ and $C$ tangent to side $B C$ at point $C$ and circumcircle of $B H C$ where $H$ is the ortocenter of triangle $A B C$. This intersection is unique and we are done.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\nG2",
"solution_match": "\n## Solution"
}
|
d434158f-847e-5995-ba0f-996020e35bf4
| 605,418
|
Let $A B C$ be a triangle with $A B<A C$ inscribed into a circle $c$. The tangent of $c$ at the point $C$ meets the parallel from $B$ to $A C$ at the point $D$. The tangent of $c$ at the point $B$ meets the parallel from $C$ to $A B$ at the point $E$ and the tangent of $c$ at the point $C$ at the point $L$. Suppose that the circumcircle $c_{1}$ of the triangle $B D C$ meets $A C$ at the point $T$ and the circumcircle $c_{2}$ of the triangle $B E C$ meets $A B$ at the point $S$. Prove that the lines $S T, B C, A L$ are concurrent.
|
We will prove first that the circle $c_{1}$ is tangent to $A B$ at the point $B$. In order to prove this, we have to prove that $\measuredangle B D C=\measuredangle A B C$. Indeed, since $B D \| A C$, we have that $\measuredangle D B C=\measuredangle A C B$. Additionally, $\angle B C D=\measuredangle B A C$ (by chord and tangent), which means that the triangles $A B C, B D C$ have two equal angles and so the third ones are also equal. It follows that $\angle B D C=\measuredangle A B C$, so $c_{1}$ is tangent to $A B$ at the point $B$.
Similarly, the circle $c_{2}$ is tangent to $A C$ at the point $C$.
As a consequence, $\measuredangle A B T=\measuredangle A C B$ (by chord and tangent) and also $\measuredangle B S C=\measuredangle A C B$.
By the above, we have that $\measuredangle A B T=\measuredangle B S C$, so the lines $B T, S C$ are parallel.
Now, let $S T$ intersect $B C$ at the point $K$. It suffice to prove that $K$ belongs to $A L$. From the trapezoid $B T C S$ we get that
$$
\frac{B K}{K C}=\frac{B T}{S C}
$$
and from the similar triangles $A B T, A S C$, we have that
$$
\frac{B T}{S C}=\frac{A B}{A S}
$$
By (1), (2) we get that
$$
\frac{B K}{K C}=\frac{A B}{A S}
$$
From the power of point theorem, we have that
$$
A C^{2}=A B \cdot A S \Rightarrow A S=\frac{A C^{2}}{A B}
$$
Going back into (3), it gives that
$$
\frac{B K}{K C}=\frac{A B^{2}}{A C^{2}}
$$
From the last one, it follows that $K$ belongs to the symmedian of the triangle $A B C$.
Finally, recall that the well known fact that since $L B$ and $L C$ are tangents, it follows that $A L$ is the symmedian of the triangle $A B C$, so $K$ belongs to $A L$, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$ inscribed into a circle $c$. The tangent of $c$ at the point $C$ meets the parallel from $B$ to $A C$ at the point $D$. The tangent of $c$ at the point $B$ meets the parallel from $C$ to $A B$ at the point $E$ and the tangent of $c$ at the point $C$ at the point $L$. Suppose that the circumcircle $c_{1}$ of the triangle $B D C$ meets $A C$ at the point $T$ and the circumcircle $c_{2}$ of the triangle $B E C$ meets $A B$ at the point $S$. Prove that the lines $S T, B C, A L$ are concurrent.
|
We will prove first that the circle $c_{1}$ is tangent to $A B$ at the point $B$. In order to prove this, we have to prove that $\measuredangle B D C=\measuredangle A B C$. Indeed, since $B D \| A C$, we have that $\measuredangle D B C=\measuredangle A C B$. Additionally, $\angle B C D=\measuredangle B A C$ (by chord and tangent), which means that the triangles $A B C, B D C$ have two equal angles and so the third ones are also equal. It follows that $\angle B D C=\measuredangle A B C$, so $c_{1}$ is tangent to $A B$ at the point $B$.
Similarly, the circle $c_{2}$ is tangent to $A C$ at the point $C$.
As a consequence, $\measuredangle A B T=\measuredangle A C B$ (by chord and tangent) and also $\measuredangle B S C=\measuredangle A C B$.
By the above, we have that $\measuredangle A B T=\measuredangle B S C$, so the lines $B T, S C$ are parallel.
Now, let $S T$ intersect $B C$ at the point $K$. It suffice to prove that $K$ belongs to $A L$. From the trapezoid $B T C S$ we get that
$$
\frac{B K}{K C}=\frac{B T}{S C}
$$
and from the similar triangles $A B T, A S C$, we have that
$$
\frac{B T}{S C}=\frac{A B}{A S}
$$
By (1), (2) we get that
$$
\frac{B K}{K C}=\frac{A B}{A S}
$$
From the power of point theorem, we have that
$$
A C^{2}=A B \cdot A S \Rightarrow A S=\frac{A C^{2}}{A B}
$$
Going back into (3), it gives that
$$
\frac{B K}{K C}=\frac{A B^{2}}{A C^{2}}
$$

From the last one, it follows that $K$ belongs to the symmedian of the triangle $A B C$.
Finally, recall that the well known fact that since $L B$ and $L C$ are tangents, it follows that $A L$ is the symmedian of the triangle $A B C$, so $K$ belongs to $A L$, as needed.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## G3",
"solution_match": "\n## Solution"
}
|
189f29e7-d484-5e39-9183-d3c1e7c5bde7
| 605,428
|
The acuteangled triangle $A B C$ with circumcenter $O$ is given. The midpoints of the sides $B C$, $C A$ and $A B$ are $D, E$ and $F$ respectivelly. An arbitrary point $M$ on the side $B C$, different of $D$, is choosen. The straight lines $A M$ and $E F$ intersects at the point $N$ and the straight line $O N$ cut again the circumscribed circle of the triangle $O D M$ at the point $P$. Prove that the reflection of the point $M$ with respect to the midpoint of the segment $D P$ belongs on the nine points circle of the triangle $A B C$.
|
The straight lines $D O, E O$ and $F O$ are the perpendicular bisectors of the sides $B C, C A$ and $A B$ respectively. It follows that $[O M]$ is the diameter of the circumscribed circle of the triangle $O D M$ and $M P \perp O N$. The point $O$ is the ortocenter of the triangle $D E F$ (see the picture)
Let $O_{1}$ be the circumcenter of the triangle $D E F$ and $H$ be the diametrically opposite point of $D$. The circumscribed circle of the triangle $D E F$ is the nine points circle of the triangle $A B C$. It follows that $E H \perp D E, F H \perp F D$ and $E D\|A F, D F\| A E$. So, the point $H$ is the ortocenter of the triangle $A E F$.
Let $A D \cap E F=\{I\}$ and $R$ is the reflection of the point N with respect to the point $I$, i.e. $R \in(E F), N I=R I$. The point $I$ is the simmetry center of the parallelogram $A E D F$. It follows that the point $I$ is the midpoint of the segment $[O H]$ and the quadrilaterals $A E D F$, $A N D R, H N O R$ are all parallelograms.
Let $Q$ be the reflection of the point $M$ with respect to the midpoint of the segment $D P$. It follows that the quadrilaterals $P Q D M$ and $M N R D$ are the parallelograms, which imply that the quadrilateral $P Q R N$ is a parallelogram. So, $N O\|H R, N P\| R Q$, which imply that the points $H, R$ and $Q$ are collinear. We obtain that $m(\angle D Q H)=90^{\circ}$, i.e. the point $Q$ belongs on the nine points circle of the triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The acuteangled triangle $A B C$ with circumcenter $O$ is given. The midpoints of the sides $B C$, $C A$ and $A B$ are $D, E$ and $F$ respectivelly. An arbitrary point $M$ on the side $B C$, different of $D$, is choosen. The straight lines $A M$ and $E F$ intersects at the point $N$ and the straight line $O N$ cut again the circumscribed circle of the triangle $O D M$ at the point $P$. Prove that the reflection of the point $M$ with respect to the midpoint of the segment $D P$ belongs on the nine points circle of the triangle $A B C$.
|
The straight lines $D O, E O$ and $F O$ are the perpendicular bisectors of the sides $B C, C A$ and $A B$ respectively. It follows that $[O M]$ is the diameter of the circumscribed circle of the triangle $O D M$ and $M P \perp O N$. The point $O$ is the ortocenter of the triangle $D E F$ (see the picture)
Let $O_{1}$ be the circumcenter of the triangle $D E F$ and $H$ be the diametrically opposite point of $D$. The circumscribed circle of the triangle $D E F$ is the nine points circle of the triangle $A B C$. It follows that $E H \perp D E, F H \perp F D$ and $E D\|A F, D F\| A E$. So, the point $H$ is the ortocenter of the triangle $A E F$.

Let $A D \cap E F=\{I\}$ and $R$ is the reflection of the point N with respect to the point $I$, i.e. $R \in(E F), N I=R I$. The point $I$ is the simmetry center of the parallelogram $A E D F$. It follows that the point $I$ is the midpoint of the segment $[O H]$ and the quadrilaterals $A E D F$, $A N D R, H N O R$ are all parallelograms.
Let $Q$ be the reflection of the point $M$ with respect to the midpoint of the segment $D P$. It follows that the quadrilaterals $P Q D M$ and $M N R D$ are the parallelograms, which imply that the quadrilateral $P Q R N$ is a parallelogram. So, $N O\|H R, N P\| R Q$, which imply that the points $H, R$ and $Q$ are collinear. We obtain that $m(\angle D Q H)=90^{\circ}$, i.e. the point $Q$ belongs on the nine points circle of the triangle $A B C$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## G4",
"solution_match": "\n## Solution."
}
|
8b076c43-1180-560c-b234-c4690c2af604
| 605,436
|
Let $A B C$ be an acute angled triangle with ortocenter $H$, centroid $G$ and circumcircle $\omega$. Let $D$ and $M$ respectively be the intersection of lines $A H$ and $A G$ with side $B C$. Rays $M H$ and $D G$ interect $\omega$ again at $P$ and $Q$ respectively. Prove that $P D$ and $Q M$ intersect on $\omega$.
|
1
Note that it is enough to prove that $\angle D P A+\angle M Q A=180^{\circ}$.
Without loss of generality assume that $A B<A C$. Let the reflection of $H$ in point $M$ be $H^{\prime}$. Since $B H C H^{\prime}$ is a paralelogram we get
$$
\measuredangle B H^{\prime} C=\angle B H C=180^{\circ}-\measuredangle B A C
$$
which means $H^{\prime}$ lies on $\omega$. Also we get
$$
\angle A B H^{\prime}=\angle A B C+\angle C B H^{\prime}=\angle A B C+\angle B C H=90^{\circ}
$$
since $C H \perp A B$. This mean $A H^{\prime}$ is the diameter of $\omega$. This means $\measuredangle M P A=\angle H^{\prime} P A=90^{\circ}$. Since $\angle M P A=\angle M D A=90^{\circ}$ we get that $M, D, P, A$ are concyclic.
This gives us $\angle D P A+\angle A M D=180^{\circ}$. So now it is enough to prove that $\measuredangle A M B=\angle M Q A$.
Taking the homothety with center $G$ and factor -2 (the homothety taking the 9 point circle to the circumcircle of $A B C$ ), we get that $Q$ and $A$ are images of $D$ and $M$ respectively.
This means $A Q \| D M$ giving $A Q \| B C$. Since $A Q \| B C$ and $A, B, C, Q$ are concyclic this means $A B C Q$ is an iscoseles trapezoid.
This means $M$ lies on the perpendicular bisector of $A Q$. This gives us $M A=M Q$. Since $A Q \| B C$ this gives us $\angle A Q M=\angle Q A M=\angle A M B$ which concludes our problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute angled triangle with ortocenter $H$, centroid $G$ and circumcircle $\omega$. Let $D$ and $M$ respectively be the intersection of lines $A H$ and $A G$ with side $B C$. Rays $M H$ and $D G$ interect $\omega$ again at $P$ and $Q$ respectively. Prove that $P D$ and $Q M$ intersect on $\omega$.
|
1
Note that it is enough to prove that $\angle D P A+\angle M Q A=180^{\circ}$.
Without loss of generality assume that $A B<A C$. Let the reflection of $H$ in point $M$ be $H^{\prime}$. Since $B H C H^{\prime}$ is a paralelogram we get
$$
\measuredangle B H^{\prime} C=\angle B H C=180^{\circ}-\measuredangle B A C
$$
which means $H^{\prime}$ lies on $\omega$. Also we get
$$
\angle A B H^{\prime}=\angle A B C+\angle C B H^{\prime}=\angle A B C+\angle B C H=90^{\circ}
$$
since $C H \perp A B$. This mean $A H^{\prime}$ is the diameter of $\omega$. This means $\measuredangle M P A=\angle H^{\prime} P A=90^{\circ}$. Since $\angle M P A=\angle M D A=90^{\circ}$ we get that $M, D, P, A$ are concyclic.

This gives us $\angle D P A+\angle A M D=180^{\circ}$. So now it is enough to prove that $\measuredangle A M B=\angle M Q A$.
Taking the homothety with center $G$ and factor -2 (the homothety taking the 9 point circle to the circumcircle of $A B C$ ), we get that $Q$ and $A$ are images of $D$ and $M$ respectively.
This means $A Q \| D M$ giving $A Q \| B C$. Since $A Q \| B C$ and $A, B, C, Q$ are concyclic this means $A B C Q$ is an iscoseles trapezoid.
This means $M$ lies on the perpendicular bisector of $A Q$. This gives us $M A=M Q$. Since $A Q \| B C$ this gives us $\angle A Q M=\angle Q A M=\angle A M B$ which concludes our problem.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## G5",
"solution_match": "\n## Solution"
}
|
3647a2cc-2e3c-552b-8ab8-2a96730a3c59
| 605,445
|
Let $A B C$ be an acute angled triangle with ortocenter $H$, centroid $G$ and circumcircle $\omega$. Let $D$ and $M$ respectively be the intersection of lines $A H$ and $A G$ with side $B C$. Rays $M H$ and $D G$ interect $\omega$ again at $P$ and $Q$ respectively. Prove that $P D$ and $Q M$ intersect on $\omega$.
|
2
We prove that $M, D, P, A$ are concyclic same as in solution 1. Let $P D$ intersect $\omega$ again at $S$ We see that this gives us $\measuredangle S A H^{\prime}=\measuredangle S P H^{\prime}=\measuredangle D P M=\measuredangle D A M$. Combining this with $\measuredangle B A H^{\prime}=\measuredangle C A D$ we get:
$$
\measuredangle S A H^{\prime}+\measuredangle S A B=\measuredangle H^{\prime} A B=\measuredangle C A D=\measuredangle D A M+\measuredangle M A C
$$
## Giving us
$$
\measuredangle S A B=\measuredangle M A C
$$
Combining (*) with $\angle A S B=\measuredangle A C B=\measuredangle A C M$ we get triangles $A S B$ and $A C M$ are similar. This gives us
$$
\frac{A B}{A M}=\frac{S B}{C M} .
$$
Analogously we get triangles $A S C$ and $A B M$ are similar. This gives us
$$
\frac{A C}{A M}=\frac{S C}{B M} .
$$
Combining ( ${ }^{* *}$ ) and ( $\left.{ }^{(* *}\right)$ we get
$$
\frac{A B}{A C}=\frac{S B}{S C}
$$
since $B M=C M$. Let $S M$ intersect $\omega$ again at $Q^{\prime}$. Let $Q^{\prime} D$ intersect $A M$ at $G^{\prime}$. We wish to prove that $Q^{\prime} \equiv Q$ and $G^{\prime} \equiv G$. It is enough to prove that $A G^{\prime}=2 G^{\prime} M$.
Since triangles SMB and $C M Q^{\prime}$ are similar we get
$$
\frac{S B}{S M}=\frac{C Q}{C M} .
$$
Analogously SMC and BMQ' are similar and we get
$$
\frac{S M}{S C^{\prime}}=\frac{B M}{B Q^{\prime}} .
$$
Multiplying (2) and (3) we get $\frac{S B}{S C}=\frac{C Q^{\prime}}{B Q^{\prime}}$. Combining that with (1) we get
$$
\frac{A B}{A C}=\frac{C Q^{\prime}}{B Q^{\prime}} .
$$
Since $Q^{\prime}$ and $A$ are on the same side of $B C$ (4) gives us $A Q^{\prime} \| B C$. This means that $A B C Q^{\prime}$ is an isosceles trapezoid.
Let $Q^{\prime} S$ intersect $A D$ at point $T$. Since $M D \| A Q^{\prime}, M A=M Q^{\prime}$ and $\angle T A Q^{\prime}=90^{\circ}$ we get that $M$ is center of the circumcircle of the right triangle TAQ'.
Applying Menelaus' theorem on $D-G^{\prime}-Q^{\prime}$ and triangle $A M T$ we get
$$
\frac{A G^{\prime}}{M G^{\prime}} \cdot \frac{M Q^{\prime}}{T Q^{\prime}} \cdot \frac{T D}{A D}=1
$$
Since $M A=M T$ and $M D \perp A T$ this means
$$
D A=D T .
$$
Also since $M$ is the circumcenter of triangle $T A Q^{\prime}$ we get
$$
2 M Q^{\prime}=T Q^{\prime} .
$$
Combining (5) with (6) and (7) we get $2 M G^{\prime}=A G^{\prime}$. This gives us $G^{\prime} \equiv G$ and $Q^{\prime} \equiv Q$, thus proving the problem statement.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute angled triangle with ortocenter $H$, centroid $G$ and circumcircle $\omega$. Let $D$ and $M$ respectively be the intersection of lines $A H$ and $A G$ with side $B C$. Rays $M H$ and $D G$ interect $\omega$ again at $P$ and $Q$ respectively. Prove that $P D$ and $Q M$ intersect on $\omega$.
|
2
We prove that $M, D, P, A$ are concyclic same as in solution 1. Let $P D$ intersect $\omega$ again at $S$ We see that this gives us $\measuredangle S A H^{\prime}=\measuredangle S P H^{\prime}=\measuredangle D P M=\measuredangle D A M$. Combining this with $\measuredangle B A H^{\prime}=\measuredangle C A D$ we get:
$$
\measuredangle S A H^{\prime}+\measuredangle S A B=\measuredangle H^{\prime} A B=\measuredangle C A D=\measuredangle D A M+\measuredangle M A C
$$
## Giving us
$$
\measuredangle S A B=\measuredangle M A C
$$

Combining (*) with $\angle A S B=\measuredangle A C B=\measuredangle A C M$ we get triangles $A S B$ and $A C M$ are similar. This gives us
$$
\frac{A B}{A M}=\frac{S B}{C M} .
$$
Analogously we get triangles $A S C$ and $A B M$ are similar. This gives us
$$
\frac{A C}{A M}=\frac{S C}{B M} .
$$
Combining ( ${ }^{* *}$ ) and ( $\left.{ }^{(* *}\right)$ we get
$$
\frac{A B}{A C}=\frac{S B}{S C}
$$
since $B M=C M$. Let $S M$ intersect $\omega$ again at $Q^{\prime}$. Let $Q^{\prime} D$ intersect $A M$ at $G^{\prime}$. We wish to prove that $Q^{\prime} \equiv Q$ and $G^{\prime} \equiv G$. It is enough to prove that $A G^{\prime}=2 G^{\prime} M$.
Since triangles SMB and $C M Q^{\prime}$ are similar we get
$$
\frac{S B}{S M}=\frac{C Q}{C M} .
$$
Analogously SMC and BMQ' are similar and we get
$$
\frac{S M}{S C^{\prime}}=\frac{B M}{B Q^{\prime}} .
$$
Multiplying (2) and (3) we get $\frac{S B}{S C}=\frac{C Q^{\prime}}{B Q^{\prime}}$. Combining that with (1) we get
$$
\frac{A B}{A C}=\frac{C Q^{\prime}}{B Q^{\prime}} .
$$
Since $Q^{\prime}$ and $A$ are on the same side of $B C$ (4) gives us $A Q^{\prime} \| B C$. This means that $A B C Q^{\prime}$ is an isosceles trapezoid.

Let $Q^{\prime} S$ intersect $A D$ at point $T$. Since $M D \| A Q^{\prime}, M A=M Q^{\prime}$ and $\angle T A Q^{\prime}=90^{\circ}$ we get that $M$ is center of the circumcircle of the right triangle TAQ'.
Applying Menelaus' theorem on $D-G^{\prime}-Q^{\prime}$ and triangle $A M T$ we get
$$
\frac{A G^{\prime}}{M G^{\prime}} \cdot \frac{M Q^{\prime}}{T Q^{\prime}} \cdot \frac{T D}{A D}=1
$$
Since $M A=M T$ and $M D \perp A T$ this means
$$
D A=D T .
$$
Also since $M$ is the circumcenter of triangle $T A Q^{\prime}$ we get
$$
2 M Q^{\prime}=T Q^{\prime} .
$$
Combining (5) with (6) and (7) we get $2 M G^{\prime}=A G^{\prime}$. This gives us $G^{\prime} \equiv G$ and $Q^{\prime} \equiv Q$, thus proving the problem statement.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## G5",
"solution_match": "\n## Solution"
}
|
3647a2cc-2e3c-552b-8ab8-2a96730a3c59
| 605,445
|
Construct outside the acute-angled triangle $A B C$ the isosceles triangles $A B A_{B}, A B B_{A}$, $A C A_{C}, A C C_{A}, B C B_{C}$ and $B C C_{B}$, so that
$$
A B=A B_{A}=B A_{B}, A C=A C_{A}=C A_{C}, B C=B C_{B}=C B_{C}
$$
and
$$
\measuredangle B A B_{A}=\measuredangle A B A_{B}=\measuredangle C A C_{A}=\measuredangle A C A_{C}=\measuredangle B C B_{C}=\measuredangle C B C_{B}=\alpha<90^{\circ} .
$$
Prove that the perpendiculars from $A$ to $B_{A} C_{A}$, from $B$ to $A_{B} C_{B}$ and from $C$ to $A_{C} B_{C}$ are concurrent.
|
Lemma. If $B C D$ is the isoceles triangle which is outside the triangle $A B C$ and has
$$
\measuredangle C B D=\measuredangle B C D=90^{\circ}-\alpha: \stackrel{\text { not }}{=} \beta,
$$
then $A D \perp B_{A} C_{A}$.
Proof of the lemma. Construct an isosceles triangle $A B E$ outside the triangle $A B C$, so that $\measuredangle A B E=\measuredangle A E B=\beta$.
Then $A E=A B=A B_{A}$ and $\measuredangle E A B_{A}=\alpha$, so a rotation of center $A$ and angle $\alpha$ sends $C_{A}$ to $C$ and $B_{A}$ to $E$, hence $\Varangle\left(\overrightarrow{B_{A} C_{A}}, \overrightarrow{E C}\right)=\alpha$ (the angle between vectors is considered oriented). Also triangles $E B A$ and $B C D$ are similar, so a rotation of center $B$ and angle $\beta$, followed by
a dilation of ratio $\frac{E B}{A B}=\frac{B C}{B D}$ sends $E$ to $A$ and $C$ to $D$, hence $\measuredangle(\overrightarrow{E C}, \overrightarrow{A D})=\beta$ (also oriented angle).
This shows that
$$
\measuredangle\left(\overrightarrow{B_{A} C_{A}}, \overrightarrow{A D}\right)=\measuredangle\left(\overrightarrow{B_{A} C_{A}}, \overrightarrow{E C}\right)+\measuredangle(\overrightarrow{E C}, \overrightarrow{A D})=\alpha+\beta=90^{\circ} .
$$
Returning to the solution of the problem, denote $A^{\prime}$ the intersection of $B C$ with the perpendicular from $A$ to $B_{A} C_{A}$. Then $A^{\prime}$ belongs to the segment $B C$ and
$$
\frac{A^{\prime} B}{A^{\prime} C}=\frac{A B \sin (B+\beta)}{A C \sin (C+\beta)}
$$
Since similar relations are true for the intersections $B^{\prime}, C^{\prime}$ of the other two perpendiculars with the opposite sides, this yields
$$
\frac{A^{\prime} B}{A^{\prime} C} \cdot \frac{B^{\prime} C}{B^{\prime} A} \cdot \frac{C^{\prime} A}{C^{\prime} B}=\frac{A B \sin (B+\beta)}{A C \sin (C+\beta)} \cdot \frac{B C \sin (C+\beta)}{B A \sin (A+\beta)} \cdot \frac{C A \sin (A+\beta)}{C B \sin (B+\beta)}=1
$$
whence the conclusion.
Remark. The conditions 'acute-angled' and ' $\alpha<90^{\circ}$ ' are not essential, but without them there are cases when $A^{\prime}$ does not belong to the segment $B C$, or the perpendiculars become parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Construct outside the acute-angled triangle $A B C$ the isosceles triangles $A B A_{B}, A B B_{A}$, $A C A_{C}, A C C_{A}, B C B_{C}$ and $B C C_{B}$, so that
$$
A B=A B_{A}=B A_{B}, A C=A C_{A}=C A_{C}, B C=B C_{B}=C B_{C}
$$
and
$$
\measuredangle B A B_{A}=\measuredangle A B A_{B}=\measuredangle C A C_{A}=\measuredangle A C A_{C}=\measuredangle B C B_{C}=\measuredangle C B C_{B}=\alpha<90^{\circ} .
$$
Prove that the perpendiculars from $A$ to $B_{A} C_{A}$, from $B$ to $A_{B} C_{B}$ and from $C$ to $A_{C} B_{C}$ are concurrent.
|
Lemma. If $B C D$ is the isoceles triangle which is outside the triangle $A B C$ and has
$$
\measuredangle C B D=\measuredangle B C D=90^{\circ}-\alpha: \stackrel{\text { not }}{=} \beta,
$$
then $A D \perp B_{A} C_{A}$.
Proof of the lemma. Construct an isosceles triangle $A B E$ outside the triangle $A B C$, so that $\measuredangle A B E=\measuredangle A E B=\beta$.
Then $A E=A B=A B_{A}$ and $\measuredangle E A B_{A}=\alpha$, so a rotation of center $A$ and angle $\alpha$ sends $C_{A}$ to $C$ and $B_{A}$ to $E$, hence $\Varangle\left(\overrightarrow{B_{A} C_{A}}, \overrightarrow{E C}\right)=\alpha$ (the angle between vectors is considered oriented). Also triangles $E B A$ and $B C D$ are similar, so a rotation of center $B$ and angle $\beta$, followed by

a dilation of ratio $\frac{E B}{A B}=\frac{B C}{B D}$ sends $E$ to $A$ and $C$ to $D$, hence $\measuredangle(\overrightarrow{E C}, \overrightarrow{A D})=\beta$ (also oriented angle).
This shows that
$$
\measuredangle\left(\overrightarrow{B_{A} C_{A}}, \overrightarrow{A D}\right)=\measuredangle\left(\overrightarrow{B_{A} C_{A}}, \overrightarrow{E C}\right)+\measuredangle(\overrightarrow{E C}, \overrightarrow{A D})=\alpha+\beta=90^{\circ} .
$$
Returning to the solution of the problem, denote $A^{\prime}$ the intersection of $B C$ with the perpendicular from $A$ to $B_{A} C_{A}$. Then $A^{\prime}$ belongs to the segment $B C$ and
$$
\frac{A^{\prime} B}{A^{\prime} C}=\frac{A B \sin (B+\beta)}{A C \sin (C+\beta)}
$$
Since similar relations are true for the intersections $B^{\prime}, C^{\prime}$ of the other two perpendiculars with the opposite sides, this yields
$$
\frac{A^{\prime} B}{A^{\prime} C} \cdot \frac{B^{\prime} C}{B^{\prime} A} \cdot \frac{C^{\prime} A}{C^{\prime} B}=\frac{A B \sin (B+\beta)}{A C \sin (C+\beta)} \cdot \frac{B C \sin (C+\beta)}{B A \sin (A+\beta)} \cdot \frac{C A \sin (A+\beta)}{C B \sin (B+\beta)}=1
$$
whence the conclusion.
Remark. The conditions 'acute-angled' and ' $\alpha<90^{\circ}$ ' are not essential, but without them there are cases when $A^{\prime}$ does not belong to the segment $B C$, or the perpendiculars become parallel.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## G6",
"solution_match": "\n## Solution."
}
|
0b8205ab-914d-5836-bd3f-0fd2171e4108
| 605,461
|
Let $A B C$ be an acute triangle with $A B \neq A C$ and circumcirle $\Gamma$. The angle bisector of $B A C$ intersects $B C$ and $\Gamma$ at $D$ and $E$ respectively. Circle with diameter $D E$ intersects $\Gamma$ again at $F \neq E$. Point $P$ is on $A F$ such that $P B=P C$ and $X$ and $Y$ are feet of perpendiculars from $P$ to $A B$ and $A C$ respectively. Let $H$ and $H^{\prime}$ be the ortocenters of $A B C$ and $A X Y$ respectively. $A H$ meets $\Gamma$ again at $Q$. If $A H^{\prime}$ and $H H^{\prime}$ intersect the circle with diameter $A H$ again at points $S$ and $T$, respectively, prove that the lines $A T, H S$ and $F Q$ are concurrent.
|
WLOG, assume $A B<A C$. Let $M$ be the midpoint of side $B C$ and let the circumcircle of $D F E$ intersect $A F$ again at $K$. Since
$$
90^{\circ}+\measuredangle M E D=180^{\circ}-\measuredangle M D E=\measuredangle A B C+\frac{\measuredangle B A C}{2}=\measuredangle A F E=\angle D F E+\angle A F D=90+\angle A F D
$$
$\measuredangle M^{\prime} C E=\measuredangle E C P$. From the angle bisector theorem we get
$$
\frac{M^{\prime} E}{P E}=\frac{C M^{\prime}}{C P}=\frac{M^{\prime} L}{P L}
$$
Multiplying (1) and (2) we get $\frac{M E}{L M}=\frac{M^{\prime} E}{M^{\prime} L}$ adding 1 on both sides we get $L M=L M^{\prime}$ from which it follows that $M \equiv M^{\prime}$ and thus $C E$ and $C L$ are the bisectors of $\measuredangle M C P$.
Now we have
Since $X$ and $Y$ are perpendicular to $A B$ and $A C$ we have $B X P M$ and $C Y P M$ are concyclic. Here we get
$$
\angle M Y C=\angle M P C=90^{\circ}-\angle B A C
$$
and it follows that $Y M \perp A X$ Similarily we get $X M \perp A Y$ and so $M$ is the ortocentar of $\triangle A X Y$ giving us $M \equiv H^{\prime}$.
Since ATHS and ATQF are both concyclic it is enough to prove that $H S F Q$ is concyclic. Since
$$
\begin{aligned}
\triangle B Q C & =180^{\circ}-\angle B A C \\
& =\angle B H C
\end{aligned}
$$
and $H Q \perp B C$ it follows that $B C$ is the perpendicular bisector of $H Q$. It is enough to prove that $B C$ is the perpendicular bisector of $S F$. Let $A M$ and $T H$ meet $\Gamma$ again at points $A^{\prime}$ and $N$ respec-
tively. Since $H N$ passes through the midpoint of side $B C$ and
$$
\angle B H C=180-\angle B A C=\angle B N C
$$
it follows that $B N C H$ is a paralelogram. From here we get that
$$
\angle N C B=\angle H B C=90^{\circ}-\angle A C B
$$
giving us $\measuredangle N C A=90^{\circ}$ and similarily $\measuredangle N B A=90^{\circ}$. This means $A N$ is the diameter of $\Gamma$, so
$$
\begin{aligned}
\angle N A^{\prime} S & =\angle N A^{\prime} A=90^{\circ} \\
& =\angle H S A=\angle H S A^{\prime}
\end{aligned}
$$
and from here we have $H S \| A^{\prime} N$. Now since $H S \| A^{\prime} N$ and $M$ is the midpoint of $H N$ (because $B H C N$ is a paralelogram) we get
that $H S N A$ is a paralelogram. Since
$$
\measuredangle F A E=\measuredangle E A M=\measuredangle E A A^{\prime}
$$
we get that $F A^{\prime} B C$ is an isocelese trapezoid which means that $M E$ is the perpendicular bisector of $F A^{\prime}$ (since it is the perpendicular bisector of $B C$ ).
This gives us $B F=C A^{\prime}=B S$ and $C F=B A^{\prime}=C S$ giving us that $S B F C$ is a deltoid, meaning that $B C$ is the perpendicular bisector of FS. This means that $H S F Q$ is an isoceles trapezoid. Now from the radical axis theorem of the circumcircles of HSFQ, HSAT and $A T Q F$ we get that $Q F$,
$H S, A T$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A B \neq A C$ and circumcirle $\Gamma$. The angle bisector of $B A C$ intersects $B C$ and $\Gamma$ at $D$ and $E$ respectively. Circle with diameter $D E$ intersects $\Gamma$ again at $F \neq E$. Point $P$ is on $A F$ such that $P B=P C$ and $X$ and $Y$ are feet of perpendiculars from $P$ to $A B$ and $A C$ respectively. Let $H$ and $H^{\prime}$ be the ortocenters of $A B C$ and $A X Y$ respectively. $A H$ meets $\Gamma$ again at $Q$. If $A H^{\prime}$ and $H H^{\prime}$ intersect the circle with diameter $A H$ again at points $S$ and $T$, respectively, prove that the lines $A T, H S$ and $F Q$ are concurrent.
|
WLOG, assume $A B<A C$. Let $M$ be the midpoint of side $B C$ and let the circumcircle of $D F E$ intersect $A F$ again at $K$. Since
$$
90^{\circ}+\measuredangle M E D=180^{\circ}-\measuredangle M D E=\measuredangle A B C+\frac{\measuredangle B A C}{2}=\measuredangle A F E=\angle D F E+\angle A F D=90+\angle A F D
$$

$\measuredangle M^{\prime} C E=\measuredangle E C P$. From the angle bisector theorem we get
$$
\frac{M^{\prime} E}{P E}=\frac{C M^{\prime}}{C P}=\frac{M^{\prime} L}{P L}
$$
Multiplying (1) and (2) we get $\frac{M E}{L M}=\frac{M^{\prime} E}{M^{\prime} L}$ adding 1 on both sides we get $L M=L M^{\prime}$ from which it follows that $M \equiv M^{\prime}$ and thus $C E$ and $C L$ are the bisectors of $\measuredangle M C P$.
Now we have

Since $X$ and $Y$ are perpendicular to $A B$ and $A C$ we have $B X P M$ and $C Y P M$ are concyclic. Here we get
$$
\angle M Y C=\angle M P C=90^{\circ}-\angle B A C
$$
and it follows that $Y M \perp A X$ Similarily we get $X M \perp A Y$ and so $M$ is the ortocentar of $\triangle A X Y$ giving us $M \equiv H^{\prime}$.
Since ATHS and ATQF are both concyclic it is enough to prove that $H S F Q$ is concyclic. Since
$$
\begin{aligned}
\triangle B Q C & =180^{\circ}-\angle B A C \\
& =\angle B H C
\end{aligned}
$$
and $H Q \perp B C$ it follows that $B C$ is the perpendicular bisector of $H Q$. It is enough to prove that $B C$ is the perpendicular bisector of $S F$. Let $A M$ and $T H$ meet $\Gamma$ again at points $A^{\prime}$ and $N$ respec-
tively. Since $H N$ passes through the midpoint of side $B C$ and
$$
\angle B H C=180-\angle B A C=\angle B N C
$$
it follows that $B N C H$ is a paralelogram. From here we get that
$$
\angle N C B=\angle H B C=90^{\circ}-\angle A C B
$$
giving us $\measuredangle N C A=90^{\circ}$ and similarily $\measuredangle N B A=90^{\circ}$. This means $A N$ is the diameter of $\Gamma$, so
$$
\begin{aligned}
\angle N A^{\prime} S & =\angle N A^{\prime} A=90^{\circ} \\
& =\angle H S A=\angle H S A^{\prime}
\end{aligned}
$$
and from here we have $H S \| A^{\prime} N$. Now since $H S \| A^{\prime} N$ and $M$ is the midpoint of $H N$ (because $B H C N$ is a paralelogram) we get

that $H S N A$ is a paralelogram. Since
$$
\measuredangle F A E=\measuredangle E A M=\measuredangle E A A^{\prime}
$$

we get that $F A^{\prime} B C$ is an isocelese trapezoid which means that $M E$ is the perpendicular bisector of $F A^{\prime}$ (since it is the perpendicular bisector of $B C$ ).
This gives us $B F=C A^{\prime}=B S$ and $C F=B A^{\prime}=C S$ giving us that $S B F C$ is a deltoid, meaning that $B C$ is the perpendicular bisector of FS. This means that $H S F Q$ is an isoceles trapezoid. Now from the radical axis theorem of the circumcircles of HSFQ, HSAT and $A T Q F$ we get that $Q F$,
$H S, A T$ are concurrent.

|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\nG7",
"solution_match": "\n## Solution"
}
|
ae7f9da9-4d64-5c04-a20c-2f6cd4284ad7
| 605,472
|
Given an acute triangle $\triangle A B C(A C \neq A B)$ and let $(C)$ be its circumcircle. The excircle $\left(C_{1}\right)$ corresponding to the vertex $A$, of center $I_{a}$, tangents to the side $B C$ at the point $D$ and to the extensions of the sides $A B, A C$ at the points $E, Z$ respectively. Let $I$ and $L$ are the intersection points of the circles $(C)$ and $\left(C_{1}\right), H$ the orthocenter of the triangle $\triangle E D Z$ and $N$ the midpoint of segment $E Z$. The parallel line through the point $I_{a}$ to the line $H L$ meets the line $H I$ at the point $G$. Prove that the perpendicular line ( $e$ ) through the point $N$ to the to the line $B C$ and the parallel line $(\delta)$ through the point $G$ to the line $I L$ meet each other on the line $\mathrm{HI}_{a}$
|
We have $(e) \perp B C$ and $I_{a} D \perp B C$, so $(e) \| I_{a} D$. Let $T$. $S$ be the midpoints of the segments $H I_{a}, H D$ respectively and $Y$ the point of intersection of the lines $H D, E Z$ Then, $T S \| I_{a} D$. $T S \perp B C$ and $S Y \perp E Z$
The Euler circle ( $\omega$ ) of the triangle EDZ passes through the points $N, Y, S$. Therefore, the segment $S N$ is a diameter of the circle $(\omega)$. Thus, the center of $(\omega)$, let $T^{\prime}$, is the midpoint of the segment $S N$
On the other hand, we know that the center of Euler circle ( $\omega$ ) is the midpoint $T$ of $\mathrm{HI}_{a}$. So $T \equiv T^{\prime}$. Therefore, the line ( $e$ ) passes through the points $T, S$.
Therefore, we get that the quadrilateral $H S I_{a} N$ is parallelogram and its diagonals meet each other at the point $T$.
We consider the inversion $I\left(I_{a}, I_{a} Z^{2}\right)$. As $I_{a} Z^{2}=I_{a} A \cdot I_{a} N$ we have $I(N)=A$. Similarly, if $M_{1}, M_{2}$ the midpoints of the segments $D E, D Z$ respectively, we get. $I\left(M_{1}\right)=B$ and $I\left(M_{2}\right)=C$.
Therefore, the circumcircle ( $C$ ) of the triangle $A B C$ is the image of the circle ( $\omega$ ) under the inversion $I$ and the points of the intersection of the circles and ( $\omega$ ) are invariant under this inversion. But it is well known that the circle of inversion passes through the points of the intersection of the circles $(C)$ and ( $\omega$ ). Thus, the Euler circle ( $\omega$ ) passes through the points I,L.
Also, we consider the inversion $J\left(H, r^{2}\right)$ with
$$
r^{2}=H X \cdot H Z=H D \cdot H Y=H W \cdot H E
$$
where $X, W, Y$ the traces of the altitudes of the triangle $E D Z$ on its sides. Then, $J(Z)=X$, $J(D)=Y$ and $J(E)=W$. Therefore, the circumcircle $\left(C_{1}\right)$ of the triangle $A B C$ is the image of the circle $(\omega)$ under the inversion $J$. Thus, the circle of inversion $J$ passes through the points $I, L$.
We conclude that $H I=H L$ and $H I_{a} \perp I L$ and since $(\delta) \| I L$, we have $H I_{a} \perp(\delta)$.
If, $R$ is the point of intersection of the lines $(\delta), H L$, we get that quadrilateral $H R I_{a} G$ is parallelogram and its diagonals meet each other at the point $T$. So, the perpendicular line (e) through the point $N$ to the to the line $B C$ and the parallel line $(\delta)$ through the point $G$ to the line $I L$, meet each other on the line $H I_{a}$.
## COMBINATORICS
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an acute triangle $\triangle A B C(A C \neq A B)$ and let $(C)$ be its circumcircle. The excircle $\left(C_{1}\right)$ corresponding to the vertex $A$, of center $I_{a}$, tangents to the side $B C$ at the point $D$ and to the extensions of the sides $A B, A C$ at the points $E, Z$ respectively. Let $I$ and $L$ are the intersection points of the circles $(C)$ and $\left(C_{1}\right), H$ the orthocenter of the triangle $\triangle E D Z$ and $N$ the midpoint of segment $E Z$. The parallel line through the point $I_{a}$ to the line $H L$ meets the line $H I$ at the point $G$. Prove that the perpendicular line ( $e$ ) through the point $N$ to the to the line $B C$ and the parallel line $(\delta)$ through the point $G$ to the line $I L$ meet each other on the line $\mathrm{HI}_{a}$
|

We have $(e) \perp B C$ and $I_{a} D \perp B C$, so $(e) \| I_{a} D$. Let $T$. $S$ be the midpoints of the segments $H I_{a}, H D$ respectively and $Y$ the point of intersection of the lines $H D, E Z$ Then, $T S \| I_{a} D$. $T S \perp B C$ and $S Y \perp E Z$
The Euler circle ( $\omega$ ) of the triangle EDZ passes through the points $N, Y, S$. Therefore, the segment $S N$ is a diameter of the circle $(\omega)$. Thus, the center of $(\omega)$, let $T^{\prime}$, is the midpoint of the segment $S N$
On the other hand, we know that the center of Euler circle ( $\omega$ ) is the midpoint $T$ of $\mathrm{HI}_{a}$. So $T \equiv T^{\prime}$. Therefore, the line ( $e$ ) passes through the points $T, S$.
Therefore, we get that the quadrilateral $H S I_{a} N$ is parallelogram and its diagonals meet each other at the point $T$.
We consider the inversion $I\left(I_{a}, I_{a} Z^{2}\right)$. As $I_{a} Z^{2}=I_{a} A \cdot I_{a} N$ we have $I(N)=A$. Similarly, if $M_{1}, M_{2}$ the midpoints of the segments $D E, D Z$ respectively, we get. $I\left(M_{1}\right)=B$ and $I\left(M_{2}\right)=C$.
Therefore, the circumcircle ( $C$ ) of the triangle $A B C$ is the image of the circle ( $\omega$ ) under the inversion $I$ and the points of the intersection of the circles and ( $\omega$ ) are invariant under this inversion. But it is well known that the circle of inversion passes through the points of the intersection of the circles $(C)$ and ( $\omega$ ). Thus, the Euler circle ( $\omega$ ) passes through the points I,L.
Also, we consider the inversion $J\left(H, r^{2}\right)$ with
$$
r^{2}=H X \cdot H Z=H D \cdot H Y=H W \cdot H E
$$
where $X, W, Y$ the traces of the altitudes of the triangle $E D Z$ on its sides. Then, $J(Z)=X$, $J(D)=Y$ and $J(E)=W$. Therefore, the circumcircle $\left(C_{1}\right)$ of the triangle $A B C$ is the image of the circle $(\omega)$ under the inversion $J$. Thus, the circle of inversion $J$ passes through the points $I, L$.
We conclude that $H I=H L$ and $H I_{a} \perp I L$ and since $(\delta) \| I L$, we have $H I_{a} \perp(\delta)$.
If, $R$ is the point of intersection of the lines $(\delta), H L$, we get that quadrilateral $H R I_{a} G$ is parallelogram and its diagonals meet each other at the point $T$. So, the perpendicular line (e) through the point $N$ to the to the line $B C$ and the parallel line $(\delta)$ through the point $G$ to the line $I L$, meet each other on the line $H I_{a}$.
## COMBINATORICS
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\nG8",
"solution_match": "\n## Solution"
}
|
9b5bb84d-ba58-54d3-83e9-f6af820c01ed
| 605,480
|
A grasshopper is sitting at an integer point in the Euclidean plane. Each second it jumps to another integer point in such a way that the jump vector is constant. A hunter that knows neither the starting point of the grasshopper nor the jump vector (but knows that the jump vector for each second is constant) wants to catch the grasshopper. Each second the hunter can choose one integer point in the plane and, if the grasshopper is there, he catches it. Can the hunter always catch the grasshopper in a finite amount of time?
|
The hunter can catch the grasshopper. Here is the strategy for him. Let $f$ be any bijection between the set of positive integers and the set $\{((x, y),(u, v)): x, y, u, v \in \mathbb{Z}\}$, and denote
$$
f(t)=\left(\left(x_{t}, y_{t}\right),\left(u_{t}, v_{t}\right)\right) .
$$
In the second $t$, the hunter should hunt at the point $\left(x_{t}+t u_{t}, y_{t}+t v_{t}\right)$. Let us show that this strategy indeed works.
Assume that the grasshopper starts at the point ( $x^{\prime}, y^{\prime}$ ) and that the jump vector is ( $u^{\prime}, v^{\prime}$ ). Then in the second $t$ the grasshopper is at the point $\left(x^{\prime}+t u^{\prime}, y^{\prime}+t v^{\prime}\right)$. Let
$$
t^{\prime}=f^{-1}\left(\left(x^{\prime}, y^{\prime}\right),\left(u^{\prime}, v^{\prime}\right)\right)
$$
The hunter's strategy dictates that in the second $t^{\prime}$ he searches for the grasshopper at the point $\left(x_{t^{\prime}}+t^{\prime} u_{t^{\prime}}, y_{t^{\prime}}+t^{\prime} v_{t^{\prime}}\right)$, which is actually $\left(x^{\prime}+t^{\prime} u^{\prime}, y^{\prime}+t^{\prime} v^{\prime}\right)$, and this is precisely the point where the grasshopper is in the second $t^{\prime}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A grasshopper is sitting at an integer point in the Euclidean plane. Each second it jumps to another integer point in such a way that the jump vector is constant. A hunter that knows neither the starting point of the grasshopper nor the jump vector (but knows that the jump vector for each second is constant) wants to catch the grasshopper. Each second the hunter can choose one integer point in the plane and, if the grasshopper is there, he catches it. Can the hunter always catch the grasshopper in a finite amount of time?
|
The hunter can catch the grasshopper. Here is the strategy for him. Let $f$ be any bijection between the set of positive integers and the set $\{((x, y),(u, v)): x, y, u, v \in \mathbb{Z}\}$, and denote
$$
f(t)=\left(\left(x_{t}, y_{t}\right),\left(u_{t}, v_{t}\right)\right) .
$$
In the second $t$, the hunter should hunt at the point $\left(x_{t}+t u_{t}, y_{t}+t v_{t}\right)$. Let us show that this strategy indeed works.
Assume that the grasshopper starts at the point ( $x^{\prime}, y^{\prime}$ ) and that the jump vector is ( $u^{\prime}, v^{\prime}$ ). Then in the second $t$ the grasshopper is at the point $\left(x^{\prime}+t u^{\prime}, y^{\prime}+t v^{\prime}\right)$. Let
$$
t^{\prime}=f^{-1}\left(\left(x^{\prime}, y^{\prime}\right),\left(u^{\prime}, v^{\prime}\right)\right)
$$
The hunter's strategy dictates that in the second $t^{\prime}$ he searches for the grasshopper at the point $\left(x_{t^{\prime}}+t^{\prime} u_{t^{\prime}}, y_{t^{\prime}}+t^{\prime} v_{t^{\prime}}\right)$, which is actually $\left(x^{\prime}+t^{\prime} u^{\prime}, y^{\prime}+t^{\prime} v^{\prime}\right)$, and this is precisely the point where the grasshopper is in the second $t^{\prime}$. This completes the proof.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\n## C1",
"solution_match": "\n## Solution"
}
|
7583b59b-ba45-50d1-8e5c-29155163b08f
| 605,493
|
Let $n, a, b, c$ be natural numbers. Every point on the coordinate plane with integer coordinates is colored in one of $n$ colors. Prove there exists $c$ triangles whose vertices are colored in the same color, which are pairwise congruent, and which have a side whose lenght is divisible by $a$ and a side whose lenght is divisible by $b$.
|
Let the colors be $d_{1}, d_{2}, d_{3} \ldots, d_{n}$. Look at the coordinates
$$
(k, 0+(n+1) a b r),(k, a b+(n+1) a b r),(k, 2 a b+(n+1) a b r), \ldots,(k, n a b+(n+1) a b r)
$$
for integers $k$ and $r$. By the pigeonhole principle there are two points of the same color. For every pair ( $k, r$ ) we say the color $d_{i}$ is $(k, r)$-good if at least two coordinates
$$
(k, 0+(n+1) a b r),(k, a b+(n+1) a b r),(k, 2 a b+(n+1) a b r), \ldots,(k, n a b+(n+1) a b r)
$$
are colored by color $d_{i}$. Fixing $r$ and taking $k=0, a b, 2 a b, \ldots, n^{2} a b$ get that some color, say $d_{1}$, was $(k, r)$-good for at least $n+1$.
Among the $n+1$ pairs $(x, y)$ there exists two which share the same $x$ cordinate. We call such quadruple $r$-great. In every $r$-great quadruple there are two triangle whose vertecies are all the same color and whose two sides are divisible by $a b$. Taking
$$
r=0.1,2, \ldots, n\left(c\left(\left(^{(n+1)\left(n^{2}+1\right)} 3{ }^{3}\right)+1\right)+1\right)+1
$$
we get that there is one color which is in a $r$-great quadruple for at least
$$
c\left(\left(^{(n+1)\left(n^{2}+1\right)} 3-1\right)+1\right.
$$
different values of $r$. Let this color be $d_{1}$. Since there are less than $\binom{\left.(n+1) n^{2}+1\right)}{3}$ possible triangles in any $r$-great quadruple (among $c\left(\left(^{(n+1)\left(n^{2}+1\right)}\right)+1\right)+1 \quad r$-great quadruples with the color $d_{1}$ ) we get that there are $c+1$ triangles which are the same and the same color $d_{1}$ and with two sides divisible by $a b$. This concludes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n, a, b, c$ be natural numbers. Every point on the coordinate plane with integer coordinates is colored in one of $n$ colors. Prove there exists $c$ triangles whose vertices are colored in the same color, which are pairwise congruent, and which have a side whose lenght is divisible by $a$ and a side whose lenght is divisible by $b$.
|
Let the colors be $d_{1}, d_{2}, d_{3} \ldots, d_{n}$. Look at the coordinates
$$
(k, 0+(n+1) a b r),(k, a b+(n+1) a b r),(k, 2 a b+(n+1) a b r), \ldots,(k, n a b+(n+1) a b r)
$$
for integers $k$ and $r$. By the pigeonhole principle there are two points of the same color. For every pair ( $k, r$ ) we say the color $d_{i}$ is $(k, r)$-good if at least two coordinates
$$
(k, 0+(n+1) a b r),(k, a b+(n+1) a b r),(k, 2 a b+(n+1) a b r), \ldots,(k, n a b+(n+1) a b r)
$$
are colored by color $d_{i}$. Fixing $r$ and taking $k=0, a b, 2 a b, \ldots, n^{2} a b$ get that some color, say $d_{1}$, was $(k, r)$-good for at least $n+1$.
Among the $n+1$ pairs $(x, y)$ there exists two which share the same $x$ cordinate. We call such quadruple $r$-great. In every $r$-great quadruple there are two triangle whose vertecies are all the same color and whose two sides are divisible by $a b$. Taking
$$
r=0.1,2, \ldots, n\left(c\left(\left(^{(n+1)\left(n^{2}+1\right)} 3{ }^{3}\right)+1\right)+1\right)+1
$$
we get that there is one color which is in a $r$-great quadruple for at least
$$
c\left(\left(^{(n+1)\left(n^{2}+1\right)} 3-1\right)+1\right.
$$
different values of $r$. Let this color be $d_{1}$. Since there are less than $\binom{\left.(n+1) n^{2}+1\right)}{3}$ possible triangles in any $r$-great quadruple (among $c\left(\left(^{(n+1)\left(n^{2}+1\right)}\right)+1\right)+1 \quad r$-great quadruples with the color $d_{1}$ ) we get that there are $c+1$ triangles which are the same and the same color $d_{1}$ and with two sides divisible by $a b$. This concludes the problem.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\nC2",
"solution_match": "\n## Solution"
}
|
e285cccc-98e3-58a3-847f-31d6552fd377
| 605,506
|
Let $a, b, c$ be positive real numbers such that $a b c=\frac{2}{3}$. Prove that
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}
$$
(FYR Macedonia)
|
By the AH mean inequality, we have
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a}=\frac{2}{3(a c+b c)}+\frac{2}{3(a b+a c)}+\frac{2}{3(a b+a c)} \geqslant \frac{3}{a b+a c+b c}
$$
so it only remains to prove that $\frac{3}{a b+a c+b c} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}$, or equivalently
$$
3\left(a^{3}+b^{3}+c^{3}\right) \geqslant(a+b+c)(a b+a c+b c)
$$
The last inequality easily follows by summing $a^{3}+b^{3} \geqslant a b(a+b), a^{3}+c^{3} \geqslant a c(a+c)$, $b^{3}+c^{3} \geqslant b c(b+c)$ and $a^{3}+b^{3}+c^{3} \geqslant 3 a b c$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=\frac{2}{3}$. Prove that
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}
$$
(FYR Macedonia)
|
By the AH mean inequality, we have
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a}=\frac{2}{3(a c+b c)}+\frac{2}{3(a b+a c)}+\frac{2}{3(a b+a c)} \geqslant \frac{3}{a b+a c+b c}
$$
so it only remains to prove that $\frac{3}{a b+a c+b c} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}$, or equivalently
$$
3\left(a^{3}+b^{3}+c^{3}\right) \geqslant(a+b+c)(a b+a c+b c)
$$
The last inequality easily follows by summing $a^{3}+b^{3} \geqslant a b(a+b), a^{3}+c^{3} \geqslant a c(a+c)$, $b^{3}+c^{3} \geqslant b c(b+c)$ and $a^{3}+b^{3}+c^{3} \geqslant 3 a b c$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nA1.",
"solution_match": "\n## Solution."
}
|
cc9e73fe-4657-5325-a44e-bb59502287d8
| 605,563
|
Show that for every positive integer $n$ we have:
$$
\sum_{k=0}^{n}\left(\frac{2 n+1-k}{k+1}\right)^{k}=\left(\frac{2 n+1}{1}\right)^{0}+\left(\frac{2 n}{2}\right)^{1}+\cdots+\left(\frac{n+1}{n+1}\right)^{n} \leqslant 2^{n}
$$
|
We shall prove that
$$
\binom{n}{k} \geqslant\left(\frac{2 n+1-k}{k+1}\right)^{k} \quad \text { for all } \quad k=0,1, \ldots, n
$$
The result will follow immediately, as $\sum_{k=0}^{n}\binom{n}{k}=2^{n}$.
Note that $(*)$ is trivial for $k=0$ and $k=n$. For $0<k<n$, by Hölder's inequality we have
$$
\binom{n}{k}=\left(1+\frac{n-k}{k}\right) \cdot\left(1+\frac{n-k}{k-1}\right) \cdots\left(1+\frac{n-k}{1}\right) \geqslant\left(1+\frac{n-k}{\sqrt[k]{k!}}\right)^{k} .
$$
Hence, it is enough to prove that
$$
1+\frac{n-k}{\sqrt[k]{k!}} \geqslant \frac{2 n+1-k}{k+1}
$$
This is equivalent to $\sqrt[k]{k!} \leqslant \frac{k+1}{2}$, which follows from $\sqrt[k]{k!} \leqslant \frac{1+2+\cdots+k}{k}=\frac{k+1}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that for every positive integer $n$ we have:
$$
\sum_{k=0}^{n}\left(\frac{2 n+1-k}{k+1}\right)^{k}=\left(\frac{2 n+1}{1}\right)^{0}+\left(\frac{2 n}{2}\right)^{1}+\cdots+\left(\frac{n+1}{n+1}\right)^{n} \leqslant 2^{n}
$$
|
We shall prove that
$$
\binom{n}{k} \geqslant\left(\frac{2 n+1-k}{k+1}\right)^{k} \quad \text { for all } \quad k=0,1, \ldots, n
$$
The result will follow immediately, as $\sum_{k=0}^{n}\binom{n}{k}=2^{n}$.
Note that $(*)$ is trivial for $k=0$ and $k=n$. For $0<k<n$, by Hölder's inequality we have
$$
\binom{n}{k}=\left(1+\frac{n-k}{k}\right) \cdot\left(1+\frac{n-k}{k-1}\right) \cdots\left(1+\frac{n-k}{1}\right) \geqslant\left(1+\frac{n-k}{\sqrt[k]{k!}}\right)^{k} .
$$
Hence, it is enough to prove that
$$
1+\frac{n-k}{\sqrt[k]{k!}} \geqslant \frac{2 n+1-k}{k+1}
$$
This is equivalent to $\sqrt[k]{k!} \leqslant \frac{k+1}{2}$, which follows from $\sqrt[k]{k!} \leqslant \frac{1+2+\cdots+k}{k}=\frac{k+1}{2}$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nA3.",
"solution_match": "\n## Solution."
}
|
2e3db6c1-8421-5b49-8260-aca4298e9aaf
| 605,606
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that the following inequality holds:
$$
2\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}\right) \geqslant 3(a+b+c+a b+b c+c a)
$$
(Romania)
|
First, we show that
$$
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geqslant a b+b c+c a \quad \text { and } \quad \frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geqslant a+b+c
$$
By AG inequality, we have
$$
\begin{aligned}
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} & =\frac{1}{3}\left(\frac{a}{b}+\frac{a}{b}+\frac{c}{a}\right)+\frac{1}{3}\left(\frac{b}{c}+\frac{b}{c}+\frac{a}{b}\right)+\frac{1}{3}\left(\frac{c}{a}+\frac{c}{a}+\frac{b}{c}\right) \\
& \geqslant \frac{\sqrt[3]{a c}}{\sqrt[3]{b^{2}}}+\frac{\sqrt[3]{b a}}{\sqrt[3]{c^{2}}}+\frac{\sqrt[3]{c b}}{\sqrt[3]{a^{2}}}=\frac{\sqrt[3]{a b c}}{b}+\frac{\sqrt[3]{a b c}}{c}+\frac{\sqrt[3]{a b c}}{a} \\
& =a b+b c+c a
\end{aligned}
$$
Similarly, we have
$$
\begin{aligned}
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} & =\frac{1}{3}\left(\frac{a}{b}+\frac{a}{b}+\frac{b}{c}\right)+\frac{1}{3}\left(\frac{b}{c}+\frac{b}{c}+\frac{c}{a}\right)+\frac{1}{3}\left(\frac{c}{a}+\frac{c}{a}+\frac{a}{b}\right) \\
& \geqslant \frac{\sqrt[3]{a^{2}}}{\sqrt[3]{b c}}+\frac{\sqrt[3]{b^{2}}}{\sqrt[3]{c a}}+\frac{\sqrt[3]{c^{2}}}{\sqrt[3]{a b}}=\frac{a}{\sqrt[3]{a b c}}+\frac{b}{\sqrt[3]{a b c}}+\frac{c}{\sqrt[3]{a b c}} \\
& =a+b+c
\end{aligned}
$$
which completes our proof of ( $\dagger$ ).
By Cauchy-Schwarz inequality we have
$$
\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{b^{2}}+\frac{1}{c^{2}}+\frac{1}{a^{2}}\right) \geqslant\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)^{2}
$$
which together with $\left(a^{2}+b^{2}+c^{2}\right)\left(1 / a^{2}+1 / b^{2}+1 / c^{2}\right) \geqslant 9$ leads to
$$
2\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}\right) \geqslant\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)^{2}+9 \geqslant 6\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)
$$
Now, the desired inequality follows from ( $\dagger$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that the following inequality holds:
$$
2\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}\right) \geqslant 3(a+b+c+a b+b c+c a)
$$
(Romania)
|
First, we show that
$$
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geqslant a b+b c+c a \quad \text { and } \quad \frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geqslant a+b+c
$$
By AG inequality, we have
$$
\begin{aligned}
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} & =\frac{1}{3}\left(\frac{a}{b}+\frac{a}{b}+\frac{c}{a}\right)+\frac{1}{3}\left(\frac{b}{c}+\frac{b}{c}+\frac{a}{b}\right)+\frac{1}{3}\left(\frac{c}{a}+\frac{c}{a}+\frac{b}{c}\right) \\
& \geqslant \frac{\sqrt[3]{a c}}{\sqrt[3]{b^{2}}}+\frac{\sqrt[3]{b a}}{\sqrt[3]{c^{2}}}+\frac{\sqrt[3]{c b}}{\sqrt[3]{a^{2}}}=\frac{\sqrt[3]{a b c}}{b}+\frac{\sqrt[3]{a b c}}{c}+\frac{\sqrt[3]{a b c}}{a} \\
& =a b+b c+c a
\end{aligned}
$$
Similarly, we have
$$
\begin{aligned}
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} & =\frac{1}{3}\left(\frac{a}{b}+\frac{a}{b}+\frac{b}{c}\right)+\frac{1}{3}\left(\frac{b}{c}+\frac{b}{c}+\frac{c}{a}\right)+\frac{1}{3}\left(\frac{c}{a}+\frac{c}{a}+\frac{a}{b}\right) \\
& \geqslant \frac{\sqrt[3]{a^{2}}}{\sqrt[3]{b c}}+\frac{\sqrt[3]{b^{2}}}{\sqrt[3]{c a}}+\frac{\sqrt[3]{c^{2}}}{\sqrt[3]{a b}}=\frac{a}{\sqrt[3]{a b c}}+\frac{b}{\sqrt[3]{a b c}}+\frac{c}{\sqrt[3]{a b c}} \\
& =a+b+c
\end{aligned}
$$
which completes our proof of ( $\dagger$ ).
By Cauchy-Schwarz inequality we have
$$
\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{b^{2}}+\frac{1}{c^{2}}+\frac{1}{a^{2}}\right) \geqslant\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)^{2}
$$
which together with $\left(a^{2}+b^{2}+c^{2}\right)\left(1 / a^{2}+1 / b^{2}+1 / c^{2}\right) \geqslant 9$ leads to
$$
2\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}\right) \geqslant\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)^{2}+9 \geqslant 6\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)
$$
Now, the desired inequality follows from ( $\dagger$ ).
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nA4.",
"solution_match": "\n## Solution."
}
|
63662bcd-26c3-51ba-9f30-203283c4d5ba
| 605,625
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that the following inequality holds:
$$
2\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}\right) \geqslant 3(a+b+c+a b+b c+c a)
$$
(Romania)
|
2.
Set $a=x^{3}, b=y^{3}, c=z^{3}$ and denote $T_{p, q, r}=\sum_{s y m} x^{p} y^{q} z^{r}=x^{p} y^{q} z^{r}+y^{p} x^{q} z^{r}+\cdots$. The given inequality is expanded into
$$
4 T_{12,6,0}+2 T_{6,6,6} \geqslant 3 T_{8,5,5}+3 T_{7,7,4}
$$
Applying the Schur inequality on triples $\left(x^{4} y^{2}, y^{4} z^{2}, z^{4} x^{2}\right)$ and $\left(x^{2} y^{4}, y^{2} z^{4}, z^{2} x^{4}\right)$ and summing them up yields
$$
T_{12,6,0}+T_{6,6,6} \geqslant T_{10,4,4}+T_{8,8,2}
$$
On the other hand, by the Muirhead inequality we have
$$
T_{12,6,0} \geqslant T_{6,6,6}, \quad T_{10,4,4} \geqslant T_{8,5,5}, \quad T_{8,8,2} \geqslant T_{7,7,4} .
$$
The four inequalities in (1) and (2) imply the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that the following inequality holds:
$$
2\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}\right) \geqslant 3(a+b+c+a b+b c+c a)
$$
(Romania)
|
2.
Set $a=x^{3}, b=y^{3}, c=z^{3}$ and denote $T_{p, q, r}=\sum_{s y m} x^{p} y^{q} z^{r}=x^{p} y^{q} z^{r}+y^{p} x^{q} z^{r}+\cdots$. The given inequality is expanded into
$$
4 T_{12,6,0}+2 T_{6,6,6} \geqslant 3 T_{8,5,5}+3 T_{7,7,4}
$$
Applying the Schur inequality on triples $\left(x^{4} y^{2}, y^{4} z^{2}, z^{4} x^{2}\right)$ and $\left(x^{2} y^{4}, y^{2} z^{4}, z^{2} x^{4}\right)$ and summing them up yields
$$
T_{12,6,0}+T_{6,6,6} \geqslant T_{10,4,4}+T_{8,8,2}
$$
On the other hand, by the Muirhead inequality we have
$$
T_{12,6,0} \geqslant T_{6,6,6}, \quad T_{10,4,4} \geqslant T_{8,5,5}, \quad T_{8,8,2} \geqslant T_{7,7,4} .
$$
The four inequalities in (1) and (2) imply the desired inequality.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nA4.",
"solution_match": "\n## Solution"
}
|
63662bcd-26c3-51ba-9f30-203283c4d5ba
| 605,625
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a concave function and let $g: \mathbb{R} \rightarrow \mathbb{R}$ be continuous. Given that
$$
f(x+y)+f(x-y)-2 f(x)=g(x) y^{2}
$$
for all $x, y \in \mathbb{R}$, prove that $f$ is a quadratic function.
(Bulgaria)
|
We plug in the pairs $(a, x),(a, 2 x),(a+x, x)$ and $(a-x, x)$ to get
$$
\begin{aligned}
f(a+x)+f(a-x)-2 f(a) & =g(a) x^{2} \\
f(a+2 x)+f(a-2 x)-2 f(a) & =4 g(a) x^{2} \\
f(a+2 x)+f(a)-2 f(a+x) & =g(a+x) x^{2} \\
f(a-2 x)+f(a)-2 f(a-x) & =g(a-x) x^{2}
\end{aligned}
$$
respectively. Combining these equations in the form $2 E_{1}-E_{2}+E_{3}+E_{4}$ the left hand side vanishes, yielding an equation in $g:(g(a+x)+g(a-x)-2 g(a)) x^{2}=0$, i.e.
$$
g(a)=\frac{g(a+x)+g(a-x)}{2}
$$
Since $g$ is continuous, it must be linear, i.e. $g(x)=c_{1} x+c_{0}$. However, the original equation for $x=y$ together with the concavity condition now gives us
$$
0 \geqslant f(2 x)+f(0)-2 f(x)=\left(x c_{1}+c_{0}\right) x^{2}
$$
for all $x$, which is only possible if $c_{1}=0$. Thus $g(x) \equiv c_{0}=2 A$ is constant and
$$
f(x+y)+f(x-y)-2 f(x)=2 A y^{2}
$$
This suggests that $f$ is a quadratic function, so we can set $f(x)=A x^{2}+f_{1}(x)$. Then $(*)$ becomes $f_{1}(x+y)+f_{1}(x-y)-2 f_{1}(x)=0$, so an easy induction gives us
$$
f_{1}(n x)-f_{1}(0)=n\left(f_{1}(x)-f_{1}(0)\right) \quad \text { for all } \quad n \in \mathbb{Z}
$$
By setting $f_{1}(0)=C$ and $f_{1}(1)=B+C$ we obtain $f_{1}(x)=B x+C$ and $f(x)=$ $A x^{2}+B x+C$ for all $x \in \mathbb{Q}$. By concavity of $f$ we conclude that $f(x)=A x^{2}+B x+C$ for all real $x$.
## Remark.
In fact, $(*)$ implies that the second derivative of $f$ is constant by taking $y \rightarrow 0$ and the problem is solved. The solution presented here avoids use of derivatives.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a concave function and let $g: \mathbb{R} \rightarrow \mathbb{R}$ be continuous. Given that
$$
f(x+y)+f(x-y)-2 f(x)=g(x) y^{2}
$$
for all $x, y \in \mathbb{R}$, prove that $f$ is a quadratic function.
(Bulgaria)
|
We plug in the pairs $(a, x),(a, 2 x),(a+x, x)$ and $(a-x, x)$ to get
$$
\begin{aligned}
f(a+x)+f(a-x)-2 f(a) & =g(a) x^{2} \\
f(a+2 x)+f(a-2 x)-2 f(a) & =4 g(a) x^{2} \\
f(a+2 x)+f(a)-2 f(a+x) & =g(a+x) x^{2} \\
f(a-2 x)+f(a)-2 f(a-x) & =g(a-x) x^{2}
\end{aligned}
$$
respectively. Combining these equations in the form $2 E_{1}-E_{2}+E_{3}+E_{4}$ the left hand side vanishes, yielding an equation in $g:(g(a+x)+g(a-x)-2 g(a)) x^{2}=0$, i.e.
$$
g(a)=\frac{g(a+x)+g(a-x)}{2}
$$
Since $g$ is continuous, it must be linear, i.e. $g(x)=c_{1} x+c_{0}$. However, the original equation for $x=y$ together with the concavity condition now gives us
$$
0 \geqslant f(2 x)+f(0)-2 f(x)=\left(x c_{1}+c_{0}\right) x^{2}
$$
for all $x$, which is only possible if $c_{1}=0$. Thus $g(x) \equiv c_{0}=2 A$ is constant and
$$
f(x+y)+f(x-y)-2 f(x)=2 A y^{2}
$$
This suggests that $f$ is a quadratic function, so we can set $f(x)=A x^{2}+f_{1}(x)$. Then $(*)$ becomes $f_{1}(x+y)+f_{1}(x-y)-2 f_{1}(x)=0$, so an easy induction gives us
$$
f_{1}(n x)-f_{1}(0)=n\left(f_{1}(x)-f_{1}(0)\right) \quad \text { for all } \quad n \in \mathbb{Z}
$$
By setting $f_{1}(0)=C$ and $f_{1}(1)=B+C$ we obtain $f_{1}(x)=B x+C$ and $f(x)=$ $A x^{2}+B x+C$ for all $x \in \mathbb{Q}$. By concavity of $f$ we conclude that $f(x)=A x^{2}+B x+C$ for all real $x$.
## Remark.
In fact, $(*)$ implies that the second derivative of $f$ is constant by taking $y \rightarrow 0$ and the problem is solved. The solution presented here avoids use of derivatives.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nA5.",
"solution_match": "\n## Solution."
}
|
2db57d65-4f42-5b54-902e-d3cce666732f
| 605,646
|
Let $n$ be a positive integer and let $x_{1}, \ldots, x_{n}$ be real numbers. Show that
$$
\sum_{i=1}^{n} x_{i}^{2} \geqslant \frac{1}{n+1}\left(\sum_{i=1}^{n} x_{i}\right)^{2}+\frac{12\left(\sum_{i=1}^{n} i x_{i}\right)^{2}}{n(n+1)(n+2)(3 n+1)}
$$
|
Let $S=\frac{1}{n+1} \sum_{i=1}^{n} x_{i}$, and $y_{i}=x_{i}-S$ for $1 \leqslant i \leqslant n$. Then we have
$$
\sum_{i=1}^{n} i x_{i}=\sum_{i=1}^{n} i y_{i}+\frac{n(n+1)}{2} S
$$
and
$$
\sum_{i=1}^{n} y_{i}^{2}=\sum_{i=1}^{n} x_{i}^{2}-2 S \sum_{i=1}^{n} x_{i}+n S^{2}=\sum_{i=1}^{n} x_{i}^{2}-\frac{1}{n+1}\left(\sum_{i=1}^{n} x_{i}\right)^{2}-S^{2}
$$
Now, by the Cauchy-Schwarz inequality
$$
\begin{aligned}
\left(\sum_{i=1}^{n} i x_{i}\right)^{2} & =\left(\sum_{i=1}^{n} i y_{i}+\frac{n(n+1)}{2} S\right)^{2} \\
& \leqslant\left(\sum_{i=1}^{n} i^{2}+\frac{n^{2}(n+1)^{2}}{4}\right)\left(\sum_{i=1}^{n} y_{i}^{2}+S^{2}\right) \\
& =\frac{n(n+1)(n+2)(3 n+1)}{12} \cdot\left(\sum_{i=1}^{n} x_{i}^{2}-\frac{1}{n+1}\left(\sum_{i=1}^{n} x_{i}\right)^{2}\right)
\end{aligned}
$$
which completes our proof.
## Remark.
It can be checked that equality holds if and only if $x_{i}=c(n(n+1)+2 i)$ for $1 \leqslant i \leqslant n$ and some $c \in \mathbb{R}$.
## Combinatorics
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer and let $x_{1}, \ldots, x_{n}$ be real numbers. Show that
$$
\sum_{i=1}^{n} x_{i}^{2} \geqslant \frac{1}{n+1}\left(\sum_{i=1}^{n} x_{i}\right)^{2}+\frac{12\left(\sum_{i=1}^{n} i x_{i}\right)^{2}}{n(n+1)(n+2)(3 n+1)}
$$
|
Let $S=\frac{1}{n+1} \sum_{i=1}^{n} x_{i}$, and $y_{i}=x_{i}-S$ for $1 \leqslant i \leqslant n$. Then we have
$$
\sum_{i=1}^{n} i x_{i}=\sum_{i=1}^{n} i y_{i}+\frac{n(n+1)}{2} S
$$
and
$$
\sum_{i=1}^{n} y_{i}^{2}=\sum_{i=1}^{n} x_{i}^{2}-2 S \sum_{i=1}^{n} x_{i}+n S^{2}=\sum_{i=1}^{n} x_{i}^{2}-\frac{1}{n+1}\left(\sum_{i=1}^{n} x_{i}\right)^{2}-S^{2}
$$
Now, by the Cauchy-Schwarz inequality
$$
\begin{aligned}
\left(\sum_{i=1}^{n} i x_{i}\right)^{2} & =\left(\sum_{i=1}^{n} i y_{i}+\frac{n(n+1)}{2} S\right)^{2} \\
& \leqslant\left(\sum_{i=1}^{n} i^{2}+\frac{n^{2}(n+1)^{2}}{4}\right)\left(\sum_{i=1}^{n} y_{i}^{2}+S^{2}\right) \\
& =\frac{n(n+1)(n+2)(3 n+1)}{12} \cdot\left(\sum_{i=1}^{n} x_{i}^{2}-\frac{1}{n+1}\left(\sum_{i=1}^{n} x_{i}\right)^{2}\right)
\end{aligned}
$$
which completes our proof.
## Remark.
It can be checked that equality holds if and only if $x_{i}=c(n(n+1)+2 i)$ for $1 \leqslant i \leqslant n$ and some $c \in \mathbb{R}$.
## Combinatorics
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nA6.",
"solution_match": "\n## Solution."
}
|
8b7649ad-b004-55f8-bce9-d0a381dae0f2
| 605,656
|
An open necklace can contain rubies, emeralds and sapphires. At every step we can perform any of the following operations:
$\left(1^{\circ}\right)$ We can replace two consecutive rubies with an emerald and a sapphire, where the emerald is on the left of the sapphire.
$\left(2^{\circ}\right)$ We can replace three consecutive emeralds with a sapphire and a ruby, where the sapphire is on the left of the ruby.
(3 ) If we find two consecutive sapphires then we can remove them.
(4 ) If we find consecutively and in this order a ruby, an emerald, and a sapphire, then we can remove them.
Furthermore we can also reverse all of the above operations. For example, by reversing $\left(3^{\circ}\right)$ we can put two consecutive sapphires on any position we wish.
Initially the necklace has one sapphire (and no other precious stones). Decide, with proof, whether there is a finite sequence of steps such that at the end of this sequence the necklace contains one emerald (and no other precious stones).
Remark. A necklace is open if its precious stones are on a line from left to right. We are not allowed to move a precious stone from the rightmost position to the leftmost as we would be able to do if the necklace was closed.
(Cyprus)
|
For each precious stone on the necklace, we define its value as $(-1)^{r} \cdot s$, where $r$ denotes the number of emeralds and sapphires preceding it, and $s$ equals $-2,1$ or -1 for a ruby, emerald or sapphire, respectively.
The value of the necklace is equal to the sum of the values of its precious stones. We claim that the value of the necklace is invariant modulo 6 .
Suppose for example that we remove two consecutive rubies, and suppose there is an even number of emeralds and sapphires preceding them. The value of each ruby is -2 so by removing them we increase the value of the necklace by 4 . The emerald that we add had an even number of emeralds and sapphires preceding it, so its value is 1 . The sapphire that we add has an odd number of emeralds and sapphires preceding it (accounting for the added emerald), so its value is 1 . No other precious stone changes value, so the total increase of the value of the necklace is 6 .
Similarly we can check that all of the other operations and their inverses also leave the value of the necklace invariant modulo 6 .
Since the necklace containing just one sapphire has value -1 , whereas the necklace containing just one emerald has value 1 , there is no desired sequence of steps.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An open necklace can contain rubies, emeralds and sapphires. At every step we can perform any of the following operations:
$\left(1^{\circ}\right)$ We can replace two consecutive rubies with an emerald and a sapphire, where the emerald is on the left of the sapphire.
$\left(2^{\circ}\right)$ We can replace three consecutive emeralds with a sapphire and a ruby, where the sapphire is on the left of the ruby.
(3 ) If we find two consecutive sapphires then we can remove them.
(4 ) If we find consecutively and in this order a ruby, an emerald, and a sapphire, then we can remove them.
Furthermore we can also reverse all of the above operations. For example, by reversing $\left(3^{\circ}\right)$ we can put two consecutive sapphires on any position we wish.
Initially the necklace has one sapphire (and no other precious stones). Decide, with proof, whether there is a finite sequence of steps such that at the end of this sequence the necklace contains one emerald (and no other precious stones).
Remark. A necklace is open if its precious stones are on a line from left to right. We are not allowed to move a precious stone from the rightmost position to the leftmost as we would be able to do if the necklace was closed.
(Cyprus)
|
For each precious stone on the necklace, we define its value as $(-1)^{r} \cdot s$, where $r$ denotes the number of emeralds and sapphires preceding it, and $s$ equals $-2,1$ or -1 for a ruby, emerald or sapphire, respectively.
The value of the necklace is equal to the sum of the values of its precious stones. We claim that the value of the necklace is invariant modulo 6 .
Suppose for example that we remove two consecutive rubies, and suppose there is an even number of emeralds and sapphires preceding them. The value of each ruby is -2 so by removing them we increase the value of the necklace by 4 . The emerald that we add had an even number of emeralds and sapphires preceding it, so its value is 1 . The sapphire that we add has an odd number of emeralds and sapphires preceding it (accounting for the added emerald), so its value is 1 . No other precious stone changes value, so the total increase of the value of the necklace is 6 .
Similarly we can check that all of the other operations and their inverses also leave the value of the necklace invariant modulo 6 .
Since the necklace containing just one sapphire has value -1 , whereas the necklace containing just one emerald has value 1 , there is no desired sequence of steps.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nC3.",
"solution_match": "\n## Solution."
}
|
b41b348c-30ca-58db-a5d1-fe1393f107ed
| 605,699
|
An open necklace can contain rubies, emeralds and sapphires. At every step we can perform any of the following operations:
$\left(1^{\circ}\right)$ We can replace two consecutive rubies with an emerald and a sapphire, where the emerald is on the left of the sapphire.
$\left(2^{\circ}\right)$ We can replace three consecutive emeralds with a sapphire and a ruby, where the sapphire is on the left of the ruby.
(3 ) If we find two consecutive sapphires then we can remove them.
(4 ) If we find consecutively and in this order a ruby, an emerald, and a sapphire, then we can remove them.
Furthermore we can also reverse all of the above operations. For example, by reversing $\left(3^{\circ}\right)$ we can put two consecutive sapphires on any position we wish.
Initially the necklace has one sapphire (and no other precious stones). Decide, with proof, whether there is a finite sequence of steps such that at the end of this sequence the necklace contains one emerald (and no other precious stones).
Remark. A necklace is open if its precious stones are on a line from left to right. We are not allowed to move a precious stone from the rightmost position to the leftmost as we would be able to do if the necklace was closed.
(Cyprus)
|
2.
Write $a, b$ and $c$ respectively for a ruby, emerald and sapphire. Each necklace corresponds to an element of a group $G$ containing elements $a, b, c$. If we impose the conditions $a^{2}=b c, b^{3}=c a, c^{2}=1$ and $a b c=1$, the allowed operations will preserve this element. In this group we have $c=a b$ (since $c^{2}=a b c$ ), i.e. $b=a^{-1} c$ and using this relation we obtain $a^{3}=c^{2}=\left(a^{-1} c\right)^{4}=1$. Thus we can take $G=\mathbb{S}_{4}, a=(1,2,3)$, $c=(1,4)$ and $b=a^{-1} c=(1,4,3,2)$. The initial and final necklaces should correspond to elements $c$ and $b$, respectively, so the desired sequence of operations does not exist.
## Geometry
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An open necklace can contain rubies, emeralds and sapphires. At every step we can perform any of the following operations:
$\left(1^{\circ}\right)$ We can replace two consecutive rubies with an emerald and a sapphire, where the emerald is on the left of the sapphire.
$\left(2^{\circ}\right)$ We can replace three consecutive emeralds with a sapphire and a ruby, where the sapphire is on the left of the ruby.
(3 ) If we find two consecutive sapphires then we can remove them.
(4 ) If we find consecutively and in this order a ruby, an emerald, and a sapphire, then we can remove them.
Furthermore we can also reverse all of the above operations. For example, by reversing $\left(3^{\circ}\right)$ we can put two consecutive sapphires on any position we wish.
Initially the necklace has one sapphire (and no other precious stones). Decide, with proof, whether there is a finite sequence of steps such that at the end of this sequence the necklace contains one emerald (and no other precious stones).
Remark. A necklace is open if its precious stones are on a line from left to right. We are not allowed to move a precious stone from the rightmost position to the leftmost as we would be able to do if the necklace was closed.
(Cyprus)
|
2.
Write $a, b$ and $c$ respectively for a ruby, emerald and sapphire. Each necklace corresponds to an element of a group $G$ containing elements $a, b, c$. If we impose the conditions $a^{2}=b c, b^{3}=c a, c^{2}=1$ and $a b c=1$, the allowed operations will preserve this element. In this group we have $c=a b$ (since $c^{2}=a b c$ ), i.e. $b=a^{-1} c$ and using this relation we obtain $a^{3}=c^{2}=\left(a^{-1} c\right)^{4}=1$. Thus we can take $G=\mathbb{S}_{4}, a=(1,2,3)$, $c=(1,4)$ and $b=a^{-1} c=(1,4,3,2)$. The initial and final necklaces should correspond to elements $c$ and $b$, respectively, so the desired sequence of operations does not exist.
## Geometry
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nC3.",
"solution_match": "\n## Solution"
}
|
b41b348c-30ca-58db-a5d1-fe1393f107ed
| 605,699
|
Let $A B C$ be a triangle inscribed in circle $\Gamma$ with center $O$ and let $H$ its orthocenter and $K$ be the midpoint of $O H$. The tangent of $\Gamma$ at $B$ meets the perpendicular bisector of $A C$ meets at $L$ and the tangent of $\Gamma$ at $C$ meets the perpendicular bisector of $A B$ at $M$. Prove that $A K \perp L M$.
(Greece)
|
The polar of $L$ with respect to $\Gamma$ is the line $\ell_{B}$ through $B$ parallel to $A C$, and the polar of $M$ with respect to $\Gamma$ is the line $\ell_{C}$ through $C$ parallel to $A B$. Therefore the pole of the line $L M$ is the intersection $A^{\prime}$ of $\ell_{B}$ and $\ell_{C}$. It follows that $O A^{\prime} \perp L M$, so it remains to show that $O D \| A K$.
Consider the reflection $O^{\prime}$ of $O$ in the midpoint $D$ of $B C$. Since $A^{\prime}$ is the reflection of $A$ in $D, A O A^{\prime} O^{\prime}$ is a parallelogram. Moreover, $A H O^{\prime} O$ is a parallelogram because $\overrightarrow{O O^{\prime}}=2 \overrightarrow{O D}=\overrightarrow{A H}$. It follows that $\overrightarrow{O A^{\prime}}=\overrightarrow{A O^{\prime}}=2 \overrightarrow{A K}$, so $O A^{\prime} \| A K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle inscribed in circle $\Gamma$ with center $O$ and let $H$ its orthocenter and $K$ be the midpoint of $O H$. The tangent of $\Gamma$ at $B$ meets the perpendicular bisector of $A C$ meets at $L$ and the tangent of $\Gamma$ at $C$ meets the perpendicular bisector of $A B$ at $M$. Prove that $A K \perp L M$.
(Greece)
|
The polar of $L$ with respect to $\Gamma$ is the line $\ell_{B}$ through $B$ parallel to $A C$, and the polar of $M$ with respect to $\Gamma$ is the line $\ell_{C}$ through $C$ parallel to $A B$. Therefore the pole of the line $L M$ is the intersection $A^{\prime}$ of $\ell_{B}$ and $\ell_{C}$. It follows that $O A^{\prime} \perp L M$, so it remains to show that $O D \| A K$.
Consider the reflection $O^{\prime}$ of $O$ in the midpoint $D$ of $B C$. Since $A^{\prime}$ is the reflection of $A$ in $D, A O A^{\prime} O^{\prime}$ is a parallelogram. Moreover, $A H O^{\prime} O$ is a parallelogram because $\overrightarrow{O O^{\prime}}=2 \overrightarrow{O D}=\overrightarrow{A H}$. It follows that $\overrightarrow{O A^{\prime}}=\overrightarrow{A O^{\prime}}=2 \overrightarrow{A K}$, so $O A^{\prime} \| A K$.

|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nG2.",
"solution_match": "\n## Solution."
}
|
53001fd8-1b4c-53b8-b5f9-92ff6dd3b971
| 605,724
|
Let $A B C$ be a triangle inscribed in circle $\Gamma$ with center $O$ and let $H$ its orthocenter and $K$ be the midpoint of $O H$. The tangent of $\Gamma$ at $B$ meets the perpendicular bisector of $A C$ meets at $L$ and the tangent of $\Gamma$ at $C$ meets the perpendicular bisector of $A B$ at $M$. Prove that $A K \perp L M$.
(Greece)
|
2.
We introduce the complex plane such that $\Gamma$ is the unit cycle. Also, let the lower-case letters denote complex numbers corresponding to the points denoted by capital letters. First, note that $o=0, \bar{a}=1 / a, \bar{b}=1 / b$ and $\bar{c}=1 / c$.
Since $B L \perp B O$, we have
$$
\frac{b-l}{\bar{b}-\bar{l}}=-\frac{b-o}{\bar{b}-\bar{o}}=-\frac{b}{\bar{b}}=-b^{2}, \quad \text { and hence } \quad \bar{l}=\frac{2 b-l}{b^{2}}
$$
Since $L O \perp A C$, we have
$$
\frac{l}{\bar{l}}=\frac{l-o}{\bar{l}-\bar{o}}=-\frac{a-c}{\bar{a}-\bar{c}}=a c, \quad \text { and hence } \quad \bar{l}=\frac{l}{a c} .
$$
Combining $(\dagger)$ and $(\ddagger)$ we get $l=\frac{2 a b c}{b^{2}+a c}$. By symmetry, $m=\frac{2 a b c}{c^{2}+a b}$ and hence
$$
l-m=\frac{2 a b c(c-b)(b+c-a)}{\left(b^{2}+a c\right)\left(c^{2}+a b\right)} \quad \text { and } \quad \bar{l}-\bar{m}=\frac{2(b-c)(a b+a c-b c)}{\left(b^{2}+a c\right)\left(c^{2}+a b\right)}
$$
By Hamilton's formula $a+b+c=h-o=h$, and hence $k=\frac{h+o}{2}=\frac{a+b+c}{2}$. So,
$$
a-k=\frac{b+c-a}{2} \quad \text { and } \quad \bar{a}-\bar{k}=\frac{a b+a c-b c}{2 a b c}
$$
and hence
$$
\frac{l-m}{\bar{l}-\bar{m}}=-\frac{a-k}{\bar{a}-\bar{k}}
$$
which implies $L M \perp A K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle inscribed in circle $\Gamma$ with center $O$ and let $H$ its orthocenter and $K$ be the midpoint of $O H$. The tangent of $\Gamma$ at $B$ meets the perpendicular bisector of $A C$ meets at $L$ and the tangent of $\Gamma$ at $C$ meets the perpendicular bisector of $A B$ at $M$. Prove that $A K \perp L M$.
(Greece)
|
2.
We introduce the complex plane such that $\Gamma$ is the unit cycle. Also, let the lower-case letters denote complex numbers corresponding to the points denoted by capital letters. First, note that $o=0, \bar{a}=1 / a, \bar{b}=1 / b$ and $\bar{c}=1 / c$.
Since $B L \perp B O$, we have
$$
\frac{b-l}{\bar{b}-\bar{l}}=-\frac{b-o}{\bar{b}-\bar{o}}=-\frac{b}{\bar{b}}=-b^{2}, \quad \text { and hence } \quad \bar{l}=\frac{2 b-l}{b^{2}}
$$
Since $L O \perp A C$, we have
$$
\frac{l}{\bar{l}}=\frac{l-o}{\bar{l}-\bar{o}}=-\frac{a-c}{\bar{a}-\bar{c}}=a c, \quad \text { and hence } \quad \bar{l}=\frac{l}{a c} .
$$
Combining $(\dagger)$ and $(\ddagger)$ we get $l=\frac{2 a b c}{b^{2}+a c}$. By symmetry, $m=\frac{2 a b c}{c^{2}+a b}$ and hence
$$
l-m=\frac{2 a b c(c-b)(b+c-a)}{\left(b^{2}+a c\right)\left(c^{2}+a b\right)} \quad \text { and } \quad \bar{l}-\bar{m}=\frac{2(b-c)(a b+a c-b c)}{\left(b^{2}+a c\right)\left(c^{2}+a b\right)}
$$
By Hamilton's formula $a+b+c=h-o=h$, and hence $k=\frac{h+o}{2}=\frac{a+b+c}{2}$. So,
$$
a-k=\frac{b+c-a}{2} \quad \text { and } \quad \bar{a}-\bar{k}=\frac{a b+a c-b c}{2 a b c}
$$
and hence
$$
\frac{l-m}{\bar{l}-\bar{m}}=-\frac{a-k}{\bar{a}-\bar{k}}
$$
which implies $L M \perp A K$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nG2.",
"solution_match": "\n## Solution"
}
|
53001fd8-1b4c-53b8-b5f9-92ff6dd3b971
| 605,724
|
A quadrilateral $A B C D$ is inscribed in a circle $k$, where $A B>C D$ and $A B$ is not parallel to $C D$. Point $M$ is the intersection of the diagonals $A C$ and $B D$ and point $H$ is the foot of the perpendicular from $M$ to $A B$. Given that $\varangle M H C=\varangle M H D$, prove that $A B$ is a diameter of $k$.
|
Let the line through $M$ parallel to $A B$ meet the segments $A D, D H, B C, C H$ at points $K, P, L, Q$, respectively. Triangle $H P Q$ is isosceles, so $M P=M Q$. Now from
$$
\frac{M P}{B H}=\frac{D M}{D B}=\frac{K M}{A B} \quad \text { and } \quad \frac{M Q}{A H}=\frac{C M}{C A}=\frac{M L}{A B}
$$
we obtain $A H / H B=K M / M L$.
Let the lines $A D$ and $B C$ meet at point $S$ and let the line $S M$ meet $A B$ at $H^{\prime}$. Then $A H^{\prime} / H^{\prime} B=K M / M L=A H / H B$, so $H^{\prime} \equiv H$, i.e. $S$ lies on the line $M H$.
The quadrilateral $A B C D$ is not a trapezoid, so $A H \neq B H$. Consider the point $A^{\prime}$ on the ray $H B$ such that $H A^{\prime}=H A$. Since $\varangle S A^{\prime} M=\varangle S A M=\varangle S B M$, quadrilateral $A^{\prime} B S M$ is cyclic and therefore $\varangle A B C=\varangle A^{\prime} B S=\varangle A^{\prime} M H=\varangle A M H=90^{\circ}-\varangle B A C$, which implies that $\varangle A C B=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A quadrilateral $A B C D$ is inscribed in a circle $k$, where $A B>C D$ and $A B$ is not parallel to $C D$. Point $M$ is the intersection of the diagonals $A C$ and $B D$ and point $H$ is the foot of the perpendicular from $M$ to $A B$. Given that $\varangle M H C=\varangle M H D$, prove that $A B$ is a diameter of $k$.
|
Let the line through $M$ parallel to $A B$ meet the segments $A D, D H, B C, C H$ at points $K, P, L, Q$, respectively. Triangle $H P Q$ is isosceles, so $M P=M Q$. Now from
$$
\frac{M P}{B H}=\frac{D M}{D B}=\frac{K M}{A B} \quad \text { and } \quad \frac{M Q}{A H}=\frac{C M}{C A}=\frac{M L}{A B}
$$
we obtain $A H / H B=K M / M L$.
Let the lines $A D$ and $B C$ meet at point $S$ and let the line $S M$ meet $A B$ at $H^{\prime}$. Then $A H^{\prime} / H^{\prime} B=K M / M L=A H / H B$, so $H^{\prime} \equiv H$, i.e. $S$ lies on the line $M H$.
The quadrilateral $A B C D$ is not a trapezoid, so $A H \neq B H$. Consider the point $A^{\prime}$ on the ray $H B$ such that $H A^{\prime}=H A$. Since $\varangle S A^{\prime} M=\varangle S A M=\varangle S B M$, quadrilateral $A^{\prime} B S M$ is cyclic and therefore $\varangle A B C=\varangle A^{\prime} B S=\varangle A^{\prime} M H=\varangle A M H=90^{\circ}-\varangle B A C$, which implies that $\varangle A C B=90^{\circ}$.

|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nG4.",
"solution_match": "\n## Solution."
}
|
25eacde4-78b4-5ab0-821a-7001f180a3c4
| 605,747
|
Let $A B C$ be an acute-angled triangle with $A B<A C<B C$ and let $D$ be an arbitrary point on the extension of $B C$ beyond $C$. The circle $\gamma(A, A D)$ intersects the rays $A C$, $A B, C B$ at points $E, F, G$, respectively. The circumcircle $\omega_{1}$ of triangle $A F G$ intersects the lines $F E, B C, G E, D F$ again at points $J, H, H^{\prime}, J^{\prime}$. The circumcircle $\omega_{2}$ of triangle $A D E$ intersects the lines $F E, B C, G E, D F$ again at points $I, K, K^{\prime}, I^{\prime}$. Prove that the quadrilaterals $H I J K$ and $H^{\prime} I^{\prime} J^{\prime} K^{\prime}$ are cyclic and that their circumcenters coincide.
(Greece)
|
From $\varangle F A H=\varangle F G H=\varangle F G D=\frac{1}{2} \varangle F A D=90^{\circ}-\varangle A F D$ we deduce that $A H \perp$ $D F$. Similarly, $\varangle D A I=180^{\circ}-\varangle D E I=180^{\circ}-\varangle D E F=\varangle D G F=\frac{1}{2} \varangle D A F$, so we also have $A I \perp D F$. Therefore, points $A, H, I$ are collinear. Analogously, we find that the triples of points $(A, K, J),\left(A, H^{\prime}, I^{\prime}\right)$ and $\left(A, K^{\prime}, J^{\prime}\right)$ are collinear.
Quadrilateral $H I J K$ is cyclic because $\varangle A I K=\varangle A D K=\varangle A G H=\varangle A J H$. Analogously, quadrilateral $H^{\prime} I^{\prime} J^{\prime} K^{\prime}$ is cyclic.
Finally, since $\varangle H^{\prime} J H=\varangle H^{\prime} G H=\varangle E G D=\varangle E F D=\varangle J F J^{\prime}=\varangle J H J^{\prime}$, quadrilateral $H J J^{\prime} H^{\prime}$ is an isosceles trapezoid with $H J \| H^{\prime} J^{\prime}$, so the perpendicular bisectors of $H J$ and $H^{\prime} J^{\prime}$ coincide. Analogously, the perpendicular bisectors of $I K$ and $I^{\prime} K^{\prime}$ coincide. Therefore the circumcenters of $H I J K$ and $H^{\prime} I^{\prime} J^{\prime} K^{\prime}$ coincide.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with $A B<A C<B C$ and let $D$ be an arbitrary point on the extension of $B C$ beyond $C$. The circle $\gamma(A, A D)$ intersects the rays $A C$, $A B, C B$ at points $E, F, G$, respectively. The circumcircle $\omega_{1}$ of triangle $A F G$ intersects the lines $F E, B C, G E, D F$ again at points $J, H, H^{\prime}, J^{\prime}$. The circumcircle $\omega_{2}$ of triangle $A D E$ intersects the lines $F E, B C, G E, D F$ again at points $I, K, K^{\prime}, I^{\prime}$. Prove that the quadrilaterals $H I J K$ and $H^{\prime} I^{\prime} J^{\prime} K^{\prime}$ are cyclic and that their circumcenters coincide.
(Greece)
|
From $\varangle F A H=\varangle F G H=\varangle F G D=\frac{1}{2} \varangle F A D=90^{\circ}-\varangle A F D$ we deduce that $A H \perp$ $D F$. Similarly, $\varangle D A I=180^{\circ}-\varangle D E I=180^{\circ}-\varangle D E F=\varangle D G F=\frac{1}{2} \varangle D A F$, so we also have $A I \perp D F$. Therefore, points $A, H, I$ are collinear. Analogously, we find that the triples of points $(A, K, J),\left(A, H^{\prime}, I^{\prime}\right)$ and $\left(A, K^{\prime}, J^{\prime}\right)$ are collinear.
Quadrilateral $H I J K$ is cyclic because $\varangle A I K=\varangle A D K=\varangle A G H=\varangle A J H$. Analogously, quadrilateral $H^{\prime} I^{\prime} J^{\prime} K^{\prime}$ is cyclic.
Finally, since $\varangle H^{\prime} J H=\varangle H^{\prime} G H=\varangle E G D=\varangle E F D=\varangle J F J^{\prime}=\varangle J H J^{\prime}$, quadrilateral $H J J^{\prime} H^{\prime}$ is an isosceles trapezoid with $H J \| H^{\prime} J^{\prime}$, so the perpendicular bisectors of $H J$ and $H^{\prime} J^{\prime}$ coincide. Analogously, the perpendicular bisectors of $I K$ and $I^{\prime} K^{\prime}$ coincide. Therefore the circumcenters of $H I J K$ and $H^{\prime} I^{\prime} J^{\prime} K^{\prime}$ coincide.

|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nG5.",
"solution_match": "\n## Solution."
}
|
89d0f9c0-819b-5bdc-9d92-a17b70eaaa4f
| 605,757
|
In a triangle $A B C$ with $A B=A C, \omega$ is the circumcircle and $O$ its center. Let $D$ be a point on the extension of $B A$ beyond $A$. The circumcircle $\omega_{1}$ of triangle $O A D$ intersects the line $A C$ and the circle $\omega$ again at points $E$ and $G$, respectively. Point $H$ is such that $D A E H$ is a parallelogram. Line $E H$ meets circle $\omega_{1}$ again at point $J$. The line through $G$ perpendicular to $G B$ meets $\omega_{1}$ again at point $N$ and the line through $G$ perpendicular to $G J$ meets $\omega$ again at point $L$. Prove that the points $L, N, H, G$ lie on a circle.
(Cyprus)
|
We first observe that $\varangle D O E=\varangle D A E=2 \varangle A B C=\varangle B O A$ and hence $\varangle D O B=$ $\varangle E O A$, which together with $O B=O A$ and $\varangle O B D=\varangle B A O=\varangle O A E$ gives us $\triangle O B D \cong \triangle O A E$. Therefore $B D=A E$.
Next, $O G=O A$ implies $\varangle O D G=\varangle O D A=\varangle O D B$ and hence $\triangle O G D \cong \triangle O B D$. It follows that $D G=D B=A E=D H$. Moreover, since $A D \| E J$, we have $D J=A E=$ $D G$. Thus, the points $B, G, H, J$ lie on a circle $\omega_{2}$ with center $D$.
We deduce that $\varangle A G H=\varangle B G H-\varangle B G A=180^{\circ}-\frac{1}{2} \varangle H D B-\varangle B C A=180^{\circ}-$ $\frac{1}{2} \varangle C A B-\varangle B C A=90^{\circ}$.
We will now invert the diagram through $G$. By $\hat{X}$ we denote the image of any point $X$. The points $\hat{H}, \hat{L}, \hat{N}$ then lie on the lines $\hat{B} \hat{J}, \hat{A} \hat{B}$ and $\hat{A} \hat{J}$, respectively, such that $\varangle \hat{A} G \hat{H}=\hat{B} G \hat{N}=\varangle \hat{J} G \hat{L}=90^{\circ}$. It remains to prove that $\hat{H}, \hat{L}$ and $\hat{N}$ are collinear, which follows from the following statement:
Lemma. Let $X Y Z$ be a triangle and let $U$ be a point in the plane. If the lines through $U$ perpendicular to $U X, U Y, U Z$ meet the lines $Y Z, Z X, X Y$ respectively at points $P, Q, R$, then the points $P, Q$ and $R$ are collinear.
$\underline{\text { Proof. Here we assume that } U \text { is inside } \triangle X Y Z \text { and the angles } X U Y, Y U Z \text { and } Z U X . . . ~}$ are all obtuse - the other cases are similar. We have
$$
\frac{\overrightarrow{Y P}}{\overrightarrow{P Z}}=-\frac{P_{Y U P}}{P_{P U Z}}, \quad \frac{\overrightarrow{Z Q}}{\overrightarrow{Q X}}=-\frac{P_{Z U Q}}{P_{Q U X}}, \quad \frac{\overrightarrow{X R}}{\overrightarrow{R Y}}=-\frac{P_{X U R}}{P_{R U Y}}
$$
On the other hand, since $\varangle Q U X=\varangle Y U P$ are equal and equally directed, we have $\frac{P_{Y U P}}{P_{Q U X}}=\frac{U P \cdot U Y}{U Q \cdot U X}$. Writing the analogous expressions for $\frac{P_{Z U Q}}{P_{R U Y}}$ and $\frac{P_{X U R}}{P_{P U Z}}$
and multiplying them out we obtain $\frac{\overrightarrow{Y P}}{\overrightarrow{P Z}} \cdot \frac{\overrightarrow{Z Q}}{\overrightarrow{Q X}} \cdot \frac{\overrightarrow{X R}}{\overrightarrow{R Y}}=-1$, and the result follows by Menelaus' theorem.
## Remark.
The result remains valid if $D$ is any point on the line $A B$.
Point $L$ does not depend on the choice of $D$. Indeed, $\varangle L C B=\varangle L G B=\varangle J G B-90^{\circ}=$ $\varangle J E A+\varangle A G B-90^{\circ}=\varangle B A C+\varangle A C B-90^{\circ}=90^{\circ}-\varangle A B C$, so $C L \perp A B$.
Also, since $\varangle A O N=\varangle A G N=90^{\circ}-\varangle B G A=90^{\circ}-\varangle B C A=\varangle O A B=\varangle O N D$, $O N D A$ is an isosceles trapezoid, i.e. $O N \| A B$.
## Alternative formulation.
Based on the Remark, the PSC proposes the following modification which hides point $J$ and defines the points in a more natural way:
A triangle $A B C$ with $A B=A C$ is inscribed in a circle $\omega$ with center $O$. Its altitude from $C$ meets $\omega$ again at point $L$. Line $\ell$ through $O$ is parallel to $A B$. A circle $\omega_{1}$ passes through points $A$ and $O$ and meets the lines $A B, A C, \ell$ and circle $\omega$ again at points $D, E, N$ and $G$, respectively. Point $H$ is such that $A D H E$ is a parallelogram.
Prove that $H$ lies on the circumcircle of triangle $G L N$.
## Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C$ with $A B=A C, \omega$ is the circumcircle and $O$ its center. Let $D$ be a point on the extension of $B A$ beyond $A$. The circumcircle $\omega_{1}$ of triangle $O A D$ intersects the line $A C$ and the circle $\omega$ again at points $E$ and $G$, respectively. Point $H$ is such that $D A E H$ is a parallelogram. Line $E H$ meets circle $\omega_{1}$ again at point $J$. The line through $G$ perpendicular to $G B$ meets $\omega_{1}$ again at point $N$ and the line through $G$ perpendicular to $G J$ meets $\omega$ again at point $L$. Prove that the points $L, N, H, G$ lie on a circle.
(Cyprus)
|
We first observe that $\varangle D O E=\varangle D A E=2 \varangle A B C=\varangle B O A$ and hence $\varangle D O B=$ $\varangle E O A$, which together with $O B=O A$ and $\varangle O B D=\varangle B A O=\varangle O A E$ gives us $\triangle O B D \cong \triangle O A E$. Therefore $B D=A E$.
Next, $O G=O A$ implies $\varangle O D G=\varangle O D A=\varangle O D B$ and hence $\triangle O G D \cong \triangle O B D$. It follows that $D G=D B=A E=D H$. Moreover, since $A D \| E J$, we have $D J=A E=$ $D G$. Thus, the points $B, G, H, J$ lie on a circle $\omega_{2}$ with center $D$.
We deduce that $\varangle A G H=\varangle B G H-\varangle B G A=180^{\circ}-\frac{1}{2} \varangle H D B-\varangle B C A=180^{\circ}-$ $\frac{1}{2} \varangle C A B-\varangle B C A=90^{\circ}$.
We will now invert the diagram through $G$. By $\hat{X}$ we denote the image of any point $X$. The points $\hat{H}, \hat{L}, \hat{N}$ then lie on the lines $\hat{B} \hat{J}, \hat{A} \hat{B}$ and $\hat{A} \hat{J}$, respectively, such that $\varangle \hat{A} G \hat{H}=\hat{B} G \hat{N}=\varangle \hat{J} G \hat{L}=90^{\circ}$. It remains to prove that $\hat{H}, \hat{L}$ and $\hat{N}$ are collinear, which follows from the following statement:

Lemma. Let $X Y Z$ be a triangle and let $U$ be a point in the plane. If the lines through $U$ perpendicular to $U X, U Y, U Z$ meet the lines $Y Z, Z X, X Y$ respectively at points $P, Q, R$, then the points $P, Q$ and $R$ are collinear.
$\underline{\text { Proof. Here we assume that } U \text { is inside } \triangle X Y Z \text { and the angles } X U Y, Y U Z \text { and } Z U X . . . ~}$ are all obtuse - the other cases are similar. We have
$$
\frac{\overrightarrow{Y P}}{\overrightarrow{P Z}}=-\frac{P_{Y U P}}{P_{P U Z}}, \quad \frac{\overrightarrow{Z Q}}{\overrightarrow{Q X}}=-\frac{P_{Z U Q}}{P_{Q U X}}, \quad \frac{\overrightarrow{X R}}{\overrightarrow{R Y}}=-\frac{P_{X U R}}{P_{R U Y}}
$$
On the other hand, since $\varangle Q U X=\varangle Y U P$ are equal and equally directed, we have $\frac{P_{Y U P}}{P_{Q U X}}=\frac{U P \cdot U Y}{U Q \cdot U X}$. Writing the analogous expressions for $\frac{P_{Z U Q}}{P_{R U Y}}$ and $\frac{P_{X U R}}{P_{P U Z}}$
and multiplying them out we obtain $\frac{\overrightarrow{Y P}}{\overrightarrow{P Z}} \cdot \frac{\overrightarrow{Z Q}}{\overrightarrow{Q X}} \cdot \frac{\overrightarrow{X R}}{\overrightarrow{R Y}}=-1$, and the result follows by Menelaus' theorem.
## Remark.
The result remains valid if $D$ is any point on the line $A B$.
Point $L$ does not depend on the choice of $D$. Indeed, $\varangle L C B=\varangle L G B=\varangle J G B-90^{\circ}=$ $\varangle J E A+\varangle A G B-90^{\circ}=\varangle B A C+\varangle A C B-90^{\circ}=90^{\circ}-\varangle A B C$, so $C L \perp A B$.
Also, since $\varangle A O N=\varangle A G N=90^{\circ}-\varangle B G A=90^{\circ}-\varangle B C A=\varangle O A B=\varangle O N D$, $O N D A$ is an isosceles trapezoid, i.e. $O N \| A B$.
## Alternative formulation.
Based on the Remark, the PSC proposes the following modification which hides point $J$ and defines the points in a more natural way:
A triangle $A B C$ with $A B=A C$ is inscribed in a circle $\omega$ with center $O$. Its altitude from $C$ meets $\omega$ again at point $L$. Line $\ell$ through $O$ is parallel to $A B$. A circle $\omega_{1}$ passes through points $A$ and $O$ and meets the lines $A B, A C, \ell$ and circle $\omega$ again at points $D, E, N$ and $G$, respectively. Point $H$ is such that $A D H E$ is a parallelogram.
Prove that $H$ lies on the circumcircle of triangle $G L N$.

## Number Theory
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nG6.",
"solution_match": "\n## Solution."
}
|
d9326439-aa3c-58e5-b92d-bd8e8f7c6c53
| 605,766
|
For positive integers $m$ and $n$, let $d(m, n)$ be the number of distinct primes that divide both $m$ and $n$. For instance, $d(60,126)=d\left(2^{2} \times 3 \times 5,2 \times 3^{2} \times 7\right)=2$. Does there exist a sequence $\left(a_{n}\right)$ of positive integers such that:
(i) $a_{1} \geqslant 2018^{2018}$;
(ii) $a_{m} \leqslant a_{n}$ whenever $m \leqslant n$;
(iii) $d(m, n)=d\left(a_{m}, a_{n}\right)$ for all positive integers $m \neq n$ ?
(United Kingdom)
|
Such a sequence does exist.
Let $p_{1}<p_{2}<p_{3}<\ldots$ be the usual list of primes, and $q_{1}<q_{2}<\ldots, r_{1}<r_{2}<\ldots$ be disjoint sequences of primes greater than $2018^{2018}$. For example, let $q_{i} \equiv 1$ and $r_{i} \equiv 3$ modulo 4. Then, if $n=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots$, where all but finitely many of the $\alpha_{i}$ will be zero, set
$$
b_{n}:=q_{1}^{\alpha_{1}} q_{2}^{\alpha_{2}} \cdots, \quad \text { for all } n \geqslant 2
$$
This sequence satisfies requirement (iii), but not the ordering conditions (i) and (ii). Iteratively, take $a_{1}=r_{1}$, then given $a_{1}, \ldots, a_{n-1}$, define $a_{n}$ by multiplying $b_{n}$ by as large a power of $r_{n}$ as necessary in order to ensure $a_{n}>a_{n-1}$. Thus $d\left(a_{m}, a_{n}\right)=d\left(b_{m}, b_{n}\right)=$ $d(m, n)$, and so all three requirements are satisfied.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For positive integers $m$ and $n$, let $d(m, n)$ be the number of distinct primes that divide both $m$ and $n$. For instance, $d(60,126)=d\left(2^{2} \times 3 \times 5,2 \times 3^{2} \times 7\right)=2$. Does there exist a sequence $\left(a_{n}\right)$ of positive integers such that:
(i) $a_{1} \geqslant 2018^{2018}$;
(ii) $a_{m} \leqslant a_{n}$ whenever $m \leqslant n$;
(iii) $d(m, n)=d\left(a_{m}, a_{n}\right)$ for all positive integers $m \neq n$ ?
(United Kingdom)
|
Such a sequence does exist.
Let $p_{1}<p_{2}<p_{3}<\ldots$ be the usual list of primes, and $q_{1}<q_{2}<\ldots, r_{1}<r_{2}<\ldots$ be disjoint sequences of primes greater than $2018^{2018}$. For example, let $q_{i} \equiv 1$ and $r_{i} \equiv 3$ modulo 4. Then, if $n=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots$, where all but finitely many of the $\alpha_{i}$ will be zero, set
$$
b_{n}:=q_{1}^{\alpha_{1}} q_{2}^{\alpha_{2}} \cdots, \quad \text { for all } n \geqslant 2
$$
This sequence satisfies requirement (iii), but not the ordering conditions (i) and (ii). Iteratively, take $a_{1}=r_{1}$, then given $a_{1}, \ldots, a_{n-1}$, define $a_{n}$ by multiplying $b_{n}$ by as large a power of $r_{n}$ as necessary in order to ensure $a_{n}>a_{n-1}$. Thus $d\left(a_{m}, a_{n}\right)=d\left(b_{m}, b_{n}\right)=$ $d(m, n)$, and so all three requirements are satisfied.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nN1.",
"solution_match": "\n## Solution."
}
|
3c63d421-1cdb-5ea3-9b50-e755b3df3a90
| 605,775
|
Let $P(x)=a_{d} x^{d}+\cdots+a_{1} x+a_{0}$ be a non-constant polynomial with nonnegative integer coefficients having $d$ rational roots. Prove that
$$
\operatorname{lcm}(P(m), P(m+1), \ldots, P(n)) \geqslant m\binom{n}{m}
$$
for all positive integers $n>m$.
|
Let $x_{i}=-\frac{p_{i}}{q_{i}}(1 \leqslant i \leqslant d)$ be the roots of $P(x)$, where $p_{i}, q_{i} \in \mathbb{N}$ and $\operatorname{gcd}\left(p_{i}, q_{i}\right)=1$. By Gauss' lemma, we have $P(x)=c\left(q_{1} x+p_{1}\right)\left(q_{2} x+p_{2}\right) \cdots\left(q_{d} x+p_{d}\right)$ for some $c \in \mathbb{N}$, so $q_{1} x+p_{1} \mid P(x)$. Thus it suffices to prove the statement for $P(x)=q_{1} x+p_{1}=q x+p$. Let
$$
\begin{array}{ll}
A=\operatorname{lcm}(q m+p, q(m+1)+p, \ldots, q n+p) & =\prod_{i=1}^{s} p_{i}^{\alpha_{i}}, \\
B=(q m+p)(q(m+1)+p) \cdots(q n+p) & =\prod_{i=1}^{s} p_{i}^{\beta_{i}}
\end{array}
$$
be the prime factorizations of $A$ and $B$.
Consider a prime divisor $p_{i}$. We have $p_{i}^{\alpha_{i}} \mid q x+p$ for some $m \leqslant x \leqslant n$. On the other hand, if $p_{i}^{r} \mid q y+p\left(r \leqslant \alpha_{i}\right)$ for some $m \leqslant y \leqslant n$ with $y \neq x$, then $p_{i}^{r} \mid q(x-y)$, i.e. $p_{i}^{r} \mid x-y$. Taking the product over all $y \neq x$ we obtain that
$$
p_{i}^{\beta_{i}} \quad \text { divides } \quad p_{i}^{\alpha_{i}} \cdot \prod_{\substack{y=m \\ y \neq x}}^{n}|x-y|, \quad \text { which divides } \quad p_{i}^{\alpha_{i}}(n-m)!
$$
It follows that $B \mid A \cdot(n-m)$ !, but $B \geqslant m(m+1) \cdots n$, so the result immediately follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $P(x)=a_{d} x^{d}+\cdots+a_{1} x+a_{0}$ be a non-constant polynomial with nonnegative integer coefficients having $d$ rational roots. Prove that
$$
\operatorname{lcm}(P(m), P(m+1), \ldots, P(n)) \geqslant m\binom{n}{m}
$$
for all positive integers $n>m$.
|
Let $x_{i}=-\frac{p_{i}}{q_{i}}(1 \leqslant i \leqslant d)$ be the roots of $P(x)$, where $p_{i}, q_{i} \in \mathbb{N}$ and $\operatorname{gcd}\left(p_{i}, q_{i}\right)=1$. By Gauss' lemma, we have $P(x)=c\left(q_{1} x+p_{1}\right)\left(q_{2} x+p_{2}\right) \cdots\left(q_{d} x+p_{d}\right)$ for some $c \in \mathbb{N}$, so $q_{1} x+p_{1} \mid P(x)$. Thus it suffices to prove the statement for $P(x)=q_{1} x+p_{1}=q x+p$. Let
$$
\begin{array}{ll}
A=\operatorname{lcm}(q m+p, q(m+1)+p, \ldots, q n+p) & =\prod_{i=1}^{s} p_{i}^{\alpha_{i}}, \\
B=(q m+p)(q(m+1)+p) \cdots(q n+p) & =\prod_{i=1}^{s} p_{i}^{\beta_{i}}
\end{array}
$$
be the prime factorizations of $A$ and $B$.
Consider a prime divisor $p_{i}$. We have $p_{i}^{\alpha_{i}} \mid q x+p$ for some $m \leqslant x \leqslant n$. On the other hand, if $p_{i}^{r} \mid q y+p\left(r \leqslant \alpha_{i}\right)$ for some $m \leqslant y \leqslant n$ with $y \neq x$, then $p_{i}^{r} \mid q(x-y)$, i.e. $p_{i}^{r} \mid x-y$. Taking the product over all $y \neq x$ we obtain that
$$
p_{i}^{\beta_{i}} \quad \text { divides } \quad p_{i}^{\alpha_{i}} \cdot \prod_{\substack{y=m \\ y \neq x}}^{n}|x-y|, \quad \text { which divides } \quad p_{i}^{\alpha_{i}}(n-m)!
$$
It follows that $B \mid A \cdot(n-m)$ !, but $B \geqslant m(m+1) \cdots n$, so the result immediately follows.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nN4.",
"solution_match": "\n## Solution."
}
|
de383b2b-aaed-5645-a8f1-c0d49f6a5f14
| 605,804
|
Let $x$ and $y$ be positive integers. If for each positive integer $n$ we have that
$$
(n y)^{2}+1 \mid x^{\varphi(n)}-1
$$
prove that $x=1$.
|
Let us take $n=3^{k}$ and suppose that $p$ is a prime divisor of $\left(3^{k} y\right)^{2}+1$ such that $p \equiv 2$ $(\bmod 3)$.
Since $p$ divides $x^{\varphi(n)}-1=x^{2 \cdot 3^{k-1}}-1$, the order of $x$ modulo $p$ divides both $p-1$ and $2 \cdot 3^{k-1}$, but $\operatorname{gcd}\left(p-1,2 \cdot 3^{k-1}\right) \mid 2$, which implies that $p \mid x^{2}-1$. The result will follow if we prove that the prime $p$ can take infinitely many values.
Suppose, to the contrary, that there are only finitely many primes $p$ with $p \equiv 2(\bmod 3)$ that divide a term of the sequence
$$
a_{k}=3^{2 k} y^{2}+1 \quad(k \geqslant 0)
$$
Let $p_{1}, p_{2}, \ldots, p_{m}$ be these primes. Clearly, we may assume without loss of generality that $3 \nmid y$. Then $a_{0}=y^{2}+1 \equiv 2(\bmod 3)$, so it has a prime divisor of the form $3 s+2$ $\left(s \in \mathbb{N}_{0}\right)$.
For $N=\left(y^{2}+1\right) p_{1} \cdots p_{m}$ we have $a_{\varphi(N)}=3^{2 \varphi(N)} y^{2}+1 \equiv y^{2}+1(\bmod N)$, which means that
$$
a_{\varphi(N)}=\left(y^{2}+1\right)\left(t p_{1} \cdots p_{m}+1\right)
$$
for some positive integer $t$. Since $y^{2}+1 \equiv 2(\bmod 3)$ and $3^{2 \varphi(N)} y^{2}+1 \equiv 1(\bmod 3)$, the number $t p_{1} \cdots p_{m}+1$ must have a prime divisor of the form $3 s+2$, but it cannot be any of the primes $p_{1}, \ldots, p_{m}$, so we have a contradiction as desired.

|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $x$ and $y$ be positive integers. If for each positive integer $n$ we have that
$$
(n y)^{2}+1 \mid x^{\varphi(n)}-1
$$
prove that $x=1$.
|
Let us take $n=3^{k}$ and suppose that $p$ is a prime divisor of $\left(3^{k} y\right)^{2}+1$ such that $p \equiv 2$ $(\bmod 3)$.
Since $p$ divides $x^{\varphi(n)}-1=x^{2 \cdot 3^{k-1}}-1$, the order of $x$ modulo $p$ divides both $p-1$ and $2 \cdot 3^{k-1}$, but $\operatorname{gcd}\left(p-1,2 \cdot 3^{k-1}\right) \mid 2$, which implies that $p \mid x^{2}-1$. The result will follow if we prove that the prime $p$ can take infinitely many values.
Suppose, to the contrary, that there are only finitely many primes $p$ with $p \equiv 2(\bmod 3)$ that divide a term of the sequence
$$
a_{k}=3^{2 k} y^{2}+1 \quad(k \geqslant 0)
$$
Let $p_{1}, p_{2}, \ldots, p_{m}$ be these primes. Clearly, we may assume without loss of generality that $3 \nmid y$. Then $a_{0}=y^{2}+1 \equiv 2(\bmod 3)$, so it has a prime divisor of the form $3 s+2$ $\left(s \in \mathbb{N}_{0}\right)$.
For $N=\left(y^{2}+1\right) p_{1} \cdots p_{m}$ we have $a_{\varphi(N)}=3^{2 \varphi(N)} y^{2}+1 \equiv y^{2}+1(\bmod N)$, which means that
$$
a_{\varphi(N)}=\left(y^{2}+1\right)\left(t p_{1} \cdots p_{m}+1\right)
$$
for some positive integer $t$. Since $y^{2}+1 \equiv 2(\bmod 3)$ and $3^{2 \varphi(N)} y^{2}+1 \equiv 1(\bmod 3)$, the number $t p_{1} \cdots p_{m}+1$ must have a prime divisor of the form $3 s+2$, but it cannot be any of the primes $p_{1}, \ldots, p_{m}$, so we have a contradiction as desired.

|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nN5.",
"solution_match": "\n## Solution."
}
|
f8ce7770-dd7b-5761-8c2e-0aef4e0c60ed
| 605,813
|
Let $a_{0}$ be an arbitrary positive integer. Consider the infinite sequence $\left(a_{n}\right)_{n \geq 1}$, defined inductively as follows: given $a_{0}, a_{1}, \ldots, a_{n-1}$ define the term $a_{n}$ as the smallest positive integer such that $a_{0}+a_{1}+\ldots+a_{n}$ is divisible by $n$. Prove that there exists a positive integer $M$ such that $a_{n+1}=a_{n}$ for all $n \geq M$.
|
Define $b_{n}=\frac{a_{0}+a_{1}+\ldots+a_{n}}{n}$ for every positive integer $n$. According to condition, $b_{n}$ is a positive integer for every positive integer $n$.
Since $a_{n+1}$ is the smallest positive integer such that $\frac{a_{0}+a_{1}+\ldots+a_{n}+a_{n+1}}{n+1}$ is a positive integer and
$$
\frac{a_{0}+a_{1}+\ldots+a_{n}+b_{n}}{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}+\frac{a_{0}+a_{1}+\ldots+a_{n}}{n}}{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}}{n}=b_{n}
$$
which is a positive integer, we get $a_{n+1} \leq b_{n}$ for every positive integer $n$.
Now from last result we have
$$
b_{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}+a_{n+1}}{n+1} \leq \frac{a_{0}+a_{1}+\ldots+a_{n}+b_{n}}{n+1}=b_{n} .
$$
Hence the infinite sequence of positive integers $b_{1}, b_{2}, \ldots$ is non-increasing. So there exists a positive integer $T$ such that for all $n \geq T$ we have
$$
\begin{gathered}
b_{n+1}=b_{n} \Rightarrow \frac{a_{0}+a_{1}+\ldots+a_{n}+a_{n+1}}{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}}{n} \Rightarrow \\
n\left(a_{0}+a_{1}+\ldots+a_{n}+a_{n+1}\right)=(n+1)\left(a_{0}+a_{1}+\ldots+a_{n}\right) \Rightarrow \\
n a_{n+1}=a_{0}+a_{1}+\ldots+a_{n} \Rightarrow a_{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}}{n}=b_{n} .
\end{gathered}
$$
Similarly we get $a_{n+2}=b_{n+1}$, which follows that $a_{n+2}=b_{n+1}=b_{n}=a_{n+1}$. Hence, taking $M=T+1$, we can state that $a_{n+1}=a_{n}$ for every $n \geq M$.
[^3]A2. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that:
$$
f(x y)=y f(x)+x+f(f(y)-f(x))
$$
for all $x, y \in \mathbb{R}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{0}$ be an arbitrary positive integer. Consider the infinite sequence $\left(a_{n}\right)_{n \geq 1}$, defined inductively as follows: given $a_{0}, a_{1}, \ldots, a_{n-1}$ define the term $a_{n}$ as the smallest positive integer such that $a_{0}+a_{1}+\ldots+a_{n}$ is divisible by $n$. Prove that there exists a positive integer $M$ such that $a_{n+1}=a_{n}$ for all $n \geq M$.
|
Define $b_{n}=\frac{a_{0}+a_{1}+\ldots+a_{n}}{n}$ for every positive integer $n$. According to condition, $b_{n}$ is a positive integer for every positive integer $n$.
Since $a_{n+1}$ is the smallest positive integer such that $\frac{a_{0}+a_{1}+\ldots+a_{n}+a_{n+1}}{n+1}$ is a positive integer and
$$
\frac{a_{0}+a_{1}+\ldots+a_{n}+b_{n}}{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}+\frac{a_{0}+a_{1}+\ldots+a_{n}}{n}}{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}}{n}=b_{n}
$$
which is a positive integer, we get $a_{n+1} \leq b_{n}$ for every positive integer $n$.
Now from last result we have
$$
b_{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}+a_{n+1}}{n+1} \leq \frac{a_{0}+a_{1}+\ldots+a_{n}+b_{n}}{n+1}=b_{n} .
$$
Hence the infinite sequence of positive integers $b_{1}, b_{2}, \ldots$ is non-increasing. So there exists a positive integer $T$ such that for all $n \geq T$ we have
$$
\begin{gathered}
b_{n+1}=b_{n} \Rightarrow \frac{a_{0}+a_{1}+\ldots+a_{n}+a_{n+1}}{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}}{n} \Rightarrow \\
n\left(a_{0}+a_{1}+\ldots+a_{n}+a_{n+1}\right)=(n+1)\left(a_{0}+a_{1}+\ldots+a_{n}\right) \Rightarrow \\
n a_{n+1}=a_{0}+a_{1}+\ldots+a_{n} \Rightarrow a_{n+1}=\frac{a_{0}+a_{1}+\ldots+a_{n}}{n}=b_{n} .
\end{gathered}
$$
Similarly we get $a_{n+2}=b_{n+1}$, which follows that $a_{n+2}=b_{n+1}=b_{n}=a_{n+1}$. Hence, taking $M=T+1$, we can state that $a_{n+1}=a_{n}$ for every $n \geq M$.
[^3]A2. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that:
$$
f(x y)=y f(x)+x+f(f(y)-f(x))
$$
for all $x, y \in \mathbb{R}$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nA1b. ${ }^{4}$",
"solution_match": "\nSolution."
}
|
53e6e720-4e7b-5d9d-b994-6b4bcb391e16
| 605,821
|
Let $a, b, c$ be real numbers such that $0 \leq a \leq b \leq c$. Prove that if
$$
a+b+c=a b+b c+c a>0,
$$
then $\sqrt{b c}(a+1) \geq 2$. When does the equality hold?
|
Let $a+b+c=a b+b c+c a=k$. Since $(a+b+c)^{2} \geq 3(a b+b c+c a)$, we get that $k^{2} \geq 3 k$. Since $k>0$, we obtain that $k \geq 3$.
We have $b c \geq c a \geq a b$, so from the above relation we deduce that $b c \geq 1$.
By AM-GM, $b+c \geq 2 \sqrt{b c}$ and consequently $b+c \geq 2$. The equality holds iff $b=c$.
The constraint gives us
$$
a=\frac{b+c-b c}{b+c-1}=1-\frac{b c-1}{b+c-1} \geq 1-\frac{b c-1}{2 \sqrt{b c}-1}=\frac{\sqrt{b c}(2-\sqrt{b c})}{2 \sqrt{b c}-1}
$$
For $\sqrt{b c}=2$ condition $a \geq 0$ gives $\sqrt{b c}(a+1) \geq 2$ with equality iff $a=0$ and $b=c=2$.
For $\sqrt{b c}<2$, taking into account the estimation for $a$, we get
$$
a \sqrt{b c} \geq \frac{b c(2-\sqrt{b c})}{2 \sqrt{b c}-1}=\frac{b c}{2 \sqrt{b c}-1}(2-\sqrt{b c}) .
$$
Since $\frac{b c}{2 \sqrt{b c}-1} \geq 1$, with equality for $b c=1$, we get $\sqrt{b c}(a+1) \geq 2$ with equality iff $a=b=c=1$.
For $\sqrt{b c}>2$ we have $\sqrt{b c}(a+1)>2(a+1) \geq 2$.
The proof is complete.
The equality holds iff $a=b=c=1$ or $a=0$ and $b=c=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers such that $0 \leq a \leq b \leq c$. Prove that if
$$
a+b+c=a b+b c+c a>0,
$$
then $\sqrt{b c}(a+1) \geq 2$. When does the equality hold?
|
Let $a+b+c=a b+b c+c a=k$. Since $(a+b+c)^{2} \geq 3(a b+b c+c a)$, we get that $k^{2} \geq 3 k$. Since $k>0$, we obtain that $k \geq 3$.
We have $b c \geq c a \geq a b$, so from the above relation we deduce that $b c \geq 1$.
By AM-GM, $b+c \geq 2 \sqrt{b c}$ and consequently $b+c \geq 2$. The equality holds iff $b=c$.
The constraint gives us
$$
a=\frac{b+c-b c}{b+c-1}=1-\frac{b c-1}{b+c-1} \geq 1-\frac{b c-1}{2 \sqrt{b c}-1}=\frac{\sqrt{b c}(2-\sqrt{b c})}{2 \sqrt{b c}-1}
$$
For $\sqrt{b c}=2$ condition $a \geq 0$ gives $\sqrt{b c}(a+1) \geq 2$ with equality iff $a=0$ and $b=c=2$.
For $\sqrt{b c}<2$, taking into account the estimation for $a$, we get
$$
a \sqrt{b c} \geq \frac{b c(2-\sqrt{b c})}{2 \sqrt{b c}-1}=\frac{b c}{2 \sqrt{b c}-1}(2-\sqrt{b c}) .
$$
Since $\frac{b c}{2 \sqrt{b c}-1} \geq 1$, with equality for $b c=1$, we get $\sqrt{b c}(a+1) \geq 2$ with equality iff $a=b=c=1$.
For $\sqrt{b c}>2$ we have $\sqrt{b c}(a+1)>2(a+1) \geq 2$.
The proof is complete.
The equality holds iff $a=b=c=1$ or $a=0$ and $b=c=2$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nA3.",
"solution_match": "\nSolution."
}
|
2ae7d15e-fbec-5b34-a032-5af90d4dc817
| 605,843
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.