problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $A B C$ be a triangle with incenter $I$, and whose incircle is tangent to $\overline{B C}, \overline{C A}$, $\overline{A B}$ at $D, E, F$, respectively. Let $K$ be the foot of the altitude from $D$ to $\overline{E F}$. Suppose that the circumcircle of $\triangle A I B$ meets the incircle at two distinct points $C_{1}$ and $C_{2}$, while the circumcircle of $\triangle A I C$ meets the incircle at two distinct points $B_{1}$ and $B_{2}$. Prove that the radical axis of the circumcircles of $\triangle B B_{1} B_{2}$ and $\triangle C C_{1} C_{2}$ passes through the midpoint $M$ of $\overline{D K}$.
|
『 Second solution (Evan Chen). As before, we just have to prove $G$ lies on the radical axis. 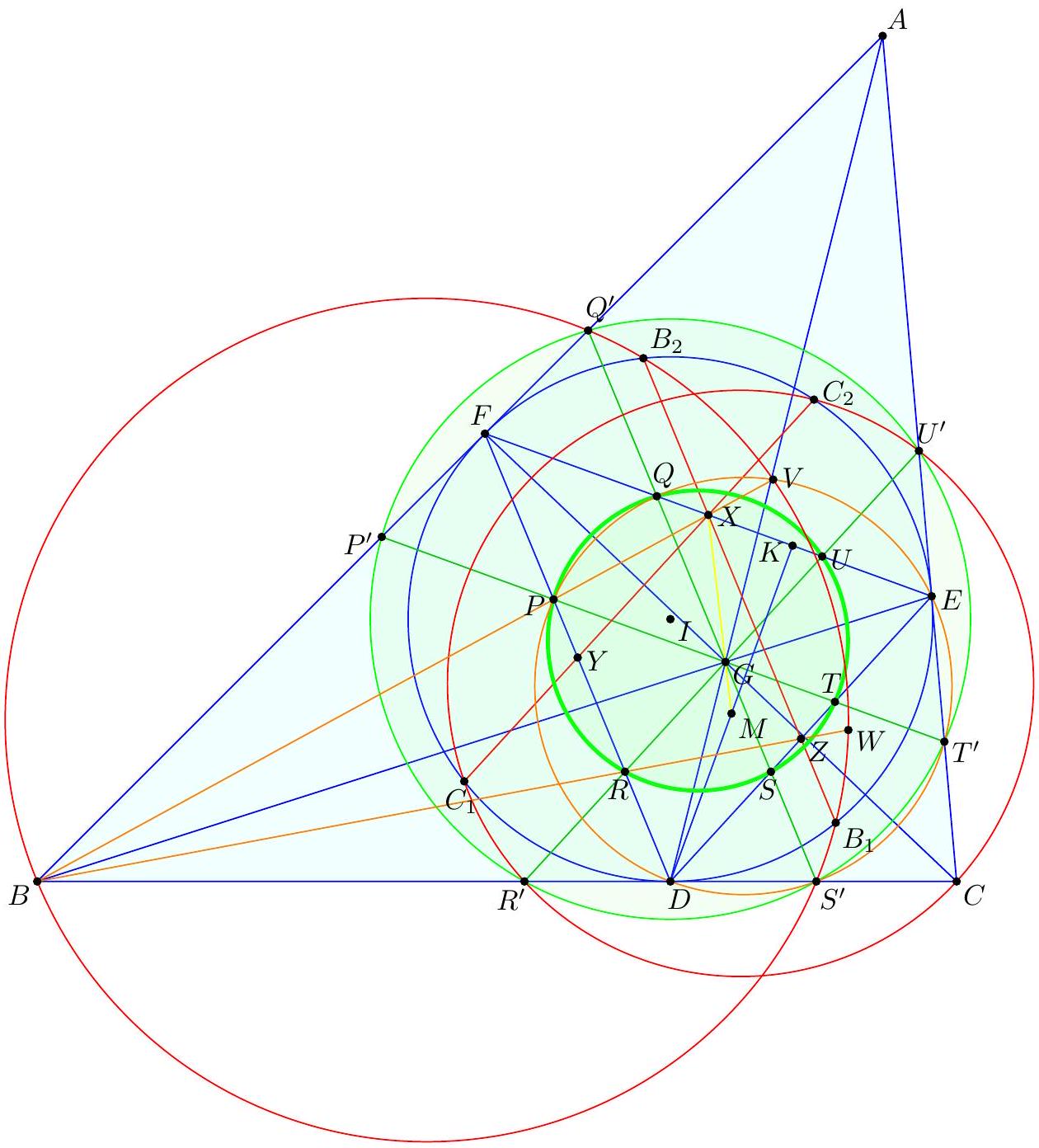 Construct parallelograms $G P F Q, G R D S, G T U E$ such that $P, R \in D F, S, T \in D E$, $Q, U \in E F$. As $F G$ bisects $P Q$ and is isogonal to $F Z$, we find $P Q E D$, hence $P Q R U$, is cyclic. Repeating the same logic and noticing $P R, S T, Q U$ not concurrent, all six points $P Q R S T U$ are cyclic. Moreover, since $P Q$ bisects $G F$, we see that a dilation with factor 2 at $G$ sends $P Q$ to $P^{\prime}, Q^{\prime} \in A B$, say, with $F$ the midpoint of $P^{\prime} Q^{\prime}$. Define $R^{\prime}, S^{\prime} \in B C$ similarly now and $T^{\prime}, U^{\prime} \in C A$. Note that $E Q P D S^{\prime}$ is in cyclic too, as $\measuredangle D S^{\prime} Q=\measuredangle D R S=\measuredangle D E F$. By homothety through $B$, points $B, P, X$ are collinear; assume they meet ( $\left.E Q P D S^{\prime}\right)$ again at $V$. Thus $E V Q P D S^{\prime}$ is cyclic, and now $$ \measuredangle B V S^{\prime}=\measuredangle P V S^{\prime}=\measuredangle P Q S=\measuredangle P T S=\measuredangle F E D=\measuredangle X E Z=\measuredangle X V Z $$ hence $V$ lies on $\left(B Q^{\prime} S^{\prime}\right)$. Since $F B \| Q P$, we get $E V F B$ is cyclic too, so $X V \cdot X B=X E \cdot X F$ now; thus $X$ lies on the radical axis of $\left(B S^{\prime} Q^{\prime}\right)$ and $(D E F)$. By the same argument with $W \in B Z$, we get $Z$ lies on the radical axis too. Thus the radical axis of $\left(B S^{\prime} Q^{\prime}\right)$ and ( $D E F$ ) must be line $X Z$, which coincides with $B_{1} B_{2}$; so $\left(B B_{1} B_{2}\right)=\left(B S^{\prime} Q^{\prime}\right)$. Analogously, $\left(C C_{1} C_{2}\right)=\left(C R^{\prime} U^{\prime}\right)$. Since $G=Q^{\prime} S^{\prime} \cap R^{\prime} U^{\prime}$, we need only prove that $Q^{\prime} R^{\prime} S^{\prime} U^{\prime}$ is cyclic. But $Q R S U$ is cyclic, so we are done. The circle ( $P Q R S T U$ ) is called the Lemoine circle of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$, and whose incircle is tangent to $\overline{B C}, \overline{C A}$, $\overline{A B}$ at $D, E, F$, respectively. Let $K$ be the foot of the altitude from $D$ to $\overline{E F}$. Suppose that the circumcircle of $\triangle A I B$ meets the incircle at two distinct points $C_{1}$ and $C_{2}$, while the circumcircle of $\triangle A I C$ meets the incircle at two distinct points $B_{1}$ and $B_{2}$. Prove that the radical axis of the circumcircles of $\triangle B B_{1} B_{2}$ and $\triangle C C_{1} C_{2}$ passes through the midpoint $M$ of $\overline{D K}$.
|
『 Second solution (Evan Chen). As before, we just have to prove $G$ lies on the radical axis.  Construct parallelograms $G P F Q, G R D S, G T U E$ such that $P, R \in D F, S, T \in D E$, $Q, U \in E F$. As $F G$ bisects $P Q$ and is isogonal to $F Z$, we find $P Q E D$, hence $P Q R U$, is cyclic. Repeating the same logic and noticing $P R, S T, Q U$ not concurrent, all six points $P Q R S T U$ are cyclic. Moreover, since $P Q$ bisects $G F$, we see that a dilation with factor 2 at $G$ sends $P Q$ to $P^{\prime}, Q^{\prime} \in A B$, say, with $F$ the midpoint of $P^{\prime} Q^{\prime}$. Define $R^{\prime}, S^{\prime} \in B C$ similarly now and $T^{\prime}, U^{\prime} \in C A$. Note that $E Q P D S^{\prime}$ is in cyclic too, as $\measuredangle D S^{\prime} Q=\measuredangle D R S=\measuredangle D E F$. By homothety through $B$, points $B, P, X$ are collinear; assume they meet ( $\left.E Q P D S^{\prime}\right)$ again at $V$. Thus $E V Q P D S^{\prime}$ is cyclic, and now $$ \measuredangle B V S^{\prime}=\measuredangle P V S^{\prime}=\measuredangle P Q S=\measuredangle P T S=\measuredangle F E D=\measuredangle X E Z=\measuredangle X V Z $$ hence $V$ lies on $\left(B Q^{\prime} S^{\prime}\right)$. Since $F B \| Q P$, we get $E V F B$ is cyclic too, so $X V \cdot X B=X E \cdot X F$ now; thus $X$ lies on the radical axis of $\left(B S^{\prime} Q^{\prime}\right)$ and $(D E F)$. By the same argument with $W \in B Z$, we get $Z$ lies on the radical axis too. Thus the radical axis of $\left(B S^{\prime} Q^{\prime}\right)$ and ( $D E F$ ) must be line $X Z$, which coincides with $B_{1} B_{2}$; so $\left(B B_{1} B_{2}\right)=\left(B S^{\prime} Q^{\prime}\right)$. Analogously, $\left(C C_{1} C_{2}\right)=\left(C R^{\prime} U^{\prime}\right)$. Since $G=Q^{\prime} S^{\prime} \cap R^{\prime} U^{\prime}$, we need only prove that $Q^{\prime} R^{\prime} S^{\prime} U^{\prime}$ is cyclic. But $Q R S U$ is cyclic, so we are done. The circle ( $P Q R S T U$ ) is called the Lemoine circle of $A B C$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
1965f734-a65e-55f1-ad1d-bc54710433bc
| 247,247 |
Let $A B C$ be a triangle with circumcircle $\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \neq A C$ and $\angle A \neq 90^{\circ}$. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\Gamma$ with the circumcircle of $\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\overline{P R} \perp \overline{O H}$.
|
【 First solution (power of a point). Let $\gamma$ denote the nine-point circle of $A B C$. 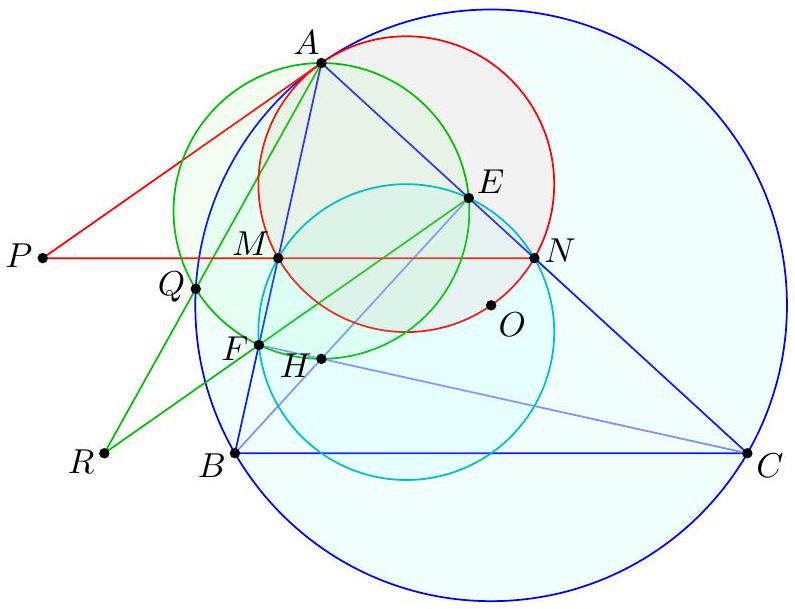 Note that - $P A^{2}=P M \cdot P N$, so $P$ lies on the radical axis of $\Gamma$ and $\gamma$. - $R A \cdot R Q=R E \cdot R F$, so $R$ lies on the radical axis of $\Gamma$ and $\gamma$. Thus $\overline{P R}$ is the radical axis of $\Gamma$ and $\gamma$, which is evidently perpendicular to $\overline{O H}$. Remark. In fact, by power of a point one may also observe that $R$ lies on $\overline{B C}$, since it is on the radical axis of $(A Q F H E),(B F E C),(A B C)$. Ironically, this fact is not used in the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \neq A C$ and $\angle A \neq 90^{\circ}$. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\Gamma$ with the circumcircle of $\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\overline{P R} \perp \overline{O H}$.
|
【 First solution (power of a point). Let $\gamma$ denote the nine-point circle of $A B C$.  Note that - $P A^{2}=P M \cdot P N$, so $P$ lies on the radical axis of $\Gamma$ and $\gamma$. - $R A \cdot R Q=R E \cdot R F$, so $R$ lies on the radical axis of $\Gamma$ and $\gamma$. Thus $\overline{P R}$ is the radical axis of $\Gamma$ and $\gamma$, which is evidently perpendicular to $\overline{O H}$. Remark. In fact, by power of a point one may also observe that $R$ lies on $\overline{B C}$, since it is on the radical axis of $(A Q F H E),(B F E C),(A B C)$. Ironically, this fact is not used in the solution.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
e9a890b5-81cc-5035-935b-000ba262e103
| 247,255 |
Let $A B C$ be a triangle with circumcircle $\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \neq A C$ and $\angle A \neq 90^{\circ}$. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\Gamma$ with the circumcircle of $\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\overline{P R} \perp \overline{O H}$.
|
II Second solution (barycentric coordinates). Again note first $R \in \overline{B C}$ (although this can be avoided too). We compute the points in much the same way as before. Since $\overline{A P} \cap \overline{B C}=\left(0: b^{2}:-c^{2}\right)$ we have $$ P=\left(b^{2}-c^{2}: b^{2}:-c^{2}\right) $$ (since $x=y+z$ is the equation of line $\overline{M N}$ ). Now in Conway notation we have $$ R=\overline{E F} \cap \overline{B C}=\left(0: S_{C}:-S_{B}\right)=\left(0: a^{2}+b^{2}-c^{2}:-a^{2}+b^{2}-c^{2}\right) . $$ Hence $$ \overrightarrow{P R}=\frac{1}{2\left(b^{2}-c^{2}\right)}\left(b^{2}-c^{2}, c^{2}-a^{2}, a^{2}-b^{2}\right) $$ On the other hand, we have $\overrightarrow{O H}=\vec{A}+\vec{B}+\vec{C}$. So it suffices to check that $$ \sum_{\mathrm{cyc}} a^{2}\left(\left(a^{2}-b^{2}\right)+\left(c^{2}-a^{2}\right)\right)=0 $$ which is immediate.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \neq A C$ and $\angle A \neq 90^{\circ}$. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\Gamma$ with the circumcircle of $\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\overline{P R} \perp \overline{O H}$.
|
II Second solution (barycentric coordinates). Again note first $R \in \overline{B C}$ (although this can be avoided too). We compute the points in much the same way as before. Since $\overline{A P} \cap \overline{B C}=\left(0: b^{2}:-c^{2}\right)$ we have $$ P=\left(b^{2}-c^{2}: b^{2}:-c^{2}\right) $$ (since $x=y+z$ is the equation of line $\overline{M N}$ ). Now in Conway notation we have $$ R=\overline{E F} \cap \overline{B C}=\left(0: S_{C}:-S_{B}\right)=\left(0: a^{2}+b^{2}-c^{2}:-a^{2}+b^{2}-c^{2}\right) . $$ Hence $$ \overrightarrow{P R}=\frac{1}{2\left(b^{2}-c^{2}\right)}\left(b^{2}-c^{2}, c^{2}-a^{2}, a^{2}-b^{2}\right) $$ On the other hand, we have $\overrightarrow{O H}=\vec{A}+\vec{B}+\vec{C}$. So it suffices to check that $$ \sum_{\mathrm{cyc}} a^{2}\left(\left(a^{2}-b^{2}\right)+\left(c^{2}-a^{2}\right)\right)=0 $$ which is immediate.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
e9a890b5-81cc-5035-935b-000ba262e103
| 247,255 |
Let $A B C$ be a triangle with circumcircle $\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \neq A C$ and $\angle A \neq 90^{\circ}$. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\Gamma$ with the circumcircle of $\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\overline{P R} \perp \overline{O H}$.
|
『 Third solution (complex numbers). Let $A B C$ be the unit circle. We first compute $P$ as the midpoint of $A$ and $\overline{A A} \cap \overline{B C}$ : $$ \begin{aligned} p & =\frac{1}{2}\left(a+\frac{a^{2}(b+c)-b c \cdot 2 a}{a^{2}-b c}\right) \\ & =\frac{a\left(a^{2}-b c\right)+a^{2}(b+c)-2 a b c}{2\left(a^{2}-b c\right)} \end{aligned} $$ Using the remark above, $R$ is the inverse of $D$ with respect to the circle with diameter $\overline{B C}$, which has radius $\left|\frac{1}{2}(b-c)\right|$. Thus $$ \begin{aligned} r-\frac{b+c}{2} & =\frac{\frac{1}{4}(b-c)\left(\frac{1}{b}-\frac{1}{c}\right)}{\frac{1}{2}\left(a-\frac{b c}{a}\right)} \\ r & =\frac{b+c}{2}+\frac{-\frac{1}{2} \frac{(b-c)^{2}}{b c}}{\frac{1}{a}-\frac{a}{b c}} \\ & =\frac{b+c}{2}+\frac{a(b-c)^{2}}{2\left(a^{2}-b c\right)} \\ & =\frac{a(b-c)^{2}+(b+c)\left(a^{2}-b c\right)}{2\left(a^{2}-b c\right)} \end{aligned} $$ Expanding and subtracting gives $$ p-r=\frac{a^{3}-a b c-a b^{2}-a c^{2}+b^{2} c+b c^{2}}{2\left(a^{2}-b c\right)}=\frac{(a+b+c)(a-b)(a-c)}{2\left(a^{2}-b c\right)} $$ which is visibly equal to the negation of its conjugate once the factor of $a+b+c$ is deleted. (Actually, one can guess this factorization ahead of time by noting that if $A=B$, then $P=B=R$, so $a-b$ must be a factor; analogously $a-c$ must be as well.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Gamma$, circumcenter $O$, and orthocenter $H$. Assume that $A B \neq A C$ and $\angle A \neq 90^{\circ}$. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$ in $\triangle A B C$, respectively. Let $P$ be the intersection point of line $M N$ with the tangent line to $\Gamma$ at $A$. Let $Q$ be the intersection point, other than $A$, of $\Gamma$ with the circumcircle of $\triangle A E F$. Let $R$ be the intersection point of lines $A Q$ and $E F$. Prove that $\overline{P R} \perp \overline{O H}$.
|
『 Third solution (complex numbers). Let $A B C$ be the unit circle. We first compute $P$ as the midpoint of $A$ and $\overline{A A} \cap \overline{B C}$ : $$ \begin{aligned} p & =\frac{1}{2}\left(a+\frac{a^{2}(b+c)-b c \cdot 2 a}{a^{2}-b c}\right) \\ & =\frac{a\left(a^{2}-b c\right)+a^{2}(b+c)-2 a b c}{2\left(a^{2}-b c\right)} \end{aligned} $$ Using the remark above, $R$ is the inverse of $D$ with respect to the circle with diameter $\overline{B C}$, which has radius $\left|\frac{1}{2}(b-c)\right|$. Thus $$ \begin{aligned} r-\frac{b+c}{2} & =\frac{\frac{1}{4}(b-c)\left(\frac{1}{b}-\frac{1}{c}\right)}{\frac{1}{2}\left(a-\frac{b c}{a}\right)} \\ r & =\frac{b+c}{2}+\frac{-\frac{1}{2} \frac{(b-c)^{2}}{b c}}{\frac{1}{a}-\frac{a}{b c}} \\ & =\frac{b+c}{2}+\frac{a(b-c)^{2}}{2\left(a^{2}-b c\right)} \\ & =\frac{a(b-c)^{2}+(b+c)\left(a^{2}-b c\right)}{2\left(a^{2}-b c\right)} \end{aligned} $$ Expanding and subtracting gives $$ p-r=\frac{a^{3}-a b c-a b^{2}-a c^{2}+b^{2} c+b c^{2}}{2\left(a^{2}-b c\right)}=\frac{(a+b+c)(a-b)(a-c)}{2\left(a^{2}-b c\right)} $$ which is visibly equal to the negation of its conjugate once the factor of $a+b+c$ is deleted. (Actually, one can guess this factorization ahead of time by noting that if $A=B$, then $P=B=R$, so $a-b$ must be a factor; analogously $a-c$ must be as well.)
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
e9a890b5-81cc-5035-935b-000ba262e103
| 247,255 |
Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\omega_{B}$ and $\omega_{C}$ be the incircles of $\triangle A B D$ and $\triangle A C D$, respectively. Suppose that $\omega_{B}$ and $\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\omega_{B}$ and $\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\triangle A B C$.
|
『 First solution (homothety). Let $Z$ be the diametrically opposite point on the incircle. We claim this is the desired intersection. 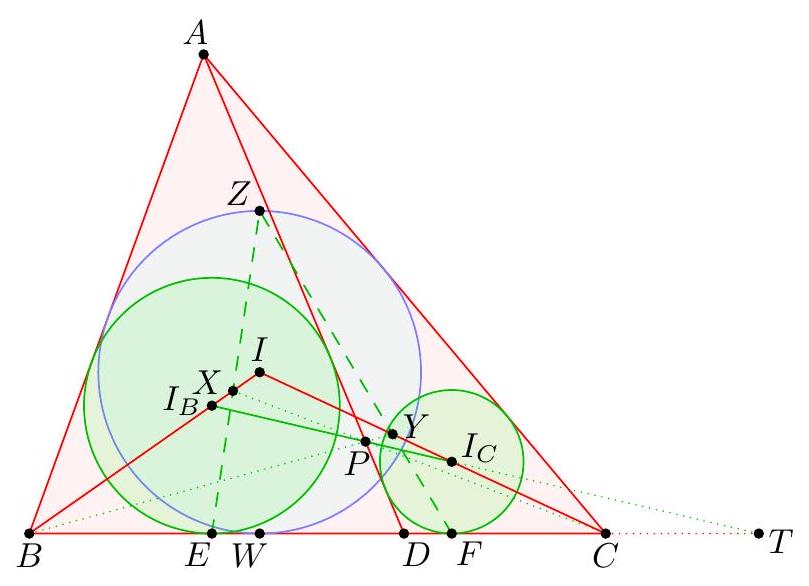 Note that: - $P$ is the insimilicenter of $\omega_{B}$ and $\omega_{C}$ - $C$ is the exsimilicenter of $\omega$ and $\omega_{C}$. Thus by Monge theorem, the insimilicenter of $\omega_{B}$ and $\omega$ lies on line $C P$. This insimilicenter should also lie on the line joining the centers of $\omega$ and $\omega_{B}$, which is $\overline{B I}$, hence it coincides with the point $X$. So $X \in \overline{E Z}$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\omega_{B}$ and $\omega_{C}$ be the incircles of $\triangle A B D$ and $\triangle A C D$, respectively. Suppose that $\omega_{B}$ and $\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\omega_{B}$ and $\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\triangle A B C$.
|
『 First solution (homothety). Let $Z$ be the diametrically opposite point on the incircle. We claim this is the desired intersection.  Note that: - $P$ is the insimilicenter of $\omega_{B}$ and $\omega_{C}$ - $C$ is the exsimilicenter of $\omega$ and $\omega_{C}$. Thus by Monge theorem, the insimilicenter of $\omega_{B}$ and $\omega$ lies on line $C P$. This insimilicenter should also lie on the line joining the centers of $\omega$ and $\omega_{B}$, which is $\overline{B I}$, hence it coincides with the point $X$. So $X \in \overline{E Z}$ as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
3e29c513-e144-57f7-9d9b-cf87806186c9
| 247,284 |
Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\omega_{B}$ and $\omega_{C}$ be the incircles of $\triangle A B D$ and $\triangle A C D$, respectively. Suppose that $\omega_{B}$ and $\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\omega_{B}$ and $\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\triangle A B C$.
|
【 Second solution (harmonic). Let $T=\overline{I_{B} I_{C}} \cap \overline{B C}$, and $W$ the foot from $I$ to $\overline{B C}$. Define $Z=\overline{F Y} \cap \overline{I W}$. Because $\angle I_{B} D I_{C}=90^{\circ}$, we have $$ -1=\left(I_{B} I_{C} ; P T\right) \stackrel{B}{\stackrel{B}{2}}\left(I I_{C} ; Y C\right) \stackrel{F}{=}(I \infty ; Z W) $$ So $I$ is the midpoint of $\overline{Z W}$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\omega_{B}$ and $\omega_{C}$ be the incircles of $\triangle A B D$ and $\triangle A C D$, respectively. Suppose that $\omega_{B}$ and $\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\omega_{B}$ and $\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\triangle A B C$.
|
【 Second solution (harmonic). Let $T=\overline{I_{B} I_{C}} \cap \overline{B C}$, and $W$ the foot from $I$ to $\overline{B C}$. Define $Z=\overline{F Y} \cap \overline{I W}$. Because $\angle I_{B} D I_{C}=90^{\circ}$, we have $$ -1=\left(I_{B} I_{C} ; P T\right) \stackrel{B}{\stackrel{B}{2}}\left(I I_{C} ; Y C\right) \stackrel{F}{=}(I \infty ; Z W) $$ So $I$ is the midpoint of $\overline{Z W}$ as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
3e29c513-e144-57f7-9d9b-cf87806186c9
| 247,284 |
Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\omega_{B}$ and $\omega_{C}$ be the incircles of $\triangle A B D$ and $\triangle A C D$, respectively. Suppose that $\omega_{B}$ and $\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\omega_{B}$ and $\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\triangle A B C$.
|
【 Third solution (outline, barycentric, Andrew Gu). Let $A D=t, B D=x, C D=y$, so $a=x+y$ and by Stewart's theorem we have $$ (x+y)\left(x y+t^{2}\right)=b^{2} x+c^{2} y $$ We then have $D=(0: y: x)$ and so $$ \overline{A I_{B}} \cap \overline{B C}=\left(0: y+\frac{t x}{c+t}: \frac{c x}{c+t}\right) $$ hence intersection with $B I$ gives $$ I_{B}=(a x: c y+a t: c x) $$ Similarly, $$ I_{C}=(a y: b y: b x+a t) $$ Then, we can compute $$ P=(2 a x y: y(a t+b x+c y): x(a t+b x+c y)) $$ since $P \in \overline{I_{B} I_{C}}$, and clearly $P \in \overline{A D}$. Intersection now gives $$ \begin{aligned} & X=(2 a x: a t+b x+c y: 2 c x) \\ & Y=(2 a y: 2 b y: a t+b x+c y) \end{aligned} $$ Finally, we have $B E=\frac{1}{2}(c+x-t)$, and similarly for $C F$. Now if we reflect $D=$ $\left(0, \frac{s-c}{a}, \frac{s-b}{a}\right)$ over $I=\left(\frac{a}{2 s}, \frac{b}{2 s}, \frac{c}{2 s}\right)$, we get the antipode $$ Q:=\left(4 a^{2}:-a^{2}+2 a b-b^{2}+c^{2}:-a^{2}+2 a c-c^{2}+b^{2}\right) . $$ We may then check $Q$ lies on each of lines $E X$ and $F Y$ (by checking $\operatorname{det}(Q, E, X)=0$ using the equation (1)).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$. Let $D$ be a point on side $B C$ and let $\omega_{B}$ and $\omega_{C}$ be the incircles of $\triangle A B D$ and $\triangle A C D$, respectively. Suppose that $\omega_{B}$ and $\omega_{C}$ are tangent to segment $B C$ at points $E$ and $F$, respectively. Let $P$ be the intersection of segment $A D$ with the line joining the centers of $\omega_{B}$ and $\omega_{C}$. Let $X$ be the intersection point of lines $B I$ and $C P$ and let $Y$ be the intersection point of lines $C I$ and $B P$. Prove that lines $E X$ and $F Y$ meet on the incircle of $\triangle A B C$.
|
【 Third solution (outline, barycentric, Andrew Gu). Let $A D=t, B D=x, C D=y$, so $a=x+y$ and by Stewart's theorem we have $$ (x+y)\left(x y+t^{2}\right)=b^{2} x+c^{2} y $$ We then have $D=(0: y: x)$ and so $$ \overline{A I_{B}} \cap \overline{B C}=\left(0: y+\frac{t x}{c+t}: \frac{c x}{c+t}\right) $$ hence intersection with $B I$ gives $$ I_{B}=(a x: c y+a t: c x) $$ Similarly, $$ I_{C}=(a y: b y: b x+a t) $$ Then, we can compute $$ P=(2 a x y: y(a t+b x+c y): x(a t+b x+c y)) $$ since $P \in \overline{I_{B} I_{C}}$, and clearly $P \in \overline{A D}$. Intersection now gives $$ \begin{aligned} & X=(2 a x: a t+b x+c y: 2 c x) \\ & Y=(2 a y: 2 b y: a t+b x+c y) \end{aligned} $$ Finally, we have $B E=\frac{1}{2}(c+x-t)$, and similarly for $C F$. Now if we reflect $D=$ $\left(0, \frac{s-c}{a}, \frac{s-b}{a}\right)$ over $I=\left(\frac{a}{2 s}, \frac{b}{2 s}, \frac{c}{2 s}\right)$, we get the antipode $$ Q:=\left(4 a^{2}:-a^{2}+2 a b-b^{2}+c^{2}:-a^{2}+2 a c-c^{2}+b^{2}\right) . $$ We may then check $Q$ lies on each of lines $E X$ and $F Y$ (by checking $\operatorname{det}(Q, E, X)=0$ using the equation (1)).
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
3e29c513-e144-57f7-9d9b-cf87806186c9
| 247,284 |
A sequence of positive integers $\left(a_{n}\right)_{n \geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?
|
【 First solution (Kevin Sun). We are going to appeal to the so-called Zeckendorf theorem: Theorem (Zeckendorf) Every positive integer can be uniquely expressed as the sum of nonconsecutive Fibonacci numbers. This means every positive integer has a Zeckendorf ("Fibonacci-binary") representation where we put 1 in the $i$ th digit from the right if $F_{i+1}$ is used. The idea is then to take the following so-called Wythoff array: - Row 1: 1, 2, 3, 5, ... - Row 101: $1+3,2+5,3+8, \ldots$ - Row 1001: $1+5,2+8,3+13, \ldots$ - Row 10001: $1+8,2+13,3+21, \ldots$ - Row 10101: $1+3+8,2+5+13,3+8+21, \ldots$ - . . .et cetera. More concretely, the array has the following rows to start: | 1 | 2 | 3 | 5 | 8 | 13 | 21 | $\ldots$ | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 4 | 7 | 11 | 18 | 29 | 47 | 76 | $\ldots$ | | 6 | 10 | 16 | 26 | 42 | 68 | 110 | $\ldots$ | | 9 | 15 | 24 | 39 | 63 | 102 | 165 | $\ldots$ | | 12 | 20 | 32 | 52 | 84 | 136 | 220 | $\ldots$ | | 14 | 23 | 37 | 60 | 97 | 157 | 254 | $\ldots$ | | 17 | 28 | 45 | 73 | 118 | 191 | 309 | $\ldots$ | | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | Here are the full details. $$ n-F_{k}<F_{k+1}-F_{k}=F_{k-1} . $$ In particular, repeatedly subtracting off the largest $F_{k}$ from $n$ will produce one such representation with no two consecutive Fibonacci numbers. On the other hand, this $F_{k}$ must be used, as $$ n \geq F_{k}>F_{k-1}+F_{k-3}+F_{k-5}+\cdots $$ This shows, by a simple inductive argument, that such a representation exists and unique. We write $n={\bar{a} k \ldots a_{1}}_{\text {Fib }}$ for the Zeckendorf representation as we described (where $a_{i}=1$ if $F_{i+1}$ is used). Now for each ${\bar{a} k \ldots a_{1}}^{\text {Fib }}$ with $a_{1}=1$, consider the sequence $$ {\overline{a_{k} \ldots a_{1}}}_{\mathrm{Fib}},{\overline{a_{k} \ldots a_{1} 0}}_{\mathrm{Fib}},{\overline{a_{k} \ldots a_{1} 00}}_{\mathrm{Fib}}, \ldots $$ These sequences are Fibonacci-type by definition, and partition the positive integers since each positive integer has exactly one Fibonacci base representation.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A sequence of positive integers $\left(a_{n}\right)_{n \geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?
|
【 First solution (Kevin Sun). We are going to appeal to the so-called Zeckendorf theorem: Theorem (Zeckendorf) Every positive integer can be uniquely expressed as the sum of nonconsecutive Fibonacci numbers. This means every positive integer has a Zeckendorf ("Fibonacci-binary") representation where we put 1 in the $i$ th digit from the right if $F_{i+1}$ is used. The idea is then to take the following so-called Wythoff array: - Row 1: 1, 2, 3, 5, ... - Row 101: $1+3,2+5,3+8, \ldots$ - Row 1001: $1+5,2+8,3+13, \ldots$ - Row 10001: $1+8,2+13,3+21, \ldots$ - Row 10101: $1+3+8,2+5+13,3+8+21, \ldots$ - . . .et cetera. More concretely, the array has the following rows to start: | 1 | 2 | 3 | 5 | 8 | 13 | 21 | $\ldots$ | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 4 | 7 | 11 | 18 | 29 | 47 | 76 | $\ldots$ | | 6 | 10 | 16 | 26 | 42 | 68 | 110 | $\ldots$ | | 9 | 15 | 24 | 39 | 63 | 102 | 165 | $\ldots$ | | 12 | 20 | 32 | 52 | 84 | 136 | 220 | $\ldots$ | | 14 | 23 | 37 | 60 | 97 | 157 | 254 | $\ldots$ | | 17 | 28 | 45 | 73 | 118 | 191 | 309 | $\ldots$ | | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | Here are the full details. $$ n-F_{k}<F_{k+1}-F_{k}=F_{k-1} . $$ In particular, repeatedly subtracting off the largest $F_{k}$ from $n$ will produce one such representation with no two consecutive Fibonacci numbers. On the other hand, this $F_{k}$ must be used, as $$ n \geq F_{k}>F_{k-1}+F_{k-3}+F_{k-5}+\cdots $$ This shows, by a simple inductive argument, that such a representation exists and unique. We write $n={\bar{a} k \ldots a_{1}}_{\text {Fib }}$ for the Zeckendorf representation as we described (where $a_{i}=1$ if $F_{i+1}$ is used). Now for each ${\bar{a} k \ldots a_{1}}^{\text {Fib }}$ with $a_{1}=1$, consider the sequence $$ {\overline{a_{k} \ldots a_{1}}}_{\mathrm{Fib}},{\overline{a_{k} \ldots a_{1} 0}}_{\mathrm{Fib}},{\overline{a_{k} \ldots a_{1} 00}}_{\mathrm{Fib}}, \ldots $$ These sequences are Fibonacci-type by definition, and partition the positive integers since each positive integer has exactly one Fibonacci base representation.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
ee458e82-3de2-51dc-8146-6ab65bc6e112
| 247,296 |
A sequence of positive integers $\left(a_{n}\right)_{n \geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?
|
\I Second solution. Call an infinite set of integers $S$ sandwiched if there exist increasing sequences $\left\{a_{i}\right\}_{i=0}^{\infty},\left\{b_{i}\right\}_{i=0}^{\infty}$ such that the following are true: - $a_{i}+a_{i+1}=a_{i+2}$ and $b_{i}+b_{i+1}=b_{i+2}$. - The intervals $\left[a_{i}+1, b_{i}-1\right]$ are disjoint and are nondecreasing in length. - $S=\bigcup_{i=0}^{\infty}\left[a_{i}+1, b_{i}-1\right]$. We claim that if $S$ is any nonempty sandwiched set, then $S$ can be partitioned into a Fibonacci-type sequence (involving the smallest element of $S$ ) and two smaller sandwiched sets. If this claim is proven, then we can start with $\mathbb{N} \backslash\{1,2,3,5, \ldots\}$, which is a sandwiched set, and repeatedly perform this partition, which will eventually sort each natural number into a Fibonacci-type sequence. Let $S$ be a sandwiched set given by $\left\{a_{i}\right\}_{i=0}^{\infty},\left\{b_{i}\right\}_{i=0}^{\infty}$, so the smallest element in $S$ is $x=a_{0}+1$. Note that $y=a_{1}+1$ is also in $S$ and $x<y$. Then consider the Fibonaccitype sequence given by $f_{0}=x, f_{1}=y$, and $f_{k+2}=f_{k+1}+f_{k}$. We can then see that $f_{i} \in\left[a_{i}+1, b_{i}-1\right]$, as the sum of numbers in the intervals $\left[a_{k}+1, b_{k}-1\right],\left[a_{k+1}+1, b_{k+1}-1\right]$ lies in the interval $$ \left[a_{k}+a_{k+1}+2, b_{k}+b_{k+1}-2\right]=\left[a_{k+2}+2, b_{k+2}-2\right] \subset\left[a_{k+2}+1, b_{k+2}-1\right] $$ Therefore, this gives a natural partition of $S$ into this sequence and two sets: $$ \begin{aligned} S_{1} & =\bigcup_{i=0}^{\infty}\left[a_{i}+1, f_{i}-1\right] \\ \text { and } S_{2} & =\bigcup_{i=0}^{\infty}\left[f_{i}+1, b_{i}-1\right] . \end{aligned} $$ (For convenience, $[x, x-1]$ will be treated as the empty set.) We now show that $S_{1}$ and $S_{2}$ are sandwiched. Since $\left\{a_{i}\right\},\left\{f_{i}\right\}$, and $\left\{b_{i}\right\}$ satisfy the Fibonacci recurrence, it is enough to check that the intervals have nondecreasing lengths. For $S_{1}$, that is equivalent to $f_{k+1}-a_{k+1} \geq f_{k}-a_{k}$ for each $k$. Fortunately, for $k \geq 1$, the difference is $f_{k-1}-a_{k-1} \geq 0$, and for $k=0, f_{1}-a_{1}=1=f_{0}-a_{0}$. Similarly for $S_{2}$, checking $b_{k+1}-f_{k+1} \geq b_{k}-f_{k}$ is easy for $k \geq 1$ as $b_{k-1}-f_{k-1} \geq 0$, and $$ \left(b_{1}-f_{1}\right)-\left(b_{0}-f_{0}\right)=\left(b_{1}-a_{1}\right)-\left(b_{0}-a_{0}\right) $$ which is nonnegative since the lengths of intervals in $S$ are nondecreasing. Therefore we have shown that $S_{1}$ and $S_{2}$ are sandwiched. (Note that some of the $\left[a_{i}+1, f_{i}-1\right]$ may be empty, which would shift some indices back.) Since this gives us a procedure to take a set $S$ and produce a Fibonacci-type sequence with its smallest element, along which two other sandwiched types, we can partition $\mathbb{N}$ into an infinite number of Fibonacci-type sequences.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A sequence of positive integers $\left(a_{n}\right)_{n \geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?
|
\I Second solution. Call an infinite set of integers $S$ sandwiched if there exist increasing sequences $\left\{a_{i}\right\}_{i=0}^{\infty},\left\{b_{i}\right\}_{i=0}^{\infty}$ such that the following are true: - $a_{i}+a_{i+1}=a_{i+2}$ and $b_{i}+b_{i+1}=b_{i+2}$. - The intervals $\left[a_{i}+1, b_{i}-1\right]$ are disjoint and are nondecreasing in length. - $S=\bigcup_{i=0}^{\infty}\left[a_{i}+1, b_{i}-1\right]$. We claim that if $S$ is any nonempty sandwiched set, then $S$ can be partitioned into a Fibonacci-type sequence (involving the smallest element of $S$ ) and two smaller sandwiched sets. If this claim is proven, then we can start with $\mathbb{N} \backslash\{1,2,3,5, \ldots\}$, which is a sandwiched set, and repeatedly perform this partition, which will eventually sort each natural number into a Fibonacci-type sequence. Let $S$ be a sandwiched set given by $\left\{a_{i}\right\}_{i=0}^{\infty},\left\{b_{i}\right\}_{i=0}^{\infty}$, so the smallest element in $S$ is $x=a_{0}+1$. Note that $y=a_{1}+1$ is also in $S$ and $x<y$. Then consider the Fibonaccitype sequence given by $f_{0}=x, f_{1}=y$, and $f_{k+2}=f_{k+1}+f_{k}$. We can then see that $f_{i} \in\left[a_{i}+1, b_{i}-1\right]$, as the sum of numbers in the intervals $\left[a_{k}+1, b_{k}-1\right],\left[a_{k+1}+1, b_{k+1}-1\right]$ lies in the interval $$ \left[a_{k}+a_{k+1}+2, b_{k}+b_{k+1}-2\right]=\left[a_{k+2}+2, b_{k+2}-2\right] \subset\left[a_{k+2}+1, b_{k+2}-1\right] $$ Therefore, this gives a natural partition of $S$ into this sequence and two sets: $$ \begin{aligned} S_{1} & =\bigcup_{i=0}^{\infty}\left[a_{i}+1, f_{i}-1\right] \\ \text { and } S_{2} & =\bigcup_{i=0}^{\infty}\left[f_{i}+1, b_{i}-1\right] . \end{aligned} $$ (For convenience, $[x, x-1]$ will be treated as the empty set.) We now show that $S_{1}$ and $S_{2}$ are sandwiched. Since $\left\{a_{i}\right\},\left\{f_{i}\right\}$, and $\left\{b_{i}\right\}$ satisfy the Fibonacci recurrence, it is enough to check that the intervals have nondecreasing lengths. For $S_{1}$, that is equivalent to $f_{k+1}-a_{k+1} \geq f_{k}-a_{k}$ for each $k$. Fortunately, for $k \geq 1$, the difference is $f_{k-1}-a_{k-1} \geq 0$, and for $k=0, f_{1}-a_{1}=1=f_{0}-a_{0}$. Similarly for $S_{2}$, checking $b_{k+1}-f_{k+1} \geq b_{k}-f_{k}$ is easy for $k \geq 1$ as $b_{k-1}-f_{k-1} \geq 0$, and $$ \left(b_{1}-f_{1}\right)-\left(b_{0}-f_{0}\right)=\left(b_{1}-a_{1}\right)-\left(b_{0}-a_{0}\right) $$ which is nonnegative since the lengths of intervals in $S$ are nondecreasing. Therefore we have shown that $S_{1}$ and $S_{2}$ are sandwiched. (Note that some of the $\left[a_{i}+1, f_{i}-1\right]$ may be empty, which would shift some indices back.) Since this gives us a procedure to take a set $S$ and produce a Fibonacci-type sequence with its smallest element, along which two other sandwiched types, we can partition $\mathbb{N}$ into an infinite number of Fibonacci-type sequences.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
ee458e82-3de2-51dc-8146-6ab65bc6e112
| 247,296 |
A sequence of positive integers $\left(a_{n}\right)_{n \geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?
|
\l Third solution. We add Fibonacci-type sequences one-by-one. At each step, let $x$ be the smallest number that has not been used in any previous sequence. We generate a new Fibonacci-type sequence as follows. Set $a_{0}=x$ and for $i \geq 1$, set $$ a_{i}=\left\lfloor\varphi a_{i-1}+\frac{1}{2}\right\rfloor $$ Equivalently, $a_{i}$ is the closest integer to $\varphi a_{i-1}$. It suffices to show that this sequence is Fibonacci-type and that no two sequences generated in this way overlap. We first show that for a positive integer $n$, $$ \left\lfloor\varphi\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor=n+\left\lfloor\varphi n+\frac{1}{2}\right\rfloor . $$ Indeed, $$ \begin{aligned} \left\lfloor\varphi\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor & =\left\lfloor\left(1+\varphi^{-1}\right)\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor \\ & =\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\left\lfloor\varphi^{-1}\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor . \end{aligned} $$ Note that $\left\lfloor\varphi n+\frac{1}{2}\right\rfloor=\varphi n+c$ for some $|c| \leq \frac{1}{2}$; this implies that $\varphi^{-1}\left\lfloor\varphi n+\frac{1}{2}\right\rfloor$ is within $\varphi^{-1} \cdot \frac{1}{2}<\frac{1}{2}$ of $n$, so its closest integer is $n$, proving the claim. Therefore these sequences are Fibonacci-type. Additionally, if $a \neq b$, then $|\varphi a-\varphi b| \geq$ $\varphi>1$. Then $$ a \neq b \Longrightarrow\left\lfloor\varphi a+\frac{1}{2}\right\rfloor \neq\left\lfloor\varphi b+\frac{1}{2}\right\rfloor, $$ and since the first term of each sequence is chosen to not overlap with any previous sequences, these sequences are disjoint. Remark. Ankan Bhattacharya points out that the same sequence essentially appears in IMO 1993, Problem 5 - in other words, a strictly increasing function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ with $f(1)=2$, and $f(f(n))=f(n)+n$. Nikolai Beluhov sent us an older reference from March 1977, where Martin Gardner wrote in his column about Wythoff's Nim. The relevant excerpt goes: "Imagine that we go through the infinite sequence of safe pairs (in the manner of Eratosthenes' sieve for sifting out primes) and cross out the infinite set of all safe pairs that are pairs in the Fibonacci sequence. The smallest pair that is not crossed out is $4 / 7$. We can now cross out a second infinite set of safe pairs, starting with $4 / 7$, that are pairs in the Lucas sequence. An infinite number of safe pairs, of which the lowest is now $6 / 10$, remain. This pair too begins another infinite Fibonacci sequence, all of whose pairs are safe. The process continues forever. Robert Silber, a mathematician at North Carolina State University, calls a safe pair "primitive" if it is the first safe pair that generates a Fibonacci sequence." The relevant article by Robert Silber is A Fibonacci Property of Wythoff Pairs, from The Fibonacci Quarterly 11/1976.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A sequence of positive integers $\left(a_{n}\right)_{n \geq 1}$ is of Fibonacci type if it satisfies the recursive relation $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 1$. Is it possible to partition the set of positive integers into an infinite number of Fibonacci type sequences?
|
\l Third solution. We add Fibonacci-type sequences one-by-one. At each step, let $x$ be the smallest number that has not been used in any previous sequence. We generate a new Fibonacci-type sequence as follows. Set $a_{0}=x$ and for $i \geq 1$, set $$ a_{i}=\left\lfloor\varphi a_{i-1}+\frac{1}{2}\right\rfloor $$ Equivalently, $a_{i}$ is the closest integer to $\varphi a_{i-1}$. It suffices to show that this sequence is Fibonacci-type and that no two sequences generated in this way overlap. We first show that for a positive integer $n$, $$ \left\lfloor\varphi\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor=n+\left\lfloor\varphi n+\frac{1}{2}\right\rfloor . $$ Indeed, $$ \begin{aligned} \left\lfloor\varphi\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor & =\left\lfloor\left(1+\varphi^{-1}\right)\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor \\ & =\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\left\lfloor\varphi^{-1}\left\lfloor\varphi n+\frac{1}{2}\right\rfloor+\frac{1}{2}\right\rfloor . \end{aligned} $$ Note that $\left\lfloor\varphi n+\frac{1}{2}\right\rfloor=\varphi n+c$ for some $|c| \leq \frac{1}{2}$; this implies that $\varphi^{-1}\left\lfloor\varphi n+\frac{1}{2}\right\rfloor$ is within $\varphi^{-1} \cdot \frac{1}{2}<\frac{1}{2}$ of $n$, so its closest integer is $n$, proving the claim. Therefore these sequences are Fibonacci-type. Additionally, if $a \neq b$, then $|\varphi a-\varphi b| \geq$ $\varphi>1$. Then $$ a \neq b \Longrightarrow\left\lfloor\varphi a+\frac{1}{2}\right\rfloor \neq\left\lfloor\varphi b+\frac{1}{2}\right\rfloor, $$ and since the first term of each sequence is chosen to not overlap with any previous sequences, these sequences are disjoint. Remark. Ankan Bhattacharya points out that the same sequence essentially appears in IMO 1993, Problem 5 - in other words, a strictly increasing function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ with $f(1)=2$, and $f(f(n))=f(n)+n$. Nikolai Beluhov sent us an older reference from March 1977, where Martin Gardner wrote in his column about Wythoff's Nim. The relevant excerpt goes: "Imagine that we go through the infinite sequence of safe pairs (in the manner of Eratosthenes' sieve for sifting out primes) and cross out the infinite set of all safe pairs that are pairs in the Fibonacci sequence. The smallest pair that is not crossed out is $4 / 7$. We can now cross out a second infinite set of safe pairs, starting with $4 / 7$, that are pairs in the Lucas sequence. An infinite number of safe pairs, of which the lowest is now $6 / 10$, remain. This pair too begins another infinite Fibonacci sequence, all of whose pairs are safe. The process continues forever. Robert Silber, a mathematician at North Carolina State University, calls a safe pair "primitive" if it is the first safe pair that generates a Fibonacci sequence." The relevant article by Robert Silber is A Fibonacci Property of Wythoff Pairs, from The Fibonacci Quarterly 11/1976.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
ee458e82-3de2-51dc-8146-6ab65bc6e112
| 247,296 |
In the nation of Onewaynia, certain pairs of cities are connected by one-way roads. Every road connects exactly two cities (roads are allowed to cross each other, e.g., via bridges), and each pair of cities has at most one road between them. Moreover, every city has exactly two roads leaving it and exactly two roads entering it. We wish to close half the roads of Onewaynia in such a way that every city has exactly one road leaving it and exactly one road entering it. Show that the number of ways to do so is a power of 2 greater than 1 (i.e. of the form $2^{n}$ for some integer $n \geq 1$ ).
|
In the language of graph theory, we have a simple digraph $G$ which is 2 -regular and we seek the number of sub-digraphs which are 1-regular. We now present two solution paths. 【 Second solution by linear algebra over $\mathbb{F}_{2}$ (Brian Lawrence). This is actually not that different from the first solution. For each edge $e$, we create an indicator variable $x_{e}$. We then require for each vertex $v$ that: - If $e_{1}$ and $e_{2}$ are the two edges leaving $v$, then we require $x_{e_{1}}+x_{e_{2}} \equiv 1(\bmod 2)$. - If $e_{3}$ and $e_{4}$ are the two edges entering $v$, then we require $x_{e_{3}}+x_{e_{4}} \equiv 1(\bmod 2)$. We thus get a large system of equations. Moreover, the solutions come in natural pairs $\vec{x}$ and $\vec{x}+\overrightarrow{1}$ and therefore the number of solutions is either zero, or a power of two. So we just have to prove there is at least one solution. For linear algebra reasons, there can only be zero solutions if some nontrivial linear combination of the equations gives the sum $0 \equiv 1$. So suppose we added up some subset $S$ of the equations for which every variable appeared on the left-hand side an even number of times. Then every variable that did appear appeared exactly twice; and accordingly we see that the edges corresponding to these variables form one or more even cycles as in the previous solution. Of course, this means $|S|$ is even, so we really have $0 \equiv 0(\bmod 2)$ as needed. Remark. The author's original proposal contained a second part asking to show that it was not always possible for the resulting $H$ to be connected, even if $G$ was strongly connected. This problem is related to IMO Shortlist 2002 C6, which gives an example of a strongly connected graph which does have a full directed Hamiltonian cycle.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In the nation of Onewaynia, certain pairs of cities are connected by one-way roads. Every road connects exactly two cities (roads are allowed to cross each other, e.g., via bridges), and each pair of cities has at most one road between them. Moreover, every city has exactly two roads leaving it and exactly two roads entering it. We wish to close half the roads of Onewaynia in such a way that every city has exactly one road leaving it and exactly one road entering it. Show that the number of ways to do so is a power of 2 greater than 1 (i.e. of the form $2^{n}$ for some integer $n \geq 1$ ).
|
In the language of graph theory, we have a simple digraph $G$ which is 2 -regular and we seek the number of sub-digraphs which are 1-regular. We now present two solution paths. 【 Second solution by linear algebra over $\mathbb{F}_{2}$ (Brian Lawrence). This is actually not that different from the first solution. For each edge $e$, we create an indicator variable $x_{e}$. We then require for each vertex $v$ that: - If $e_{1}$ and $e_{2}$ are the two edges leaving $v$, then we require $x_{e_{1}}+x_{e_{2}} \equiv 1(\bmod 2)$. - If $e_{3}$ and $e_{4}$ are the two edges entering $v$, then we require $x_{e_{3}}+x_{e_{4}} \equiv 1(\bmod 2)$. We thus get a large system of equations. Moreover, the solutions come in natural pairs $\vec{x}$ and $\vec{x}+\overrightarrow{1}$ and therefore the number of solutions is either zero, or a power of two. So we just have to prove there is at least one solution. For linear algebra reasons, there can only be zero solutions if some nontrivial linear combination of the equations gives the sum $0 \equiv 1$. So suppose we added up some subset $S$ of the equations for which every variable appeared on the left-hand side an even number of times. Then every variable that did appear appeared exactly twice; and accordingly we see that the edges corresponding to these variables form one or more even cycles as in the previous solution. Of course, this means $|S|$ is even, so we really have $0 \equiv 0(\bmod 2)$ as needed. Remark. The author's original proposal contained a second part asking to show that it was not always possible for the resulting $H$ to be connected, even if $G$ was strongly connected. This problem is related to IMO Shortlist 2002 C6, which gives an example of a strongly connected graph which does have a full directed Hamiltonian cycle.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
97547b5b-2271-5a93-a181-573fdcb91574
| 605,520 |
Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\Gamma$. Let $M$ be the midpoint of $\overline{A B}$. Ray $A I$ meets $\overline{B C}$ at $D$. Denote by $\omega$ and $\gamma$ the circumcircles of $\triangle B I C$ and $\triangle B A D$, respectively. Line $M O$ meets $\omega$ at $X$ and $Y$, while line $C O$ meets $\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\triangle A B C$ and $\angle A Q M=\angle A C B$. Consider the tangents to $\omega$ at $X$ and $Y$ and the tangents to $\gamma$ at $A$ and $D$. Given that $\angle B A C \neq 60^{\circ}$, prove that these four lines are concurrent on $\Gamma$.
|
Henceforth assume $\angle A \neq 60^{\circ}$; we prove the concurrence. Let $L$ denote the center of $\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\omega$ such that $\overline{K L} \| \overline{A B}$ and $\overline{K C} \| \overline{A L}$. Then $\overline{K A}$ is tangent to $\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\overline{K A}$ is tangent to $\gamma$ as well since $$ \measuredangle K A D=\measuredangle K A L=\measuredangle K A C+\measuredangle C A L=\measuredangle K B C+\measuredangle A B K=\measuredangle A B C . $$ 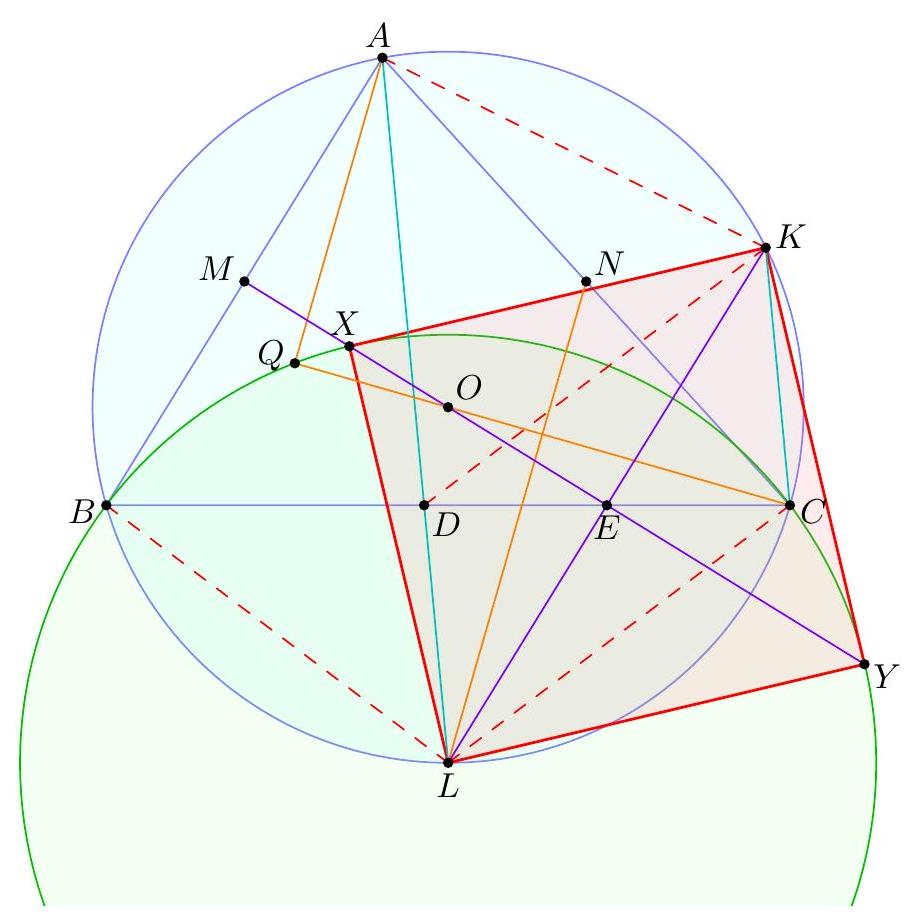 Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \neq O$, since $\angle A \neq 60^{\circ} \Longrightarrow O \notin \omega$. Moreover, we have $\angle A O M=\angle A C B$ too. Since $O$ and $Q$ both lie inside $\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \neq O$ we conclude $\angle C Q A=90^{\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\overline{K X}$ and $\overline{K Y}$ are tangent to $\omega$. First proof of Claim, communicated by Milan Haiman. Observe that $\triangle Q L C \sim \triangle L O C$ since both triangles are isosceles and share a base angle. Hence, $C L^{2}=C O \cdot C Q$. Let $N$ be the midpoint of $\overline{A C}$, which lies on $(A M O Q)$. Then, $$ x^{2}=C L^{2}=C O \cdot C Q=C N \cdot C A=\frac{1}{2} C A^{2}=\frac{1}{2} L K^{2} $$ where we have also used the fact $A Q O N$ is cyclic. Thus $L K=\sqrt{2} x$ and so the rhombus $L X K Y$ is actually a square.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\Gamma$. Let $M$ be the midpoint of $\overline{A B}$. Ray $A I$ meets $\overline{B C}$ at $D$. Denote by $\omega$ and $\gamma$ the circumcircles of $\triangle B I C$ and $\triangle B A D$, respectively. Line $M O$ meets $\omega$ at $X$ and $Y$, while line $C O$ meets $\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\triangle A B C$ and $\angle A Q M=\angle A C B$. Consider the tangents to $\omega$ at $X$ and $Y$ and the tangents to $\gamma$ at $A$ and $D$. Given that $\angle B A C \neq 60^{\circ}$, prove that these four lines are concurrent on $\Gamma$.
|
Henceforth assume $\angle A \neq 60^{\circ}$; we prove the concurrence. Let $L$ denote the center of $\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\omega$ such that $\overline{K L} \| \overline{A B}$ and $\overline{K C} \| \overline{A L}$. Then $\overline{K A}$ is tangent to $\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\overline{K A}$ is tangent to $\gamma$ as well since $$ \measuredangle K A D=\measuredangle K A L=\measuredangle K A C+\measuredangle C A L=\measuredangle K B C+\measuredangle A B K=\measuredangle A B C . $$  Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \neq O$, since $\angle A \neq 60^{\circ} \Longrightarrow O \notin \omega$. Moreover, we have $\angle A O M=\angle A C B$ too. Since $O$ and $Q$ both lie inside $\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \neq O$ we conclude $\angle C Q A=90^{\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\overline{K X}$ and $\overline{K Y}$ are tangent to $\omega$. First proof of Claim, communicated by Milan Haiman. Observe that $\triangle Q L C \sim \triangle L O C$ since both triangles are isosceles and share a base angle. Hence, $C L^{2}=C O \cdot C Q$. Let $N$ be the midpoint of $\overline{A C}$, which lies on $(A M O Q)$. Then, $$ x^{2}=C L^{2}=C O \cdot C Q=C N \cdot C A=\frac{1}{2} C A^{2}=\frac{1}{2} L K^{2} $$ where we have also used the fact $A Q O N$ is cyclic. Thus $L K=\sqrt{2} x$ and so the rhombus $L X K Y$ is actually a square.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
cc76d3e9-b2ee-57e4-9120-106e2fed90fd
| 605,540 |
Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\Gamma$. Let $M$ be the midpoint of $\overline{A B}$. Ray $A I$ meets $\overline{B C}$ at $D$. Denote by $\omega$ and $\gamma$ the circumcircles of $\triangle B I C$ and $\triangle B A D$, respectively. Line $M O$ meets $\omega$ at $X$ and $Y$, while line $C O$ meets $\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\triangle A B C$ and $\angle A Q M=\angle A C B$. Consider the tangents to $\omega$ at $X$ and $Y$ and the tangents to $\gamma$ at $A$ and $D$. Given that $\angle B A C \neq 60^{\circ}$, prove that these four lines are concurrent on $\Gamma$.
|
Henceforth assume $\angle A \neq 60^{\circ}$; we prove the concurrence. Let $L$ denote the center of $\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\omega$ such that $\overline{K L} \| \overline{A B}$ and $\overline{K C} \| \overline{A L}$. Then $\overline{K A}$ is tangent to $\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\overline{K A}$ is tangent to $\gamma$ as well since $$ \measuredangle K A D=\measuredangle K A L=\measuredangle K A C+\measuredangle C A L=\measuredangle K B C+\measuredangle A B K=\measuredangle A B C . $$  Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \neq O$, since $\angle A \neq 60^{\circ} \Longrightarrow O \notin \omega$. Moreover, we have $\angle A O M=\angle A C B$ too. Since $O$ and $Q$ both lie inside $\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \neq O$ we conclude $\angle C Q A=90^{\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\overline{K X}$ and $\overline{K Y}$ are tangent to $\omega$. Second proof of Claim, Evan Chen. Observe that $Q$ lies on the circle with diameter $\overline{A C}$, centered at $N$, say. This means that $O$ lies on the radical axis of $\omega$ and $(N)$, hence $\overline{N L} \perp \overline{C O}$ implying $$ \begin{aligned} N O^{2}+C L^{2} & =N C^{2}+L O^{2}=N C^{2}+O C^{2}=N C^{2}+N O^{2}+N C^{2} \\ \Longrightarrow x^{2} & =2 N C^{2} \\ \Longrightarrow x & =\sqrt{2} N C=\frac{1}{\sqrt{2}} A C=\frac{1}{\sqrt{2}} L K \end{aligned} $$ So $L X K Y$ is a rhombus with $L K=\sqrt{2} x$. Hence it is a square.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\Gamma$. Let $M$ be the midpoint of $\overline{A B}$. Ray $A I$ meets $\overline{B C}$ at $D$. Denote by $\omega$ and $\gamma$ the circumcircles of $\triangle B I C$ and $\triangle B A D$, respectively. Line $M O$ meets $\omega$ at $X$ and $Y$, while line $C O$ meets $\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\triangle A B C$ and $\angle A Q M=\angle A C B$. Consider the tangents to $\omega$ at $X$ and $Y$ and the tangents to $\gamma$ at $A$ and $D$. Given that $\angle B A C \neq 60^{\circ}$, prove that these four lines are concurrent on $\Gamma$.
|
Henceforth assume $\angle A \neq 60^{\circ}$; we prove the concurrence. Let $L$ denote the center of $\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\omega$ such that $\overline{K L} \| \overline{A B}$ and $\overline{K C} \| \overline{A L}$. Then $\overline{K A}$ is tangent to $\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\overline{K A}$ is tangent to $\gamma$ as well since $$ \measuredangle K A D=\measuredangle K A L=\measuredangle K A C+\measuredangle C A L=\measuredangle K B C+\measuredangle A B K=\measuredangle A B C . $$  Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \neq O$, since $\angle A \neq 60^{\circ} \Longrightarrow O \notin \omega$. Moreover, we have $\angle A O M=\angle A C B$ too. Since $O$ and $Q$ both lie inside $\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \neq O$ we conclude $\angle C Q A=90^{\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\overline{K X}$ and $\overline{K Y}$ are tangent to $\omega$. Second proof of Claim, Evan Chen. Observe that $Q$ lies on the circle with diameter $\overline{A C}$, centered at $N$, say. This means that $O$ lies on the radical axis of $\omega$ and $(N)$, hence $\overline{N L} \perp \overline{C O}$ implying $$ \begin{aligned} N O^{2}+C L^{2} & =N C^{2}+L O^{2}=N C^{2}+O C^{2}=N C^{2}+N O^{2}+N C^{2} \\ \Longrightarrow x^{2} & =2 N C^{2} \\ \Longrightarrow x & =\sqrt{2} N C=\frac{1}{\sqrt{2}} A C=\frac{1}{\sqrt{2}} L K \end{aligned} $$ So $L X K Y$ is a rhombus with $L K=\sqrt{2} x$. Hence it is a square.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
cc76d3e9-b2ee-57e4-9120-106e2fed90fd
| 605,540 |
Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\Gamma$. Let $M$ be the midpoint of $\overline{A B}$. Ray $A I$ meets $\overline{B C}$ at $D$. Denote by $\omega$ and $\gamma$ the circumcircles of $\triangle B I C$ and $\triangle B A D$, respectively. Line $M O$ meets $\omega$ at $X$ and $Y$, while line $C O$ meets $\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\triangle A B C$ and $\angle A Q M=\angle A C B$. Consider the tangents to $\omega$ at $X$ and $Y$ and the tangents to $\gamma$ at $A$ and $D$. Given that $\angle B A C \neq 60^{\circ}$, prove that these four lines are concurrent on $\Gamma$.
|
Henceforth assume $\angle A \neq 60^{\circ}$; we prove the concurrence. Let $L$ denote the center of $\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\omega$ such that $\overline{K L} \| \overline{A B}$ and $\overline{K C} \| \overline{A L}$. Then $\overline{K A}$ is tangent to $\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\overline{K A}$ is tangent to $\gamma$ as well since $$ \measuredangle K A D=\measuredangle K A L=\measuredangle K A C+\measuredangle C A L=\measuredangle K B C+\measuredangle A B K=\measuredangle A B C . $$  Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \neq O$, since $\angle A \neq 60^{\circ} \Longrightarrow O \notin \omega$. Moreover, we have $\angle A O M=\angle A C B$ too. Since $O$ and $Q$ both lie inside $\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \neq O$ we conclude $\angle C Q A=90^{\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\overline{K X}$ and $\overline{K Y}$ are tangent to $\omega$. Third proof of Claim. A solution by trig is also possible. As in the previous claims, it suffices to show that $A C=\sqrt{2} x$. First, we compute the length $C Q$ in two ways; by angle chasing one can show $\angle C B Q=$ $180^{\circ}-(\angle B Q C+\angle Q C B)=\frac{1}{2} \angle A$, and so $$ \begin{aligned} A C \sin B=C Q & =\frac{B C}{\sin \left(90^{\circ}+\frac{1}{2} \angle A\right)} \cdot \sin \frac{1}{2} \angle A \\ \Longleftrightarrow \sin ^{2} B & =\frac{\sin A \cdot \sin \frac{1}{2} \angle A}{\cos \frac{1}{2} \angle A} \\ \Longleftrightarrow \sin ^{2} B & =2 \sin ^{2} \frac{1}{2} \angle A \\ \Longleftrightarrow \sin B & =\sqrt{2} \sin \frac{1}{2} \angle A \\ \Longleftrightarrow 2 R \sin B & =\sqrt{2}\left(2 R \sin \frac{1}{2} \angle A\right) \\ \Longleftrightarrow A C & =\sqrt{2} x \end{aligned} $$ as desired (we have here used the fact $\triangle A B C$ is acute to take square roots). It is interesting to note that $\sin ^{2} B=2 \sin ^{2} \frac{1}{2} \angle A$ can be rewritten as $$ \cos A=\cos ^{2} B $$ since $\cos ^{2} B=1-\sin ^{2} B=1-2 \sin ^{2} \frac{1}{2} \angle A=\cos A$; this is the condition for the existence of the point $Q$. We finish by proving that $$ K D=K A $$ and hence line $\overline{K D}$ is tangent to $\gamma$. Let $E=\overline{B C} \cap \overline{K L}$. Then $$ L E \cdot L K=L C^{2}=L X^{2}=\frac{1}{2} L K^{2} $$ and so $E$ is the midpoint of $\overline{L K}$. Thus $\overline{M X O Y}, \overline{B C}, \overline{K L}$ are concurrent at $E$. As $\overline{D L} \| \overline{K C}$, we find that $D L C K$ is a parallelogram, so $K D=C L=K A$ as well. Thus $\overline{K D}$ and $\overline{K A}$ are tangent to $\gamma$. Remark. The condition $\angle A \neq 60^{\circ}$ cannot be dropped, since if $Q=O$ the problem is not true. \ Authorship comments. In the notation of the present points, the question originally sent to me by Yannick Yao read: Circles $(L)$ and $(O)$ are drawn, meeting at $B$ and $C$, with $L$ on $(O)$. Ray $C O$ meets $(L)$ at $Q$, and $A$ is on $(O)$ such that $\angle C Q A=90^{\circ}$. The angle bisector of $\angle A O B$ meets $(L)$ at $X$ and $Y$. Show that $\angle X L Y=90^{\circ}$. Notice the points $M$ and $K$ are absent from the problem. I am told this was found as part of the computer game "Euclidea". Using this as the starting point, I constructed the TSTST problem by recognizing the significance of that special point $K$, which became the center of attention.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with incenter $I$, circumcenter $O$, and circumcircle $\Gamma$. Let $M$ be the midpoint of $\overline{A B}$. Ray $A I$ meets $\overline{B C}$ at $D$. Denote by $\omega$ and $\gamma$ the circumcircles of $\triangle B I C$ and $\triangle B A D$, respectively. Line $M O$ meets $\omega$ at $X$ and $Y$, while line $C O$ meets $\omega$ at $C$ and $Q$. Assume that $Q$ lies inside $\triangle A B C$ and $\angle A Q M=\angle A C B$. Consider the tangents to $\omega$ at $X$ and $Y$ and the tangents to $\gamma$ at $A$ and $D$. Given that $\angle B A C \neq 60^{\circ}$, prove that these four lines are concurrent on $\Gamma$.
|
Henceforth assume $\angle A \neq 60^{\circ}$; we prove the concurrence. Let $L$ denote the center of $\omega$, which is the midpoint of minor arc $B C$. Claim - Let $K$ be the point on $\omega$ such that $\overline{K L} \| \overline{A B}$ and $\overline{K C} \| \overline{A L}$. Then $\overline{K A}$ is tangent to $\gamma$, and we may put $$ x=K A=L B=L C=L X=L Y=K X=K Y . $$ Moreover, $\overline{K A}$ is tangent to $\gamma$ as well since $$ \measuredangle K A D=\measuredangle K A L=\measuredangle K A C+\measuredangle C A L=\measuredangle K B C+\measuredangle A B K=\measuredangle A B C . $$  Up to now we have not used the existence of $Q$; we henceforth do so. Note that $Q \neq O$, since $\angle A \neq 60^{\circ} \Longrightarrow O \notin \omega$. Moreover, we have $\angle A O M=\angle A C B$ too. Since $O$ and $Q$ both lie inside $\triangle A B C$, this implies that $A, M, O, Q$ are concyclic. As $Q \neq O$ we conclude $\angle C Q A=90^{\circ}$. The main claim is now: Claim - Assuming $Q$ exists, the rhombus $L X K Y$ is a square. In particular, $\overline{K X}$ and $\overline{K Y}$ are tangent to $\omega$. Third proof of Claim. A solution by trig is also possible. As in the previous claims, it suffices to show that $A C=\sqrt{2} x$. First, we compute the length $C Q$ in two ways; by angle chasing one can show $\angle C B Q=$ $180^{\circ}-(\angle B Q C+\angle Q C B)=\frac{1}{2} \angle A$, and so $$ \begin{aligned} A C \sin B=C Q & =\frac{B C}{\sin \left(90^{\circ}+\frac{1}{2} \angle A\right)} \cdot \sin \frac{1}{2} \angle A \\ \Longleftrightarrow \sin ^{2} B & =\frac{\sin A \cdot \sin \frac{1}{2} \angle A}{\cos \frac{1}{2} \angle A} \\ \Longleftrightarrow \sin ^{2} B & =2 \sin ^{2} \frac{1}{2} \angle A \\ \Longleftrightarrow \sin B & =\sqrt{2} \sin \frac{1}{2} \angle A \\ \Longleftrightarrow 2 R \sin B & =\sqrt{2}\left(2 R \sin \frac{1}{2} \angle A\right) \\ \Longleftrightarrow A C & =\sqrt{2} x \end{aligned} $$ as desired (we have here used the fact $\triangle A B C$ is acute to take square roots). It is interesting to note that $\sin ^{2} B=2 \sin ^{2} \frac{1}{2} \angle A$ can be rewritten as $$ \cos A=\cos ^{2} B $$ since $\cos ^{2} B=1-\sin ^{2} B=1-2 \sin ^{2} \frac{1}{2} \angle A=\cos A$; this is the condition for the existence of the point $Q$. We finish by proving that $$ K D=K A $$ and hence line $\overline{K D}$ is tangent to $\gamma$. Let $E=\overline{B C} \cap \overline{K L}$. Then $$ L E \cdot L K=L C^{2}=L X^{2}=\frac{1}{2} L K^{2} $$ and so $E$ is the midpoint of $\overline{L K}$. Thus $\overline{M X O Y}, \overline{B C}, \overline{K L}$ are concurrent at $E$. As $\overline{D L} \| \overline{K C}$, we find that $D L C K$ is a parallelogram, so $K D=C L=K A$ as well. Thus $\overline{K D}$ and $\overline{K A}$ are tangent to $\gamma$. Remark. The condition $\angle A \neq 60^{\circ}$ cannot be dropped, since if $Q=O$ the problem is not true. \ Authorship comments. In the notation of the present points, the question originally sent to me by Yannick Yao read: Circles $(L)$ and $(O)$ are drawn, meeting at $B$ and $C$, with $L$ on $(O)$. Ray $C O$ meets $(L)$ at $Q$, and $A$ is on $(O)$ such that $\angle C Q A=90^{\circ}$. The angle bisector of $\angle A O B$ meets $(L)$ at $X$ and $Y$. Show that $\angle X L Y=90^{\circ}$. Notice the points $M$ and $K$ are absent from the problem. I am told this was found as part of the computer game "Euclidea". Using this as the starting point, I constructed the TSTST problem by recognizing the significance of that special point $K$, which became the center of attention.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
cc76d3e9-b2ee-57e4-9120-106e2fed90fd
| 605,540 |
For an integer $n>0$, denote by $\mathcal{F}(n)$ the set of integers $m>0$ for which the polynomial $p(x)=x^{2}+m x+n$ has an integer root. (a) Let $S$ denote the set of integers $n>0$ for which $\mathcal{F}(n)$ contains two consecutive integers. Show that $S$ is infinite but $$ \sum_{n \in S} \frac{1}{n} \leq 1 $$ (b) Prove that there are infinitely many positive integers $n$ such that $\mathcal{F}(n)$ contains three consecutive integers.
|
We prove the following. Claim - The set $S$ is given explicitly by $S=\{x(x+1) y(y+1) \mid x, y>0\}$. $$ \begin{aligned} m^{2}-4 n & =p^{2} \\ (m+1)^{2}-4 n & =q^{2} \end{aligned} $$ Subtraction gives $2 m+1=q^{2}-p^{2}$, so $p$ and $q$ are different parities. We can thus let $q-p=2 x+1, q+p=2 y+1$, where $y \geq x \geq 0$ are integers. It follows that $$ \begin{aligned} 4 n & =m^{2}-p^{2} \\ & =\left(\frac{q^{2}-p^{2}-1}{2}\right)^{2}-p^{2}=\left(\frac{q^{2}-p^{2}-1}{2}-p\right)\left(\frac{q^{2}-p^{2}-1}{2}+p\right) \\ & =\frac{q^{2}-\left(p^{2}+2 p+1\right)}{2} \cdot \frac{q^{2}-\left(p^{2}-2 p+1\right)}{2} \\ & =\frac{1}{4}(q-p-1)(q-p+1)(q+p-1)(q+p+1)=\frac{1}{4}(2 x)(2 x+2)(2 y)(2 y+2) \\ \Longrightarrow n & =x(x+1) y(y+1) . \end{aligned} $$ Since $n>0$ we require $x, y>0$. Conversely, if $n=x(x+1) y(y+1)$ for positive $x$ and $y$ then $m=\sqrt{p^{2}+4 n}=\sqrt{(y-x)^{2}+4 n}=2 x y+x+y=x(y+1)+(x+1) y$ and $m+1=2 x y+x+y+1=x y+(x+1)(y+1)$. Thus we conclude the main claim. From this, part (a) follows as $$ \sum_{n \in S} n^{-1} \leq\left(\sum_{x \geq 1} \frac{1}{x(x+1)}\right)\left(\sum_{y \geq 1} \frac{1}{y(y+1)}\right)=1 \cdot 1=1 $$ $$ \begin{aligned} r^{2} & =(m+2)^{2}-4 n=m^{2}-4 n+4 m+4=p^{2}+2+2(2 m+1) \\ & =p^{2}+2\left(q^{2}-p^{2}\right)+2=2 q^{2}-p^{2}+2 \\ \Longleftrightarrow 2 q^{2}+2 & =p^{2}+r^{2} \quad(\dagger) \end{aligned} $$ with $q>p$ of different parity and $n=\frac{1}{16}(q-p-1)(q-p+1)(q+p-1)(q+p+1)$. Note that (by taking modulo 8 ) we have $q \not \equiv p \equiv r(\bmod 2)$, and so there are no parity issues and we will always assume $p<q<r$ in ( $\dagger$ ). Now, for every $q$, the equation ( $\dagger$ ) has a canonical solution $(p, r)=(q-1, q+1)$, but this leaves $n=0$. Thus we want to show for infinitely many $q$ there is a third way to write $2 q^{2}+2$ as a sum of squares, which will give the desired $p$. To do this, choose large integers $q$ such that $q^{2}+1$ is divisible by at least three distinct $1 \bmod 4$ primes. Since each such prime can be written as a sum of two squares, using Lagrange identity, we can deduce that $2 q^{2}+2$ can be written as a sum of two squares in at least three different ways, as desired. Remark. We can see that $n=144$ is the smallest integer such that $\mathcal{F}(n)$ contains three consecutive integers and $n=15120$ is the smallest integer such that $\mathcal{F}(n)$ contains four consecutive integers. It would be interesting to determine whether the number of consecutive elements in $\mathcal{F}(n)$ can be arbitrarily large or is bounded.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For an integer $n>0$, denote by $\mathcal{F}(n)$ the set of integers $m>0$ for which the polynomial $p(x)=x^{2}+m x+n$ has an integer root. (a) Let $S$ denote the set of integers $n>0$ for which $\mathcal{F}(n)$ contains two consecutive integers. Show that $S$ is infinite but $$ \sum_{n \in S} \frac{1}{n} \leq 1 $$ (b) Prove that there are infinitely many positive integers $n$ such that $\mathcal{F}(n)$ contains three consecutive integers.
|
We prove the following. Claim - The set $S$ is given explicitly by $S=\{x(x+1) y(y+1) \mid x, y>0\}$. $$ \begin{aligned} m^{2}-4 n & =p^{2} \\ (m+1)^{2}-4 n & =q^{2} \end{aligned} $$ Subtraction gives $2 m+1=q^{2}-p^{2}$, so $p$ and $q$ are different parities. We can thus let $q-p=2 x+1, q+p=2 y+1$, where $y \geq x \geq 0$ are integers. It follows that $$ \begin{aligned} 4 n & =m^{2}-p^{2} \\ & =\left(\frac{q^{2}-p^{2}-1}{2}\right)^{2}-p^{2}=\left(\frac{q^{2}-p^{2}-1}{2}-p\right)\left(\frac{q^{2}-p^{2}-1}{2}+p\right) \\ & =\frac{q^{2}-\left(p^{2}+2 p+1\right)}{2} \cdot \frac{q^{2}-\left(p^{2}-2 p+1\right)}{2} \\ & =\frac{1}{4}(q-p-1)(q-p+1)(q+p-1)(q+p+1)=\frac{1}{4}(2 x)(2 x+2)(2 y)(2 y+2) \\ \Longrightarrow n & =x(x+1) y(y+1) . \end{aligned} $$ Since $n>0$ we require $x, y>0$. Conversely, if $n=x(x+1) y(y+1)$ for positive $x$ and $y$ then $m=\sqrt{p^{2}+4 n}=\sqrt{(y-x)^{2}+4 n}=2 x y+x+y=x(y+1)+(x+1) y$ and $m+1=2 x y+x+y+1=x y+(x+1)(y+1)$. Thus we conclude the main claim. From this, part (a) follows as $$ \sum_{n \in S} n^{-1} \leq\left(\sum_{x \geq 1} \frac{1}{x(x+1)}\right)\left(\sum_{y \geq 1} \frac{1}{y(y+1)}\right)=1 \cdot 1=1 $$ $$ \begin{aligned} r^{2} & =(m+2)^{2}-4 n=m^{2}-4 n+4 m+4=p^{2}+2+2(2 m+1) \\ & =p^{2}+2\left(q^{2}-p^{2}\right)+2=2 q^{2}-p^{2}+2 \\ \Longleftrightarrow 2 q^{2}+2 & =p^{2}+r^{2} \quad(\dagger) \end{aligned} $$ with $q>p$ of different parity and $n=\frac{1}{16}(q-p-1)(q-p+1)(q+p-1)(q+p+1)$. Note that (by taking modulo 8 ) we have $q \not \equiv p \equiv r(\bmod 2)$, and so there are no parity issues and we will always assume $p<q<r$ in ( $\dagger$ ). Now, for every $q$, the equation ( $\dagger$ ) has a canonical solution $(p, r)=(q-1, q+1)$, but this leaves $n=0$. Thus we want to show for infinitely many $q$ there is a third way to write $2 q^{2}+2$ as a sum of squares, which will give the desired $p$. To do this, choose large integers $q$ such that $q^{2}+1$ is divisible by at least three distinct $1 \bmod 4$ primes. Since each such prime can be written as a sum of two squares, using Lagrange identity, we can deduce that $2 q^{2}+2$ can be written as a sum of two squares in at least three different ways, as desired. Remark. We can see that $n=144$ is the smallest integer such that $\mathcal{F}(n)$ contains three consecutive integers and $n=15120$ is the smallest integer such that $\mathcal{F}(n)$ contains four consecutive integers. It would be interesting to determine whether the number of consecutive elements in $\mathcal{F}(n)$ can be arbitrarily large or is bounded.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
9847b0a7-5b0d-54c4-a7cb-20b2a2d72b33
| 605,570 |
On an infinite square grid we place finitely many cars, which each occupy a single cell and face in one of the four cardinal directions. Cars may never occupy the same cell. It is given that the cell immediately in front of each car is empty, and moreover no two cars face towards each other (no right-facing car is to the left of a left-facing car within a row, etc.). In a move, one chooses a car and shifts it one cell forward to a vacant cell. Prove that there exists an infinite sequence of valid moves using each car infinitely many times.
|
Let $S$ be any rectangle containing all the cars. Partition $S$ into horizontal strips of height 1 , and color them red and green in an alternating fashion. It is enough to prove all the cars may exit $S$. 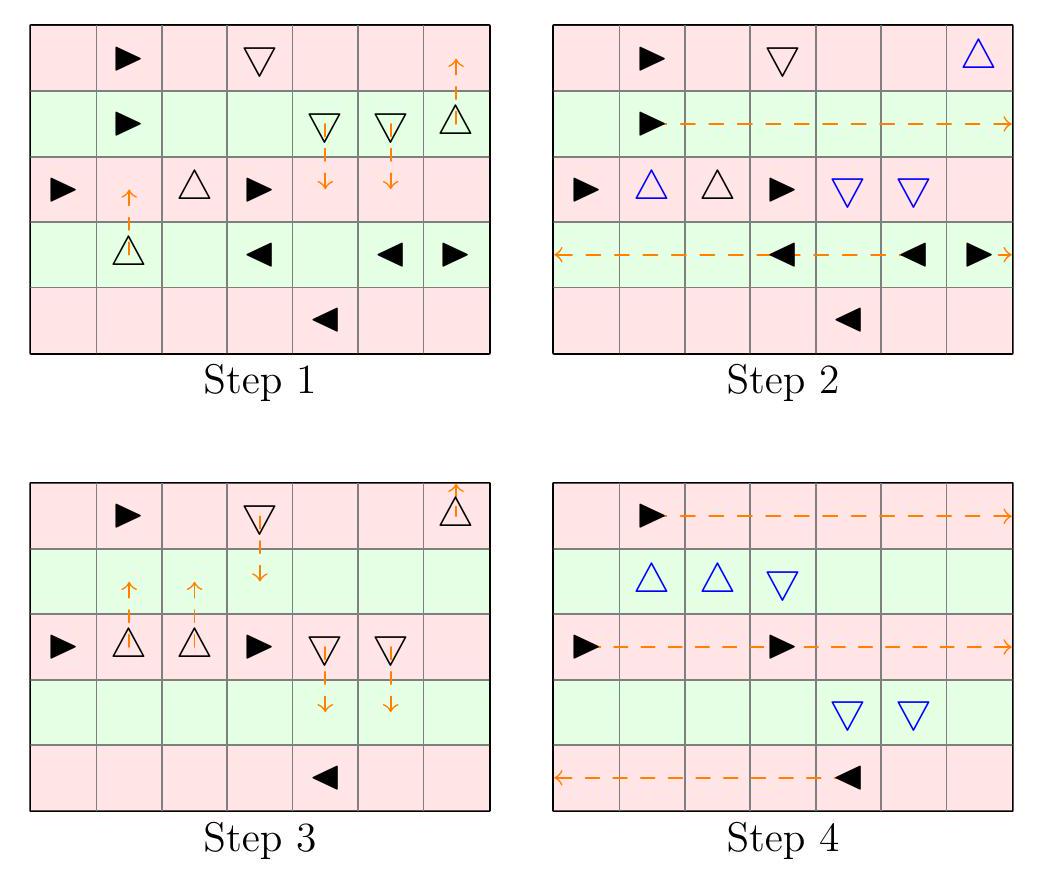 To do so, we outline a five-stage plan for the cars. 1. All vertical cars in a green cell may advance one cell into a red cell (or exit $S$ altogether), by the given condition. (This is the only place where the hypothesis about empty space is used!) 2. All horizontal cars on green cells may exit $S$, as no vertical cars occupy green cells. 3. All vertical cars in a red cell may advance one cell into a green cell (or exit $S$ altogether), as all green cells are empty. 4. All horizontal cars within red cells may exit $S$, as no vertical car occupy red cells. 5. The remaining cars exit $S$, as they are all vertical. The solution is complete. Remark (Higher-dimensional generalization by author). The natural higher-dimensional generalization is true, and can be proved in largely the same fashion. For example, in three dimensions, one may let $S$ be a rectangular prism and partition $S$ into horizontal slabs and color them red and green in an alternating fashion. Stages 1, 3, and 5 generalize immediately, and stages 2 and 4 reduce to an application of the two-dimensional problem. In the same way, the general problem is handled by induction on the dimension. Remark (Historical comments). For $k>1$, we could consider a variant of the problem where cars are $1 \times k$ rectangles (moving parallel to the longer edge) instead of occupying single cells. In that case, if there are $2 k-1$ empty spaces in front of each car, the above proof works (with the red and green strips having height $k$ instead). On the other hand, at least $k$ empty spaces are necessary. We don't know the best constant in this case.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On an infinite square grid we place finitely many cars, which each occupy a single cell and face in one of the four cardinal directions. Cars may never occupy the same cell. It is given that the cell immediately in front of each car is empty, and moreover no two cars face towards each other (no right-facing car is to the left of a left-facing car within a row, etc.). In a move, one chooses a car and shifts it one cell forward to a vacant cell. Prove that there exists an infinite sequence of valid moves using each car infinitely many times.
|
Let $S$ be any rectangle containing all the cars. Partition $S$ into horizontal strips of height 1 , and color them red and green in an alternating fashion. It is enough to prove all the cars may exit $S$.  To do so, we outline a five-stage plan for the cars. 1. All vertical cars in a green cell may advance one cell into a red cell (or exit $S$ altogether), by the given condition. (This is the only place where the hypothesis about empty space is used!) 2. All horizontal cars on green cells may exit $S$, as no vertical cars occupy green cells. 3. All vertical cars in a red cell may advance one cell into a green cell (or exit $S$ altogether), as all green cells are empty. 4. All horizontal cars within red cells may exit $S$, as no vertical car occupy red cells. 5. The remaining cars exit $S$, as they are all vertical. The solution is complete. Remark (Higher-dimensional generalization by author). The natural higher-dimensional generalization is true, and can be proved in largely the same fashion. For example, in three dimensions, one may let $S$ be a rectangular prism and partition $S$ into horizontal slabs and color them red and green in an alternating fashion. Stages 1, 3, and 5 generalize immediately, and stages 2 and 4 reduce to an application of the two-dimensional problem. In the same way, the general problem is handled by induction on the dimension. Remark (Historical comments). For $k>1$, we could consider a variant of the problem where cars are $1 \times k$ rectangles (moving parallel to the longer edge) instead of occupying single cells. In that case, if there are $2 k-1$ empty spaces in front of each car, the above proof works (with the red and green strips having height $k$ instead). On the other hand, at least $k$ empty spaces are necessary. We don't know the best constant in this case.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
55ffdc97-1160-544c-8593-6076bc3ec700
| 247,397 |
Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\triangle A E F$, and suppose line $A K$ intersects $\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\overline{B C}$ meet on $\Gamma$.
|
『 First solution (Andrew Gu). We begin with the following two observations. Claim - Point $K$ lies on the radical axis of $(B E H)$ and $(C F H)$. $$ \measuredangle H E K=90^{\circ}-\measuredangle E A F=90^{\circ}-\measuredangle B A C=\measuredangle H B E $$ implying the result. Since $K E=K F$, this implies the result. Claim - The second intersection $M$ of $(B E H)$ and $(C F H)$ lies on $\Gamma$.  In particular, $M, H, K$ are collinear. Let $X$ be on $\Gamma$ with $\overline{D X} \perp \overline{B C}$; we then wish to show $X$ lies on the line $M H K$ we found. This is angle chasing: compute $$ \measuredangle X M B=\measuredangle X D B=90^{\circ}-\measuredangle D B C=90^{\circ}-\measuredangle D A C $$ $$ =90^{\circ}-\measuredangle K A F=\measuredangle F E A=\measuredangle H E B=\measuredangle H M B $$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\triangle A E F$, and suppose line $A K$ intersects $\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\overline{B C}$ meet on $\Gamma$.
|
『 First solution (Andrew Gu). We begin with the following two observations. Claim - Point $K$ lies on the radical axis of $(B E H)$ and $(C F H)$. $$ \measuredangle H E K=90^{\circ}-\measuredangle E A F=90^{\circ}-\measuredangle B A C=\measuredangle H B E $$ implying the result. Since $K E=K F$, this implies the result. Claim - The second intersection $M$ of $(B E H)$ and $(C F H)$ lies on $\Gamma$.  In particular, $M, H, K$ are collinear. Let $X$ be on $\Gamma$ with $\overline{D X} \perp \overline{B C}$; we then wish to show $X$ lies on the line $M H K$ we found. This is angle chasing: compute $$ \measuredangle X M B=\measuredangle X D B=90^{\circ}-\measuredangle D B C=90^{\circ}-\measuredangle D A C $$ $$ =90^{\circ}-\measuredangle K A F=\measuredangle F E A=\measuredangle H E B=\measuredangle H M B $$ as needed.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
f52b53c6-9873-5b2a-bc92-3d0c2e6d9935
| 247,418 |
Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\triangle A E F$, and suppose line $A K$ intersects $\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\overline{B C}$ meet on $\Gamma$.
|
II Second solution (Ankan Bhattacharya). We let $D^{\prime}$ be the second intersection of $\overline{E F}$ with $(B H C)$ and redefine $D$ as the reflection of $D^{\prime}$ across $\overline{B C}$. We will first prove that this point $D$ coincides with the point $D$ given in the problem statement. The idea is that: Claim - $A$ is the $D$-excenter of $\triangle D E F$. $$ \begin{aligned} \measuredangle D^{\prime} D B & =\measuredangle B D^{\prime} D=\measuredangle D^{\prime} B C+90^{\circ}=\measuredangle D^{\prime} H C+90^{\circ} \\ & =\measuredangle D^{\prime} H C+\measuredangle(H C, A B)=\measuredangle\left(D^{\prime} H, A B\right)=\measuredangle D^{\prime} E B \end{aligned} $$ Now as $B D=B D^{\prime}$, we obtain $\overline{B E A}$ externally bisects $\angle D E D^{\prime} \cong \angle D E F$. Likewise $\overline{F A}$ externally bisects $\angle D F E$, so $A$ is the $D$-excenter of $\triangle D E F$. Hence, by the so-called "Fact 5 ", point $K$ lies on $\overline{D A}$, so this point $D$ is the one given in the problem statement.  Now choose point $X$ on $(A B C)$ satisfying $\overline{D X} \perp \overline{B C}$. Claim - Point $K$ lies on line $H X$. $$ \frac{K D}{K A}=\frac{K D}{K E}=\frac{D E+D F}{E F} $$ On the other hand, if we let $r_{D}$ denote the $D$-exradius of $\triangle D E F$ then $$ \frac{X D}{X D^{\prime}}=\frac{[D E X]+[D F X]}{[X E F]}=\frac{[D E X]+[D F X]}{[A E F]}=\frac{D E \cdot r_{D}+D F \cdot r_{D}}{E F \cdot r_{D}}=\frac{D E+D F}{E F} $$ Thus $$ [A K X]=\frac{K A}{K D} \cdot[D K X]=\frac{K A}{K D} \cdot \frac{X D}{X D^{\prime}} \cdot\left[K D^{\prime} X\right]=\left[D^{\prime} K X\right] $$ This is sufficient to prove $K$ lies on $\overline{H X}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\triangle A E F$, and suppose line $A K$ intersects $\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\overline{B C}$ meet on $\Gamma$.
|
II Second solution (Ankan Bhattacharya). We let $D^{\prime}$ be the second intersection of $\overline{E F}$ with $(B H C)$ and redefine $D$ as the reflection of $D^{\prime}$ across $\overline{B C}$. We will first prove that this point $D$ coincides with the point $D$ given in the problem statement. The idea is that: Claim - $A$ is the $D$-excenter of $\triangle D E F$. $$ \begin{aligned} \measuredangle D^{\prime} D B & =\measuredangle B D^{\prime} D=\measuredangle D^{\prime} B C+90^{\circ}=\measuredangle D^{\prime} H C+90^{\circ} \\ & =\measuredangle D^{\prime} H C+\measuredangle(H C, A B)=\measuredangle\left(D^{\prime} H, A B\right)=\measuredangle D^{\prime} E B \end{aligned} $$ Now as $B D=B D^{\prime}$, we obtain $\overline{B E A}$ externally bisects $\angle D E D^{\prime} \cong \angle D E F$. Likewise $\overline{F A}$ externally bisects $\angle D F E$, so $A$ is the $D$-excenter of $\triangle D E F$. Hence, by the so-called "Fact 5 ", point $K$ lies on $\overline{D A}$, so this point $D$ is the one given in the problem statement.  Now choose point $X$ on $(A B C)$ satisfying $\overline{D X} \perp \overline{B C}$. Claim - Point $K$ lies on line $H X$. $$ \frac{K D}{K A}=\frac{K D}{K E}=\frac{D E+D F}{E F} $$ On the other hand, if we let $r_{D}$ denote the $D$-exradius of $\triangle D E F$ then $$ \frac{X D}{X D^{\prime}}=\frac{[D E X]+[D F X]}{[X E F]}=\frac{[D E X]+[D F X]}{[A E F]}=\frac{D E \cdot r_{D}+D F \cdot r_{D}}{E F \cdot r_{D}}=\frac{D E+D F}{E F} $$ Thus $$ [A K X]=\frac{K A}{K D} \cdot[D K X]=\frac{K A}{K D} \cdot \frac{X D}{X D^{\prime}} \cdot\left[K D^{\prime} X\right]=\left[D^{\prime} K X\right] $$ This is sufficient to prove $K$ lies on $\overline{H X}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
f52b53c6-9873-5b2a-bc92-3d0c2e6d9935
| 247,418 |
Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\triangle A E F$, and suppose line $A K$ intersects $\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\overline{B C}$ meet on $\Gamma$.
|
【 Seventh solution using moving points (Zack Chroman). We state the converse of the problem as follows: Take a point $D$ on $\Gamma$, and let $G \in \Gamma$ such that $\overline{D G} \perp \overline{B C}$. Then define $K$ to lie on $\overline{G H}, \overline{A D}$, and take $L \in \overline{A D}$ such that $K$ is the midpoint of $\overline{A L}$. Then if we define $E$ and $F$ as the projections of $L$ onto $\overline{A B}$ and $\overline{A C}$ we want to show that $E, H, F$ are collinear. It's clear that solving this problem will solve the original. In fact we will show later that each line $E F$ through $H$ corresponds bijectively to the point $D$. We animate $D$ projectively on $\Gamma$ (hence $\operatorname{deg} D=2$ ). Since $D \mapsto G$ is a projective map $\Gamma \rightarrow \Gamma$, it follows $\operatorname{deg} G=2$. By Zack's lemma, $\operatorname{deg}(\overline{A D}) \leq 0+2-1=1$ (since $D$ can coincide with $A$ ), and $\operatorname{deg}(\overline{H G}) \leq 0+2-0=2$. So again by Zack's lemma, $\operatorname{deg} K \leq 1+2-1=2$, since lines $A D$ and $G H$ can coincide once if $D$ is the reflection of $H$ over $\overline{B C}$. It follows $\operatorname{deg} L=2$, since it is obtained by dilating $K$ by a factor of 2 across the fixed point $A$. Let $\infty_{C}$ be the point at infinity on the line perpendicular to $A C$, and similarly $\infty_{B}$. Then $$ F=\overline{A C} \cap \overline{\infty_{C} L}, \quad E=\overline{A B} \cap \overline{\infty_{B} L} . $$ We want to use Zack's lemma again on line $\overline{\infty_{B} L}$. Consider the case $G=B$; we get $\overline{H G} \| \overline{A D}$, so $A D G H$ is a parallelogram, and then $K=L=\infty_{B}$. Thus there is at least one $t$ where $L=\infty_{B}$ and by Zack's lemma we get $\operatorname{deg}\left(\overline{\infty_{B} L}\right) \leq 0+2-1=1$. Again by Zack's lemma, we conclude $\operatorname{deg} E \leq 0+1-0=1$. Similarly, $\operatorname{deg} F \leq 1$. We were aiming to show $E, F, H$ collinear which is a condition of degree at most $1+1+0=2$. So it suffices to verify the problem for three distinct choices of $D$. - If $D=A$, then line $G H$ is line $A H$, and $L=\overline{A D} \cap \overline{A H}=A$. So $E=F=A$ and the statement is true. - If $D=B, G$ is the antipode of $C$ on $\Gamma$. Then $K=\overline{H G} \cap \overline{A D}$ is the midpoint of $\overline{A B}$, so $L=B$. Then $E=B$ and $F$ is the projection of $B$ onto $A C$, so $E, H, F$ collinear. - We finish similarly when $D=C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with orthocenter $H$ and circumcircle $\Gamma$. A line through $H$ intersects segments $A B$ and $A C$ at $E$ and $F$, respectively. Let $K$ be the circumcenter of $\triangle A E F$, and suppose line $A K$ intersects $\Gamma$ again at a point $D$. Prove that line $H K$ and the line through $D$ perpendicular to $\overline{B C}$ meet on $\Gamma$.
|
【 Seventh solution using moving points (Zack Chroman). We state the converse of the problem as follows: Take a point $D$ on $\Gamma$, and let $G \in \Gamma$ such that $\overline{D G} \perp \overline{B C}$. Then define $K$ to lie on $\overline{G H}, \overline{A D}$, and take $L \in \overline{A D}$ such that $K$ is the midpoint of $\overline{A L}$. Then if we define $E$ and $F$ as the projections of $L$ onto $\overline{A B}$ and $\overline{A C}$ we want to show that $E, H, F$ are collinear. It's clear that solving this problem will solve the original. In fact we will show later that each line $E F$ through $H$ corresponds bijectively to the point $D$. We animate $D$ projectively on $\Gamma$ (hence $\operatorname{deg} D=2$ ). Since $D \mapsto G$ is a projective map $\Gamma \rightarrow \Gamma$, it follows $\operatorname{deg} G=2$. By Zack's lemma, $\operatorname{deg}(\overline{A D}) \leq 0+2-1=1$ (since $D$ can coincide with $A$ ), and $\operatorname{deg}(\overline{H G}) \leq 0+2-0=2$. So again by Zack's lemma, $\operatorname{deg} K \leq 1+2-1=2$, since lines $A D$ and $G H$ can coincide once if $D$ is the reflection of $H$ over $\overline{B C}$. It follows $\operatorname{deg} L=2$, since it is obtained by dilating $K$ by a factor of 2 across the fixed point $A$. Let $\infty_{C}$ be the point at infinity on the line perpendicular to $A C$, and similarly $\infty_{B}$. Then $$ F=\overline{A C} \cap \overline{\infty_{C} L}, \quad E=\overline{A B} \cap \overline{\infty_{B} L} . $$ We want to use Zack's lemma again on line $\overline{\infty_{B} L}$. Consider the case $G=B$; we get $\overline{H G} \| \overline{A D}$, so $A D G H$ is a parallelogram, and then $K=L=\infty_{B}$. Thus there is at least one $t$ where $L=\infty_{B}$ and by Zack's lemma we get $\operatorname{deg}\left(\overline{\infty_{B} L}\right) \leq 0+2-1=1$. Again by Zack's lemma, we conclude $\operatorname{deg} E \leq 0+1-0=1$. Similarly, $\operatorname{deg} F \leq 1$. We were aiming to show $E, F, H$ collinear which is a condition of degree at most $1+1+0=2$. So it suffices to verify the problem for three distinct choices of $D$. - If $D=A$, then line $G H$ is line $A H$, and $L=\overline{A D} \cap \overline{A H}=A$. So $E=F=A$ and the statement is true. - If $D=B, G$ is the antipode of $C$ on $\Gamma$. Then $K=\overline{H G} \cap \overline{A D}$ is the midpoint of $\overline{A B}$, so $L=B$. Then $E=B$ and $F$ is the projection of $B$ onto $A C$, so $E, H, F$ collinear. - We finish similarly when $D=C$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
f52b53c6-9873-5b2a-bc92-3d0c2e6d9935
| 247,418 |
Suppose $P$ is a polynomial with integer coefficients such that for every positive integer $n$, the sum of the decimal digits of $|P(n)|$ is not a Fibonacci number. Must $P$ be constant?
|
The answer is yes, $P$ must be constant. By $S(n)$ we mean the sum of the decimal digits of $|n|$. We need two claims. Claim - If $P(x) \in \mathbb{Z}[x]$ is nonconstant with positive leading coefficient, then there exists an integer polynomial $F(x)$ such that all coefficients of $P \circ F$ are positive except for the second one, which is negative. First, consider $T_{0}(x)=x^{3}+x+1$. Observe that in $T_{0}^{\operatorname{deg} P}$, every coefficient is strictly positive, except for the second one, which is zero. Then, let $T_{1}(x)=x^{3}-\frac{1}{D} x^{2}+x+1$. Using continuity as $D \rightarrow \infty$, it follows that if $D$ is large enough (in terms of $\operatorname{deg} P$ ), then $T_{1}^{\operatorname{deg} P}$ is good, with $-\frac{3}{D} x^{3 \operatorname{deg} P-1}$ being the only negative coefficient. Finally, we can let $F(x)=C T_{1}(x)$ where $C$ is a sufficiently large multiple of $D$ (in terms of the coefficients of $P$ ); thus the coefficients of $\left(C T_{1}(x)\right)^{\operatorname{deg} P}$ dominate (and are integers), as needed. Claim - There are infinitely many Fibonacci numbers in each residue class modulo 9. $$ \begin{aligned} F_{0}=0 & \equiv 0 \quad(\bmod 9) \\ F_{1}=1 & \equiv 1 \quad(\bmod 9) \\ F_{3}=2 & \equiv 2 \quad(\bmod 9) \\ F_{4}=3 & \equiv 3 \quad(\bmod 9) \\ F_{7}=13 & \equiv 4 \quad(\bmod 9) \\ F_{5}=5 & \equiv 5 \quad(\bmod 9) \\ F_{-4}=-3 & \equiv 6 \quad(\bmod 9) \\ F_{9}=34 & \equiv 7 \quad(\bmod 9) \\ F_{6}=8 & \equiv 8 \quad(\bmod 9) . \end{aligned} $$ We now show how to solve the problem with the two claims. WLOG $P$ satisfies the conditions of the first claim, and choose $F$ as above. Let $$ P(F(x))=c_{N} x^{N}-c_{N-1} x^{N-1}+c_{N-2} x^{N-2}+\cdots+c_{0} $$ where $c_{i}>0$ (and $N=3 \operatorname{deg} P$ ). Then if we select $x=10^{e}$ for $e$ large enough (say $\left.x>10 \max _{i} c_{i}\right)$, the decimal representation $P\left(F\left(10^{e}\right)\right)$ consists of the concatenation of - the decimal representation of $c_{N}-1$, - the decimal representation of $10^{e}-c_{N-1}$ - the decimal representation of $c_{N-2}$, with several leading zeros, - the decimal representation of $c_{N-3}$, with several leading zeros, - ... - the decimal representation of $c_{0}$, with several leading zeros. (For example, if $P(F(x))=15 x^{3}-7 x^{2}+4 x+19$, then $P(F(1000))=14,993,004,019$.) Thus, the sum of the digits of this expression is equal to $$ S\left(P\left(F\left(10^{e}\right)\right)\right)=9 e+k $$ for some constant $k$ depending only on $P$ and $F$, independent of $e$. But this will eventually hit a Fibonacci number by the second claim, contradiction. Remark. It is important to control the number of negative coefficients in the created polynomial. If one tries to use this approach on a polynomial $P$ with $m>0$ negative coefficients, then one would require that the Fibonacci sequence is surjective modulo $9 m$ for any $m>1$, which is not true: for example the Fibonacci sequence avoids all numbers congruent to $4 \bmod 11($ and thus $4 \bmod 99)$. In bases $b$ for which surjectivity modulo $b-1$ fails, the problem is false. For example, $P(x)=11 x+4$ will avoid all Fibonacci numbers if we take sum of digits in base 12, since that base-12 sum is necessarily $4(\bmod 11)$, hence not a Fibonacci number.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Suppose $P$ is a polynomial with integer coefficients such that for every positive integer $n$, the sum of the decimal digits of $|P(n)|$ is not a Fibonacci number. Must $P$ be constant?
|
The answer is yes, $P$ must be constant. By $S(n)$ we mean the sum of the decimal digits of $|n|$. We need two claims. Claim - If $P(x) \in \mathbb{Z}[x]$ is nonconstant with positive leading coefficient, then there exists an integer polynomial $F(x)$ such that all coefficients of $P \circ F$ are positive except for the second one, which is negative. First, consider $T_{0}(x)=x^{3}+x+1$. Observe that in $T_{0}^{\operatorname{deg} P}$, every coefficient is strictly positive, except for the second one, which is zero. Then, let $T_{1}(x)=x^{3}-\frac{1}{D} x^{2}+x+1$. Using continuity as $D \rightarrow \infty$, it follows that if $D$ is large enough (in terms of $\operatorname{deg} P$ ), then $T_{1}^{\operatorname{deg} P}$ is good, with $-\frac{3}{D} x^{3 \operatorname{deg} P-1}$ being the only negative coefficient. Finally, we can let $F(x)=C T_{1}(x)$ where $C$ is a sufficiently large multiple of $D$ (in terms of the coefficients of $P$ ); thus the coefficients of $\left(C T_{1}(x)\right)^{\operatorname{deg} P}$ dominate (and are integers), as needed. Claim - There are infinitely many Fibonacci numbers in each residue class modulo 9. $$ \begin{aligned} F_{0}=0 & \equiv 0 \quad(\bmod 9) \\ F_{1}=1 & \equiv 1 \quad(\bmod 9) \\ F_{3}=2 & \equiv 2 \quad(\bmod 9) \\ F_{4}=3 & \equiv 3 \quad(\bmod 9) \\ F_{7}=13 & \equiv 4 \quad(\bmod 9) \\ F_{5}=5 & \equiv 5 \quad(\bmod 9) \\ F_{-4}=-3 & \equiv 6 \quad(\bmod 9) \\ F_{9}=34 & \equiv 7 \quad(\bmod 9) \\ F_{6}=8 & \equiv 8 \quad(\bmod 9) . \end{aligned} $$ We now show how to solve the problem with the two claims. WLOG $P$ satisfies the conditions of the first claim, and choose $F$ as above. Let $$ P(F(x))=c_{N} x^{N}-c_{N-1} x^{N-1}+c_{N-2} x^{N-2}+\cdots+c_{0} $$ where $c_{i}>0$ (and $N=3 \operatorname{deg} P$ ). Then if we select $x=10^{e}$ for $e$ large enough (say $\left.x>10 \max _{i} c_{i}\right)$, the decimal representation $P\left(F\left(10^{e}\right)\right)$ consists of the concatenation of - the decimal representation of $c_{N}-1$, - the decimal representation of $10^{e}-c_{N-1}$ - the decimal representation of $c_{N-2}$, with several leading zeros, - the decimal representation of $c_{N-3}$, with several leading zeros, - ... - the decimal representation of $c_{0}$, with several leading zeros. (For example, if $P(F(x))=15 x^{3}-7 x^{2}+4 x+19$, then $P(F(1000))=14,993,004,019$.) Thus, the sum of the digits of this expression is equal to $$ S\left(P\left(F\left(10^{e}\right)\right)\right)=9 e+k $$ for some constant $k$ depending only on $P$ and $F$, independent of $e$. But this will eventually hit a Fibonacci number by the second claim, contradiction. Remark. It is important to control the number of negative coefficients in the created polynomial. If one tries to use this approach on a polynomial $P$ with $m>0$ negative coefficients, then one would require that the Fibonacci sequence is surjective modulo $9 m$ for any $m>1$, which is not true: for example the Fibonacci sequence avoids all numbers congruent to $4 \bmod 11($ and thus $4 \bmod 99)$. In bases $b$ for which surjectivity modulo $b-1$ fails, the problem is false. For example, $P(x)=11 x+4$ will avoid all Fibonacci numbers if we take sum of digits in base 12, since that base-12 sum is necessarily $4(\bmod 11)$, hence not a Fibonacci number.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
24b27b99-11cc-5653-8370-22b026c9fe2f
| 247,426 |
Let $f: \mathbb{Z} \rightarrow\left\{1,2, \ldots, 10^{100}\right\}$ be a function satisfying $$ \operatorname{gcd}(f(x), f(y))=\operatorname{gcd}(f(x), x-y) $$ for all integers $x$ and $y$. Show that there exist positive integers $m$ and $n$ such that $f(x)=\operatorname{gcd}(m+x, n)$ for all integers $x$.
|
Let $\mathcal{P}$ be the set of primes not exceeding $10^{100}$. For each $p \in \mathcal{P}$, let $e_{p}=\max _{x} \nu_{p}(f(x))$ and let $c_{p} \in \operatorname{argmax}_{x} \nu_{p}(f(x))$. We show that this is good enough to compute all values of $x$, by looking at the exponent at each individual prime. Claim - For any $p \in \mathcal{P}$, we have $$ \nu_{p}(f(x))=\min \left(\nu_{p}\left(x-c_{p}\right), e_{p}\right) $$ $$ \operatorname{gcd}\left(f\left(c_{p}\right), f(x)\right)=\operatorname{gcd}\left(f\left(c_{p}\right), x-c_{p}\right) $$ We then take $\nu_{p}$ of both sides and recall $\nu_{p}(f(x)) \leq \nu_{p}\left(f\left(c_{p}\right)\right)=e_{p}$; this implies the result. This essentially determines $f$, and so now we just follow through. Choose $n$ and $m$ such that $$ \begin{aligned} n & =\prod_{p \in \mathcal{P}} p^{e_{p}} \\ m & \equiv-c_{p} \quad\left(\bmod p^{e_{p}}\right) \quad \forall p \in \mathcal{P} \end{aligned} $$ the latter being possible by Chinese remainder theorem. Then, from the claim we have $$ \begin{aligned} f(x) & =\prod_{p \in \mathcal{P}} p^{\nu_{p}(f(x))}=\prod_{p \mid n} p^{\min \left(\nu_{p}\left(x-c_{p}\right), e_{p}\right)} \\ & =\prod_{p \mid n} p^{\min \left(\nu_{p}(x+m), \nu_{p}(n)\right)}=\operatorname{gcd}(x+m, n) \end{aligned} $$ for every $x \in \mathbb{Z}$, as desired. Remark. The functions $f(x)=x$ and $f(x)=|2 x-1|$ are examples satisfying the gcd equation (the latter always being strictly positive). Hence the hypothesis $f$ bounded cannot be dropped. Remark. The pair $(m, n)$ is essentially unique: every other pair is obtained by shifting $m$ by a multiple of $n$. Hence there is not really any choice in choosing $m$ and $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f: \mathbb{Z} \rightarrow\left\{1,2, \ldots, 10^{100}\right\}$ be a function satisfying $$ \operatorname{gcd}(f(x), f(y))=\operatorname{gcd}(f(x), x-y) $$ for all integers $x$ and $y$. Show that there exist positive integers $m$ and $n$ such that $f(x)=\operatorname{gcd}(m+x, n)$ for all integers $x$.
|
Let $\mathcal{P}$ be the set of primes not exceeding $10^{100}$. For each $p \in \mathcal{P}$, let $e_{p}=\max _{x} \nu_{p}(f(x))$ and let $c_{p} \in \operatorname{argmax}_{x} \nu_{p}(f(x))$. We show that this is good enough to compute all values of $x$, by looking at the exponent at each individual prime. Claim - For any $p \in \mathcal{P}$, we have $$ \nu_{p}(f(x))=\min \left(\nu_{p}\left(x-c_{p}\right), e_{p}\right) $$ $$ \operatorname{gcd}\left(f\left(c_{p}\right), f(x)\right)=\operatorname{gcd}\left(f\left(c_{p}\right), x-c_{p}\right) $$ We then take $\nu_{p}$ of both sides and recall $\nu_{p}(f(x)) \leq \nu_{p}\left(f\left(c_{p}\right)\right)=e_{p}$; this implies the result. This essentially determines $f$, and so now we just follow through. Choose $n$ and $m$ such that $$ \begin{aligned} n & =\prod_{p \in \mathcal{P}} p^{e_{p}} \\ m & \equiv-c_{p} \quad\left(\bmod p^{e_{p}}\right) \quad \forall p \in \mathcal{P} \end{aligned} $$ the latter being possible by Chinese remainder theorem. Then, from the claim we have $$ \begin{aligned} f(x) & =\prod_{p \in \mathcal{P}} p^{\nu_{p}(f(x))}=\prod_{p \mid n} p^{\min \left(\nu_{p}\left(x-c_{p}\right), e_{p}\right)} \\ & =\prod_{p \mid n} p^{\min \left(\nu_{p}(x+m), \nu_{p}(n)\right)}=\operatorname{gcd}(x+m, n) \end{aligned} $$ for every $x \in \mathbb{Z}$, as desired. Remark. The functions $f(x)=x$ and $f(x)=|2 x-1|$ are examples satisfying the gcd equation (the latter always being strictly positive). Hence the hypothesis $f$ bounded cannot be dropped. Remark. The pair $(m, n)$ is essentially unique: every other pair is obtained by shifting $m$ by a multiple of $n$. Hence there is not really any choice in choosing $m$ and $n$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
2f318191-0345-5e82-a564-9df75a836f46
| 605,756 |
Let $A B C$ be a triangle with incenter $I$. Points $K$ and $L$ are chosen on segment $B C$ such that the incircles of $\triangle A B K$ and $\triangle A B L$ are tangent at $P$, and the incircles of $\triangle A C K$ and $\triangle A C L$ are tangent at $Q$. Prove that $I P=I Q$.
|
【 First solution, mostly elementary (original). Let $I_{B}, J_{B}, I_{C}, J_{C}$ be the incenters of $\triangle A B K, \triangle A B L, \triangle A C K, \triangle A C L$ respectively.  We begin with the following claim which does not depend on the existence of tangency points $P$ and $Q$. Claim - Lines $B C, I_{B} J_{C}, J_{B} I_{C}$ meet at a point $R$ (possibly at infinity). $$ A\left(B I ; I_{B} J_{B}\right)=A\left(I C ; I_{C} J_{C}\right) . $$ It follows $\left(B I ; I_{B} J_{B}\right)=\left(I C ; I_{C} J_{C}\right)=\left(C I ; J_{C} I_{C}\right)$. (One could also check directly that both cross ratios equal $\frac{\sin \angle B A K / 2}{\sin \angle C A K / 2} \div \frac{\sin \angle B A L / 2}{\sin \angle C A L / 2}$, rather than using rotation.) Therefore, the concurrence follows from the so-called prism lemma on $\overline{I B I_{B} J_{B}}$ and $\overline{I C J_{C} I_{C}}$. Remark (Nikolai Beluhov). This result is known; it appears as 4.5.32 in Akopyan's Geometry in Figures. The cross ratio is not necessary to prove this claim: it can be proven by length chasing with circumscribed quadrilaterals. (The generalization mentioned later also admits a trig-free proof for the analogous step.) We now bring $P$ and $Q$ into the problem. Claim - Line $P Q$ also passes through $R$. $$ \frac{I_{B} P}{P I} \cdot \frac{I Q}{Q J_{C}} \cdot \frac{J_{C} R}{R I_{B}}=-1 \Longrightarrow I P=I Q $$ Remark (Author's comments on drawing the diagram). Drawing the diagram directly is quite difficult. If one draws $\triangle A B C$ first, they must locate both $K$ and $L$, which likely involves some trial and error due to the complex interplay between the two points. There are alternative simpler ways. For example, one may draw $\triangle A K L$ first; then the remaining points $B$ and $C$ are not related and the task is much simpler (though some trial and error is still required). In fact, by breaking symmetry, we may only require one application of guesswork. Start by drawing $\triangle A B K$ and its incircle; then the incircle of $\triangle A B L$ may be constructed, and so point $L$ may be drawn. Thus only the location of point $C$ needs to be guessed. I would be interested in a method to create a general diagram without any trial and error.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$. Points $K$ and $L$ are chosen on segment $B C$ such that the incircles of $\triangle A B K$ and $\triangle A B L$ are tangent at $P$, and the incircles of $\triangle A C K$ and $\triangle A C L$ are tangent at $Q$. Prove that $I P=I Q$.
|
【 First solution, mostly elementary (original). Let $I_{B}, J_{B}, I_{C}, J_{C}$ be the incenters of $\triangle A B K, \triangle A B L, \triangle A C K, \triangle A C L$ respectively.  We begin with the following claim which does not depend on the existence of tangency points $P$ and $Q$. Claim - Lines $B C, I_{B} J_{C}, J_{B} I_{C}$ meet at a point $R$ (possibly at infinity). $$ A\left(B I ; I_{B} J_{B}\right)=A\left(I C ; I_{C} J_{C}\right) . $$ It follows $\left(B I ; I_{B} J_{B}\right)=\left(I C ; I_{C} J_{C}\right)=\left(C I ; J_{C} I_{C}\right)$. (One could also check directly that both cross ratios equal $\frac{\sin \angle B A K / 2}{\sin \angle C A K / 2} \div \frac{\sin \angle B A L / 2}{\sin \angle C A L / 2}$, rather than using rotation.) Therefore, the concurrence follows from the so-called prism lemma on $\overline{I B I_{B} J_{B}}$ and $\overline{I C J_{C} I_{C}}$. Remark (Nikolai Beluhov). This result is known; it appears as 4.5.32 in Akopyan's Geometry in Figures. The cross ratio is not necessary to prove this claim: it can be proven by length chasing with circumscribed quadrilaterals. (The generalization mentioned later also admits a trig-free proof for the analogous step.) We now bring $P$ and $Q$ into the problem. Claim - Line $P Q$ also passes through $R$. $$ \frac{I_{B} P}{P I} \cdot \frac{I Q}{Q J_{C}} \cdot \frac{J_{C} R}{R I_{B}}=-1 \Longrightarrow I P=I Q $$ Remark (Author's comments on drawing the diagram). Drawing the diagram directly is quite difficult. If one draws $\triangle A B C$ first, they must locate both $K$ and $L$, which likely involves some trial and error due to the complex interplay between the two points. There are alternative simpler ways. For example, one may draw $\triangle A K L$ first; then the remaining points $B$ and $C$ are not related and the task is much simpler (though some trial and error is still required). In fact, by breaking symmetry, we may only require one application of guesswork. Start by drawing $\triangle A B K$ and its incircle; then the incircle of $\triangle A B L$ may be constructed, and so point $L$ may be drawn. Thus only the location of point $C$ needs to be guessed. I would be interested in a method to create a general diagram without any trial and error.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
63e39be8-8cc5-5897-8e3c-8890dcff8579
| 247,456 |
Let $A B C$ be a triangle with incenter $I$. Points $K$ and $L$ are chosen on segment $B C$ such that the incircles of $\triangle A B K$ and $\triangle A B L$ are tangent at $P$, and the incircles of $\triangle A C K$ and $\triangle A C L$ are tangent at $Q$. Prove that $I P=I Q$.
|
【 Second solution, inversion (Nikolai Beluhov). As above, the lines $B C, I_{B} J_{C}, J_{B} I_{C}$ meet at some point $R$ (possibly at infinity). Let $\omega_{1}, \omega_{2}, \omega_{3}, \omega_{4}$ be the incircles of $\triangle A B K$, $\triangle A C L, \triangle A B L$, and $\triangle A C K$. Claim - There exists an inversion $\iota$ at $R$ swapping $\left\{\omega_{1}, \omega_{2}\right\}$ and $\left\{\omega_{3}, \omega_{4}\right\}$. Claim - Circles $\omega_{1}, \omega_{2}, \omega_{3}, \omega_{4}$ share a common radical center. Then $k$ is actually orthogonal to $\Omega, \omega_{1}, \omega_{3}$, so $k$ is fixed under $\iota$ and $k$ is also orthogonal to $\omega_{2}$ and $\omega_{4}$. Thus the center of $k$ is the desired radical center. The desired statement immediately follows. Indeed, letting $S$ be the radical center, it follows that $\overline{S P}$ and $\overline{S Q}$ are the common internal tangents to $\left\{\omega_{1}, \omega_{3}\right\}$ and $\left\{\omega_{2}, \omega_{4}\right\}$. Since $S$ is the radical center, $S P=S Q$. In light of $\angle S P I=\angle S Q I=90^{\circ}$, it follows that $I P=I Q$, as desired. Remark (Nikolai Beluhov). There exists a circle tangent to all four incircles, because circle $k$ is orthogonal to all four, and line $B C$ is tangent to all four; thus the inverse of line $B C$ in $k$ is a circle tangent to all four incircles. The amusing thing here is that Casey's theorem is completely unhelpful for proving this fact: all it can tell us is that there is a line or circle tangent to these incircles, and line $B C$ already satisfies this property. Remark (Generalization by Nikolai Beluhov). The following generalization holds: Let $A B C D$ be a quadrilateral circumscribed about a circle with center $I$. A line through $A$ meets $\overrightarrow{B C}$ and $\overrightarrow{D C}$ at $K$ and $L$; another line through $A$ meets $\overrightarrow{B C}$ and $\overrightarrow{D C}$ at $M$ and $N$. Suppose that the incircles of $\triangle A B K$ and $\triangle A B M$ are tangent at $P$, and the incircles of $\triangle A C L$ and $\triangle A C N$ are tangent at $Q$. Prove that $I P=I Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$. Points $K$ and $L$ are chosen on segment $B C$ such that the incircles of $\triangle A B K$ and $\triangle A B L$ are tangent at $P$, and the incircles of $\triangle A C K$ and $\triangle A C L$ are tangent at $Q$. Prove that $I P=I Q$.
|
【 Second solution, inversion (Nikolai Beluhov). As above, the lines $B C, I_{B} J_{C}, J_{B} I_{C}$ meet at some point $R$ (possibly at infinity). Let $\omega_{1}, \omega_{2}, \omega_{3}, \omega_{4}$ be the incircles of $\triangle A B K$, $\triangle A C L, \triangle A B L$, and $\triangle A C K$. Claim - There exists an inversion $\iota$ at $R$ swapping $\left\{\omega_{1}, \omega_{2}\right\}$ and $\left\{\omega_{3}, \omega_{4}\right\}$. Claim - Circles $\omega_{1}, \omega_{2}, \omega_{3}, \omega_{4}$ share a common radical center. Then $k$ is actually orthogonal to $\Omega, \omega_{1}, \omega_{3}$, so $k$ is fixed under $\iota$ and $k$ is also orthogonal to $\omega_{2}$ and $\omega_{4}$. Thus the center of $k$ is the desired radical center. The desired statement immediately follows. Indeed, letting $S$ be the radical center, it follows that $\overline{S P}$ and $\overline{S Q}$ are the common internal tangents to $\left\{\omega_{1}, \omega_{3}\right\}$ and $\left\{\omega_{2}, \omega_{4}\right\}$. Since $S$ is the radical center, $S P=S Q$. In light of $\angle S P I=\angle S Q I=90^{\circ}$, it follows that $I P=I Q$, as desired. Remark (Nikolai Beluhov). There exists a circle tangent to all four incircles, because circle $k$ is orthogonal to all four, and line $B C$ is tangent to all four; thus the inverse of line $B C$ in $k$ is a circle tangent to all four incircles. The amusing thing here is that Casey's theorem is completely unhelpful for proving this fact: all it can tell us is that there is a line or circle tangent to these incircles, and line $B C$ already satisfies this property. Remark (Generalization by Nikolai Beluhov). The following generalization holds: Let $A B C D$ be a quadrilateral circumscribed about a circle with center $I$. A line through $A$ meets $\overrightarrow{B C}$ and $\overrightarrow{D C}$ at $K$ and $L$; another line through $A$ meets $\overrightarrow{B C}$ and $\overrightarrow{D C}$ at $M$ and $N$. Suppose that the incircles of $\triangle A B K$ and $\triangle A B M$ are tangent at $P$, and the incircles of $\triangle A C L$ and $\triangle A C N$ are tangent at $Q$. Prove that $I P=I Q$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
63e39be8-8cc5-5897-8e3c-8890dcff8579
| 247,456 |
Let $A B C$ be a scalene triangle with incenter $I$. The incircle of $A B C$ touches $\overline{B C}$, $\overline{C A}, \overline{A B}$ at points $D, E, F$, respectively. Let $P$ be the foot of the altitude from $D$ to $\overline{E F}$, and let $M$ be the midpoint of $\overline{B C}$. The rays $A P$ and $I P$ intersect the circumcircle of triangle $A B C$ again at points $G$ and $Q$, respectively. Show that the incenter of triangle $G Q M$ coincides with $D$.
|
Refer to the figure below. 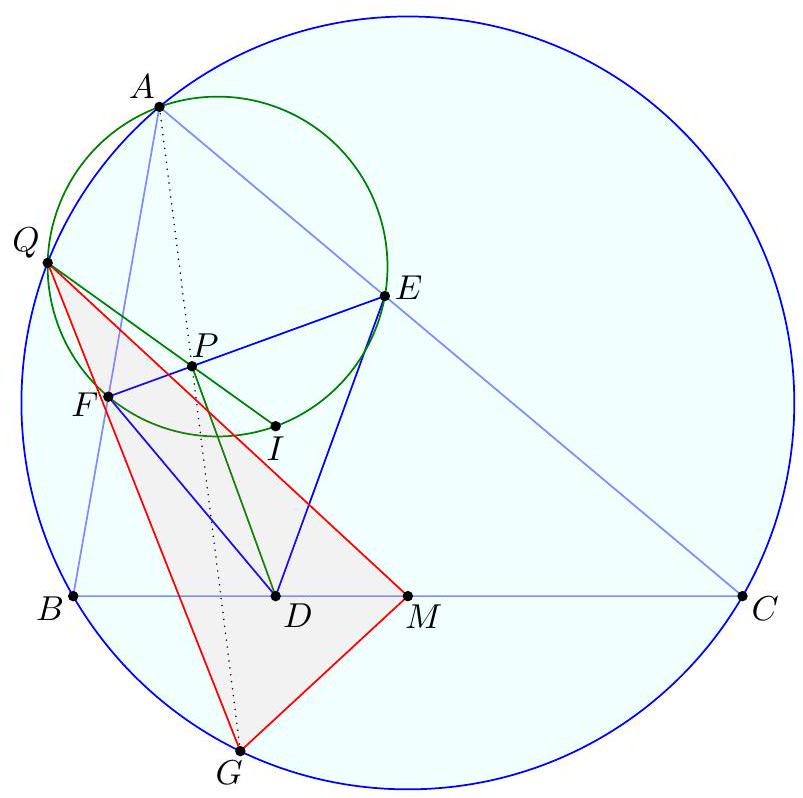 Claim - The point $Q$ is the Miquel point of $B F E C$. Also, $\overline{Q D}$ bisects $\angle B Q C$. The spiral similarity mentioned then gives $\frac{Q B}{B F}=\frac{Q C}{C E}$, so $\overline{Q D}$ bisects $\angle B Q C$. Remark. The point $Q$ and its properties mentioned in the first claim have appeared in other references. See for example Canada 2007/5, ELMO 2010/6, HMMT 2016 T-10, USA TST 2017/2, USA TST 2019/6 for a few examples. Claim - We have $(Q G ; B C)=-1$, so in particular $\overline{G D}$ bisects $\angle B G C$. $$ -1=(A I ; E F) \stackrel{Q}{=}(\overline{A Q} \cap \overline{E F}, P ; E, F) \stackrel{A}{=}(Q G ; B C) $$ The last statement follows from Apollonian circle, or more bluntly $\frac{G B}{G C}=\frac{Q B}{Q C}=\frac{B D}{D C}$. Hence $\overline{Q D}$ and $\overline{G D}$ are angle bisectors of $\angle B Q C$ and $\angle B G C$. However, $\overline{Q M}$ and $\overline{Q G}$ are isogonal in $\angle B Q C$ (as median and symmedian), and similarly for $\angle B G C$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with incenter $I$. The incircle of $A B C$ touches $\overline{B C}$, $\overline{C A}, \overline{A B}$ at points $D, E, F$, respectively. Let $P$ be the foot of the altitude from $D$ to $\overline{E F}$, and let $M$ be the midpoint of $\overline{B C}$. The rays $A P$ and $I P$ intersect the circumcircle of triangle $A B C$ again at points $G$ and $Q$, respectively. Show that the incenter of triangle $G Q M$ coincides with $D$.
|
Refer to the figure below.  Claim - The point $Q$ is the Miquel point of $B F E C$. Also, $\overline{Q D}$ bisects $\angle B Q C$. The spiral similarity mentioned then gives $\frac{Q B}{B F}=\frac{Q C}{C E}$, so $\overline{Q D}$ bisects $\angle B Q C$. Remark. The point $Q$ and its properties mentioned in the first claim have appeared in other references. See for example Canada 2007/5, ELMO 2010/6, HMMT 2016 T-10, USA TST 2017/2, USA TST 2019/6 for a few examples. Claim - We have $(Q G ; B C)=-1$, so in particular $\overline{G D}$ bisects $\angle B G C$. $$ -1=(A I ; E F) \stackrel{Q}{=}(\overline{A Q} \cap \overline{E F}, P ; E, F) \stackrel{A}{=}(Q G ; B C) $$ The last statement follows from Apollonian circle, or more bluntly $\frac{G B}{G C}=\frac{Q B}{Q C}=\frac{B D}{D C}$. Hence $\overline{Q D}$ and $\overline{G D}$ are angle bisectors of $\angle B Q C$ and $\angle B G C$. However, $\overline{Q M}$ and $\overline{Q G}$ are isogonal in $\angle B Q C$ (as median and symmedian), and similarly for $\angle B G C$, as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
ef648da6-cd60-551e-aee1-230f005bf5fe
| 247,472 |
Let $\mathbb{N}^{2}$ denote the set of ordered pairs of positive integers. A finite subset $S$ of $\mathbb{N}^{2}$ is stable if whenever $(x, y)$ is in $S$, then so are all points $\left(x^{\prime}, y^{\prime}\right)$ of $\mathbb{N}^{2}$ with both $x^{\prime} \leq x$ and $y^{\prime} \leq y$. Prove that if $S$ is a stable set, then among all stable subsets of $S$ (including the empty set and $S$ itself), at least half of them have an even number of elements.
|
Suppose $|S| \geq 2$. For any $p \in S$, let $R(p)$ denote the stable rectangle with upper-right corner $p$. We say such $p$ is pivotal if $p+(1,1) \notin S$ and $|R(p)|$ is even.  Claim - If $|S| \geq 2$, then a pivotal $p$ always exists. - If it has length at least 2 , one of the two rightmost points in it is pivotal. - Otherwise, the top row has length 1. Now either the top point or the point below it (which exists as $|S| \geq 2$ ) is pivotal. We describe how to complete the induction, given some pivotal $p \in S$. There is a partition $$ S=R(p) \sqcup S_{1} \sqcup S_{2} $$ where $S_{1}$ and $S_{2}$ are the sets of points in $S$ above and to the right of $p$ (possibly empty). Claim - The desired inequality holds for stable subsets containing $p$. Since $|R(p)|$ is even, exactly $E_{1} E_{2}+O_{1} O_{2}$ stable subsets containing $p$ are even, and exactly $E_{1} O_{2}+E_{2} O_{1}$ are odd. As $E_{1} \geq O_{1}$ and $E_{2} \geq O_{2}$ by inductive hypothesis, we obtain $E_{1} E_{2}+O_{1} O_{2} \geq E_{1} O_{2}+E_{2} O_{1}$ as desired. By the inductive hypothesis, the desired inequality also holds for stable subsets not containing $p$, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $\mathbb{N}^{2}$ denote the set of ordered pairs of positive integers. A finite subset $S$ of $\mathbb{N}^{2}$ is stable if whenever $(x, y)$ is in $S$, then so are all points $\left(x^{\prime}, y^{\prime}\right)$ of $\mathbb{N}^{2}$ with both $x^{\prime} \leq x$ and $y^{\prime} \leq y$. Prove that if $S$ is a stable set, then among all stable subsets of $S$ (including the empty set and $S$ itself), at least half of them have an even number of elements.
|
Suppose $|S| \geq 2$. For any $p \in S$, let $R(p)$ denote the stable rectangle with upper-right corner $p$. We say such $p$ is pivotal if $p+(1,1) \notin S$ and $|R(p)|$ is even.  Claim - If $|S| \geq 2$, then a pivotal $p$ always exists. - If it has length at least 2 , one of the two rightmost points in it is pivotal. - Otherwise, the top row has length 1. Now either the top point or the point below it (which exists as $|S| \geq 2$ ) is pivotal. We describe how to complete the induction, given some pivotal $p \in S$. There is a partition $$ S=R(p) \sqcup S_{1} \sqcup S_{2} $$ where $S_{1}$ and $S_{2}$ are the sets of points in $S$ above and to the right of $p$ (possibly empty). Claim - The desired inequality holds for stable subsets containing $p$. Since $|R(p)|$ is even, exactly $E_{1} E_{2}+O_{1} O_{2}$ stable subsets containing $p$ are even, and exactly $E_{1} O_{2}+E_{2} O_{1}$ are odd. As $E_{1} \geq O_{1}$ and $E_{2} \geq O_{2}$ by inductive hypothesis, we obtain $E_{1} E_{2}+O_{1} O_{2} \geq E_{1} O_{2}+E_{2} O_{1}$ as desired. By the inductive hypothesis, the desired inequality also holds for stable subsets not containing $p$, so we are done.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
300872e1-b631-560e-80d3-46564c7d4d56
| 605,860 |
Let $A, B, C, D$ be four points such that no three are collinear and $D$ is not the orthocenter of triangle $A B C$. Let $P, Q, R$ be the orthocenters of $\triangle B C D, \triangle C A D$, $\triangle A B D$, respectively. Suppose that lines $A P, B Q, C R$ are pairwise distinct and are concurrent. Show that the four points $A, B, C, D$ lie on a circle.
|
Let $T$ be the concurrency point, and let $H$ be the orthocenter of $\triangle A B C$.  Claim (Key claim) - $T$ is the midpoint of $\overline{A P}, \overline{B Q}, \overline{C R}, \overline{D H}$, and $D$ is the orthocenter of $\triangle P Q R$. By symmetric reasoning, we get that $A Q C P B R$ is a hexagon with opposite sides parallel and concurrent diagonals as $\overline{A P}, \overline{B Q}, \overline{C R}$ meet at $T$. This implies that the hexagon is centrally symmetric about $T$; indeed $$ \frac{A T}{T P}=\frac{T Q}{B T}=\frac{C T}{T R}=\frac{T P}{A T} $$ so all the ratios are equal to +1 . Next, $\overline{P D} \perp \overline{B C} \| \overline{Q R}$, so by symmetry we get $D$ is the orthocenter of $\triangle P Q R$. This means that $T$ is the midpoint of $\overline{D H}$ as well. ## Corollary The configuration is now symmetric: we have four points $A, B, C, D$, and their reflections in $T$ are four orthocenters $P, Q, R, H$. Let $S$ be the centroid of $\{A, B, C, D\}$, and let $O$ be the reflection of $T$ in $S$. We are ready to conclude: Claim - $A, B, C, D$ are equidistant from $O$. Then $T^{\prime}$ is the midpoint of $\overline{A^{\prime} D^{\prime}}$, so $S^{\prime}=\frac{1}{4}\left(A^{\prime}+D^{\prime}+B+C\right)$ gives that $O^{\prime}$ is the midpoint of $\overline{B C}$. Thus $O B=O C$ and we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, C, D$ be four points such that no three are collinear and $D$ is not the orthocenter of triangle $A B C$. Let $P, Q, R$ be the orthocenters of $\triangle B C D, \triangle C A D$, $\triangle A B D$, respectively. Suppose that lines $A P, B Q, C R$ are pairwise distinct and are concurrent. Show that the four points $A, B, C, D$ lie on a circle.
|
Let $T$ be the concurrency point, and let $H$ be the orthocenter of $\triangle A B C$.  Claim (Key claim) - $T$ is the midpoint of $\overline{A P}, \overline{B Q}, \overline{C R}, \overline{D H}$, and $D$ is the orthocenter of $\triangle P Q R$. By symmetric reasoning, we get that $A Q C P B R$ is a hexagon with opposite sides parallel and concurrent diagonals as $\overline{A P}, \overline{B Q}, \overline{C R}$ meet at $T$. This implies that the hexagon is centrally symmetric about $T$; indeed $$ \frac{A T}{T P}=\frac{T Q}{B T}=\frac{C T}{T R}=\frac{T P}{A T} $$ so all the ratios are equal to +1 . Next, $\overline{P D} \perp \overline{B C} \| \overline{Q R}$, so by symmetry we get $D$ is the orthocenter of $\triangle P Q R$. This means that $T$ is the midpoint of $\overline{D H}$ as well. ## Corollary The configuration is now symmetric: we have four points $A, B, C, D$, and their reflections in $T$ are four orthocenters $P, Q, R, H$. Let $S$ be the centroid of $\{A, B, C, D\}$, and let $O$ be the reflection of $T$ in $S$. We are ready to conclude: Claim - $A, B, C, D$ are equidistant from $O$. Then $T^{\prime}$ is the midpoint of $\overline{A^{\prime} D^{\prime}}$, so $S^{\prime}=\frac{1}{4}\left(A^{\prime}+D^{\prime}+B+C\right)$ gives that $O^{\prime}$ is the midpoint of $\overline{B C}$. Thus $O B=O C$ and we're done.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
3883ef38-95ff-59e5-abf8-7264a9c617bb
| 247,504 |
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
『 First solution, angle chasing only (Ankit Bisain). Let lines $B Q$ and $D P$ meet $(A B C D)$ again at $D^{\prime}$ and $B^{\prime}$, respectively.  Then $B B^{\prime} \| P X$ and $D D^{\prime} \| Q Y$ by Reim's theorem. Segments $B B^{\prime}, D D^{\prime}$, and $P Q$ share a perpendicular bisector which passes through $O$, so $O P=O Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
『 First solution, angle chasing only (Ankit Bisain). Let lines $B Q$ and $D P$ meet $(A B C D)$ again at $D^{\prime}$ and $B^{\prime}$, respectively.  Then $B B^{\prime} \| P X$ and $D D^{\prime} \| Q Y$ by Reim's theorem. Segments $B B^{\prime}, D D^{\prime}$, and $P Q$ share a perpendicular bisector which passes through $O$, so $O P=O Q$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0def9412-9295-5e69-9eac-0e29c6e12e4b
| 247,540 |
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Second solution via isosceles triangles (from contestants). Let $T=\overline{B Q} \cap \overline{D P}$. 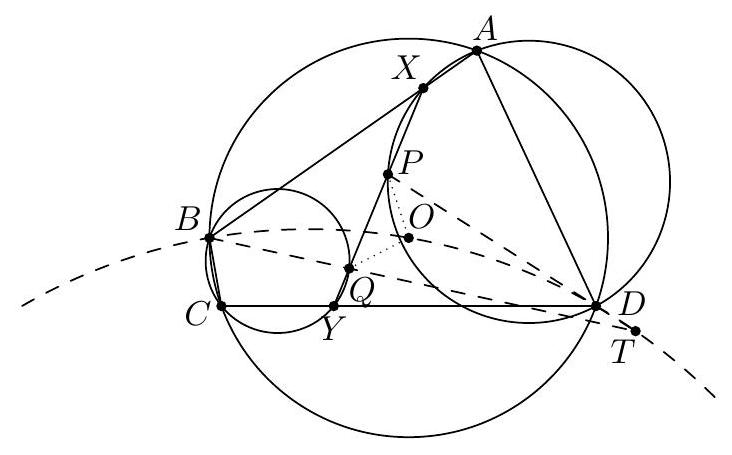 Note that $P Q T$ is isosceles because $$ \measuredangle P Q T=\measuredangle Y Q B=\measuredangle B C D=\measuredangle B A D=\measuredangle X P D=\measuredangle T P Q $$ Then $(B O D T)$ is cyclic because $$ \measuredangle B O D=2 \measuredangle B C D=\measuredangle P Q T+\measuredangle T P Q=\measuredangle B T D . $$ Since $B O=O D, \overline{T O}$ is an angle bisector of $\measuredangle B T D$. Since $\triangle P Q T$ is isosceles, $\overline{T O} \perp \overline{P Q}$, so $O P=O Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Second solution via isosceles triangles (from contestants). Let $T=\overline{B Q} \cap \overline{D P}$.  Note that $P Q T$ is isosceles because $$ \measuredangle P Q T=\measuredangle Y Q B=\measuredangle B C D=\measuredangle B A D=\measuredangle X P D=\measuredangle T P Q $$ Then $(B O D T)$ is cyclic because $$ \measuredangle B O D=2 \measuredangle B C D=\measuredangle P Q T+\measuredangle T P Q=\measuredangle B T D . $$ Since $B O=O D, \overline{T O}$ is an angle bisector of $\measuredangle B T D$. Since $\triangle P Q T$ is isosceles, $\overline{T O} \perp \overline{P Q}$, so $O P=O Q$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0def9412-9295-5e69-9eac-0e29c6e12e4b
| 247,540 |
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
ब Third solution using a parallelogram (from contestants). Let $(B C Y)$ meet $\overline{A B}$ again at $W$ and let $(A D X)$ meet $\overline{C D}$ again at $Z$. Additionally, let $O_{1}$ be the center of $(A D X)$ and $O_{2}$ be the center of $(B C Y)$. 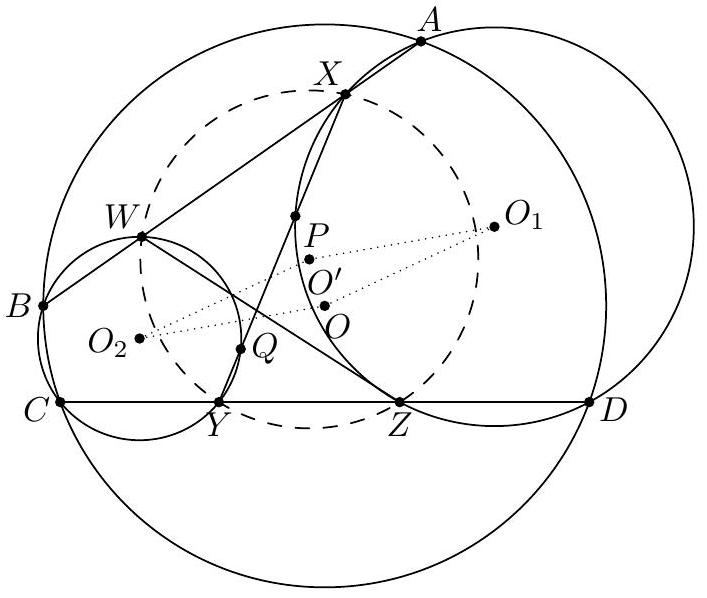 Note that $(W X Y Z)$ is cyclic since $$ \measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ} $$ so let $O^{\prime}$ be the center of ( $W X Y Z$ ). Since $\overline{A D} \| \overline{W Y}$ and $\overline{B C} \| \overline{X Z}$ by Reim's theorem, $O O_{1} O^{\prime} O_{2}$ is a parallelogram. To finish the problem, note that projecting $O_{1}, O_{2}$, and $O^{\prime}$ onto $\overline{X Y}$ gives the midpoints of $\overline{P X}, \overline{Q Y}$, and $\overline{X Y}$. Since $O O_{1} O^{\prime} O_{2}$ is a parallelogram, projecting $O$ onto $\overline{X Y}$ must give the midpoint of $\overline{P Q}$, so $O P=O Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
ब Third solution using a parallelogram (from contestants). Let $(B C Y)$ meet $\overline{A B}$ again at $W$ and let $(A D X)$ meet $\overline{C D}$ again at $Z$. Additionally, let $O_{1}$ be the center of $(A D X)$ and $O_{2}$ be the center of $(B C Y)$.  Note that $(W X Y Z)$ is cyclic since $$ \measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ} $$ so let $O^{\prime}$ be the center of ( $W X Y Z$ ). Since $\overline{A D} \| \overline{W Y}$ and $\overline{B C} \| \overline{X Z}$ by Reim's theorem, $O O_{1} O^{\prime} O_{2}$ is a parallelogram. To finish the problem, note that projecting $O_{1}, O_{2}$, and $O^{\prime}$ onto $\overline{X Y}$ gives the midpoints of $\overline{P X}, \overline{Q Y}$, and $\overline{X Y}$. Since $O O_{1} O^{\prime} O_{2}$ is a parallelogram, projecting $O$ onto $\overline{X Y}$ must give the midpoint of $\overline{P Q}$, so $O P=O Q$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0def9412-9295-5e69-9eac-0e29c6e12e4b
| 247,540 |
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
ब Fourth solution using congruent circles (from contestants). Let the angle bisector of $\measuredangle B O D$ meet $\overline{X Y}$ at $K$. 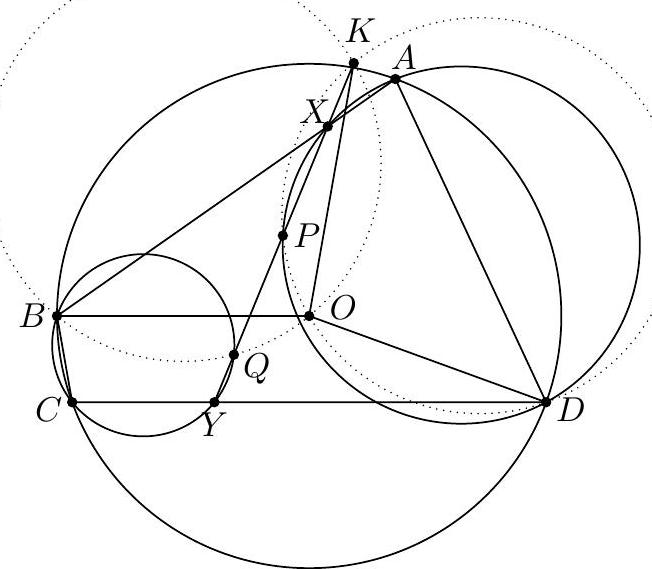 Then $(B Q O K)$ is cyclic because $\measuredangle K O D=\measuredangle B A D=\measuredangle K P D$, and $(D O P K)$ is cyclic similarly. By symmetry over $K O$, these circles have the same radius $r$, so $$ O P=2 r \sin \angle O K P=2 r \sin \angle O K Q=O Q $$ by the Law of Sines.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
ब Fourth solution using congruent circles (from contestants). Let the angle bisector of $\measuredangle B O D$ meet $\overline{X Y}$ at $K$.  Then $(B Q O K)$ is cyclic because $\measuredangle K O D=\measuredangle B A D=\measuredangle K P D$, and $(D O P K)$ is cyclic similarly. By symmetry over $K O$, these circles have the same radius $r$, so $$ O P=2 r \sin \angle O K P=2 r \sin \angle O K Q=O Q $$ by the Law of Sines.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0def9412-9295-5e69-9eac-0e29c6e12e4b
| 247,540 |
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Fifth solution by ratio calculation (from contestants). Let $\overline{X Y}$ meet $(A B C D)$ at $X^{\prime}$ and $Y^{\prime}$. 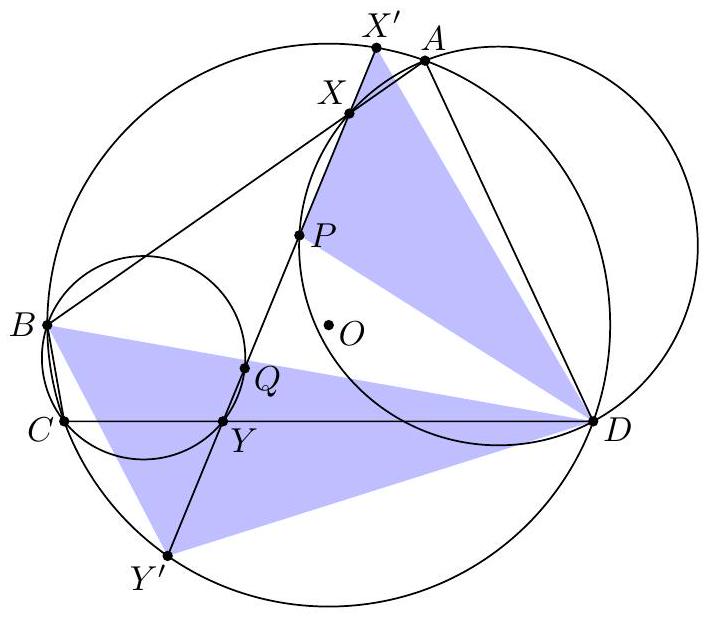 Since $\measuredangle Y^{\prime} B D=\measuredangle P X^{\prime} D$ and $\measuredangle B Y^{\prime} D=\measuredangle B A D=\measuredangle X^{\prime} P D$, $$ \triangle B Y^{\prime} D \sim \triangle X P^{\prime} D \Longrightarrow P X^{\prime}=B Y^{\prime} \cdot \frac{D X^{\prime}}{B D} $$ Similarly, $$ \triangle B X^{\prime} D \sim \triangle B Q Y^{\prime} \Longrightarrow Q Y^{\prime}=D X^{\prime} \cdot \frac{B Y^{\prime}}{B D} $$ Thus $P X^{\prime}=Q Y^{\prime}$, which gives $O P=O Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Fifth solution by ratio calculation (from contestants). Let $\overline{X Y}$ meet $(A B C D)$ at $X^{\prime}$ and $Y^{\prime}$.  Since $\measuredangle Y^{\prime} B D=\measuredangle P X^{\prime} D$ and $\measuredangle B Y^{\prime} D=\measuredangle B A D=\measuredangle X^{\prime} P D$, $$ \triangle B Y^{\prime} D \sim \triangle X P^{\prime} D \Longrightarrow P X^{\prime}=B Y^{\prime} \cdot \frac{D X^{\prime}}{B D} $$ Similarly, $$ \triangle B X^{\prime} D \sim \triangle B Q Y^{\prime} \Longrightarrow Q Y^{\prime}=D X^{\prime} \cdot \frac{B Y^{\prime}}{B D} $$ Thus $P X^{\prime}=Q Y^{\prime}$, which gives $O P=O Q$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0def9412-9295-5e69-9eac-0e29c6e12e4b
| 247,540 |
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
I Sixth solution using radical axis (from author). Without loss of generality, assume $\overline{A D} \nVdash \overline{B C}$, as this case holds by continuity. Let $(B C Y)$ meet $\overline{A B}$ again at $W$, let $(A D X)$ meet $\overline{C D}$ again at $Z$, and let $\overline{W Z}$ meet $(A D X)$ and $(B C Y)$ again at $R$ and $S$. 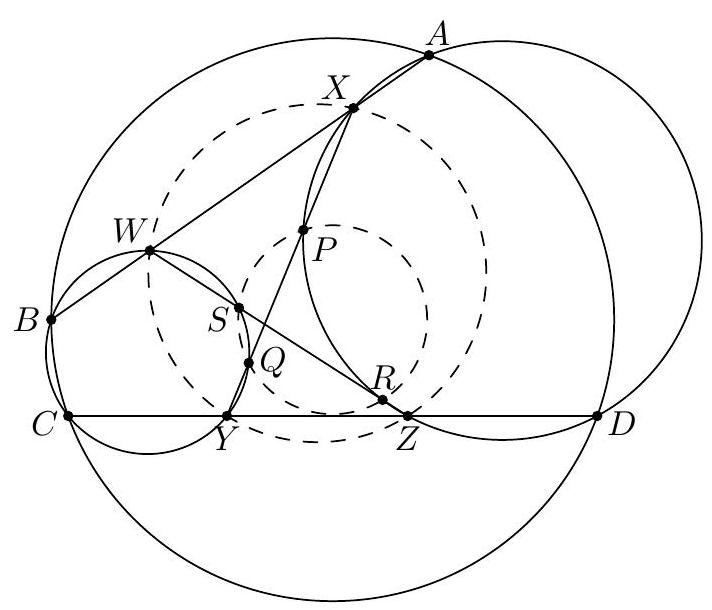 Note that $(W X Y Z)$ is cyclic since $$ \measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ} $$ and $(P Q R S)$ is cyclic since $$ \measuredangle P Q S=\measuredangle Y Q S=\measuredangle Y W S=\measuredangle P X Z=\measuredangle P R Z=\measuredangle S R P $$ Additionally, $\overline{A D} \| \overline{P R}$ since $$ \measuredangle D A X+\measuredangle A X P+\measuredangle X P R=\measuredangle Y W X+\measuredangle W X Y+\measuredangle X Y W=0^{\circ}, $$ and $\overline{B C} \| \overline{S Q}$ similarly. Lastly, $(A B C D)$ and $(P Q R S)$ are concentric; if not, using the radical axis theorem twice shows that their radical axis must be parallel to both $\overline{A D}$ and $\overline{B C}$, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
I Sixth solution using radical axis (from author). Without loss of generality, assume $\overline{A D} \nVdash \overline{B C}$, as this case holds by continuity. Let $(B C Y)$ meet $\overline{A B}$ again at $W$, let $(A D X)$ meet $\overline{C D}$ again at $Z$, and let $\overline{W Z}$ meet $(A D X)$ and $(B C Y)$ again at $R$ and $S$.  Note that $(W X Y Z)$ is cyclic since $$ \measuredangle X W Y+\measuredangle Y Z X=\measuredangle Y W B+\measuredangle X Z D=\measuredangle Y C B+\measuredangle X A D=0^{\circ} $$ and $(P Q R S)$ is cyclic since $$ \measuredangle P Q S=\measuredangle Y Q S=\measuredangle Y W S=\measuredangle P X Z=\measuredangle P R Z=\measuredangle S R P $$ Additionally, $\overline{A D} \| \overline{P R}$ since $$ \measuredangle D A X+\measuredangle A X P+\measuredangle X P R=\measuredangle Y W X+\measuredangle W X Y+\measuredangle X Y W=0^{\circ}, $$ and $\overline{B C} \| \overline{S Q}$ similarly. Lastly, $(A B C D)$ and $(P Q R S)$ are concentric; if not, using the radical axis theorem twice shows that their radical axis must be parallel to both $\overline{A D}$ and $\overline{B C}$, contradiction.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0def9412-9295-5e69-9eac-0e29c6e12e4b
| 247,540 |
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Seventh solution using Cayley-Bacharach (author). Define points $W, Z, R, S$ as in the previous solution. 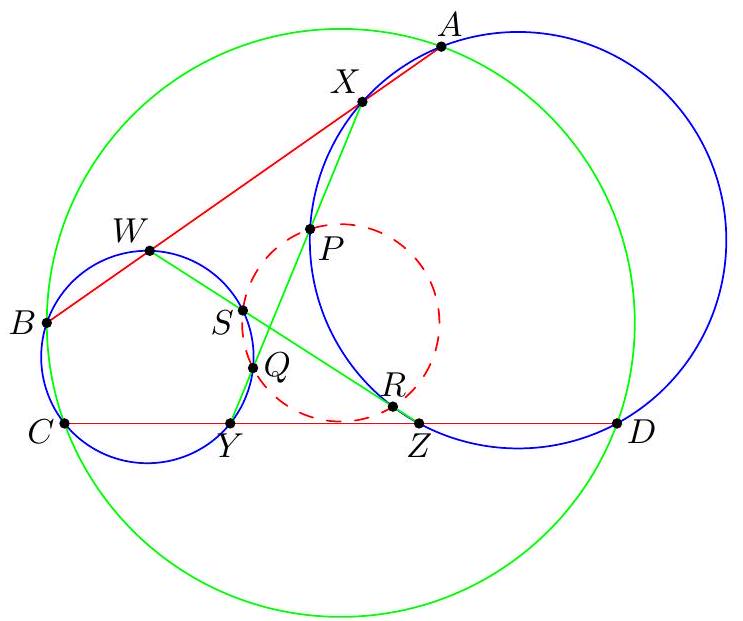 The quartics $(A D X Z) \cup(B C W Y)$ and $\overline{X Y} \cup \overline{W Z} \cup(A B C D)$ meet at the 16 points $$ A, B, C, D, W, X, Y, Z, P, Q, R, S, I, I, J, J $$ where $I$ and $J$ are the circular points at infinity. Since $\overline{A B} \cup \overline{C D} \cup(P Q R)$ contains the 13 points $$ A, B, C, D, P, Q, R, W, X, Y, Z, I, J $$ it must contain $S, I$, and $J$ as well, by quartic Cayley-Bacharach. Thus, $(P Q R S)$ is cyclic and intersects $(A B C D)$ at $I, I, J$, and $J$, implying that the two circles are concentric, as desired. Remark (Author comments). Holden says he came up with this problem via the CayleyBacharach solution, by trying to get two quartics to intersect.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Points $X$ and $Y$ lie on sides $A B$ and $C D$, respectively. Suppose the circumcircles of $A D X$ and $B C Y$ meet line $X Y$ again at $P$ and $Q$, respectively. Show that $O P=O Q$.
|
【 Seventh solution using Cayley-Bacharach (author). Define points $W, Z, R, S$ as in the previous solution.  The quartics $(A D X Z) \cup(B C W Y)$ and $\overline{X Y} \cup \overline{W Z} \cup(A B C D)$ meet at the 16 points $$ A, B, C, D, W, X, Y, Z, P, Q, R, S, I, I, J, J $$ where $I$ and $J$ are the circular points at infinity. Since $\overline{A B} \cup \overline{C D} \cup(P Q R)$ contains the 13 points $$ A, B, C, D, P, Q, R, W, X, Y, Z, I, J $$ it must contain $S, I$, and $J$ as well, by quartic Cayley-Bacharach. Thus, $(P Q R S)$ is cyclic and intersects $(A B C D)$ at $I, I, J$, and $J$, implying that the two circles are concentric, as desired. Remark (Author comments). Holden says he came up with this problem via the CayleyBacharach solution, by trying to get two quartics to intersect.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0def9412-9295-5e69-9eac-0e29c6e12e4b
| 247,540 |
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 1 (Merlijn Staps). We argue by contradiction, so suppose that for each $\lambda$ for which the set $S_{\lambda}=\left\{k: a_{k} / k=\lambda\right\}$ is non-empty, it contains at least two elements. Note that $S_{\lambda}$ is always a finite set because $a_{k}=k \lambda$ implies $k<1 / \lambda$. Write $m_{\lambda}$ and $M_{\lambda}$ for the smallest and largest element of $S_{\lambda}$, respectively, and define $T_{\lambda}=\left\{m_{\lambda}, m_{\lambda}+1, \ldots, M_{\lambda}\right\}$ as the smallest set of consecutive positive integers that contains $S_{\lambda}$. Then all $T_{\lambda}$ are sets of at least two consecutive positive integers, and moreover the $T_{\lambda}$ cover $\mathbb{N}$. Additionally, each positive integer is covered finitely many times because there are only finitely many possible values of $m_{\lambda}$ smaller than any fixed integer. Recall that if three intervals have a point in common then one of them is contained in the union of the other two. Thus, if any positive integer is covered more than twice by the sets $T_{\lambda}$, we may throw out one set while maintaining the property that the $T_{\lambda}$ cover $\mathbb{N}$. By using the fact that each positive integer is covered finitely many times, we can apply this process so that each positive integer is eventually covered at most twice. Let $\Lambda$ denote the set of the $\lambda$-values for which $T_{\lambda}$ remains in our collection of sets; then $\bigcup_{\lambda \in \Lambda} T_{\lambda}=\mathbb{N}$ and each positive integer is contained in at most two sets $T_{\lambda}$. We now obtain $$ \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \leq 2 \sum_{k \geq 1}\left(a_{k+1}-a_{k}\right) \leq 2 $$ On the other hand, because $a_{m_{\lambda}}=\lambda m_{\lambda}$ and $a_{M_{\lambda}}=\lambda M_{\lambda}$, we have $$ \begin{aligned} 2 \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) & \geq 2 \sum_{m_{\lambda} \leq k<M_{\lambda}}\left(a_{k+1}-a_{k}\right)=2\left(a_{M_{\lambda}}-a_{m_{\lambda}}\right)=2\left(M_{\lambda}-m_{\lambda}\right) \lambda \\ & =2\left(M_{\lambda}-m_{\lambda}\right) \cdot \frac{a_{m_{\lambda}}}{m_{\lambda}} \geq\left(M_{\lambda}-m_{\lambda}+1\right) \cdot \frac{a_{1}}{m_{\lambda}} \geq a_{1} \cdot \sum_{k \in T_{\lambda}} \frac{1}{k} . \end{aligned} $$ Combining this with our first estimate, and using the fact that the $T_{\lambda}$ cover $\mathbb{N}$, we obtain $$ 4 \geq 2 \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \geq a_{1} \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}} \frac{1}{k} \geq a_{1} \sum_{k \geq 1} \frac{1}{k} $$ contradicting the fact that the harmonic series diverges.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 1 (Merlijn Staps). We argue by contradiction, so suppose that for each $\lambda$ for which the set $S_{\lambda}=\left\{k: a_{k} / k=\lambda\right\}$ is non-empty, it contains at least two elements. Note that $S_{\lambda}$ is always a finite set because $a_{k}=k \lambda$ implies $k<1 / \lambda$. Write $m_{\lambda}$ and $M_{\lambda}$ for the smallest and largest element of $S_{\lambda}$, respectively, and define $T_{\lambda}=\left\{m_{\lambda}, m_{\lambda}+1, \ldots, M_{\lambda}\right\}$ as the smallest set of consecutive positive integers that contains $S_{\lambda}$. Then all $T_{\lambda}$ are sets of at least two consecutive positive integers, and moreover the $T_{\lambda}$ cover $\mathbb{N}$. Additionally, each positive integer is covered finitely many times because there are only finitely many possible values of $m_{\lambda}$ smaller than any fixed integer. Recall that if three intervals have a point in common then one of them is contained in the union of the other two. Thus, if any positive integer is covered more than twice by the sets $T_{\lambda}$, we may throw out one set while maintaining the property that the $T_{\lambda}$ cover $\mathbb{N}$. By using the fact that each positive integer is covered finitely many times, we can apply this process so that each positive integer is eventually covered at most twice. Let $\Lambda$ denote the set of the $\lambda$-values for which $T_{\lambda}$ remains in our collection of sets; then $\bigcup_{\lambda \in \Lambda} T_{\lambda}=\mathbb{N}$ and each positive integer is contained in at most two sets $T_{\lambda}$. We now obtain $$ \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \leq 2 \sum_{k \geq 1}\left(a_{k+1}-a_{k}\right) \leq 2 $$ On the other hand, because $a_{m_{\lambda}}=\lambda m_{\lambda}$ and $a_{M_{\lambda}}=\lambda M_{\lambda}$, we have $$ \begin{aligned} 2 \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) & \geq 2 \sum_{m_{\lambda} \leq k<M_{\lambda}}\left(a_{k+1}-a_{k}\right)=2\left(a_{M_{\lambda}}-a_{m_{\lambda}}\right)=2\left(M_{\lambda}-m_{\lambda}\right) \lambda \\ & =2\left(M_{\lambda}-m_{\lambda}\right) \cdot \frac{a_{m_{\lambda}}}{m_{\lambda}} \geq\left(M_{\lambda}-m_{\lambda}+1\right) \cdot \frac{a_{1}}{m_{\lambda}} \geq a_{1} \cdot \sum_{k \in T_{\lambda}} \frac{1}{k} . \end{aligned} $$ Combining this with our first estimate, and using the fact that the $T_{\lambda}$ cover $\mathbb{N}$, we obtain $$ 4 \geq 2 \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}}\left(a_{k+1}-a_{k}\right) \geq a_{1} \sum_{\lambda \in \Lambda} \sum_{k \in T_{\lambda}} \frac{1}{k} \geq a_{1} \sum_{k \geq 1} \frac{1}{k} $$ contradicting the fact that the harmonic series diverges.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
993976ff-055a-5b7e-9f55-6efc300795e6
| 605,993 |
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 2 (Sanjana Das). Assume for the sake of contradiction that no number appears exactly once in the sequence. For every $i<j$ with $a_{i} / i=a_{j} / j$, draw an edge between $i$ and $j$, so every $i$ has an edge (and being connected by an edge is a transitive property). Call $i$ good if it has an edge with some $j>i$. First, each $i$ has finite degree - otherwise $$ \frac{a_{x_{1}}}{x_{1}}=\frac{a_{x_{2}}}{x_{2}}=\cdots $$ for an infinite increasing sequence of positive integers $x_{i}$, but then the $a_{x_{i}}$ are unbounded. Now we use the following process to build a sequence of indices whose $a_{i}$ we can lower-bound: - Start at $x_{1}=1$, which is good. - If we're currently at good index $x_{i}$, then let $s_{i}$ be the largest positive integer such that $x_{i}$ has an edge to $x_{i}+s_{i}$. (This exists because the degrees are finite.) - Let $t_{i}$ be the smallest positive integer for which $x_{i}+s_{i}+t_{i}$ is good, and let this be $x_{i+1}$. This exists because if all numbers $k \leq x \leq 2 k$ are bad, they must each connect to some number less than $k$ (if two connect to each other, the smaller one is good), but then two connect to the same number, and therefore to each other this is the idea we will use later to bound the $t_{i}$ as well. Then $x_{i}=1+s_{1}+t_{1}+\cdots+s_{i-1}+t_{i-1}$, and we have $$ a_{x_{i+1}}>a_{x_{i}+s_{i}}=\frac{x_{i}+s_{i}}{x_{i}} a_{x_{i}}=\frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} a_{x_{i}} $$ This means $$ c_{n}:=\frac{a_{x_{n}}}{a_{1}}>\prod_{i=1}^{n-1} \frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} $$ ## Lemma $t_{1}+\cdots+t_{n} \leq s_{1}+\cdots+s_{n}$ for each $n$. First we claim that if $x \in\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$, then $x$ cannot have an edge to $x_{j}$ for any $j \leq i$. This is because $x>x_{i}+s_{i} \geq x_{j}+s_{j}$, contradicting the fact that $x_{j}+s_{j}$ is the largest neighbor of $x_{j}$. This also means $x$ doesn't have an edge to $x_{j}+s_{j}$ for any $j \leq i$, since if it did, it would have an edge to $x_{j}$. Second, no two bad values of $x$ can have an edge, since then the smaller one is good. This also means no two bad $x$ can have an edge to the same $y$. Then each of the $\sum\left(t_{i}-1\right)$ values in the intervals $\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$ for $1 \leq i \leq n$ must have an edge to an unique $y$ in one of the intervals $\left(x_{i}, x_{i}+s_{i}\right)$ (not necessarily with the same $i$ ). Therefore $$ \sum\left(t_{i}-1\right) \leq \sum\left(s_{i}-1\right) \Longrightarrow \sum t_{i} \leq \sum s_{i} $$ Now note that if $a>b$, then $\frac{a+x}{b+x}=1+\frac{a-b}{b+x}$ is decreasing in $x$. This means $$ c_{n}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+2 s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}} $$ By multiplying both products, we have a telescoping product, which results in $$ c_{n}^{2} \geq 1+2 s_{1}+\cdots+2 s_{n}+2 s_{n+1} $$ The right hand side is unbounded since the $s_{i}$ are positive integers, while $c_{n}=a_{x_{n}} / a_{1}<$ $1 / a_{1}$ is bounded, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 2 (Sanjana Das). Assume for the sake of contradiction that no number appears exactly once in the sequence. For every $i<j$ with $a_{i} / i=a_{j} / j$, draw an edge between $i$ and $j$, so every $i$ has an edge (and being connected by an edge is a transitive property). Call $i$ good if it has an edge with some $j>i$. First, each $i$ has finite degree - otherwise $$ \frac{a_{x_{1}}}{x_{1}}=\frac{a_{x_{2}}}{x_{2}}=\cdots $$ for an infinite increasing sequence of positive integers $x_{i}$, but then the $a_{x_{i}}$ are unbounded. Now we use the following process to build a sequence of indices whose $a_{i}$ we can lower-bound: - Start at $x_{1}=1$, which is good. - If we're currently at good index $x_{i}$, then let $s_{i}$ be the largest positive integer such that $x_{i}$ has an edge to $x_{i}+s_{i}$. (This exists because the degrees are finite.) - Let $t_{i}$ be the smallest positive integer for which $x_{i}+s_{i}+t_{i}$ is good, and let this be $x_{i+1}$. This exists because if all numbers $k \leq x \leq 2 k$ are bad, they must each connect to some number less than $k$ (if two connect to each other, the smaller one is good), but then two connect to the same number, and therefore to each other this is the idea we will use later to bound the $t_{i}$ as well. Then $x_{i}=1+s_{1}+t_{1}+\cdots+s_{i-1}+t_{i-1}$, and we have $$ a_{x_{i+1}}>a_{x_{i}+s_{i}}=\frac{x_{i}+s_{i}}{x_{i}} a_{x_{i}}=\frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} a_{x_{i}} $$ This means $$ c_{n}:=\frac{a_{x_{n}}}{a_{1}}>\prod_{i=1}^{n-1} \frac{1+\left(s_{1}+\cdots+s_{i-1}+s_{i}\right)+\left(t_{1}+\cdots+t_{i-1}\right)}{1+\left(s_{1}+\cdots+s_{i-1}\right)+\left(t_{1}+\cdots+t_{i-1}\right)} $$ ## Lemma $t_{1}+\cdots+t_{n} \leq s_{1}+\cdots+s_{n}$ for each $n$. First we claim that if $x \in\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$, then $x$ cannot have an edge to $x_{j}$ for any $j \leq i$. This is because $x>x_{i}+s_{i} \geq x_{j}+s_{j}$, contradicting the fact that $x_{j}+s_{j}$ is the largest neighbor of $x_{j}$. This also means $x$ doesn't have an edge to $x_{j}+s_{j}$ for any $j \leq i$, since if it did, it would have an edge to $x_{j}$. Second, no two bad values of $x$ can have an edge, since then the smaller one is good. This also means no two bad $x$ can have an edge to the same $y$. Then each of the $\sum\left(t_{i}-1\right)$ values in the intervals $\left(x_{i}+s_{i}, x_{i}+s_{i}+t_{i}\right)$ for $1 \leq i \leq n$ must have an edge to an unique $y$ in one of the intervals $\left(x_{i}, x_{i}+s_{i}\right)$ (not necessarily with the same $i$ ). Therefore $$ \sum\left(t_{i}-1\right) \leq \sum\left(s_{i}-1\right) \Longrightarrow \sum t_{i} \leq \sum s_{i} $$ Now note that if $a>b$, then $\frac{a+x}{b+x}=1+\frac{a-b}{b+x}$ is decreasing in $x$. This means $$ c_{n}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}}>\prod_{i=1}^{n-1} \frac{1+2 s_{1}+\cdots+2 s_{i-1}+2 s_{i}}{1+2 s_{1}+\cdots+2 s_{i-1}+s_{i}} $$ By multiplying both products, we have a telescoping product, which results in $$ c_{n}^{2} \geq 1+2 s_{1}+\cdots+2 s_{n}+2 s_{n+1} $$ The right hand side is unbounded since the $s_{i}$ are positive integers, while $c_{n}=a_{x_{n}} / a_{1}<$ $1 / a_{1}$ is bounded, contradiction.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
993976ff-055a-5b7e-9f55-6efc300795e6
| 605,993 |
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 3 (Gopal Goel). Suppose for sake of contradiction that the problem is false. Call an index $i$ a pin if $$ \frac{a_{j}}{j}=\frac{a_{i}}{i} \Longrightarrow j \geq i $$ ## Lemma There exists $k$ such that if we have $\frac{a_{i}}{i}=\frac{a_{j}}{j}$ with $j>i \geq k$, then $j \leq 1.1 i$. Suppose no such $k$ exists. Then, take a pair $j_{1}>i_{1}$ such that $\frac{a_{j_{1}}}{j_{1}}=\frac{a_{i_{1}}}{i_{1}}$ and $j_{1}>1.1 i_{1}$, or $a_{j_{1}}>1.1 a_{i_{1}}$. Now, since $k=j_{1}$ can't work, there exists a pair $j_{2}>i_{2} \geq i_{1}$ such that $\frac{a_{j_{2}}}{j_{2}}=\frac{a_{i_{2}}}{i_{2}}$ and $j_{2}>1.1 i_{2}$, or $a_{j_{2}}>1.1 a_{i_{2}}$. Continuing in this fashion, we see that $$ a_{j_{\ell}}>1.1 a_{i_{\ell}}>1.1 a_{j_{\ell-1}} $$ so we have that $a_{j_{\ell}}>1.1^{\ell} a_{i_{1}}$. Taking $\ell>\log _{1.1}\left(1 / a_{1}\right)$ gives the desired contradiction. ## Lemma For $N>k^{2}$, there are at most $0.8 N$ pins in $[\sqrt{N}, N)$. $$ p-N\left(1-\frac{1}{1.1}\right) \leq N-p $$ so $p \leq 0.8 N$, as desired. We say that $i$ is the pin of $j$ if it is the smallest index such that $\frac{a_{i}}{i}=\frac{a_{j}}{j}$. The pin of $j$ is always a pin. Given an index $i$, let $f(i)$ denote the largest index less than $i$ that is not a pin (we leave the function undefined when no such index exists, as we are only interested in the behavior for large $i$ ). Then $f$ is weakly increasing and unbounded by the first lemma. Let $N_{0}$ be a positive integer such that $f\left(\sqrt{N_{0}}\right)>k$. Take any $N>N_{0}$ such that $N$ is not a pin. Let $b_{0}=N$, and $b_{1}$ be the pin of $b_{0}$. Recursively define $b_{2 i}=f\left(b_{2 i-1}\right)$, and $b_{2 i+1}$ to be the pin of $b_{2 i}$. Let $\ell$ be the largest odd index such that $b_{\ell} \geq \sqrt{N}$. We first show that $b_{\ell} \leq 100 \sqrt{N}$. Since $N>N_{0}$, we have $b_{\ell+1}>k$. By the choice of $\ell$ we have $b_{\ell+2}<\sqrt{N}$, so $$ b_{\ell+1}<1.1 b_{\ell+2}<1.1 \sqrt{N} $$ by the first lemma. We see that all the indices from $b_{\ell+1}+1$ to $b_{\ell}$ must be pins, so we have at least $b_{\ell}-1.1 \sqrt{N}$ pins in $\left[\sqrt{N}, b_{\ell}\right)$. Combined with the second lemma, this shows that $b_{\ell} \leq 100 \sqrt{N}$. Now, we have that $a_{b_{2 i}}=\frac{b_{2 i}}{b_{2 i+1}} a_{b_{2 i+1}}$ and $a_{b_{2 i+1}}>a_{b_{2 i+2}}$, so combining gives us $$ \frac{a_{b_{0}}}{a_{b_{\ell}}}>\frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} . $$ Note that there are at least $$ \left(b_{1}-b_{2}\right)+\left(b_{3}-b_{4}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right) $$ pins in $[\sqrt{N}, N)$, so by the second lemma, that sum is at most $0.8 N$. Thus, $$ \begin{aligned} \left(b_{0}-b_{1}\right)+\left(b_{2}-b_{3}\right)+\cdots+\left(b_{\ell-1}-b_{\ell}\right) & =b_{0}-\left[\left(b_{1}-b_{2}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right)\right]-b_{\ell} \\ & \geq 0.2 N-100 \sqrt{N} . \end{aligned} $$ Then $$ \begin{aligned} \frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} & \geq 1+\frac{b_{0}-b_{1}}{b_{1}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{\ell}} \\ & >1+\frac{b_{0}-b_{1}}{b_{0}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{0}} \\ & \geq 1+\frac{0.2 N-100 \sqrt{N}}{N} \end{aligned} $$ which is at least 1.01 if $N_{0}$ is large enough. Thus, we see that $$ a_{N}>1.01 a_{b_{\ell}} \geq 1.01 a_{\lfloor\sqrt{N}\rfloor} $$ if $N>N_{0}$ is not a pin. Since there are arbitrarily large non-pins, this implies that the sequence $\left(a_{n}\right)$ is unbounded, which is the desired contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}<a_{2}<a_{3}<a_{4}<\cdots$ be an infinite sequence of real numbers in the interval $(0,1)$. Show that there exists a number that occurs exactly once in the sequence $$ \frac{a_{1}}{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \frac{a_{4}}{4}, \ldots $$
|
【 Solution 3 (Gopal Goel). Suppose for sake of contradiction that the problem is false. Call an index $i$ a pin if $$ \frac{a_{j}}{j}=\frac{a_{i}}{i} \Longrightarrow j \geq i $$ ## Lemma There exists $k$ such that if we have $\frac{a_{i}}{i}=\frac{a_{j}}{j}$ with $j>i \geq k$, then $j \leq 1.1 i$. Suppose no such $k$ exists. Then, take a pair $j_{1}>i_{1}$ such that $\frac{a_{j_{1}}}{j_{1}}=\frac{a_{i_{1}}}{i_{1}}$ and $j_{1}>1.1 i_{1}$, or $a_{j_{1}}>1.1 a_{i_{1}}$. Now, since $k=j_{1}$ can't work, there exists a pair $j_{2}>i_{2} \geq i_{1}$ such that $\frac{a_{j_{2}}}{j_{2}}=\frac{a_{i_{2}}}{i_{2}}$ and $j_{2}>1.1 i_{2}$, or $a_{j_{2}}>1.1 a_{i_{2}}$. Continuing in this fashion, we see that $$ a_{j_{\ell}}>1.1 a_{i_{\ell}}>1.1 a_{j_{\ell-1}} $$ so we have that $a_{j_{\ell}}>1.1^{\ell} a_{i_{1}}$. Taking $\ell>\log _{1.1}\left(1 / a_{1}\right)$ gives the desired contradiction. ## Lemma For $N>k^{2}$, there are at most $0.8 N$ pins in $[\sqrt{N}, N)$. $$ p-N\left(1-\frac{1}{1.1}\right) \leq N-p $$ so $p \leq 0.8 N$, as desired. We say that $i$ is the pin of $j$ if it is the smallest index such that $\frac{a_{i}}{i}=\frac{a_{j}}{j}$. The pin of $j$ is always a pin. Given an index $i$, let $f(i)$ denote the largest index less than $i$ that is not a pin (we leave the function undefined when no such index exists, as we are only interested in the behavior for large $i$ ). Then $f$ is weakly increasing and unbounded by the first lemma. Let $N_{0}$ be a positive integer such that $f\left(\sqrt{N_{0}}\right)>k$. Take any $N>N_{0}$ such that $N$ is not a pin. Let $b_{0}=N$, and $b_{1}$ be the pin of $b_{0}$. Recursively define $b_{2 i}=f\left(b_{2 i-1}\right)$, and $b_{2 i+1}$ to be the pin of $b_{2 i}$. Let $\ell$ be the largest odd index such that $b_{\ell} \geq \sqrt{N}$. We first show that $b_{\ell} \leq 100 \sqrt{N}$. Since $N>N_{0}$, we have $b_{\ell+1}>k$. By the choice of $\ell$ we have $b_{\ell+2}<\sqrt{N}$, so $$ b_{\ell+1}<1.1 b_{\ell+2}<1.1 \sqrt{N} $$ by the first lemma. We see that all the indices from $b_{\ell+1}+1$ to $b_{\ell}$ must be pins, so we have at least $b_{\ell}-1.1 \sqrt{N}$ pins in $\left[\sqrt{N}, b_{\ell}\right)$. Combined with the second lemma, this shows that $b_{\ell} \leq 100 \sqrt{N}$. Now, we have that $a_{b_{2 i}}=\frac{b_{2 i}}{b_{2 i+1}} a_{b_{2 i+1}}$ and $a_{b_{2 i+1}}>a_{b_{2 i+2}}$, so combining gives us $$ \frac{a_{b_{0}}}{a_{b_{\ell}}}>\frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} . $$ Note that there are at least $$ \left(b_{1}-b_{2}\right)+\left(b_{3}-b_{4}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right) $$ pins in $[\sqrt{N}, N)$, so by the second lemma, that sum is at most $0.8 N$. Thus, $$ \begin{aligned} \left(b_{0}-b_{1}\right)+\left(b_{2}-b_{3}\right)+\cdots+\left(b_{\ell-1}-b_{\ell}\right) & =b_{0}-\left[\left(b_{1}-b_{2}\right)+\cdots+\left(b_{\ell-2}-b_{\ell-1}\right)\right]-b_{\ell} \\ & \geq 0.2 N-100 \sqrt{N} . \end{aligned} $$ Then $$ \begin{aligned} \frac{b_{0}}{b_{1}} \frac{b_{2}}{b_{3}} \cdots \frac{b_{\ell-1}}{b_{\ell}} & \geq 1+\frac{b_{0}-b_{1}}{b_{1}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{\ell}} \\ & >1+\frac{b_{0}-b_{1}}{b_{0}}+\cdots+\frac{b_{\ell-1}-b_{\ell}}{b_{0}} \\ & \geq 1+\frac{0.2 N-100 \sqrt{N}}{N} \end{aligned} $$ which is at least 1.01 if $N_{0}$ is large enough. Thus, we see that $$ a_{N}>1.01 a_{b_{\ell}} \geq 1.01 a_{\lfloor\sqrt{N}\rfloor} $$ if $N>N_{0}$ is not a pin. Since there are arbitrarily large non-pins, this implies that the sequence $\left(a_{n}\right)$ is unbounded, which is the desired contradiction.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
993976ff-055a-5b7e-9f55-6efc300795e6
| 605,993 |
Let $a$ and $b$ be positive integers. Suppose that there are infinitely many pairs of positive integers $(m, n)$ for which $m^{2}+a n+b$ and $n^{2}+a m+b$ are both perfect squares. Prove that $a$ divides $2 b$.
|
Treating $a$ and $b$ as fixed, we are given that there are infinitely many quadrpules $(m, n, r, s)$ which satisfy the system $$ \begin{aligned} m^{2}+a n+b & =(m+r)^{2} \\ n^{2}+a m+b & =(n+s)^{2} \end{aligned} $$ We say that $(r, s)$ is exceptional if there exists infinitely many $(m, n)$ that satisfy. Claim - If $(r, s)$ is exceptional, then either - $0<r<a / 2$, and $0<s<\frac{1}{4} a^{2}$; or - $0<s<a / 2$, and $0<r<\frac{1}{4} a^{2}$; or - $r^{2}+s^{2} \leq 2 b$. In particular, finitely many pairs $(r, s)$ can be exceptional. $$ r^{2}+s^{2}-2 b=(a-2 r) m+(a-2 s) n $$ If $0<r<a / 2$, then the idea is to use the bound $a n+b \geq 2 m+1$ to get $m \leq \frac{a n+b-1}{2}$. Consequently, $$ (n+s)^{2}=n^{2}+a m+b \leq n^{2}+a \cdot \frac{a n+b-1}{2}+b $$ For this to hold for infinitely many integers $n$, we need $2 s \leq \frac{a^{2}}{2}$, by comparing coefficients. A similar case occurs when $0<s<a / 2$. If $\min (r, s)>a / 2$, then $(\dagger)$ forces $r^{2}+s^{2} \leq 2 b$, giving the last case. Hence, there exists some particular pair $(r, s)$ for which there are infinitely many solutions $(m, n)$. Simplifying the system gives $$ \begin{aligned} & a n=2 r m+r^{2}-b \\ & 2 s n=a m+b-s^{2} \end{aligned} $$ Since the system is linear, for there to be infinitely many solutions $(m, n)$ the system must be dependent. This gives $$ \frac{a}{2 s}=\frac{2 r}{a}=\frac{r^{2}-b}{b-s^{2}} $$ so $a=2 \sqrt{r s}$ and $b=\frac{s^{2} \sqrt{r}+r^{2} \sqrt{s}}{\sqrt{r}+\sqrt{s}}$. Since $r s$ must be square, we can reparametrize as $r=k x^{2}, s=k y^{2}$, and $\operatorname{gcd}(x, y)=1$. This gives $$ \begin{aligned} a & =2 k x y \\ b & =k^{2} x y\left(x^{2}-x y+y^{2}\right) \end{aligned} $$ Thus, $a \mid 2 b$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be positive integers. Suppose that there are infinitely many pairs of positive integers $(m, n)$ for which $m^{2}+a n+b$ and $n^{2}+a m+b$ are both perfect squares. Prove that $a$ divides $2 b$.
|
Treating $a$ and $b$ as fixed, we are given that there are infinitely many quadrpules $(m, n, r, s)$ which satisfy the system $$ \begin{aligned} m^{2}+a n+b & =(m+r)^{2} \\ n^{2}+a m+b & =(n+s)^{2} \end{aligned} $$ We say that $(r, s)$ is exceptional if there exists infinitely many $(m, n)$ that satisfy. Claim - If $(r, s)$ is exceptional, then either - $0<r<a / 2$, and $0<s<\frac{1}{4} a^{2}$; or - $0<s<a / 2$, and $0<r<\frac{1}{4} a^{2}$; or - $r^{2}+s^{2} \leq 2 b$. In particular, finitely many pairs $(r, s)$ can be exceptional. $$ r^{2}+s^{2}-2 b=(a-2 r) m+(a-2 s) n $$ If $0<r<a / 2$, then the idea is to use the bound $a n+b \geq 2 m+1$ to get $m \leq \frac{a n+b-1}{2}$. Consequently, $$ (n+s)^{2}=n^{2}+a m+b \leq n^{2}+a \cdot \frac{a n+b-1}{2}+b $$ For this to hold for infinitely many integers $n$, we need $2 s \leq \frac{a^{2}}{2}$, by comparing coefficients. A similar case occurs when $0<s<a / 2$. If $\min (r, s)>a / 2$, then $(\dagger)$ forces $r^{2}+s^{2} \leq 2 b$, giving the last case. Hence, there exists some particular pair $(r, s)$ for which there are infinitely many solutions $(m, n)$. Simplifying the system gives $$ \begin{aligned} & a n=2 r m+r^{2}-b \\ & 2 s n=a m+b-s^{2} \end{aligned} $$ Since the system is linear, for there to be infinitely many solutions $(m, n)$ the system must be dependent. This gives $$ \frac{a}{2 s}=\frac{2 r}{a}=\frac{r^{2}-b}{b-s^{2}} $$ so $a=2 \sqrt{r s}$ and $b=\frac{s^{2} \sqrt{r}+r^{2} \sqrt{s}}{\sqrt{r}+\sqrt{s}}$. Since $r s$ must be square, we can reparametrize as $r=k x^{2}, s=k y^{2}$, and $\operatorname{gcd}(x, y)=1$. This gives $$ \begin{aligned} a & =2 k x y \\ b & =k^{2} x y\left(x^{2}-x y+y^{2}\right) \end{aligned} $$ Thus, $a \mid 2 b$, as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd090cb4-57f1-5eac-9da8-3433431a3084
| 247,567 |
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 1 (Ankan Bhattacharya, Jeffery Li). ## Lemma If $S$ is an independent set of $T$, then $$ \sum_{v \in S} \operatorname{deg}(v) \leq n-1 $$ Equality holds if and only if $S$ is one of the two components of the unique 2-coloring of $T$. We are given that there exists an independent set of at least $\frac{n+k-1}{2}$ vertices. By greedily choosing vertices of smallest degree, the sum of the degrees of these vertices is at least $$ k+2 \cdot \frac{n-k-1}{2}=n-1 $$ Thus equality holds everywhere, which implies that the independent set contains every leaf and is one of the components of the 2 -coloring.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 1 (Ankan Bhattacharya, Jeffery Li). ## Lemma If $S$ is an independent set of $T$, then $$ \sum_{v \in S} \operatorname{deg}(v) \leq n-1 $$ Equality holds if and only if $S$ is one of the two components of the unique 2-coloring of $T$. We are given that there exists an independent set of at least $\frac{n+k-1}{2}$ vertices. By greedily choosing vertices of smallest degree, the sum of the degrees of these vertices is at least $$ k+2 \cdot \frac{n-k-1}{2}=n-1 $$ Thus equality holds everywhere, which implies that the independent set contains every leaf and is one of the components of the 2 -coloring.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
e9d26087-d3c0-5e35-8466-b15cd06c66b2
| 247,575 |
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 2 (Andrew Gu). ## Lemma The vertices of $T$ can be partitioned into $k-1$ paths (i.e. the induced subgraph on each set of vertices is a path) such that all edges of $T$ which are not part of a path are incident to an endpoint of a path. Now given a path of $a$ vertices, at most $\frac{a+1}{2}$ of those vertices can be in an independent set of $T$. By the lemma, $T$ can be partitioned into $k-1$ paths of $a_{1}, \ldots, a_{k-1}$ vertices, so the maximum size of an independent set of $T$ is $$ \sum \frac{a_{i}+1}{2}=\frac{n+k-1}{2} . $$ For equality to hold, each path in the partition must have an odd number of vertices, and has a unique 2 -coloring in red and blue where the endpoints are red. The unique independent set of $T$ of size $\frac{n+k-1}{2}$ is then the set of red vertices. By the lemma, the edges of $T$ which are not part of a path connect an endpoint of a path (which is colored red) to another vertex (which must be blue, because the red vertices are independent). Thus the coloring of the paths extends to the unique 2 -coloring of $T$. The leaves of $T$ are endpoints of paths, so they are all red.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $T$ be a tree on $n$ vertices with exactly $k$ leaves. Suppose that there exists a subset of at least $\frac{n+k-1}{2}$ vertices of $T$, no two of which are adjacent. Show that the longest path in $T$ contains an even number of edges.
|
The longest path in $T$ must go between two leaves. The solutions presented here will solve the problem by showing that in the unique 2-coloring of $T$, all leaves are the same color. ## 【 Solution 2 (Andrew Gu). ## Lemma The vertices of $T$ can be partitioned into $k-1$ paths (i.e. the induced subgraph on each set of vertices is a path) such that all edges of $T$ which are not part of a path are incident to an endpoint of a path. Now given a path of $a$ vertices, at most $\frac{a+1}{2}$ of those vertices can be in an independent set of $T$. By the lemma, $T$ can be partitioned into $k-1$ paths of $a_{1}, \ldots, a_{k-1}$ vertices, so the maximum size of an independent set of $T$ is $$ \sum \frac{a_{i}+1}{2}=\frac{n+k-1}{2} . $$ For equality to hold, each path in the partition must have an odd number of vertices, and has a unique 2 -coloring in red and blue where the endpoints are red. The unique independent set of $T$ of size $\frac{n+k-1}{2}$ is then the set of red vertices. By the lemma, the edges of $T$ which are not part of a path connect an endpoint of a path (which is colored red) to another vertex (which must be blue, because the red vertices are independent). Thus the coloring of the paths extends to the unique 2 -coloring of $T$. The leaves of $T$ are endpoints of paths, so they are all red.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
e9d26087-d3c0-5e35-8466-b15cd06c66b2
| 247,575 |
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) Let the second tangent to $\omega$ parallel to $E F$ meet lines $A B$ and $A C$ at $P$ and $Q$, respectively, and let the second tangent to $\omega$ parallel to $B C$ meet lines $D E$ and $D F$ at $R$ and $S$, respectively. Furthermore, let $\omega$ touch $P Q$ and $R S$ at $U$ and $V$, respectively. Let $h$ be inversion with respect to $\omega$. Then $h$ maps $A, B$, and $C$ onto the midpoints of the sides of triangle $D_{1} E_{1} F_{1}$. So $h$ maps $k$ onto the Euler circle of triangle $D_{1} E_{1} F_{1}$. Similarly, $h$ maps $k$ onto the Euler circle of triangle $A_{1} B_{1} C_{1}$. Therefore, triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$ share a common nine-point circle $\gamma$. Let $K$ be its center; its radius equals $\frac{1}{2} r$. Let $H$ be the reflection of $I$ in $K$. Then $H$ is the common orthocenter of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$. Let $\gamma_{U}$ of center $K_{U}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $U E_{1} F_{1}$, and let $\gamma_{V}$ of center $K_{V}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $V B_{1} C_{1}$. Let $H_{U}$ be the orthocenter of triangle $U E_{1} F_{1}$. Since quadrilateral $D_{1} E_{1} F_{1} U$ is cyclic, vectors $\overrightarrow{H H_{U}}$ and $\overrightarrow{D_{1} U}$ are equal. Consequently, $\overrightarrow{K K_{U}}=\frac{1}{2} \overrightarrow{D_{1} U}$. Similarly, $\overrightarrow{K K_{V}}=$ $\frac{1}{2} \overrightarrow{A_{1} V}$. Since both of $A_{1} U$ and $D_{1} V$ are diameters in $\omega$, vectors $\overrightarrow{D_{1} U}$ and $\overrightarrow{A_{1} V}$ are equal. Therefore, $K_{U}$ and $K_{V}$ coincide, and so do $\gamma_{U}$ and $\gamma_{V}$. As above, $h$ maps $\gamma_{U}$ onto the circumcircle of triangle $A P Q$ and $\gamma_{V}$ onto the circumcircle of triangle $D R S$. Therefore, triangles $A P Q$ and $D R S$ are inscribed inside the same circle $\Omega_{A D}$. Since $E F$ and $P Q$ are parallel, triangles $\Delta_{A}$ and $A P Q$ are homothetic, and so are figures $\Omega_{A} \cup \omega_{A}$ and $\Omega_{A D} \cup \omega$. Consequently, we have $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right), $$ which solves part (a).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) Let the second tangent to $\omega$ parallel to $E F$ meet lines $A B$ and $A C$ at $P$ and $Q$, respectively, and let the second tangent to $\omega$ parallel to $B C$ meet lines $D E$ and $D F$ at $R$ and $S$, respectively. Furthermore, let $\omega$ touch $P Q$ and $R S$ at $U$ and $V$, respectively. Let $h$ be inversion with respect to $\omega$. Then $h$ maps $A, B$, and $C$ onto the midpoints of the sides of triangle $D_{1} E_{1} F_{1}$. So $h$ maps $k$ onto the Euler circle of triangle $D_{1} E_{1} F_{1}$. Similarly, $h$ maps $k$ onto the Euler circle of triangle $A_{1} B_{1} C_{1}$. Therefore, triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$ share a common nine-point circle $\gamma$. Let $K$ be its center; its radius equals $\frac{1}{2} r$. Let $H$ be the reflection of $I$ in $K$. Then $H$ is the common orthocenter of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$. Let $\gamma_{U}$ of center $K_{U}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $U E_{1} F_{1}$, and let $\gamma_{V}$ of center $K_{V}$ and radius $\frac{1}{2} r$ be the Euler circle of triangle $V B_{1} C_{1}$. Let $H_{U}$ be the orthocenter of triangle $U E_{1} F_{1}$. Since quadrilateral $D_{1} E_{1} F_{1} U$ is cyclic, vectors $\overrightarrow{H H_{U}}$ and $\overrightarrow{D_{1} U}$ are equal. Consequently, $\overrightarrow{K K_{U}}=\frac{1}{2} \overrightarrow{D_{1} U}$. Similarly, $\overrightarrow{K K_{V}}=$ $\frac{1}{2} \overrightarrow{A_{1} V}$. Since both of $A_{1} U$ and $D_{1} V$ are diameters in $\omega$, vectors $\overrightarrow{D_{1} U}$ and $\overrightarrow{A_{1} V}$ are equal. Therefore, $K_{U}$ and $K_{V}$ coincide, and so do $\gamma_{U}$ and $\gamma_{V}$. As above, $h$ maps $\gamma_{U}$ onto the circumcircle of triangle $A P Q$ and $\gamma_{V}$ onto the circumcircle of triangle $D R S$. Therefore, triangles $A P Q$ and $D R S$ are inscribed inside the same circle $\Omega_{A D}$. Since $E F$ and $P Q$ are parallel, triangles $\Delta_{A}$ and $A P Q$ are homothetic, and so are figures $\Omega_{A} \cup \omega_{A}$ and $\Omega_{A D} \cup \omega$. Consequently, we have $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right), $$ which solves part (a).
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6f1f510-5cb6-5a29-8a6c-833556e68a61
| 606,070 |
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (Michael Ren) As in the previous solution, let the second tangent to $\omega$ parallel to $E F$ meet $A B$ and $A C$ at $P$ and $Q$, respectively. Let $(A P Q)$ meet $\Omega$ again at $D^{\prime}$, so that $D^{\prime}$ is the Miquel point of $\{A B, A C, B C, P Q\}$. Since the quadrilateral formed by these lines has incircle $\omega$, it is classical that $D^{\prime} I$ bisects $\angle P D^{\prime} C$ and $B D^{\prime} Q$ (e.g. by DDIT). Let $\ell$ be the tangent to $\Omega$ at $D^{\prime}$ and $D^{\prime} I$ meet $\Omega$ again at $M$. We have $$ \measuredangle\left(\ell, D^{\prime} B\right)=\measuredangle D^{\prime} C B=\measuredangle D^{\prime} Q P=\measuredangle\left(D^{\prime} Q, E F\right) . $$ Therefore $D^{\prime} I$ also bisects the angle between $\ell$ and the line parallel to $E F$ through $D^{\prime}$. This means that $M$ is one of the arc midpoints of $E F$. Additionally, $D^{\prime}$ lies on $\operatorname{arc} B C$ not containing $A$, so $D^{\prime}=D$. Similarly, letting the second tangent to $\omega$ parallel to $B C$ meet $D E$ and $D F$ again at $R$ and $S$, we have $A D R S$ cyclic. ## Lemma There exists a circle $\Omega_{A D}$ tangent to $\Omega_{A}$ and $\Omega_{D}$ at $A$ and $D$, respectively. $$ \measuredangle O A O_{A}=\measuredangle(\perp E F, \perp B C)=\measuredangle(E F, B C) . $$ (Here, $\perp E F$ means the direction perpendicular to $E F$.) By symmetry, this is equal to $\measuredangle O_{D} D O$. The circle $(A D P Q)$ passes through $A$ and $D$, and is tangent to $\Omega_{A}$ by homothety. Therefore it coincides with $\Omega_{A D}$, as does ( $A D R S$ ). Like the previous solution, we finish with $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) . $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (Michael Ren) As in the previous solution, let the second tangent to $\omega$ parallel to $E F$ meet $A B$ and $A C$ at $P$ and $Q$, respectively. Let $(A P Q)$ meet $\Omega$ again at $D^{\prime}$, so that $D^{\prime}$ is the Miquel point of $\{A B, A C, B C, P Q\}$. Since the quadrilateral formed by these lines has incircle $\omega$, it is classical that $D^{\prime} I$ bisects $\angle P D^{\prime} C$ and $B D^{\prime} Q$ (e.g. by DDIT). Let $\ell$ be the tangent to $\Omega$ at $D^{\prime}$ and $D^{\prime} I$ meet $\Omega$ again at $M$. We have $$ \measuredangle\left(\ell, D^{\prime} B\right)=\measuredangle D^{\prime} C B=\measuredangle D^{\prime} Q P=\measuredangle\left(D^{\prime} Q, E F\right) . $$ Therefore $D^{\prime} I$ also bisects the angle between $\ell$ and the line parallel to $E F$ through $D^{\prime}$. This means that $M$ is one of the arc midpoints of $E F$. Additionally, $D^{\prime}$ lies on $\operatorname{arc} B C$ not containing $A$, so $D^{\prime}=D$. Similarly, letting the second tangent to $\omega$ parallel to $B C$ meet $D E$ and $D F$ again at $R$ and $S$, we have $A D R S$ cyclic. ## Lemma There exists a circle $\Omega_{A D}$ tangent to $\Omega_{A}$ and $\Omega_{D}$ at $A$ and $D$, respectively. $$ \measuredangle O A O_{A}=\measuredangle(\perp E F, \perp B C)=\measuredangle(E F, B C) . $$ (Here, $\perp E F$ means the direction perpendicular to $E F$.) By symmetry, this is equal to $\measuredangle O_{D} D O$. The circle $(A D P Q)$ passes through $A$ and $D$, and is tangent to $\Omega_{A}$ by homothety. Therefore it coincides with $\Omega_{A D}$, as does ( $A D R S$ ). Like the previous solution, we finish with $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{A D} \cup \omega\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) . $$
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6f1f510-5cb6-5a29-8a6c-833556e68a61
| 606,070 |
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Andrew Gu) Construct triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$ (with positive ratio) which have the same circumcircle; it suffices to show that these copies have the same incircle as well. Let $O$ be the center of this common circumcircle, which we take to be the origin, and $M_{X Y}$ denote the point on the circle such that the tangent at that point is parallel to line $X Y$ (from the two possible choices, we make the choice that corresponds to the arc midpoint on $\Omega$, e.g. $M_{A B}$ should correspond to the arc midpoint on the internal angle bisector of $A C B$ ). The left diagram below shows the original triangles $A B C$ and $D E F$, while the right diagram shows the triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$.  Using the fact that the incenter is the orthocenter of the arc midpoints, the incenter of $\Delta_{A}$ in this reference frame is $M_{A B}+M_{A C}-M_{E F}$ and the incenter of $\Delta_{D}$ in this reference frame is $M_{D E}+M_{D F}-M_{B C}$. Since $A B C$ and $D E F$ share a common incenter, we have $$ M_{A B}+M_{B C}+M_{C A}=M_{D E}+M_{E F}+M_{F D} $$ Thus the copies of $\Delta_{A}$ and $\Delta_{D}$ have the same incenter, and therefore the same incircle as well (Euler's theorem determines the inradius).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Andrew Gu) Construct triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$ (with positive ratio) which have the same circumcircle; it suffices to show that these copies have the same incircle as well. Let $O$ be the center of this common circumcircle, which we take to be the origin, and $M_{X Y}$ denote the point on the circle such that the tangent at that point is parallel to line $X Y$ (from the two possible choices, we make the choice that corresponds to the arc midpoint on $\Omega$, e.g. $M_{A B}$ should correspond to the arc midpoint on the internal angle bisector of $A C B$ ). The left diagram below shows the original triangles $A B C$ and $D E F$, while the right diagram shows the triangles homothetic to $\Delta_{A}$ and $\Delta_{D}$.  Using the fact that the incenter is the orthocenter of the arc midpoints, the incenter of $\Delta_{A}$ in this reference frame is $M_{A B}+M_{A C}-M_{E F}$ and the incenter of $\Delta_{D}$ in this reference frame is $M_{D E}+M_{D F}-M_{B C}$. Since $A B C$ and $D E F$ share a common incenter, we have $$ M_{A B}+M_{B C}+M_{C A}=M_{D E}+M_{E F}+M_{F D} $$ Thus the copies of $\Delta_{A}$ and $\Delta_{D}$ have the same incenter, and therefore the same incircle as well (Euler's theorem determines the inradius).
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6f1f510-5cb6-5a29-8a6c-833556e68a61
| 606,070 |
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) By Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Therefore, $T_{A}=A D \cap I_{A} I_{D}$. Let $p$ be pole-and-polar correspondence with respect to $\omega$. Then $p$ maps $A$ onto line $E_{1} F_{1}$ and $D$ onto line $B_{1} C_{1}$. Consequently, $p$ maps line $A D$ onto $X_{A}=B_{1} C_{1} \cap E_{1} F_{1}$. Furthermore, $p$ maps the line that bisects the angle formed by lines $A B$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} F_{1}$. Similarly, $p$ maps the line that bisects the angle formed by lines $A C$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} E_{1}$. So $p$ maps $I_{A}$ onto the midline of triangle $A_{1} E_{1} F_{1}$ opposite $A_{1}$. Similarly, $p$ maps $I_{D}$ onto the midline of triangle $D_{1} B_{1} C_{1}$ opposite $D_{1}$. Consequently, $p$ maps line $I_{A} I_{D}$ onto the intersection point $Y_{A}$ of this pair of midlines, and $p$ maps $T_{A}$ onto line $X_{A} Y_{A}$. Since the reflection of $H$ in line $B_{1} C_{1}$ lies on $\omega, A_{1} H \cdot H H_{A}$ equals half the power of $H$ with respect to $\omega$. Similarly, $D_{1} H \cdot H H_{D}$ equals half the power of $H$ with respect to $\omega$. Then $A_{1} H \cdot H H_{A}=D_{1} H \cdot H H_{D}$ and $A_{1} H H_{D} \sim D_{1} H H_{A}$. Since $\angle H H_{D} L_{A}=90^{\circ}=$ $\angle H H_{A} L_{D}$, figures $A_{1} H H_{D} L_{A}$ and $D_{1} H H_{A} L_{D}$ are similar as well. Consequently, $$ \frac{H L_{A}}{L_{A} A_{1}}=\frac{H L_{D}}{L_{D} D_{1}}=s $$ as a signed ratio. Let the line through $A_{1}$ parallel to $E_{1} F_{1}$ and the line through $D_{1}$ parallel to $B_{1} C_{1}$ meet at $Z_{A}$. Then $H X_{A} / X_{A} Z_{A}=s$ and $Y_{A}$ is the midpoint of segment $X_{A} Z_{A}$. Therefore, $H$ lies on line $X_{A} Y_{A}$. This means that $T_{A}$ lies on the polar of $H$ with respect to $\omega$, and by symmetry so do $T_{B}$ and $T_{C}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 1 (author) By Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Therefore, $T_{A}=A D \cap I_{A} I_{D}$. Let $p$ be pole-and-polar correspondence with respect to $\omega$. Then $p$ maps $A$ onto line $E_{1} F_{1}$ and $D$ onto line $B_{1} C_{1}$. Consequently, $p$ maps line $A D$ onto $X_{A}=B_{1} C_{1} \cap E_{1} F_{1}$. Furthermore, $p$ maps the line that bisects the angle formed by lines $A B$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} F_{1}$. Similarly, $p$ maps the line that bisects the angle formed by lines $A C$ and $E F$ and does not contain $I$ onto the midpoint of segment $A_{1} E_{1}$. So $p$ maps $I_{A}$ onto the midline of triangle $A_{1} E_{1} F_{1}$ opposite $A_{1}$. Similarly, $p$ maps $I_{D}$ onto the midline of triangle $D_{1} B_{1} C_{1}$ opposite $D_{1}$. Consequently, $p$ maps line $I_{A} I_{D}$ onto the intersection point $Y_{A}$ of this pair of midlines, and $p$ maps $T_{A}$ onto line $X_{A} Y_{A}$. Since the reflection of $H$ in line $B_{1} C_{1}$ lies on $\omega, A_{1} H \cdot H H_{A}$ equals half the power of $H$ with respect to $\omega$. Similarly, $D_{1} H \cdot H H_{D}$ equals half the power of $H$ with respect to $\omega$. Then $A_{1} H \cdot H H_{A}=D_{1} H \cdot H H_{D}$ and $A_{1} H H_{D} \sim D_{1} H H_{A}$. Since $\angle H H_{D} L_{A}=90^{\circ}=$ $\angle H H_{A} L_{D}$, figures $A_{1} H H_{D} L_{A}$ and $D_{1} H H_{A} L_{D}$ are similar as well. Consequently, $$ \frac{H L_{A}}{L_{A} A_{1}}=\frac{H L_{D}}{L_{D} D_{1}}=s $$ as a signed ratio. Let the line through $A_{1}$ parallel to $E_{1} F_{1}$ and the line through $D_{1}$ parallel to $B_{1} C_{1}$ meet at $Z_{A}$. Then $H X_{A} / X_{A} Z_{A}=s$ and $Y_{A}$ is the midpoint of segment $X_{A} Z_{A}$. Therefore, $H$ lies on line $X_{A} Y_{A}$. This means that $T_{A}$ lies on the polar of $H$ with respect to $\omega$, and by symmetry so do $T_{B}$ and $T_{C}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6f1f510-5cb6-5a29-8a6c-833556e68a61
| 606,070 |
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (author) As in the first solution to part (a), let $h$ be inversion with respect to $\omega$, let $\gamma$ of center $K$ be the common Euler circle of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$, and let $H$ be their common orthocenter. Let $K_{A}$ and $K_{D}$ be the centers of $\gamma_{A}$ and $\gamma_{D}$, respectively, and let $\ell_{A}$ be the perpendicular bisector of segment $K_{A} K_{D}$. Since $\gamma_{A}$ and $\gamma_{D}$ are congruent (both of them are of radius $\left.\frac{1}{2} r\right)$, they are reflections of each other across $\ell_{A}$. Inversion $h$ maps the two common external tangents of $\Omega_{A}$ and $\Omega_{D}$ onto the two circles $\alpha$ and $\beta$ through $I$ that are tangent to both of $\gamma_{A}$ and $\gamma_{D}$ in the same way. (That is, either internally to both or externally to both.) Consequently, $\alpha$ and $\beta$ are reflections of each other in $\ell_{A}$ and so their second point of intersection $S_{A}$, which $h$ maps $T_{A}$ onto, is the reflection of $I$ in $\ell_{A}$. Define $\ell_{B}, \ell_{C}, S_{B}$, and $S_{C}$ similarly. Then $S_{B}$ is the reflection of $I$ in $\ell_{B}$ and $S_{C}$ is the reflection of $I$ in $\ell_{C}$. Therefore, all four points $I, S_{A}, S_{B}$, and $S_{C}$ lie on the circle of center $K$ that contains $I$. (This is also the circle on diameter $I H$.) Since points $S_{A}, S_{B}$, and $S_{C}$ are concyclic with $I$, their images $T_{A}, T_{B}$, and $T_{C}$ under $h$ are collinear, and the solution is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 2 (author) As in the first solution to part (a), let $h$ be inversion with respect to $\omega$, let $\gamma$ of center $K$ be the common Euler circle of triangles $A_{1} B_{1} C_{1}$ and $D_{1} E_{1} F_{1}$, and let $H$ be their common orthocenter. Let $K_{A}$ and $K_{D}$ be the centers of $\gamma_{A}$ and $\gamma_{D}$, respectively, and let $\ell_{A}$ be the perpendicular bisector of segment $K_{A} K_{D}$. Since $\gamma_{A}$ and $\gamma_{D}$ are congruent (both of them are of radius $\left.\frac{1}{2} r\right)$, they are reflections of each other across $\ell_{A}$. Inversion $h$ maps the two common external tangents of $\Omega_{A}$ and $\Omega_{D}$ onto the two circles $\alpha$ and $\beta$ through $I$ that are tangent to both of $\gamma_{A}$ and $\gamma_{D}$ in the same way. (That is, either internally to both or externally to both.) Consequently, $\alpha$ and $\beta$ are reflections of each other in $\ell_{A}$ and so their second point of intersection $S_{A}$, which $h$ maps $T_{A}$ onto, is the reflection of $I$ in $\ell_{A}$. Define $\ell_{B}, \ell_{C}, S_{B}$, and $S_{C}$ similarly. Then $S_{B}$ is the reflection of $I$ in $\ell_{B}$ and $S_{C}$ is the reflection of $I$ in $\ell_{C}$. Therefore, all four points $I, S_{A}, S_{B}$, and $S_{C}$ lie on the circle of center $K$ that contains $I$. (This is also the circle on diameter $I H$.) Since points $S_{A}, S_{B}$, and $S_{C}$ are concyclic with $I$, their images $T_{A}, T_{B}$, and $T_{C}$ under $h$ are collinear, and the solution is complete.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6f1f510-5cb6-5a29-8a6c-833556e68a61
| 606,070 |
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Ankan Bhattacharya) From either of the first two solutions to part (a), we know that there is a circle $\Omega_{A D}$ passing through $A$ and $D$ which is (internally) tangent to $\Omega_{A}$ and $\Omega_{D}$. By Monge's theorem applied to $\Omega_{A}, \Omega_{D}$, and $\Omega_{A D}$, it follows that $A, D$, and $T_{A}$ are collinear. The inversion at $T_{A}$ swapping $\Omega_{A}$ with $\Omega_{D}$ also swaps $A$ with $D$ because $T_{A}$ lies on $A D$ and $A$ is not homologous to $D$. Let $\Omega_{A}$ and $\Omega_{D}$ meet $\Omega$ again at $L_{A}$ and $L_{D}$. Since $A D L_{A} L_{D}$ is cyclic, the same inversion at $T_{A}$ also swaps $L_{A}$ and $L_{D}$, so $T_{A}=A D \cap L_{A} L_{D}$. By Taiwan TST 2014, $L_{A}$ and $L_{D}$ are the tangency points of the $A$-mixtilinear and $D$-mixtilinear incircles, respectively, with $\Omega$. Therefore $A L_{A} \cap D L_{D}$ is the exsimilicenter $X$ of $\Omega$ and $\omega$. Then $T_{A}, T_{B}$, and $T_{C}$ all lie on the polar of $X$ with respect to $\Omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 3 (Ankan Bhattacharya) From either of the first two solutions to part (a), we know that there is a circle $\Omega_{A D}$ passing through $A$ and $D$ which is (internally) tangent to $\Omega_{A}$ and $\Omega_{D}$. By Monge's theorem applied to $\Omega_{A}, \Omega_{D}$, and $\Omega_{A D}$, it follows that $A, D$, and $T_{A}$ are collinear. The inversion at $T_{A}$ swapping $\Omega_{A}$ with $\Omega_{D}$ also swaps $A$ with $D$ because $T_{A}$ lies on $A D$ and $A$ is not homologous to $D$. Let $\Omega_{A}$ and $\Omega_{D}$ meet $\Omega$ again at $L_{A}$ and $L_{D}$. Since $A D L_{A} L_{D}$ is cyclic, the same inversion at $T_{A}$ also swaps $L_{A}$ and $L_{D}$, so $T_{A}=A D \cap L_{A} L_{D}$. By Taiwan TST 2014, $L_{A}$ and $L_{D}$ are the tangency points of the $A$-mixtilinear and $D$-mixtilinear incircles, respectively, with $\Omega$. Therefore $A L_{A} \cap D L_{D}$ is the exsimilicenter $X$ of $\Omega$ and $\omega$. Then $T_{A}, T_{B}$, and $T_{C}$ all lie on the polar of $X$ with respect to $\Omega$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6f1f510-5cb6-5a29-8a6c-833556e68a61
| 606,070 |
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 4 (Andrew Gu) We show that $T_{A}$ lies on the radical axis of the point circle at $I$ and $\Omega$, which will solve the problem. Let $I_{A}$ and $I_{D}$ be the centers of $\omega_{A}$ and $\omega_{D}$ respectively. By the Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Additionally, these other triples are collinear: $\left(A, I_{A}, I\right),\left(D, I_{D}, I\right),\left(I_{A}, I_{D}, T\right)$. By Menelaus's theorem, we have $$ \frac{T_{A} D}{T_{A} A}=\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} . $$ If $s$ is the length of the side opposite $A$ in $\Delta_{A}$, then we compute $$ \begin{aligned} \frac{I_{A} I}{I_{A} A} & =\frac{s / \cos (A / 2)}{r_{A} / \sin (A / 2)} \\ & =\frac{2 R_{A} \sin (A) \sin (A / 2)}{\cos (A / 2)} \\ & =\frac{4 R_{A} \sin ^{2}(A / 2)}{r_{A}} \\ & =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} . \end{aligned} $$ From part (a), we know that $\frac{R_{A}}{r_{A}}=\frac{R_{D}}{r_{D}}$. Therefore, doing a similar calculation for $\frac{I_{D} D}{I_{D} I}$, we get $$ \begin{aligned} \frac{T_{A} D}{T_{A} A} & =\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} \\ & =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} \cdot \frac{r_{D} D I^{2}}{4 R_{D} r^{2}} \\ & =\frac{D I^{2}}{A I^{2}} \end{aligned} $$ Thus $T_{A}$ is the point where the tangent to $(A I D)$ at $I$ meets $A D$ and $T_{A} I^{2}=T_{A} A \cdot T_{A} D$. This shows what we claimed at the start.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangles $A B C$ and $D E F$ share circumcircle $\Omega$ and incircle $\omega$ so that points $A, F$, $B, D, C$, and $E$ occur in this order along $\Omega$. Let $\Delta_{A}$ be the triangle formed by lines $A B, A C$, and $E F$, and define triangles $\Delta_{B}, \Delta_{C}, \ldots, \Delta_{F}$ similarly. Furthermore, let $\Omega_{A}$ and $\omega_{A}$ be the circumcircle and incircle of triangle $\Delta_{A}$, respectively, and define circles $\Omega_{B}, \omega_{B}, \ldots, \Omega_{F}, \omega_{F}$ similarly. (a) Prove that the two common external tangents to circles $\Omega_{A}$ and $\Omega_{D}$ and the two common external tangents to circles $\omega_{A}$ and $\omega_{D}$ are either concurrent or pairwise parallel. (b) Suppose that these four lines meet at point $T_{A}$, and define points $T_{B}$ and $T_{C}$ similarly. Prove that points $T_{A}, T_{B}$, and $T_{C}$ are collinear.
|
 Let $I$ and $r$ be the center and radius of $\omega$, and let $O$ and $R$ be the center and radius of $\Omega$. Let $O_{A}$ and $I_{A}$ be the circumcenter and incenter of triangle $\Delta_{A}$, and define $O_{B}$, $I_{B}, \ldots, I_{F}$ similarly. Let $\omega$ touch $E F$ at $A_{1}$, and define $B_{1}, C_{1}, \ldots, F_{1}$ similarly. $$ \left(\Omega_{A} \cup \omega_{A}\right) \sim\left(\Omega_{D} \cup \omega_{D}\right) $$ The four lines will concur at the homothetic center of these figures (possibly at infinity). Solution 4 (Andrew Gu) We show that $T_{A}$ lies on the radical axis of the point circle at $I$ and $\Omega$, which will solve the problem. Let $I_{A}$ and $I_{D}$ be the centers of $\omega_{A}$ and $\omega_{D}$ respectively. By the Monge's theorem applied to $\omega, \omega_{A}$, and $\omega_{D}$, points $A, D$, and $T_{A}$ are collinear. Additionally, these other triples are collinear: $\left(A, I_{A}, I\right),\left(D, I_{D}, I\right),\left(I_{A}, I_{D}, T\right)$. By Menelaus's theorem, we have $$ \frac{T_{A} D}{T_{A} A}=\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} . $$ If $s$ is the length of the side opposite $A$ in $\Delta_{A}$, then we compute $$ \begin{aligned} \frac{I_{A} I}{I_{A} A} & =\frac{s / \cos (A / 2)}{r_{A} / \sin (A / 2)} \\ & =\frac{2 R_{A} \sin (A) \sin (A / 2)}{\cos (A / 2)} \\ & =\frac{4 R_{A} \sin ^{2}(A / 2)}{r_{A}} \\ & =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} . \end{aligned} $$ From part (a), we know that $\frac{R_{A}}{r_{A}}=\frac{R_{D}}{r_{D}}$. Therefore, doing a similar calculation for $\frac{I_{D} D}{I_{D} I}$, we get $$ \begin{aligned} \frac{T_{A} D}{T_{A} A} & =\frac{I_{A} I}{I_{A} A} \cdot \frac{I_{D} D}{I_{D} I} \\ & =\frac{4 R_{A} r^{2}}{r_{A} A I^{2}} \cdot \frac{r_{D} D I^{2}}{4 R_{D} r^{2}} \\ & =\frac{D I^{2}}{A I^{2}} \end{aligned} $$ Thus $T_{A}$ is the point where the tangent to $(A I D)$ at $I$ meets $A D$ and $T_{A} I^{2}=T_{A} A \cdot T_{A} D$. This shows what we claimed at the start.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6f1f510-5cb6-5a29-8a6c-833556e68a61
| 606,070 |
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
【 Solution 1. We prove the statement by induction on $n$. We use $n=0$ as a base case, where the statement follows from $1 \geq 2^{-|M|}$. For the inductive step, let $n>0$. There exists at least one mine-avoiding path, which must pass through either $(0,1)$ or $(1,0)$. We consider two cases: Case 1: there exist mine-avoiding paths starting at both $(1,0)$ and $(0,1)$. By the inductive hypothesis, there are at least $2^{n-1-|M|}$ mine-avoiding paths starting from each of $(1,0)$ and $(0,1)$. Then the total number of mine-avoiding paths is at least $2^{n-1-|M|}+2^{n-1-|M|}=2^{n-|M|}$. Case 2: only one of $(1,0)$ and $(0,1)$ is on a mine-avoiding path. Without loss of generality, suppose no mine-avoiding path starts at $(0,1)$. Then some element of $M$ must be of the form $(0, k)$ for $1 \leq k \leq n$ in order to block the path along the $y$-axis. This element can be ignored for any mine-avoiding path starting at (1,0). By the inductive hypothesis, there are at least $2^{n-1-(|M|-1)}=2^{n-|M|}$ mine-avoiding paths. This completes the induction step, which solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
【 Solution 1. We prove the statement by induction on $n$. We use $n=0$ as a base case, where the statement follows from $1 \geq 2^{-|M|}$. For the inductive step, let $n>0$. There exists at least one mine-avoiding path, which must pass through either $(0,1)$ or $(1,0)$. We consider two cases: Case 1: there exist mine-avoiding paths starting at both $(1,0)$ and $(0,1)$. By the inductive hypothesis, there are at least $2^{n-1-|M|}$ mine-avoiding paths starting from each of $(1,0)$ and $(0,1)$. Then the total number of mine-avoiding paths is at least $2^{n-1-|M|}+2^{n-1-|M|}=2^{n-|M|}$. Case 2: only one of $(1,0)$ and $(0,1)$ is on a mine-avoiding path. Without loss of generality, suppose no mine-avoiding path starts at $(0,1)$. Then some element of $M$ must be of the form $(0, k)$ for $1 \leq k \leq n$ in order to block the path along the $y$-axis. This element can be ignored for any mine-avoiding path starting at (1,0). By the inductive hypothesis, there are at least $2^{n-1-(|M|-1)}=2^{n-|M|}$ mine-avoiding paths. This completes the induction step, which solves the problem.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
ef69e4c5-5810-5f09-bb48-b329c45cb9a5
| 247,597 |
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
## 【 Solution 2. ## Lemma If $|M|<n$, there is more than one mine-avoiding path. - Make the first $i+1$ points $P_{0}, P_{1}, \ldots, P_{i}$. - If $P_{i} \rightarrow P_{i+1}$ is one unit up, go right until $\left(n-y_{i}, y_{i}\right)$. - If $P_{i} \rightarrow P_{i+1}$ is one unit right, go up until $\left(x_{i}, n-x_{i}\right)$.  The diagram above is an example for $n=5$ with the new segments formed by the $Q_{i}$ in red, and the line $x+y=n$ in blue. By definition, $M$ has less than $n$ points, none of which are in the original path. Since all $Q_{i}$ only intersect in the original path, each mine is in at most one of $Q_{0}, Q_{1}, \ldots, Q_{n-1}$. By the Pigeonhole Principle, one of the $Q_{i}$ is mine-avoiding. Now, consider the following process: - Start at $(0,0)$. - If there is only one choice of next step that is part of a mine-avoiding path, make that choice. - Repeat the above until at a point with two possible steps that are part of mineavoiding paths. - Add a mine to the choice of next step with more mine-avoiding paths through it. If both have the same number of mine-avoiding paths through them, add a mine arbitrarily.  For instance, consider the above diagram for $n=4$. Lattice points are replaced with squares. Mines are black squares and each non-mine is labelled with the number of mine-avoiding paths passing through it. This process would start at $(0,0)$, go to $(1,0)$, then place a mine at $(1,1)$. This path increases the size of $M$ by one, and reduces the number of mine-avoiding paths to a nonzero number at most half of the original. Repeat this process until there is only one path left. By our lemma, the number of mines must be at least $n$ by the end of the process, so the process was iterated at least $n-|M|$ times. By the halving property, there must have been at least $2^{n-|M|}$ mine-avoiding paths before the process, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $M$ be a finite set of lattice points and $n$ be a positive integer. A mine-avoiding path is a path of lattice points with length $n$, beginning at $(0,0)$ and ending at a point on the line $x+y=n$, that does not contain any point in $M$. Prove that if there exists a mine-avoiding path, then there exist at least $2^{n-|M|}$ mine-avoiding paths.
|
## 【 Solution 2. ## Lemma If $|M|<n$, there is more than one mine-avoiding path. - Make the first $i+1$ points $P_{0}, P_{1}, \ldots, P_{i}$. - If $P_{i} \rightarrow P_{i+1}$ is one unit up, go right until $\left(n-y_{i}, y_{i}\right)$. - If $P_{i} \rightarrow P_{i+1}$ is one unit right, go up until $\left(x_{i}, n-x_{i}\right)$.  The diagram above is an example for $n=5$ with the new segments formed by the $Q_{i}$ in red, and the line $x+y=n$ in blue. By definition, $M$ has less than $n$ points, none of which are in the original path. Since all $Q_{i}$ only intersect in the original path, each mine is in at most one of $Q_{0}, Q_{1}, \ldots, Q_{n-1}$. By the Pigeonhole Principle, one of the $Q_{i}$ is mine-avoiding. Now, consider the following process: - Start at $(0,0)$. - If there is only one choice of next step that is part of a mine-avoiding path, make that choice. - Repeat the above until at a point with two possible steps that are part of mineavoiding paths. - Add a mine to the choice of next step with more mine-avoiding paths through it. If both have the same number of mine-avoiding paths through them, add a mine arbitrarily.  For instance, consider the above diagram for $n=4$. Lattice points are replaced with squares. Mines are black squares and each non-mine is labelled with the number of mine-avoiding paths passing through it. This process would start at $(0,0)$, go to $(1,0)$, then place a mine at $(1,1)$. This path increases the size of $M$ by one, and reduces the number of mine-avoiding paths to a nonzero number at most half of the original. Repeat this process until there is only one path left. By our lemma, the number of mines must be at least $n$ by the end of the process, so the process was iterated at least $n-|M|$ times. By the halving property, there must have been at least $2^{n-|M|}$ mine-avoiding paths before the process, as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
ef69e4c5-5810-5f09-bb48-b329c45cb9a5
| 247,597 |
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
ब Solution 1 (author). We'll use the following lemma. ## Lemma Suppose that $P Q R S$ is a convex quadrilateral with $\angle P=\angle R$. Then there is a point $T$ on $Q S$ such that $\angle Q P T=\angle S R P, \angle T R Q=\angle R P S$, and $P T=R T$. Before proving the lemma, we will show how it solves the problem. The lemma applied for the quadrilateral $A B_{1} A_{1} C_{1}$ with $\angle A=\angle A_{1}$ shows that $\angle B_{1} A_{1} A_{2}=\angle C_{1} A A_{1}$. This implies that the point $A_{2}$ in $\triangle A_{1} B_{1} C_{1}$ corresponds to the point $A_{1}$ in $\triangle A B C$. Then $\triangle A_{2} B_{2} C_{2} \sim \triangle A_{1} B_{1} C_{1} \sim \triangle A B C$, as desired. Additionally, $P T=R T$ is a corollary of the angle conditions because $$ \measuredangle P R T=\measuredangle S R Q-\measuredangle T R Q-\measuredangle S R P=\measuredangle Q P S-\measuredangle R P S-\measuredangle Q P T=\measuredangle T P R $$ Therefore we only need to prove the angle conditions. 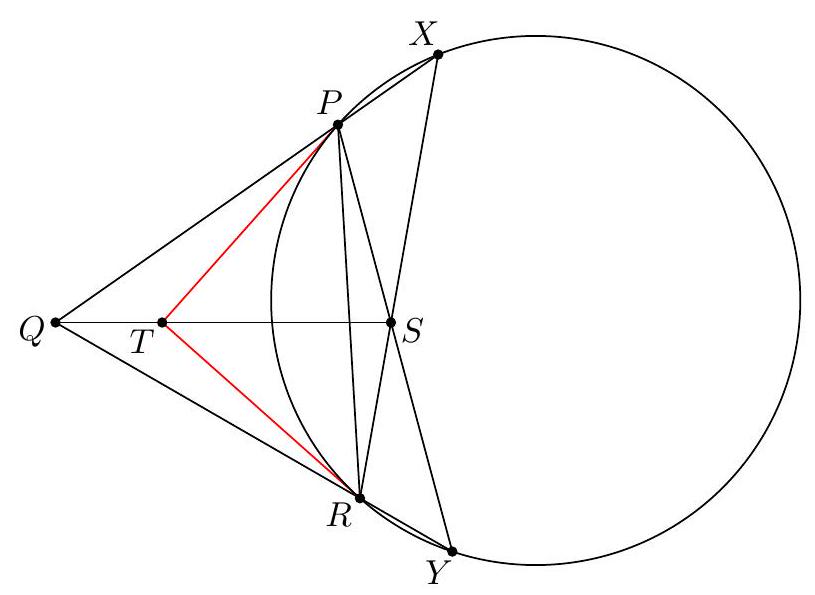 $$ \begin{aligned} \measuredangle P X T & =\measuredangle R^{\prime} P Q+\measuredangle P Q S \\ & =\measuredangle R^{\prime} S Q+\measuredangle P Q S \\ & =\measuredangle Q S R+\measuredangle P Q S \\ & =\measuredangle(P Q, S R) \\ & =\measuredangle Q P R+\measuredangle P R S . \end{aligned} $$ This means that $$ \begin{aligned} \measuredangle Q P T & =\measuredangle Q P R-\measuredangle T P R \\ & =\measuredangle Q P R-\measuredangle T X R \\ & =\measuredangle Q P R-\measuredangle P X T \\ & =\measuredangle Q P R-\measuredangle Q P R-\measuredangle P R S \\ & =\measuredangle S R P . \end{aligned} $$ Similarly, $\measuredangle Q R T=\measuredangle S P R$, so we're done. 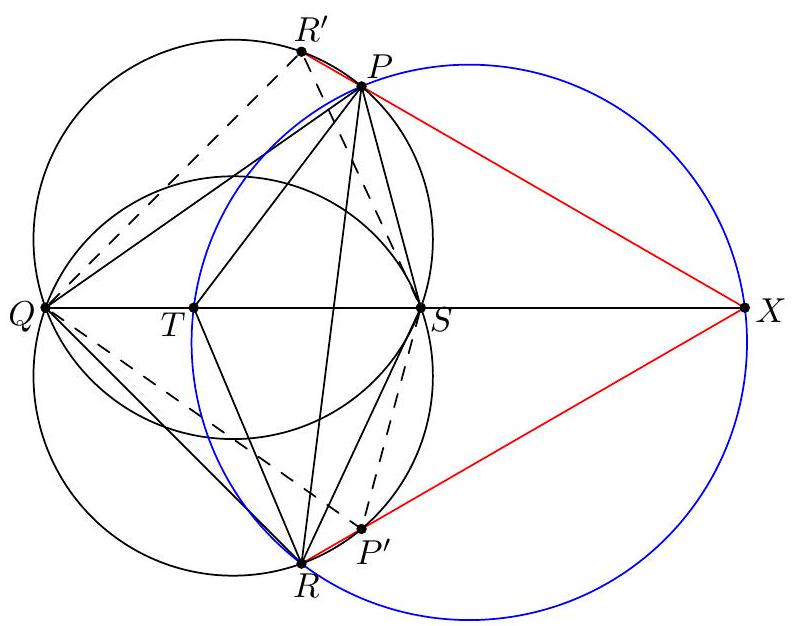 $$ \frac{Q T}{T S}=\frac{\sin Q P T \cdot P T / \sin P Q T}{\sin T P S \cdot P T / \sin T S P}=\frac{P Q / \sin P R Q}{P S / \sin S R P}=\frac{R(\triangle P Q R)}{R(\triangle P R S)} $$ which is symmetric in $P$ and $R$, so we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
ब Solution 1 (author). We'll use the following lemma. ## Lemma Suppose that $P Q R S$ is a convex quadrilateral with $\angle P=\angle R$. Then there is a point $T$ on $Q S$ such that $\angle Q P T=\angle S R P, \angle T R Q=\angle R P S$, and $P T=R T$. Before proving the lemma, we will show how it solves the problem. The lemma applied for the quadrilateral $A B_{1} A_{1} C_{1}$ with $\angle A=\angle A_{1}$ shows that $\angle B_{1} A_{1} A_{2}=\angle C_{1} A A_{1}$. This implies that the point $A_{2}$ in $\triangle A_{1} B_{1} C_{1}$ corresponds to the point $A_{1}$ in $\triangle A B C$. Then $\triangle A_{2} B_{2} C_{2} \sim \triangle A_{1} B_{1} C_{1} \sim \triangle A B C$, as desired. Additionally, $P T=R T$ is a corollary of the angle conditions because $$ \measuredangle P R T=\measuredangle S R Q-\measuredangle T R Q-\measuredangle S R P=\measuredangle Q P S-\measuredangle R P S-\measuredangle Q P T=\measuredangle T P R $$ Therefore we only need to prove the angle conditions.  $$ \begin{aligned} \measuredangle P X T & =\measuredangle R^{\prime} P Q+\measuredangle P Q S \\ & =\measuredangle R^{\prime} S Q+\measuredangle P Q S \\ & =\measuredangle Q S R+\measuredangle P Q S \\ & =\measuredangle(P Q, S R) \\ & =\measuredangle Q P R+\measuredangle P R S . \end{aligned} $$ This means that $$ \begin{aligned} \measuredangle Q P T & =\measuredangle Q P R-\measuredangle T P R \\ & =\measuredangle Q P R-\measuredangle T X R \\ & =\measuredangle Q P R-\measuredangle P X T \\ & =\measuredangle Q P R-\measuredangle Q P R-\measuredangle P R S \\ & =\measuredangle S R P . \end{aligned} $$ Similarly, $\measuredangle Q R T=\measuredangle S P R$, so we're done.  $$ \frac{Q T}{T S}=\frac{\sin Q P T \cdot P T / \sin P Q T}{\sin T P S \cdot P T / \sin T S P}=\frac{P Q / \sin P R Q}{P S / \sin S R P}=\frac{R(\triangle P Q R)}{R(\triangle P R S)} $$ which is symmetric in $P$ and $R$, so we're done.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
4c07bf4b-5125-51ef-9850-f4f98901617b
| 247,604 |
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
Solution 2 (Ankan Bhattacharya). We prove the main claim $\frac{B_{1} A_{2}}{A_{2} C_{1}}=\frac{B A_{1}}{A_{1} C}$. Let $\triangle A_{0} B_{0} C_{0}$ be the medial triangle of $\triangle A B C$. In addition, let $A_{1}^{\prime}$ be the reflection of $A_{1}$ over $\overline{B_{1} C_{1}}$, and let $X$ be the point satisfying $\triangle X B C \approx \triangle A B_{1} C_{1}$, so that we have a compound similarity $$ \triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A . $$ Finally, let $O_{A}$ be the circumcenter of $\triangle A_{1}^{\prime} B_{1} C_{1}$, and let $A_{2}^{*}$ be the point on $\overline{B_{1} C_{1}}$ satisfying $\frac{B_{1} A_{2}^{*}}{A_{2}^{*} C_{1}}=\frac{B A_{1}}{A_{1} C}$. Recall that $O$ is the Miquel point of $\triangle A_{1} B_{1} C_{1}$, as well as its orthocenter. Claim $-\overline{A A_{1}^{\prime}} \| \overline{B C}$. $$ \text { Claim }-\overline{A X} \| \overline{B_{1} C_{1}} . $$ $$ \measuredangle(\overline{B C}, \overline{A X})=\measuredangle\left(\overline{A A_{1}^{\prime}}, \overline{B_{1} C_{1}}\right) . $$ As $\overline{A A_{1}^{\prime}} \| \overline{B C}$, we obtain $\overline{A X} \| \overline{B_{1} C_{1}}$. $$ \text { Claim }-\overline{A X} \perp \overline{A_{1} O} . $$ $$ \text { Claim }-\overline{A A_{1}^{\prime}} \perp \overline{A_{2}^{*} O_{A}} $$ $$ \triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A . $$ Claim $-A A_{2}^{*}=A_{1}^{\prime} A_{2}$. Finally, $A_{1}^{\prime} A_{2}^{*}=A_{1} A_{2}^{*}$ by reflections, so $A A_{2}^{*}=A_{1} A_{2}^{*}$, and $A_{2}^{*}=A_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle. Points $A_{1}, B_{1}$ and $C_{1}$ are chosen on segments $B C$, $C A$, and $A B$, respectively, such that $\triangle A_{1} B_{1} C_{1}$ and $\triangle A B C$ are similar. Let $A_{2}$ be the unique point on line $B_{1} C_{1}$ such that $A A_{2}=A_{1} A_{2}$. Points $B_{2}$ and $C_{2}$ are defined similarly. Prove that $\triangle A_{2} B_{2} C_{2}$ and $\triangle A B C$ are similar.
|
Solution 2 (Ankan Bhattacharya). We prove the main claim $\frac{B_{1} A_{2}}{A_{2} C_{1}}=\frac{B A_{1}}{A_{1} C}$. Let $\triangle A_{0} B_{0} C_{0}$ be the medial triangle of $\triangle A B C$. In addition, let $A_{1}^{\prime}$ be the reflection of $A_{1}$ over $\overline{B_{1} C_{1}}$, and let $X$ be the point satisfying $\triangle X B C \approx \triangle A B_{1} C_{1}$, so that we have a compound similarity $$ \triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A . $$ Finally, let $O_{A}$ be the circumcenter of $\triangle A_{1}^{\prime} B_{1} C_{1}$, and let $A_{2}^{*}$ be the point on $\overline{B_{1} C_{1}}$ satisfying $\frac{B_{1} A_{2}^{*}}{A_{2}^{*} C_{1}}=\frac{B A_{1}}{A_{1} C}$. Recall that $O$ is the Miquel point of $\triangle A_{1} B_{1} C_{1}$, as well as its orthocenter. Claim $-\overline{A A_{1}^{\prime}} \| \overline{B C}$. $$ \text { Claim }-\overline{A X} \| \overline{B_{1} C_{1}} . $$ $$ \measuredangle(\overline{B C}, \overline{A X})=\measuredangle\left(\overline{A A_{1}^{\prime}}, \overline{B_{1} C_{1}}\right) . $$ As $\overline{A A_{1}^{\prime}} \| \overline{B C}$, we obtain $\overline{A X} \| \overline{B_{1} C_{1}}$. $$ \text { Claim }-\overline{A X} \perp \overline{A_{1} O} . $$ $$ \text { Claim }-\overline{A A_{1}^{\prime}} \perp \overline{A_{2}^{*} O_{A}} $$ $$ \triangle A B C \sqcup X \approx \triangle A_{1}^{\prime} B_{1} C_{1} \sqcup A . $$ Claim $-A A_{2}^{*}=A_{1}^{\prime} A_{2}$. Finally, $A_{1}^{\prime} A_{2}^{*}=A_{1} A_{2}^{*}$ by reflections, so $A A_{2}^{*}=A_{1} A_{2}^{*}$, and $A_{2}^{*}=A_{2}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
4c07bf4b-5125-51ef-9850-f4f98901617b
| 247,604 |
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which $$ \theta<\frac{1}{2} \min (\angle A, \angle B, \angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$. Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 First solution, by author. Let $X$ be the projection from $C$ to $A P_{A}, Y$ be the projection from $B$ to $A Q_{A}$. 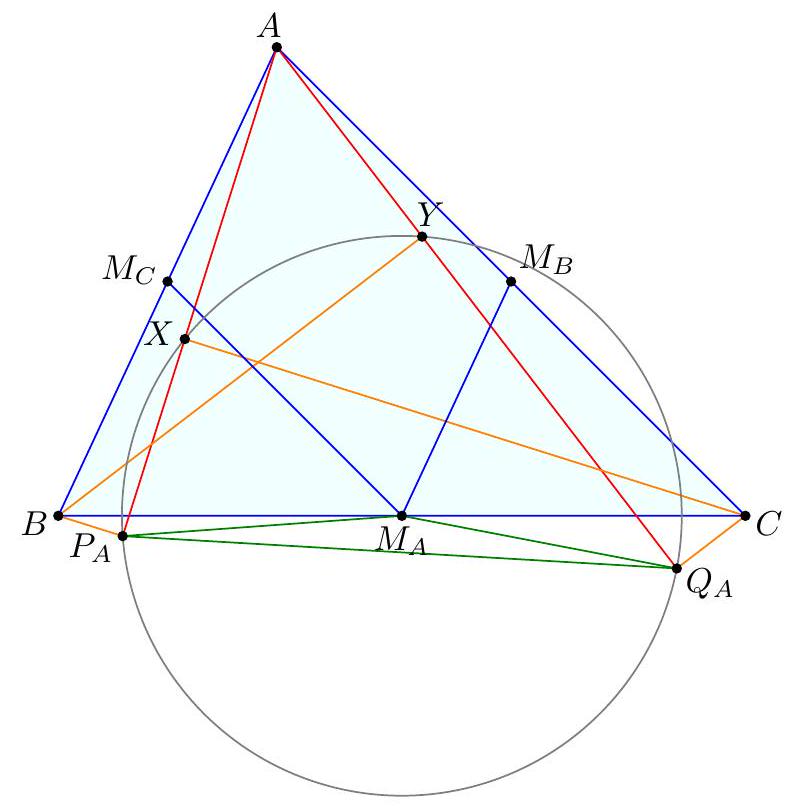 Claim - Line $\ell_{A}$ passes through $M_{A}$, the midpoint of $B C$. Also, quadrilateral $P_{A} Q_{A} Y X$ is cyclic with circumcenter $M_{A}$. $$ A P_{A} \cdot A X=A B \cdot A C \cdot \cos \theta \cos (\angle A-\theta)=A Q_{A} \cdot A Y $$ it follows that $P_{A}, Q_{A}, Y, X$ are concyclic by power of a point. Moreover, by projection, the perpendicular bisector of $P_{A} X$ passes through $M_{A}$, similar for $Q_{A} Y$, implying that $M_{A}$ is the center of $P_{A} Q_{A} Y X$. Hence $\ell_{A}$ passes through $M_{A}$. $$ \text { Claim }-\measuredangle\left(M_{A} M_{C}, \ell_{A}\right)=\measuredangle Y P_{A} Q_{A} $$ Therefore, $$ \frac{\sin \angle\left(M_{A} M_{C}, \ell_{A}\right)}{\sin \angle\left(\ell_{A}, M_{A} M_{B}\right)}=\frac{\sin \angle Y P_{A} Q_{A}}{\sin \angle P_{A} Q_{A} X}=\frac{Y Q_{A}}{X P_{A}}=\frac{B C \sin (\angle C+\theta)}{B C \sin (\angle B+\theta)}=\frac{\sin (\angle C+\theta)}{\sin (\angle B+\theta)}, $$ and we conclude by trig Ceva theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which $$ \theta<\frac{1}{2} \min (\angle A, \angle B, \angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$. Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 First solution, by author. Let $X$ be the projection from $C$ to $A P_{A}, Y$ be the projection from $B$ to $A Q_{A}$.  Claim - Line $\ell_{A}$ passes through $M_{A}$, the midpoint of $B C$. Also, quadrilateral $P_{A} Q_{A} Y X$ is cyclic with circumcenter $M_{A}$. $$ A P_{A} \cdot A X=A B \cdot A C \cdot \cos \theta \cos (\angle A-\theta)=A Q_{A} \cdot A Y $$ it follows that $P_{A}, Q_{A}, Y, X$ are concyclic by power of a point. Moreover, by projection, the perpendicular bisector of $P_{A} X$ passes through $M_{A}$, similar for $Q_{A} Y$, implying that $M_{A}$ is the center of $P_{A} Q_{A} Y X$. Hence $\ell_{A}$ passes through $M_{A}$. $$ \text { Claim }-\measuredangle\left(M_{A} M_{C}, \ell_{A}\right)=\measuredangle Y P_{A} Q_{A} $$ Therefore, $$ \frac{\sin \angle\left(M_{A} M_{C}, \ell_{A}\right)}{\sin \angle\left(\ell_{A}, M_{A} M_{B}\right)}=\frac{\sin \angle Y P_{A} Q_{A}}{\sin \angle P_{A} Q_{A} X}=\frac{Y Q_{A}}{X P_{A}}=\frac{B C \sin (\angle C+\theta)}{B C \sin (\angle B+\theta)}=\frac{\sin (\angle C+\theta)}{\sin (\angle B+\theta)}, $$ and we conclude by trig Ceva theorem.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"problem_match": null,
"solution_match": null
}
|
6158aa28-b0ac-557a-baa8-3454c43950dc
| 606,238 |
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which $$ \theta<\frac{1}{2} \min (\angle A, \angle B, \angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$. Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 Second solution via Jacobi, by Maxim Li. Let $D$ be the foot of the $A$-altitude. Note that line $B C$ is the external angle bisector of $\angle P_{A} D Q_{A}$. Claim - $\left(D P_{A} Q_{A}\right)$ passes through the midpoint $M_{A}$ of $B C$. It follows that $M_{A}$ lies on $\ell_{A}$; we need to identify a second point. We'll use the circumcenter $O_{A}$ of $\left(D P_{A} Q_{A}\right)$. The perpendicular bisector of $D P_{A}$ passes through $M_{C}$; indeed, we can easily show the angle it makes with $M_{C} M_{A}$ is $90^{\circ}-\theta-C$, so $\angle O_{A} M_{C} M_{A}=90-\theta-C$, and then by analogous angle-chasing we can finish with Jacobi's theorem on $\triangle M_{A} M_{B} M_{C}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Let $\theta$ be a fixed angle for which $$ \theta<\frac{1}{2} \min (\angle A, \angle B, \angle C) $$ Points $S_{A}$ and $T_{A}$ lie on segment $B C$ such that $\angle B A S_{A}=\angle T_{A} A C=\theta$. Let $P_{A}$ and $Q_{A}$ be the feet from $B$ and $C$ to $\overline{A S_{A}}$ and $\overline{A T_{A}}$ respectively. Then $\ell_{A}$ is defined as the perpendicular bisector of $\overline{P_{A} Q_{A}}$. Define $\ell_{B}$ and $\ell_{C}$ analogously by repeating this construction two more times (using the same value of $\theta$ ). Prove that $\ell_{A}, \ell_{B}$, and $\ell_{C}$ are concurrent or all parallel.
|
We discard the points $S_{A}$ and $T_{A}$ since they are only there to direct the angles correctly in the problem statement. 【 Second solution via Jacobi, by Maxim Li. Let $D$ be the foot of the $A$-altitude. Note that line $B C$ is the external angle bisector of $\angle P_{A} D Q_{A}$. Claim - $\left(D P_{A} Q_{A}\right)$ passes through the midpoint $M_{A}$ of $B C$. It follows that $M_{A}$ lies on $\ell_{A}$; we need to identify a second point. We'll use the circumcenter $O_{A}$ of $\left(D P_{A} Q_{A}\right)$. The perpendicular bisector of $D P_{A}$ passes through $M_{C}$; indeed, we can easily show the angle it makes with $M_{C} M_{A}$ is $90^{\circ}-\theta-C$, so $\angle O_{A} M_{C} M_{A}=90-\theta-C$, and then by analogous angle-chasing we can finish with Jacobi's theorem on $\triangle M_{A} M_{B} M_{C}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"problem_match": null,
"solution_match": null
}
|
6158aa28-b0ac-557a-baa8-3454c43950dc
| 606,238 |
A function $f: \mathbb{N} \rightarrow \mathbb{N}$ has the property that for all positive integers $m$ and $n$, exactly one of the $f(n)$ numbers $$ f(m+1), f(m+2), \ldots, f(m+f(n)) $$ is divisible by $n$. Prove that $f(n)=n$ for infinitely many positive integers $n$.
|
We start with the following claim: $$ \text { Claim - If } a \mid b \text { then } f(a) \mid f(b) $$ In what follows, let $a \geq 2$ be any positive integer. Because $f(a)$ and $f(2 a)$ are both divisible by $f(a)$, there are $a+1$ consecutive values of $f$ of which at least two divisible by $f(a)$. It follows that $f(f(a)) \leq a$. However, we also know that exactly one of $f(2), f(3), \ldots, f(1+f(a))$ is divisible by $a$; let this be $f(t)$. Then we have $S_{a}=\{t, t+f(a), t+2 f(a), \ldots\}$. Because $a|f(t)| f(2 t)$, we know that $2 t \in S_{a}$, so $t$ is a multiple of $f(a)$. Because $2 \leq t \leq 1+f(a)$, and $f(a) \geq 2$ for $a \geq 2$, we conclude that we must have $t=f(a)$, so $f(f(a))$ is a multiple of $a$. Together with $f(f(a)) \leq a$, this yields $f(f(a))=a$. Because $f(f(a))=a$ also holds for $a=1$ (from the given condition for $n=1$ it immediately follows that $f(1)=1$ ), we conclude that $f(f(a))=a$ for all $a$, and hence $f$ is a bijection. Moreover, we now have that $f(a) \mid f(b)$ implies $f(f(a)) \mid f(f(b))$, i.e. $a \mid b$, so $a \mid b$ if and only if $f(a) \mid f(b)$. Together with the fact that $f$ is a bijection, this implies that $f(n)$ has the same number of divisors of $n$. Let $p$ be a prime. Then $f(p)=q$ must be a prime as well. If $q \neq p$, then from $f(p) \mid f(p q)$ and $f(q) \mid f(p q)$ it follows that $p q \mid f(p q)$, so $f(p q)=p q$ because $f(p q)$ and $p q$ must have the same number of divisors. Therefore, for every prime number $p$ we either have that $f(p)=p$ or $f(p f(p))=p f(p)$. From here, it is easy to see that $f(n)=n$ for infinitely many $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A function $f: \mathbb{N} \rightarrow \mathbb{N}$ has the property that for all positive integers $m$ and $n$, exactly one of the $f(n)$ numbers $$ f(m+1), f(m+2), \ldots, f(m+f(n)) $$ is divisible by $n$. Prove that $f(n)=n$ for infinitely many positive integers $n$.
|
We start with the following claim: $$ \text { Claim - If } a \mid b \text { then } f(a) \mid f(b) $$ In what follows, let $a \geq 2$ be any positive integer. Because $f(a)$ and $f(2 a)$ are both divisible by $f(a)$, there are $a+1$ consecutive values of $f$ of which at least two divisible by $f(a)$. It follows that $f(f(a)) \leq a$. However, we also know that exactly one of $f(2), f(3), \ldots, f(1+f(a))$ is divisible by $a$; let this be $f(t)$. Then we have $S_{a}=\{t, t+f(a), t+2 f(a), \ldots\}$. Because $a|f(t)| f(2 t)$, we know that $2 t \in S_{a}$, so $t$ is a multiple of $f(a)$. Because $2 \leq t \leq 1+f(a)$, and $f(a) \geq 2$ for $a \geq 2$, we conclude that we must have $t=f(a)$, so $f(f(a))$ is a multiple of $a$. Together with $f(f(a)) \leq a$, this yields $f(f(a))=a$. Because $f(f(a))=a$ also holds for $a=1$ (from the given condition for $n=1$ it immediately follows that $f(1)=1$ ), we conclude that $f(f(a))=a$ for all $a$, and hence $f$ is a bijection. Moreover, we now have that $f(a) \mid f(b)$ implies $f(f(a)) \mid f(f(b))$, i.e. $a \mid b$, so $a \mid b$ if and only if $f(a) \mid f(b)$. Together with the fact that $f$ is a bijection, this implies that $f(n)$ has the same number of divisors of $n$. Let $p$ be a prime. Then $f(p)=q$ must be a prime as well. If $q \neq p$, then from $f(p) \mid f(p q)$ and $f(q) \mid f(p q)$ it follows that $p q \mid f(p q)$, so $f(p q)=p q$ because $f(p q)$ and $p q$ must have the same number of divisors. Therefore, for every prime number $p$ we either have that $f(p)=p$ or $f(p f(p))=p f(p)$. From here, it is easy to see that $f(n)=n$ for infinitely many $n$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"problem_match": null,
"solution_match": null
}
|
5ec4e6d7-b07e-558d-92b3-dc7c5aff1258
| 606,268 |
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
\ First solution, by author. Let $\odot O X_{A} Y_{A}$ intersects $A B, A C$ again at $U, V$. Then by Reim's theorem $U V C B$ are concyclic. Hence the radical axis of $\odot O X_{A} Y_{A}, \odot O B C$ and $\odot(U V C B)$ are concurrent, i.e. $O K_{A}, B C, U V$ are concurrent, Denote the intersection as $K_{A}^{*}$, which is indeed the inversion of $K_{A}$ with respect to $\odot O$. (The inversion sends $\odot O B C$ to the line $B C$ ). Let $P_{A}, P_{B}, P_{C}$ be the circumcenters of $\triangle O B C, \triangle O C A, \triangle O A B$ respectively. Claim $-K_{A}^{*}$ coincides with the intersection of $P_{B} P_{C}$ and $B C$. Finally by Desargue's theorem, it suffices to show that $A P_{A}, B P_{B}, C P_{C}$ are concurrent. Note that $$ \begin{aligned} & d\left(P_{A}, A B\right)=P_{A} B \sin \left(90^{\circ}+\angle C-\angle A\right) \\ & d\left(P_{A}, A C\right)=P_{A} C \sin \left(90^{\circ}+\angle B-\angle A\right) \end{aligned} $$ Hence the symmetric product and trig Ceva finishes the proof. 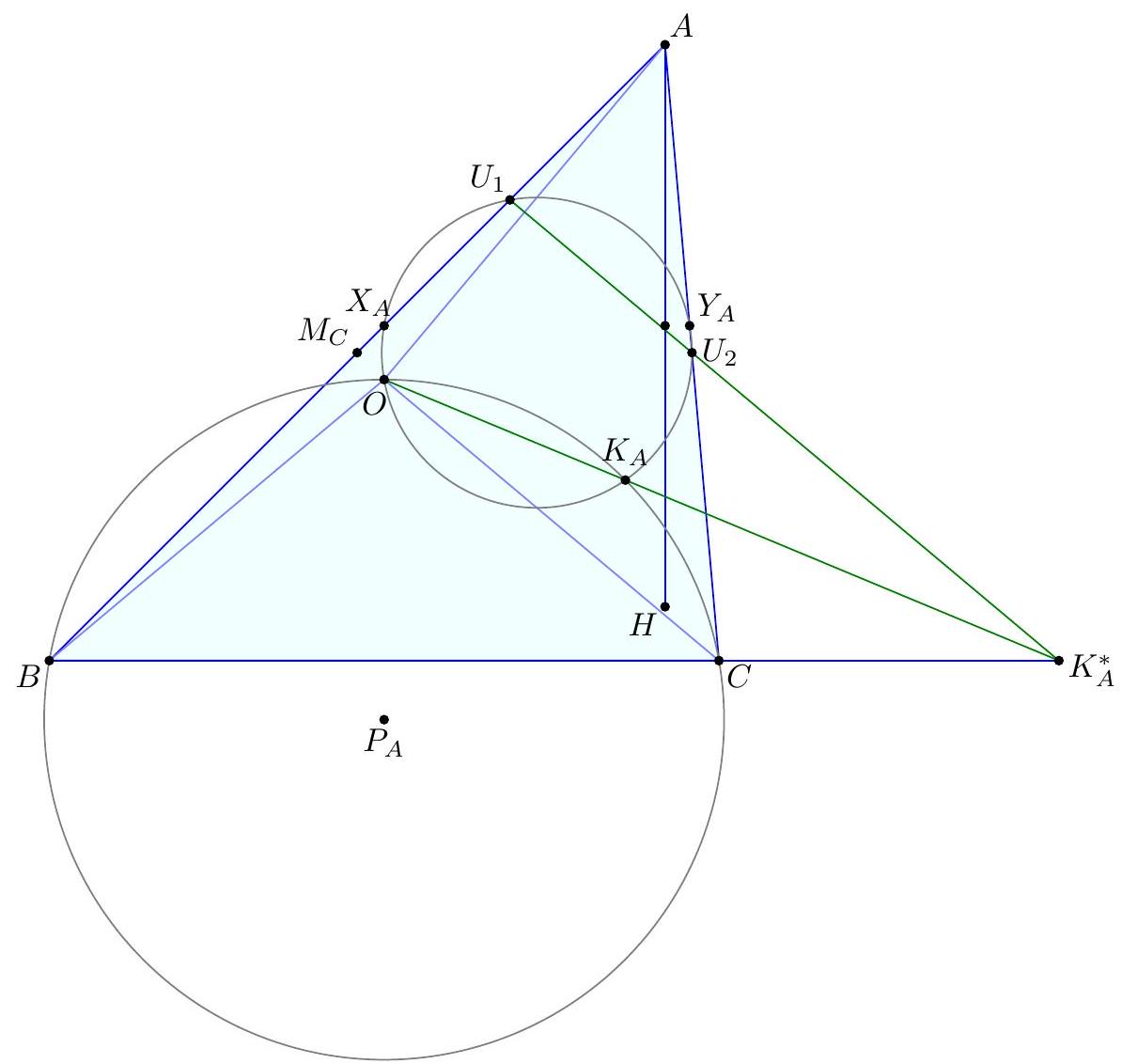
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
\ First solution, by author. Let $\odot O X_{A} Y_{A}$ intersects $A B, A C$ again at $U, V$. Then by Reim's theorem $U V C B$ are concyclic. Hence the radical axis of $\odot O X_{A} Y_{A}, \odot O B C$ and $\odot(U V C B)$ are concurrent, i.e. $O K_{A}, B C, U V$ are concurrent, Denote the intersection as $K_{A}^{*}$, which is indeed the inversion of $K_{A}$ with respect to $\odot O$. (The inversion sends $\odot O B C$ to the line $B C$ ). Let $P_{A}, P_{B}, P_{C}$ be the circumcenters of $\triangle O B C, \triangle O C A, \triangle O A B$ respectively. Claim $-K_{A}^{*}$ coincides with the intersection of $P_{B} P_{C}$ and $B C$. Finally by Desargue's theorem, it suffices to show that $A P_{A}, B P_{B}, C P_{C}$ are concurrent. Note that $$ \begin{aligned} & d\left(P_{A}, A B\right)=P_{A} B \sin \left(90^{\circ}+\angle C-\angle A\right) \\ & d\left(P_{A}, A C\right)=P_{A} C \sin \left(90^{\circ}+\angle B-\angle A\right) \end{aligned} $$ Hence the symmetric product and trig Ceva finishes the proof. 
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e0ec005-4055-5ed7-9822-569d404058e5
| 606,283 |
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
I Second solution, from Jeffrey Kwan. Let $O_{A}$ be the circumcenter of $\triangle A X_{A} Y_{A}$. The key claim is that: Claim $-O_{A} X_{A} Y_{A} O$ is cyclic. $$ \frac{A X_{A}}{A B}=\frac{A H / 2}{A D}=\frac{R \cos A}{A D} $$ and so $$ \frac{A O}{A D}=R \cdot \frac{A X_{A}}{A B \cdot R \cos A}=\frac{A X_{A}}{A E}=\frac{A Y_{A}}{A F} $$ Hence $\angle X_{A} O Y_{A}=180^{\circ}-2 \angle A=180^{\circ}-\angle X_{A} O_{A} Y_{A}$, which proves the claim. Let $P_{A}$ be the circumcenter of $\triangle O B C$, and define $P_{B}, P_{C}$ similarly. By the claim, $A$ is the exsimilicenter of $\left(O X_{A} Y_{A}\right)$ and $(O B C)$, so $A P_{A}$ is the line between their two centers. In particular, $A P_{A}$ is the perpendicular bisector of $O K_{A}$. 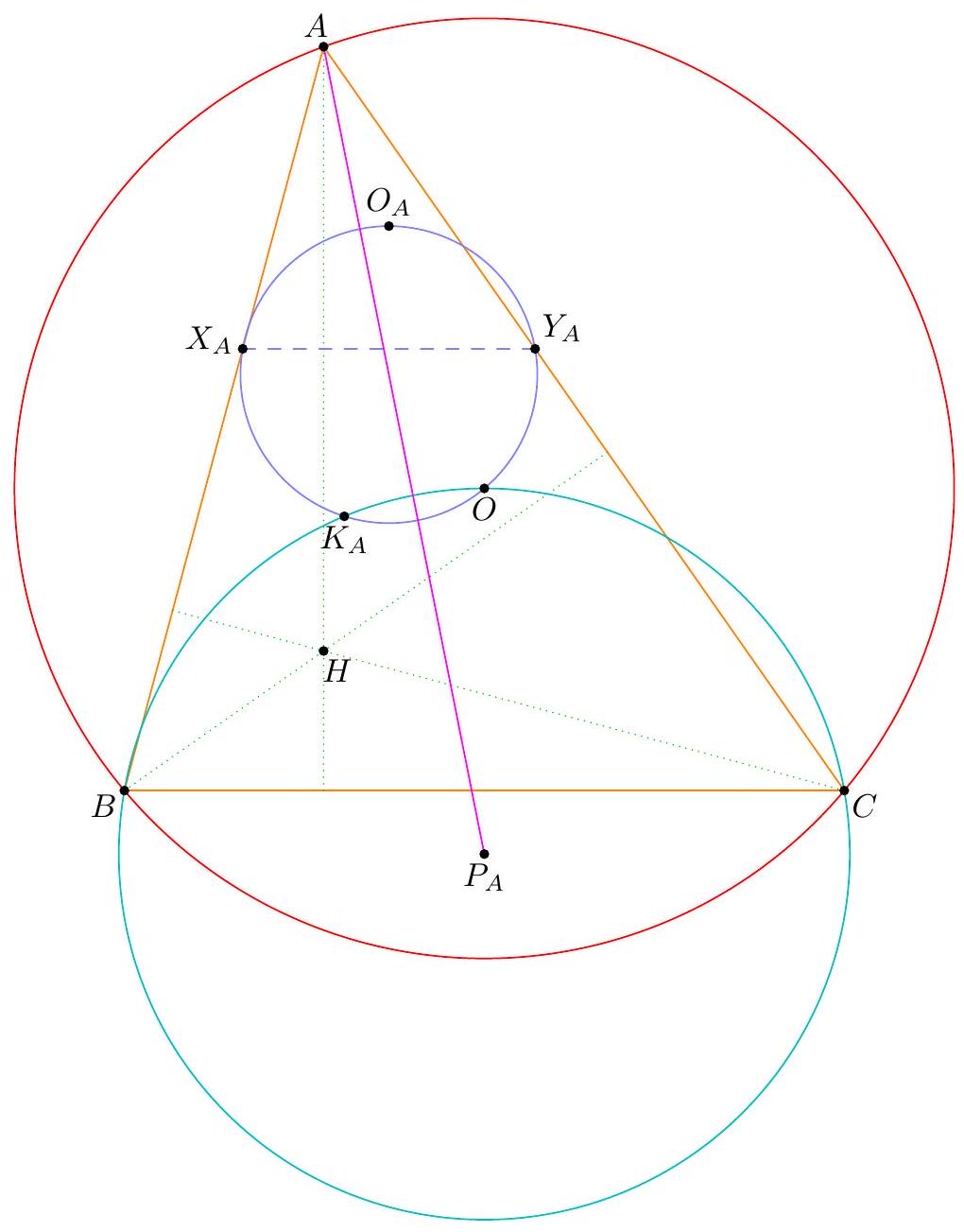 Claim $-A P_{A}, B P_{B}, C P_{C}$ concur at $T$. Now $T$ lies on the perpendicular bisectors of $O K_{A}, O K_{B}$, and $O K_{C}$. Hence $O K_{A} K_{B} K_{C}$ is cyclic with center $T$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ and $H$ be the circumcenter and orthocenter, respectively, of an acute scalene triangle $A B C$. The perpendicular bisector of $\overline{A H}$ intersects $\overline{A B}$ and $\overline{A C}$ at $X_{A}$ and $Y_{A}$ respectively. Let $K_{A}$ denote the intersection of the circumcircles of triangles $O X_{A} Y_{A}$ and $B O C$ other than $O$. Define $K_{B}$ and $K_{C}$ analogously by repeating this construction two more times. Prove that $K_{A}, K_{B}, K_{C}$, and $O$ are concyclic.
|
I Second solution, from Jeffrey Kwan. Let $O_{A}$ be the circumcenter of $\triangle A X_{A} Y_{A}$. The key claim is that: Claim $-O_{A} X_{A} Y_{A} O$ is cyclic. $$ \frac{A X_{A}}{A B}=\frac{A H / 2}{A D}=\frac{R \cos A}{A D} $$ and so $$ \frac{A O}{A D}=R \cdot \frac{A X_{A}}{A B \cdot R \cos A}=\frac{A X_{A}}{A E}=\frac{A Y_{A}}{A F} $$ Hence $\angle X_{A} O Y_{A}=180^{\circ}-2 \angle A=180^{\circ}-\angle X_{A} O_{A} Y_{A}$, which proves the claim. Let $P_{A}$ be the circumcenter of $\triangle O B C$, and define $P_{B}, P_{C}$ similarly. By the claim, $A$ is the exsimilicenter of $\left(O X_{A} Y_{A}\right)$ and $(O B C)$, so $A P_{A}$ is the line between their two centers. In particular, $A P_{A}$ is the perpendicular bisector of $O K_{A}$.  Claim $-A P_{A}, B P_{B}, C P_{C}$ concur at $T$. Now $T$ lies on the perpendicular bisectors of $O K_{A}, O K_{B}$, and $O K_{C}$. Hence $O K_{A} K_{B} K_{C}$ is cyclic with center $T$, as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e0ec005-4055-5ed7-9822-569d404058e5
| 606,283 |
Let $A B C D$ be a parallelogram. Point $E$ lies on segment $C D$ such that $$ 2 \angle A E B=\angle A D B+\angle A C B, $$ and point $F$ lies on segment $B C$ such that $$ 2 \angle D F A=\angle D C A+\angle D B A . $$ Let $K$ be the circumcenter of triangle $A B D$. Prove that $K E=K F$.
|
Let the circle through $A, B$, and $E$ intersect $C D$ again at $E^{\prime}$, and let the circle through $D$, $A$, and $F$ intersect $B C$ again at $F^{\prime}$. Now $A B E E^{\prime}$ and $D A F^{\prime} F$ are cyclic quadrilaterals with two parallel sides, so they are isosceles trapezoids. From $K A=K B$, it now follows that $K E=K E^{\prime}$, whereas from $K A=K D$ it follows that $K F=K F^{\prime}$. Next, let the circle through $A, B$, and $E$ intersect $A C$ again at $S$. Then $$ \angle A S B=\angle A E B=\frac{1}{2}(\angle A D B+\angle A C B)=\frac{1}{2}(\angle A D B+\angle D A C)=\frac{1}{2} \angle A M B, $$ where $M$ is the intersection of $A C$ and $B D$. From $\angle A S B=\frac{1}{2} \angle A M B$, it follows that $M S=M B$, so $S$ is the point on $M C$ such that $M S=M B=M D$. By symmetry, the circle through $A, D$, and $F$ also passes through $S$, and it follows that the line $A S$ is the radical axis of the circles $(A B E)$ and $(A D F)$. By power of a point, we now obtain $$ C E \cdot C E^{\prime}=C S \cdot C A=C F \cdot C F^{\prime}, $$ from which it follows that $E, F, E^{\prime}$, and $F^{\prime}$ are concyclic. The segments $E E^{\prime}$ and $F F^{\prime}$ are not parallel, so their perpendicular bisectors only meet at one point, which is $K$. Hence $K E=K F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram. Point $E$ lies on segment $C D$ such that $$ 2 \angle A E B=\angle A D B+\angle A C B, $$ and point $F$ lies on segment $B C$ such that $$ 2 \angle D F A=\angle D C A+\angle D B A . $$ Let $K$ be the circumcenter of triangle $A B D$. Prove that $K E=K F$.
|
Let the circle through $A, B$, and $E$ intersect $C D$ again at $E^{\prime}$, and let the circle through $D$, $A$, and $F$ intersect $B C$ again at $F^{\prime}$. Now $A B E E^{\prime}$ and $D A F^{\prime} F$ are cyclic quadrilaterals with two parallel sides, so they are isosceles trapezoids. From $K A=K B$, it now follows that $K E=K E^{\prime}$, whereas from $K A=K D$ it follows that $K F=K F^{\prime}$. Next, let the circle through $A, B$, and $E$ intersect $A C$ again at $S$. Then $$ \angle A S B=\angle A E B=\frac{1}{2}(\angle A D B+\angle A C B)=\frac{1}{2}(\angle A D B+\angle D A C)=\frac{1}{2} \angle A M B, $$ where $M$ is the intersection of $A C$ and $B D$. From $\angle A S B=\frac{1}{2} \angle A M B$, it follows that $M S=M B$, so $S$ is the point on $M C$ such that $M S=M B=M D$. By symmetry, the circle through $A, D$, and $F$ also passes through $S$, and it follows that the line $A S$ is the radical axis of the circles $(A B E)$ and $(A D F)$. By power of a point, we now obtain $$ C E \cdot C E^{\prime}=C S \cdot C A=C F \cdot C F^{\prime}, $$ from which it follows that $E, F, E^{\prime}$, and $F^{\prime}$ are concyclic. The segments $E E^{\prime}$ and $F F^{\prime}$ are not parallel, so their perpendicular bisectors only meet at one point, which is $K$. Hence $K E=K F$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"problem_match": null,
"solution_match": null
}
|
87963110-5767-5e81-a02c-8993454c8870
| 606,296 |
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
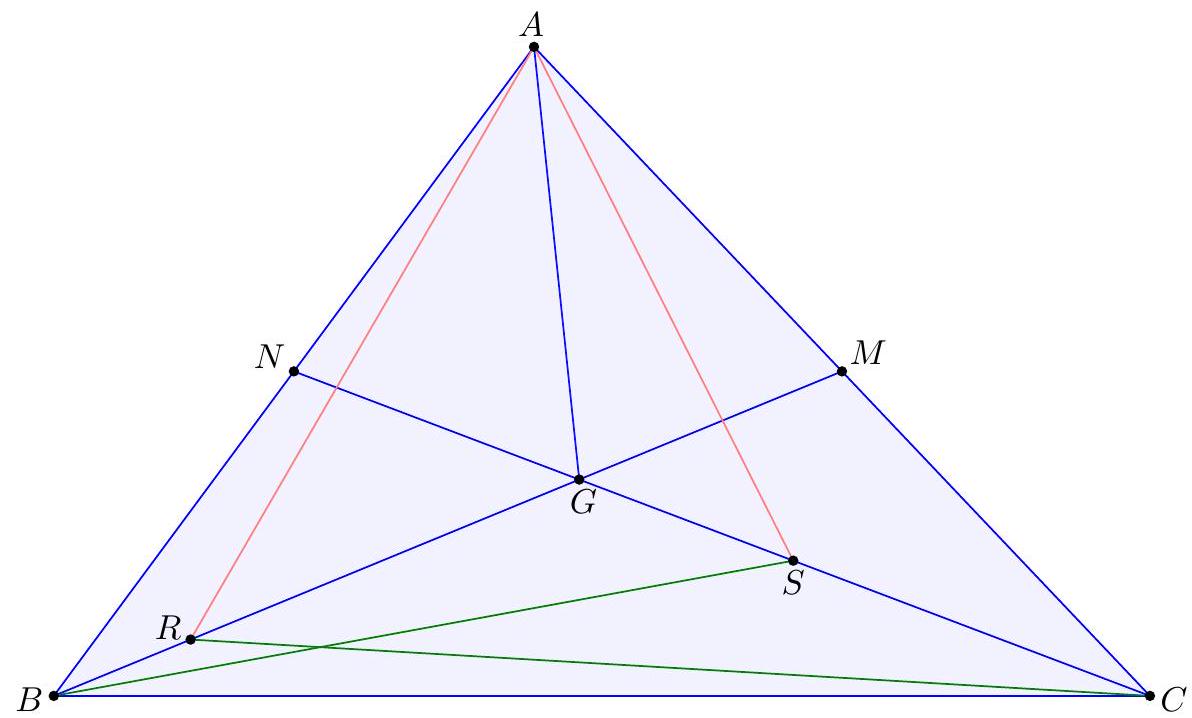 【 Solution 1 using power of a point. From the given condition that $\measuredangle A C R=\measuredangle C G M$, we get that $$ M A^{2}=M C^{2}=M G \cdot M R \Longrightarrow \measuredangle R A C=\measuredangle M G A $$ Analogously, $$ \measuredangle B A S=\measuredangle A G N $$ Hence, $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle M G A+\measuredangle A G N=\measuredangle M G N=\measuredangle B G C . $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 【 Solution 1 using power of a point. From the given condition that $\measuredangle A C R=\measuredangle C G M$, we get that $$ M A^{2}=M C^{2}=M G \cdot M R \Longrightarrow \measuredangle R A C=\measuredangle M G A $$ Analogously, $$ \measuredangle B A S=\measuredangle A G N $$ Hence, $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle M G A+\measuredangle A G N=\measuredangle M G N=\measuredangle B G C . $$
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4d0fb9d-67d1-5355-bb96-d3bbd63654fe
| 606,310 |
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 ब Solution 2 using similar triangles. As before, $\triangle M G C \sim \triangle M C R$ and $\triangle N G B \sim$ $\triangle N B S$. We obtain $$ \frac{|A C|}{|C R|}=\frac{2|M C|}{|C R|}=\frac{2|M G|}{|G C|}=\frac{|G B|}{2|N G|}=\frac{|B S|}{2|B N|}=\frac{|B S|}{|A B|} $$ which together with $\angle A C R=\angle A B S$ yields $$ \triangle A C R \sim \triangle S B A \Longrightarrow \measuredangle B A S=\measuredangle C R A $$ Hence $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle R A C+\measuredangle C R A=-\measuredangle A C R=\measuredangle B G C, $$ which proves the statement.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 ब Solution 2 using similar triangles. As before, $\triangle M G C \sim \triangle M C R$ and $\triangle N G B \sim$ $\triangle N B S$. We obtain $$ \frac{|A C|}{|C R|}=\frac{2|M C|}{|C R|}=\frac{2|M G|}{|G C|}=\frac{|G B|}{2|N G|}=\frac{|B S|}{2|B N|}=\frac{|B S|}{|A B|} $$ which together with $\angle A C R=\angle A B S$ yields $$ \triangle A C R \sim \triangle S B A \Longrightarrow \measuredangle B A S=\measuredangle C R A $$ Hence $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle R A C+\measuredangle C R A=-\measuredangle A C R=\measuredangle B G C, $$ which proves the statement.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4d0fb9d-67d1-5355-bb96-d3bbd63654fe
| 606,310 |
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 I Solution 3 using parallelograms. Let $M$ and $N$ be defined as above. Let $P$ be the reflection of $G$ in $M$ and let $Q$ the reflection of $G$ in $N$. Then $A G C P$ and $A G B Q$ are parallelograms. 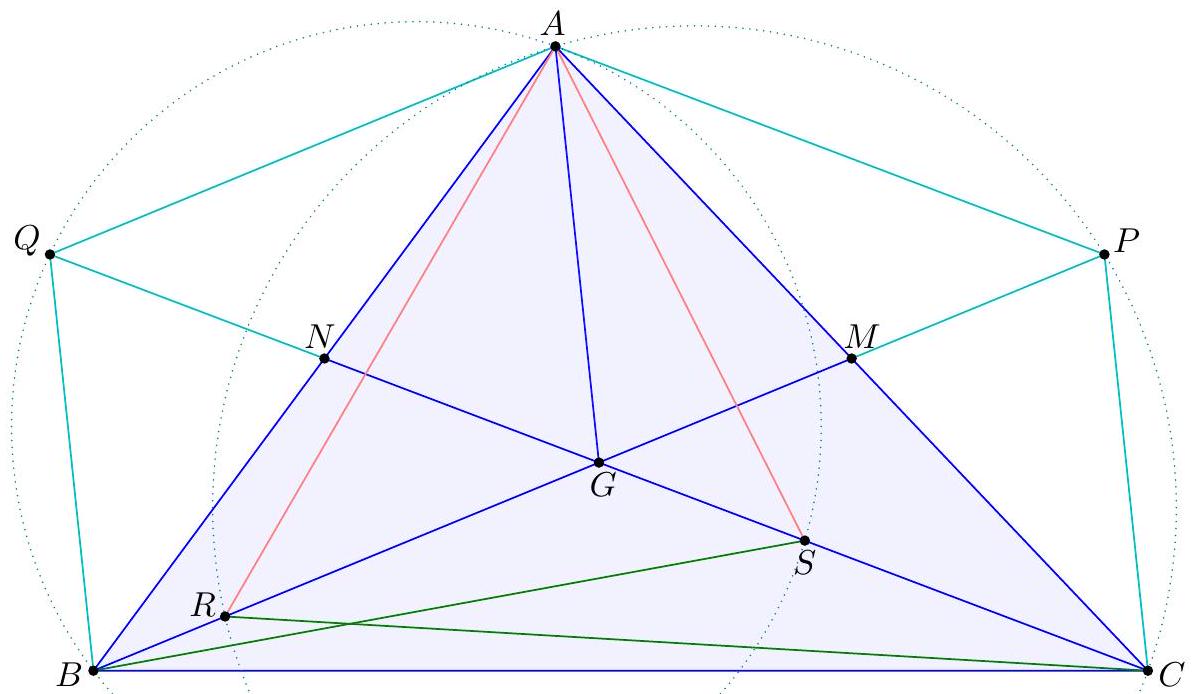 Claim - Quadrilaterals $A P C R$ and $A Q B S$ are concyclic. Thus from $\overline{P C} \| \overline{G A}$ we get $$ \measuredangle R A C=\measuredangle R P C=\measuredangle G P C=\measuredangle P G A $$ and similarly $$ \measuredangle B A S=\measuredangle B Q S=\measuredangle B Q G=\measuredangle A G Q $$ We conclude that $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle P G A+\measuredangle A G Q=\measuredangle P G Q=\measuredangle B G C $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 I Solution 3 using parallelograms. Let $M$ and $N$ be defined as above. Let $P$ be the reflection of $G$ in $M$ and let $Q$ the reflection of $G$ in $N$. Then $A G C P$ and $A G B Q$ are parallelograms.  Claim - Quadrilaterals $A P C R$ and $A Q B S$ are concyclic. Thus from $\overline{P C} \| \overline{G A}$ we get $$ \measuredangle R A C=\measuredangle R P C=\measuredangle G P C=\measuredangle P G A $$ and similarly $$ \measuredangle B A S=\measuredangle B Q S=\measuredangle B Q G=\measuredangle A G Q $$ We conclude that $$ \measuredangle R A S+\measuredangle B A C=\measuredangle R A C+\measuredangle B A S=\measuredangle P G A+\measuredangle A G Q=\measuredangle P G Q=\measuredangle B G C $$
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4d0fb9d-67d1-5355-bb96-d3bbd63654fe
| 606,310 |
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 ब Solution 4 also using parallelograms, by Ankan Bhattacharya. Construct parallelograms $A R C K$ and $A S B L$. Since $$ \measuredangle C A K=\measuredangle A C R=\measuredangle C G B=\measuredangle C G K, $$ it follows that $A G C K$ is cyclic. Similarly, $A G B L$ is also cyclic. 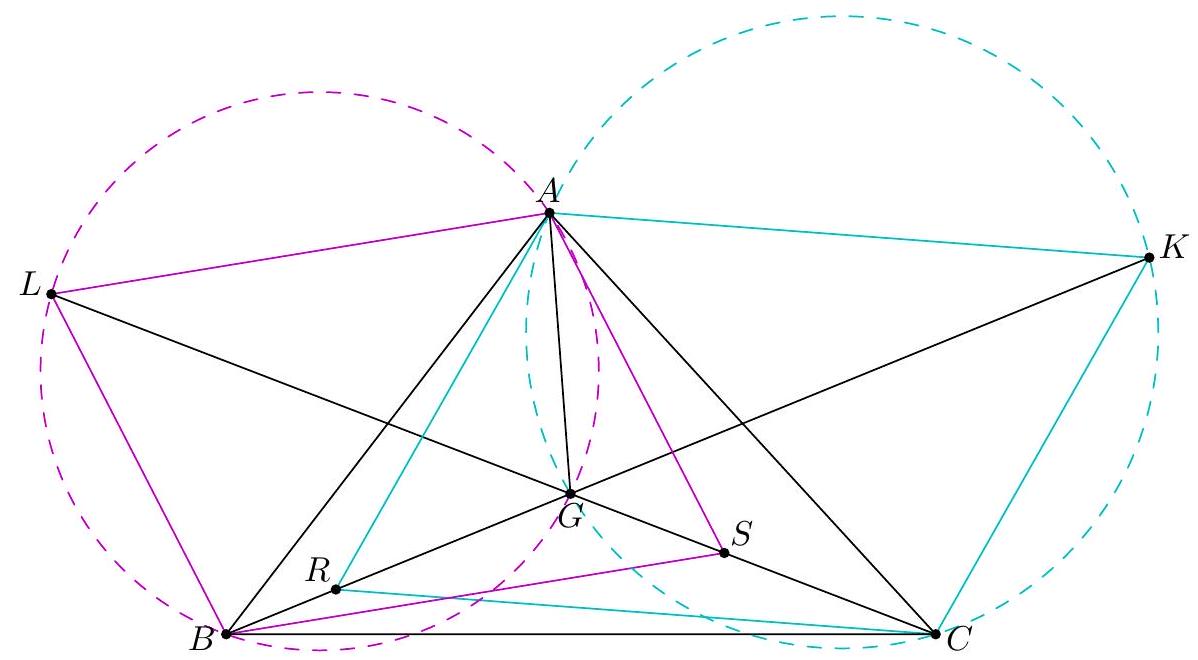 Finally, observe that $$ \begin{aligned} \angle R A S+\angle B A C & =\measuredangle B A S+\measuredangle R A C \\ & =\measuredangle A B L+\measuredangle K C A \\ & =\measuredangle A G L+\measuredangle K G A \\ & =\measuredangle K G L \\ & =\angle B G C \end{aligned} $$ as requested.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 ब Solution 4 also using parallelograms, by Ankan Bhattacharya. Construct parallelograms $A R C K$ and $A S B L$. Since $$ \measuredangle C A K=\measuredangle A C R=\measuredangle C G B=\measuredangle C G K, $$ it follows that $A G C K$ is cyclic. Similarly, $A G B L$ is also cyclic.  Finally, observe that $$ \begin{aligned} \angle R A S+\angle B A C & =\measuredangle B A S+\measuredangle R A C \\ & =\measuredangle A B L+\measuredangle K C A \\ & =\measuredangle A G L+\measuredangle K G A \\ & =\measuredangle K G L \\ & =\angle B G C \end{aligned} $$ as requested.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4d0fb9d-67d1-5355-bb96-d3bbd63654fe
| 606,310 |
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 『 Solution 5 using complex numbers, by Milan Haiman. Note that $\angle R A S+\angle B A C=$ $\angle B A S+\angle R A C$. We compute $\angle B A S$ in complex numbers; then $\angle R A C$ will then be known by symmetry. Let $a, b, c$ be points on the unit circle representing $A, B, C$ respectively. Let $g=\frac{1}{3}(a+b+c)$ represent the centroid $G$, and let $s$ represent $S$. ## Claim - We have $$ \frac{s-a}{b-a}=\frac{a b-2 b c+c a}{2 a b-b c-c a} . $$ $$ s=\frac{a+b}{2}+t(c-g) $$ for some $t \in \mathbb{R}$. By the given angle condition, we have that $$ \frac{(s-b) /(b-a)}{(c-g) /(g-b)} \in \mathbb{R} $$ Note that $$ \frac{s-b}{b-a}=t \frac{c-g}{b-a}-\frac{1}{2} $$ So, $$ t \frac{g-b}{b-a}-\frac{g-b}{2(c-g)} \in \mathbb{R} $$ Thus $$ t=\frac{\operatorname{Im}\left(\frac{g-b}{2(c-g)}\right)}{\operatorname{Im}\left(\frac{g-b}{b-a}\right)}=\frac{1}{2} \cdot \frac{\left(\frac{g-b}{c-g}\right)-\overline{\left(\frac{g-b}{c-g}\right)}}{\left(\frac{g-b}{b-a}\right)-\overline{\left(\frac{g-b}{b-a}\right)}} $$ Let $N$ and $D$ be the numerator and denominator of the second factor above. We want to compute $$ \frac{s-a}{b-a}=\frac{1}{2}+t \frac{c-g}{b-a}=\frac{(b-a)+2 t(c-g)}{2(b-a)}=\frac{(b-a) D+(c-g) N}{2(b-a) D} $$ We have $$ \begin{aligned} (c-g) N & =g-b-(c-g) \overline{\left(\frac{g-b}{c-g}\right)} \\ & =\frac{a+b+c}{3}-b-\left(c-\frac{a+b+c}{3}\right) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{c}-\frac{1}{a}-\frac{1}{b}-\frac{1}{c}} \\ & =\frac{(a+c-2 b)(2 a b-b c-c a)-(2 c-a-b)(a b+b c-2 c a)}{3(2 a b-b c-c a)} \\ & =\frac{3\left(a^{2} b+b^{2} c+c^{2} a-a b^{2}-b c^{2}-c a^{2}\right)}{3(2 a b-b c-c a)} \\ & =\frac{(a-b)(b-c)(a-c)}{2 a b-b c-c a} \end{aligned} $$ We also compute $$ \begin{aligned} (b-a) D & =g-b-(b-a) \overline{\left(\frac{g-b}{b-a}\right)} \\ & =\frac{a+b+c}{3}-b-(b-a) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{b}-\frac{3}{a}} \\ & =\frac{(a+c-2 b) c+(a b+b c-2 c a)}{3 c} \\ & =\frac{a b-b c-c a+c^{2}}{3 c} \\ & =\frac{(a-c)(b-c)}{3 c} \end{aligned} $$ So, we obtain $$ \frac{s-a}{b-a}=\frac{\frac{1}{3 c}+\frac{a-b}{2 a b-b c-c a}}{\frac{2}{3 c}}=\frac{2 a b-b c-c a+3 c(a-b)}{2(2 a b-b c-c a)}=\frac{a b-2 b c+c a}{2 a b-b c-c a} $$ By symmetry, $$ \frac{r-a}{c-a}=\frac{a b-2 b c+c a}{2 c a-a b-b c} $$ Hence their ratio $$ \frac{s-a}{b-a} \div \frac{r-a}{c-a}=\frac{2 a b-b c-c a}{2 c a-a b-b c} $$ has argument $\angle R A C+\angle B A S$. We also have that $\angle B G C$ is the argument of $$ \frac{b-g}{c-g}=\frac{2 b-a-c}{2 c-a-b} $$ Note that these two complex numbers are inverse-conjugates, and thus have the same argument. So we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Points $R$ and $S$ are chosen on rays $G B$ and $G C$, respectively, such that $$ \angle A B S=\angle A C R=180^{\circ}-\angle B G C . $$ Prove that $\angle R A S+\angle B A C=\angle B G C$.
|
 『 Solution 5 using complex numbers, by Milan Haiman. Note that $\angle R A S+\angle B A C=$ $\angle B A S+\angle R A C$. We compute $\angle B A S$ in complex numbers; then $\angle R A C$ will then be known by symmetry. Let $a, b, c$ be points on the unit circle representing $A, B, C$ respectively. Let $g=\frac{1}{3}(a+b+c)$ represent the centroid $G$, and let $s$ represent $S$. ## Claim - We have $$ \frac{s-a}{b-a}=\frac{a b-2 b c+c a}{2 a b-b c-c a} . $$ $$ s=\frac{a+b}{2}+t(c-g) $$ for some $t \in \mathbb{R}$. By the given angle condition, we have that $$ \frac{(s-b) /(b-a)}{(c-g) /(g-b)} \in \mathbb{R} $$ Note that $$ \frac{s-b}{b-a}=t \frac{c-g}{b-a}-\frac{1}{2} $$ So, $$ t \frac{g-b}{b-a}-\frac{g-b}{2(c-g)} \in \mathbb{R} $$ Thus $$ t=\frac{\operatorname{Im}\left(\frac{g-b}{2(c-g)}\right)}{\operatorname{Im}\left(\frac{g-b}{b-a}\right)}=\frac{1}{2} \cdot \frac{\left(\frac{g-b}{c-g}\right)-\overline{\left(\frac{g-b}{c-g}\right)}}{\left(\frac{g-b}{b-a}\right)-\overline{\left(\frac{g-b}{b-a}\right)}} $$ Let $N$ and $D$ be the numerator and denominator of the second factor above. We want to compute $$ \frac{s-a}{b-a}=\frac{1}{2}+t \frac{c-g}{b-a}=\frac{(b-a)+2 t(c-g)}{2(b-a)}=\frac{(b-a) D+(c-g) N}{2(b-a) D} $$ We have $$ \begin{aligned} (c-g) N & =g-b-(c-g) \overline{\left(\frac{g-b}{c-g}\right)} \\ & =\frac{a+b+c}{3}-b-\left(c-\frac{a+b+c}{3}\right) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{c}-\frac{1}{a}-\frac{1}{b}-\frac{1}{c}} \\ & =\frac{(a+c-2 b)(2 a b-b c-c a)-(2 c-a-b)(a b+b c-2 c a)}{3(2 a b-b c-c a)} \\ & =\frac{3\left(a^{2} b+b^{2} c+c^{2} a-a b^{2}-b c^{2}-c a^{2}\right)}{3(2 a b-b c-c a)} \\ & =\frac{(a-b)(b-c)(a-c)}{2 a b-b c-c a} \end{aligned} $$ We also compute $$ \begin{aligned} (b-a) D & =g-b-(b-a) \overline{\left(\frac{g-b}{b-a}\right)} \\ & =\frac{a+b+c}{3}-b-(b-a) \frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{b}}{\frac{3}{b}-\frac{3}{a}} \\ & =\frac{(a+c-2 b) c+(a b+b c-2 c a)}{3 c} \\ & =\frac{a b-b c-c a+c^{2}}{3 c} \\ & =\frac{(a-c)(b-c)}{3 c} \end{aligned} $$ So, we obtain $$ \frac{s-a}{b-a}=\frac{\frac{1}{3 c}+\frac{a-b}{2 a b-b c-c a}}{\frac{2}{3 c}}=\frac{2 a b-b c-c a+3 c(a-b)}{2(2 a b-b c-c a)}=\frac{a b-2 b c+c a}{2 a b-b c-c a} $$ By symmetry, $$ \frac{r-a}{c-a}=\frac{a b-2 b c+c a}{2 c a-a b-b c} $$ Hence their ratio $$ \frac{s-a}{b-a} \div \frac{r-a}{c-a}=\frac{2 a b-b c-c a}{2 c a-a b-b c} $$ has argument $\angle R A C+\angle B A S$. We also have that $\angle B G C$ is the argument of $$ \frac{b-g}{c-g}=\frac{2 b-a-c}{2 c-a-b} $$ Note that these two complex numbers are inverse-conjugates, and thus have the same argument. So we're done.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4d0fb9d-67d1-5355-bb96-d3bbd63654fe
| 606,310 |
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
【 First solution (authors). By Cauchy-Schwarz, we have $$ \begin{aligned} \sum_{k=m}^{n} \frac{k+1}{k^{3}} & =\sum_{k=m}^{n} \frac{\left(\frac{1}{k^{2}}\right)^{2}}{\frac{1}{k(k+1)}} \\ & \geq \frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m(m+1)}+\frac{1}{(m+1)(m+2)}+\cdots+\frac{1}{n(n+1)}} \\ & =\frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m}-\frac{1}{n+1}} \\ & >\frac{\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2}}{\frac{1}{m}} \end{aligned} $$ as desired. Remark (Bound on error). Let $A=\sum_{k=m}^{n} k^{-2}$ and $B=\sum_{k=m}^{n} k^{-3}$. The inequality above becomes tighter for large $m$ and $n \gg m$. If we use Lagrange's identity in place of Cauchy-Schwarz, we get $$ A+B-m A^{2}=m \cdot \sum_{m \leq a<b} \frac{(a-b)^{2}}{a^{3} b^{3}(a+1)(b+1)} $$ We can upper bound this error by $$ \leq m \cdot \sum_{m \leq a<b} \frac{1}{a^{3}(a+1) b(b+1)}=m \cdot \sum_{m \leq a} \frac{1}{a^{3}(a+1)^{2}} \approx m \cdot \frac{1}{m^{4}}=\frac{1}{m^{3}}, $$ which is still generous as $(a-b)^{2} \ll b^{2}$ for $b$ not much larger than $a$, so the real error is probably around $\frac{1}{10 \mathrm{~m}^{3}}$. This exhibits the tightness of the inequality since it implies $$ m A^{2}+O(B / m)>A+B $$ Remark (Construction commentary, from author). My motivation was to write an inequality where Titu could be applied creatively to yield a telescoping sum. This can be difficult because most of the time, such a reverse-engineered inequality will be so loose it's trivial anyways. My first attempt was the not-so-amazing inequality $$ \frac{n^{2}+3 n}{2}=\sum_{1}^{n} i+1=\sum_{1}^{n} \frac{\frac{1}{i}}{\frac{1}{i(i+1)}}>\left(\sum_{1}^{n} \frac{1}{\sqrt{i}}\right)^{2} $$ which is really not surprising given that $\sum \frac{1}{\sqrt{i}} \ll \frac{n}{\sqrt{2}}$. The key here is that we need "near-equality" as dictated by the Cauchy-Schwarz equality case, i.e. the square root of the numerators should be approximately proportional to the denominators. This motivates using $\frac{1}{i^{4}}$ as the numerator, which works like a charm. After working out the resulting statement, the LHS and RHS even share a sum, which adds to the simplicity of the problem. The final touch was to unrestrict the starting value of the sum, since this allows the strength of the estimate $\frac{1}{i^{2}} \approx \frac{1}{i(i+1)}$ to be fully exploited.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
【 First solution (authors). By Cauchy-Schwarz, we have $$ \begin{aligned} \sum_{k=m}^{n} \frac{k+1}{k^{3}} & =\sum_{k=m}^{n} \frac{\left(\frac{1}{k^{2}}\right)^{2}}{\frac{1}{k(k+1)}} \\ & \geq \frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m(m+1)}+\frac{1}{(m+1)(m+2)}+\cdots+\frac{1}{n(n+1)}} \\ & =\frac{\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}+\cdots+\frac{1}{n^{2}}\right)^{2}}{\frac{1}{m}-\frac{1}{n+1}} \\ & >\frac{\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2}}{\frac{1}{m}} \end{aligned} $$ as desired. Remark (Bound on error). Let $A=\sum_{k=m}^{n} k^{-2}$ and $B=\sum_{k=m}^{n} k^{-3}$. The inequality above becomes tighter for large $m$ and $n \gg m$. If we use Lagrange's identity in place of Cauchy-Schwarz, we get $$ A+B-m A^{2}=m \cdot \sum_{m \leq a<b} \frac{(a-b)^{2}}{a^{3} b^{3}(a+1)(b+1)} $$ We can upper bound this error by $$ \leq m \cdot \sum_{m \leq a<b} \frac{1}{a^{3}(a+1) b(b+1)}=m \cdot \sum_{m \leq a} \frac{1}{a^{3}(a+1)^{2}} \approx m \cdot \frac{1}{m^{4}}=\frac{1}{m^{3}}, $$ which is still generous as $(a-b)^{2} \ll b^{2}$ for $b$ not much larger than $a$, so the real error is probably around $\frac{1}{10 \mathrm{~m}^{3}}$. This exhibits the tightness of the inequality since it implies $$ m A^{2}+O(B / m)>A+B $$ Remark (Construction commentary, from author). My motivation was to write an inequality where Titu could be applied creatively to yield a telescoping sum. This can be difficult because most of the time, such a reverse-engineered inequality will be so loose it's trivial anyways. My first attempt was the not-so-amazing inequality $$ \frac{n^{2}+3 n}{2}=\sum_{1}^{n} i+1=\sum_{1}^{n} \frac{\frac{1}{i}}{\frac{1}{i(i+1)}}>\left(\sum_{1}^{n} \frac{1}{\sqrt{i}}\right)^{2} $$ which is really not surprising given that $\sum \frac{1}{\sqrt{i}} \ll \frac{n}{\sqrt{2}}$. The key here is that we need "near-equality" as dictated by the Cauchy-Schwarz equality case, i.e. the square root of the numerators should be approximately proportional to the denominators. This motivates using $\frac{1}{i^{4}}$ as the numerator, which works like a charm. After working out the resulting statement, the LHS and RHS even share a sum, which adds to the simplicity of the problem. The final touch was to unrestrict the starting value of the sum, since this allows the strength of the estimate $\frac{1}{i^{2}} \approx \frac{1}{i(i+1)}$ to be fully exploited.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
1dd28739-57cb-5bf9-9aeb-c78d295c7421
| 606,320 |
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
【 Second approach by inducting down, Luke Robitaille and Carl Schildkraut. Fix $n$; we'll induct downwards on $m$. For the base case of $n=m$ the result is easy, since the left side is $\frac{m+1}{m^{3}}$ and the right side is $\frac{m}{m^{4}}=\frac{1}{m^{3}}$. For the inductive step, suppose we have shown the result for $m+1$. Let $$ A=\sum_{k=m+1}^{n} \frac{1}{k^{2}} \quad \text { and } \quad B=\sum_{k=m+1}^{n} \frac{1}{k^{3}} $$ We know $A+B \geq(m+1) A^{2}$, and we want to show $$ \left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right) \geq m\left(A+\frac{1}{m^{2}}\right)^{2} $$ Indeed, $$ \begin{aligned} \left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right)-m\left(A+\frac{1}{m^{2}}\right)^{2} & =A+B+\frac{m+1}{m^{3}}-m A^{2}-\frac{2 A}{m}-\frac{1}{m^{3}} \\ & =\left(A+B-(m+1) A^{2}\right)+\left(A-\frac{1}{m}\right)^{2} \geq 0 \end{aligned} $$ and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
【 Second approach by inducting down, Luke Robitaille and Carl Schildkraut. Fix $n$; we'll induct downwards on $m$. For the base case of $n=m$ the result is easy, since the left side is $\frac{m+1}{m^{3}}$ and the right side is $\frac{m}{m^{4}}=\frac{1}{m^{3}}$. For the inductive step, suppose we have shown the result for $m+1$. Let $$ A=\sum_{k=m+1}^{n} \frac{1}{k^{2}} \quad \text { and } \quad B=\sum_{k=m+1}^{n} \frac{1}{k^{3}} $$ We know $A+B \geq(m+1) A^{2}$, and we want to show $$ \left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right) \geq m\left(A+\frac{1}{m^{2}}\right)^{2} $$ Indeed, $$ \begin{aligned} \left(A+\frac{1}{m^{2}}\right)+\left(B+\frac{1}{m^{3}}\right)-m\left(A+\frac{1}{m^{2}}\right)^{2} & =A+B+\frac{m+1}{m^{3}}-m A^{2}-\frac{2 A}{m}-\frac{1}{m^{3}} \\ & =\left(A+B-(m+1) A^{2}\right)+\left(A-\frac{1}{m}\right)^{2} \geq 0 \end{aligned} $$ and we are done.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
1dd28739-57cb-5bf9-9aeb-c78d295c7421
| 606,320 |
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
I Third approach by reducing $n \rightarrow \infty$, Michael Ren and Carl Schildkraut. First, we give: Claim (Reduction to $n \rightarrow \infty$ ) - If the problem is true when $n \rightarrow \infty$, it is true for all $n$. However, the region is bounded by a convex curve, and the sequence of points $(0,0)$, $\left(\frac{1}{m^{2}}, \frac{1}{m^{3}}\right),\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}, \frac{1}{m^{3}}+\frac{1}{(m+1)^{3}}\right), \ldots$ has successively decreasing slopes between consecutive points. Thus it suffices to check that the inequality is true when $n \rightarrow \infty$. Set $n=\infty$ henceforth. Let $$ A=\sum_{k=m}^{\infty} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{\infty} \frac{1}{k^{3}} $$ we want to show $B \geq m A^{2}-A$, which rearranges to $$ 1+4 m B \geq(2 m A-1)^{2} $$ Write $$ C=\sum_{k=m}^{\infty} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{\infty} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ Then $$ \frac{2}{2 k-1}-\frac{2}{2 k+1}=\frac{1}{k^{2}}+\frac{1}{k^{2}(2 k-1)(2 k+1)} $$ and $$ \frac{2}{(2 k-1)^{2}}-\frac{2}{(2 k+1)^{2}}=\frac{1}{k^{3}}+\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}, $$ so that $$ A=\frac{2}{2 m-1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-D $$ Our inequality we wish to show becomes $$ \frac{2 m+1}{2 m-1} C \geq D+m C^{2} $$ We in fact show two claims: Claim - We have $$ \frac{2 m+1 / 2}{2 m-1} C \geq D $$ $$ \frac{2 m+1 / 2}{2 m-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ for $k \geq m$. It suffices to show $$ \frac{2 k+1 / 2}{2 k-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ which is equivalent to $k(2 k+1 / 2)(2 k+1) \geq 8 k^{2}-1$. This holds for all $k \geq 1$. ## Claim - We have $$ \frac{1 / 2}{2 m-1} C \geq m C^{2} $$ $$ \frac{1}{2 m(2 m-1)}=\sum_{k=m}^{\infty}\left(\frac{1}{2 k(2 k-1)}-\frac{1}{2(k+1)(2 k+1)}\right)=\sum_{k=m}^{\infty} \frac{4 k+1}{2 k(2 k-1)(k+1)(2 k+1)} $$ comparing term-wise with the definition of $C$ and using the inequality $k(4 k+1) \geq 2(k+1)$ for $k \geq 1$ gives the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
I Third approach by reducing $n \rightarrow \infty$, Michael Ren and Carl Schildkraut. First, we give: Claim (Reduction to $n \rightarrow \infty$ ) - If the problem is true when $n \rightarrow \infty$, it is true for all $n$. However, the region is bounded by a convex curve, and the sequence of points $(0,0)$, $\left(\frac{1}{m^{2}}, \frac{1}{m^{3}}\right),\left(\frac{1}{m^{2}}+\frac{1}{(m+1)^{2}}, \frac{1}{m^{3}}+\frac{1}{(m+1)^{3}}\right), \ldots$ has successively decreasing slopes between consecutive points. Thus it suffices to check that the inequality is true when $n \rightarrow \infty$. Set $n=\infty$ henceforth. Let $$ A=\sum_{k=m}^{\infty} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{\infty} \frac{1}{k^{3}} $$ we want to show $B \geq m A^{2}-A$, which rearranges to $$ 1+4 m B \geq(2 m A-1)^{2} $$ Write $$ C=\sum_{k=m}^{\infty} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{\infty} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ Then $$ \frac{2}{2 k-1}-\frac{2}{2 k+1}=\frac{1}{k^{2}}+\frac{1}{k^{2}(2 k-1)(2 k+1)} $$ and $$ \frac{2}{(2 k-1)^{2}}-\frac{2}{(2 k+1)^{2}}=\frac{1}{k^{3}}+\frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}}, $$ so that $$ A=\frac{2}{2 m-1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-D $$ Our inequality we wish to show becomes $$ \frac{2 m+1}{2 m-1} C \geq D+m C^{2} $$ We in fact show two claims: Claim - We have $$ \frac{2 m+1 / 2}{2 m-1} C \geq D $$ $$ \frac{2 m+1 / 2}{2 m-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ for $k \geq m$. It suffices to show $$ \frac{2 k+1 / 2}{2 k-1} \cdot \frac{1}{k^{2}(2 k-1)(2 k+1)} \geq \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ which is equivalent to $k(2 k+1 / 2)(2 k+1) \geq 8 k^{2}-1$. This holds for all $k \geq 1$. ## Claim - We have $$ \frac{1 / 2}{2 m-1} C \geq m C^{2} $$ $$ \frac{1}{2 m(2 m-1)}=\sum_{k=m}^{\infty}\left(\frac{1}{2 k(2 k-1)}-\frac{1}{2(k+1)(2 k+1)}\right)=\sum_{k=m}^{\infty} \frac{4 k+1}{2 k(2 k-1)(k+1)(2 k+1)} $$ comparing term-wise with the definition of $C$ and using the inequality $k(4 k+1) \geq 2(k+1)$ for $k \geq 1$ gives the desired result.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
1dd28739-57cb-5bf9-9aeb-c78d295c7421
| 606,320 |
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
『 Fourth approach by bashing, Carl Schildkraut. With a bit more work, the third approach can be adapted to avoid the $n \rightarrow \infty$ reduction. Similarly to before, define $$ A=\sum_{k=m}^{n} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{n} \frac{1}{k^{3}} $$ we want to show $1+4 m B \geq(2 m A-1)^{2}$. Writing $$ C=\sum_{k=m}^{n} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{n} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ We compute $$ A=\frac{2}{2 m-1}-\frac{2}{2 n+1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-\frac{2}{(2 n+1)^{2}}-D . $$ Then, the inequality we wish to show reduces (as in the previous solution) to $$ \frac{2 m+1}{2 m-1} C+\frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq D+m C^{2}+\frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C $$ We deal first with the terms not containing the variable $n$, i.e. we show that $$ \frac{2 m+1}{2 m-1} C \geq D+m C^{2} $$ For this part, the two claims from the previous solution go through exactly as written above, and we have $C \leq 1 /(2 m(2 m-1))$. We now need to show $$ \frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq \frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C $$ (this is just the inequality between the remaining terms); our bound on $C$ reduces this to proving $$ \frac{4(2 m+1)(n-m+1)}{(2 m-1)(2 n+1)^{2}} \geq \frac{2}{(2 m-1)(2 n+1)} $$ Expanding and writing in terms of $n$, this is equivalent to $$ n \geq \frac{1+2(m-1)(2 m+1)}{4 m}=m-\frac{2 m+1}{4 m} $$ which holds for all $n \geq m$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq m \geq 1$ be integers. Prove that $$ \sum_{k=m}^{n}\left(\frac{1}{k^{2}}+\frac{1}{k^{3}}\right) \geq m \cdot\left(\sum_{k=m}^{n} \frac{1}{k^{2}}\right)^{2} $$
|
『 Fourth approach by bashing, Carl Schildkraut. With a bit more work, the third approach can be adapted to avoid the $n \rightarrow \infty$ reduction. Similarly to before, define $$ A=\sum_{k=m}^{n} \frac{1}{k^{2}} \text { and } B=\sum_{k=m}^{n} \frac{1}{k^{3}} $$ we want to show $1+4 m B \geq(2 m A-1)^{2}$. Writing $$ C=\sum_{k=m}^{n} \frac{1}{k^{2}(2 k-1)(2 k+1)} \text { and } D=\sum_{k=m}^{n} \frac{8 k^{2}-1}{k^{3}(2 k-1)^{2}(2 k+1)^{2}} $$ We compute $$ A=\frac{2}{2 m-1}-\frac{2}{2 n+1}-C \text { and } B=\frac{2}{(2 m-1)^{2}}-\frac{2}{(2 n+1)^{2}}-D . $$ Then, the inequality we wish to show reduces (as in the previous solution) to $$ \frac{2 m+1}{2 m-1} C+\frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq D+m C^{2}+\frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C $$ We deal first with the terms not containing the variable $n$, i.e. we show that $$ \frac{2 m+1}{2 m-1} C \geq D+m C^{2} $$ For this part, the two claims from the previous solution go through exactly as written above, and we have $C \leq 1 /(2 m(2 m-1))$. We now need to show $$ \frac{2(2 m+1)}{(2 m-1)(2 n+1)} \geq \frac{2(2 m+1)}{(2 n+1)^{2}}+\frac{4 m}{2 n+1} C $$ (this is just the inequality between the remaining terms); our bound on $C$ reduces this to proving $$ \frac{4(2 m+1)(n-m+1)}{(2 m-1)(2 n+1)^{2}} \geq \frac{2}{(2 m-1)(2 n+1)} $$ Expanding and writing in terms of $n$, this is equivalent to $$ n \geq \frac{1+2(m-1)(2 m+1)}{4 m}=m-\frac{2 m+1}{4 m} $$ which holds for all $n \geq m$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
1dd28739-57cb-5bf9-9aeb-c78d295c7421
| 606,320 |
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
『 Solution 1 (Ankit Bisain). Let $H$ be the orthocenter of $A B C$, and construct $P^{\prime}$ using the following claim. Claim - There is a point $P^{\prime}$ for which $$ \measuredangle A P H+\measuredangle A P^{\prime} H=\measuredangle B P H+\measuredangle B P^{\prime} H=\measuredangle C P H+\measuredangle C P^{\prime} H=0 . $$ Now, let $X, Y$, and $Z$ be the reflections of $P$ over $\overline{A H}, \overline{B H}$, and $\overline{C H}$ respectively. Additionally, let $Q^{\prime}$ be the image of $Q$ under inversion about ( $P X Y Z$ ). 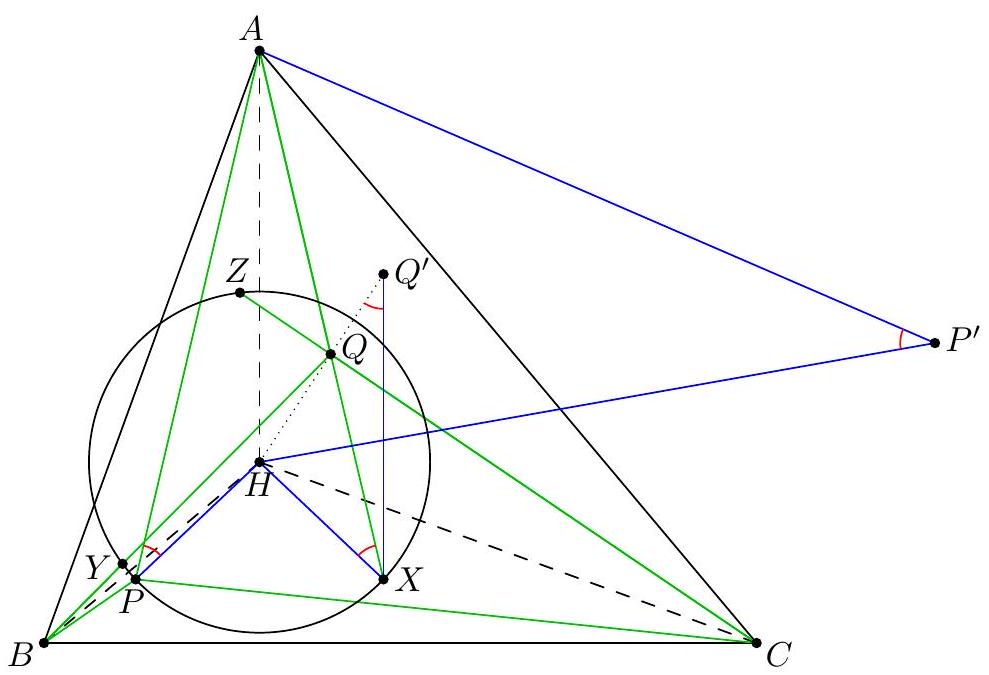 $$ \text { Claim }-A B C P^{\prime} \approx X Y Z Q^{\prime} $$ $$ \measuredangle Y X Z=\measuredangle Y P Z=\measuredangle(\overline{B H}, \overline{C H})=-\measuredangle B A C $$ and cyclic variants, triangles $A B C$ and $X Y Z$ are similar. Additionally, $$ \measuredangle H Q^{\prime} X=-\measuredangle H X Q=-\measuredangle H X A=\measuredangle H P A=-\measuredangle H P^{\prime} A $$ and cyclic variants, so summing in pairs gives $\measuredangle Y Q^{\prime} Z=-\measuredangle B P^{\prime} C$ and cyclic variants; this implies the similarity. Claim - $Q^{\prime}$ lies on the Euler line of triangle $X Y Z$. To finish the problem, let $G_{1}$ be the centroid of $A B C$ and $G_{2}$ be the centroid of $X Y Z$. Then with signed areas, $$ \begin{aligned} {\left[G_{1} H P\right]+\left[G_{1} H Q\right] } & =\frac{[A H P]+[B H P]+[C H P]}{3}+\frac{[A H Q]+[B H Q]+[C H Q]}{3} \\ & =\frac{[A H Q]-[A H X]+[B H Q]-[B H Y]+[C H Q]-[C H Z]}{3} \\ & =\frac{[H Q X]+[H Q Y]+[H Q Z]}{3} \\ & =\left[Q G_{2} H\right] \\ & =0 \end{aligned} $$ where the last line follows from the last claim. Therefore $\overline{G_{1} H}$ bisects $\overline{P Q}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
『 Solution 1 (Ankit Bisain). Let $H$ be the orthocenter of $A B C$, and construct $P^{\prime}$ using the following claim. Claim - There is a point $P^{\prime}$ for which $$ \measuredangle A P H+\measuredangle A P^{\prime} H=\measuredangle B P H+\measuredangle B P^{\prime} H=\measuredangle C P H+\measuredangle C P^{\prime} H=0 . $$ Now, let $X, Y$, and $Z$ be the reflections of $P$ over $\overline{A H}, \overline{B H}$, and $\overline{C H}$ respectively. Additionally, let $Q^{\prime}$ be the image of $Q$ under inversion about ( $P X Y Z$ ).  $$ \text { Claim }-A B C P^{\prime} \approx X Y Z Q^{\prime} $$ $$ \measuredangle Y X Z=\measuredangle Y P Z=\measuredangle(\overline{B H}, \overline{C H})=-\measuredangle B A C $$ and cyclic variants, triangles $A B C$ and $X Y Z$ are similar. Additionally, $$ \measuredangle H Q^{\prime} X=-\measuredangle H X Q=-\measuredangle H X A=\measuredangle H P A=-\measuredangle H P^{\prime} A $$ and cyclic variants, so summing in pairs gives $\measuredangle Y Q^{\prime} Z=-\measuredangle B P^{\prime} C$ and cyclic variants; this implies the similarity. Claim - $Q^{\prime}$ lies on the Euler line of triangle $X Y Z$. To finish the problem, let $G_{1}$ be the centroid of $A B C$ and $G_{2}$ be the centroid of $X Y Z$. Then with signed areas, $$ \begin{aligned} {\left[G_{1} H P\right]+\left[G_{1} H Q\right] } & =\frac{[A H P]+[B H P]+[C H P]}{3}+\frac{[A H Q]+[B H Q]+[C H Q]}{3} \\ & =\frac{[A H Q]-[A H X]+[B H Q]-[B H Y]+[C H Q]-[C H Z]}{3} \\ & =\frac{[H Q X]+[H Q Y]+[H Q Z]}{3} \\ & =\left[Q G_{2} H\right] \\ & =0 \end{aligned} $$ where the last line follows from the last claim. Therefore $\overline{G_{1} H}$ bisects $\overline{P Q}$, as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
cb9da5f6-9199-507a-ba9f-ada7a979408c
| 247,749 |
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
Solution 2 using complex numbers (Carl Schildkraut and Milan Haiman). Let $(A B C)$ be the unit circle in the complex plane, and let $A=a, B=b, C=c$ such that $|a|=|b|=|c|=1$. Let $P=p$ and $Q=q$, and $O=0$ and $H=h=a+b+c$ be the circumcenter and orthocenter of $A B C$ respectively. The first step is to translate the given geometric conditions into a single usable equation: Claim - We have the equation $$ (p+q) \sum_{\mathrm{cyc}} a^{3}\left(b^{2}-c^{2}\right)=(\bar{p}+\bar{q}) a b c \sum_{\mathrm{cyc}}\left(b c\left(b^{2}-c^{2}\right)\right) $$ $$ \begin{aligned} & \frac{(p-a)(q-a)}{(h-a)^{2}}=\frac{(p-a)(q-a)}{(b+c)^{2}} \in \mathbb{R} \\ \Longrightarrow & \frac{(p-a)(q-a)}{(b+c)^{2}}=\frac{\left(\frac{(p-a)(q-a)}{(b+c)^{2}}\right)}{}=\frac{(a \bar{p}-1)(a \bar{q}-1) b^{2} c^{2}}{(b+c)^{2} a^{2}} \\ \Longrightarrow & a^{2}(p-a)(q-a)=b^{2} c^{2}(a \bar{p}-1)(a \bar{q}-1) \\ \Longrightarrow & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) . \end{aligned} $$ Writing the symmetric conditions that $\overline{B H}$ and $\overline{C H}$ bisect $\angle P B Q$ and $\angle P C Q$ gives three equations: $$ \begin{aligned} & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) \\ & b^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(b^{4}-c^{2} a^{2}\right)=b^{3}(p+q)-b c^{2} a^{2}(\bar{p}+\bar{q}) \end{aligned} $$ $$ c^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(c^{4}-a^{2} b^{2}\right)=c^{3}(p+q)-c a^{2} b^{2}(\bar{p}+\bar{q}) $$ Now, sum $\left(b^{2}-c^{2}\right)$ times the first equation, $\left(c^{2}-a^{2}\right)$ times the second equation, and $\left(a^{2}-b^{2}\right)$ times the third equation. On the left side, the coefficients of $p q$ and $\overline{p q}$ are 0 . Additionally, the coefficient of 1 (the parenthesized terms on the left sides of each equation) sum to 0 , since $$ \sum_{\mathrm{cyc}}\left(a^{4}-b^{2} c^{2}\right)\left(b^{2}-c^{2}\right)=\sum_{\mathrm{cyc}}\left(a^{4} b^{2}-b^{4} c^{2}-a^{4} c^{2}+c^{4} b^{2}\right) $$ This gives (1) as desired. We can then factor (1): Claim - The left-hand side of (1) factors as $$ -(p+q)(a-b)(b-c)(c-a)(a b+b c+c a) $$ while the right-hand side factors as $$ -(\bar{p}+\bar{q})(a-b)(b-c)(c-a)(a+b+c) $$ Consider the cyclic sum on the left as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a^{3}\left(a^{2}-c^{2}\right)+a^{3}\left(c^{2}-a^{2}\right)+c^{3}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $f(a, b, c)(a-b)(b-c)(c-a)$ for some symmetric quadratic polynomial $f$, and thus it is some linear combination of $a^{2}+b^{2}+c^{2}$ and $a b+b c+c a$. When $a=0$, the whole expression is $b^{2} c^{2}(b-c)$, so $f(0, b, c)=-b c$, which implies that $f(a, b, c)=-(a b+b c+c a)$. Similarly, consider the cyclic sum on the right as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a c\left(a^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)+a^{2}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $g(a, b, c)(a-b)(b-c)(c-a)$ where $g$ is a symmetric linear polynomial; hence, it is a scalar multiple of $a+b+c$. When $a=0$, the whole expression is $b c\left(b^{2}-c^{2}\right)$, so $g(0, b, c)=-b-c$, which implies that $g(a, b, c)=-(a+b+c)$. Since $A, B$, and $C$ are distinct, we may divide by $(a-b)(b-c)(c-a)$ to obtain $$ (p+q)(a b+b c+c a)=(\bar{p}+\bar{q}) a b c(a+b+c) \Longrightarrow(p+q) \bar{h}=(\bar{p}+\bar{q}) h $$ This implies that $\frac{\frac{p+q}{h}-0}{h-0}$ is real, so the midpoint of $\overline{P Q}$ lies on line $\overline{O H}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
Solution 2 using complex numbers (Carl Schildkraut and Milan Haiman). Let $(A B C)$ be the unit circle in the complex plane, and let $A=a, B=b, C=c$ such that $|a|=|b|=|c|=1$. Let $P=p$ and $Q=q$, and $O=0$ and $H=h=a+b+c$ be the circumcenter and orthocenter of $A B C$ respectively. The first step is to translate the given geometric conditions into a single usable equation: Claim - We have the equation $$ (p+q) \sum_{\mathrm{cyc}} a^{3}\left(b^{2}-c^{2}\right)=(\bar{p}+\bar{q}) a b c \sum_{\mathrm{cyc}}\left(b c\left(b^{2}-c^{2}\right)\right) $$ $$ \begin{aligned} & \frac{(p-a)(q-a)}{(h-a)^{2}}=\frac{(p-a)(q-a)}{(b+c)^{2}} \in \mathbb{R} \\ \Longrightarrow & \frac{(p-a)(q-a)}{(b+c)^{2}}=\frac{\left(\frac{(p-a)(q-a)}{(b+c)^{2}}\right)}{}=\frac{(a \bar{p}-1)(a \bar{q}-1) b^{2} c^{2}}{(b+c)^{2} a^{2}} \\ \Longrightarrow & a^{2}(p-a)(q-a)=b^{2} c^{2}(a \bar{p}-1)(a \bar{q}-1) \\ \Longrightarrow & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) . \end{aligned} $$ Writing the symmetric conditions that $\overline{B H}$ and $\overline{C H}$ bisect $\angle P B Q$ and $\angle P C Q$ gives three equations: $$ \begin{aligned} & a^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(a^{4}-b^{2} c^{2}\right)=a^{3}(p+q)-a b^{2} c^{2}(\bar{p}+\bar{q}) \\ & b^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(b^{4}-c^{2} a^{2}\right)=b^{3}(p+q)-b c^{2} a^{2}(\bar{p}+\bar{q}) \end{aligned} $$ $$ c^{2} p q-a^{2} b^{2} c^{2} \overline{p q}+\left(c^{4}-a^{2} b^{2}\right)=c^{3}(p+q)-c a^{2} b^{2}(\bar{p}+\bar{q}) $$ Now, sum $\left(b^{2}-c^{2}\right)$ times the first equation, $\left(c^{2}-a^{2}\right)$ times the second equation, and $\left(a^{2}-b^{2}\right)$ times the third equation. On the left side, the coefficients of $p q$ and $\overline{p q}$ are 0 . Additionally, the coefficient of 1 (the parenthesized terms on the left sides of each equation) sum to 0 , since $$ \sum_{\mathrm{cyc}}\left(a^{4}-b^{2} c^{2}\right)\left(b^{2}-c^{2}\right)=\sum_{\mathrm{cyc}}\left(a^{4} b^{2}-b^{4} c^{2}-a^{4} c^{2}+c^{4} b^{2}\right) $$ This gives (1) as desired. We can then factor (1): Claim - The left-hand side of (1) factors as $$ -(p+q)(a-b)(b-c)(c-a)(a b+b c+c a) $$ while the right-hand side factors as $$ -(\bar{p}+\bar{q})(a-b)(b-c)(c-a)(a+b+c) $$ Consider the cyclic sum on the left as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a^{3}\left(a^{2}-c^{2}\right)+a^{3}\left(c^{2}-a^{2}\right)+c^{3}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $f(a, b, c)(a-b)(b-c)(c-a)$ for some symmetric quadratic polynomial $f$, and thus it is some linear combination of $a^{2}+b^{2}+c^{2}$ and $a b+b c+c a$. When $a=0$, the whole expression is $b^{2} c^{2}(b-c)$, so $f(0, b, c)=-b c$, which implies that $f(a, b, c)=-(a b+b c+c a)$. Similarly, consider the cyclic sum on the right as a polynomial in $a, b$, and $c$. If $a=b$, then it simplifies as $a c\left(a^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)+a^{2}\left(a^{2}-a^{2}\right)=0$, so $a-b$ divides this polynomial. Similarly, $a-c$ and $b-c$ divide it, so it can be written as $g(a, b, c)(a-b)(b-c)(c-a)$ where $g$ is a symmetric linear polynomial; hence, it is a scalar multiple of $a+b+c$. When $a=0$, the whole expression is $b c\left(b^{2}-c^{2}\right)$, so $g(0, b, c)=-b-c$, which implies that $g(a, b, c)=-(a+b+c)$. Since $A, B$, and $C$ are distinct, we may divide by $(a-b)(b-c)(c-a)$ to obtain $$ (p+q)(a b+b c+c a)=(\bar{p}+\bar{q}) a b c(a+b+c) \Longrightarrow(p+q) \bar{h}=(\bar{p}+\bar{q}) h $$ This implies that $\frac{\frac{p+q}{h}-0}{h-0}$ is real, so the midpoint of $\overline{P Q}$ lies on line $\overline{O H}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
cb9da5f6-9199-507a-ba9f-ada7a979408c
| 247,749 |
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
【 Solution 3 also using complex numbers (Michael Ren). We use complex numbers as in the previous solution. The angle conditions imply that $\frac{(a-p)(a-q)}{(b-c)^{2}}, \frac{(b-p)(b-q)}{(c-a)^{2}}$, and $\frac{(c-p)(c-q)}{(a-b)^{2}}$ are real numbers. Take a linear combination of these with real coefficients $X$, $Y$, and $Z$ to be determined; after expansion, we obtain $$ \begin{aligned} & {\left[\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right] p q } \\ - & {\left[\frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}\right](p+q) } \end{aligned} $$ $$ +\left[\frac{a^{2} X}{(b-c)^{2}}+\frac{b^{2} Y}{(c-a)^{2}}+\frac{c^{2} Z}{(a-b)^{2}}\right] $$ which is a real number. To get something about the midpoint of $P Q$, the $p q$ coefficient should be zero, which motivates the following lemma. ## Lemma There exist real $X, Y, Z$ for which $$ \begin{aligned} & \frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}=0 \text { and } \\ & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}} \neq 0 . \end{aligned} $$ $$ \begin{aligned} & \frac{(b-a) Y}{(c-a)^{2}}+\frac{(c-a) Z}{(a-b)^{2}} \\ = & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}-a\left(\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right) \\ = & 0 \end{aligned} $$ We can easily check that $(Y, Z)=(0,0)$ is impossible, therefore $\frac{(b-a)^{3}}{(c-a)^{3}}=-\frac{Z}{Y}$ is real. This means $\angle B A C=60^{\circ}$ or $120^{\circ}$. By symmetry, the same is true of $\angle C B A$ and $\angle A C B$. This is impossible because $A B C$ is scalene. With the choice of $X, Y, Z$ as in the lemma, there exist complex numbers $\alpha$ and $\beta$, depending only on $a, b$, and $c$, such that $\alpha \neq 0$ and $\alpha(p+q)+\beta$ is real. Therefore the midpoint of $P Q$, which corresponds to $\frac{p+q}{2}$, lies on a fixed line. It remains to show that this line is the Euler line. First, choose $P=Q$ to be the orthocenter to show that the orthocenter lies on the line. Secondly, choose $P$ and $Q$ to be the foci of the Steiner circumellipse to show that the centroid lies on the line. (By some ellipse properties, the external angle bisector of $\angle P A Q$ is the tangent to the circumellipse at $A$, which is the line through $A$ parallel to $B C$. Therefore these points are valid.) Therefore the fixed line of the midpoint is the Euler line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle and let $P$ and $Q$ be two distinct points in its interior. Suppose that the angle bisectors of $\angle P A Q, \angle P B Q$, and $\angle P C Q$ are the altitudes of triangle $A B C$. Prove that the midpoint of $\overline{P Q}$ lies on the Euler line of $A B C$.
|
【 Solution 3 also using complex numbers (Michael Ren). We use complex numbers as in the previous solution. The angle conditions imply that $\frac{(a-p)(a-q)}{(b-c)^{2}}, \frac{(b-p)(b-q)}{(c-a)^{2}}$, and $\frac{(c-p)(c-q)}{(a-b)^{2}}$ are real numbers. Take a linear combination of these with real coefficients $X$, $Y$, and $Z$ to be determined; after expansion, we obtain $$ \begin{aligned} & {\left[\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right] p q } \\ - & {\left[\frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}\right](p+q) } \end{aligned} $$ $$ +\left[\frac{a^{2} X}{(b-c)^{2}}+\frac{b^{2} Y}{(c-a)^{2}}+\frac{c^{2} Z}{(a-b)^{2}}\right] $$ which is a real number. To get something about the midpoint of $P Q$, the $p q$ coefficient should be zero, which motivates the following lemma. ## Lemma There exist real $X, Y, Z$ for which $$ \begin{aligned} & \frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}=0 \text { and } \\ & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}} \neq 0 . \end{aligned} $$ $$ \begin{aligned} & \frac{(b-a) Y}{(c-a)^{2}}+\frac{(c-a) Z}{(a-b)^{2}} \\ = & \frac{a X}{(b-c)^{2}}+\frac{b Y}{(c-a)^{2}}+\frac{c Z}{(a-b)^{2}}-a\left(\frac{X}{(b-c)^{2}}+\frac{Y}{(c-a)^{2}}+\frac{Z}{(a-b)^{2}}\right) \\ = & 0 \end{aligned} $$ We can easily check that $(Y, Z)=(0,0)$ is impossible, therefore $\frac{(b-a)^{3}}{(c-a)^{3}}=-\frac{Z}{Y}$ is real. This means $\angle B A C=60^{\circ}$ or $120^{\circ}$. By symmetry, the same is true of $\angle C B A$ and $\angle A C B$. This is impossible because $A B C$ is scalene. With the choice of $X, Y, Z$ as in the lemma, there exist complex numbers $\alpha$ and $\beta$, depending only on $a, b$, and $c$, such that $\alpha \neq 0$ and $\alpha(p+q)+\beta$ is real. Therefore the midpoint of $P Q$, which corresponds to $\frac{p+q}{2}$, lies on a fixed line. It remains to show that this line is the Euler line. First, choose $P=Q$ to be the orthocenter to show that the orthocenter lies on the line. Secondly, choose $P$ and $Q$ to be the foci of the Steiner circumellipse to show that the centroid lies on the line. (By some ellipse properties, the external angle bisector of $\angle P A Q$ is the tangent to the circumellipse at $A$, which is the line through $A$ parallel to $B C$. Therefore these points are valid.) Therefore the fixed line of the midpoint is the Euler line.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
cb9da5f6-9199-507a-ba9f-ada7a979408c
| 247,749 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.