problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $a$ and $b$ be positive integers. Every cell of an $(a+b+1) \times(a+b+1)$ grid is colored either amber or bronze such that there are at least $a^{2}+a b-b$ amber cells and at least $b^{2}+a b-a$ bronze cells. Prove that it is possible to choose $a$ amber cells and $b$ bronze cells such that no two of the $a+b$ chosen cells lie in the same row or column.
|
Claim - There exists a transversal $T_{a}$ with at least $a$ amber cells. Analogously, there exists a transversal $T_{b}$ with at least $b$ bronze cells. $$ \frac{a^{2}+a b-b}{a+b+1}=(a-1)+\frac{1}{a+b+1}>a-1 $$ Now imagine we transform $T_{a}$ to $T_{b}$ in some number of steps, by repeatedly choosing cells $c$ and $c^{\prime}$ and swapping them with the two other corners of the rectangle formed by their row/column, as shown in the figure. 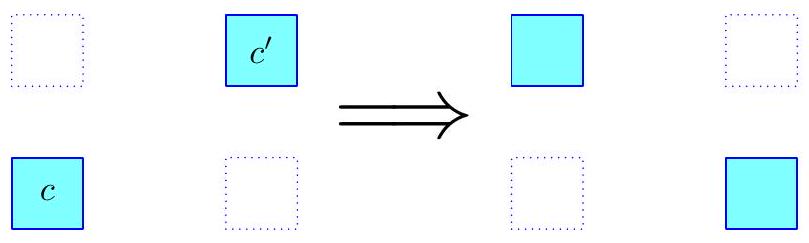 By "discrete intermediate value theorem", the number of amber cells will be either $a$ or $a+1$ at some point during this transformation. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $a$ and $b$ be positive integers. Every cell of an $(a+b+1) \times(a+b+1)$ grid is colored either amber or bronze such that there are at least $a^{2}+a b-b$ amber cells and at least $b^{2}+a b-a$ bronze cells. Prove that it is possible to choose $a$ amber cells and $b$ bronze cells such that no two of the $a+b$ chosen cells lie in the same row or column.
|
Claim - There exists a transversal $T_{a}$ with at least $a$ amber cells. Analogously, there exists a transversal $T_{b}$ with at least $b$ bronze cells. $$ \frac{a^{2}+a b-b}{a+b+1}=(a-1)+\frac{1}{a+b+1}>a-1 $$ Now imagine we transform $T_{a}$ to $T_{b}$ in some number of steps, by repeatedly choosing cells $c$ and $c^{\prime}$ and swapping them with the two other corners of the rectangle formed by their row/column, as shown in the figure.  By "discrete intermediate value theorem", the number of amber cells will be either $a$ or $a+1$ at some point during this transformation. This completes the proof.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2022-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8c4f1aab-d759-5c44-9a36-84792c78c27b
| 246,226 |
Let $b \geq 2$ and $w \geq 2$ be fixed integers, and $n=b+w$. Given are $2 b$ identical black rods and $2 w$ identical white rods, each of side length 1. We assemble a regular $2 n$-gon using these rods so that parallel sides are the same color. Then, a convex $2 b$-gon $B$ is formed by translating the black rods, and a convex $2 w$-gon $W$ is formed by translating the white rods. An example of one way of doing the assembly when $b=3$ and $w=2$ is shown below, as well as the resulting polygons $B$ and $W$. 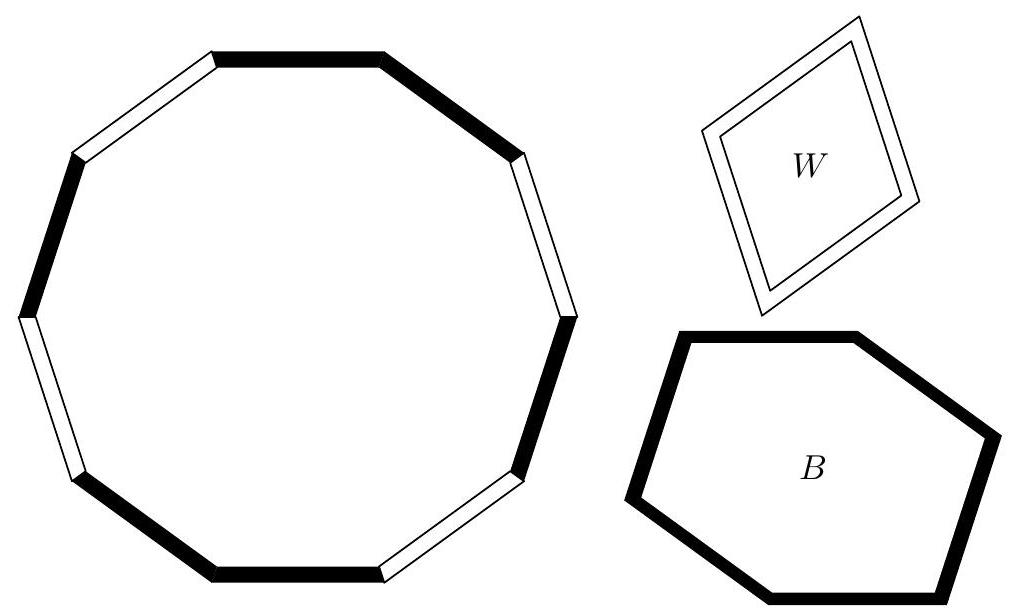 Prove that the difference of the areas of $B$ and $W$ depends only on the numbers $b$ and $w$, and not on how the $2 n$-gon was assembled.
|
We are going to prove that one may swap a black rod with an adjacent white rod (as well as the rods parallel to them) without affecting the difference in the areas of $B-W$. Let $\vec{u}$ and $\vec{v}$ denote the originally black and white vectors that were adjacent on the $2 n$-gon and are now going to be swapped. Let $\vec{x}$ denote the sum of all the other black vectors between $\vec{u}$ and $-\vec{u}$, and define $\vec{y}$ similarly. See the diagram below, where $B_{0}$ and $W_{0}$ are the polygons before the swap, and $B_{1}$ and $W_{1}$ are the resulting changed polygons. 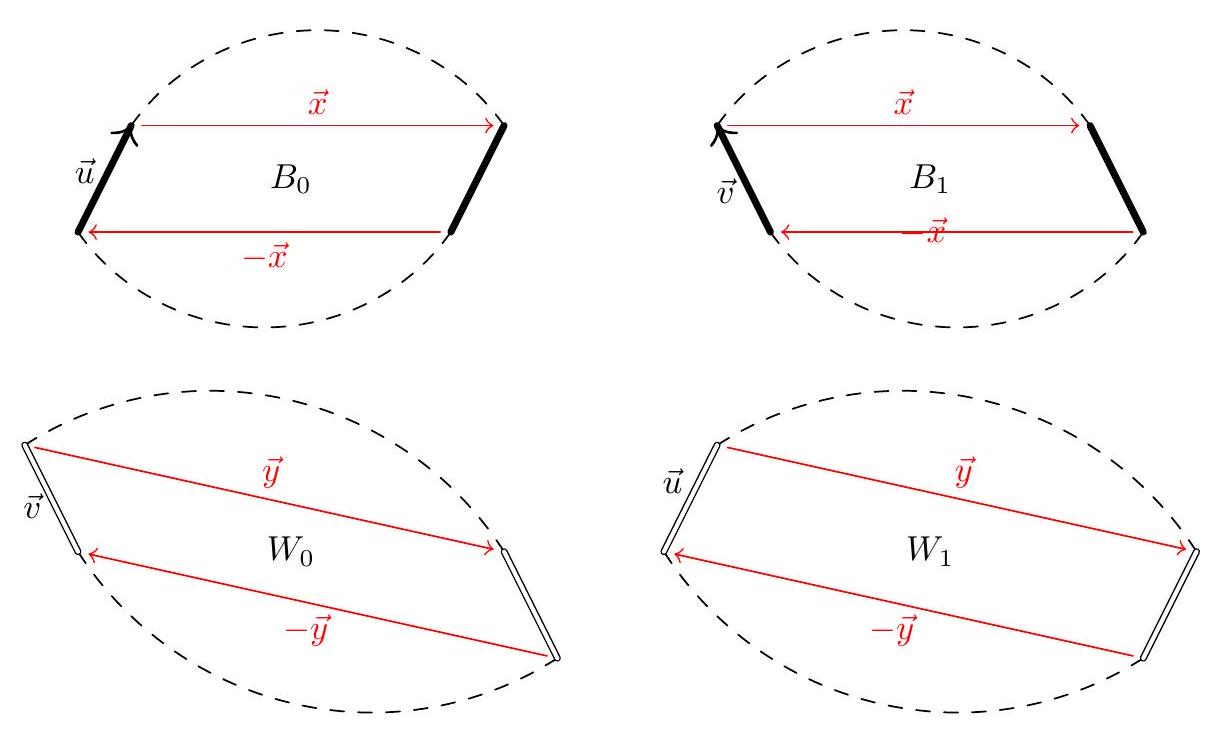 Observe that the only change in $B$ and $W$ is in the parallelograms shown above in each diagram. Letting $\wedge$ denote the wedge product, we need to show that $$ \vec{u} \wedge \vec{x}-\vec{v} \wedge \vec{y}=\vec{v} \wedge \vec{x}-\vec{u} \wedge \vec{y} $$ which can be rewritten as $$ (\vec{u}-\vec{v}) \wedge(\vec{x}+\vec{y})=0 $$ In other words, it would suffice to show $\vec{u}-\vec{v}$ and $\vec{x}+\vec{y}$ are parallel. (Students not familiar with wedge products can replace every $\wedge$ with the cross product $\times$ instead.) Claim - Both $\vec{u}-\vec{v}$ and $\vec{x}+\vec{y}$ are perpendicular to vector $\vec{u}+\vec{v}$. For the other perpendicularity, note that $\vec{u}+\vec{v}+\vec{x}+\vec{y}$ traces out a diameter of the circumcircle of the original $2 n$-gon; call this diameter $A B$, so $$ A+\vec{u}+\vec{v}+\vec{x}+\vec{y}=B $$ Now point $A+\vec{u}+\vec{v}$ is a point on this semicircle, which means (by the inscribed angle theorem) the angle between $\vec{u}+\vec{v}$ and $\vec{x}+\vec{y}$ is $90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $b \geq 2$ and $w \geq 2$ be fixed integers, and $n=b+w$. Given are $2 b$ identical black rods and $2 w$ identical white rods, each of side length 1. We assemble a regular $2 n$-gon using these rods so that parallel sides are the same color. Then, a convex $2 b$-gon $B$ is formed by translating the black rods, and a convex $2 w$-gon $W$ is formed by translating the white rods. An example of one way of doing the assembly when $b=3$ and $w=2$ is shown below, as well as the resulting polygons $B$ and $W$.  Prove that the difference of the areas of $B$ and $W$ depends only on the numbers $b$ and $w$, and not on how the $2 n$-gon was assembled.
|
We are going to prove that one may swap a black rod with an adjacent white rod (as well as the rods parallel to them) without affecting the difference in the areas of $B-W$. Let $\vec{u}$ and $\vec{v}$ denote the originally black and white vectors that were adjacent on the $2 n$-gon and are now going to be swapped. Let $\vec{x}$ denote the sum of all the other black vectors between $\vec{u}$ and $-\vec{u}$, and define $\vec{y}$ similarly. See the diagram below, where $B_{0}$ and $W_{0}$ are the polygons before the swap, and $B_{1}$ and $W_{1}$ are the resulting changed polygons.  Observe that the only change in $B$ and $W$ is in the parallelograms shown above in each diagram. Letting $\wedge$ denote the wedge product, we need to show that $$ \vec{u} \wedge \vec{x}-\vec{v} \wedge \vec{y}=\vec{v} \wedge \vec{x}-\vec{u} \wedge \vec{y} $$ which can be rewritten as $$ (\vec{u}-\vec{v}) \wedge(\vec{x}+\vec{y})=0 $$ In other words, it would suffice to show $\vec{u}-\vec{v}$ and $\vec{x}+\vec{y}$ are parallel. (Students not familiar with wedge products can replace every $\wedge$ with the cross product $\times$ instead.) Claim - Both $\vec{u}-\vec{v}$ and $\vec{x}+\vec{y}$ are perpendicular to vector $\vec{u}+\vec{v}$. For the other perpendicularity, note that $\vec{u}+\vec{v}+\vec{x}+\vec{y}$ traces out a diameter of the circumcircle of the original $2 n$-gon; call this diameter $A B$, so $$ A+\vec{u}+\vec{v}+\vec{x}+\vec{y}=B $$ Now point $A+\vec{u}+\vec{v}$ is a point on this semicircle, which means (by the inscribed angle theorem) the angle between $\vec{u}+\vec{v}$ and $\vec{x}+\vec{y}$ is $90^{\circ}$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2022-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
12ab7410-a841-5261-b7a5-9bf6d464cdf9
| 605,909 |
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
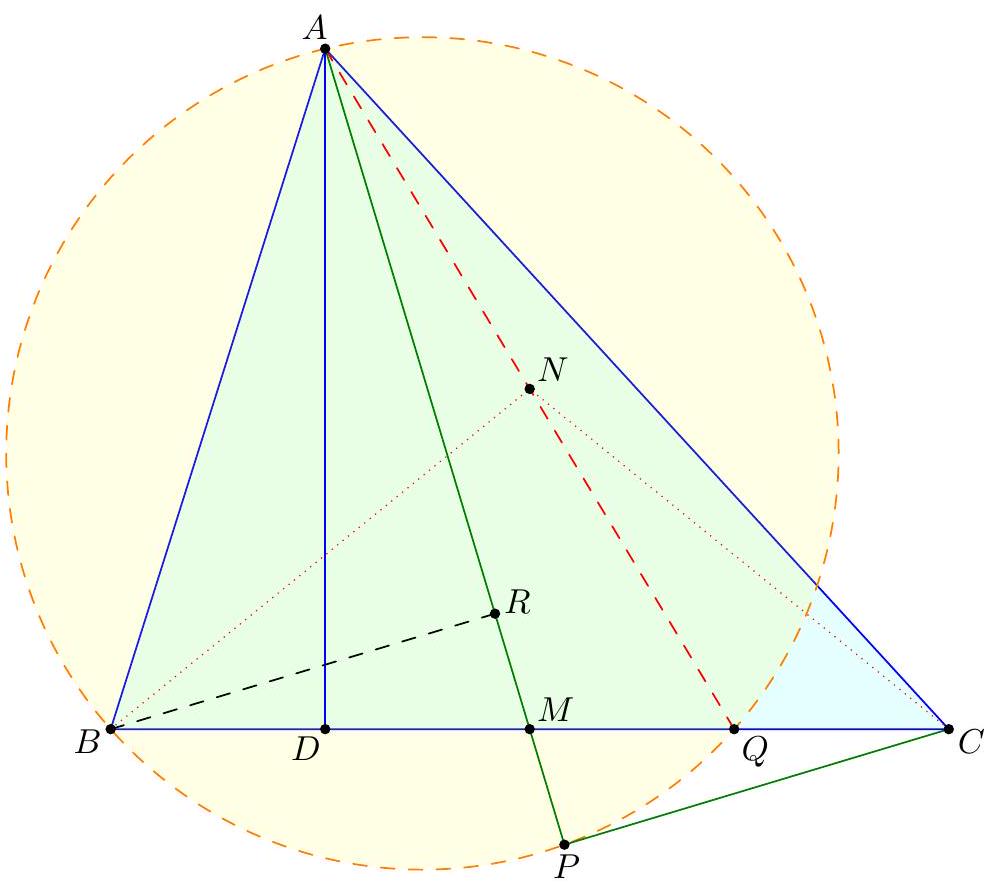 【 Most common synthetic approach. The solution hinges on the following claim: Claim - $Q$ coincides with the reflection of $D$ across $M$. $$ M B \cdot M Q=M A \cdot M P=M C \cdot M D $$ Since $M B=M C$, the claim follows. It follows that $\overline{M N} \| \overline{A D}$, as $M$ and $N$ are respectively the midpoints of $\overline{A Q}$ and $\overline{D Q}$. Thus $\overline{M N} \perp \overline{B C}$, and so $N$ lies on the perpendicular bisector of $\overline{B C}$, as needed. Remark (David Lin). One can prove the main claim without power of a point as well, as follows: Let $R$ be the foot from $B$ to $\overline{A M}$, so $B R C P$ is a parallelogram. Note that $A B D R$ is cyclic, and hence $$ \measuredangle D R M=\measuredangle D B A=Q B A=\measuredangle Q P A=\measuredangle Q P M $$ Thus, $\overline{D R} \| \overline{P Q}$, so $D R Q P$ is also a parallelogram.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Most common synthetic approach. The solution hinges on the following claim: Claim - $Q$ coincides with the reflection of $D$ across $M$. $$ M B \cdot M Q=M A \cdot M P=M C \cdot M D $$ Since $M B=M C$, the claim follows. It follows that $\overline{M N} \| \overline{A D}$, as $M$ and $N$ are respectively the midpoints of $\overline{A Q}$ and $\overline{D Q}$. Thus $\overline{M N} \perp \overline{B C}$, and so $N$ lies on the perpendicular bisector of $\overline{B C}$, as needed. Remark (David Lin). One can prove the main claim without power of a point as well, as follows: Let $R$ be the foot from $B$ to $\overline{A M}$, so $B R C P$ is a parallelogram. Note that $A B D R$ is cyclic, and hence $$ \measuredangle D R M=\measuredangle D B A=Q B A=\measuredangle Q P A=\measuredangle Q P M $$ Thus, $\overline{D R} \| \overline{P Q}$, so $D R Q P$ is also a parallelogram.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281 |
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 ## ब Synthetic approach with no additional points at all. ## Claim - $\triangle B P C \sim \triangle A N M$ (oppositely oriented). $$ \frac{B M}{B P}=\frac{A M}{A Q} \Longrightarrow \frac{2 B M}{B P}=\frac{A M}{A Q / 2} \Longrightarrow \frac{B C}{B P}=\frac{A M}{A N} $$ implying the similarity (since $\measuredangle M A Q=\measuredangle B P M$ ). This similarity gives us the equality of directed angles $$ \measuredangle(B C, M N)=-\measuredangle(P C, A M)=90^{\circ} $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 ## ब Synthetic approach with no additional points at all. ## Claim - $\triangle B P C \sim \triangle A N M$ (oppositely oriented). $$ \frac{B M}{B P}=\frac{A M}{A Q} \Longrightarrow \frac{2 B M}{B P}=\frac{A M}{A Q / 2} \Longrightarrow \frac{B C}{B P}=\frac{A M}{A N} $$ implying the similarity (since $\measuredangle M A Q=\measuredangle B P M$ ). This similarity gives us the equality of directed angles $$ \measuredangle(B C, M N)=-\measuredangle(P C, A M)=90^{\circ} $$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281 |
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Cartesian coordinates approach without power of a point (outline). After computing $A$ and $P$ as above, one could also directly calculate $$ \begin{aligned} & \text { Perpendicular bisector of } \overline{A B}: y=-\frac{a+1}{b} x+\frac{a^{2}+b^{2}-1}{2 b} \\ & \text { Perpendicular bisector of } \overline{P B}: y=-\left(\frac{2 a}{b}+\frac{b}{a}\right) x-\frac{b}{2 a} \\ & \text { Perpendicular bisector of } \overline{P A}: y=-\frac{a}{b} x+\frac{a+a^{2}+b^{2}}{2 b} \\ & \text { Circumcenter of } \triangle P A B=\left(-\frac{a+1}{2}, \frac{2 a^{2}+2 a+b^{2}}{2 b}\right) \end{aligned} $$ This is enough to extract the coordinates of $Q=(\bullet, 0)$, because $B=(-1,0)$ is given, and the $x$-coordinate of the circumcenter should be the average of the $x$-coordinates of $B$ and $Q$. In other words, $Q=(-a, 0)$. Hence, $N=\left(0, \frac{b}{2}\right)$, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Cartesian coordinates approach without power of a point (outline). After computing $A$ and $P$ as above, one could also directly calculate $$ \begin{aligned} & \text { Perpendicular bisector of } \overline{A B}: y=-\frac{a+1}{b} x+\frac{a^{2}+b^{2}-1}{2 b} \\ & \text { Perpendicular bisector of } \overline{P B}: y=-\left(\frac{2 a}{b}+\frac{b}{a}\right) x-\frac{b}{2 a} \\ & \text { Perpendicular bisector of } \overline{P A}: y=-\frac{a}{b} x+\frac{a+a^{2}+b^{2}}{2 b} \\ & \text { Circumcenter of } \triangle P A B=\left(-\frac{a+1}{2}, \frac{2 a^{2}+2 a+b^{2}}{2 b}\right) \end{aligned} $$ This is enough to extract the coordinates of $Q=(\bullet, 0)$, because $B=(-1,0)$ is given, and the $x$-coordinate of the circumcenter should be the average of the $x$-coordinates of $B$ and $Q$. In other words, $Q=(-a, 0)$. Hence, $N=\left(0, \frac{b}{2}\right)$, as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281 |
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 \I III-advised barycentric approach (outline). Use reference triangle $A B C$. The $A$ median is parametrized by $(t: 1: 1)$ for $t \in \mathbb{R}$. So because of $\overline{C P} \perp \overline{A M}$, we are looking for $t$ such that $$ \left(\frac{t \vec{A}+\vec{B}+\vec{C}}{t+2}-\vec{C}\right) \perp\left(A-\frac{\vec{B}+\vec{C}}{2}\right) $$ This is equivalent to $$ (t \vec{A}+\vec{B}-(t+1) \vec{C}) \perp(2 \vec{A}-\vec{B}-\vec{C}) $$ By the perpendicularity formula for barycentric coordinates (EGMO 7.16), this is equivalent to $$ \begin{aligned} 0 & =a^{2} t-b^{2} \cdot(3 t+2)+c^{2} \cdot(2-t) \\ & =\left(a^{2}-3 b^{2}-c^{2}\right) t-2\left(b^{2}-c^{2}\right) \\ \Longrightarrow t & =\frac{2\left(b^{2}-c^{2}\right)}{a^{2}-3 b^{2}-c^{2}} \end{aligned} $$ In other words, $$ P=\left(2\left(b^{2}-c^{2}\right): a^{2}-3 b^{2}-c^{2}: a^{2}-3 b^{2}-c^{2}\right) . $$ A long calculation gives $a^{2} y_{P} z_{P}+b^{2} z_{P} x_{P}+c^{2} x_{P} y_{P}=\left(a^{2}-3 b^{2}-c^{2}\right)\left(a^{2}-b^{2}+c^{2}\right)\left(a^{2}-\right.$ $\left.2 b^{2}-2 c^{2}\right)$. Together with $x_{P}+y_{P}+z_{P}=2 a^{2}-4 b^{2}-4 c^{2}$, this makes the equation of $(A B P)$ as $$ 0=-a^{2} y z-b^{2} z x-c^{2} x y+\frac{a^{2}-b^{2}+c^{2}}{2} z(x+y+z) $$ To solve for $Q$, set $x=0$ to get to get $$ a^{2} y z=\frac{a^{2}-b^{2}+c^{2}}{2} z(y+z) \Longrightarrow \frac{y}{z}=\frac{a^{2}-b^{2}+c^{2}}{a^{2}+b^{2}-c^{2}} $$ In other words, $$ Q=\left(0: a^{2}-b^{2}+c^{2}: a^{2}+b^{2}-c^{2}\right) $$ Taking the average with $A=(1,0,0)$ then gives $$ N=\left(2 a^{2}: a^{2}-b^{2}+c^{2}: a^{2}+b^{2}-c^{2}\right) . $$ The equation for the perpendicular bisector of $\overline{B C}$ is given by (see EGMO 7.19) $$ 0=a^{2}(z-y)+x\left(c^{2}-b^{2}\right) $$ which contains $N$, as needed. $$ p=\frac{(a-m) \bar{c}+(\bar{a}-\bar{m}) c+\bar{a} m-a \bar{m}}{2(\bar{a}-\bar{m})}=\frac{a^{2} b-a^{2} c-a b^{2}-2 a b c-a c^{2}+b^{2} c+3 b c^{2}}{4 b c-2 a(b+c)} $$ Meanwhile, an extremely ugly calculation will eventually yield $$ q=\frac{\frac{b c}{a}+b+c-a}{2} $$ SO $$ n=\frac{a+q}{2}=\frac{a+b+c+\frac{b c}{a}}{4}=\frac{(a+b)(a+c)}{2 a} $$ There are a few ways to then verify $N B=N C$. The simplest seems to be to verify that $$ \frac{n-\frac{b+c}{2}}{b-c}=\frac{a-b-c+\frac{b c}{a}}{4(b-c)}=\frac{(a-b)(a-c)}{2 a(b-c)} $$ is pure imaginary, which is clear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 \I III-advised barycentric approach (outline). Use reference triangle $A B C$. The $A$ median is parametrized by $(t: 1: 1)$ for $t \in \mathbb{R}$. So because of $\overline{C P} \perp \overline{A M}$, we are looking for $t$ such that $$ \left(\frac{t \vec{A}+\vec{B}+\vec{C}}{t+2}-\vec{C}\right) \perp\left(A-\frac{\vec{B}+\vec{C}}{2}\right) $$ This is equivalent to $$ (t \vec{A}+\vec{B}-(t+1) \vec{C}) \perp(2 \vec{A}-\vec{B}-\vec{C}) $$ By the perpendicularity formula for barycentric coordinates (EGMO 7.16), this is equivalent to $$ \begin{aligned} 0 & =a^{2} t-b^{2} \cdot(3 t+2)+c^{2} \cdot(2-t) \\ & =\left(a^{2}-3 b^{2}-c^{2}\right) t-2\left(b^{2}-c^{2}\right) \\ \Longrightarrow t & =\frac{2\left(b^{2}-c^{2}\right)}{a^{2}-3 b^{2}-c^{2}} \end{aligned} $$ In other words, $$ P=\left(2\left(b^{2}-c^{2}\right): a^{2}-3 b^{2}-c^{2}: a^{2}-3 b^{2}-c^{2}\right) . $$ A long calculation gives $a^{2} y_{P} z_{P}+b^{2} z_{P} x_{P}+c^{2} x_{P} y_{P}=\left(a^{2}-3 b^{2}-c^{2}\right)\left(a^{2}-b^{2}+c^{2}\right)\left(a^{2}-\right.$ $\left.2 b^{2}-2 c^{2}\right)$. Together with $x_{P}+y_{P}+z_{P}=2 a^{2}-4 b^{2}-4 c^{2}$, this makes the equation of $(A B P)$ as $$ 0=-a^{2} y z-b^{2} z x-c^{2} x y+\frac{a^{2}-b^{2}+c^{2}}{2} z(x+y+z) $$ To solve for $Q$, set $x=0$ to get to get $$ a^{2} y z=\frac{a^{2}-b^{2}+c^{2}}{2} z(y+z) \Longrightarrow \frac{y}{z}=\frac{a^{2}-b^{2}+c^{2}}{a^{2}+b^{2}-c^{2}} $$ In other words, $$ Q=\left(0: a^{2}-b^{2}+c^{2}: a^{2}+b^{2}-c^{2}\right) $$ Taking the average with $A=(1,0,0)$ then gives $$ N=\left(2 a^{2}: a^{2}-b^{2}+c^{2}: a^{2}+b^{2}-c^{2}\right) . $$ The equation for the perpendicular bisector of $\overline{B C}$ is given by (see EGMO 7.19) $$ 0=a^{2}(z-y)+x\left(c^{2}-b^{2}\right) $$ which contains $N$, as needed. $$ p=\frac{(a-m) \bar{c}+(\bar{a}-\bar{m}) c+\bar{a} m-a \bar{m}}{2(\bar{a}-\bar{m})}=\frac{a^{2} b-a^{2} c-a b^{2}-2 a b c-a c^{2}+b^{2} c+3 b c^{2}}{4 b c-2 a(b+c)} $$ Meanwhile, an extremely ugly calculation will eventually yield $$ q=\frac{\frac{b c}{a}+b+c-a}{2} $$ SO $$ n=\frac{a+q}{2}=\frac{a+b+c+\frac{b c}{a}}{4}=\frac{(a+b)(a+c)}{2 a} $$ There are a few ways to then verify $N B=N C$. The simplest seems to be to verify that $$ \frac{n-\frac{b+c}{2}}{b-c}=\frac{a-b-c+\frac{b c}{a}}{4(b-c)}=\frac{(a-b)(a-c)}{2 a(b-c)} $$ is pure imaginary, which is clear.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281 |
Positive integers $a$ and $N$ are fixed, and $N$ positive integers are written on a blackboard. Alice and Bob play the following game. On Alice's turn, she must replace some integer $n$ on the board with $n+a$, and on Bob's turn he must replace some even integer $n$ on the board with $n / 2$. Alice goes first and they alternate turns. If on his turn Bob has no valid moves, the game ends. After analyzing the $N$ integers on the board, Bob realizes that, regardless of what moves Alice makes, he will be able to force the game to end eventually. Show that, in fact, for this value of $a$ and these $N$ integers on the board, the game is guaranteed to end regardless of Alice's or Bob's moves.
|
For $N=1$, there is nothing to prove. We address $N \geq 2$ only henceforth. Let $S$ denote the numbers on the board. Claim - When $N \geq 2$, if $\nu_{2}(x)<\nu_{2}(a)$ for all $x \in S$, the game must terminate no matter what either player does. Hence, in fact the game will always terminate in exactly $\sum_{x \in S} \nu_{2}(x)$ moves in this case, regardless of what either player does. Claim - When $N \geq 2$, if there exists a number $x$ on the board such that $\nu_{2}(x) \geq$ $\nu_{2}(a)$, then Alice can cause the game to go on forever. - Operate on the first entry if $\nu_{2}(x)=\nu_{2}(a)$ (the new entry thus has $\nu_{2}(x+a)>\nu_{2}(a)$ ); - Operate on any other entry besides the first one, otherwise. A double induction then shows that - Just before each of Bob's turns, $\nu_{2}(x)>\nu_{2}(a)$ always holds; and - After each of Bob's turns, $\nu_{2}(x) \geq \nu_{2}(a)$ always holds. In particular Bob will never run out of legal moves, since halving $x$ is always legal.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Positive integers $a$ and $N$ are fixed, and $N$ positive integers are written on a blackboard. Alice and Bob play the following game. On Alice's turn, she must replace some integer $n$ on the board with $n+a$, and on Bob's turn he must replace some even integer $n$ on the board with $n / 2$. Alice goes first and they alternate turns. If on his turn Bob has no valid moves, the game ends. After analyzing the $N$ integers on the board, Bob realizes that, regardless of what moves Alice makes, he will be able to force the game to end eventually. Show that, in fact, for this value of $a$ and these $N$ integers on the board, the game is guaranteed to end regardless of Alice's or Bob's moves.
|
For $N=1$, there is nothing to prove. We address $N \geq 2$ only henceforth. Let $S$ denote the numbers on the board. Claim - When $N \geq 2$, if $\nu_{2}(x)<\nu_{2}(a)$ for all $x \in S$, the game must terminate no matter what either player does. Hence, in fact the game will always terminate in exactly $\sum_{x \in S} \nu_{2}(x)$ moves in this case, regardless of what either player does. Claim - When $N \geq 2$, if there exists a number $x$ on the board such that $\nu_{2}(x) \geq$ $\nu_{2}(a)$, then Alice can cause the game to go on forever. - Operate on the first entry if $\nu_{2}(x)=\nu_{2}(a)$ (the new entry thus has $\nu_{2}(x+a)>\nu_{2}(a)$ ); - Operate on any other entry besides the first one, otherwise. A double induction then shows that - Just before each of Bob's turns, $\nu_{2}(x)>\nu_{2}(a)$ always holds; and - After each of Bob's turns, $\nu_{2}(x) \geq \nu_{2}(a)$ always holds. In particular Bob will never run out of legal moves, since halving $x$ is always legal.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5a0c2e05-3fc5-5fdf-b1b1-dd37f92d4e76
| 605,776 |
Let $A B C$ be a triangle with incenter $I$ and excenters $I_{a}, I_{b}, I_{c}$ opposite $A, B$, and $C$, respectively. Given an arbitrary point $D$ on the circumcircle of $\triangle A B C$ that does not lie on any of the lines $I I_{a}, I_{b} I_{c}$, or $B C$, suppose the circumcircles of $\triangle D I I_{a}$ and $\triangle D I_{b} I_{c}$ intersect at two distinct points $D$ and $F$. If $E$ is the intersection of lines $D F$ and $B C$, prove that $\angle B A D=\angle E A C$.
|
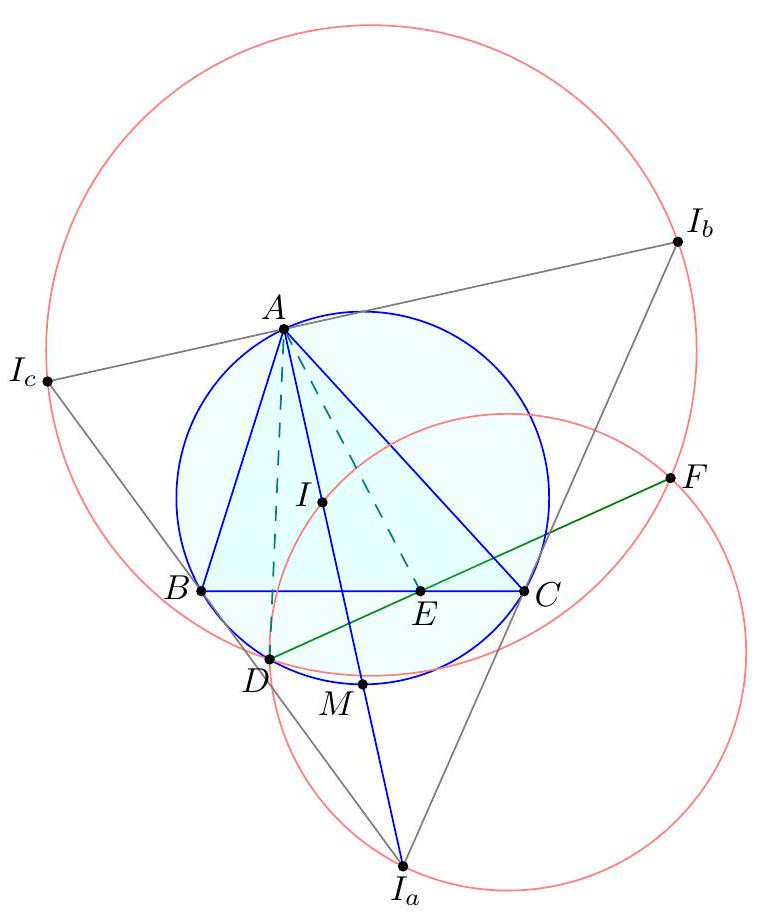 \I Barycentric coordinates (Carl Schildkraut). With reference triangle $\triangle A B C$, set $D=(r: s: t)$. Claim - The equations of $\left(D I I_{a}\right)$ and $\left(D I_{b} I_{c}\right)$ are, respectively, $$ \begin{aligned} & 0=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z) \cdot\left(b c x-\frac{b c r}{c s-b t}(c y-b z)\right) \\ & 0=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z) \cdot\left(-b c x+\frac{b c r}{c s+b t}(c y+b z)\right) . \end{aligned} $$ By EGMO Lemma 7.24, the radical axis is then given by $$ \overline{D F}: b c x-\frac{b c r}{c s-b t}(c y-b z)=-b c x+\frac{b c r}{c s+b t}(c y+b z) . $$ Now the point $$ \left(0: \frac{b^{2}}{s}: \frac{c^{2}}{t}\right)=\left(0: b^{2} t: c^{2} s\right) $$ lies on line $D F$ by inspection, and is obviously on line $B C$, hence it coincides with $E$. This lies on the isogonal of $\overline{A D}$ (by EGMO Lemma 7.6), as needed. 『 Synthetic approach (Anant Mudgal). Focus on just $\left(D I I_{a}\right)$. Let $P$ be the second intersection of $\left(D I I_{a}\right)$ with $(A B C)$, and let $M$ be the midpoint of minor arc $\widehat{B C}$. Then by radical axis, lines $A M, D P$, and $B C$ are concurrent at a point $K$. Let $E^{\prime}=\overline{P M} \cap \overline{B C}$. 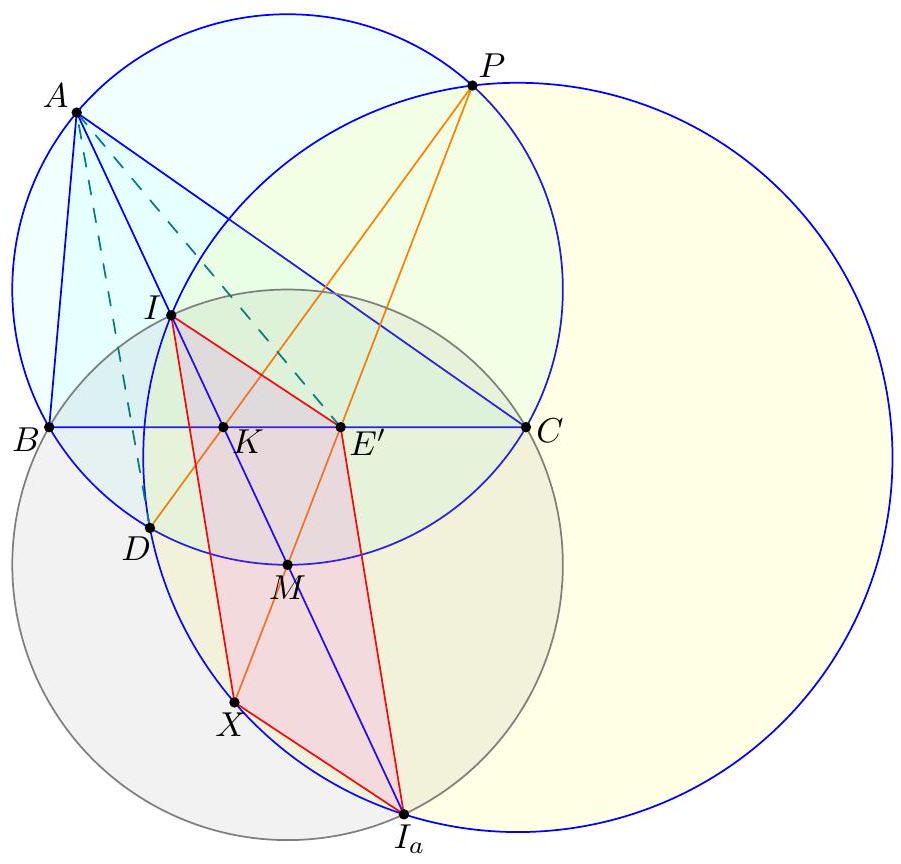 Claim - We have $\measuredangle B A D=\measuredangle E^{\prime} A C$. $$ \measuredangle K A E^{\prime}=\measuredangle K P E^{\prime}=\measuredangle D P M=\measuredangle D A M $$ Claim - The power of point $E^{\prime}$ with respect to $\left(D I I_{a}\right)$ is $2 E^{\prime} B \cdot E^{\prime} C$. $$ \measuredangle X I_{a} I=\measuredangle I_{a} I E^{\prime}=\measuredangle M I E^{\prime}=\measuredangle M P I=\measuredangle X P I $$ Hence $X$ lies on $\left(D I I_{a}\right)$, and $E^{\prime} X \cdot E^{\prime} P=2 E^{\prime} M \cdot E^{\prime} P=2 E^{\prime} B \cdot E^{\prime} C$. Repeat the argument on $\left(D I_{b} I_{c}\right)$; the same point $E^{\prime}$ (because of the first claim) then has power $2 E^{\prime} B \cdot E^{\prime} C$ with respect to $\left(D I_{b} I_{c}\right)$. Hence $E^{\prime}$ lies on the radical axis of $\left(D I I_{a}\right)$ and $\left(D I_{b} I_{c}\right)$, ergo $E^{\prime}=E$. The first claim then solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$ and excenters $I_{a}, I_{b}, I_{c}$ opposite $A, B$, and $C$, respectively. Given an arbitrary point $D$ on the circumcircle of $\triangle A B C$ that does not lie on any of the lines $I I_{a}, I_{b} I_{c}$, or $B C$, suppose the circumcircles of $\triangle D I I_{a}$ and $\triangle D I_{b} I_{c}$ intersect at two distinct points $D$ and $F$. If $E$ is the intersection of lines $D F$ and $B C$, prove that $\angle B A D=\angle E A C$.
|
 \I Barycentric coordinates (Carl Schildkraut). With reference triangle $\triangle A B C$, set $D=(r: s: t)$. Claim - The equations of $\left(D I I_{a}\right)$ and $\left(D I_{b} I_{c}\right)$ are, respectively, $$ \begin{aligned} & 0=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z) \cdot\left(b c x-\frac{b c r}{c s-b t}(c y-b z)\right) \\ & 0=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z) \cdot\left(-b c x+\frac{b c r}{c s+b t}(c y+b z)\right) . \end{aligned} $$ By EGMO Lemma 7.24, the radical axis is then given by $$ \overline{D F}: b c x-\frac{b c r}{c s-b t}(c y-b z)=-b c x+\frac{b c r}{c s+b t}(c y+b z) . $$ Now the point $$ \left(0: \frac{b^{2}}{s}: \frac{c^{2}}{t}\right)=\left(0: b^{2} t: c^{2} s\right) $$ lies on line $D F$ by inspection, and is obviously on line $B C$, hence it coincides with $E$. This lies on the isogonal of $\overline{A D}$ (by EGMO Lemma 7.6), as needed. 『 Synthetic approach (Anant Mudgal). Focus on just $\left(D I I_{a}\right)$. Let $P$ be the second intersection of $\left(D I I_{a}\right)$ with $(A B C)$, and let $M$ be the midpoint of minor arc $\widehat{B C}$. Then by radical axis, lines $A M, D P$, and $B C$ are concurrent at a point $K$. Let $E^{\prime}=\overline{P M} \cap \overline{B C}$.  Claim - We have $\measuredangle B A D=\measuredangle E^{\prime} A C$. $$ \measuredangle K A E^{\prime}=\measuredangle K P E^{\prime}=\measuredangle D P M=\measuredangle D A M $$ Claim - The power of point $E^{\prime}$ with respect to $\left(D I I_{a}\right)$ is $2 E^{\prime} B \cdot E^{\prime} C$. $$ \measuredangle X I_{a} I=\measuredangle I_{a} I E^{\prime}=\measuredangle M I E^{\prime}=\measuredangle M P I=\measuredangle X P I $$ Hence $X$ lies on $\left(D I I_{a}\right)$, and $E^{\prime} X \cdot E^{\prime} P=2 E^{\prime} M \cdot E^{\prime} P=2 E^{\prime} B \cdot E^{\prime} C$. Repeat the argument on $\left(D I_{b} I_{c}\right)$; the same point $E^{\prime}$ (because of the first claim) then has power $2 E^{\prime} B \cdot E^{\prime} C$ with respect to $\left(D I_{b} I_{c}\right)$. Hence $E^{\prime}$ lies on the radical axis of $\left(D I I_{a}\right)$ and $\left(D I_{b} I_{c}\right)$, ergo $E^{\prime}=E$. The first claim then solves the problem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
88d64202-d001-539f-aa5e-43de57a170cb
| 249,213 |
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
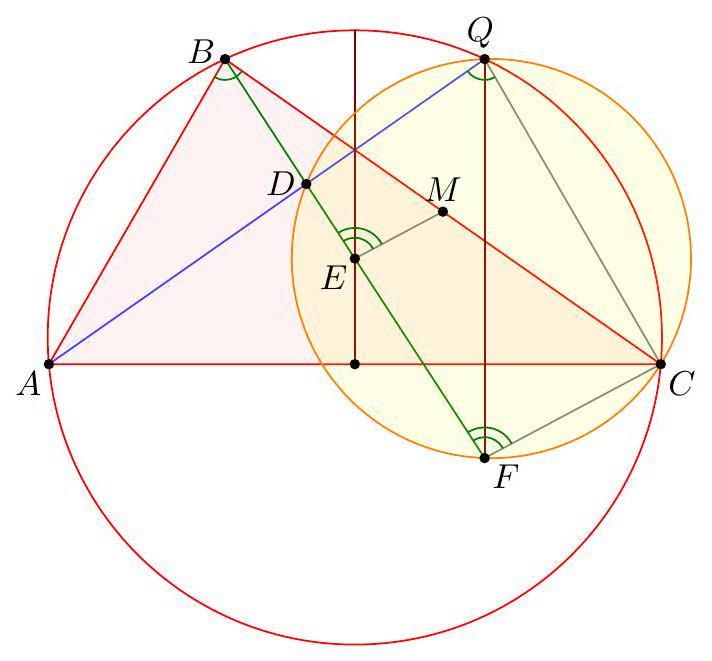 Claim - We have DQCF is cyclic. $$ \begin{aligned} \measuredangle F D C & =-\measuredangle C D B=180^{\circ}-\left(90^{\circ}+\measuredangle C A B\right)=90^{\circ}-\measuredangle C A B \\ & =90^{\circ}-\measuredangle Q C A=\measuredangle F Q C . \end{aligned} $$ To conclude, note that $$ \measuredangle B E M=\measuredangle B F C=\measuredangle D F C=\measuredangle D Q C=\measuredangle A Q C=\measuredangle A B C=\measuredangle A B M . $$ Remark (Motivation). Here is one possible way to come up with the construction of point $F$ (at least this is what led Evan to find it). If one directs all the angles in the obvious way, there are really two points $D$ and $D^{\prime}$ that are possible, although one is outside the triangle; they give corresponding points $E$ and $E^{\prime}$. The circles $B E M$ and $B E^{\prime} M$ must then actually coincide since they are both alleged to be tangent to line $A B$. See the figure below. 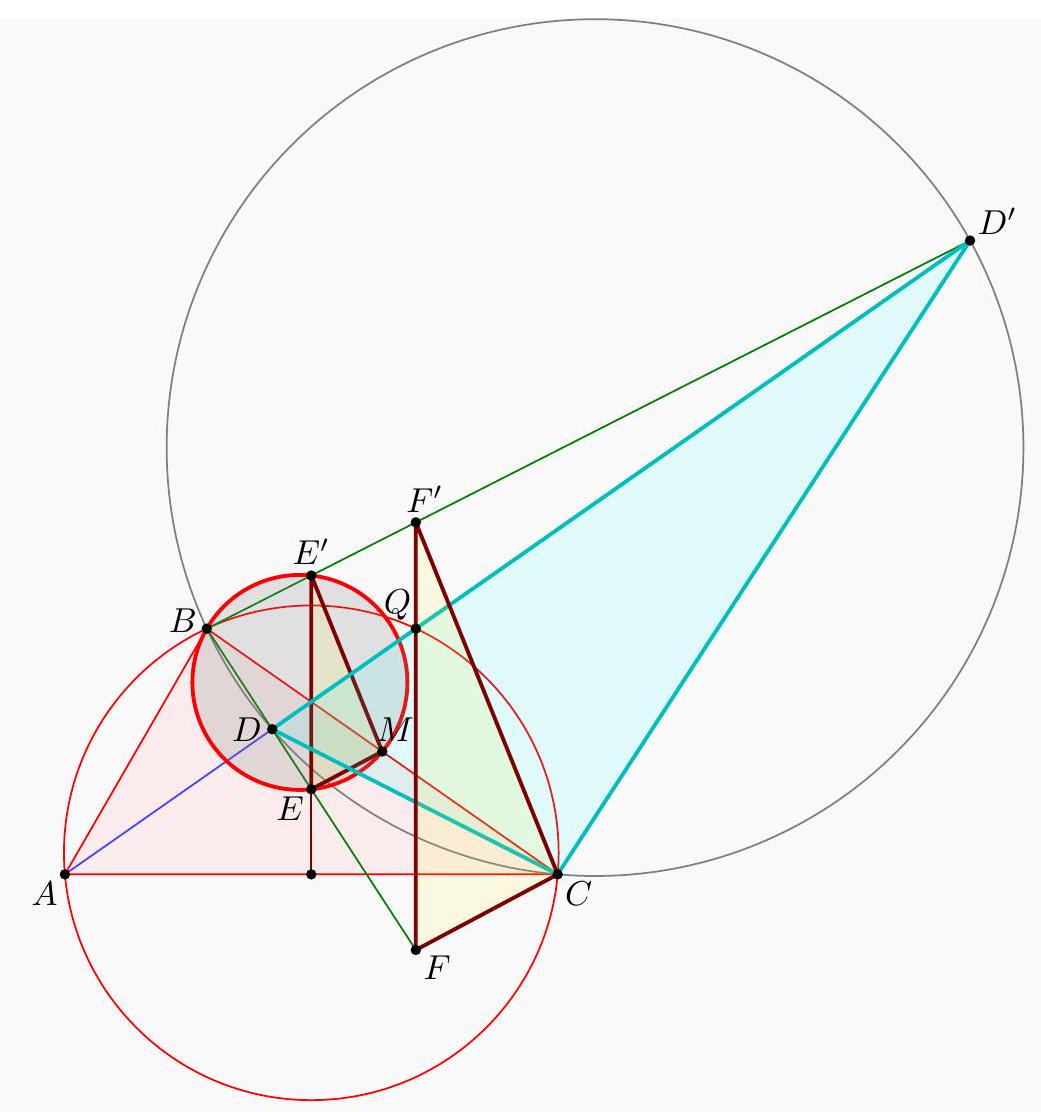 One can already prove using angle chasing that $\overline{A B}$ is tangent to $\left(B E E^{\prime}\right)$. So the point of the problem is to show that $M$ lies on this circle too. However, from looking at the diagram, one may realize that in fact it seems $$ \triangle M E E^{\prime} \stackrel{\triangle}{\sim} \triangle C D D^{\prime} $$ is going to be true from just those marked in the figure (and this would certainly imply the desired concyclic conclusion). Since $M$ is a midpoint, it makes sense to dilate $\triangle E M E^{\prime}$ from $B$ by a factor of 2 to get $\triangle F C F^{\prime}$ so that the desired similarity is actually a spiral similarity at $C$. Then the spiral similarity lemma says that the desired similarity is equivalent to requiring $\overline{D D^{\prime}} \cap \overline{F F^{\prime}}=Q$ to lie on both $(C D F)$ and $\left(C D^{\prime} F^{\prime}\right)$. Hence the key construction and claim from the solution are both discovered naturally, and we find the solution above. (The points $D^{\prime}, E^{\prime}, F^{\prime}$ can then be deleted to hide the motivation.) Another short solution. Let $Z$ be on line $B D E$ such that $\angle B A Z=90^{\circ}$. This lets us interpret the angle condition as follows: Claim - Points $A, D, Z, C$ are cyclic.  Define $W$ as the midpoint of $\overline{B Z}$, so $\overline{M W} \| \overline{C Z}$. And let $O$ denote the center of $(A B C)$. Claim - Points $M, E, O, W$ are cyclic. $$ \begin{aligned} \measuredangle M O E & =\measuredangle(\overline{O M}, \overline{B C})+\measuredangle(\overline{B C}, \overline{A C})+\measuredangle(\overline{A C}, \overline{O E}) \\ & =90^{\circ}+\measuredangle B C A+90^{\circ} \\ & =\measuredangle B C A=\measuredangle C A D=\measuredangle C Z D=\measuredangle M W D=\measuredangle M W E . \end{aligned} $$ To finish, note $$ \begin{aligned} \measuredangle M E B & =\measuredangle M E W=\measuredangle M O W \\ & =\measuredangle(\overline{M O}, \overline{B C})+\measuredangle(\overline{B C}, \overline{A B})+\measuredangle(\overline{A B}, \overline{O W}) \\ & =90^{\circ}+\measuredangle C B A+90^{\circ}=\measuredangle C B A=\measuredangle M B A . \end{aligned} $$ This implies the desired tangency.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
 Claim - We have DQCF is cyclic. $$ \begin{aligned} \measuredangle F D C & =-\measuredangle C D B=180^{\circ}-\left(90^{\circ}+\measuredangle C A B\right)=90^{\circ}-\measuredangle C A B \\ & =90^{\circ}-\measuredangle Q C A=\measuredangle F Q C . \end{aligned} $$ To conclude, note that $$ \measuredangle B E M=\measuredangle B F C=\measuredangle D F C=\measuredangle D Q C=\measuredangle A Q C=\measuredangle A B C=\measuredangle A B M . $$ Remark (Motivation). Here is one possible way to come up with the construction of point $F$ (at least this is what led Evan to find it). If one directs all the angles in the obvious way, there are really two points $D$ and $D^{\prime}$ that are possible, although one is outside the triangle; they give corresponding points $E$ and $E^{\prime}$. The circles $B E M$ and $B E^{\prime} M$ must then actually coincide since they are both alleged to be tangent to line $A B$. See the figure below.  One can already prove using angle chasing that $\overline{A B}$ is tangent to $\left(B E E^{\prime}\right)$. So the point of the problem is to show that $M$ lies on this circle too. However, from looking at the diagram, one may realize that in fact it seems $$ \triangle M E E^{\prime} \stackrel{\triangle}{\sim} \triangle C D D^{\prime} $$ is going to be true from just those marked in the figure (and this would certainly imply the desired concyclic conclusion). Since $M$ is a midpoint, it makes sense to dilate $\triangle E M E^{\prime}$ from $B$ by a factor of 2 to get $\triangle F C F^{\prime}$ so that the desired similarity is actually a spiral similarity at $C$. Then the spiral similarity lemma says that the desired similarity is equivalent to requiring $\overline{D D^{\prime}} \cap \overline{F F^{\prime}}=Q$ to lie on both $(C D F)$ and $\left(C D^{\prime} F^{\prime}\right)$. Hence the key construction and claim from the solution are both discovered naturally, and we find the solution above. (The points $D^{\prime}, E^{\prime}, F^{\prime}$ can then be deleted to hide the motivation.) Another short solution. Let $Z$ be on line $B D E$ such that $\angle B A Z=90^{\circ}$. This lets us interpret the angle condition as follows: Claim - Points $A, D, Z, C$ are cyclic.  Define $W$ as the midpoint of $\overline{B Z}$, so $\overline{M W} \| \overline{C Z}$. And let $O$ denote the center of $(A B C)$. Claim - Points $M, E, O, W$ are cyclic. $$ \begin{aligned} \measuredangle M O E & =\measuredangle(\overline{O M}, \overline{B C})+\measuredangle(\overline{B C}, \overline{A C})+\measuredangle(\overline{A C}, \overline{O E}) \\ & =90^{\circ}+\measuredangle B C A+90^{\circ} \\ & =\measuredangle B C A=\measuredangle C A D=\measuredangle C Z D=\measuredangle M W D=\measuredangle M W E . \end{aligned} $$ To finish, note $$ \begin{aligned} \measuredangle M E B & =\measuredangle M E W=\measuredangle M O W \\ & =\measuredangle(\overline{M O}, \overline{B C})+\measuredangle(\overline{B C}, \overline{A B})+\measuredangle(\overline{A B}, \overline{O W}) \\ & =90^{\circ}+\measuredangle C B A+90^{\circ}=\measuredangle C B A=\measuredangle M B A . \end{aligned} $$ This implies the desired tangency.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
0082373f-0732-5cf0-8d49-df0179f668fd
| 605,912 |
Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of integers, with the property that every consecutive group of $a_{i}$ 's averages to a perfect square. More precisely, for all positive integers $n$ and $k$, the quantity $$ \frac{a_{n}+a_{n+1}+\cdots+a_{n+k-1}}{k} $$ is always the square of an integer. Prove that the sequence must be constant (all $a_{i}$ are equal to the same perfect square).
|
Let $\nu_{p}(n)$ denote the largest exponent of $p$ dividing $n$. The problem follows from the following proposition. ## Proposition Let $\left(a_{n}\right)$ be a sequence of integers and let $p$ be a prime. Suppose that every consecutive group of $a_{i}$ 's with length at most $p$ averages to a perfect square. Then $\nu_{p}\left(a_{i}\right)$ is independent of $i$. We proceed by induction on the smallest value of $\nu_{p}\left(a_{i}\right)$ as $i$ ranges (which must be even, as each of the $a_{i}$ are themselves a square). First we prove two claims. Claim - If $j \equiv k(\bmod p)$ then $a_{j} \equiv a_{k}(\bmod p)$. Claim - If some $a_{i}$ is divisible by $p$ then all of them are. $$ S_{n}=a_{1}+a_{2}+\cdots+a_{n} \equiv a_{2}+\cdots+a_{n} \quad(\bmod p) $$ Call an integer $k$ with $2 \leq k<p$ a pivot if $1-k^{-1}$ is a quadratic nonresidue modulo $p$. We claim that for any pivot $k, S_{k} \equiv 0(\bmod p)$. If not, then $$ \frac{a_{1}+a_{2}+\cdots+a_{k}}{k} \text { and } \frac{a_{2}+\cdots+a_{k}}{k-1} $$ are both qudaratic residues. Division implies that $\frac{k-1}{k}=1-k^{-1}$ is a quadratic residue, contradiction. Next we claim that there is an integer $m$ with $S_{m} \equiv S_{m+1} \equiv 0(\bmod p)$, which implies $p \mid a_{m+1}$. If 2 is a pivot, then we simply take $m=1$. Otherwise, there are $\frac{1}{2}(p-1)$ pivots, one for each nonresidue (which includes neither 0 nor 1 ), and all pivots lie in [3, $p-1]$, so we can find an $m$ such that $m$ and $m+1$ are both pivots. Repeating this procedure starting with $a_{m+1}$ shows that $a_{2 m+1}, a_{3 m+1}, \ldots$ must all be divisible by $p$. Combined with the first claim and the fact that $m<p$, we find that all the $a_{i}$ are divisible by $p$. The second claim establishes the base case of our induction. Now assume all $a_{i}$ are divisible by $p$ and hence $p^{2}$. Then all the averages in our proposition (with length at $\operatorname{most} p$ ) are divisible by $p$ and hence $p^{2}$. Thus the map $a_{i} \mapsto \frac{1}{p^{2}} a_{i}$ gives a new sequence satisfying the proposition, and our inductive hypothesis completes the proof. Remark. There is a subtle bug that arises if one omits the condition that $k \leq p$ in the proposition. When $k=p^{2}$ the average $\frac{a_{1}+\cdots+a_{p^{2}}}{p^{2}}$ is not necessarily divisible by $p$ even if all the $a_{i}$ are. Hence it is not valid to divide through by $p$. This is why the condition $k \leq p$ was added.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of integers, with the property that every consecutive group of $a_{i}$ 's averages to a perfect square. More precisely, for all positive integers $n$ and $k$, the quantity $$ \frac{a_{n}+a_{n+1}+\cdots+a_{n+k-1}}{k} $$ is always the square of an integer. Prove that the sequence must be constant (all $a_{i}$ are equal to the same perfect square).
|
Let $\nu_{p}(n)$ denote the largest exponent of $p$ dividing $n$. The problem follows from the following proposition. ## Proposition Let $\left(a_{n}\right)$ be a sequence of integers and let $p$ be a prime. Suppose that every consecutive group of $a_{i}$ 's with length at most $p$ averages to a perfect square. Then $\nu_{p}\left(a_{i}\right)$ is independent of $i$. We proceed by induction on the smallest value of $\nu_{p}\left(a_{i}\right)$ as $i$ ranges (which must be even, as each of the $a_{i}$ are themselves a square). First we prove two claims. Claim - If $j \equiv k(\bmod p)$ then $a_{j} \equiv a_{k}(\bmod p)$. Claim - If some $a_{i}$ is divisible by $p$ then all of them are. $$ S_{n}=a_{1}+a_{2}+\cdots+a_{n} \equiv a_{2}+\cdots+a_{n} \quad(\bmod p) $$ Call an integer $k$ with $2 \leq k<p$ a pivot if $1-k^{-1}$ is a quadratic nonresidue modulo $p$. We claim that for any pivot $k, S_{k} \equiv 0(\bmod p)$. If not, then $$ \frac{a_{1}+a_{2}+\cdots+a_{k}}{k} \text { and } \frac{a_{2}+\cdots+a_{k}}{k-1} $$ are both qudaratic residues. Division implies that $\frac{k-1}{k}=1-k^{-1}$ is a quadratic residue, contradiction. Next we claim that there is an integer $m$ with $S_{m} \equiv S_{m+1} \equiv 0(\bmod p)$, which implies $p \mid a_{m+1}$. If 2 is a pivot, then we simply take $m=1$. Otherwise, there are $\frac{1}{2}(p-1)$ pivots, one for each nonresidue (which includes neither 0 nor 1 ), and all pivots lie in [3, $p-1]$, so we can find an $m$ such that $m$ and $m+1$ are both pivots. Repeating this procedure starting with $a_{m+1}$ shows that $a_{2 m+1}, a_{3 m+1}, \ldots$ must all be divisible by $p$. Combined with the first claim and the fact that $m<p$, we find that all the $a_{i}$ are divisible by $p$. The second claim establishes the base case of our induction. Now assume all $a_{i}$ are divisible by $p$ and hence $p^{2}$. Then all the averages in our proposition (with length at $\operatorname{most} p$ ) are divisible by $p$ and hence $p^{2}$. Thus the map $a_{i} \mapsto \frac{1}{p^{2}} a_{i}$ gives a new sequence satisfying the proposition, and our inductive hypothesis completes the proof. Remark. There is a subtle bug that arises if one omits the condition that $k \leq p$ in the proposition. When $k=p^{2}$ the average $\frac{a_{1}+\cdots+a_{p^{2}}}{p^{2}}$ is not necessarily divisible by $p$ even if all the $a_{i}$ are. Hence it is not valid to divide through by $p$. This is why the condition $k \leq p$ was added.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
d2f4797f-cb24-5edc-99d5-7466559f3521
| 606,177 |
Let $n$ be an even positive integer, and let $G$ be an $n$-vertex (simple) graph with exactly $\frac{n^{2}}{4}$ edges. An unordered pair of distinct vertices $\{x, y\}$ is said to be amicable if they have a common neighbor (there is a vertex $z$ such that $x z$ and $y z$ are both edges). Prove that $G$ has at least $2\binom{n / 2}{2}$ pairs of vertices which are amicable.
|
First, we prove the following lemma. (https://en.wikipedia.org/wiki/Friendship_ paradox). Lemma (On average, your friends are more popular than you) For a vertex $v$, let $a(v)$ denote the average degree of the neighbors of $v$ (setting $a(v)=0$ if $\operatorname{deg} v=0)$. Then $$ \sum_{v} a(v) \geq \sum_{v} \operatorname{deg} v=2 \# E $$ $$ \begin{aligned} \sum_{v} a(v) & =\sum_{v} \frac{\sum_{w \sim v} \operatorname{deg} w}{\operatorname{deg} v} \\ & =\sum_{v} \sum_{w \sim v} \frac{\operatorname{deg} w}{\operatorname{deg} v} \\ & =\sum_{\text {edges } v w}\left(\frac{\operatorname{deg} w}{\operatorname{deg} v}+\frac{\operatorname{deg} v}{\operatorname{deg} w}\right) \\ & \stackrel{\text { AM-GM }}{\geq} \sum_{\text {edges } v w} 2=2 \# E=\sum_{v} \operatorname{deg} v \end{aligned} $$ as desired. Corollary (On average, your most popular friend is more popular than you) For a vertex $v$, let $m(v)$ denote the maximum degree of the neighbors of $v$ (setting $m(v)=0$ if $\operatorname{deg} v=0)$. Then $$ \sum_{v} m(v) \geq \sum_{v} \operatorname{deg} v=2 \# E \text {. } $$ We can use this to count amicable pairs by noting that any particular vertex $v$ is in at least $m(v)-1$ amicable pairs. So, the number of amicable pairs is at least $$ \frac{1}{2} \sum_{v}(m(v)-1) \geq \# E-\frac{1}{2} \# V $$ Note that up until now we haven't used any information about $G$. But now if we plug in $\# E=n^{2} / 4, \# V=n$, then we get exactly the desired answer. (Equality holds for $G=K_{n / 2, n / 2}$.)
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be an even positive integer, and let $G$ be an $n$-vertex (simple) graph with exactly $\frac{n^{2}}{4}$ edges. An unordered pair of distinct vertices $\{x, y\}$ is said to be amicable if they have a common neighbor (there is a vertex $z$ such that $x z$ and $y z$ are both edges). Prove that $G$ has at least $2\binom{n / 2}{2}$ pairs of vertices which are amicable.
|
First, we prove the following lemma. (https://en.wikipedia.org/wiki/Friendship_ paradox). Lemma (On average, your friends are more popular than you) For a vertex $v$, let $a(v)$ denote the average degree of the neighbors of $v$ (setting $a(v)=0$ if $\operatorname{deg} v=0)$. Then $$ \sum_{v} a(v) \geq \sum_{v} \operatorname{deg} v=2 \# E $$ $$ \begin{aligned} \sum_{v} a(v) & =\sum_{v} \frac{\sum_{w \sim v} \operatorname{deg} w}{\operatorname{deg} v} \\ & =\sum_{v} \sum_{w \sim v} \frac{\operatorname{deg} w}{\operatorname{deg} v} \\ & =\sum_{\text {edges } v w}\left(\frac{\operatorname{deg} w}{\operatorname{deg} v}+\frac{\operatorname{deg} v}{\operatorname{deg} w}\right) \\ & \stackrel{\text { AM-GM }}{\geq} \sum_{\text {edges } v w} 2=2 \# E=\sum_{v} \operatorname{deg} v \end{aligned} $$ as desired. Corollary (On average, your most popular friend is more popular than you) For a vertex $v$, let $m(v)$ denote the maximum degree of the neighbors of $v$ (setting $m(v)=0$ if $\operatorname{deg} v=0)$. Then $$ \sum_{v} m(v) \geq \sum_{v} \operatorname{deg} v=2 \# E \text {. } $$ We can use this to count amicable pairs by noting that any particular vertex $v$ is in at least $m(v)-1$ amicable pairs. So, the number of amicable pairs is at least $$ \frac{1}{2} \sum_{v}(m(v)-1) \geq \# E-\frac{1}{2} \# V $$ Note that up until now we haven't used any information about $G$. But now if we plug in $\# E=n^{2} / 4, \# V=n$, then we get exactly the desired answer. (Equality holds for $G=K_{n / 2, n / 2}$.)
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
68c5c8b9-11ea-546e-878c-c2413953db3c
| 246,399 |
Let $n$ be a positive even integer, and let $c_{1}, c_{2}, \ldots, c_{n-1}$ be real numbers satisfying $$ \sum_{i=1}^{n-1}\left|c_{i}-1\right|<1 $$ Prove that $$ 2 x^{n}-c_{n-1} x^{n-1}+c_{n-2} x^{n-2}-\cdots-c_{1} x^{1}+2 $$ has no real roots.
|
We will prove the polynomial is positive for all $x \in \mathbb{R}$. As $c_{i}>0$, the result is vacuous for $x \leq 0$, so we restrict attention to $x>0$. Then letting $c_{i}=1-d_{i}$ for each $i$, the inequality we want to prove becomes $$ x^{n}+1+\frac{x^{n+1}+1}{x+1}>\sum_{1}^{n-1} d_{i} x^{i} \quad \text { given } \sum\left|d_{i}\right|<1 $$ But obviously $x^{n}+1>x^{i}$ for any $1 \leq i \leq n-1$ and $x>0$. So in fact $x^{n}+1>\sum_{1}^{n-1}\left|d_{i}\right| x^{i}$ holds for $x>0$, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n$ be a positive even integer, and let $c_{1}, c_{2}, \ldots, c_{n-1}$ be real numbers satisfying $$ \sum_{i=1}^{n-1}\left|c_{i}-1\right|<1 $$ Prove that $$ 2 x^{n}-c_{n-1} x^{n-1}+c_{n-2} x^{n-2}-\cdots-c_{1} x^{1}+2 $$ has no real roots.
|
We will prove the polynomial is positive for all $x \in \mathbb{R}$. As $c_{i}>0$, the result is vacuous for $x \leq 0$, so we restrict attention to $x>0$. Then letting $c_{i}=1-d_{i}$ for each $i$, the inequality we want to prove becomes $$ x^{n}+1+\frac{x^{n+1}+1}{x+1}>\sum_{1}^{n-1} d_{i} x^{i} \quad \text { given } \sum\left|d_{i}\right|<1 $$ But obviously $x^{n}+1>x^{i}$ for any $1 \leq i \leq n-1$ and $x>0$. So in fact $x^{n}+1>\sum_{1}^{n-1}\left|d_{i}\right| x^{i}$ holds for $x>0$, as needed.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5f58ec9-8cee-5eda-9c48-31ea2f00688d
| 606,211 |
Let $A B C D$ be a cyclic quadrilateral, and let $E, F, G$, and $H$ be the midpoints of $A B, B C, C D$, and $D A$ respectively. Let $W, X, Y$ and $Z$ be the orthocenters of triangles $A H E, B E F, C F G$ and $D G H$, respectively. Prove that the quadrilaterals $A B C D$ and $W X Y Z$ have the same area.
|
We begin with: Claim - Point $W$ has coordinates $\frac{1}{2}(2 a+b+d)$. By symmetry, we have $$ \begin{aligned} w & =\frac{1}{2}(2 a+b+d) \\ x & =\frac{1}{2}(2 b+c+a) \\ y & =\frac{1}{2}(2 c+d+b) \\ z & =\frac{1}{2}(2 d+a+c) . \end{aligned} $$ We see that $w-y=a-c, x-z=b-d$. So the diagonals of $W X Y Z$ have the same length as those of $A B C D$ as well as the same directed angle between them. This implies the areas are equal, too.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral, and let $E, F, G$, and $H$ be the midpoints of $A B, B C, C D$, and $D A$ respectively. Let $W, X, Y$ and $Z$ be the orthocenters of triangles $A H E, B E F, C F G$ and $D G H$, respectively. Prove that the quadrilaterals $A B C D$ and $W X Y Z$ have the same area.
|
We begin with: Claim - Point $W$ has coordinates $\frac{1}{2}(2 a+b+d)$. By symmetry, we have $$ \begin{aligned} w & =\frac{1}{2}(2 a+b+d) \\ x & =\frac{1}{2}(2 b+c+a) \\ y & =\frac{1}{2}(2 c+d+b) \\ z & =\frac{1}{2}(2 d+a+c) . \end{aligned} $$ We see that $w-y=a-c, x-z=b-d$. So the diagonals of $W X Y Z$ have the same length as those of $A B C D$ as well as the same directed angle between them. This implies the areas are equal, too.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
4f02435e-223d-5ad2-ad2c-0ec3cf9ec493
| 246,420 |
For a prime $p$, a subset $S$ of residues modulo $p$ is called a sum-free multiplicative subgroup of $\mathbb{F}_{p}$ if - there is a nonzero residue $\alpha$ modulo $p$ such that $S=\left\{1, \alpha^{1}, \alpha^{2}, \ldots\right\}$ (all considered $\bmod p$ ), and - there are no $a, b, c \in S$ (not necessarily distinct) such that $a+b \equiv c(\bmod p)$. Prove that for every integer $N$, there is a prime $p$ and a sum-free multiplicative subgroup $S$ of $\mathbb{F}_{p}$ such that $|S| \geq N$.
|
We first prove the following general lemma. ## Lemma If $f, g \in \mathbb{Z}[X]$ are relatively prime nonconstant polynomials, then for sufficiently large primes $p$, they have no common root modulo $p$. $$ a(X) f(X)+b(X) g(X) \equiv c $$ So, plugging in $X=r$ we get $p \mid c$, so the set of permissible primes $p$ is finite. With this we can give the construction. ## Claim - Suppose that - $n$ is a positive integer with $n \not \equiv 0(\bmod 3)$; - $p$ is a prime which is $1 \bmod n$; and - $\alpha$ is a primitive $n^{\prime}$ th root of unity modulo $p$. Then $|S|=n$ and, if $p$ is sufficiently large in $n$, is also sum-free. $$ 1+\alpha^{k} \equiv \alpha^{m} \quad(\bmod p) $$ for some integers $k, m \in \mathbb{Z}$. This means $(X+1)^{n}-1$ and $X^{n}-1$ have common root $X=\alpha^{k}$. But $$ \underset{\mathbb{Z}[x]}{\operatorname{gcd}}\left((X+1)^{n}-1, X^{n}-1\right)=1 \quad \forall n \not \equiv 0 \quad(\bmod 3) $$ because when $3 \nmid n$ the two polynomials have no common complex roots. (Indeed, if $|\omega|=|1+\omega|=1$ then $\omega=-\frac{1}{2} \pm \frac{\sqrt{3}}{2} i$.) Thus $p$ is bounded by the lemma, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a prime $p$, a subset $S$ of residues modulo $p$ is called a sum-free multiplicative subgroup of $\mathbb{F}_{p}$ if - there is a nonzero residue $\alpha$ modulo $p$ such that $S=\left\{1, \alpha^{1}, \alpha^{2}, \ldots\right\}$ (all considered $\bmod p$ ), and - there are no $a, b, c \in S$ (not necessarily distinct) such that $a+b \equiv c(\bmod p)$. Prove that for every integer $N$, there is a prime $p$ and a sum-free multiplicative subgroup $S$ of $\mathbb{F}_{p}$ such that $|S| \geq N$.
|
We first prove the following general lemma. ## Lemma If $f, g \in \mathbb{Z}[X]$ are relatively prime nonconstant polynomials, then for sufficiently large primes $p$, they have no common root modulo $p$. $$ a(X) f(X)+b(X) g(X) \equiv c $$ So, plugging in $X=r$ we get $p \mid c$, so the set of permissible primes $p$ is finite. With this we can give the construction. ## Claim - Suppose that - $n$ is a positive integer with $n \not \equiv 0(\bmod 3)$; - $p$ is a prime which is $1 \bmod n$; and - $\alpha$ is a primitive $n^{\prime}$ th root of unity modulo $p$. Then $|S|=n$ and, if $p$ is sufficiently large in $n$, is also sum-free. $$ 1+\alpha^{k} \equiv \alpha^{m} \quad(\bmod p) $$ for some integers $k, m \in \mathbb{Z}$. This means $(X+1)^{n}-1$ and $X^{n}-1$ have common root $X=\alpha^{k}$. But $$ \underset{\mathbb{Z}[x]}{\operatorname{gcd}}\left((X+1)^{n}-1, X^{n}-1\right)=1 \quad \forall n \not \equiv 0 \quad(\bmod 3) $$ because when $3 \nmid n$ the two polynomials have no common complex roots. (Indeed, if $|\omega|=|1+\omega|=1$ then $\omega=-\frac{1}{2} \pm \frac{\sqrt{3}}{2} i$.) Thus $p$ is bounded by the lemma, as desired.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
00bd68ee-569b-5b37-a644-04c6ee3c6427
| 606,239 |
Let $A B C$ be a scalene triangle with incenter $I$ whose incircle is tangent to $\overline{B C}$, $\overline{C A}, \overline{A B}$ at $D, E, F$, respectively. Denote by $M$ the midpoint of $\overline{B C}$ and let $P$ be a point in the interior of $\triangle A B C$ so that $M D=M P$ and $\angle P A B=\angle P A C$. Let $Q$ be a point on the incircle such that $\angle A Q D=90^{\circ}$. Prove that either $\angle P Q E=90^{\circ}$ or $\angle P Q F=90^{\circ}$.
|
 First, we claim that $D, P, E$ are collinear. Let $N$ be the midpoint of $\overline{A B}$. It is well-known that the three lines $M N, D E, A I$ are concurrent at a point (see for example problem 6 of USAJMO 2014). Let $P^{\prime}$ be this intersection point, noting that $P^{\prime}$ actually lies on segment $D E$. Then $P^{\prime}$ lies inside $\triangle A B C$ and moreover $$ \triangle D P^{\prime} M \sim \triangle D E C $$ so $M P^{\prime}=M D$. Hence $P^{\prime}=P$, proving the claim. Let $S$ be the point diametrically opposite $D$ on the incircle, which is also the second intersection of $\overline{A Q}$ with the incircle. Let $T=\overline{A Q} \cap \overline{B C}$. Then $T$ is the contact point of the $A$-excircle; consequently, $$ M D=M P=M T $$ and we obtain a circle with diameter $\overline{D T}$. Since $\angle D Q T=\angle D Q S=90^{\circ}$ we have $Q$ on this circle as well. As $\overline{S D}$ is tangent to the circle with diameter $\overline{D T}$, we obtain $$ \angle P Q D=\angle S D P=\angle S D E=\angle S Q E . $$ Since $\angle D Q S=90^{\circ}, \angle P Q E=90^{\circ}$ too. 【 Solution using spiral similarity. We will ignore for now the point $P$. As before define $S, T$ and note $\overline{A Q S T}$ collinear, as well as $D P Q T$ cyclic on circle $\omega$ with diameter $\overline{D T}$. Let $\tau$ be the spiral similarity at $Q$ sending $\omega$ to the incircle. We have $\tau(T)=D$, $\tau(D)=S, \tau(Q)=Q$. Now $$ I=\overline{D D} \cap \overline{Q Q} \Longrightarrow \tau(I)=\overline{S S} \cap \overline{Q Q} $$ and hence we conclude $\tau(I)$ is the pole of $\overline{A S Q T}$ with respect to the incircle, which lies on line $E F$. Then since $\overline{A I} \perp \overline{E F}$ too, we deduce $\tau$ sends line $A I$ to line $E F$, hence $\tau(P)$ must be either $E$ or $F$ as desired. 【 Authorship comments. Written April 2014. I found this problem while playing with GeoGebra. Specifically, I started by drawing in the points $A, B, C, I, D, M, T$, common points. I decided to add in the circle with diameter $D T$, because of the synergy it had with the rest of the picture. After a while of playing around, I intersected ray $A I$ with the circle to get $P$, and was surprised to find that $D, P, E$ were collinear, which I thought was impossible since the setup should have been symmetric. On further reflection, I realized it was because $A I$ intersected the circle twice, and set about trying to prove this. I noticed the relation $\angle P Q E=90^{\circ}$ in my attempts to prove the result, even though this ended up being a corollary rather than a useful lemma.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with incenter $I$ whose incircle is tangent to $\overline{B C}$, $\overline{C A}, \overline{A B}$ at $D, E, F$, respectively. Denote by $M$ the midpoint of $\overline{B C}$ and let $P$ be a point in the interior of $\triangle A B C$ so that $M D=M P$ and $\angle P A B=\angle P A C$. Let $Q$ be a point on the incircle such that $\angle A Q D=90^{\circ}$. Prove that either $\angle P Q E=90^{\circ}$ or $\angle P Q F=90^{\circ}$.
|
 First, we claim that $D, P, E$ are collinear. Let $N$ be the midpoint of $\overline{A B}$. It is well-known that the three lines $M N, D E, A I$ are concurrent at a point (see for example problem 6 of USAJMO 2014). Let $P^{\prime}$ be this intersection point, noting that $P^{\prime}$ actually lies on segment $D E$. Then $P^{\prime}$ lies inside $\triangle A B C$ and moreover $$ \triangle D P^{\prime} M \sim \triangle D E C $$ so $M P^{\prime}=M D$. Hence $P^{\prime}=P$, proving the claim. Let $S$ be the point diametrically opposite $D$ on the incircle, which is also the second intersection of $\overline{A Q}$ with the incircle. Let $T=\overline{A Q} \cap \overline{B C}$. Then $T$ is the contact point of the $A$-excircle; consequently, $$ M D=M P=M T $$ and we obtain a circle with diameter $\overline{D T}$. Since $\angle D Q T=\angle D Q S=90^{\circ}$ we have $Q$ on this circle as well. As $\overline{S D}$ is tangent to the circle with diameter $\overline{D T}$, we obtain $$ \angle P Q D=\angle S D P=\angle S D E=\angle S Q E . $$ Since $\angle D Q S=90^{\circ}, \angle P Q E=90^{\circ}$ too. 【 Solution using spiral similarity. We will ignore for now the point $P$. As before define $S, T$ and note $\overline{A Q S T}$ collinear, as well as $D P Q T$ cyclic on circle $\omega$ with diameter $\overline{D T}$. Let $\tau$ be the spiral similarity at $Q$ sending $\omega$ to the incircle. We have $\tau(T)=D$, $\tau(D)=S, \tau(Q)=Q$. Now $$ I=\overline{D D} \cap \overline{Q Q} \Longrightarrow \tau(I)=\overline{S S} \cap \overline{Q Q} $$ and hence we conclude $\tau(I)$ is the pole of $\overline{A S Q T}$ with respect to the incircle, which lies on line $E F$. Then since $\overline{A I} \perp \overline{E F}$ too, we deduce $\tau$ sends line $A I$ to line $E F$, hence $\tau(P)$ must be either $E$ or $F$ as desired. 【 Authorship comments. Written April 2014. I found this problem while playing with GeoGebra. Specifically, I started by drawing in the points $A, B, C, I, D, M, T$, common points. I decided to add in the circle with diameter $D T$, because of the synergy it had with the rest of the picture. After a while of playing around, I intersected ray $A I$ with the circle to get $P$, and was surprised to find that $D, P, E$ were collinear, which I thought was impossible since the setup should have been symmetric. On further reflection, I realized it was because $A I$ intersected the circle twice, and set about trying to prove this. I noticed the relation $\angle P Q E=90^{\circ}$ in my attempts to prove the result, even though this ended up being a corollary rather than a useful lemma.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
7f0ee4da-b647-5729-b53a-287b1a07852d
| 606,245 |
Prove that for every positive integer $n$, there exists a set $S$ of $n$ positive integers such that for any two distinct $a, b \in S, a-b$ divides $a$ and $b$ but none of the other elements of $S$.
|
The idea is to look for a sequence $d_{1}, \ldots, d_{n-1}$ of "differences" such that the following two conditions hold. Let $s_{i}=d_{1}+\cdots+d_{i-1}$, and $t_{i, j}=d_{i}+\cdots+d_{j-1}$ for $i \leq j$. (i) No two of the $t_{i, j}$ divide each other. (ii) There exists an integer $a$ satisfying the CRT equivalences $$ a \equiv-s_{i} \quad\left(\bmod t_{i, j}\right) \quad \forall i \leq j $$ Then the sequence $a+s_{1}, a+s_{2}, \ldots, a+s_{n}$ will work. For example, when $n=3$ we can take $\left(d_{1}, d_{2}\right)=(2,3)$ giving  because the only conditions we need satisfy are $$ \begin{aligned} a & \equiv 0 \quad(\bmod 2) \\ a & \equiv 0 \quad(\bmod 5) \\ a & \equiv-2 \quad(\bmod 3) . \end{aligned} $$ But with this setup we can just construct the $d_{i}$ inductively. To go from $n$ to $n+1$, take a $d_{1}, \ldots, d_{n-1}$ and let $p$ be a prime not dividing any of the $d_{i}$. Moreover, let $M$ be a multiple of $\prod_{i \leq j} t_{i, j}$ coprime to $p$. Then we claim that $d_{1} M, d_{2} M, \ldots, d_{n-1} M, p$ is such a difference sequence. For example, the previous example extends as follows with $M=300$ and $p=7$.  The new numbers $p, p+M t_{n-1, n}, p+M t_{n-2, n}, \ldots$ are all relatively prime to everything else. Hence (i) still holds. To see that (ii) still holds, just note that we can still get a family of solutions for the first $n$ terms, and then the last $(n+1)$ st term can be made to work by Chinese Remainder Theorem since all the new $p+M t_{n-2, n}$ are coprime to everything.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every positive integer $n$, there exists a set $S$ of $n$ positive integers such that for any two distinct $a, b \in S, a-b$ divides $a$ and $b$ but none of the other elements of $S$.
|
The idea is to look for a sequence $d_{1}, \ldots, d_{n-1}$ of "differences" such that the following two conditions hold. Let $s_{i}=d_{1}+\cdots+d_{i-1}$, and $t_{i, j}=d_{i}+\cdots+d_{j-1}$ for $i \leq j$. (i) No two of the $t_{i, j}$ divide each other. (ii) There exists an integer $a$ satisfying the CRT equivalences $$ a \equiv-s_{i} \quad\left(\bmod t_{i, j}\right) \quad \forall i \leq j $$ Then the sequence $a+s_{1}, a+s_{2}, \ldots, a+s_{n}$ will work. For example, when $n=3$ we can take $\left(d_{1}, d_{2}\right)=(2,3)$ giving  because the only conditions we need satisfy are $$ \begin{aligned} a & \equiv 0 \quad(\bmod 2) \\ a & \equiv 0 \quad(\bmod 5) \\ a & \equiv-2 \quad(\bmod 3) . \end{aligned} $$ But with this setup we can just construct the $d_{i}$ inductively. To go from $n$ to $n+1$, take a $d_{1}, \ldots, d_{n-1}$ and let $p$ be a prime not dividing any of the $d_{i}$. Moreover, let $M$ be a multiple of $\prod_{i \leq j} t_{i, j}$ coprime to $p$. Then we claim that $d_{1} M, d_{2} M, \ldots, d_{n-1} M, p$ is such a difference sequence. For example, the previous example extends as follows with $M=300$ and $p=7$.  The new numbers $p, p+M t_{n-1, n}, p+M t_{n-2, n}, \ldots$ are all relatively prime to everything else. Hence (i) still holds. To see that (ii) still holds, just note that we can still get a family of solutions for the first $n$ terms, and then the last $(n+1)$ st term can be made to work by Chinese Remainder Theorem since all the new $p+M t_{n-2, n}$ are coprime to everything.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
efdaf453-a6ad-5f6f-b59e-6beb8a097638
| 246,450 |
Let $f: \mathbb{Q} \rightarrow \mathbb{Q}$ be a function such that for any $x, y \in \mathbb{Q}$, the number $f(x+y)-$ $f(x)-f(y)$ is an integer. Decide whether there must exist a constant $c$ such that $f(x)-c x$ is an integer for every rational number $x$.
|
No, such a constant need not exist. $$ \begin{aligned} & 2 x_{1}=x_{0} \\ & 2 x_{2}=x_{1}+1 \\ & 2 x_{3}=x_{2} \\ & 2 x_{4}=x_{3}+1 \\ & 2 x_{5}=x_{4} \\ & 2 x_{6}=x_{5}+1 \end{aligned} $$ Set $f\left(2^{-k}\right)=x_{k}$ and $f\left(2^{k}\right)=2^{k}$ for $k=0,1, \ldots$ Then, let $$ f\left(a \cdot 2^{k}+\frac{b}{c}\right)=a f\left(2^{k}\right)+\frac{b}{c} $$ for odd integers $a, b, c$. One can verify this works. $$ f\left(\frac{p}{q}\right)=\frac{p}{q}(1!+2!+\cdots+q!) . $$ Remark. Silly note: despite appearances, $f(x)=\lfloor x\rfloor$ is not a counterexample since one can take $c=0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f: \mathbb{Q} \rightarrow \mathbb{Q}$ be a function such that for any $x, y \in \mathbb{Q}$, the number $f(x+y)-$ $f(x)-f(y)$ is an integer. Decide whether there must exist a constant $c$ such that $f(x)-c x$ is an integer for every rational number $x$.
|
No, such a constant need not exist. $$ \begin{aligned} & 2 x_{1}=x_{0} \\ & 2 x_{2}=x_{1}+1 \\ & 2 x_{3}=x_{2} \\ & 2 x_{4}=x_{3}+1 \\ & 2 x_{5}=x_{4} \\ & 2 x_{6}=x_{5}+1 \end{aligned} $$ Set $f\left(2^{-k}\right)=x_{k}$ and $f\left(2^{k}\right)=2^{k}$ for $k=0,1, \ldots$ Then, let $$ f\left(a \cdot 2^{k}+\frac{b}{c}\right)=a f\left(2^{k}\right)+\frac{b}{c} $$ for odd integers $a, b, c$. One can verify this works. $$ f\left(\frac{p}{q}\right)=\frac{p}{q}(1!+2!+\cdots+q!) . $$ Remark. Silly note: despite appearances, $f(x)=\lfloor x\rfloor$ is not a counterexample since one can take $c=0$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
97451845-a819-5ec5-847b-fa3f8fa19560
| 246,469 |
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 【 First solution by barycentric coordinates (Evan Chen). Let $A X$ meet $M_{b} M_{c}$ at $D$, and let $X$ reflected over $M_{b} M_{c}^{\prime}$ 's midpoint be $X^{\prime}$. Let $Y^{\prime}, Z^{\prime}, E, F$ be similarly defined. 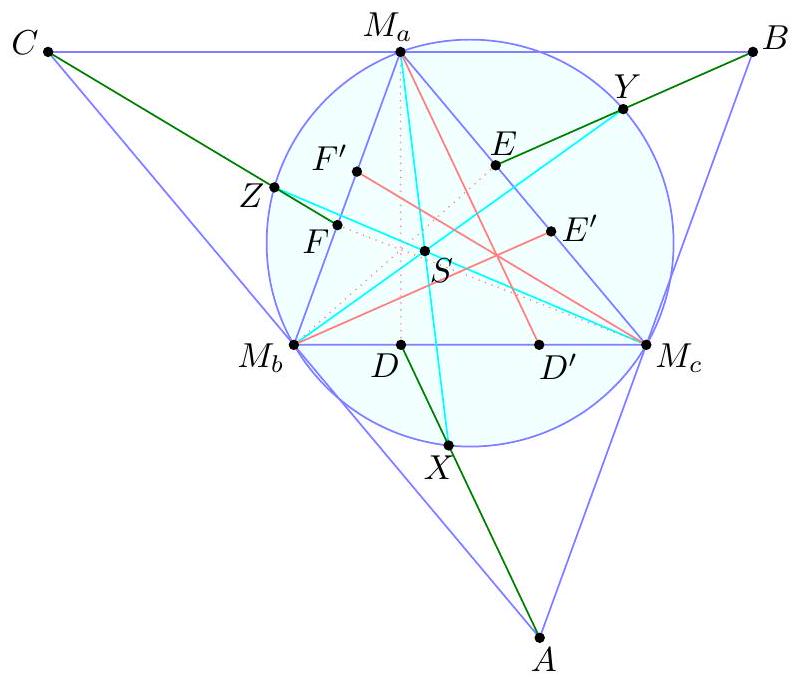 By Cevian Nest Theorem it suffices to prove that $M_{a} D, M_{b} E, M_{c} F$ are concurrent. Taking the isotomic conjugate and recalling that $M_{a} M_{b} A M_{c}$ is a parallelogram, we see that it suffices to prove $M_{a} X^{\prime}, M_{b} Y^{\prime}, M_{c} Z^{\prime}$ are concurrent. We now use barycentric coordinates on $\triangle M_{a} M_{b} M_{c}$. Let $$ S=\left(a^{2} S_{A}+t: b^{2} S_{B}+t: c^{2} S_{C}+t\right) $$ (possibly $t=\infty$ if $S$ is the centroid). Let $v=b^{2} S_{B}+t, w=c^{2} S_{C}+t$. Hence $$ X=\left(-a^{2} v w:\left(b^{2} w+c^{2} v\right) v:\left(b^{2} w+c^{2} v\right) w\right) $$ Consequently, $$ X^{\prime}=\left(a^{2} v w:-a^{2} v w+\left(b^{2} w+c^{2} v\right) w:-a^{2} v w+\left(b^{2} w+c^{2} v\right) v\right) $$ We can compute $$ b^{2} w+c^{2} v=(b c)^{2}\left(S_{B}+S_{C}\right)+\left(b^{2}+c^{2}\right) t=(a b c)^{2}+\left(b^{2}+c^{2}\right) t $$ Thus $$ -a^{2} v+b^{2} w+c^{2} v=\left(b^{2}+c^{2}\right) t+(a b c)^{2}-(a b)^{2} S_{B}-a^{2} t=S_{A}\left((a b)^{2}+t\right) $$ Finally $$ X^{\prime}=\left(a^{2} v w: S_{A}\left(c^{2} S_{C}+t\right)\left((a b)^{2}+2 t\right): S_{A}\left(b^{2} S_{B}+t\right)\left((a c)^{2}+2 t\right)\right) $$ and from this it's evident that $A X^{\prime}, B Y^{\prime}, C Z^{\prime}$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 【 First solution by barycentric coordinates (Evan Chen). Let $A X$ meet $M_{b} M_{c}$ at $D$, and let $X$ reflected over $M_{b} M_{c}^{\prime}$ 's midpoint be $X^{\prime}$. Let $Y^{\prime}, Z^{\prime}, E, F$ be similarly defined.  By Cevian Nest Theorem it suffices to prove that $M_{a} D, M_{b} E, M_{c} F$ are concurrent. Taking the isotomic conjugate and recalling that $M_{a} M_{b} A M_{c}$ is a parallelogram, we see that it suffices to prove $M_{a} X^{\prime}, M_{b} Y^{\prime}, M_{c} Z^{\prime}$ are concurrent. We now use barycentric coordinates on $\triangle M_{a} M_{b} M_{c}$. Let $$ S=\left(a^{2} S_{A}+t: b^{2} S_{B}+t: c^{2} S_{C}+t\right) $$ (possibly $t=\infty$ if $S$ is the centroid). Let $v=b^{2} S_{B}+t, w=c^{2} S_{C}+t$. Hence $$ X=\left(-a^{2} v w:\left(b^{2} w+c^{2} v\right) v:\left(b^{2} w+c^{2} v\right) w\right) $$ Consequently, $$ X^{\prime}=\left(a^{2} v w:-a^{2} v w+\left(b^{2} w+c^{2} v\right) w:-a^{2} v w+\left(b^{2} w+c^{2} v\right) v\right) $$ We can compute $$ b^{2} w+c^{2} v=(b c)^{2}\left(S_{B}+S_{C}\right)+\left(b^{2}+c^{2}\right) t=(a b c)^{2}+\left(b^{2}+c^{2}\right) t $$ Thus $$ -a^{2} v+b^{2} w+c^{2} v=\left(b^{2}+c^{2}\right) t+(a b c)^{2}-(a b)^{2} S_{B}-a^{2} t=S_{A}\left((a b)^{2}+t\right) $$ Finally $$ X^{\prime}=\left(a^{2} v w: S_{A}\left(c^{2} S_{C}+t\right)\left((a b)^{2}+2 t\right): S_{A}\left(b^{2} S_{B}+t\right)\left((a c)^{2}+2 t\right)\right) $$ and from this it's evident that $A X^{\prime}, B Y^{\prime}, C Z^{\prime}$ are concurrent.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4acb25c-b95d-5413-b21b-519897d53696
| 246,488 |
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. \ Second solution by moving points (Anant Mudgal). Let $H_{a}, H_{b}, H_{c}$ be feet of altitudes, and let $\gamma$ denote the nine-point circle. The main claim is that: Claim - Lines $X H_{a}, Y H_{b}, Z H_{c}$ are concurrent, $$ \begin{aligned} & \ell \rightarrow \gamma \rightarrow \ell \\ & S \mapsto X \mapsto S_{a}:=\ell \cap \overline{H_{a} X} \end{aligned} $$ is projective, because it consists of two perspectivities. So we want the analogous maps $S \mapsto S_{b}, S \mapsto S_{c}$ to coincide. For this it suffices to check three positions of $S$; since you're such a good customer here are four. - If $S$ is the orthocenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the circumcenter of $\triangle A B C$ ) then $S_{a}$ coincides with the circumcenter of $M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C)$. By symmetry $S_{b}$ and $S_{c}$ are too. - If $S$ is the circumcenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C$ ) then $S_{a}$ coincides with the de Longchamps point of $\triangle M_{a} M_{b} M_{c}$ (equivalently orthocenter of $\triangle A B C)$. By symmetry $S_{b}$ and $S_{c}$ are too. - If $S$ is either of the intersections of the Euler line with $\gamma$, then $S=S_{a}=S_{b}=S_{c}$ (as $S=X=Y=Z$ ). 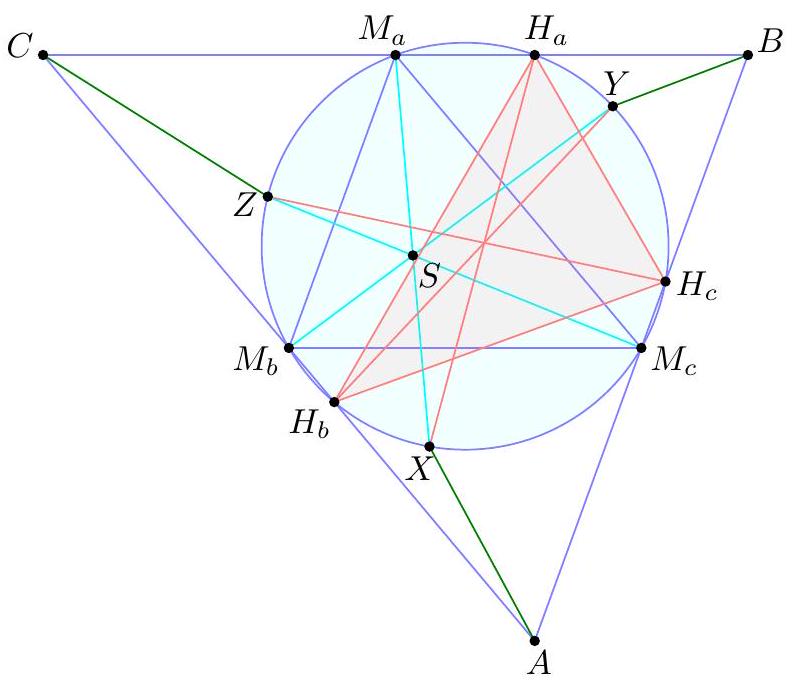 We now use Trig Ceva to carry over the concurrence. By sine law, $$ \frac{\sin \angle M_{c} A X}{\sin \angle A M_{c} X}=\frac{M_{c} X}{A X} $$ and a similar relation for $M_{b}$ gives that $$ \frac{\sin \angle M_{c} A X}{\sin \angle M_{b} A X}=\frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \cdot \frac{M_{c} X}{M_{b} X}=\frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \cdot \frac{\sin \angle X M_{a} M_{c}}{\sin \angle X M_{a} M_{b}} . $$ Thus multiplying cyclically gives $$ \prod_{\text {cyc }} \frac{\sin \angle M_{c} A X}{\sin \angle M_{b} A X}=\prod_{\text {cyc }} \frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \prod_{\text {cyc }} \frac{\sin \angle X M_{a} M_{c}}{\sin \angle X M_{a} M_{b}} . $$ The latter product on the right-hand side equals 1 by Trig Ceva on $\triangle M_{a} M_{b} M_{c}$ with cevians $\overline{M_{a} X}, \overline{M_{b} Y}, \overline{M_{c} Z}$. The former product also equals 1 by Trig Ceva for the concurrence in the previous claim (and the fact that $\angle A M_{c} X=\angle H_{c} H_{a} X$ ). Hence the left-hand side equals 1 , implying the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. \ Second solution by moving points (Anant Mudgal). Let $H_{a}, H_{b}, H_{c}$ be feet of altitudes, and let $\gamma$ denote the nine-point circle. The main claim is that: Claim - Lines $X H_{a}, Y H_{b}, Z H_{c}$ are concurrent, $$ \begin{aligned} & \ell \rightarrow \gamma \rightarrow \ell \\ & S \mapsto X \mapsto S_{a}:=\ell \cap \overline{H_{a} X} \end{aligned} $$ is projective, because it consists of two perspectivities. So we want the analogous maps $S \mapsto S_{b}, S \mapsto S_{c}$ to coincide. For this it suffices to check three positions of $S$; since you're such a good customer here are four. - If $S$ is the orthocenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the circumcenter of $\triangle A B C$ ) then $S_{a}$ coincides with the circumcenter of $M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C)$. By symmetry $S_{b}$ and $S_{c}$ are too. - If $S$ is the circumcenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C$ ) then $S_{a}$ coincides with the de Longchamps point of $\triangle M_{a} M_{b} M_{c}$ (equivalently orthocenter of $\triangle A B C)$. By symmetry $S_{b}$ and $S_{c}$ are too. - If $S$ is either of the intersections of the Euler line with $\gamma$, then $S=S_{a}=S_{b}=S_{c}$ (as $S=X=Y=Z$ ).  We now use Trig Ceva to carry over the concurrence. By sine law, $$ \frac{\sin \angle M_{c} A X}{\sin \angle A M_{c} X}=\frac{M_{c} X}{A X} $$ and a similar relation for $M_{b}$ gives that $$ \frac{\sin \angle M_{c} A X}{\sin \angle M_{b} A X}=\frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \cdot \frac{M_{c} X}{M_{b} X}=\frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \cdot \frac{\sin \angle X M_{a} M_{c}}{\sin \angle X M_{a} M_{b}} . $$ Thus multiplying cyclically gives $$ \prod_{\text {cyc }} \frac{\sin \angle M_{c} A X}{\sin \angle M_{b} A X}=\prod_{\text {cyc }} \frac{\sin \angle A M_{c} X}{\sin \angle A M_{b} X} \prod_{\text {cyc }} \frac{\sin \angle X M_{a} M_{c}}{\sin \angle X M_{a} M_{b}} . $$ The latter product on the right-hand side equals 1 by Trig Ceva on $\triangle M_{a} M_{b} M_{c}$ with cevians $\overline{M_{a} X}, \overline{M_{b} Y}, \overline{M_{c} Z}$. The former product also equals 1 by Trig Ceva for the concurrence in the previous claim (and the fact that $\angle A M_{c} X=\angle H_{c} H_{a} X$ ). Hence the left-hand side equals 1 , implying the result.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4acb25c-b95d-5413-b21b-519897d53696
| 246,488 |
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 『 Third solution by moving points (Gopal Goel). In this solution, we will instead use barycentric coordinates with resect to $\triangle A B C$ to bound the degrees suitably, and then verify for seven distinct choices of $S$. We let $R$ denote the radius of $\triangle A B C$, and $N$ the nine-point center. First, imagine solving for $X$ in the following way. Suppose $\vec{X}=\left(1-t_{a}\right) \vec{M}_{a}+t_{a} \vec{S}$. Then, using the dot product (with $|\vec{v}|^{2}=\vec{v} \cdot \vec{v}$ in general) $$ \begin{aligned} \frac{1}{4} R^{2} & =|\vec{X}-\vec{N}|^{2} \\ & =\left|t_{a}\left(\vec{S}-\vec{M}_{a}\right)+\vec{M}_{a}-\vec{N}\right|^{2} \\ & =\left|t_{a}\left(\vec{S}-\vec{M}_{a}\right)\right|^{2}+2 t_{a}\left(\vec{S}-\vec{M}_{a}\right) \cdot\left(\vec{M}_{a}-\vec{N}\right)+\left|\vec{M}_{a}-\vec{N}\right|^{2} \\ & =t_{a}^{2}\left|\left(\vec{S}-\vec{M}_{a}\right)\right|^{2}+2 t_{a}\left(\vec{S}-\vec{M}_{a}\right) \cdot\left(\vec{M}_{a}-\vec{N}\right)+\frac{1}{4} R^{2} \end{aligned} $$ Since $t_{a} \neq 0$ we may solve to obtain $$ t_{a}=-\frac{2\left(\vec{M}_{a}-\vec{N}\right) \cdot\left(\vec{S}-\vec{M}_{a}\right)}{\left|\vec{S}-\vec{M}_{a}\right|^{2}} $$ Now imagine $S$ varies along the Euler line, meaning there should exist linear functions $\alpha, \beta, \gamma: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ S=(\alpha(s), \beta(s), \gamma(s)) \quad s \in \mathbb{R} $$ with $\alpha(s)+\beta(s)+\gamma(s)=1$. Thus $t_{a}=\frac{f_{a}}{g_{a}}=\frac{f_{a}(s)}{g_{a}(s)}$ is the quotient of a linear function $f_{a}(s)$ and a quadratic function $g_{a}(s)$. So we may write: $$ \begin{aligned} X & =\left(1-t_{a}\right)\left(0, \frac{1}{2}, \frac{1}{2}\right)+t_{a}(\alpha, \beta, \gamma) \\ & =\left(t_{a} \alpha, \frac{1}{2}\left(1-t_{a}\right)+t_{a} \beta, \frac{1}{2}\left(1-t_{a}\right)+t_{a} \gamma\right) \end{aligned} $$ $$ =\left(2 f_{a} \alpha: g_{a}-f_{a}+2 f_{a} \beta: g_{a}-f_{a}+2 f_{a} \gamma\right) . $$ Thus the coordinates of $X$ are quadratic polynomials in $s$ when written in this way. In a similar way, the coordinates of $Y$ and $Z$ should be quadratic polynomials in $s$. The Ceva concurrence condition $$ \prod_{\text {cyc }} \frac{g_{a}-f_{a}+2 f_{a} \beta}{g_{a}-f_{a}+2 f_{a} \gamma}=1 $$ is thus a polynomial in $s$ of degree at most six. Our goal is to verify it is identically zero, thus it suffices to check seven positions of $S$. - If $S$ is the circumcenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C$ ) then $\overline{A X}, \overline{B Y}, \overline{C Z}$ are altitudes of $\triangle A B C$. - If $S$ is the centroid of $\triangle M_{a} M_{b} M_{c}$ (equivalently the centroid of $\triangle A B C$ ), then $\overline{A X}$, $\overline{B Y}, \overline{C Z}$ are medians of $\triangle A B C$. - If $S$ is either of the intersections of the Euler line with $\gamma$, then $S=X=Y=Z$ and all cevians concur at $S$. - If $S$ lies on the $\overline{M_{a} M_{b}}$, then $Y=M_{a}, X=M_{c}$, and thus $\overline{A X} \cap \overline{B Y}=C$, which is of course concurrent with $\overline{C Z}$ (regardless of $Z$ ). Similarly if $S$ lies on the other sides of $\triangle M_{a} M_{b} M_{c}$. Thus we are also done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 『 Third solution by moving points (Gopal Goel). In this solution, we will instead use barycentric coordinates with resect to $\triangle A B C$ to bound the degrees suitably, and then verify for seven distinct choices of $S$. We let $R$ denote the radius of $\triangle A B C$, and $N$ the nine-point center. First, imagine solving for $X$ in the following way. Suppose $\vec{X}=\left(1-t_{a}\right) \vec{M}_{a}+t_{a} \vec{S}$. Then, using the dot product (with $|\vec{v}|^{2}=\vec{v} \cdot \vec{v}$ in general) $$ \begin{aligned} \frac{1}{4} R^{2} & =|\vec{X}-\vec{N}|^{2} \\ & =\left|t_{a}\left(\vec{S}-\vec{M}_{a}\right)+\vec{M}_{a}-\vec{N}\right|^{2} \\ & =\left|t_{a}\left(\vec{S}-\vec{M}_{a}\right)\right|^{2}+2 t_{a}\left(\vec{S}-\vec{M}_{a}\right) \cdot\left(\vec{M}_{a}-\vec{N}\right)+\left|\vec{M}_{a}-\vec{N}\right|^{2} \\ & =t_{a}^{2}\left|\left(\vec{S}-\vec{M}_{a}\right)\right|^{2}+2 t_{a}\left(\vec{S}-\vec{M}_{a}\right) \cdot\left(\vec{M}_{a}-\vec{N}\right)+\frac{1}{4} R^{2} \end{aligned} $$ Since $t_{a} \neq 0$ we may solve to obtain $$ t_{a}=-\frac{2\left(\vec{M}_{a}-\vec{N}\right) \cdot\left(\vec{S}-\vec{M}_{a}\right)}{\left|\vec{S}-\vec{M}_{a}\right|^{2}} $$ Now imagine $S$ varies along the Euler line, meaning there should exist linear functions $\alpha, \beta, \gamma: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ S=(\alpha(s), \beta(s), \gamma(s)) \quad s \in \mathbb{R} $$ with $\alpha(s)+\beta(s)+\gamma(s)=1$. Thus $t_{a}=\frac{f_{a}}{g_{a}}=\frac{f_{a}(s)}{g_{a}(s)}$ is the quotient of a linear function $f_{a}(s)$ and a quadratic function $g_{a}(s)$. So we may write: $$ \begin{aligned} X & =\left(1-t_{a}\right)\left(0, \frac{1}{2}, \frac{1}{2}\right)+t_{a}(\alpha, \beta, \gamma) \\ & =\left(t_{a} \alpha, \frac{1}{2}\left(1-t_{a}\right)+t_{a} \beta, \frac{1}{2}\left(1-t_{a}\right)+t_{a} \gamma\right) \end{aligned} $$ $$ =\left(2 f_{a} \alpha: g_{a}-f_{a}+2 f_{a} \beta: g_{a}-f_{a}+2 f_{a} \gamma\right) . $$ Thus the coordinates of $X$ are quadratic polynomials in $s$ when written in this way. In a similar way, the coordinates of $Y$ and $Z$ should be quadratic polynomials in $s$. The Ceva concurrence condition $$ \prod_{\text {cyc }} \frac{g_{a}-f_{a}+2 f_{a} \beta}{g_{a}-f_{a}+2 f_{a} \gamma}=1 $$ is thus a polynomial in $s$ of degree at most six. Our goal is to verify it is identically zero, thus it suffices to check seven positions of $S$. - If $S$ is the circumcenter of $\triangle M_{a} M_{b} M_{c}$ (equivalently the nine-point center of $\triangle A B C$ ) then $\overline{A X}, \overline{B Y}, \overline{C Z}$ are altitudes of $\triangle A B C$. - If $S$ is the centroid of $\triangle M_{a} M_{b} M_{c}$ (equivalently the centroid of $\triangle A B C$ ), then $\overline{A X}$, $\overline{B Y}, \overline{C Z}$ are medians of $\triangle A B C$. - If $S$ is either of the intersections of the Euler line with $\gamma$, then $S=X=Y=Z$ and all cevians concur at $S$. - If $S$ lies on the $\overline{M_{a} M_{b}}$, then $Y=M_{a}, X=M_{c}$, and thus $\overline{A X} \cap \overline{B Y}=C$, which is of course concurrent with $\overline{C Z}$ (regardless of $Z$ ). Similarly if $S$ lies on the other sides of $\triangle M_{a} M_{b} M_{c}$. Thus we are also done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4acb25c-b95d-5413-b21b-519897d53696
| 246,488 |
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 【 Fourth solution using Pascal (official one). We give a different proof of the claim that $\overline{X H_{a}}, \overline{Y H_{b}}, \overline{Z H_{c}}$ are concurrent (and then proceed as in the end of the second solution). Let $H$ denote the orthocenter, $N$ the nine-point center, and moreover let $N_{a}, N_{b}, N_{c}$ denote the midpoints of $\overline{A H}, \overline{B H}, \overline{C H}$, which also lie on the nine-point circle (and are the antipodes of $M_{a}, M_{b}, M_{c}$ ). - By Pascal's theorem on $M_{b} N_{b} H_{b} M_{c} N_{c} H_{c}$, the point $P=\overline{M_{c} H_{b}} \cap \overline{M_{b} H_{c}}$ is collinear with $N=\overline{M_{b} N_{b}} \cap \overline{M_{c} N_{c}}$, and $H=\overline{N_{b} H_{b}} \cap \overline{N_{c} H_{c}}$. So $P$ lies on the Euler line. - By Pascal's theorem on $M_{b} Y H_{b} M_{c} Z H_{c}$, the point $\overline{Y H_{b}} \cap \overline{Z H_{c}}$ is collinear with $S=\overline{M_{b} Y} \cap \overline{M_{c} Z}$ and $P=\overline{M_{b} H_{c}} \cap \overline{M_{c} H_{b}}$. Hence $Y H_{b}$ and $Z H_{c}$ meet on the Euler line, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a non-equilateral triangle and let $M_{a}, M_{b}, M_{c}$ be the midpoints of the sides $B C, C A, A B$, respectively. Let $S$ be a point lying on the Euler line. Denote by $X, Y, Z$ the second intersections of $M_{a} S, M_{b} S, M_{c} S$ with the nine-point circle. Prove that $A X, B Y, C Z$ are concurrent.
|
We assume now and forever that $A B C$ is scalene since the problem follows by symmetry in the isosceles case. We present four solutions. 【 Fourth solution using Pascal (official one). We give a different proof of the claim that $\overline{X H_{a}}, \overline{Y H_{b}}, \overline{Z H_{c}}$ are concurrent (and then proceed as in the end of the second solution). Let $H$ denote the orthocenter, $N$ the nine-point center, and moreover let $N_{a}, N_{b}, N_{c}$ denote the midpoints of $\overline{A H}, \overline{B H}, \overline{C H}$, which also lie on the nine-point circle (and are the antipodes of $M_{a}, M_{b}, M_{c}$ ). - By Pascal's theorem on $M_{b} N_{b} H_{b} M_{c} N_{c} H_{c}$, the point $P=\overline{M_{c} H_{b}} \cap \overline{M_{b} H_{c}}$ is collinear with $N=\overline{M_{b} N_{b}} \cap \overline{M_{c} N_{c}}$, and $H=\overline{N_{b} H_{b}} \cap \overline{N_{c} H_{c}}$. So $P$ lies on the Euler line. - By Pascal's theorem on $M_{b} Y H_{b} M_{c} Z H_{c}$, the point $\overline{Y H_{b}} \cap \overline{Z H_{c}}$ is collinear with $S=\overline{M_{b} Y} \cap \overline{M_{c} Z}$ and $P=\overline{M_{b} H_{c}} \cap \overline{M_{c} H_{b}}$. Hence $Y H_{b}$ and $Z H_{c}$ meet on the Euler line, as needed.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4acb25c-b95d-5413-b21b-519897d53696
| 246,488 |
Let $A B C$ be a scalene triangle with circumcircle $\Omega$, and suppose the incircle of $A B C$ touches $B C$ at $D$. The angle bisector of $\angle A$ meets $B C$ and $\Omega$ at $K$ and $M$. The circumcircle of $\triangle D K M$ intersects the $A$-excircle at $S_{1}, S_{2}$, and $\Omega$ at $T \neq M$. Prove that line $A T$ passes through either $S_{1}$ or $S_{2}$.
|
【 First solution (angle chasing). Assume for simplicity $A B<A C$. Let $E$ be the contact point of the $A$-excircle on $B C$; also let ray $T D$ meet $\Omega$ again at $L$. From the fact that $\angle M T L=\angle M T D=180^{\circ}-\angle M K D$, we can deduce that $\angle M T L=\angle A C M$, meaning that $L$ is the reflection of $A$ across the perpendicular bisector $\ell$ of $B C$. If we reflect $T, D$, $L$ over $\ell$, we deduce $A, E$ and the reflection of $T$ across $\ell$ are collinear, which implies that $\angle B A T=\angle C A E$. Now, consider the reflection point $E$ across line $A I$, say $S$. Since ray $A I$ passes through the $A$-excenter, $S$ lies on the $A$-excircle. Since $\angle B A T=\angle C A E, S$ also lies on ray $A T$. But the circumcircles of triangles $D K M$ and $K M E$ are congruent (from $D M=E M$ ), so $S$ lies on the circumcircle of $\triangle D K M$ too. Hence $S$ is the desired intersection point. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with circumcircle $\Omega$, and suppose the incircle of $A B C$ touches $B C$ at $D$. The angle bisector of $\angle A$ meets $B C$ and $\Omega$ at $K$ and $M$. The circumcircle of $\triangle D K M$ intersects the $A$-excircle at $S_{1}, S_{2}$, and $\Omega$ at $T \neq M$. Prove that line $A T$ passes through either $S_{1}$ or $S_{2}$.
|
【 First solution (angle chasing). Assume for simplicity $A B<A C$. Let $E$ be the contact point of the $A$-excircle on $B C$; also let ray $T D$ meet $\Omega$ again at $L$. From the fact that $\angle M T L=\angle M T D=180^{\circ}-\angle M K D$, we can deduce that $\angle M T L=\angle A C M$, meaning that $L$ is the reflection of $A$ across the perpendicular bisector $\ell$ of $B C$. If we reflect $T, D$, $L$ over $\ell$, we deduce $A, E$ and the reflection of $T$ across $\ell$ are collinear, which implies that $\angle B A T=\angle C A E$. Now, consider the reflection point $E$ across line $A I$, say $S$. Since ray $A I$ passes through the $A$-excenter, $S$ lies on the $A$-excircle. Since $\angle B A T=\angle C A E, S$ also lies on ray $A T$. But the circumcircles of triangles $D K M$ and $K M E$ are congruent (from $D M=E M$ ), so $S$ lies on the circumcircle of $\triangle D K M$ too. Hence $S$ is the desired intersection point. 
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
dcf7ebc8-ee61-5531-8942-1009daac5003
| 246,508 |
Let $A B C$ be a scalene triangle with circumcircle $\Omega$, and suppose the incircle of $A B C$ touches $B C$ at $D$. The angle bisector of $\angle A$ meets $B C$ and $\Omega$ at $K$ and $M$. The circumcircle of $\triangle D K M$ intersects the $A$-excircle at $S_{1}, S_{2}$, and $\Omega$ at $T \neq M$. Prove that line $A T$ passes through either $S_{1}$ or $S_{2}$.
|
Second solution (advanced). It's known that $T$ is the touch-point of the $A$-mixtilinear incircle. Let $E$ be contact point of $A$-excircle on $B C$. Now the circumcircles of $\triangle D K M$ and $\triangle K M E$ are congruent, since $D M=M E$ and the angles at $K$ are supplementary. Let $S$ be the reflection of $E$ across line $K M$, which by the above the above comment lies on the circumcircle of $\triangle D K M$. Since $K M$ passes through the $A$-excenter, $S$ also lies on the $A$-excircle. But $S$ also lies on line $A T$, since lines $A T$ and $A E$ are isogonal (the mixtilinear cevian is isogonal to the Nagel line). Thus $S$ is the desired intersection point. 【 Authorship comments. This problem comes from an observation of mine: let $A B C$ be a triangle, let the $\angle A$ bisector meet $\overline{B C}$ and $(A B C)$ at $E$ and $M$. Let $W$ be the tangency point of the $A$-mixtilinear excircle with the circumcircle of $A B C$. Then $A$ Nagel line passed through a common intersection of the circumcircle of $\triangle M E W$ and the $A$-mixtilinear incircle. This problem is the inverted version of this observation.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with circumcircle $\Omega$, and suppose the incircle of $A B C$ touches $B C$ at $D$. The angle bisector of $\angle A$ meets $B C$ and $\Omega$ at $K$ and $M$. The circumcircle of $\triangle D K M$ intersects the $A$-excircle at $S_{1}, S_{2}$, and $\Omega$ at $T \neq M$. Prove that line $A T$ passes through either $S_{1}$ or $S_{2}$.
|
Second solution (advanced). It's known that $T$ is the touch-point of the $A$-mixtilinear incircle. Let $E$ be contact point of $A$-excircle on $B C$. Now the circumcircles of $\triangle D K M$ and $\triangle K M E$ are congruent, since $D M=M E$ and the angles at $K$ are supplementary. Let $S$ be the reflection of $E$ across line $K M$, which by the above the above comment lies on the circumcircle of $\triangle D K M$. Since $K M$ passes through the $A$-excenter, $S$ also lies on the $A$-excircle. But $S$ also lies on line $A T$, since lines $A T$ and $A E$ are isogonal (the mixtilinear cevian is isogonal to the Nagel line). Thus $S$ is the desired intersection point. 【 Authorship comments. This problem comes from an observation of mine: let $A B C$ be a triangle, let the $\angle A$ bisector meet $\overline{B C}$ and $(A B C)$ at $E$ and $M$. Let $W$ be the tangency point of the $A$-mixtilinear excircle with the circumcircle of $A B C$. Then $A$ Nagel line passed through a common intersection of the circumcircle of $\triangle M E W$ and the $A$-mixtilinear incircle. This problem is the inverted version of this observation.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
dcf7ebc8-ee61-5531-8942-1009daac5003
| 246,508 |
Let $p$ be a prime number. Let $\mathbb{F}_{p}$ denote the integers modulo $p$, and let $\mathbb{F}_{p}[x]$ be the set of polynomials with coefficients in $\mathbb{F}_{p}$. Define $\Psi: \mathbb{F}_{p}[x] \rightarrow \mathbb{F}_{p}[x]$ by $$ \Psi\left(\sum_{i=0}^{n} a_{i} x^{i}\right)=\sum_{i=0}^{n} a_{i} x^{x^{i}} . $$ Prove that for nonzero polynomials $F, G \in \mathbb{F}_{p}[x]$, $$ \Psi(\operatorname{gcd}(F, G))=\operatorname{gcd}(\Psi(F), \Psi(G)) $$
|
Observe that $\Psi$ is also a linear map of $\mathbb{F}_{p}$ vector spaces, and that $\Psi(x P)=\Psi(P)^{p}$ for any $P \in \mathbb{F}_{p}[x]$. (In particular, $\Psi(1)=x$, not 1 , take caution!) 『 First solution (Ankan Bhattacharya). We start with: Claim - If $P \mid Q$ then $\Psi(P) \mid \Psi(Q)$. $$ \Psi(Q)=\Psi\left(P \sum_{i=0}^{k} r_{i} x^{i}\right)=\sum_{i=0}^{k} \Psi\left(P \cdot r_{i} x^{i}\right)=\sum_{i=0}^{k} r_{i} \Psi(P)^{p^{i}} $$ which is divisible by $\Psi(P)$. This already implies $$ \Psi(\operatorname{gcd}(F, G)) \mid \operatorname{gcd}(\Psi(F), \Psi(G)) $$ For the converse, by Bezout there exists $A, B \in \mathbb{F}_{p}[x]$ such that $A F+B G=\operatorname{gcd}(F, G)$, so taking $\Psi$ of both sides gives $$ \Psi(A F)+\Psi(B G)=\Psi(\operatorname{gcd}(F, G)) $$ The left-hand side is divisible by $\operatorname{gcd}(\Psi(F), \Psi(G))$ since the first term is divisible by $\Psi(F)$ and the second term is divisible by $\Psi(G)$. So $\operatorname{gcd}(\Psi(F), \Psi(G)) \mid \Psi(\operatorname{gcd}(F, G))$ and noting both sides are monic we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $p$ be a prime number. Let $\mathbb{F}_{p}$ denote the integers modulo $p$, and let $\mathbb{F}_{p}[x]$ be the set of polynomials with coefficients in $\mathbb{F}_{p}$. Define $\Psi: \mathbb{F}_{p}[x] \rightarrow \mathbb{F}_{p}[x]$ by $$ \Psi\left(\sum_{i=0}^{n} a_{i} x^{i}\right)=\sum_{i=0}^{n} a_{i} x^{x^{i}} . $$ Prove that for nonzero polynomials $F, G \in \mathbb{F}_{p}[x]$, $$ \Psi(\operatorname{gcd}(F, G))=\operatorname{gcd}(\Psi(F), \Psi(G)) $$
|
Observe that $\Psi$ is also a linear map of $\mathbb{F}_{p}$ vector spaces, and that $\Psi(x P)=\Psi(P)^{p}$ for any $P \in \mathbb{F}_{p}[x]$. (In particular, $\Psi(1)=x$, not 1 , take caution!) 『 First solution (Ankan Bhattacharya). We start with: Claim - If $P \mid Q$ then $\Psi(P) \mid \Psi(Q)$. $$ \Psi(Q)=\Psi\left(P \sum_{i=0}^{k} r_{i} x^{i}\right)=\sum_{i=0}^{k} \Psi\left(P \cdot r_{i} x^{i}\right)=\sum_{i=0}^{k} r_{i} \Psi(P)^{p^{i}} $$ which is divisible by $\Psi(P)$. This already implies $$ \Psi(\operatorname{gcd}(F, G)) \mid \operatorname{gcd}(\Psi(F), \Psi(G)) $$ For the converse, by Bezout there exists $A, B \in \mathbb{F}_{p}[x]$ such that $A F+B G=\operatorname{gcd}(F, G)$, so taking $\Psi$ of both sides gives $$ \Psi(A F)+\Psi(B G)=\Psi(\operatorname{gcd}(F, G)) $$ The left-hand side is divisible by $\operatorname{gcd}(\Psi(F), \Psi(G))$ since the first term is divisible by $\Psi(F)$ and the second term is divisible by $\Psi(G)$. So $\operatorname{gcd}(\Psi(F), \Psi(G)) \mid \Psi(\operatorname{gcd}(F, G))$ and noting both sides are monic we are done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
631d7241-f0cf-541f-aee0-426a7d5d0920
| 606,327 |
Let $p$ be a prime number. Let $\mathbb{F}_{p}$ denote the integers modulo $p$, and let $\mathbb{F}_{p}[x]$ be the set of polynomials with coefficients in $\mathbb{F}_{p}$. Define $\Psi: \mathbb{F}_{p}[x] \rightarrow \mathbb{F}_{p}[x]$ by $$ \Psi\left(\sum_{i=0}^{n} a_{i} x^{i}\right)=\sum_{i=0}^{n} a_{i} x^{x^{i}} . $$ Prove that for nonzero polynomials $F, G \in \mathbb{F}_{p}[x]$, $$ \Psi(\operatorname{gcd}(F, G))=\operatorname{gcd}(\Psi(F), \Psi(G)) $$
|
Observe that $\Psi$ is also a linear map of $\mathbb{F}_{p}$ vector spaces, and that $\Psi(x P)=\Psi(P)^{p}$ for any $P \in \mathbb{F}_{p}[x]$. (In particular, $\Psi(1)=x$, not 1 , take caution!) 【 Second solution. Here is an alternative (longer but more conceptual) way to finish without Bezout lemma. Let $\beth \subseteq \mathbb{F}_{p}[x]$ denote the set of polynomials in the image of $\Psi$, thus $\Psi: \mathbb{F}_{p}[x] \rightarrow \beth$ is a bijection on the level of sets. Claim - If $A, B \in \beth$ then $\operatorname{gcd}(A, B) \in \beth$. $$ \begin{aligned} x^{p^{k}} & \equiv\left(c_{2} x^{p^{k-2}}+c_{3} x^{p^{k-3}}+\cdots+c_{k}\right)^{p} \quad(\bmod B) \\ & \equiv c_{2} x^{p^{k-1}}+c_{3} x^{p^{k-2}} \cdots+c_{k} \quad(\bmod B) \end{aligned} $$ since exponentiation by $p$ commutes with addition in $\mathbb{F}_{p}$. This is enough to imply the conclusion. The proof if $\operatorname{deg} B$ is smaller less than $p^{k-1}$ is similar. Thus, if we view $\mathbb{F}_{p}[x]$ and $\beth$ as partially ordered sets under polynomial division, then gcd is the "greatest lower bound" or "meet" in both partially ordered sets. We will now prove that $\Psi$ is an isomorphism of the posets. We have already seen that $P|Q \Longrightarrow \Psi(P)| \Psi(Q)$ from the first solution. For the converse: Claim - If $\Psi(P) \mid \Psi(Q)$ then $P \mid Q$. Remark. In fact $\Psi: \mathbb{F}_{p}[x] \rightarrow \beth$ is a ring isomorphism if we equip $\beth$ with function composition as the ring multiplication. Indeed in the proof of the first claim (that $P|Q \Longrightarrow \Psi(P)|$ $\Psi(Q)$ ) we saw that $$ \Psi(R P)=\sum_{i=0}^{k} r_{i} \Psi(P)^{p^{i}}=\Psi(R) \circ \Psi(P) $$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $p$ be a prime number. Let $\mathbb{F}_{p}$ denote the integers modulo $p$, and let $\mathbb{F}_{p}[x]$ be the set of polynomials with coefficients in $\mathbb{F}_{p}$. Define $\Psi: \mathbb{F}_{p}[x] \rightarrow \mathbb{F}_{p}[x]$ by $$ \Psi\left(\sum_{i=0}^{n} a_{i} x^{i}\right)=\sum_{i=0}^{n} a_{i} x^{x^{i}} . $$ Prove that for nonzero polynomials $F, G \in \mathbb{F}_{p}[x]$, $$ \Psi(\operatorname{gcd}(F, G))=\operatorname{gcd}(\Psi(F), \Psi(G)) $$
|
Observe that $\Psi$ is also a linear map of $\mathbb{F}_{p}$ vector spaces, and that $\Psi(x P)=\Psi(P)^{p}$ for any $P \in \mathbb{F}_{p}[x]$. (In particular, $\Psi(1)=x$, not 1 , take caution!) 【 Second solution. Here is an alternative (longer but more conceptual) way to finish without Bezout lemma. Let $\beth \subseteq \mathbb{F}_{p}[x]$ denote the set of polynomials in the image of $\Psi$, thus $\Psi: \mathbb{F}_{p}[x] \rightarrow \beth$ is a bijection on the level of sets. Claim - If $A, B \in \beth$ then $\operatorname{gcd}(A, B) \in \beth$. $$ \begin{aligned} x^{p^{k}} & \equiv\left(c_{2} x^{p^{k-2}}+c_{3} x^{p^{k-3}}+\cdots+c_{k}\right)^{p} \quad(\bmod B) \\ & \equiv c_{2} x^{p^{k-1}}+c_{3} x^{p^{k-2}} \cdots+c_{k} \quad(\bmod B) \end{aligned} $$ since exponentiation by $p$ commutes with addition in $\mathbb{F}_{p}$. This is enough to imply the conclusion. The proof if $\operatorname{deg} B$ is smaller less than $p^{k-1}$ is similar. Thus, if we view $\mathbb{F}_{p}[x]$ and $\beth$ as partially ordered sets under polynomial division, then gcd is the "greatest lower bound" or "meet" in both partially ordered sets. We will now prove that $\Psi$ is an isomorphism of the posets. We have already seen that $P|Q \Longrightarrow \Psi(P)| \Psi(Q)$ from the first solution. For the converse: Claim - If $\Psi(P) \mid \Psi(Q)$ then $P \mid Q$. Remark. In fact $\Psi: \mathbb{F}_{p}[x] \rightarrow \beth$ is a ring isomorphism if we equip $\beth$ with function composition as the ring multiplication. Indeed in the proof of the first claim (that $P|Q \Longrightarrow \Psi(P)|$ $\Psi(Q)$ ) we saw that $$ \Psi(R P)=\sum_{i=0}^{k} r_{i} \Psi(P)^{p^{i}}=\Psi(R) \circ \Psi(P) $$
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
631d7241-f0cf-541f-aee0-426a7d5d0920
| 606,327 |
Let $\sqrt{3}=1 . b_{1} b_{2} b_{3} \cdots(2)$ be the binary representation of $\sqrt{3}$. Prove that for any positive integer $n$, at least one of the digits $b_{n}, b_{n+1}, \ldots, b_{2 n}$ equals 1 .
|
Assume the contrary, so that for some integer $k$ we have $$ k<2^{n-1} \sqrt{3}<k+\frac{1}{2^{n+1}} . $$ Squaring gives $$ \begin{aligned} k^{2}<3 \cdot 2^{2 n-2} & <k^{2}+\frac{k}{2^{n}}+\frac{1}{2^{2 n+2}} \\ & \leq k^{2}+\frac{2^{n-1} \sqrt{3}}{2^{n}}+\frac{1}{2^{2 n+2}} \\ & =k^{2}+\frac{\sqrt{3}}{2}+\frac{1}{2^{2 n+2}} \\ & \leq k^{2}+\frac{\sqrt{3}}{2}+\frac{1}{16} \\ & <k^{2}+1 \end{aligned} $$ and this is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\sqrt{3}=1 . b_{1} b_{2} b_{3} \cdots(2)$ be the binary representation of $\sqrt{3}$. Prove that for any positive integer $n$, at least one of the digits $b_{n}, b_{n+1}, \ldots, b_{2 n}$ equals 1 .
|
Assume the contrary, so that for some integer $k$ we have $$ k<2^{n-1} \sqrt{3}<k+\frac{1}{2^{n+1}} . $$ Squaring gives $$ \begin{aligned} k^{2}<3 \cdot 2^{2 n-2} & <k^{2}+\frac{k}{2^{n}}+\frac{1}{2^{2 n+2}} \\ & \leq k^{2}+\frac{2^{n-1} \sqrt{3}}{2^{n}}+\frac{1}{2^{2 n+2}} \\ & =k^{2}+\frac{\sqrt{3}}{2}+\frac{1}{2^{2 n+2}} \\ & \leq k^{2}+\frac{\sqrt{3}}{2}+\frac{1}{16} \\ & <k^{2}+1 \end{aligned} $$ and this is a contradiction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
35097223-1dac-5f51-b43b-6e36591ed5bb
| 606,330 |
Let $A B C$ be an acute scalene triangle with circumcenter $O$, and let $T$ be on line $B C$ such that $\angle T A O=90^{\circ}$. The circle with diameter $\overline{A T}$ intersects the circumcircle of $\triangle B O C$ at two points $A_{1}$ and $A_{2}$, where $O A_{1}<O A_{2}$. Points $B_{1}, B_{2}, C_{1}, C_{2}$ are defined analogously. (a) Prove that $\overline{A A_{1}}, \overline{B B_{1}}, \overline{C C_{1}}$ are concurrent. (b) Prove that $\overline{A A_{2}}, \overline{B B_{2}}, \overline{C C_{2}}$ are concurrent on the Euler line of triangle $A B C$.
|
Let triangle $A B C$ have circumcircle $\Gamma$. Let $\triangle X Y Z$ be the tangential triangle of $\triangle A B C$ (hence $\Gamma$ is the incircle of $\triangle X Y Z$ ), and denote by $\Omega$ its circumcircle. Suppose the symmedian $\overline{A X}$ meets $\Gamma$ again at $D$, and let $M$ be the midpoint of $\overline{A D}$. Finally, let $K$ be the Miquel point of quadrilateral $Z B C Y$, meaning it is the intersection of $\Omega$ and the circumcircle of $\triangle B O C$ (other than $X$ ).  We first claim that $M$ and $K$ are $A_{1}$ and $A_{2}$. In that case $O M<O A<O K$, so $M=A_{1}, K=A_{2}$. To see that $M=A_{1}$, note that $\angle O M X=90^{\circ}$, and moreover that $\overline{T A}, \overline{T D}$ are tangents to $\Gamma$, whence we also have $M=\overline{T O} \cap \overline{A D}$. Thus $M$ lies on both $(B O C)$ and $(A T)$. This solves part (a) of the problem: the concurrency point is the symmedian point of $\triangle A B C$. Now, note that since $K$ is the Miquel point, $$ \frac{Z K}{Y K}=\frac{Z B}{Y C}=\frac{Z A}{Y A} $$ and hence $\overline{K A}$ is an angle bisector of $\angle Z K Y$. Thus from $(T A ; Y Z)=-1$ we obtain $\angle T K A=90^{\circ}$. It remains to show $\overline{A K}$ passes through a fixed point on the Euler line. We claim it is the exsimilicenter of $\Gamma$ and $\Omega$. Let $L$ be the midpoint of the $\operatorname{arc} Y Z$ of $\triangle X Y Z$ not containing $X$. Then we know that $K, A, L$ are collinear. Now the positive homothety sending $\Gamma$ to $\Omega$ maps $A$ to $L$; this proves the claim. Finally, it is well-known that the line through $O$ and the circumcenter of $\triangle X Y Z$ coincides with the Euler line of $\triangle A B C$; hence done. I Authorship comments. This problem was inspired by the fact that $K, A, L$ are collinear in the figure, which was produced by one of my students (Ryan Kim) in a solution to a homework problem. I realized for example that this implied that line $A K$ passed through the $X_{56}$ point of $\triangle X Y Z$ (which lies on the Euler line of $\triangle A B C$ ). This problem was the result of playing around with the resulting very nice picture: all the power comes from the "magic" point $K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute scalene triangle with circumcenter $O$, and let $T$ be on line $B C$ such that $\angle T A O=90^{\circ}$. The circle with diameter $\overline{A T}$ intersects the circumcircle of $\triangle B O C$ at two points $A_{1}$ and $A_{2}$, where $O A_{1}<O A_{2}$. Points $B_{1}, B_{2}, C_{1}, C_{2}$ are defined analogously. (a) Prove that $\overline{A A_{1}}, \overline{B B_{1}}, \overline{C C_{1}}$ are concurrent. (b) Prove that $\overline{A A_{2}}, \overline{B B_{2}}, \overline{C C_{2}}$ are concurrent on the Euler line of triangle $A B C$.
|
Let triangle $A B C$ have circumcircle $\Gamma$. Let $\triangle X Y Z$ be the tangential triangle of $\triangle A B C$ (hence $\Gamma$ is the incircle of $\triangle X Y Z$ ), and denote by $\Omega$ its circumcircle. Suppose the symmedian $\overline{A X}$ meets $\Gamma$ again at $D$, and let $M$ be the midpoint of $\overline{A D}$. Finally, let $K$ be the Miquel point of quadrilateral $Z B C Y$, meaning it is the intersection of $\Omega$ and the circumcircle of $\triangle B O C$ (other than $X$ ).  We first claim that $M$ and $K$ are $A_{1}$ and $A_{2}$. In that case $O M<O A<O K$, so $M=A_{1}, K=A_{2}$. To see that $M=A_{1}$, note that $\angle O M X=90^{\circ}$, and moreover that $\overline{T A}, \overline{T D}$ are tangents to $\Gamma$, whence we also have $M=\overline{T O} \cap \overline{A D}$. Thus $M$ lies on both $(B O C)$ and $(A T)$. This solves part (a) of the problem: the concurrency point is the symmedian point of $\triangle A B C$. Now, note that since $K$ is the Miquel point, $$ \frac{Z K}{Y K}=\frac{Z B}{Y C}=\frac{Z A}{Y A} $$ and hence $\overline{K A}$ is an angle bisector of $\angle Z K Y$. Thus from $(T A ; Y Z)=-1$ we obtain $\angle T K A=90^{\circ}$. It remains to show $\overline{A K}$ passes through a fixed point on the Euler line. We claim it is the exsimilicenter of $\Gamma$ and $\Omega$. Let $L$ be the midpoint of the $\operatorname{arc} Y Z$ of $\triangle X Y Z$ not containing $X$. Then we know that $K, A, L$ are collinear. Now the positive homothety sending $\Gamma$ to $\Omega$ maps $A$ to $L$; this proves the claim. Finally, it is well-known that the line through $O$ and the circumcenter of $\triangle X Y Z$ coincides with the Euler line of $\triangle A B C$; hence done. I Authorship comments. This problem was inspired by the fact that $K, A, L$ are collinear in the figure, which was produced by one of my students (Ryan Kim) in a solution to a homework problem. I realized for example that this implied that line $A K$ passed through the $X_{56}$ point of $\triangle X Y Z$ (which lies on the Euler line of $\triangle A B C$ ). This problem was the result of playing around with the resulting very nice picture: all the power comes from the "magic" point $K$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6c6b29a-2443-58fb-90ac-acd464d38baf
| 606,350 |
Let $P, Q \in \mathbb{R}[x]$ be relatively prime nonconstant polynomials. Show that there can be at most three real numbers $\lambda$ such that $P+\lambda Q$ is the square of a polynomial.
|
This is true even with $\mathbb{R}$ replaced by $\mathbb{C}$, and it will be necessary to work in this generality. 【 First solution using transformations. We will prove the claim in the following form: Claim - Assume $P, Q \in \mathbb{C}[x]$ are relatively prime. If $\alpha P+\beta Q$ is a square for four different choices of the ratio $[\alpha: \beta]$ then $P$ and $Q$ must be constant. Call pairs $(P, Q)$ as in the claim bad; so we wish to show the only bad pairs are pairs of constant polynomials. Assume not, and take a bad pair with $\operatorname{deg} P+\operatorname{deg} Q$ minimal. By a suitable Möbius transformation, we may transform $(P, Q)$ so that the four ratios are $[1: 0],[0: 1],[1:-1]$ and $[1:-k]$, so we find there are polynomials $A$ and $B$ such that $$ \begin{aligned} A^{2}-B^{2} & =C^{2} \\ A^{2}-k B^{2} & =D^{2} \end{aligned} $$ where $A^{2}=P+\lambda_{1} Q, B^{2}=P+\lambda_{2} Q$, say. Of course $\operatorname{gcd}(A, B)=1$. Consequently, we have $C^{2}=(A+B)(A-B)$ and $D^{2}=(A+\mu B)(A-\mu B)$ where $\mu^{2}=k$. Now $\operatorname{gcd}(A, B)=1$, so $A+B, A-B, A+\mu B$ and $A-\mu B$ are squares; id est $(A, B)$ is bad. This is a contradiction, since $\operatorname{deg} A+\operatorname{deg} B<\operatorname{deg} P+\operatorname{deg} Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P, Q \in \mathbb{R}[x]$ be relatively prime nonconstant polynomials. Show that there can be at most three real numbers $\lambda$ such that $P+\lambda Q$ is the square of a polynomial.
|
This is true even with $\mathbb{R}$ replaced by $\mathbb{C}$, and it will be necessary to work in this generality. 【 First solution using transformations. We will prove the claim in the following form: Claim - Assume $P, Q \in \mathbb{C}[x]$ are relatively prime. If $\alpha P+\beta Q$ is a square for four different choices of the ratio $[\alpha: \beta]$ then $P$ and $Q$ must be constant. Call pairs $(P, Q)$ as in the claim bad; so we wish to show the only bad pairs are pairs of constant polynomials. Assume not, and take a bad pair with $\operatorname{deg} P+\operatorname{deg} Q$ minimal. By a suitable Möbius transformation, we may transform $(P, Q)$ so that the four ratios are $[1: 0],[0: 1],[1:-1]$ and $[1:-k]$, so we find there are polynomials $A$ and $B$ such that $$ \begin{aligned} A^{2}-B^{2} & =C^{2} \\ A^{2}-k B^{2} & =D^{2} \end{aligned} $$ where $A^{2}=P+\lambda_{1} Q, B^{2}=P+\lambda_{2} Q$, say. Of course $\operatorname{gcd}(A, B)=1$. Consequently, we have $C^{2}=(A+B)(A-B)$ and $D^{2}=(A+\mu B)(A-\mu B)$ where $\mu^{2}=k$. Now $\operatorname{gcd}(A, B)=1$, so $A+B, A-B, A+\mu B$ and $A-\mu B$ are squares; id est $(A, B)$ is bad. This is a contradiction, since $\operatorname{deg} A+\operatorname{deg} B<\operatorname{deg} P+\operatorname{deg} Q$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
fcd1b06a-de4e-52bb-9b44-f44ce84d8d9a
| 246,574 |
Let $P, Q \in \mathbb{R}[x]$ be relatively prime nonconstant polynomials. Show that there can be at most three real numbers $\lambda$ such that $P+\lambda Q$ is the square of a polynomial.
|
This is true even with $\mathbb{R}$ replaced by $\mathbb{C}$, and it will be necessary to work in this generality. 【 Second solution using derivatives (by Zack Chroman). We will assume without loss of generality that $\operatorname{deg} P \neq \operatorname{deg} Q$; if not, then one can replace $(P, Q)$ with $(P+c Q, Q)$ for a suitable constant $c$. Then, there exist $\lambda_{i} \in \mathbb{C}$ and polynomials $R_{i}$ for $i=1,2,3,4$ such that $$ \begin{aligned} & P+\lambda_{i} Q=R_{i}^{2} \\ \Longrightarrow & P^{\prime}+\lambda_{i} Q^{\prime}=2 R_{i} R_{i}^{\prime} \\ & \Longrightarrow R_{i} \mid Q^{\prime}\left(P+\lambda_{i} Q\right)-Q\left(P^{\prime}+\lambda_{i} Q^{\prime}\right)=Q^{\prime} P-Q P^{\prime} \end{aligned} $$ On the other hand by Euclidean algorithm it follows that $R_{i}$ are relatively prime to each other. Therefore $$ R_{1} R_{2} R_{3} R_{4} \mid Q^{\prime} P-Q P^{\prime} $$ However, we have $$ \begin{aligned} \sum_{1}^{4} \operatorname{deg} R_{i} & \geq \frac{3 \max (\operatorname{deg} P, \operatorname{deg} Q)+\min (\operatorname{deg} P, \operatorname{deg} Q)}{2} \\ & \geq \operatorname{deg} P+\operatorname{deg} Q>\operatorname{deg}\left(Q^{\prime} P-Q P^{\prime}\right) \end{aligned} $$ This can only occur if $Q^{\prime} P-Q P^{\prime}=0$ or $(P / Q)^{\prime}=0$ by the quotient rule! But $P / Q$ can't be constant, the end. Remark. The result is previously known; see e.g. Lemma 1.6 of http://math.mit.edu/ ebelmont/ec-notes.pdf or Exercise 6.5.L(a) of Vakil's notes.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P, Q \in \mathbb{R}[x]$ be relatively prime nonconstant polynomials. Show that there can be at most three real numbers $\lambda$ such that $P+\lambda Q$ is the square of a polynomial.
|
This is true even with $\mathbb{R}$ replaced by $\mathbb{C}$, and it will be necessary to work in this generality. 【 Second solution using derivatives (by Zack Chroman). We will assume without loss of generality that $\operatorname{deg} P \neq \operatorname{deg} Q$; if not, then one can replace $(P, Q)$ with $(P+c Q, Q)$ for a suitable constant $c$. Then, there exist $\lambda_{i} \in \mathbb{C}$ and polynomials $R_{i}$ for $i=1,2,3,4$ such that $$ \begin{aligned} & P+\lambda_{i} Q=R_{i}^{2} \\ \Longrightarrow & P^{\prime}+\lambda_{i} Q^{\prime}=2 R_{i} R_{i}^{\prime} \\ & \Longrightarrow R_{i} \mid Q^{\prime}\left(P+\lambda_{i} Q\right)-Q\left(P^{\prime}+\lambda_{i} Q^{\prime}\right)=Q^{\prime} P-Q P^{\prime} \end{aligned} $$ On the other hand by Euclidean algorithm it follows that $R_{i}$ are relatively prime to each other. Therefore $$ R_{1} R_{2} R_{3} R_{4} \mid Q^{\prime} P-Q P^{\prime} $$ However, we have $$ \begin{aligned} \sum_{1}^{4} \operatorname{deg} R_{i} & \geq \frac{3 \max (\operatorname{deg} P, \operatorname{deg} Q)+\min (\operatorname{deg} P, \operatorname{deg} Q)}{2} \\ & \geq \operatorname{deg} P+\operatorname{deg} Q>\operatorname{deg}\left(Q^{\prime} P-Q P^{\prime}\right) \end{aligned} $$ This can only occur if $Q^{\prime} P-Q P^{\prime}=0$ or $(P / Q)^{\prime}=0$ by the quotient rule! But $P / Q$ can't be constant, the end. Remark. The result is previously known; see e.g. Lemma 1.6 of http://math.mit.edu/ ebelmont/ec-notes.pdf or Exercise 6.5.L(a) of Vakil's notes.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
fcd1b06a-de4e-52bb-9b44-f44ce84d8d9a
| 246,574 |
Let $A B C$ be a triangle with altitude $\overline{A E}$. The $A$-excircle touches $\overline{B C}$ at $D$, and intersects the circumcircle at two points $F$ and $G$. Prove that one can select points $V$ and $N$ on lines $D G$ and $D F$ such that quadrilateral $E V A N$ is a rhombus.
|
Let $I$ denote the incenter, $J$ the $A$-excenter, and $L$ the midpoint of $\overline{A E}$. Denote by $\overline{I Y}$, $\overline{I Z}$ the tangents from $I$ to the $A$-excircle. Note that lines $\overline{B C}, \overline{G F}, \overline{Y Z}$ then concur at $H$ (unless $A B=A C$, but this case is obvious), as it's the radical center of cyclic hexagon $B I C Y J Z$, the circumcircle and the $A$-excircle.  Now let $\overline{H D}$ and $\overline{H T}$ be the tangents from $H$ to the $A$-excircle. It follows that $\overline{D T}$ is the symmedian of $\triangle D Z Y$, hence passes through $I=\overline{Y Y} \cap \overline{Z Z}$. Moreover, it's well known that $\overline{D I}$ passes through $L$, the midpoint of the $A$-altitude (for example by homothety). Finally, $(D T ; F G)=-1$, hence project through $D$ onto the line through $L$ parallel to $\overline{B C}$ to obtain $(\infty L ; V N)=-1$ as desired. 【 Authorship comments. This is a joint proposal with Danielle Wang (mostly by her). The formulation given was that the tangents to the $A$-excircle at $F$ and $G$ was on line $\overline{D I}$; I solved this formulation using the radical axis argument above. I then got the idea to involve the point $L$, already knowing it was on $\overline{D I}$. Observing the harmonic quadrilateral, I took perspectivity through $M$ onto the line through $L$ parallel to $\overline{B C}$ (before this I had tried to use the $A$-altitude with little luck). This yields the rhombus in the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with altitude $\overline{A E}$. The $A$-excircle touches $\overline{B C}$ at $D$, and intersects the circumcircle at two points $F$ and $G$. Prove that one can select points $V$ and $N$ on lines $D G$ and $D F$ such that quadrilateral $E V A N$ is a rhombus.
|
Let $I$ denote the incenter, $J$ the $A$-excenter, and $L$ the midpoint of $\overline{A E}$. Denote by $\overline{I Y}$, $\overline{I Z}$ the tangents from $I$ to the $A$-excircle. Note that lines $\overline{B C}, \overline{G F}, \overline{Y Z}$ then concur at $H$ (unless $A B=A C$, but this case is obvious), as it's the radical center of cyclic hexagon $B I C Y J Z$, the circumcircle and the $A$-excircle.  Now let $\overline{H D}$ and $\overline{H T}$ be the tangents from $H$ to the $A$-excircle. It follows that $\overline{D T}$ is the symmedian of $\triangle D Z Y$, hence passes through $I=\overline{Y Y} \cap \overline{Z Z}$. Moreover, it's well known that $\overline{D I}$ passes through $L$, the midpoint of the $A$-altitude (for example by homothety). Finally, $(D T ; F G)=-1$, hence project through $D$ onto the line through $L$ parallel to $\overline{B C}$ to obtain $(\infty L ; V N)=-1$ as desired. 【 Authorship comments. This is a joint proposal with Danielle Wang (mostly by her). The formulation given was that the tangents to the $A$-excircle at $F$ and $G$ was on line $\overline{D I}$; I solved this formulation using the radical axis argument above. I then got the idea to involve the point $L$, already knowing it was on $\overline{D I}$. Observing the harmonic quadrilateral, I took perspectivity through $M$ onto the line through $L$ parallel to $\overline{B C}$ (before this I had tried to use the $A$-altitude with little luck). This yields the rhombus in the problem.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
384a2b3f-31a7-559b-9710-7b552ef0c7f9
| 246,592 |
Prove that there are infinitely many triples $(a, b, p)$ of integers, with $p$ prime and $0<a \leq b<p$, for which $p^{5}$ divides $(a+b)^{p}-a^{p}-b^{p}$.
|
The key claim is that if $p \equiv 1(\bmod 3)$, then $$ p\left(x^{2}+x y+y^{2}\right)^{2} \text { divides }(x+y)^{p}-x^{p}-y^{p} $$ as polynomials in $x$ and $y$. Since it's known that one can select $a$ and $b$ such that $p^{2} \mid a^{2}+a b+b^{2}$, the conclusion follows. (The theory of quadratic forms tells us we can do it with $p^{2}=a^{2}+a b+b^{2}$; Thue's lemma lets us do it by solving $x^{2}+x+1 \equiv 0\left(\bmod p^{2}\right)$.) To prove this, it is the same to show that $$ \left(x^{2}+x+1\right)^{2} \text { divides } F(x):=(x+1)^{p}-x^{p}-1 $$ since the binomial coefficients $\binom{p}{k}$ are clearly divisible by $p$. Let $\zeta$ be a third root of unity. Then $F(\zeta)=(1+\zeta)^{p}-\zeta^{p}-1=-\zeta^{2}-\zeta-1=0$. Moreover, $F^{\prime}(x)=p(x+1)^{p-1}-p x^{p-1}$, so $F^{\prime}(\zeta)=p-p=0$. Hence $\zeta$ is a double root of $F$ as needed. (Incidentally, $p=2017$ works!) $$ (x+1)^{7}-x^{7}-1=7 x(x+1)\left(x^{4}+2 x^{3}+3 x^{2}+2 x+1\right) $$ The key is now to notice that the last factor is $\left(x^{2}+x+1\right)^{2}$, which suggests the entire solution. In fact, even if $p \equiv 2(\bmod 3)$, the polynomial $x^{2}+x+1$ still divides $(x+1)^{p}-x^{p}-1$. So even the $p=5$ case can motivate the main idea.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there are infinitely many triples $(a, b, p)$ of integers, with $p$ prime and $0<a \leq b<p$, for which $p^{5}$ divides $(a+b)^{p}-a^{p}-b^{p}$.
|
The key claim is that if $p \equiv 1(\bmod 3)$, then $$ p\left(x^{2}+x y+y^{2}\right)^{2} \text { divides }(x+y)^{p}-x^{p}-y^{p} $$ as polynomials in $x$ and $y$. Since it's known that one can select $a$ and $b$ such that $p^{2} \mid a^{2}+a b+b^{2}$, the conclusion follows. (The theory of quadratic forms tells us we can do it with $p^{2}=a^{2}+a b+b^{2}$; Thue's lemma lets us do it by solving $x^{2}+x+1 \equiv 0\left(\bmod p^{2}\right)$.) To prove this, it is the same to show that $$ \left(x^{2}+x+1\right)^{2} \text { divides } F(x):=(x+1)^{p}-x^{p}-1 $$ since the binomial coefficients $\binom{p}{k}$ are clearly divisible by $p$. Let $\zeta$ be a third root of unity. Then $F(\zeta)=(1+\zeta)^{p}-\zeta^{p}-1=-\zeta^{2}-\zeta-1=0$. Moreover, $F^{\prime}(x)=p(x+1)^{p-1}-p x^{p-1}$, so $F^{\prime}(\zeta)=p-p=0$. Hence $\zeta$ is a double root of $F$ as needed. (Incidentally, $p=2017$ works!) $$ (x+1)^{7}-x^{7}-1=7 x(x+1)\left(x^{4}+2 x^{3}+3 x^{2}+2 x+1\right) $$ The key is now to notice that the last factor is $\left(x^{2}+x+1\right)^{2}$, which suggests the entire solution. In fact, even if $p \equiv 2(\bmod 3)$, the polynomial $x^{2}+x+1$ still divides $(x+1)^{p}-x^{p}-1$. So even the $p=5$ case can motivate the main idea.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
57b2cfbf-ffd6-5c36-813b-cfbcf979a147
| 246,602 |
Let $n \geq 2$ be a positive integer, and let $\sigma(n)$ denote the sum of the positive divisors of $n$. Prove that the $n^{\text {th }}$ smallest positive integer relatively prime to $n$ is at least $\sigma(n)$, and determine for which $n$ equality holds.
|
The equality case is $n=p^{e}$ for $p$ prime and a positive integer $e$. It is easy to check that this works. 【 First solution. In what follows, by $[a, b]$ we mean $\{a, a+1, \ldots, b\}$. First, we make the following easy observation. Claim - If $a$ and $d$ are positive integers, then precisely $\varphi(d)$ elements of $[a, a+d-1]$ are relatively prime to $d$. Let $d_{1}, d_{2}, \ldots, d_{k}$ denote denote the divisors of $n$ in some order. Consider the intervals $$ \begin{aligned} I_{1} & =\left[1, d_{1}\right] \\ I_{2} & =\left[d_{1}+1, d_{1}+d_{2}\right] \\ & \vdots \\ I_{k} & =\left[d_{1}+\cdots+d_{k-1}+1, d_{1}+\cdots+d_{k}\right] . \end{aligned} $$ of length $d_{1}, \ldots, d_{k}$ respectively. The $j$ th interval will have exactly $\varphi\left(d_{j}\right)$ elements which are relatively prime $d_{j}$, hence at most $\varphi\left(d_{j}\right)$ which are relatively prime to $n$. Consequently, in $I=\bigcup_{j=1}^{k} I_{k}$ there are at most $$ \sum_{j=1}^{k} \varphi\left(d_{j}\right)=\sum_{d \mid n} \varphi(d)=n $$ integers relatively prime to $n$. On the other hand $I=[1, \sigma(n)]$ so this implies the inequality. We see that the equality holds for $n=p^{e}$. Assume now $p<q$ are distinct primes dividing $n$. Reorder the divisors $d_{i}$ so that $d_{1}=q$. Then $p, q \in I_{1}$, and so $I_{1}$ should contain strictly fewer than $\varphi\left(d_{1}\right)=q-1$ elements relatively prime to $n$, hence the inequality is strict.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geq 2$ be a positive integer, and let $\sigma(n)$ denote the sum of the positive divisors of $n$. Prove that the $n^{\text {th }}$ smallest positive integer relatively prime to $n$ is at least $\sigma(n)$, and determine for which $n$ equality holds.
|
The equality case is $n=p^{e}$ for $p$ prime and a positive integer $e$. It is easy to check that this works. 【 First solution. In what follows, by $[a, b]$ we mean $\{a, a+1, \ldots, b\}$. First, we make the following easy observation. Claim - If $a$ and $d$ are positive integers, then precisely $\varphi(d)$ elements of $[a, a+d-1]$ are relatively prime to $d$. Let $d_{1}, d_{2}, \ldots, d_{k}$ denote denote the divisors of $n$ in some order. Consider the intervals $$ \begin{aligned} I_{1} & =\left[1, d_{1}\right] \\ I_{2} & =\left[d_{1}+1, d_{1}+d_{2}\right] \\ & \vdots \\ I_{k} & =\left[d_{1}+\cdots+d_{k-1}+1, d_{1}+\cdots+d_{k}\right] . \end{aligned} $$ of length $d_{1}, \ldots, d_{k}$ respectively. The $j$ th interval will have exactly $\varphi\left(d_{j}\right)$ elements which are relatively prime $d_{j}$, hence at most $\varphi\left(d_{j}\right)$ which are relatively prime to $n$. Consequently, in $I=\bigcup_{j=1}^{k} I_{k}$ there are at most $$ \sum_{j=1}^{k} \varphi\left(d_{j}\right)=\sum_{d \mid n} \varphi(d)=n $$ integers relatively prime to $n$. On the other hand $I=[1, \sigma(n)]$ so this implies the inequality. We see that the equality holds for $n=p^{e}$. Assume now $p<q$ are distinct primes dividing $n$. Reorder the divisors $d_{i}$ so that $d_{1}=q$. Then $p, q \in I_{1}$, and so $I_{1}$ should contain strictly fewer than $\varphi\left(d_{1}\right)=q-1$ elements relatively prime to $n$, hence the inequality is strict.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
1641f737-b465-59d0-a72a-dca5d3e50bcc
| 246,614 |
Let $n \geq 2$ be a positive integer, and let $\sigma(n)$ denote the sum of the positive divisors of $n$. Prove that the $n^{\text {th }}$ smallest positive integer relatively prime to $n$ is at least $\sigma(n)$, and determine for which $n$ equality holds.
|
The equality case is $n=p^{e}$ for $p$ prime and a positive integer $e$. It is easy to check that this works. I Second solution (Ivan Borsenco and Evan Chen). Let $n=p_{1}^{e_{1}} \ldots p_{k}^{e_{k}}$, where $p_{1}<p_{2}<\ldots$. We are going to assume $k \geq 2$, since the $k=1$ case was resolved in the very beginning, and prove the strict inequality. For a general $N$, the number of relatively prime integers in $[1, N]$ is given exactly by $$ f(N)=N-\sum_{i}\left\lfloor\frac{N}{p_{i}}\right\rfloor+\sum_{i<j}\left\lfloor\frac{N}{p_{i} p_{j}}\right\rfloor-\ldots $$ according to the inclusion-exclusion principle. So, we wish to show that $f(\sigma(n))<n$ (as $k \geq 2$ ). Discarding the error terms from the floors (noting that we get at most 1 from the negative floors) gives $$ \begin{aligned} f(N) & <2^{k-1}+N-\sum_{i} \frac{N}{p_{i}}+\sum_{i<j} \frac{N}{p_{i} p_{j}}-\ldots \\ & =2^{k-1}+N \prod_{i}\left(1-p_{i}^{-1}\right) \\ & =2^{k-1}+\prod_{i}\left(1-p_{i}^{-1}\right)\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{e_{i}}\right) \\ & =2^{k-1}+\prod_{i}\left(p_{i}^{e_{i}}-p_{i}^{-1}\right) . \end{aligned} $$ $$ \begin{aligned} f(N) & <2+\left(p_{1}^{e_{1}}-p_{1}^{-1}\right)\left(p_{2}^{e_{2}}-p_{2}^{-1}\right) \\ & =2+n-\frac{p_{2}^{e_{2}}}{p_{1}}-\frac{p_{1}^{e_{1}}}{p_{2}}+\frac{1}{p_{1} p_{2}} \\ & \leq 2+n-\frac{p_{2}}{p_{1}}-\frac{p_{1}}{p_{2}}+\frac{1}{p_{1} p_{2}} \\ & =n+\frac{1-\left(p_{1}-p_{2}\right)^{2}}{p_{1} p_{2}} \leq n \end{aligned} $$ On the other hand if $k \geq 3$ we may now write $$ \begin{aligned} f(N) & <2^{k-1}+\left[\prod_{i=2}^{k-1}\left(p_{i}^{e_{i}}\right)\right]\left(p_{1}^{e_{1}}-p_{1}^{-1}\right) \\ & =2^{k-1}+n-\frac{p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}}{p_{1}} \\ & \leq 2^{k-1}+n-\frac{p_{2} p_{3} \ldots p_{k}}{p_{1}} . \end{aligned} $$ If $p_{1}=2$, then one can show by induction that $p_{2} p_{3} \ldots p_{k} \geq 2^{k+1}-1$, which implies the result. If $p_{1}>2$, then one can again show by induction $p_{3} \ldots p_{k} \geq 2^{k}-1$ (since $p_{3} \geq 7$ ), which also implies the result.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geq 2$ be a positive integer, and let $\sigma(n)$ denote the sum of the positive divisors of $n$. Prove that the $n^{\text {th }}$ smallest positive integer relatively prime to $n$ is at least $\sigma(n)$, and determine for which $n$ equality holds.
|
The equality case is $n=p^{e}$ for $p$ prime and a positive integer $e$. It is easy to check that this works. I Second solution (Ivan Borsenco and Evan Chen). Let $n=p_{1}^{e_{1}} \ldots p_{k}^{e_{k}}$, where $p_{1}<p_{2}<\ldots$. We are going to assume $k \geq 2$, since the $k=1$ case was resolved in the very beginning, and prove the strict inequality. For a general $N$, the number of relatively prime integers in $[1, N]$ is given exactly by $$ f(N)=N-\sum_{i}\left\lfloor\frac{N}{p_{i}}\right\rfloor+\sum_{i<j}\left\lfloor\frac{N}{p_{i} p_{j}}\right\rfloor-\ldots $$ according to the inclusion-exclusion principle. So, we wish to show that $f(\sigma(n))<n$ (as $k \geq 2$ ). Discarding the error terms from the floors (noting that we get at most 1 from the negative floors) gives $$ \begin{aligned} f(N) & <2^{k-1}+N-\sum_{i} \frac{N}{p_{i}}+\sum_{i<j} \frac{N}{p_{i} p_{j}}-\ldots \\ & =2^{k-1}+N \prod_{i}\left(1-p_{i}^{-1}\right) \\ & =2^{k-1}+\prod_{i}\left(1-p_{i}^{-1}\right)\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{e_{i}}\right) \\ & =2^{k-1}+\prod_{i}\left(p_{i}^{e_{i}}-p_{i}^{-1}\right) . \end{aligned} $$ $$ \begin{aligned} f(N) & <2+\left(p_{1}^{e_{1}}-p_{1}^{-1}\right)\left(p_{2}^{e_{2}}-p_{2}^{-1}\right) \\ & =2+n-\frac{p_{2}^{e_{2}}}{p_{1}}-\frac{p_{1}^{e_{1}}}{p_{2}}+\frac{1}{p_{1} p_{2}} \\ & \leq 2+n-\frac{p_{2}}{p_{1}}-\frac{p_{1}}{p_{2}}+\frac{1}{p_{1} p_{2}} \\ & =n+\frac{1-\left(p_{1}-p_{2}\right)^{2}}{p_{1} p_{2}} \leq n \end{aligned} $$ On the other hand if $k \geq 3$ we may now write $$ \begin{aligned} f(N) & <2^{k-1}+\left[\prod_{i=2}^{k-1}\left(p_{i}^{e_{i}}\right)\right]\left(p_{1}^{e_{1}}-p_{1}^{-1}\right) \\ & =2^{k-1}+n-\frac{p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}}{p_{1}} \\ & \leq 2^{k-1}+n-\frac{p_{2} p_{3} \ldots p_{k}}{p_{1}} . \end{aligned} $$ If $p_{1}=2$, then one can show by induction that $p_{2} p_{3} \ldots p_{k} \geq 2^{k+1}-1$, which implies the result. If $p_{1}>2$, then one can again show by induction $p_{3} \ldots p_{k} \geq 2^{k}-1$ (since $p_{3} \geq 7$ ), which also implies the result.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
1641f737-b465-59d0-a72a-dca5d3e50bcc
| 246,614 |
Let $n$ be a positive integer and let $S \subseteq\{0,1\}^{n}$ be a set of binary strings of length $n$. Given an odd number $x_{1}, \ldots, x_{2 k+1} \in S$ of binary strings (not necessarily distinct), their majority is defined as the binary string $y \in\{0,1\}^{n}$ for which the $i^{\text {th }}$ bit of $y$ is the most common bit among the $i^{\text {th }}$ bits of $x_{1}, \ldots, x_{2 k+1}$. (For example, if $n=4$ the majority of $0000,0000,1101,1100,0101$ is 0100 .) Suppose that for some positive integer $k, S$ has the property $P_{k}$ that the majority of any $2 k+1$ binary strings in $S$ (possibly with repetition) is also in $S$. Prove that $S$ has the same property $P_{k}$ for all positive integers $k$.
|
Let $M$ denote the majority function (of any length). 【 First solution (induction). We prove all $P_{k}$ are equivalent by induction on $n \geq 2$, with the base case $n=2$ being easy to check by hand. (The case $n=1$ is also vacuous; however, the inductive step is not able to go from $n=1$ to $n=2$.) For the inductive step, we proceed by contradiction; assume $S$ satisfies $P_{\ell}$, but not $P_{k}$, so there exist $x_{1}, \ldots, x_{2 k+1} \in S$ whose majority $y=M\left(x_{1}, \ldots, x_{k}\right)$ is not in $S$. We contend that: Claim - Let $y_{i}$ be the string which differs from $y$ only in the $i^{\text {th }}$ bit. Then $y_{i} \in S$. $$ T=\{\hat{s} \mid s \in S\} $$ Since $S$ satisfies $P_{\ell}$, so does $T$; thus by the induction hypothesis on $n, T$ satisfies $P_{k}$. Consequently, $T \ni M\left(\hat{x}_{1}, \ldots, \hat{x}_{2 k+1}\right)=\hat{y}$. Thus there exists $s \in S$ such that $\hat{s}=\hat{y}$. This implies $s=y$ or $s=y_{i}$. But since we assumed $y \notin S$ it follows $y_{i} \in S$ instead. Now take any $2 \ell+1$ copies of the $y_{i}$, about equally often (i.e. the number of times any two $y_{i}$ are taken differs by at most 1 ). We see the majority of these is $y$ itself, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer and let $S \subseteq\{0,1\}^{n}$ be a set of binary strings of length $n$. Given an odd number $x_{1}, \ldots, x_{2 k+1} \in S$ of binary strings (not necessarily distinct), their majority is defined as the binary string $y \in\{0,1\}^{n}$ for which the $i^{\text {th }}$ bit of $y$ is the most common bit among the $i^{\text {th }}$ bits of $x_{1}, \ldots, x_{2 k+1}$. (For example, if $n=4$ the majority of $0000,0000,1101,1100,0101$ is 0100 .) Suppose that for some positive integer $k, S$ has the property $P_{k}$ that the majority of any $2 k+1$ binary strings in $S$ (possibly with repetition) is also in $S$. Prove that $S$ has the same property $P_{k}$ for all positive integers $k$.
|
Let $M$ denote the majority function (of any length). 【 First solution (induction). We prove all $P_{k}$ are equivalent by induction on $n \geq 2$, with the base case $n=2$ being easy to check by hand. (The case $n=1$ is also vacuous; however, the inductive step is not able to go from $n=1$ to $n=2$.) For the inductive step, we proceed by contradiction; assume $S$ satisfies $P_{\ell}$, but not $P_{k}$, so there exist $x_{1}, \ldots, x_{2 k+1} \in S$ whose majority $y=M\left(x_{1}, \ldots, x_{k}\right)$ is not in $S$. We contend that: Claim - Let $y_{i}$ be the string which differs from $y$ only in the $i^{\text {th }}$ bit. Then $y_{i} \in S$. $$ T=\{\hat{s} \mid s \in S\} $$ Since $S$ satisfies $P_{\ell}$, so does $T$; thus by the induction hypothesis on $n, T$ satisfies $P_{k}$. Consequently, $T \ni M\left(\hat{x}_{1}, \ldots, \hat{x}_{2 k+1}\right)=\hat{y}$. Thus there exists $s \in S$ such that $\hat{s}=\hat{y}$. This implies $s=y$ or $s=y_{i}$. But since we assumed $y \notin S$ it follows $y_{i} \in S$ instead. Now take any $2 \ell+1$ copies of the $y_{i}$, about equally often (i.e. the number of times any two $y_{i}$ are taken differs by at most 1 ). We see the majority of these is $y$ itself, contradiction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2bc175e7-0f89-5236-967b-2e3c9ed09dee
| 606,387 |
Let $n$ be a positive integer and let $S \subseteq\{0,1\}^{n}$ be a set of binary strings of length $n$. Given an odd number $x_{1}, \ldots, x_{2 k+1} \in S$ of binary strings (not necessarily distinct), their majority is defined as the binary string $y \in\{0,1\}^{n}$ for which the $i^{\text {th }}$ bit of $y$ is the most common bit among the $i^{\text {th }}$ bits of $x_{1}, \ldots, x_{2 k+1}$. (For example, if $n=4$ the majority of $0000,0000,1101,1100,0101$ is 0100 .) Suppose that for some positive integer $k, S$ has the property $P_{k}$ that the majority of any $2 k+1$ binary strings in $S$ (possibly with repetition) is also in $S$. Prove that $S$ has the same property $P_{k}$ for all positive integers $k$.
|
Let $M$ denote the majority function (of any length). 【 Second solution (circuit construction). Note that $P_{k} \Longrightarrow P_{1}$ for any $k$, since $$ M(\underbrace{a, \ldots, a}_{k}, \underbrace{b, \ldots, b}_{k}, c)=M(a, b, c) $$ for any $a, b, c$. We will now prove $P_{1}+P_{k} \Longrightarrow P_{k+1}$ for any $k$, which will prove the result. Actually, we will show that the majority of any $2 k+3$ strings $x_{1}, \ldots, x_{2 k+3}$ can be expressed by 3 and $(2 k+1)$-majorities. WLOG assume that $M\left(x_{1}, \ldots, x_{2 k+3}\right)=0 \ldots 0$, and let $\odot$ denote binary AND. Claim - We have $M\left(x_{1}, x_{2}, M\left(x_{3}, \ldots, x_{2 k+3}\right)\right)=x_{1} \odot x_{2}$. By analogy we can construct any $x_{i} \odot x_{j}$. Finally, note that $$ M\left(x_{1} \odot x_{2}, x_{2} \odot x_{3}, \ldots, x_{2 k+1} \odot x_{2 k+2}\right)=0 \ldots 0 $$ as desired. (Indeed, if we look at any index, there were at most $k+1$ 's in the $x_{i}$ strings, and hence there will be at most $k$ 's among $x_{i} \odot x_{i+1}$ for $i=1, \ldots, 2 k+1$.)
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer and let $S \subseteq\{0,1\}^{n}$ be a set of binary strings of length $n$. Given an odd number $x_{1}, \ldots, x_{2 k+1} \in S$ of binary strings (not necessarily distinct), their majority is defined as the binary string $y \in\{0,1\}^{n}$ for which the $i^{\text {th }}$ bit of $y$ is the most common bit among the $i^{\text {th }}$ bits of $x_{1}, \ldots, x_{2 k+1}$. (For example, if $n=4$ the majority of $0000,0000,1101,1100,0101$ is 0100 .) Suppose that for some positive integer $k, S$ has the property $P_{k}$ that the majority of any $2 k+1$ binary strings in $S$ (possibly with repetition) is also in $S$. Prove that $S$ has the same property $P_{k}$ for all positive integers $k$.
|
Let $M$ denote the majority function (of any length). 【 Second solution (circuit construction). Note that $P_{k} \Longrightarrow P_{1}$ for any $k$, since $$ M(\underbrace{a, \ldots, a}_{k}, \underbrace{b, \ldots, b}_{k}, c)=M(a, b, c) $$ for any $a, b, c$. We will now prove $P_{1}+P_{k} \Longrightarrow P_{k+1}$ for any $k$, which will prove the result. Actually, we will show that the majority of any $2 k+3$ strings $x_{1}, \ldots, x_{2 k+3}$ can be expressed by 3 and $(2 k+1)$-majorities. WLOG assume that $M\left(x_{1}, \ldots, x_{2 k+3}\right)=0 \ldots 0$, and let $\odot$ denote binary AND. Claim - We have $M\left(x_{1}, x_{2}, M\left(x_{3}, \ldots, x_{2 k+3}\right)\right)=x_{1} \odot x_{2}$. By analogy we can construct any $x_{i} \odot x_{j}$. Finally, note that $$ M\left(x_{1} \odot x_{2}, x_{2} \odot x_{3}, \ldots, x_{2 k+1} \odot x_{2 k+2}\right)=0 \ldots 0 $$ as desired. (Indeed, if we look at any index, there were at most $k+1$ 's in the $x_{i}$ strings, and hence there will be at most $k$ 's among $x_{i} \odot x_{i+1}$ for $i=1, \ldots, 2 k+1$.)
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
2bc175e7-0f89-5236-967b-2e3c9ed09dee
| 606,387 |
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$.  The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. I First proof (original solution). Let $P$ be the circumcenter of $B T S D$. The properties of the Miquel point imply $P$ lies on the common bisector $\overline{E H}$ already, and it also lies on the perpendicular bisector of $\overline{B D}$, hence it must be the midpoint of $\overline{H F}$. We now contend quadrilaterals $B M P S$ and $D N P T$ are cyclic. Obviously $\overline{M P}$ is the external angle bisector of $\angle B M S$, and $P B=P S$, so $P$ is the arc midpoint of $(B M S)$. The proof for $D N P T$ is analogous. It remains to show $\angle B E N=\angle M E D$, or equivalently $\angle B E M=\angle N E D$. By properties of Miquel point we have $E \in(B M P S) \cap(T P N D)$, so $$ \measuredangle B E M=\measuredangle B P M=\measuredangle P B D=\measuredangle B D P=\measuredangle N P D=\measuredangle N E D $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$.  The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. I First proof (original solution). Let $P$ be the circumcenter of $B T S D$. The properties of the Miquel point imply $P$ lies on the common bisector $\overline{E H}$ already, and it also lies on the perpendicular bisector of $\overline{B D}$, hence it must be the midpoint of $\overline{H F}$. We now contend quadrilaterals $B M P S$ and $D N P T$ are cyclic. Obviously $\overline{M P}$ is the external angle bisector of $\angle B M S$, and $P B=P S$, so $P$ is the arc midpoint of $(B M S)$. The proof for $D N P T$ is analogous. It remains to show $\angle B E N=\angle M E D$, or equivalently $\angle B E M=\angle N E D$. By properties of Miquel point we have $E \in(B M P S) \cap(T P N D)$, so $$ \measuredangle B E M=\measuredangle B P M=\measuredangle P B D=\measuredangle B D P=\measuredangle N P D=\measuredangle N E D $$ as desired.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
bc52ddf0-22df-58c5-b6ea-83cc27d73953
| 606,390 |
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$.  The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. 【 Second proof (2011 G4). By 2011 G 4 , the circumcircle of $\triangle E M N$ is tangent to the circumcircle of $A B C D$. Hence if we extend $\overline{E M}$ and $\overline{E N}$ to meet $(A B C D)$ again at $X$ and $Y$, we get $\overline{X Y}\|\overline{M N}\| \overline{B D}$. Thus $\measuredangle B E M=\measuredangle B E X=\measuredangle Y E D=\measuredangle N E D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$.  The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. 【 Second proof (2011 G4). By 2011 G 4 , the circumcircle of $\triangle E M N$ is tangent to the circumcircle of $A B C D$. Hence if we extend $\overline{E M}$ and $\overline{E N}$ to meet $(A B C D)$ again at $X$ and $Y$, we get $\overline{X Y}\|\overline{M N}\| \overline{B D}$. Thus $\measuredangle B E M=\measuredangle B E X=\measuredangle Y E D=\measuredangle N E D$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
bc52ddf0-22df-58c5-b6ea-83cc27d73953
| 606,390 |
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$.  The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. I Third proof (involutions, submitted by Daniel Liu). Let $G=\overline{B N} \cap \overline{M D}$ denote the centroid of $\triangle B C D$, and note that it lies on $\overline{E H F}$. Now consider the dual of Desargues involution theorem on complete quadrilateral $B M D N C G$ at point $E$. We get $$ (E B, E D), \quad(E M, E N), \quad(E C, E G) $$ form an involutive pairing. However, the bisector of $\angle B E D$, say $\ell$, is also the angle bisector of $\angle C E F$ (since $\overline{C F} \| \overline{B D})$. So the involution we found must coincide with reflection across $\ell$. This means $\angle M E N$ is bisected by $\ell$ as well, as desired. 【 Authorship comments. This diagram actually comes from the inverted picture in IMO 2014/3 (which I attended). I had heard for many years that one could solve this problem quickly by inversion at $H$ afterwards. But when I actually tried to do it during an OTIS class years later, I ended up with the picture in the TST problem, and couldn't see why it was true! In the process of trying to reconstruct this rumored solution, I ended up finding most of the properties that ended up in the January TST problem (but were overkill for the original IMO problem). Let us make the equivalence explicit by deducing the IMO problem from our work. Let rays $E M$ and $E N$ meet the circumcircles of $\triangle B H C$ and $\triangle B N C$ again at $X$ and $Y$, with $E M<E X$ and $E N<E Y$. As above we concluded $E M / E X=E N / E Y$ and so $\overline{M N} \| \overline{X Y} \Longrightarrow \overline{X Y} \perp \overline{A H C}$. Now consider an inversion at $H$ which swaps $B \leftrightarrow D$ and $A \leftrightarrow C$. The point $E$ goes to $E^{*}$ diametrically opposite $A$. Points $X$ and $Y$ go to points on $X^{*} \in \overline{A D}$ and $Y^{*} \in \overline{A B}$. Since the reflection of $E$ across $\overline{P X}$ is supposed to lie on $(B A E)$, it follows that the circumcenter of $\triangle H X^{*} E^{*}$ lies on $\overline{A D}$. Consequently $X^{*}$ plays the role of point " $T$ " in the IMO problem. Then $Y^{*}$ plays the role of point " $S$ " in the IMO problem. Now the fact that $\left(H X^{*} Y^{*}\right)$ is tangent to $\overline{B D}$ is equivalent to $\overline{X Y} \perp \overline{A H C}$ which we already knew.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex cyclic quadrilateral which is not a kite, but whose diagonals are perpendicular and meet at $H$. Denote by $M$ and $N$ the midpoints of $\overline{B C}$ and $\overline{C D}$. Rays $M H$ and $N H$ meet $\overline{A D}$ and $\overline{A B}$ at $S$ and $T$, respectively. Prove there exists a point $E$, lying outside quadrilateral $A B C D$, such that - ray $E H$ bisects both angles $\angle B E S, \angle T E D$, and - $\angle B E N=\angle M E D$.
|
The main claim is that $E$ is the intersection of $(A B C D)$ with the circle with diameter $\overline{A H}$.  The following observation can be quickly made without reference to $E$. ## Lemma We have $\angle H S A=\angle H T A=90^{\circ}$. Consequently, quadrilateral $B T S D$ is cyclic. From here it follows that $E$ is the Miquel point of cyclic quadrilateral $B T S D$. Define $F$ to be the point diametrically opposite $A$, so that $E, H, F$ are collinear, $\overline{C F} \| \overline{B D}$. By now we already have $$ \measuredangle B E H=\measuredangle B E F=\measuredangle B A F=\measuredangle C A D=\measuredangle H A S=\measuredangle H E S $$ so $\overline{E H}$ bisects $\angle B E S$, and $\angle T E D$. Hence it only remains to show $\angle B E M=\angle N E D$; we present several proofs below. I Third proof (involutions, submitted by Daniel Liu). Let $G=\overline{B N} \cap \overline{M D}$ denote the centroid of $\triangle B C D$, and note that it lies on $\overline{E H F}$. Now consider the dual of Desargues involution theorem on complete quadrilateral $B M D N C G$ at point $E$. We get $$ (E B, E D), \quad(E M, E N), \quad(E C, E G) $$ form an involutive pairing. However, the bisector of $\angle B E D$, say $\ell$, is also the angle bisector of $\angle C E F$ (since $\overline{C F} \| \overline{B D})$. So the involution we found must coincide with reflection across $\ell$. This means $\angle M E N$ is bisected by $\ell$ as well, as desired. 【 Authorship comments. This diagram actually comes from the inverted picture in IMO 2014/3 (which I attended). I had heard for many years that one could solve this problem quickly by inversion at $H$ afterwards. But when I actually tried to do it during an OTIS class years later, I ended up with the picture in the TST problem, and couldn't see why it was true! In the process of trying to reconstruct this rumored solution, I ended up finding most of the properties that ended up in the January TST problem (but were overkill for the original IMO problem). Let us make the equivalence explicit by deducing the IMO problem from our work. Let rays $E M$ and $E N$ meet the circumcircles of $\triangle B H C$ and $\triangle B N C$ again at $X$ and $Y$, with $E M<E X$ and $E N<E Y$. As above we concluded $E M / E X=E N / E Y$ and so $\overline{M N} \| \overline{X Y} \Longrightarrow \overline{X Y} \perp \overline{A H C}$. Now consider an inversion at $H$ which swaps $B \leftrightarrow D$ and $A \leftrightarrow C$. The point $E$ goes to $E^{*}$ diametrically opposite $A$. Points $X$ and $Y$ go to points on $X^{*} \in \overline{A D}$ and $Y^{*} \in \overline{A B}$. Since the reflection of $E$ across $\overline{P X}$ is supposed to lie on $(B A E)$, it follows that the circumcenter of $\triangle H X^{*} E^{*}$ lies on $\overline{A D}$. Consequently $X^{*}$ plays the role of point " $T$ " in the IMO problem. Then $Y^{*}$ plays the role of point " $S$ " in the IMO problem. Now the fact that $\left(H X^{*} Y^{*}\right)$ is tangent to $\overline{B D}$ is equivalent to $\overline{X Y} \perp \overline{A H C}$ which we already knew.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
bc52ddf0-22df-58c5-b6ea-83cc27d73953
| 606,390 |
Alice and Bob play a game. First, Alice secretly picks a finite set $S$ of lattice points in the Cartesian plane. Then, for every line $\ell$ in the plane which is horizontal, vertical, or has slope +1 or -1 , she tells Bob the number of points of $S$ that lie on $\ell$. Bob wins if he can then determine the set $S$. Prove that if Alice picks $S$ to be of the form $$ S=\left\{(x, y) \in \mathbb{Z}^{2} \mid m \leq x^{2}+y^{2} \leq n\right\} $$ for some positive integers $m$ and $n$, then Bob can win. (Bob does not know in advance that $S$ is of this form.)
|
Clearly Bob can compute the number $N$ of points. The main claim is that: Claim - Fix $m$ and $n$ as in the problem statement. Among all sets $T \subseteq \mathbb{Z}^{2}$ with $N$ points, the set $S$ is the unique one which maximizes the value of $$ F(T):=\sum_{(x, y) \in T}\left(x^{2}+y^{2}\right)\left(m+n-\left(x^{2}+y^{2}\right)\right) . $$ As a result of this observation, it suffices to show that Bob has enough information to compute $F(S)$ from the data given. (There is no issue with fixing $m$ and $n$, since Bob can find an upper bound on the magnitude of the points and then check all pairs ( $m, n$ ) smaller than that.) The idea is that he knows the full distribution of each of $X, Y$, $X+Y, X-Y$ and hence can compute sums over $T$ of any power of a single one of those linear functions. By taking linear combinations we can hence compute $F(S)$. Let us make the relations explicit. For ease of exposition we take $Z=(X, Y)$ to be a uniformly random point from the set $S$. The information is precisely the individual distributions of $X, Y, X+Y$, and $X-Y$. Now compute $$ \begin{aligned} \frac{F(S)}{N} & =\mathbb{E}\left[(m+n)\left(X^{2}+Y^{2}\right)-\left(X^{2}+Y^{2}\right)^{2}\right] \\ & =(m+n)\left(\mathbb{E}\left[X^{2}\right]+\mathbb{E}\left[Y^{2}\right]\right)-\mathbb{E}\left[X^{4}\right]-\mathbb{E}\left[Y^{4}\right]-2 \mathbb{E}\left[X^{2} Y^{2}\right] \end{aligned} $$ On the other hand, $$ \mathbb{E}\left[X^{2} Y^{2}\right]=\frac{\mathbb{E}\left[(X+Y)^{4}\right]+\mathbb{E}\left[(X-Y)^{4}\right]-2 \mathbb{E}\left[X^{4}\right]-2 \mathbb{E}\left[Y^{4}\right]}{12} $$ Thus we have written $F(S)$ in terms of the distributions of $X, Y, X-Y, X+Y$ which completes the proof. - An obstruction to purely combinatorial arguments is that if you take an octagon with points $( \pm a, \pm b)$ and $( \pm b, \pm a)$ then the two ways to pick every other point (going around clockwise) are indistinguishable by Bob. This at least shows that Bob's task is far from possible in general, and hints at proving an inequality. - A related and more standard fact (among a certain type of person) is that given a probability distribution $\mu$ on $\mathbb{R}^{n}$, if I tell you the distribution of all 1-dimensional projections of $\mu$, that determines $\mu$ uniquely. This works because this information gives me the Fourier transform $\hat{\mu}$, and Fourier transforms are injective. For the continuum version of this problem, this connection gives a much larger family of counterexamples to any proposed extension to arbitrary non-annular shapes. Indeed, take a fast-decaying smooth function $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ which vanishes on the four lines $$ x=0, y=0, x+y=0, x-y=0 . $$ Then the Fourier transform $\hat{f}$ will have mean 0 on each line $\ell$ as in the problem statement. Hence the positive and negative parts of $\hat{f}$ will not be distinguishable by Bob.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Alice and Bob play a game. First, Alice secretly picks a finite set $S$ of lattice points in the Cartesian plane. Then, for every line $\ell$ in the plane which is horizontal, vertical, or has slope +1 or -1 , she tells Bob the number of points of $S$ that lie on $\ell$. Bob wins if he can then determine the set $S$. Prove that if Alice picks $S$ to be of the form $$ S=\left\{(x, y) \in \mathbb{Z}^{2} \mid m \leq x^{2}+y^{2} \leq n\right\} $$ for some positive integers $m$ and $n$, then Bob can win. (Bob does not know in advance that $S$ is of this form.)
|
Clearly Bob can compute the number $N$ of points. The main claim is that: Claim - Fix $m$ and $n$ as in the problem statement. Among all sets $T \subseteq \mathbb{Z}^{2}$ with $N$ points, the set $S$ is the unique one which maximizes the value of $$ F(T):=\sum_{(x, y) \in T}\left(x^{2}+y^{2}\right)\left(m+n-\left(x^{2}+y^{2}\right)\right) . $$ As a result of this observation, it suffices to show that Bob has enough information to compute $F(S)$ from the data given. (There is no issue with fixing $m$ and $n$, since Bob can find an upper bound on the magnitude of the points and then check all pairs ( $m, n$ ) smaller than that.) The idea is that he knows the full distribution of each of $X, Y$, $X+Y, X-Y$ and hence can compute sums over $T$ of any power of a single one of those linear functions. By taking linear combinations we can hence compute $F(S)$. Let us make the relations explicit. For ease of exposition we take $Z=(X, Y)$ to be a uniformly random point from the set $S$. The information is precisely the individual distributions of $X, Y, X+Y$, and $X-Y$. Now compute $$ \begin{aligned} \frac{F(S)}{N} & =\mathbb{E}\left[(m+n)\left(X^{2}+Y^{2}\right)-\left(X^{2}+Y^{2}\right)^{2}\right] \\ & =(m+n)\left(\mathbb{E}\left[X^{2}\right]+\mathbb{E}\left[Y^{2}\right]\right)-\mathbb{E}\left[X^{4}\right]-\mathbb{E}\left[Y^{4}\right]-2 \mathbb{E}\left[X^{2} Y^{2}\right] \end{aligned} $$ On the other hand, $$ \mathbb{E}\left[X^{2} Y^{2}\right]=\frac{\mathbb{E}\left[(X+Y)^{4}\right]+\mathbb{E}\left[(X-Y)^{4}\right]-2 \mathbb{E}\left[X^{4}\right]-2 \mathbb{E}\left[Y^{4}\right]}{12} $$ Thus we have written $F(S)$ in terms of the distributions of $X, Y, X-Y, X+Y$ which completes the proof. - An obstruction to purely combinatorial arguments is that if you take an octagon with points $( \pm a, \pm b)$ and $( \pm b, \pm a)$ then the two ways to pick every other point (going around clockwise) are indistinguishable by Bob. This at least shows that Bob's task is far from possible in general, and hints at proving an inequality. - A related and more standard fact (among a certain type of person) is that given a probability distribution $\mu$ on $\mathbb{R}^{n}$, if I tell you the distribution of all 1-dimensional projections of $\mu$, that determines $\mu$ uniquely. This works because this information gives me the Fourier transform $\hat{\mu}$, and Fourier transforms are injective. For the continuum version of this problem, this connection gives a much larger family of counterexamples to any proposed extension to arbitrary non-annular shapes. Indeed, take a fast-decaying smooth function $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ which vanishes on the four lines $$ x=0, y=0, x+y=0, x-y=0 . $$ Then the Fourier transform $\hat{f}$ will have mean 0 on each line $\ell$ as in the problem statement. Hence the positive and negative parts of $\hat{f}$ will not be distinguishable by Bob.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
75937eef-a79d-5425-8db2-2a822e60e82d
| 606,396 |
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
『 First solution using symmedians (Merlijn Staps). Let $\overline{X Y}$ be the other tangent from $X$ to $(A M N)$. Claim - Line $\overline{X M}$ is tangent to $(B M Y)$; hence $Y$ lies on $\omega_{B}$.  Similarly, $\omega_{C}$ is the circumcircle of triangle $C N Y$. As $A M Y N$ is cyclic too, it follows that $\omega_{B}$ and $\omega_{C}$ intersect on $\overline{B C}$, by Miquel's theorem. Remark. The converse of Miquel's theorem is true, which means the problem is equivalent to showing that the second intersection of the $\omega_{B}$ and $\omega_{C}$ moves along $(A M N)$. Thus the construction of $Y$ above is not so unnatural.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
『 First solution using symmedians (Merlijn Staps). Let $\overline{X Y}$ be the other tangent from $X$ to $(A M N)$. Claim - Line $\overline{X M}$ is tangent to $(B M Y)$; hence $Y$ lies on $\omega_{B}$.  Similarly, $\omega_{C}$ is the circumcircle of triangle $C N Y$. As $A M Y N$ is cyclic too, it follows that $\omega_{B}$ and $\omega_{C}$ intersect on $\overline{B C}$, by Miquel's theorem. Remark. The converse of Miquel's theorem is true, which means the problem is equivalent to showing that the second intersection of the $\omega_{B}$ and $\omega_{C}$ moves along $(A M N)$. Thus the construction of $Y$ above is not so unnatural.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
089a9306-7e00-588b-bca5-a1448f7fd14f
| 246,666 |
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
【 Second solution (Jetze Zoethout). Let $\omega_{B}$ intersect $\overline{B C}$ again at $S$ and let $\overline{M S}$ intersect $\overline{A C}$ again at $Y$. Angle chasing gives $\measuredangle X M Y=\measuredangle X M S=\measuredangle M B S=\measuredangle A B C=$ $\measuredangle X A C=\measuredangle X A Y$, so $Y$ is on the circumcircle of triangle $A M X$. Furthermore, from $\measuredangle X M Y=\measuredangle A B C$ and $\measuredangle A C B=\measuredangle X A B=\measuredangle X Y M$ it follows that $\triangle A B C \sim \triangle X M Y$ and from $\measuredangle X A Y=\measuredangle M B S$ and $\measuredangle Y X A=\measuredangle Y M A=\measuredangle B M S$ it follows that $\triangle A X Y \sim$ $\triangle B M S$.  We now find $$ \frac{A N}{A X}=\frac{A N / B M}{A X / B M}=\frac{A C / A B}{M S / X Y}=\frac{A B / A B}{M S / X M}=\frac{X M}{M S} $$ which together with $\angle X M S=\angle X A N$ yields $\triangle X M S \sim \triangle X A N$. From $\measuredangle X S Y=$ $\measuredangle X S M=\measuredangle X N A=\measuredangle X N Y$ we now have that $S$ is on the circumcircle of triangle $X N Y$. Finally, we have $\measuredangle X N S=\measuredangle X Y S=\measuredangle X Y M=\measuredangle A C B=\measuredangle N C S$ so $\overline{X N}$ is tangent to the circle through $C, N$, and $S$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
【 Second solution (Jetze Zoethout). Let $\omega_{B}$ intersect $\overline{B C}$ again at $S$ and let $\overline{M S}$ intersect $\overline{A C}$ again at $Y$. Angle chasing gives $\measuredangle X M Y=\measuredangle X M S=\measuredangle M B S=\measuredangle A B C=$ $\measuredangle X A C=\measuredangle X A Y$, so $Y$ is on the circumcircle of triangle $A M X$. Furthermore, from $\measuredangle X M Y=\measuredangle A B C$ and $\measuredangle A C B=\measuredangle X A B=\measuredangle X Y M$ it follows that $\triangle A B C \sim \triangle X M Y$ and from $\measuredangle X A Y=\measuredangle M B S$ and $\measuredangle Y X A=\measuredangle Y M A=\measuredangle B M S$ it follows that $\triangle A X Y \sim$ $\triangle B M S$.  We now find $$ \frac{A N}{A X}=\frac{A N / B M}{A X / B M}=\frac{A C / A B}{M S / X Y}=\frac{A B / A B}{M S / X M}=\frac{X M}{M S} $$ which together with $\angle X M S=\angle X A N$ yields $\triangle X M S \sim \triangle X A N$. From $\measuredangle X S Y=$ $\measuredangle X S M=\measuredangle X N A=\measuredangle X N Y$ we now have that $S$ is on the circumcircle of triangle $X N Y$. Finally, we have $\measuredangle X N S=\measuredangle X Y S=\measuredangle X Y M=\measuredangle A C B=\measuredangle N C S$ so $\overline{X N}$ is tangent to the circle through $C, N$, and $S$, as desired.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
089a9306-7e00-588b-bca5-a1448f7fd14f
| 246,666 |
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
【 Third solution by moving points method. Fix triangle $A B C$ and animate $X$ along the tangent at $A$. We let $D$ denote the second intersection point of $\omega_{C}$ with line $\overline{B C}$. Claim - The composed map $X \mapsto D$ is a fractional linear transformation (i.e. a projective map) in terms of a real coordinate on line $\overline{A A}, \overline{B C}$. We claim that the composed map $$ \begin{aligned} & \overline{A A} \rightarrow \ell \rightarrow \ell \rightarrow \overline{B C} \rightarrow \overline{B C} \\ & \text { by } \quad X \mapsto P \mapsto S \mapsto T \mapsto D \end{aligned} $$ is projective, by showing each individual map is projective. 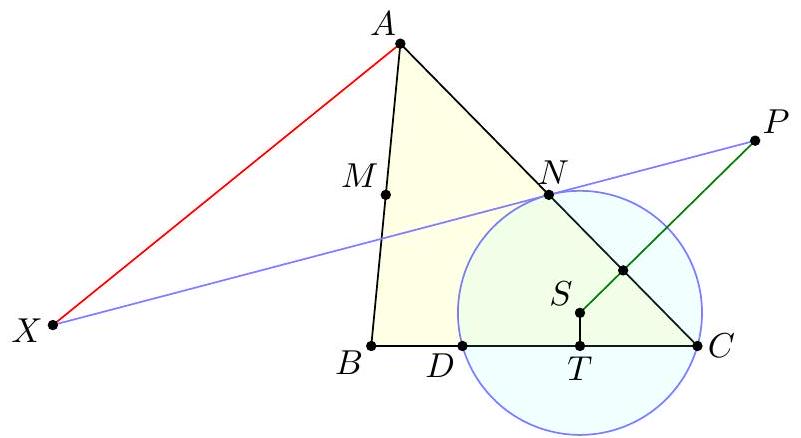 - The map $X \mapsto P$ is projective since it is a perspectivity through $N$ from $\overline{A A}$ to $\ell$. - The map $P \mapsto S$ is projective since it is equivalent to a negative inversion on $\ell$ at the midpoint of $\overline{N C}$ with radius $\frac{1}{2} N C$. (Note $\angle P N S=90^{\circ}$ is fixed.) - The map $S \mapsto T$ is projective since it is a perspectivity $\ell \rightarrow \overline{B C}$ through the point at infinity perpendicular to $\overline{B C}$ (in fact, it is linear). - The map $T \mapsto D$ is projective (in fact, linear) since it is a homothety through $C$ with fixed ratio 2 . Thus the composed map is projective as well. Similarly, if we define $D^{\prime}$ so that $\overline{X M}$ is tangent to $\left(B M D^{\prime}\right)$, the map $X \mapsto D^{\prime}$ is projective as well. We aim to show $D=D^{\prime}$, and since the maps correspond to fractional linear transformations in projective coordinates, it suffices to verify it for three distinct choices of $X$. We do so: - If $X=\overline{A A} \cap \overline{M N}$, then $D$ and $D^{\prime}$ satisfy $M B=M D^{\prime}, N C=N D$. This means they are the feet of the $A$-altitude on $\overline{B C}$. - If $X$ is a point at infinity along $\overline{A A}$, then $D$ and $D^{\prime}$ coincide with the midpoint of $\overline{B C}$. Remark (Anant Mudgal). An alternative (shorter) way to show $X \mapsto D$ is projective is to notice $\measuredangle X N D$ is a constant angle. I left the longer "original" proof for instructional reasons.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
【 Third solution by moving points method. Fix triangle $A B C$ and animate $X$ along the tangent at $A$. We let $D$ denote the second intersection point of $\omega_{C}$ with line $\overline{B C}$. Claim - The composed map $X \mapsto D$ is a fractional linear transformation (i.e. a projective map) in terms of a real coordinate on line $\overline{A A}, \overline{B C}$. We claim that the composed map $$ \begin{aligned} & \overline{A A} \rightarrow \ell \rightarrow \ell \rightarrow \overline{B C} \rightarrow \overline{B C} \\ & \text { by } \quad X \mapsto P \mapsto S \mapsto T \mapsto D \end{aligned} $$ is projective, by showing each individual map is projective.  - The map $X \mapsto P$ is projective since it is a perspectivity through $N$ from $\overline{A A}$ to $\ell$. - The map $P \mapsto S$ is projective since it is equivalent to a negative inversion on $\ell$ at the midpoint of $\overline{N C}$ with radius $\frac{1}{2} N C$. (Note $\angle P N S=90^{\circ}$ is fixed.) - The map $S \mapsto T$ is projective since it is a perspectivity $\ell \rightarrow \overline{B C}$ through the point at infinity perpendicular to $\overline{B C}$ (in fact, it is linear). - The map $T \mapsto D$ is projective (in fact, linear) since it is a homothety through $C$ with fixed ratio 2 . Thus the composed map is projective as well. Similarly, if we define $D^{\prime}$ so that $\overline{X M}$ is tangent to $\left(B M D^{\prime}\right)$, the map $X \mapsto D^{\prime}$ is projective as well. We aim to show $D=D^{\prime}$, and since the maps correspond to fractional linear transformations in projective coordinates, it suffices to verify it for three distinct choices of $X$. We do so: - If $X=\overline{A A} \cap \overline{M N}$, then $D$ and $D^{\prime}$ satisfy $M B=M D^{\prime}, N C=N D$. This means they are the feet of the $A$-altitude on $\overline{B C}$. - If $X$ is a point at infinity along $\overline{A A}$, then $D$ and $D^{\prime}$ coincide with the midpoint of $\overline{B C}$. Remark (Anant Mudgal). An alternative (shorter) way to show $X \mapsto D$ is projective is to notice $\measuredangle X N D$ is a constant angle. I left the longer "original" proof for instructional reasons.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
089a9306-7e00-588b-bca5-a1448f7fd14f
| 246,666 |
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
ब Fourth solution by isogonal conjugates (Anant Mudgal). Let $Y$ be the isogonal conjugate of $X$ in $\triangle A M N$ and $Z$ be the reflection of $Y$ in $\overline{M N}$. As $\overline{A X}$ is tangent to the circumcircle of $\triangle A M N$, it follows that $\overline{A Y} \| \overline{M N}$. Thus $Z$ lies on $\overline{B C}$ since $\overline{M N}$ bisects the strip made by $\overline{A Y}$ and $\overline{B C}$. 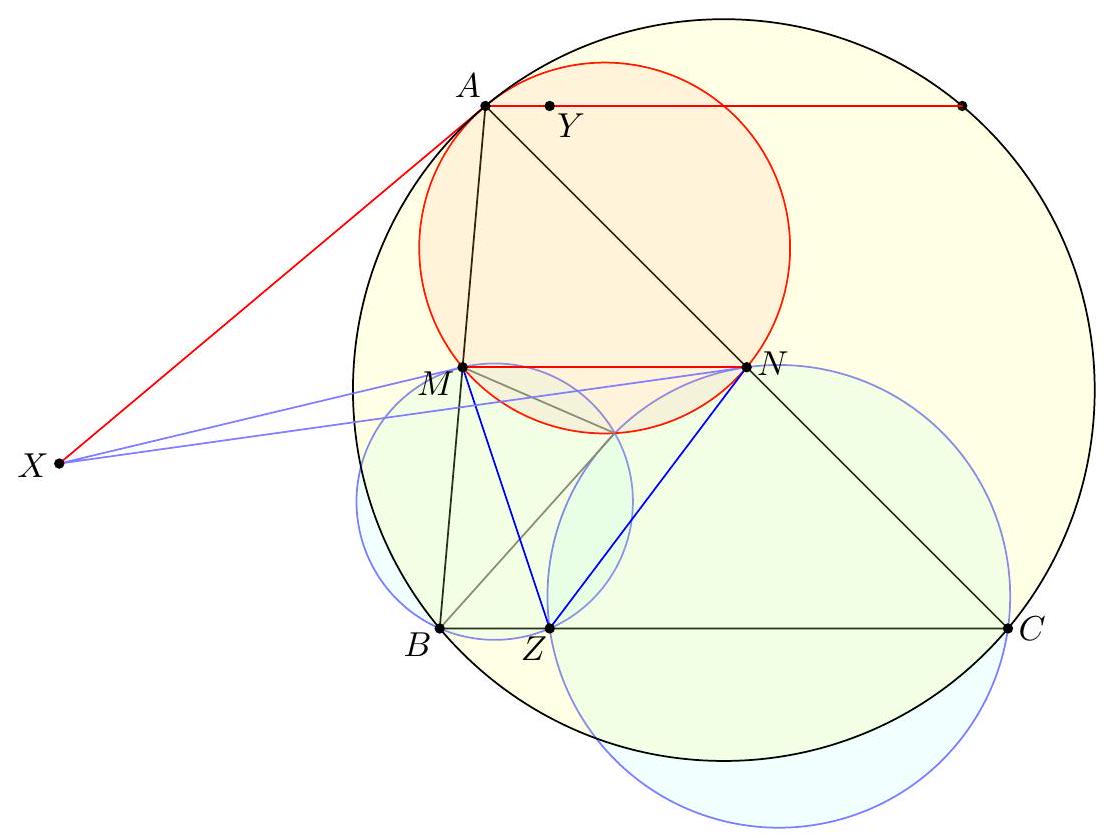 Finally, $$ \measuredangle Z M X=\measuredangle Z M N+\measuredangle N M X=\measuredangle N M Y+\measuredangle Y M A=\measuredangle N M A=\measuredangle Z B M $$ so $\overline{X M}$ is tangent to the circumcircle of $\triangle Z M B$, hence $Z$ lies on $\omega_{B}$. Similarly, $Z$ lies on $\omega_{C}$ and we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $M$ and $N$ denote the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Let $X$ be a point such that $\overline{A X}$ is tangent to the circumcircle of triangle $A B C$. Denote by $\omega_{B}$ the circle through $M$ and $B$ tangent to $\overline{M X}$, and by $\omega_{C}$ the circle through $N$ and $C$ tangent to $\overline{N X}$. Show that $\omega_{B}$ and $\omega_{C}$ intersect on line $B C$.
|
ब Fourth solution by isogonal conjugates (Anant Mudgal). Let $Y$ be the isogonal conjugate of $X$ in $\triangle A M N$ and $Z$ be the reflection of $Y$ in $\overline{M N}$. As $\overline{A X}$ is tangent to the circumcircle of $\triangle A M N$, it follows that $\overline{A Y} \| \overline{M N}$. Thus $Z$ lies on $\overline{B C}$ since $\overline{M N}$ bisects the strip made by $\overline{A Y}$ and $\overline{B C}$.  Finally, $$ \measuredangle Z M X=\measuredangle Z M N+\measuredangle N M X=\measuredangle N M Y+\measuredangle Y M A=\measuredangle N M A=\measuredangle Z B M $$ so $\overline{X M}$ is tangent to the circumcircle of $\triangle Z M B$, hence $Z$ lies on $\omega_{B}$. Similarly, $Z$ lies on $\omega_{C}$ and we're done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
089a9306-7e00-588b-bca5-a1448f7fd14f
| 246,666 |
We say a function $f: \mathbb{Z}_{\geq 0} \times \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}$ is great if for any nonnegative integers $m$ and $n$, $$ f(m+1, n+1) f(m, n)-f(m+1, n) f(m, n+1)=1 $$ If $A=\left(a_{0}, a_{1}, \ldots\right)$ and $B=\left(b_{0}, b_{1}, \ldots\right)$ are two sequences of integers, we write $A \sim B$ if there exists a great function $f$ satisfying $f(n, 0)=a_{n}$ and $f(0, n)=b_{n}$ for every nonnegative integer $n$ (in particular, $a_{0}=b_{0}$ ). Prove that if $A, B, C$, and $D$ are four sequences of integers satisfying $A \sim B$, $B \sim C$, and $C \sim D$, then $D \sim A$.
|
【 First solution (Nikolai Beluhov). Let $k=a_{0}=b_{0}=c_{0}=d_{0}$. We let $f, g, h$ be great functions for $(A, B),(B, C),(C, D)$ and write the following infinite array: $$ \left[\begin{array}{ccccccc} & \vdots & \vdots & b_{3} & \vdots & \vdots & \\ \cdots & g(2,2) & g(2,1) & b_{2} & f(1,2) & f(2,2) & \cdots \\ \cdots & g(1,2) & g(1,1) & b_{1} & f(1,1) & f(2,1) & \cdots \\ c_{3} & c_{2} & c_{1} & k & a_{1} & a_{2} & a_{3} \\ \cdots & h(2,1) & h(1,1) & d_{1} & & & \\ \cdots & h(2,2) & h(1,2) & d_{2} & & & \\ & \vdots & \vdots & d_{3} & & & \ddots \end{array}\right] $$ The greatness condition is then equivalent to saying that any $2 \times 2$ sub-grid has determinant $\pm 1$ (the sign is +1 in two quadrants and -1 in the other two), and we wish to fill in the lower-right quadrant. To this end, it suffices to prove the following. ## Lemma Suppose we have a $3 \times 3$ sub-grid $$ \left[\begin{array}{lll} a & b & c \\ x & y & z \\ p & q & \end{array}\right] $$ satisfying the determinant conditions. Then we can fill in the ninth entry in the lower right with an integer while retaining greatness. If $y=0$ we have $-1=b z=b x=x q$, hence $q z=-1$, and we can fill in the entry arbitrarily. Otherwise, we have $b x \equiv x q \equiv b z \equiv-1(\bmod y)$. This is enough to imply $q z \equiv-1$ $(\bmod y)$, and so we can fill in the integer $\frac{q z+1}{y}$. Remark. In this case (of all +1 determinants), I think it turns out the bottom entry is exactly equal to $q z a-c y p-c-p$, which is obviously an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
We say a function $f: \mathbb{Z}_{\geq 0} \times \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}$ is great if for any nonnegative integers $m$ and $n$, $$ f(m+1, n+1) f(m, n)-f(m+1, n) f(m, n+1)=1 $$ If $A=\left(a_{0}, a_{1}, \ldots\right)$ and $B=\left(b_{0}, b_{1}, \ldots\right)$ are two sequences of integers, we write $A \sim B$ if there exists a great function $f$ satisfying $f(n, 0)=a_{n}$ and $f(0, n)=b_{n}$ for every nonnegative integer $n$ (in particular, $a_{0}=b_{0}$ ). Prove that if $A, B, C$, and $D$ are four sequences of integers satisfying $A \sim B$, $B \sim C$, and $C \sim D$, then $D \sim A$.
|
【 First solution (Nikolai Beluhov). Let $k=a_{0}=b_{0}=c_{0}=d_{0}$. We let $f, g, h$ be great functions for $(A, B),(B, C),(C, D)$ and write the following infinite array: $$ \left[\begin{array}{ccccccc} & \vdots & \vdots & b_{3} & \vdots & \vdots & \\ \cdots & g(2,2) & g(2,1) & b_{2} & f(1,2) & f(2,2) & \cdots \\ \cdots & g(1,2) & g(1,1) & b_{1} & f(1,1) & f(2,1) & \cdots \\ c_{3} & c_{2} & c_{1} & k & a_{1} & a_{2} & a_{3} \\ \cdots & h(2,1) & h(1,1) & d_{1} & & & \\ \cdots & h(2,2) & h(1,2) & d_{2} & & & \\ & \vdots & \vdots & d_{3} & & & \ddots \end{array}\right] $$ The greatness condition is then equivalent to saying that any $2 \times 2$ sub-grid has determinant $\pm 1$ (the sign is +1 in two quadrants and -1 in the other two), and we wish to fill in the lower-right quadrant. To this end, it suffices to prove the following. ## Lemma Suppose we have a $3 \times 3$ sub-grid $$ \left[\begin{array}{lll} a & b & c \\ x & y & z \\ p & q & \end{array}\right] $$ satisfying the determinant conditions. Then we can fill in the ninth entry in the lower right with an integer while retaining greatness. If $y=0$ we have $-1=b z=b x=x q$, hence $q z=-1$, and we can fill in the entry arbitrarily. Otherwise, we have $b x \equiv x q \equiv b z \equiv-1(\bmod y)$. This is enough to imply $q z \equiv-1$ $(\bmod y)$, and so we can fill in the integer $\frac{q z+1}{y}$. Remark. In this case (of all +1 determinants), I think it turns out the bottom entry is exactly equal to $q z a-c y p-c-p$, which is obviously an integer.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
0d0737c3-2cc3-5f31-be07-bd3b314b8a84
| 606,420 |
We say a function $f: \mathbb{Z}_{\geq 0} \times \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}$ is great if for any nonnegative integers $m$ and $n$, $$ f(m+1, n+1) f(m, n)-f(m+1, n) f(m, n+1)=1 $$ If $A=\left(a_{0}, a_{1}, \ldots\right)$ and $B=\left(b_{0}, b_{1}, \ldots\right)$ are two sequences of integers, we write $A \sim B$ if there exists a great function $f$ satisfying $f(n, 0)=a_{n}$ and $f(0, n)=b_{n}$ for every nonnegative integer $n$ (in particular, $a_{0}=b_{0}$ ). Prove that if $A, B, C$, and $D$ are four sequences of integers satisfying $A \sim B$, $B \sim C$, and $C \sim D$, then $D \sim A$.
|
Second solution (Ankan Bhattacharya). We will give an explicit classification of great sequences: ## Lemma The pair $(A, B)$ is great if and only if $a_{0}=b_{0}, a_{0} \mid a_{1} b_{1}+1$, and $a_{n} \mid a_{n-1}+a_{n+1}$ and $b_{n} \mid b_{n-1}+b_{n+1}$ for all $n$. Now, focus on six entries $f(x, y)$ with $x \in\{n-1, n, n+1\}$ and $y \in\{0,1\}$. Let $f(n-1,1)=u, f(n, 1)=v$, and $f(n+1,1)=w$, so $$ \begin{aligned} v a_{n-1}-u a_{n} & =1 \\ w a_{n}-v a_{n+1} & =1 \end{aligned} $$ Then $$ u+w=\frac{v\left(a_{n-1}+a_{n+1}\right)}{a_{n}} $$ and from above $\operatorname{gcd}\left(v, a_{n}\right)=1$, so $a_{n} \mid a_{n-1}+a_{n+1}$; similarly for $b_{n}$. (If $a_{n}=0$, we have $v a_{n-1}=1$ and $v a_{n+1}=-1$, so this is OK.) First we set $f(1,1)$ so that $a_{0} f(1,1)=a_{1} b_{1}+1$, which is possible. Consider an uninitialized $f(s, t)$; without loss of generality suppose $s \geq 2$. Then we know five values of $f$ and wish to set a sixth one $z$, as in the matrix below: $$ \begin{array}{cc} u & x \\ v & y \\ w & z \end{array} $$ (We imagine $a$-indices to increase southwards and $b$-indices to increase eastwards.) If $v \neq 0$, then the choice $y \cdot \frac{u+w}{v}-x$ works as $u y-v x=1$. If $v=0$, it easily follows that $\{u, w\}=\{1,-1\}$ and $y=w$ as $y w=1$. Then we set the uninitialized entry to anything. Now we verify that this is compatible with the inductive hypothesis. From the determinant 1 condition, it easily follows that $\operatorname{gcd}(w, z)=\operatorname{gcd}(v, z)=1$. The proof that $y \mid x+z$ is almost identical to a step performed in the "necessary" part of the lemma and we do not repeat it here. By induction, a desired great function $f$ exists. Remark. To simplify the problem, we may restrict the codomain of great functions and elements in great pairs of sequences to $\mathbb{Z}_{>0}$. This allows the parts of the solution dealing with zero entries to be ignored. $$ f(x+1, y+1) f(x, y)-f(x+1, y) f(x, y+1)=-1 $$ A quick counterexample to transitivity of $\sim$ as is without the condition $f(0,0)=1$, for concreteness: let $a_{n}=c_{n}=3+n$ and $b_{n}=3+2 n$ for $n \geq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
We say a function $f: \mathbb{Z}_{\geq 0} \times \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}$ is great if for any nonnegative integers $m$ and $n$, $$ f(m+1, n+1) f(m, n)-f(m+1, n) f(m, n+1)=1 $$ If $A=\left(a_{0}, a_{1}, \ldots\right)$ and $B=\left(b_{0}, b_{1}, \ldots\right)$ are two sequences of integers, we write $A \sim B$ if there exists a great function $f$ satisfying $f(n, 0)=a_{n}$ and $f(0, n)=b_{n}$ for every nonnegative integer $n$ (in particular, $a_{0}=b_{0}$ ). Prove that if $A, B, C$, and $D$ are four sequences of integers satisfying $A \sim B$, $B \sim C$, and $C \sim D$, then $D \sim A$.
|
Second solution (Ankan Bhattacharya). We will give an explicit classification of great sequences: ## Lemma The pair $(A, B)$ is great if and only if $a_{0}=b_{0}, a_{0} \mid a_{1} b_{1}+1$, and $a_{n} \mid a_{n-1}+a_{n+1}$ and $b_{n} \mid b_{n-1}+b_{n+1}$ for all $n$. Now, focus on six entries $f(x, y)$ with $x \in\{n-1, n, n+1\}$ and $y \in\{0,1\}$. Let $f(n-1,1)=u, f(n, 1)=v$, and $f(n+1,1)=w$, so $$ \begin{aligned} v a_{n-1}-u a_{n} & =1 \\ w a_{n}-v a_{n+1} & =1 \end{aligned} $$ Then $$ u+w=\frac{v\left(a_{n-1}+a_{n+1}\right)}{a_{n}} $$ and from above $\operatorname{gcd}\left(v, a_{n}\right)=1$, so $a_{n} \mid a_{n-1}+a_{n+1}$; similarly for $b_{n}$. (If $a_{n}=0$, we have $v a_{n-1}=1$ and $v a_{n+1}=-1$, so this is OK.) First we set $f(1,1)$ so that $a_{0} f(1,1)=a_{1} b_{1}+1$, which is possible. Consider an uninitialized $f(s, t)$; without loss of generality suppose $s \geq 2$. Then we know five values of $f$ and wish to set a sixth one $z$, as in the matrix below: $$ \begin{array}{cc} u & x \\ v & y \\ w & z \end{array} $$ (We imagine $a$-indices to increase southwards and $b$-indices to increase eastwards.) If $v \neq 0$, then the choice $y \cdot \frac{u+w}{v}-x$ works as $u y-v x=1$. If $v=0$, it easily follows that $\{u, w\}=\{1,-1\}$ and $y=w$ as $y w=1$. Then we set the uninitialized entry to anything. Now we verify that this is compatible with the inductive hypothesis. From the determinant 1 condition, it easily follows that $\operatorname{gcd}(w, z)=\operatorname{gcd}(v, z)=1$. The proof that $y \mid x+z$ is almost identical to a step performed in the "necessary" part of the lemma and we do not repeat it here. By induction, a desired great function $f$ exists. Remark. To simplify the problem, we may restrict the codomain of great functions and elements in great pairs of sequences to $\mathbb{Z}_{>0}$. This allows the parts of the solution dealing with zero entries to be ignored. $$ f(x+1, y+1) f(x, y)-f(x+1, y) f(x, y+1)=-1 $$ A quick counterexample to transitivity of $\sim$ as is without the condition $f(0,0)=1$, for concreteness: let $a_{n}=c_{n}=3+n$ and $b_{n}=3+2 n$ for $n \geq 0$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
0d0737c3-2cc3-5f31-be07-bd3b314b8a84
| 606,420 |
Let $n$ be a positive integer. Tasty and Stacy are given a circular necklace with $3 n$ sapphire beads and $3 n$ turquoise beads, such that no three consecutive beads have the same color. They play a cooperative game where they alternate turns removing three consecutive beads, subject to the following conditions: - Tasty must remove three consecutive beads which are turquoise, sapphire, and turquoise, in that order, on each of his turns. - Stacy must remove three consecutive beads which are sapphire, turquoise, and sapphire, in that order, on each of her turns. They win if all the beads are removed in $2 n$ turns. Prove that if they can win with Tasty going first, they can also win with Stacy going first.
|
In the necklace, we draw a divider between any two beads of the same color. Unless there are no dividers, this divides the necklace into several zigzags in which the beads in each zigzag alternate. Each zigzag has two endpoints (adjacent to dividers). Observe that the condition about not having three consecutive matching beads is equivalent to saying there are no zigzags of lengths 1.  The main claim is that the game is winnable (for either player going first) if and only if there are at most $2 n$ dividers. We prove this in two parts, the first part not using the hypothesis about three consecutive letters. Claim - The game cannot be won with Tasty going first if there are more than $2 n$ dividers. Consider removing a TST in some zigzag (necessarily of length at least 3). We illustrate the three possibilities in the following table, with Tasty's move shown in red. | Before | After | Change | | :---: | :---: | :---: | | . ST \| TST | TS . | ST \| TS . | One less divider; two zigzags merge | | . . ST \| TSTST . | STST | One less divider; two zigzags merge | | .STSTS . . | ..S\|S... | One more divider; a zigzag splits in t | The analysis for Stacy's move is identical. Claim - If there are at most $2 n$ dividers and there are no zigzags of length 1 then the game can be won (with either player going first). At any point if there are no dividers at all, then the necklace alternates $T S T S T \ldots$ and the game can be won. So we will prove that on each of Tasty's turns, if there exists at least one divider, then Tasty and Stacy can each make a move at an endpoint of some zigzag (i.e. the first two cases above). As we saw in the previous proof, such moves will (a) decrease the number of dividers by exactly one, (b) not introduce any singleton zigzags (because the old zigzags merge, rather than split). Since there are fewer than $2 n$ dividers, our duo can eliminate all dividers and then win. Note that as the number of $S$ and $T$ 's are equal, there must be an equal number of - zigzags of odd length ( $\geq 3$ ) with $T$ at the endpoints (i.e. one more $T$ than $S$ ), and - zigzags of odd length $(\geq 3)$ with $S$ at the endpoints (i.e. one more $S$ than $T$ ). Now iff there is at least one of each, then Tasty removes a TST from the end of such a zigzag while Stacy removes an $S T S$ from the end of such a zigzag. Otherwise suppose all zigzags have even size. Then Tasty finds any zigzag of length $\geq 4$ (which must exist since the average zigzag length is 3 ) and removes TST from the end containing $T$. The resulting merged zigzag is odd and hence $S$ endpoints, hence Stacy can move as well. Remark. There are many equivalent ways to phrase the solution. For example, the number of dividers is equal to the number of pairs of two consecutive letters (rather than singleton letters). So the win condition can also be phrased in terms of the number of adjacent pairs of letters being at least $2 n$, or equivalently the number of differing pairs being at least $4 n$. If one thinks about the game as a process, this is a natural "monovariant" to consider anyways, so the solution is not so unmotivated. Remark. The constraint of no three consecutive identical beads is actually needed: a counterexample without this constraint is TTSTSTSTTSSS. (They win if Tasty goes first and lose if Stacy goes first.) Remark (Why induction is unlikely to work). Many contestants attempted induction. However, in doing so they often implicitly proved a different problem: "prove that if they can win with Tasty going first without ever creating a triplet, they can also win in such a way with Stacy going first". This essentially means nearly all induction attempts fail. Amusingly, even the modified problem (which is much more amenable to induction) sill seems difficult without some sort of global argument. Consider a position in which Tasty wins going first, with the sequence of winning moves being Tasty's first move in red below and Stacy's second move in blue below:  There is no "nearby" STS that Stacy can remove instead on her first turn, without introducing a triple- $T$ and also preventing Tasty from taking a TST. So it does not seem possible to easily change a Tasty-first winning sequence to a Stacy-first one, even in the modified version.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. Tasty and Stacy are given a circular necklace with $3 n$ sapphire beads and $3 n$ turquoise beads, such that no three consecutive beads have the same color. They play a cooperative game where they alternate turns removing three consecutive beads, subject to the following conditions: - Tasty must remove three consecutive beads which are turquoise, sapphire, and turquoise, in that order, on each of his turns. - Stacy must remove three consecutive beads which are sapphire, turquoise, and sapphire, in that order, on each of her turns. They win if all the beads are removed in $2 n$ turns. Prove that if they can win with Tasty going first, they can also win with Stacy going first.
|
In the necklace, we draw a divider between any two beads of the same color. Unless there are no dividers, this divides the necklace into several zigzags in which the beads in each zigzag alternate. Each zigzag has two endpoints (adjacent to dividers). Observe that the condition about not having three consecutive matching beads is equivalent to saying there are no zigzags of lengths 1.  The main claim is that the game is winnable (for either player going first) if and only if there are at most $2 n$ dividers. We prove this in two parts, the first part not using the hypothesis about three consecutive letters. Claim - The game cannot be won with Tasty going first if there are more than $2 n$ dividers. Consider removing a TST in some zigzag (necessarily of length at least 3). We illustrate the three possibilities in the following table, with Tasty's move shown in red. | Before | After | Change | | :---: | :---: | :---: | | . ST \| TST | TS . | ST \| TS . | One less divider; two zigzags merge | | . . ST \| TSTST . | STST | One less divider; two zigzags merge | | .STSTS . . | ..S\|S... | One more divider; a zigzag splits in t | The analysis for Stacy's move is identical. Claim - If there are at most $2 n$ dividers and there are no zigzags of length 1 then the game can be won (with either player going first). At any point if there are no dividers at all, then the necklace alternates $T S T S T \ldots$ and the game can be won. So we will prove that on each of Tasty's turns, if there exists at least one divider, then Tasty and Stacy can each make a move at an endpoint of some zigzag (i.e. the first two cases above). As we saw in the previous proof, such moves will (a) decrease the number of dividers by exactly one, (b) not introduce any singleton zigzags (because the old zigzags merge, rather than split). Since there are fewer than $2 n$ dividers, our duo can eliminate all dividers and then win. Note that as the number of $S$ and $T$ 's are equal, there must be an equal number of - zigzags of odd length ( $\geq 3$ ) with $T$ at the endpoints (i.e. one more $T$ than $S$ ), and - zigzags of odd length $(\geq 3)$ with $S$ at the endpoints (i.e. one more $S$ than $T$ ). Now iff there is at least one of each, then Tasty removes a TST from the end of such a zigzag while Stacy removes an $S T S$ from the end of such a zigzag. Otherwise suppose all zigzags have even size. Then Tasty finds any zigzag of length $\geq 4$ (which must exist since the average zigzag length is 3 ) and removes TST from the end containing $T$. The resulting merged zigzag is odd and hence $S$ endpoints, hence Stacy can move as well. Remark. There are many equivalent ways to phrase the solution. For example, the number of dividers is equal to the number of pairs of two consecutive letters (rather than singleton letters). So the win condition can also be phrased in terms of the number of adjacent pairs of letters being at least $2 n$, or equivalently the number of differing pairs being at least $4 n$. If one thinks about the game as a process, this is a natural "monovariant" to consider anyways, so the solution is not so unmotivated. Remark. The constraint of no three consecutive identical beads is actually needed: a counterexample without this constraint is TTSTSTSTTSSS. (They win if Tasty goes first and lose if Stacy goes first.) Remark (Why induction is unlikely to work). Many contestants attempted induction. However, in doing so they often implicitly proved a different problem: "prove that if they can win with Tasty going first without ever creating a triplet, they can also win in such a way with Stacy going first". This essentially means nearly all induction attempts fail. Amusingly, even the modified problem (which is much more amenable to induction) sill seems difficult without some sort of global argument. Consider a position in which Tasty wins going first, with the sequence of winning moves being Tasty's first move in red below and Stacy's second move in blue below:  There is no "nearby" STS that Stacy can remove instead on her first turn, without introducing a triple- $T$ and also preventing Tasty from taking a TST. So it does not seem possible to easily change a Tasty-first winning sequence to a Stacy-first one, even in the modified version.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
829ab5b7-0b9c-5d49-8f0f-dadf85a0c3a4
| 606,425 |
Let $A B C$ be a triangle with incenter $I$, and let $D$ be a point on line $B C$ satisfying $\angle A I D=90^{\circ}$. Let the excircle of triangle $A B C$ opposite the vertex $A$ be tangent to $\overline{B C}$ at point $A_{1}$. Define points $B_{1}$ on $\overline{C A}$ and $C_{1}$ on $\overline{A B}$ analogously, using the excircles opposite $B$ and $C$, respectively. Prove that if quadrilateral $A B_{1} A_{1} C_{1}$ is cyclic, then $\overline{A D}$ is tangent to the circumcircle of $\triangle D B_{1} C_{1}$.
|
【 First solution using spiral similarity (Ankan Bhattacharya). First, we prove the part of the problem which does not depend on the condition $A B_{1} A_{1} C_{1}$ is cyclic. ## Lemma Let $A B C$ be a triangle and define $I, D, B_{1}, C_{1}$ as in the problem. Moreover, let $M$ denote the midpoint of $\overline{A D}$. Then $\overline{A D}$ is tangent to $\left(A B_{1} C_{1}\right)$, and moreover $\overline{B_{1} C_{1}} \| \overline{I M}$. Note that $A, Z, D$ are collinear, by radical axis on $(A B C),(A F I E),(B I C)$. 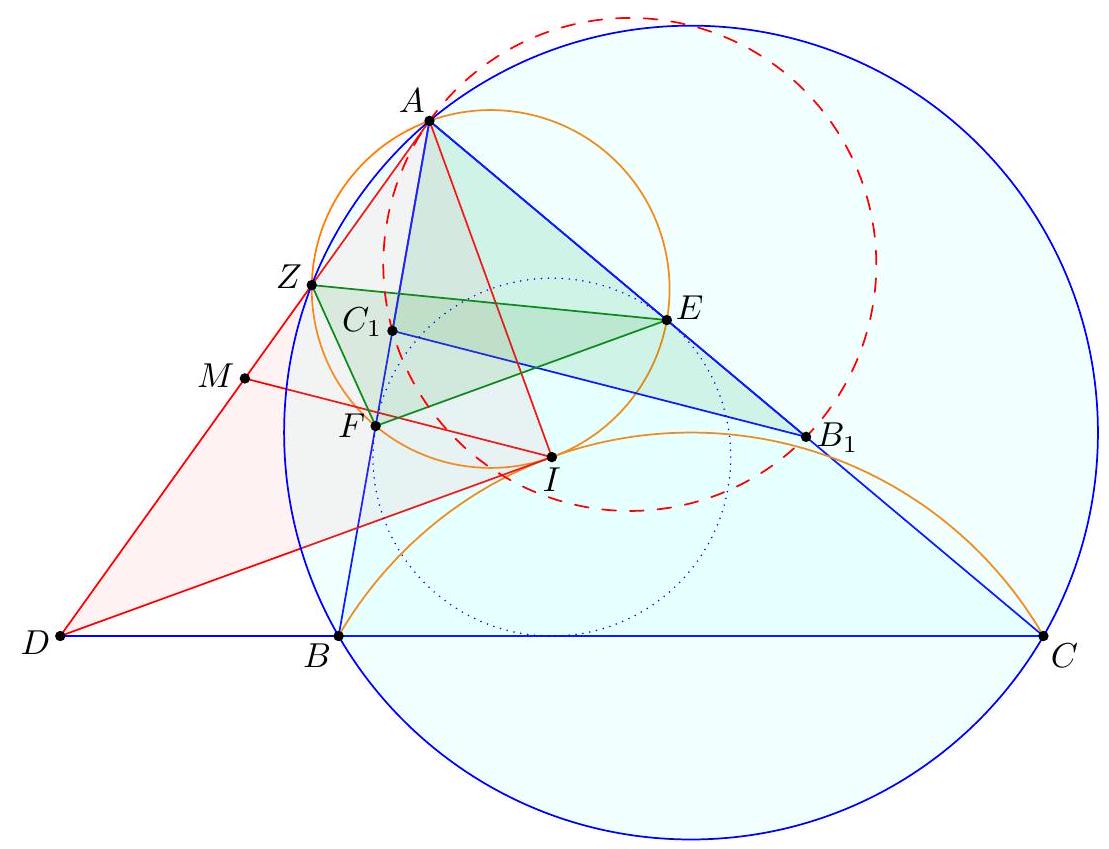 Then the spiral similarity gives us $$ \frac{Z F}{Z E}=\frac{B F}{C E}=\frac{A C_{1}}{A B_{1}} $$ which together with $\measuredangle F Z E=\measuredangle F A E=\measuredangle B A C$ implies that $\triangle Z F E$ and $\triangle A C_{1} B_{1}$ are (directly) similar. (See IMO Shortlist 2006 G9 for a similar application of spiral similarity.) $$ \measuredangle D A C_{1}=\measuredangle Z A F=\measuredangle Z E F=\measuredangle A B_{1} C_{1} $$ we have $\overline{A D}$ is tangent to $\left(A B_{1} C_{1}\right)$. Moreover, to see that $\overline{I M} \| \overline{B_{1} C_{1}}$, write $$ \begin{aligned} \measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right) & =\measuredangle I A C+\measuredangle A B_{1} C_{1}=\measuredangle B A I+\measuredangle Z E F=\measuredangle F A I+\measuredangle Z A F \\ & =\measuredangle Z A I=\measuredangle M A I=\measuredangle A I M \end{aligned} $$ the last step since $\triangle A I D$ is right with hypotenuse $\overline{A D}$, and median $\overline{I M}$. Now we return to the present problem with the additional condition. 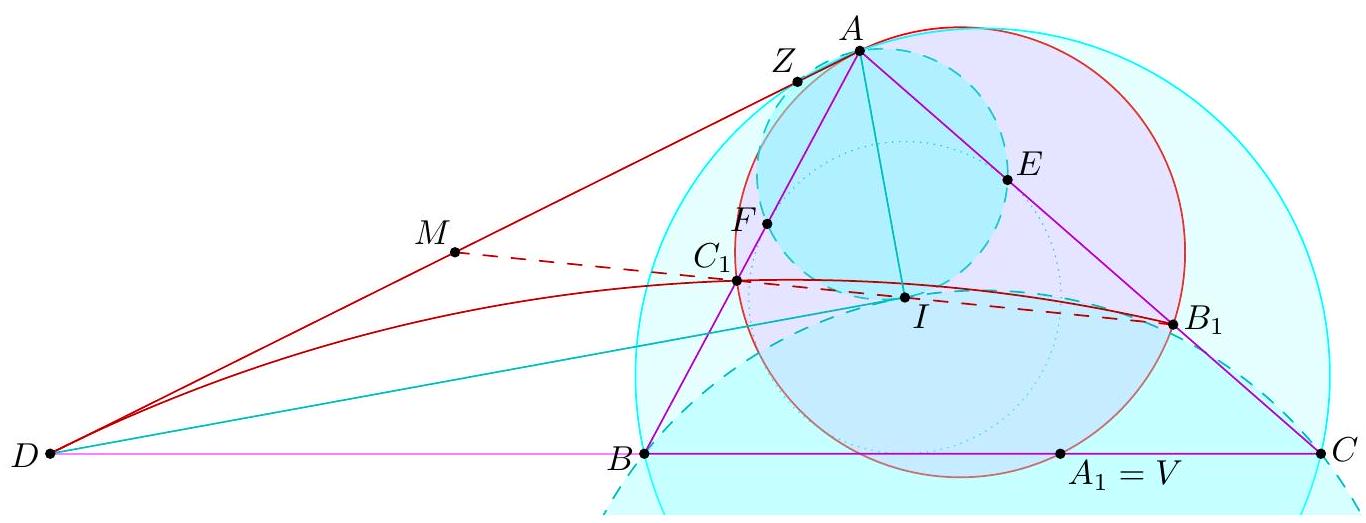 Claim - Given the condition, we actually have $\angle A B_{1} A_{1}=\angle A C_{1} A_{1}=90^{\circ}$. Now $\triangle A B_{1} C_{1}$ has circumdiameter $\overline{A V}$. We are given $A_{1}$ lies on this circle, so if $V \neq A_{1}$ then $\overline{A A_{1}} \perp \overline{A_{1} V}$. But $\overline{A_{1} V} \perp \overline{B C}$ by definition, which would imply $\overline{A A_{1}} \| \overline{B C}$, which is absurd. Claim - Given the condition the points $B_{1}, I, C_{1}$ are collinear (hence with $M$ ). To finish, since $\overline{D M A}$ was tangent to the circumcircle of $\triangle A B_{1} C_{1}$, we have $M D^{2}=$ $M A^{2}=M C_{1} \cdot M B_{1}$, implying the required tangency. Remark. The triangles satisfying the problem hypothesis are exactly the ones satisfying $r_{A}=2 R$, where $R$ and $r_{A}$ denote the circumradius and $A$-exradius. Remark. If $P$ is the foot of the $A$-altitude then this should also imply $A B_{1} P C_{1}$ is harmonic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$, and let $D$ be a point on line $B C$ satisfying $\angle A I D=90^{\circ}$. Let the excircle of triangle $A B C$ opposite the vertex $A$ be tangent to $\overline{B C}$ at point $A_{1}$. Define points $B_{1}$ on $\overline{C A}$ and $C_{1}$ on $\overline{A B}$ analogously, using the excircles opposite $B$ and $C$, respectively. Prove that if quadrilateral $A B_{1} A_{1} C_{1}$ is cyclic, then $\overline{A D}$ is tangent to the circumcircle of $\triangle D B_{1} C_{1}$.
|
【 First solution using spiral similarity (Ankan Bhattacharya). First, we prove the part of the problem which does not depend on the condition $A B_{1} A_{1} C_{1}$ is cyclic. ## Lemma Let $A B C$ be a triangle and define $I, D, B_{1}, C_{1}$ as in the problem. Moreover, let $M$ denote the midpoint of $\overline{A D}$. Then $\overline{A D}$ is tangent to $\left(A B_{1} C_{1}\right)$, and moreover $\overline{B_{1} C_{1}} \| \overline{I M}$. Note that $A, Z, D$ are collinear, by radical axis on $(A B C),(A F I E),(B I C)$.  Then the spiral similarity gives us $$ \frac{Z F}{Z E}=\frac{B F}{C E}=\frac{A C_{1}}{A B_{1}} $$ which together with $\measuredangle F Z E=\measuredangle F A E=\measuredangle B A C$ implies that $\triangle Z F E$ and $\triangle A C_{1} B_{1}$ are (directly) similar. (See IMO Shortlist 2006 G9 for a similar application of spiral similarity.) $$ \measuredangle D A C_{1}=\measuredangle Z A F=\measuredangle Z E F=\measuredangle A B_{1} C_{1} $$ we have $\overline{A D}$ is tangent to $\left(A B_{1} C_{1}\right)$. Moreover, to see that $\overline{I M} \| \overline{B_{1} C_{1}}$, write $$ \begin{aligned} \measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right) & =\measuredangle I A C+\measuredangle A B_{1} C_{1}=\measuredangle B A I+\measuredangle Z E F=\measuredangle F A I+\measuredangle Z A F \\ & =\measuredangle Z A I=\measuredangle M A I=\measuredangle A I M \end{aligned} $$ the last step since $\triangle A I D$ is right with hypotenuse $\overline{A D}$, and median $\overline{I M}$. Now we return to the present problem with the additional condition.  Claim - Given the condition, we actually have $\angle A B_{1} A_{1}=\angle A C_{1} A_{1}=90^{\circ}$. Now $\triangle A B_{1} C_{1}$ has circumdiameter $\overline{A V}$. We are given $A_{1}$ lies on this circle, so if $V \neq A_{1}$ then $\overline{A A_{1}} \perp \overline{A_{1} V}$. But $\overline{A_{1} V} \perp \overline{B C}$ by definition, which would imply $\overline{A A_{1}} \| \overline{B C}$, which is absurd. Claim - Given the condition the points $B_{1}, I, C_{1}$ are collinear (hence with $M$ ). To finish, since $\overline{D M A}$ was tangent to the circumcircle of $\triangle A B_{1} C_{1}$, we have $M D^{2}=$ $M A^{2}=M C_{1} \cdot M B_{1}$, implying the required tangency. Remark. The triangles satisfying the problem hypothesis are exactly the ones satisfying $r_{A}=2 R$, where $R$ and $r_{A}$ denote the circumradius and $A$-exradius. Remark. If $P$ is the foot of the $A$-altitude then this should also imply $A B_{1} P C_{1}$ is harmonic.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
9c54d1c0-73f2-5266-bdc9-ac46057d6a21
| 604,168 |
Let $A B C$ be a triangle with incenter $I$, and let $D$ be a point on line $B C$ satisfying $\angle A I D=90^{\circ}$. Let the excircle of triangle $A B C$ opposite the vertex $A$ be tangent to $\overline{B C}$ at point $A_{1}$. Define points $B_{1}$ on $\overline{C A}$ and $C_{1}$ on $\overline{A B}$ analogously, using the excircles opposite $B$ and $C$, respectively. Prove that if quadrilateral $A B_{1} A_{1} C_{1}$ is cyclic, then $\overline{A D}$ is tangent to the circumcircle of $\triangle D B_{1} C_{1}$.
|
【 Second solution by inversion and mixtilinears (Anant Mudgal). As in the end of the preceding solution, we have $\angle A B_{1} A_{1}=\angle A C_{1} A_{1}=90^{\circ}$ and $I \in \overline{B_{1} C_{1}}$. Let $M$ be the midpoint of minor arc $B C$ and $N$ be the midpoint of $\operatorname{arc} \widehat{B A C}$. Let $L$ be the intouch point on $\overline{B C}$. Let $O$ be the circumcenter of $\triangle A B C$. Let $K=\overline{A I} \cap \overline{B C}$. 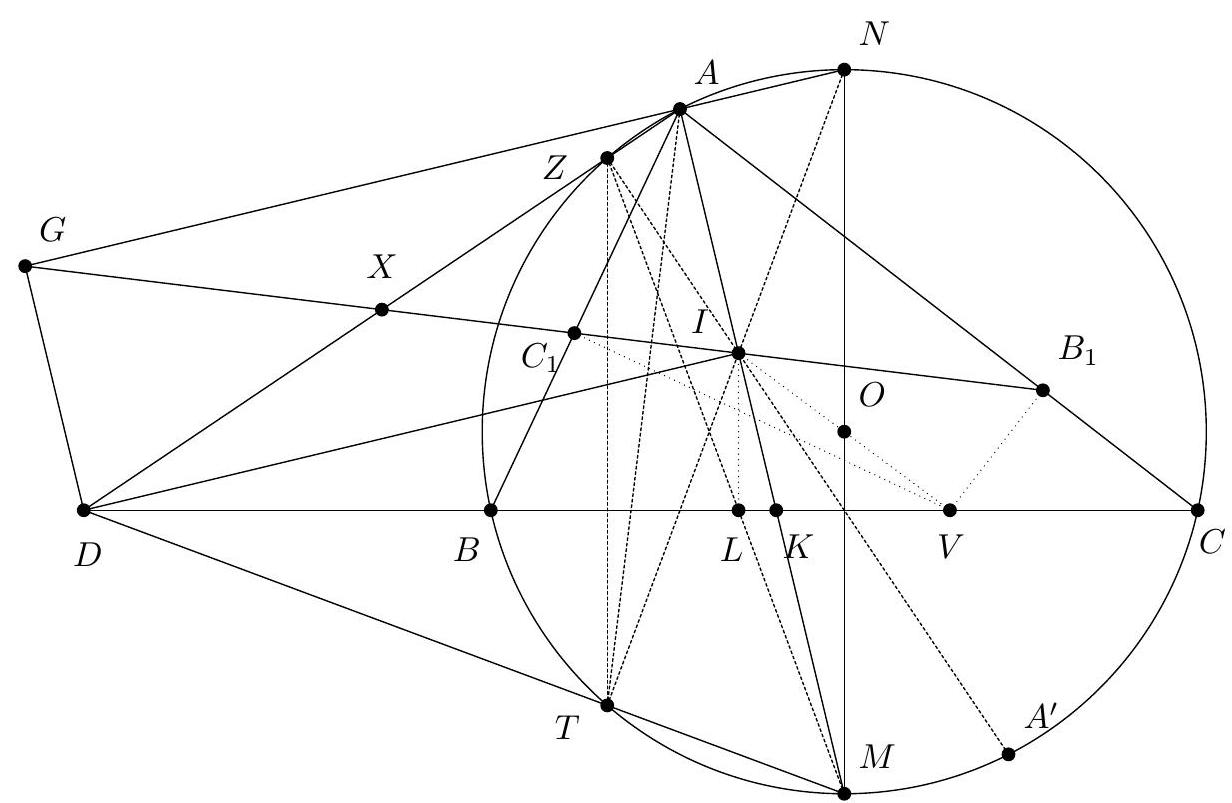 Claim — We have $\angle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)=\angle I A D$. Inversion in $(B I C)$ maps $\overline{A I}$ to $\overline{K I}$ and $(A B C)$ to $\overline{B C}$. Thus, $Z$ maps to $L$, so $Z, L, M$ are collinear. Since $B L=C V$ and $O I=O V$, we see that MLIN is a trapezoid with $\overline{I L} \| \overline{M N}$. Thus, $\overline{Z T} \| \overline{M N}$. It is known that $\overline{A T}$ and $\overline{A A_{1}}$ are isogonal in angle $B A C$. Since $\overline{A V}$ is a circumdiameter in $\left(A B_{1} C_{1}\right)$, so $\overline{A T} \perp \overline{B_{1} C_{1}}$. So $\measuredangle Z A I=\measuredangle N M T=90^{\circ}-\measuredangle T A I=\measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)$. Let $X$ be the midpoint of $\overline{A D}$ and $G$ be the reflection of $I$ in $X$. Since $A I D G$ is a rectangle, we have $\measuredangle A I G=\measuredangle Z A I=\measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)$, by the previous claim. So $\overline{I G}$ coincides with $\overline{B_{1} C_{1}}$. Now $\overline{A I}$ bisects $\angle B_{1} A C_{1}$ and $\angle I A G=90^{\circ}$, so $\left(\overline{I G} ; \overline{B_{1} C_{1}}\right)=-1$. Since $\angle I D G=90^{\circ}$, we see that $\overline{D I}$ and $\overline{D G}$ are bisectors of angle $B_{1} D C_{1}$. Now $\angle X D I=\angle X I D \Longrightarrow \angle X D C_{1}=\angle X I D-\angle I D B_{1}=\angle D B_{1} C_{1}$, so $\overline{X D}$ is tangent to $\left(D B_{1} C_{1}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$, and let $D$ be a point on line $B C$ satisfying $\angle A I D=90^{\circ}$. Let the excircle of triangle $A B C$ opposite the vertex $A$ be tangent to $\overline{B C}$ at point $A_{1}$. Define points $B_{1}$ on $\overline{C A}$ and $C_{1}$ on $\overline{A B}$ analogously, using the excircles opposite $B$ and $C$, respectively. Prove that if quadrilateral $A B_{1} A_{1} C_{1}$ is cyclic, then $\overline{A D}$ is tangent to the circumcircle of $\triangle D B_{1} C_{1}$.
|
【 Second solution by inversion and mixtilinears (Anant Mudgal). As in the end of the preceding solution, we have $\angle A B_{1} A_{1}=\angle A C_{1} A_{1}=90^{\circ}$ and $I \in \overline{B_{1} C_{1}}$. Let $M$ be the midpoint of minor arc $B C$ and $N$ be the midpoint of $\operatorname{arc} \widehat{B A C}$. Let $L$ be the intouch point on $\overline{B C}$. Let $O$ be the circumcenter of $\triangle A B C$. Let $K=\overline{A I} \cap \overline{B C}$.  Claim — We have $\angle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)=\angle I A D$. Inversion in $(B I C)$ maps $\overline{A I}$ to $\overline{K I}$ and $(A B C)$ to $\overline{B C}$. Thus, $Z$ maps to $L$, so $Z, L, M$ are collinear. Since $B L=C V$ and $O I=O V$, we see that MLIN is a trapezoid with $\overline{I L} \| \overline{M N}$. Thus, $\overline{Z T} \| \overline{M N}$. It is known that $\overline{A T}$ and $\overline{A A_{1}}$ are isogonal in angle $B A C$. Since $\overline{A V}$ is a circumdiameter in $\left(A B_{1} C_{1}\right)$, so $\overline{A T} \perp \overline{B_{1} C_{1}}$. So $\measuredangle Z A I=\measuredangle N M T=90^{\circ}-\measuredangle T A I=\measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)$. Let $X$ be the midpoint of $\overline{A D}$ and $G$ be the reflection of $I$ in $X$. Since $A I D G$ is a rectangle, we have $\measuredangle A I G=\measuredangle Z A I=\measuredangle\left(\overline{A I}, \overline{B_{1} C_{1}}\right)$, by the previous claim. So $\overline{I G}$ coincides with $\overline{B_{1} C_{1}}$. Now $\overline{A I}$ bisects $\angle B_{1} A C_{1}$ and $\angle I A G=90^{\circ}$, so $\left(\overline{I G} ; \overline{B_{1} C_{1}}\right)=-1$. Since $\angle I D G=90^{\circ}$, we see that $\overline{D I}$ and $\overline{D G}$ are bisectors of angle $B_{1} D C_{1}$. Now $\angle X D I=\angle X I D \Longrightarrow \angle X D C_{1}=\angle X I D-\angle I D B_{1}=\angle D B_{1} C_{1}$, so $\overline{X D}$ is tangent to $\left(D B_{1} C_{1}\right)$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
9c54d1c0-73f2-5266-bdc9-ac46057d6a21
| 604,168 |
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
ब First solution, elementary (original). We have $\triangle Y A C \sim \triangle Y B D$, from which it follows $$ \frac{d(Y, A C)}{d(Y, B D)}=\frac{A C}{B D} $$ Moreover, if we denote by $r_{1}$ and $r_{2}$ the radii of $\Gamma_{1}$ and $\Gamma_{2}$, then $$ \frac{d(T, A C)}{d(T, B D)}=\frac{T A \sin \angle\left(A C, \ell_{1}\right)}{T B \sin \angle\left(B D, \ell_{2}\right)}=\frac{2 r_{1} \sin \angle\left(A C, \ell_{1}\right)}{2 r_{2} \sin \angle\left(B D, \ell_{2}\right)}=\frac{A C}{B D} $$ the last step by the law of sines.  This solves the problem up to configuration issues: we claim that $Y$ and $T$ both lie inside $\angle A X B \equiv \angle C X D$. WLOG $T A<T B$. - The former is since $Y$ lies outside segments $B C$ and $A D$, since we assumed $A B C D$ was convex. - For the latter, we note that $X$ lies inside both $\Gamma_{1}$ and $\Gamma_{2}$ in fact on the radical axis of the two circles (since $X$ was an interior point of both chords $A C$ and $B D$ ). In particular, $X$ is contained inside $\angle A T B$, and moreover $\angle A T B<90^{\circ}$, and this is enough to imply the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
ब First solution, elementary (original). We have $\triangle Y A C \sim \triangle Y B D$, from which it follows $$ \frac{d(Y, A C)}{d(Y, B D)}=\frac{A C}{B D} $$ Moreover, if we denote by $r_{1}$ and $r_{2}$ the radii of $\Gamma_{1}$ and $\Gamma_{2}$, then $$ \frac{d(T, A C)}{d(T, B D)}=\frac{T A \sin \angle\left(A C, \ell_{1}\right)}{T B \sin \angle\left(B D, \ell_{2}\right)}=\frac{2 r_{1} \sin \angle\left(A C, \ell_{1}\right)}{2 r_{2} \sin \angle\left(B D, \ell_{2}\right)}=\frac{A C}{B D} $$ the last step by the law of sines.  This solves the problem up to configuration issues: we claim that $Y$ and $T$ both lie inside $\angle A X B \equiv \angle C X D$. WLOG $T A<T B$. - The former is since $Y$ lies outside segments $B C$ and $A D$, since we assumed $A B C D$ was convex. - For the latter, we note that $X$ lies inside both $\Gamma_{1}$ and $\Gamma_{2}$ in fact on the radical axis of the two circles (since $X$ was an interior point of both chords $A C$ and $B D$ ). In particular, $X$ is contained inside $\angle A T B$, and moreover $\angle A T B<90^{\circ}$, and this is enough to imply the result.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
bcd41107-a877-5159-a45e-4d8fb4f3eafc
| 604,220 |
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
『 Second solution, inversive. This is based on the solution posted by kapilpavase on AoPS. Consider the inversion at $T$ swapping $\Gamma_{1}$ and $\Gamma_{2}$; we let it send $A$ to $E, B$ to $F$, $C$ to $V, D$ to $W$, as shown. Draw circles $A D W E$ and $B C V F$.  Claim - Points $T$ and $Y$ lie on the radical axis of $(A D E)$ and $(B C F)$. Claim - Point $X$ has equal power to $(A D E)$ and $(B C F)$. But since $A E=B F$ and moreover $$ \begin{aligned} \measuredangle B C F+\measuredangle A D E & =(\measuredangle B C A+\measuredangle A C F)+(\measuredangle A D B+\measuredangle B D E) \\ & =(\measuredangle B C A+\measuredangle A D B)+(\measuredangle A C F+\measuredangle B D E)=0+0=0 \end{aligned} $$ we conclude that $(A D E)$ and $(B C F)$ are congruent. As $X$ was the center of negative inversion between them, we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
『 Second solution, inversive. This is based on the solution posted by kapilpavase on AoPS. Consider the inversion at $T$ swapping $\Gamma_{1}$ and $\Gamma_{2}$; we let it send $A$ to $E, B$ to $F$, $C$ to $V, D$ to $W$, as shown. Draw circles $A D W E$ and $B C V F$.  Claim - Points $T$ and $Y$ lie on the radical axis of $(A D E)$ and $(B C F)$. Claim - Point $X$ has equal power to $(A D E)$ and $(B C F)$. But since $A E=B F$ and moreover $$ \begin{aligned} \measuredangle B C F+\measuredangle A D E & =(\measuredangle B C A+\measuredangle A C F)+(\measuredangle A D B+\measuredangle B D E) \\ & =(\measuredangle B C A+\measuredangle A D B)+(\measuredangle A C F+\measuredangle B D E)=0+0=0 \end{aligned} $$ we conclude that $(A D E)$ and $(B C F)$ are congruent. As $X$ was the center of negative inversion between them, we're done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
bcd41107-a877-5159-a45e-4d8fb4f3eafc
| 604,220 |
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
【 Third solution, projective (Nikolai Beluhov). We start with some definitions. Let $\ell_{1}$ touch $\Gamma_{2}$ at $E, \ell_{2}$ touch $\Gamma_{1}$ at $F, K=\ell_{1} \cap \overline{B D}, L=\ell_{2} \cap \overline{A C}$, line $F X$ meet $\Gamma_{1}$ again at $M$, line $E X$ meet $\Gamma_{2}$ again at $N$, and lines $A B, A D$, and $B C$ meet line $T X$ at $Z, Y_{1}$, and $Y_{2}$. Thus the desired statement is equivalent to $Y_{1}=Y_{2}$. $$ \text { Claim - }(E B ; N D)_{\Gamma_{2}}=(F A ; M C)_{\Gamma_{1}} $$ Consider the inversion with center $T$ which swaps $\Gamma_{1}$ and $\Gamma_{2} ;$ it also swaps the pairs $\{A, E\}$ and $\{B, F\}$. Since $A E C N$ is cyclic, $C$ is on $\Gamma_{1}$, and $N$ is on $\Gamma_{2}$, it also swaps $\{C, N\}$; similarly it swaps $\{D, M\}$. Thus $(E B ; N D)_{\Gamma_{2}}=(A F ; C M)_{\Gamma_{1}}=(F A ; M C)_{\Gamma_{1}}$ as desired. $\left(T Z ; X Y_{1}\right) \stackrel{A}{=}(K B ; X D) \stackrel{E}{=}(E B ; N D)_{\Gamma_{2}}=(F A ; M C)_{\Gamma_{1}} \stackrel{F}{=}(L A ; X C) \stackrel{B}{=}\left(T Z ; X Y_{2}\right)$ implies $Y_{1}=Y_{2}$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
【 Third solution, projective (Nikolai Beluhov). We start with some definitions. Let $\ell_{1}$ touch $\Gamma_{2}$ at $E, \ell_{2}$ touch $\Gamma_{1}$ at $F, K=\ell_{1} \cap \overline{B D}, L=\ell_{2} \cap \overline{A C}$, line $F X$ meet $\Gamma_{1}$ again at $M$, line $E X$ meet $\Gamma_{2}$ again at $N$, and lines $A B, A D$, and $B C$ meet line $T X$ at $Z, Y_{1}$, and $Y_{2}$. Thus the desired statement is equivalent to $Y_{1}=Y_{2}$. $$ \text { Claim - }(E B ; N D)_{\Gamma_{2}}=(F A ; M C)_{\Gamma_{1}} $$ Consider the inversion with center $T$ which swaps $\Gamma_{1}$ and $\Gamma_{2} ;$ it also swaps the pairs $\{A, E\}$ and $\{B, F\}$. Since $A E C N$ is cyclic, $C$ is on $\Gamma_{1}$, and $N$ is on $\Gamma_{2}$, it also swaps $\{C, N\}$; similarly it swaps $\{D, M\}$. Thus $(E B ; N D)_{\Gamma_{2}}=(A F ; C M)_{\Gamma_{1}}=(F A ; M C)_{\Gamma_{1}}$ as desired. $\left(T Z ; X Y_{1}\right) \stackrel{A}{=}(K B ; X D) \stackrel{E}{=}(E B ; N D)_{\Gamma_{2}}=(F A ; M C)_{\Gamma_{1}} \stackrel{F}{=}(L A ; X C) \stackrel{B}{=}\left(T Z ; X Y_{2}\right)$ implies $Y_{1}=Y_{2}$ as desired.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
bcd41107-a877-5159-a45e-4d8fb4f3eafc
| 604,220 |
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
【 Fourth solution by untethered moving points. Fix $\ell_{1}, \ell_{2}, T, \Gamma_{1}$ and $\Gamma_{2}$, and let $\Gamma_{1}$ and $\Gamma_{2}$ meet at $U$ and $V$. By the radical axis theorem, $X$ lies on $U V$. Thus we instead treat $X$ as a variable point on line $U V$ and let $C=A X \cap \Gamma_{1}$, $D=B X \cap \Gamma_{2}$. By definition, $X$ has degree 1 and $T$ has degree 0 . We apply Zack's lemma to untethered point $Y$. Note that $C$ and $D$ move projectively on conics, and therefore have degree 2 . Then, lines $A D$ and $B C$ each have degree at most $\operatorname{deg}(A)+\operatorname{deg}(D)=0+2=2$, and so their intersection $Y$ has degree at most $2+2=4$. But when $X \in A B$, the lines $A D$ and $B C$ are the same, so Zack's lemma implies that $$ \operatorname{deg} Y \leq 4-1=3 . $$ Thus the assertion that $T, X, Y$ are collinear (which for example can be seen as a certain vanishing determinant) is a statement of degree at most $0+1+3=4$. Thus it suffices to find 5 values of $X$ (other than $X \in \overline{A B}$, which we used already). This is remarkably easy: 1. When $X=U$ or $X=V$, then $X=C=D=Y$ and the statement is obvious. 2. When $X \in \ell_{1}$, say, then $A=C$ and so $Y$ lies on $A C=\ell_{1}$ as well. The case $X \in \ell_{2}$ is symmetric. 3. Finally, take $X$ at infinity along $U V$. Then $C$ and $D$ are the other tangency points of the circles with $\ell_{1}, \ell_{2}$, and so $A C=\ell_{1}, B D=\ell_{2}$, so $Y=T$. This finishes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles $\Gamma_{1}$ and $\Gamma_{2}$ have common external tangents $\ell_{1}$ and $\ell_{2}$ meeting at $T$. Suppose $\ell_{1}$ touches $\Gamma_{1}$ at $A$ and $\ell_{2}$ touches $\Gamma_{2}$ at $B$. A circle $\Omega$ through $A$ and $B$ intersects $\Gamma_{1}$ again at $C$ and $\Gamma_{2}$ again at $D$, such that quadrilateral $A B C D$ is convex. Suppose lines $A C$ and $B D$ meet at point $X$, while lines $A D$ and $B C$ meet at point $Y$. Show that $T, X, Y$ are collinear.
|
【 Fourth solution by untethered moving points. Fix $\ell_{1}, \ell_{2}, T, \Gamma_{1}$ and $\Gamma_{2}$, and let $\Gamma_{1}$ and $\Gamma_{2}$ meet at $U$ and $V$. By the radical axis theorem, $X$ lies on $U V$. Thus we instead treat $X$ as a variable point on line $U V$ and let $C=A X \cap \Gamma_{1}$, $D=B X \cap \Gamma_{2}$. By definition, $X$ has degree 1 and $T$ has degree 0 . We apply Zack's lemma to untethered point $Y$. Note that $C$ and $D$ move projectively on conics, and therefore have degree 2 . Then, lines $A D$ and $B C$ each have degree at most $\operatorname{deg}(A)+\operatorname{deg}(D)=0+2=2$, and so their intersection $Y$ has degree at most $2+2=4$. But when $X \in A B$, the lines $A D$ and $B C$ are the same, so Zack's lemma implies that $$ \operatorname{deg} Y \leq 4-1=3 . $$ Thus the assertion that $T, X, Y$ are collinear (which for example can be seen as a certain vanishing determinant) is a statement of degree at most $0+1+3=4$. Thus it suffices to find 5 values of $X$ (other than $X \in \overline{A B}$, which we used already). This is remarkably easy: 1. When $X=U$ or $X=V$, then $X=C=D=Y$ and the statement is obvious. 2. When $X \in \ell_{1}$, say, then $A=C$ and so $Y$ lies on $A C=\ell_{1}$ as well. The case $X \in \ell_{2}$ is symmetric. 3. Finally, take $X$ at infinity along $U V$. Then $C$ and $D$ are the other tangency points of the circles with $\ell_{1}, \ell_{2}$, and so $A C=\ell_{1}, B D=\ell_{2}$, so $Y=T$. This finishes the problem.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
bcd41107-a877-5159-a45e-4d8fb4f3eafc
| 604,220 |
For a finite simple graph $G$, we define $G^{\prime}$ to be the graph on the same vertex set as $G$, where for any two vertices $u \neq v$, the pair $\{u, v\}$ is an edge of $G^{\prime}$ if and only if $u$ and $v$ have a common neighbor in $G$. Prove that if $G$ is a finite simple graph which is isomorphic to $\left(G^{\prime}\right)^{\prime}$, then $G$ is also isomorphic to $G^{\prime}$.
|
We say a vertex of a graph is fatal if it has degree at least 3, and some two of its neighbors are not adjacent. Claim - The graph $G^{\prime}$ has at least as many triangles as $G$, and has strictly more if $G$ has any fatal vertices. Thus we only need to consider graphs $G$ with no fatal vertices. Looking at the connected components, the only possibilities are cliques (including single vertices), cycles, and paths. So in what follows we restrict our attention to graphs $G$ only consisting of such components. Remark (Warning). Beware: assuming $G$ is connected loses generality. For example, it could be that $G=G_{1} \sqcup G_{2}$, where $G_{1}^{\prime} \cong G_{2}$ and $G_{2}^{\prime} \cong G_{1}$. First, note that the following are stable under the operation: - an isolated vertex, - a cycle of odd length, or - a clique with at least three vertices. In particular, $G \cong G^{\prime \prime}$ holds for such graphs. On the other hand, cycles of even length or paths of nonzero length will break into more connected components. For this reason, a graph $G$ with any of these components will not satisfy $G \cong G^{\prime \prime}$ because $G^{\prime}$ will have strictly more connected components than $G$, and $G^{\prime \prime}$ will have at least as many as $G^{\prime}$. Therefore $G \cong G^{\prime \prime}$ if and only if $G$ is a disjoint union of the three types of connected components named earlier. Since $G \cong G^{\prime}$ holds for such graphs as well, the problem statement follows right away. Remark. The proposers included a variant of the problem where given any graph $G$, the operation stabilized after at most $O(\log n)$ operations, where $n$ was the number of vertices of $G$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For a finite simple graph $G$, we define $G^{\prime}$ to be the graph on the same vertex set as $G$, where for any two vertices $u \neq v$, the pair $\{u, v\}$ is an edge of $G^{\prime}$ if and only if $u$ and $v$ have a common neighbor in $G$. Prove that if $G$ is a finite simple graph which is isomorphic to $\left(G^{\prime}\right)^{\prime}$, then $G$ is also isomorphic to $G^{\prime}$.
|
We say a vertex of a graph is fatal if it has degree at least 3, and some two of its neighbors are not adjacent. Claim - The graph $G^{\prime}$ has at least as many triangles as $G$, and has strictly more if $G$ has any fatal vertices. Thus we only need to consider graphs $G$ with no fatal vertices. Looking at the connected components, the only possibilities are cliques (including single vertices), cycles, and paths. So in what follows we restrict our attention to graphs $G$ only consisting of such components. Remark (Warning). Beware: assuming $G$ is connected loses generality. For example, it could be that $G=G_{1} \sqcup G_{2}$, where $G_{1}^{\prime} \cong G_{2}$ and $G_{2}^{\prime} \cong G_{1}$. First, note that the following are stable under the operation: - an isolated vertex, - a cycle of odd length, or - a clique with at least three vertices. In particular, $G \cong G^{\prime \prime}$ holds for such graphs. On the other hand, cycles of even length or paths of nonzero length will break into more connected components. For this reason, a graph $G$ with any of these components will not satisfy $G \cong G^{\prime \prime}$ because $G^{\prime}$ will have strictly more connected components than $G$, and $G^{\prime \prime}$ will have at least as many as $G^{\prime}$. Therefore $G \cong G^{\prime \prime}$ if and only if $G$ is a disjoint union of the three types of connected components named earlier. Since $G \cong G^{\prime}$ holds for such graphs as well, the problem statement follows right away. Remark. The proposers included a variant of the problem where given any graph $G$, the operation stabilized after at most $O(\log n)$ operations, where $n$ was the number of vertices of $G$.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2020.jsonl",
"problem_match": null,
"solution_match": null
}
|
94c6cdb3-6ec5-5ed6-ab74-cfb820266fab
| 246,744 |
Points $A, V_{1}, V_{2}, B, U_{2}, U_{1}$ lie fixed on a circle $\Gamma$, in that order, and such that $B U_{2}>A U_{1}>B V_{2}>A V_{1}$. Let $X$ be a variable point on the $\operatorname{arc} V_{1} V_{2}$ of $\Gamma$ not containing $A$ or $B$. Line $X A$ meets line $U_{1} V_{1}$ at $C$, while line $X B$ meets line $U_{2} V_{2}$ at $D$. Prove there exists a fixed point $K$, independent of $X$, such that the power of $K$ to the circumcircle of $\triangle X C D$ is constant.
|
For brevity, we let $\ell_{i}$ denote line $U_{i} V_{i}$ for $i=1,2$. We first give an explicit description of the fixed point $K$. Let $E$ and $F$ be points on $\Gamma$ such that $\overline{A E} \| \ell_{1}$ and $\overline{B F} \| \ell_{2}$. The problem conditions imply that $E$ lies between $U_{1}$ and $A$ while $F$ lies between $U_{2}$ and $B$. Then we let $$ K=\overline{A F} \cap \overline{B E} $$ This point exists because $A E F B$ are the vertices of a convex quadrilateral. Remark (How to identify the fixed point). If we drop the condition that $X$ lies on the arc, then the choice above is motivated by choosing $X \in\{E, F\}$. Essentially, when one chooses $X \rightarrow E$, the point $C$ approaches an infinity point. So in this degenerate case, the only points whose power is finite to $(X C D)$ are bounded are those on line $B E$. The same logic shows that $K$ must lie on line $A F$. Therefore, if the problem is going to work, the fixed point must be exactly $\overline{A F} \cap \overline{B E}$. 【 First approach by Vincent Huang. We need the following claim: Claim - Suppose distinct lines $A C$ and $B D$ meet at $X$. Then for any point $K$ $$ \operatorname{pow}(K, X A B)+\operatorname{pow}(K, X C D)=\operatorname{pow}(K, X A D)+\operatorname{pow}(K, X B C) $$ Construct the points $P=\ell_{1} \cap \overline{B E}$ and $Q=\ell_{2} \cap \overline{A F}$, which do not depend on $X$. Claim - Quadrilaterals $B P C X$ and $A Q D X$ are cyclic.  Now, for the particular $K$ we choose, we have $$ \begin{aligned} \operatorname{pow}(K, X C D) & =\operatorname{pow}(K, X A D)+\operatorname{pow}(K, X B C)-\operatorname{pow}(K, X A B) \\ & =K A \cdot K Q+K B \cdot K P-\operatorname{pow}(K, \Gamma) . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $A, V_{1}, V_{2}, B, U_{2}, U_{1}$ lie fixed on a circle $\Gamma$, in that order, and such that $B U_{2}>A U_{1}>B V_{2}>A V_{1}$. Let $X$ be a variable point on the $\operatorname{arc} V_{1} V_{2}$ of $\Gamma$ not containing $A$ or $B$. Line $X A$ meets line $U_{1} V_{1}$ at $C$, while line $X B$ meets line $U_{2} V_{2}$ at $D$. Prove there exists a fixed point $K$, independent of $X$, such that the power of $K$ to the circumcircle of $\triangle X C D$ is constant.
|
For brevity, we let $\ell_{i}$ denote line $U_{i} V_{i}$ for $i=1,2$. We first give an explicit description of the fixed point $K$. Let $E$ and $F$ be points on $\Gamma$ such that $\overline{A E} \| \ell_{1}$ and $\overline{B F} \| \ell_{2}$. The problem conditions imply that $E$ lies between $U_{1}$ and $A$ while $F$ lies between $U_{2}$ and $B$. Then we let $$ K=\overline{A F} \cap \overline{B E} $$ This point exists because $A E F B$ are the vertices of a convex quadrilateral. Remark (How to identify the fixed point). If we drop the condition that $X$ lies on the arc, then the choice above is motivated by choosing $X \in\{E, F\}$. Essentially, when one chooses $X \rightarrow E$, the point $C$ approaches an infinity point. So in this degenerate case, the only points whose power is finite to $(X C D)$ are bounded are those on line $B E$. The same logic shows that $K$ must lie on line $A F$. Therefore, if the problem is going to work, the fixed point must be exactly $\overline{A F} \cap \overline{B E}$. 【 First approach by Vincent Huang. We need the following claim: Claim - Suppose distinct lines $A C$ and $B D$ meet at $X$. Then for any point $K$ $$ \operatorname{pow}(K, X A B)+\operatorname{pow}(K, X C D)=\operatorname{pow}(K, X A D)+\operatorname{pow}(K, X B C) $$ Construct the points $P=\ell_{1} \cap \overline{B E}$ and $Q=\ell_{2} \cap \overline{A F}$, which do not depend on $X$. Claim - Quadrilaterals $B P C X$ and $A Q D X$ are cyclic.  Now, for the particular $K$ we choose, we have $$ \begin{aligned} \operatorname{pow}(K, X C D) & =\operatorname{pow}(K, X A D)+\operatorname{pow}(K, X B C)-\operatorname{pow}(K, X A B) \\ & =K A \cdot K Q+K B \cdot K P-\operatorname{pow}(K, \Gamma) . \end{aligned} $$
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0db2603b-6cf4-5d2f-9268-1678d9dfd5eb
| 604,338 |
Points $A, V_{1}, V_{2}, B, U_{2}, U_{1}$ lie fixed on a circle $\Gamma$, in that order, and such that $B U_{2}>A U_{1}>B V_{2}>A V_{1}$. Let $X$ be a variable point on the $\operatorname{arc} V_{1} V_{2}$ of $\Gamma$ not containing $A$ or $B$. Line $X A$ meets line $U_{1} V_{1}$ at $C$, while line $X B$ meets line $U_{2} V_{2}$ at $D$. Prove there exists a fixed point $K$, independent of $X$, such that the power of $K$ to the circumcircle of $\triangle X C D$ is constant.
|
For brevity, we let $\ell_{i}$ denote line $U_{i} V_{i}$ for $i=1,2$. We first give an explicit description of the fixed point $K$. Let $E$ and $F$ be points on $\Gamma$ such that $\overline{A E} \| \ell_{1}$ and $\overline{B F} \| \ell_{2}$. The problem conditions imply that $E$ lies between $U_{1}$ and $A$ while $F$ lies between $U_{2}$ and $B$. Then we let $$ K=\overline{A F} \cap \overline{B E} $$ This point exists because $A E F B$ are the vertices of a convex quadrilateral. Remark (How to identify the fixed point). If we drop the condition that $X$ lies on the arc, then the choice above is motivated by choosing $X \in\{E, F\}$. Essentially, when one chooses $X \rightarrow E$, the point $C$ approaches an infinity point. So in this degenerate case, the only points whose power is finite to $(X C D)$ are bounded are those on line $B E$. The same logic shows that $K$ must lie on line $A F$. Therefore, if the problem is going to work, the fixed point must be exactly $\overline{A F} \cap \overline{B E}$. 【 Second approach by authors. Let $Y$ be the second intersection of $(X C D)$ with $\Gamma$. Let $S=\overline{E Y} \cap \ell_{1}$ and $T=\overline{F Y} \cap \ell_{2}$. Claim - Points $S$ and $T$ lies on ( $X C D)$ as well. Now let $X^{\prime}$ be any other choice of $X$, and define $C^{\prime}$ and $D^{\prime}$ in the obvious way. We are going to show that $K$ lies on the radical axis of $(X C D)$ and $\left(X^{\prime} C^{\prime} D^{\prime}\right)$.  The main idea is as follows: Claim - The point $L=\overline{E Y} \cap \overline{A X^{\prime}}$ lies on the radical axis. By symmetry, so does the point $M=\overline{F Y} \cap \overline{B X^{\prime}}$ (not pictured). $$ \operatorname{pow}\left(L, X^{\prime} C^{\prime} D^{\prime}\right)=L C^{\prime} \cdot L X^{\prime}=L S \cdot L Y=\operatorname{pow}(L, X C D) $$ To conclude, note that by Pascal theorem on $$ E Y F A X^{\prime} B $$ it follows $K, L, M$ are collinear, as needed. Remark. All the conditions about $U_{1}, V_{1}, U_{2}, V_{2}$ at the beginning are there to eliminate configuration issues, making the problem less obnoxious to the contestant. In particular, without the various assumptions, there exist configurations in which the point $K$ is at infinity. In these cases, the center of $X C D$ moves along a fixed line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $A, V_{1}, V_{2}, B, U_{2}, U_{1}$ lie fixed on a circle $\Gamma$, in that order, and such that $B U_{2}>A U_{1}>B V_{2}>A V_{1}$. Let $X$ be a variable point on the $\operatorname{arc} V_{1} V_{2}$ of $\Gamma$ not containing $A$ or $B$. Line $X A$ meets line $U_{1} V_{1}$ at $C$, while line $X B$ meets line $U_{2} V_{2}$ at $D$. Prove there exists a fixed point $K$, independent of $X$, such that the power of $K$ to the circumcircle of $\triangle X C D$ is constant.
|
For brevity, we let $\ell_{i}$ denote line $U_{i} V_{i}$ for $i=1,2$. We first give an explicit description of the fixed point $K$. Let $E$ and $F$ be points on $\Gamma$ such that $\overline{A E} \| \ell_{1}$ and $\overline{B F} \| \ell_{2}$. The problem conditions imply that $E$ lies between $U_{1}$ and $A$ while $F$ lies between $U_{2}$ and $B$. Then we let $$ K=\overline{A F} \cap \overline{B E} $$ This point exists because $A E F B$ are the vertices of a convex quadrilateral. Remark (How to identify the fixed point). If we drop the condition that $X$ lies on the arc, then the choice above is motivated by choosing $X \in\{E, F\}$. Essentially, when one chooses $X \rightarrow E$, the point $C$ approaches an infinity point. So in this degenerate case, the only points whose power is finite to $(X C D)$ are bounded are those on line $B E$. The same logic shows that $K$ must lie on line $A F$. Therefore, if the problem is going to work, the fixed point must be exactly $\overline{A F} \cap \overline{B E}$. 【 Second approach by authors. Let $Y$ be the second intersection of $(X C D)$ with $\Gamma$. Let $S=\overline{E Y} \cap \ell_{1}$ and $T=\overline{F Y} \cap \ell_{2}$. Claim - Points $S$ and $T$ lies on ( $X C D)$ as well. Now let $X^{\prime}$ be any other choice of $X$, and define $C^{\prime}$ and $D^{\prime}$ in the obvious way. We are going to show that $K$ lies on the radical axis of $(X C D)$ and $\left(X^{\prime} C^{\prime} D^{\prime}\right)$.  The main idea is as follows: Claim - The point $L=\overline{E Y} \cap \overline{A X^{\prime}}$ lies on the radical axis. By symmetry, so does the point $M=\overline{F Y} \cap \overline{B X^{\prime}}$ (not pictured). $$ \operatorname{pow}\left(L, X^{\prime} C^{\prime} D^{\prime}\right)=L C^{\prime} \cdot L X^{\prime}=L S \cdot L Y=\operatorname{pow}(L, X C D) $$ To conclude, note that by Pascal theorem on $$ E Y F A X^{\prime} B $$ it follows $K, L, M$ are collinear, as needed. Remark. All the conditions about $U_{1}, V_{1}, U_{2}, V_{2}$ at the beginning are there to eliminate configuration issues, making the problem less obnoxious to the contestant. In particular, without the various assumptions, there exist configurations in which the point $K$ is at infinity. In these cases, the center of $X C D$ moves along a fixed line.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2021.jsonl",
"problem_match": null,
"solution_match": null
}
|
0db2603b-6cf4-5d2f-9268-1678d9dfd5eb
| 604,338 |
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
\I Inversion solution submitted by Ankan Bhattacharya and Nikolai Beluhov. Let $H$ be the orthocenter of $\triangle A B C$. We use inversion in the circle with diameter $\overline{B C}$. We identify a few images: - The circumcircles of $\triangle B M E$ and $\triangle C M F$ are mapped to lines $B E$ and $C F$. - The common external tangents are mapped to the two circles through $M$ which are tangent to lines $B E$ and $C F$. - The image of $K$, denoted $K^{*}$, is the second intersection of these circles. - The assertion that $K$ lies on $(A B C)$ is equivalent to $K^{*}$ lying on $(B H C)$. However, now $K^{*}$ is simple to identify directly: it's just the reflection of $M$ in the bisector of $\angle B H C$.  In particular, $\overline{H K^{*}}$ is a symmedian of $\triangle B H C$. However, since $K^{*}$ lies on $(B H C)$, this means $\left(H K^{*} ; B C\right)=-1$. Then, we obtain that $\overline{B C}$ bisects $\angle H M K^{*} \equiv \angle H M K$. However, $K$ also lies on $(A B C)$, which forces $K$ to be the reflection of $H$ in $\overline{B C}$. Thus $\overline{A K} \perp \overline{B C}$, as wanted.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
\I Inversion solution submitted by Ankan Bhattacharya and Nikolai Beluhov. Let $H$ be the orthocenter of $\triangle A B C$. We use inversion in the circle with diameter $\overline{B C}$. We identify a few images: - The circumcircles of $\triangle B M E$ and $\triangle C M F$ are mapped to lines $B E$ and $C F$. - The common external tangents are mapped to the two circles through $M$ which are tangent to lines $B E$ and $C F$. - The image of $K$, denoted $K^{*}$, is the second intersection of these circles. - The assertion that $K$ lies on $(A B C)$ is equivalent to $K^{*}$ lying on $(B H C)$. However, now $K^{*}$ is simple to identify directly: it's just the reflection of $M$ in the bisector of $\angle B H C$.  In particular, $\overline{H K^{*}}$ is a symmedian of $\triangle B H C$. However, since $K^{*}$ lies on $(B H C)$, this means $\left(H K^{*} ; B C\right)=-1$. Then, we obtain that $\overline{B C}$ bisects $\angle H M K^{*} \equiv \angle H M K$. However, $K$ also lies on $(A B C)$, which forces $K$ to be the reflection of $H$ in $\overline{B C}$. Thus $\overline{A K} \perp \overline{B C}$, as wanted.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
b34786e4-25c5-5c69-9e9f-a8e3f130d86b
| 246,802 |
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
ๆ Solution with coaxial circles (Pitchayut Saengrungkongka). Let $H$ be the orthocenter of $\triangle A B C$. Let $Q$ be the second intersection of $\odot(B M E)$ and $\odot(C M F)$. We first prove the following well-known properties of $Q$. Claim - $Q$ is the Miquel point of $B C E F$. In particular, $Q$ lies on both $\odot(A E F)$ and $\odot(A B C)$. Claim - $A(Q, H ; B, C)=-1$. Claim - $Q T$ is tangent to $\odot(B Q C)$. $$ \begin{aligned} \frac{B T}{T C} & =\frac{T B \cdot T M}{T C \cdot T M} \\ & =\frac{\operatorname{pow}(T, \odot(B M E))}{\operatorname{pow}(T, \odot(C M F))} \\ & =\frac{\operatorname{pow}(K, \odot(B M E))}{\operatorname{pow}(K, \odot(C M F))} \\ & =\left(\frac{r_{\odot(B M E)}}{r_{\odot(C M F)}}\right)^{2} \\ & =\left(\frac{B Q / \sin \angle Q M B}{C Q / \sin \angle Q M C}\right)^{2} \\ & =\frac{B Q^{2}}{C Q^{2}} \end{aligned} $$ implying the result. To finish, let $O$ be the center of $\odot(A B C)$. Then, from the claim, $\angle O Q T=90^{\circ}=$ $\angle O M T$, so $O$ also lies on $\odot(Q M T K)$. Thus, $\angle O K T=90^{\circ}$, so $K T$ is also tangent to $\odot(A B C)$ as well. This implies that $Q B K C$ is harmonic quadrilateral, and the result follows from the second claim.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
ๆ Solution with coaxial circles (Pitchayut Saengrungkongka). Let $H$ be the orthocenter of $\triangle A B C$. Let $Q$ be the second intersection of $\odot(B M E)$ and $\odot(C M F)$. We first prove the following well-known properties of $Q$. Claim - $Q$ is the Miquel point of $B C E F$. In particular, $Q$ lies on both $\odot(A E F)$ and $\odot(A B C)$. Claim - $A(Q, H ; B, C)=-1$. Claim - $Q T$ is tangent to $\odot(B Q C)$. $$ \begin{aligned} \frac{B T}{T C} & =\frac{T B \cdot T M}{T C \cdot T M} \\ & =\frac{\operatorname{pow}(T, \odot(B M E))}{\operatorname{pow}(T, \odot(C M F))} \\ & =\frac{\operatorname{pow}(K, \odot(B M E))}{\operatorname{pow}(K, \odot(C M F))} \\ & =\left(\frac{r_{\odot(B M E)}}{r_{\odot(C M F)}}\right)^{2} \\ & =\left(\frac{B Q / \sin \angle Q M B}{C Q / \sin \angle Q M C}\right)^{2} \\ & =\frac{B Q^{2}}{C Q^{2}} \end{aligned} $$ implying the result. To finish, let $O$ be the center of $\odot(A B C)$. Then, from the claim, $\angle O Q T=90^{\circ}=$ $\angle O M T$, so $O$ also lies on $\odot(Q M T K)$. Thus, $\angle O K T=90^{\circ}$, so $K T$ is also tangent to $\odot(A B C)$ as well. This implies that $Q B K C$ is harmonic quadrilateral, and the result follows from the second claim.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
b34786e4-25c5-5c69-9e9f-a8e3f130d86b
| 246,802 |
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
【 Solution by Luke Robitaille. Let $Q$ be the second intersection of $\odot(B M E)$ and $\odot(C M F)$. We use the first two claims of the previous solution. In particular, $Q \in$ $\odot(A B C)$. We have the following claim. Claim (Also appeared in ISL 2017 G7) - We have $\measuredangle Q K M=\measuredangle Q B M+\measuredangle Q C M$. $$ \begin{aligned} \measuredangle Q K M & =\measuredangle Q^{\prime} Q M^{\prime}+\measuredangle Q M^{\prime} M \\ & =\measuredangle Q C M+\measuredangle Q B M, \end{aligned} $$ as desired. Now, we extend $K M$ to meet $\odot(A B C)$ again at $Q_{1}$. We have $$ \begin{aligned} \measuredangle Q_{1} Q B=\measuredangle Q_{1} K B & =\measuredangle Q_{1} K Q+\measuredangle Q C B \\ & =\measuredangle M K Q+\measuredangle Q K B \\ & =(\measuredangle M B Q+\measuredangle M C Q)+\measuredangle Q C B \\ & =\measuredangle C B Q, \end{aligned} $$ implying that $Q Q_{1} \| B C$. This implies that $Q B K C$ is harmonic quadrilateral, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
【 Solution by Luke Robitaille. Let $Q$ be the second intersection of $\odot(B M E)$ and $\odot(C M F)$. We use the first two claims of the previous solution. In particular, $Q \in$ $\odot(A B C)$. We have the following claim. Claim (Also appeared in ISL 2017 G7) - We have $\measuredangle Q K M=\measuredangle Q B M+\measuredangle Q C M$. $$ \begin{aligned} \measuredangle Q K M & =\measuredangle Q^{\prime} Q M^{\prime}+\measuredangle Q M^{\prime} M \\ & =\measuredangle Q C M+\measuredangle Q B M, \end{aligned} $$ as desired. Now, we extend $K M$ to meet $\odot(A B C)$ again at $Q_{1}$. We have $$ \begin{aligned} \measuredangle Q_{1} Q B=\measuredangle Q_{1} K B & =\measuredangle Q_{1} K Q+\measuredangle Q C B \\ & =\measuredangle M K Q+\measuredangle Q K B \\ & =(\measuredangle M B Q+\measuredangle M C Q)+\measuredangle Q C B \\ & =\measuredangle C B Q, \end{aligned} $$ implying that $Q Q_{1} \| B C$. This implies that $Q B K C$ is harmonic quadrilateral, so we are done.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
b34786e4-25c5-5c69-9e9f-a8e3f130d86b
| 246,802 |
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
I Synthetic solution due to Andrew Gu (Harvard 2026). Define $O_{1}$ and $O_{2}$ as the circumcenters of $(B M E)$ and $(C M F)$. Let $T$ be the point on $(A B C)$ such that $\overline{A T} \perp \overline{B C}$. Denote by $L$ the midpoint of minor arc $\overparen{B C}$. We are going to ignore the condition that $K$ lies on the circumcircle of $A B C$, and prove the following unconditional result: ## Proposition The points $T, L, K$ are collinear. This will solve the problem because if $K$ is on the circumcircle of $A B C$, it follows $K=T$ or $K=L$; but $K=L$ can never occur since $O_{1}$ and $O_{2}$ are obviously on different sides of line $L M$ so line $L M$ must meet $O_{1} O_{2}$ inside segment $O_{1} O_{2}$, and $K$ lies outside this segment.  Claim - Lines $A C$ and $L M$ meet at the antipode $Q_{1}$ of $B$ on $(B M E)$, so that $B P_{1} Q_{1} M$ is a rectangle. Similarly, lines $A B$ and $L M$ meet at the antipode $Q_{2}$ of $C$ on $(C M F)$, so that $C P_{2} Q_{2} M$ is a rectangle. From this, it follows that $P_{1} Q_{1}=B M=\frac{1}{2} B C=M C=P_{2} Q_{2}$. Letting $r_{1}$ denote the radius of $\omega_{1}$ (and similarly for $\omega_{2}$ ), we deduce that $C Q_{1}=B Q_{1}=2 r_{1}$. Claim - $K M=K L$. $$ \measuredangle Q_{1} C L=\measuredangle A C L=\measuredangle A B L=\measuredangle Q_{2} B L=\measuredangle Q_{2} C L $$ The external angle bisector theorem then gives an equality of directed ratios $$ \frac{L Q_{1}}{L Q_{2}}=\frac{\left|C Q_{1}\right|}{\left|C Q_{2}\right|}=\frac{\left|B Q_{1}\right|}{\left|C Q_{2}\right|}=\frac{2 r_{1}}{2 r_{2}}=\frac{r_{1}}{r_{2}} $$ Let the reflection of $M$ over $K$ be $P$; then $P$ lies on $\overline{P_{1} P_{2}}$ and $$ \frac{P P_{1}}{P P_{2}}=\frac{2 K O_{1}}{2 K O_{2}}=\frac{K O_{1}}{K O_{2}}=\frac{r_{1}}{r_{2}}=\frac{L Q_{1}}{L Q_{2}} $$ where again the ratios are directed. Projecting everything onto line $L M$, so that $P_{1}$ lands at $Q_{1}$ and $P_{2}$ lands at $Q_{2}$, we find that the projection of $P$ must land exactly at $L$. Claim - Line $K M$ is an external angle bisector of $\angle O_{1} M O_{2}$. To finish, note that we know that $\overline{M P_{1}} \| \overline{C Q_{1}} \equiv \overline{A C}$ and $\overline{M P_{2}} \| \overline{B Q_{2}} \equiv \overline{A B}$, meaning the angles $\angle O_{1} M O_{2}$ and $\angle C A B$ have parallel legs. Hence, if $N$ is the antipode of $L$, it follows that $\overline{M K} \| \overline{A N}$. Now from $M K=K L$ and the fact that $A N L T$ is an isosceles trapezoid, we deduce that $\overline{L T}$ and $\overline{L K}$ are lines in the same direction (namely, the reflection of $M K \| A N$ across $\overline{B C}$ ), as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
I Synthetic solution due to Andrew Gu (Harvard 2026). Define $O_{1}$ and $O_{2}$ as the circumcenters of $(B M E)$ and $(C M F)$. Let $T$ be the point on $(A B C)$ such that $\overline{A T} \perp \overline{B C}$. Denote by $L$ the midpoint of minor arc $\overparen{B C}$. We are going to ignore the condition that $K$ lies on the circumcircle of $A B C$, and prove the following unconditional result: ## Proposition The points $T, L, K$ are collinear. This will solve the problem because if $K$ is on the circumcircle of $A B C$, it follows $K=T$ or $K=L$; but $K=L$ can never occur since $O_{1}$ and $O_{2}$ are obviously on different sides of line $L M$ so line $L M$ must meet $O_{1} O_{2}$ inside segment $O_{1} O_{2}$, and $K$ lies outside this segment.  Claim - Lines $A C$ and $L M$ meet at the antipode $Q_{1}$ of $B$ on $(B M E)$, so that $B P_{1} Q_{1} M$ is a rectangle. Similarly, lines $A B$ and $L M$ meet at the antipode $Q_{2}$ of $C$ on $(C M F)$, so that $C P_{2} Q_{2} M$ is a rectangle. From this, it follows that $P_{1} Q_{1}=B M=\frac{1}{2} B C=M C=P_{2} Q_{2}$. Letting $r_{1}$ denote the radius of $\omega_{1}$ (and similarly for $\omega_{2}$ ), we deduce that $C Q_{1}=B Q_{1}=2 r_{1}$. Claim - $K M=K L$. $$ \measuredangle Q_{1} C L=\measuredangle A C L=\measuredangle A B L=\measuredangle Q_{2} B L=\measuredangle Q_{2} C L $$ The external angle bisector theorem then gives an equality of directed ratios $$ \frac{L Q_{1}}{L Q_{2}}=\frac{\left|C Q_{1}\right|}{\left|C Q_{2}\right|}=\frac{\left|B Q_{1}\right|}{\left|C Q_{2}\right|}=\frac{2 r_{1}}{2 r_{2}}=\frac{r_{1}}{r_{2}} $$ Let the reflection of $M$ over $K$ be $P$; then $P$ lies on $\overline{P_{1} P_{2}}$ and $$ \frac{P P_{1}}{P P_{2}}=\frac{2 K O_{1}}{2 K O_{2}}=\frac{K O_{1}}{K O_{2}}=\frac{r_{1}}{r_{2}}=\frac{L Q_{1}}{L Q_{2}} $$ where again the ratios are directed. Projecting everything onto line $L M$, so that $P_{1}$ lands at $Q_{1}$ and $P_{2}$ lands at $Q_{2}$, we find that the projection of $P$ must land exactly at $L$. Claim - Line $K M$ is an external angle bisector of $\angle O_{1} M O_{2}$. To finish, note that we know that $\overline{M P_{1}} \| \overline{C Q_{1}} \equiv \overline{A C}$ and $\overline{M P_{2}} \| \overline{B Q_{2}} \equiv \overline{A B}$, meaning the angles $\angle O_{1} M O_{2}$ and $\angle C A B$ have parallel legs. Hence, if $N$ is the antipode of $L$, it follows that $\overline{M K} \| \overline{A N}$. Now from $M K=K L$ and the fact that $A N L T$ is an isosceles trapezoid, we deduce that $\overline{L T}$ and $\overline{L K}$ are lines in the same direction (namely, the reflection of $M K \| A N$ across $\overline{B C}$ ), as needed.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
b34786e4-25c5-5c69-9e9f-a8e3f130d86b
| 246,802 |
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
【 Complex numbers approach with Apollonian circles, by Carl Schildkraut. We use complex numbers. As in the first approach, we will ignore the hypothesis that $K$ lies on ( $A B C$ ). Let $Q:=(A H) \cap(A B C) \cap(A E F) \neq A$ be the Miquel point of $B F E C$ again. Construct the point $T$ on $(A B C)$ for which $A T \perp B C$; note that $T=-\frac{b c}{a}$. This time the unconditional result is: ## Proposition We have $Q, M, T, K$ are concyclic (or collinear) on an Apollonian circle of $\overline{O_{1} O_{2}}$. This will solve the original problem since once $K$ lies on $(A B C)$ it must be either $Q$ or $T$. But since $K$ is not on $(B M E), K \neq Q$, it will have to be $T$. We now prove the proposition. Suppose $(A B C)$ is the unit circle and let $A=a, B=b$, $C=c$. Let $H=a+b+c$ be the orthocenter of $\triangle A B C$. By the usual formulas, $$ E:=\frac{1}{2}\left(a+b+c-\frac{b c}{a}\right) . $$ Let $O_{1}$ be the center of $(B M E)$ and $O_{2}$ be the center of $(C M F)$. Claim (Calculation of the Miquel point) - We have $Q=\frac{2 a+b+c}{a\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+1}$. $$ 0=\frac{q-h}{q-a}+\frac{1 / q-\bar{h}}{1 / q-1 / a}=\frac{q-h}{q-a}-\frac{a(1-q \bar{h})}{q-a} $$ This solves to $q=\frac{h+a}{a \bar{h}+1}=\frac{2 a+b+c}{a \bar{h}+1}$. Claim (Calculation of $O_{1}$ and $\left.O_{2}\right)-$ We have $O_{1}=\frac{b(2 a+b+c)}{2(a+b)}$ and $O_{2}=\frac{c(2 a+b+c)}{2(a+c)}$. $$ \begin{aligned} O_{1} & =\operatorname{Circum}(B, M, E) \\ & =b+\frac{1}{2} \operatorname{Circum}\left(0, c-b, \frac{(a-b)(b-c)}{b}\right) \\ & =b-\frac{b-c}{2 b} \operatorname{Circum}(0, b, b-a) \\ & =b-\frac{b-c}{2 b}(b-\operatorname{Circum}(0, b, a)) \\ & =b-\frac{b-c}{2 b}\left(b-\frac{a b}{a+b}\right)=b-\frac{b(b-c)}{2(a+b)}=\frac{b(2 a+b+c)}{2(a+b)} \end{aligned} $$ Similarly, $O_{2}=\frac{c(2 a+b+c)}{2(a+c)}$. We are now going to prove the following: Claim - We have $$ \frac{T O_{1}}{T O_{2}}=\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}} $$ $$ M O_{1}=B O_{1}=\left|b-\frac{b(2 a+b+c)}{2(a+b)}\right|=\left|\frac{b(b-c)}{2(a+b)}\right|=\frac{1}{2}\left|\frac{b-c}{a+b}\right| $$ and $Q O_{1}=\left|r-\frac{b(2 a+b+c)}{2(a+b)}\right|=\left|1-\frac{b(a+h)}{2(a+b) r}\right|=\left|1-\frac{b(a \bar{h}+1)}{2(a+b)}\right|=\left|\frac{a-\frac{a b}{c}}{2(a+b)}\right|=\frac{1}{2}\left|\frac{b-c}{a+b}\right|$. This implies both (by symmetry) that $\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}}=\left|\frac{a+c}{a+b}\right|$ and that $Q$ is on (BME) and $(C M F)$. Also, $$ \frac{T O_{1}}{T O_{2}}=\frac{\left|\frac{b(2 a+b+c)}{2(a+b)}+\frac{b c}{a}\right|}{\left|\frac{c(2 a+b+c)}{2(a+c)}+\frac{b c}{a}\right|}=\left|\frac{\frac{b\left(2 a^{2}+a b+a c+2 a c+2 b c\right)}{2 a(a+b)}}{\frac{c\left(2 a^{2}+a b+a c+2 a b+2 b c\right)}{2 a(a+c)}}\right|=\left|\frac{a+c}{a+b}\right| \cdot\left|\frac{2 a^{2}+2 b c+a b+3 a c}{2 a^{2}+2 b c+3 a b+a c}\right| $$ if $z=2 a^{2}+2 b c+a b+3 a c$, then $a^{2} b c \bar{z}=2 a^{2}+2 b c+3 a b+a c$, so the second term has magnitude 1. This means $\frac{T O_{1}}{T O_{2}}=\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}}$, as desired. To finish, note that this common ratio is the ratio between the radii of these two circles, so it is also $\frac{K O_{1}}{K O_{2}}$. By Apollonian circles the points $\{Q, M, T, K\}$ lie on a circle or a line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $M$ be the midpoint of side $B C$, and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Suppose that the common external tangents to the circumcircles of triangles $B M E$ and $C M F$ intersect at a point $K$, and that $K$ lies on the circumcircle of $A B C$. Prove that line $A K$ is perpendicular to line $B C$.
|
【 Complex numbers approach with Apollonian circles, by Carl Schildkraut. We use complex numbers. As in the first approach, we will ignore the hypothesis that $K$ lies on ( $A B C$ ). Let $Q:=(A H) \cap(A B C) \cap(A E F) \neq A$ be the Miquel point of $B F E C$ again. Construct the point $T$ on $(A B C)$ for which $A T \perp B C$; note that $T=-\frac{b c}{a}$. This time the unconditional result is: ## Proposition We have $Q, M, T, K$ are concyclic (or collinear) on an Apollonian circle of $\overline{O_{1} O_{2}}$. This will solve the original problem since once $K$ lies on $(A B C)$ it must be either $Q$ or $T$. But since $K$ is not on $(B M E), K \neq Q$, it will have to be $T$. We now prove the proposition. Suppose $(A B C)$ is the unit circle and let $A=a, B=b$, $C=c$. Let $H=a+b+c$ be the orthocenter of $\triangle A B C$. By the usual formulas, $$ E:=\frac{1}{2}\left(a+b+c-\frac{b c}{a}\right) . $$ Let $O_{1}$ be the center of $(B M E)$ and $O_{2}$ be the center of $(C M F)$. Claim (Calculation of the Miquel point) - We have $Q=\frac{2 a+b+c}{a\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+1}$. $$ 0=\frac{q-h}{q-a}+\frac{1 / q-\bar{h}}{1 / q-1 / a}=\frac{q-h}{q-a}-\frac{a(1-q \bar{h})}{q-a} $$ This solves to $q=\frac{h+a}{a \bar{h}+1}=\frac{2 a+b+c}{a \bar{h}+1}$. Claim (Calculation of $O_{1}$ and $\left.O_{2}\right)-$ We have $O_{1}=\frac{b(2 a+b+c)}{2(a+b)}$ and $O_{2}=\frac{c(2 a+b+c)}{2(a+c)}$. $$ \begin{aligned} O_{1} & =\operatorname{Circum}(B, M, E) \\ & =b+\frac{1}{2} \operatorname{Circum}\left(0, c-b, \frac{(a-b)(b-c)}{b}\right) \\ & =b-\frac{b-c}{2 b} \operatorname{Circum}(0, b, b-a) \\ & =b-\frac{b-c}{2 b}(b-\operatorname{Circum}(0, b, a)) \\ & =b-\frac{b-c}{2 b}\left(b-\frac{a b}{a+b}\right)=b-\frac{b(b-c)}{2(a+b)}=\frac{b(2 a+b+c)}{2(a+b)} \end{aligned} $$ Similarly, $O_{2}=\frac{c(2 a+b+c)}{2(a+c)}$. We are now going to prove the following: Claim - We have $$ \frac{T O_{1}}{T O_{2}}=\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}} $$ $$ M O_{1}=B O_{1}=\left|b-\frac{b(2 a+b+c)}{2(a+b)}\right|=\left|\frac{b(b-c)}{2(a+b)}\right|=\frac{1}{2}\left|\frac{b-c}{a+b}\right| $$ and $Q O_{1}=\left|r-\frac{b(2 a+b+c)}{2(a+b)}\right|=\left|1-\frac{b(a+h)}{2(a+b) r}\right|=\left|1-\frac{b(a \bar{h}+1)}{2(a+b)}\right|=\left|\frac{a-\frac{a b}{c}}{2(a+b)}\right|=\frac{1}{2}\left|\frac{b-c}{a+b}\right|$. This implies both (by symmetry) that $\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}}=\left|\frac{a+c}{a+b}\right|$ and that $Q$ is on (BME) and $(C M F)$. Also, $$ \frac{T O_{1}}{T O_{2}}=\frac{\left|\frac{b(2 a+b+c)}{2(a+b)}+\frac{b c}{a}\right|}{\left|\frac{c(2 a+b+c)}{2(a+c)}+\frac{b c}{a}\right|}=\left|\frac{\frac{b\left(2 a^{2}+a b+a c+2 a c+2 b c\right)}{2 a(a+b)}}{\frac{c\left(2 a^{2}+a b+a c+2 a b+2 b c\right)}{2 a(a+c)}}\right|=\left|\frac{a+c}{a+b}\right| \cdot\left|\frac{2 a^{2}+2 b c+a b+3 a c}{2 a^{2}+2 b c+3 a b+a c}\right| $$ if $z=2 a^{2}+2 b c+a b+3 a c$, then $a^{2} b c \bar{z}=2 a^{2}+2 b c+3 a b+a c$, so the second term has magnitude 1. This means $\frac{T O_{1}}{T O_{2}}=\frac{M O_{1}}{M O_{2}}=\frac{Q O_{1}}{Q O_{2}}$, as desired. To finish, note that this common ratio is the ratio between the radii of these two circles, so it is also $\frac{K O_{1}}{K O_{2}}$. By Apollonian circles the points $\{Q, M, T, K\}$ lie on a circle or a line.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
b34786e4-25c5-5c69-9e9f-a8e3f130d86b
| 246,802 |
Fix a function $f: \mathbb{N} \rightarrow \mathbb{N}$ and for any $m, n \in \mathbb{N}$ define $$ \Delta(m, n)=\underbrace{f(f(\ldots f}_{f(n) \text { times }}(m) \ldots))-\underbrace{f(f(\ldots f}_{f(m) \text { times }}(n) \ldots)) . $$ Suppose $\Delta(m, n) \neq 0$ for any distinct $m, n \in \mathbb{N}$. Show that $\Delta$ is unbounded, meaning that for any constant $C$ there exist $m, n \in \mathbb{N}$ with $|\Delta(m, n)|>C$.
|
Suppose for the sake of contradiction that $|\Delta(m, n)| \leq N$ for all $m, n$. Note that $f$ is injective, as $$ f(m)=f(n) \Longrightarrow \Delta(m, n)=0 \Longrightarrow m=n $$ as desired. Let $G$ be the "arrow graph" of $f$, which is the directed graph with vertex set $\mathbb{N}$ and edges $n \rightarrow f(n)$. The first step in the solution is to classify the structure of $G$. Injectivity implies that $G$ is a disjoint collection of chains (infinite and half-infinite) and cycles. We have the following sequence of claims that further refine the structure. Claim - The graph $G$ has no cycles. $$ f^{f(n)}\left(m_{1}\right)=f^{f(n)}\left(m_{2}\right) $$ for some $m_{1} \neq m_{2}$, which contradicts injectivity. Claim - The graph $G$ has at most $2 N+1$ chains. $$ \left|\Delta\left(m_{i}, f^{B-f\left(m_{i}\right)}(1)\right)\right| \leq N \Longrightarrow\left|f^{B}(1)-f^{f B-f\left(m_{i}\right)+1}(1)\left(m_{i}\right)\right| \leq N . $$ Since the $m_{i} \mathrm{~S}$ are in different chains, we have that $f^{f\left(-f\left(m_{i}\right)+1\right.}(1)\left(m_{i}\right)$ are distinct for each $i$, which implies that $k \leq 2 N+1$, as desired. Claim - The graph $G$ consists of exactly one half-infinite chain. Since there are only finitely many chains, $f^{f(c)}(n)$ achieves all sufficiently large positive integers, say all positive integers at least $M$. Fix $A$ and $B$ such that $B>A \geq M$. If $f^{f(c)}(n) \in[A, B]$, then $f^{f(n)}(c) \in[A-N, B+N]$, and distinct $n$ generate distinct $f^{f(n)}(c)$ due to the structure of $G$. Therefore, we have at least $B-A+1$ good numbers in $[A-N, B+N]$, so there are at most $2 N$ bad numbers in $[A-N, B+N]$. Varying $B$, this shows there are at most $2 N$ bad numbers at least $A-N$. Let $c$ be the starting point of the chain, so every integer is of the form $f^{k}(c)$, where $k \geq 0$. Define a function $g: \mathbb{Z}_{\geq 0} \rightarrow \mathbb{N}$ by $$ g(k):=f^{k}(c) $$ Due to the structure of $G, g$ is a bijection. Define $$ \delta(a, b):=\Delta\left(f^{a}(c), f^{b}(c)\right)=g(g(b+1)+a)-g(g(a+1)+b) $$ so the conditions are equivalent to $|\delta(a, b)| \leq N$ for all $a, b \in \mathbb{Z}_{\geq 0}$ and $\delta(a, b) \neq 0$ for $a \neq b$, which is equivalent to $g(a+1)-a \neq g(b+1)-b$ for $a \neq b$. This tells us that $g(x)-x$ is injective for $x \geq 1$. ## Lemma For all $M$, there exists a nonnegative integer $x$ with $g(x) \leq x-M$. Now pick $B$ such that $g(B)+N \leq B$ and $g(B)>N$. Note that infinitely many such $B$ exist, since we can take $M$ to be arbitrarily small in the above lemma. Let $$ t=\max \left\{g^{-1}(g(B)-N), g^{-1}(g(B)-N+1), \ldots, g^{-1}(g(B)+N)\right\} $$ Note that $g(t) \leq g(B)+N \leq B$, so we have $$ |\delta(t-1, B-g(t))|=|g(B)-g(t-1+g(B+1-g(t)))| \leq N $$ so $$ t-1+g(B+1-g(t)) \in\left\{g^{-1}(g(B)-N), g^{-1}(g(B)-N+1), \ldots, g^{-1}(g(B)+N)\right\} $$ so by the maximality of $t$, we must have $g(B+1-g(t))=1$, so $B+1-g(t)=g^{-1}(1)$. We have $|g(t)-g(B)| \leq N$, so $$ \left|(B-g(B))+1-g^{-1}(1)\right| \leq N . $$ This is true for infinitely many values of $B$, so infinitely many values of $B-g(B)$ (by injectivity of $g(x)-x)$, which is a contradiction. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Fix a function $f: \mathbb{N} \rightarrow \mathbb{N}$ and for any $m, n \in \mathbb{N}$ define $$ \Delta(m, n)=\underbrace{f(f(\ldots f}_{f(n) \text { times }}(m) \ldots))-\underbrace{f(f(\ldots f}_{f(m) \text { times }}(n) \ldots)) . $$ Suppose $\Delta(m, n) \neq 0$ for any distinct $m, n \in \mathbb{N}$. Show that $\Delta$ is unbounded, meaning that for any constant $C$ there exist $m, n \in \mathbb{N}$ with $|\Delta(m, n)|>C$.
|
Suppose for the sake of contradiction that $|\Delta(m, n)| \leq N$ for all $m, n$. Note that $f$ is injective, as $$ f(m)=f(n) \Longrightarrow \Delta(m, n)=0 \Longrightarrow m=n $$ as desired. Let $G$ be the "arrow graph" of $f$, which is the directed graph with vertex set $\mathbb{N}$ and edges $n \rightarrow f(n)$. The first step in the solution is to classify the structure of $G$. Injectivity implies that $G$ is a disjoint collection of chains (infinite and half-infinite) and cycles. We have the following sequence of claims that further refine the structure. Claim - The graph $G$ has no cycles. $$ f^{f(n)}\left(m_{1}\right)=f^{f(n)}\left(m_{2}\right) $$ for some $m_{1} \neq m_{2}$, which contradicts injectivity. Claim - The graph $G$ has at most $2 N+1$ chains. $$ \left|\Delta\left(m_{i}, f^{B-f\left(m_{i}\right)}(1)\right)\right| \leq N \Longrightarrow\left|f^{B}(1)-f^{f B-f\left(m_{i}\right)+1}(1)\left(m_{i}\right)\right| \leq N . $$ Since the $m_{i} \mathrm{~S}$ are in different chains, we have that $f^{f\left(-f\left(m_{i}\right)+1\right.}(1)\left(m_{i}\right)$ are distinct for each $i$, which implies that $k \leq 2 N+1$, as desired. Claim - The graph $G$ consists of exactly one half-infinite chain. Since there are only finitely many chains, $f^{f(c)}(n)$ achieves all sufficiently large positive integers, say all positive integers at least $M$. Fix $A$ and $B$ such that $B>A \geq M$. If $f^{f(c)}(n) \in[A, B]$, then $f^{f(n)}(c) \in[A-N, B+N]$, and distinct $n$ generate distinct $f^{f(n)}(c)$ due to the structure of $G$. Therefore, we have at least $B-A+1$ good numbers in $[A-N, B+N]$, so there are at most $2 N$ bad numbers in $[A-N, B+N]$. Varying $B$, this shows there are at most $2 N$ bad numbers at least $A-N$. Let $c$ be the starting point of the chain, so every integer is of the form $f^{k}(c)$, where $k \geq 0$. Define a function $g: \mathbb{Z}_{\geq 0} \rightarrow \mathbb{N}$ by $$ g(k):=f^{k}(c) $$ Due to the structure of $G, g$ is a bijection. Define $$ \delta(a, b):=\Delta\left(f^{a}(c), f^{b}(c)\right)=g(g(b+1)+a)-g(g(a+1)+b) $$ so the conditions are equivalent to $|\delta(a, b)| \leq N$ for all $a, b \in \mathbb{Z}_{\geq 0}$ and $\delta(a, b) \neq 0$ for $a \neq b$, which is equivalent to $g(a+1)-a \neq g(b+1)-b$ for $a \neq b$. This tells us that $g(x)-x$ is injective for $x \geq 1$. ## Lemma For all $M$, there exists a nonnegative integer $x$ with $g(x) \leq x-M$. Now pick $B$ such that $g(B)+N \leq B$ and $g(B)>N$. Note that infinitely many such $B$ exist, since we can take $M$ to be arbitrarily small in the above lemma. Let $$ t=\max \left\{g^{-1}(g(B)-N), g^{-1}(g(B)-N+1), \ldots, g^{-1}(g(B)+N)\right\} $$ Note that $g(t) \leq g(B)+N \leq B$, so we have $$ |\delta(t-1, B-g(t))|=|g(B)-g(t-1+g(B+1-g(t)))| \leq N $$ so $$ t-1+g(B+1-g(t)) \in\left\{g^{-1}(g(B)-N), g^{-1}(g(B)-N+1), \ldots, g^{-1}(g(B)+N)\right\} $$ so by the maximality of $t$, we must have $g(B+1-g(t))=1$, so $B+1-g(t)=g^{-1}(1)$. We have $|g(t)-g(B)| \leq N$, so $$ \left|(B-g(B))+1-g^{-1}(1)\right| \leq N . $$ This is true for infinitely many values of $B$, so infinitely many values of $B-g(B)$ (by injectivity of $g(x)-x)$, which is a contradiction. This completes the proof.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
5bb3a883-3d83-5405-b6ad-f29dbac9269b
| 604,512 |
Find all real-valued functions $f$ defined on pairs of real numbers, having the following property: for all real numbers $a, b, c$, the median of $f(a, b), f(b, c), f(c, a)$ equals the median of $a, b, c$. (The median of three real numbers, not necessarily distinct, is the number that is in the middle when the three numbers are arranged in nondecreasing order.)
|
We prove the following main claim, from which repeated applications can deduce the problem. Claim - Let $a<b<c$ be arbitrary. On $\{a, b, c\}^{2}, f$ takes one of the following two forms, where the column indicates the $x$-value and the row indicates the $y$-value. | $f$ | $a$ | $b$ | $c$ | | ---: | ---: | ---: | ---: | | $a$ | $a$ | $b$ | $\geq c$ | | $b$ | $\leq a$ | $b$ | $\geq c$ | | $c$ | $\leq a$ | $b$ | $c$ | or | $f$ | $a$ | $b$ | $c$ | | ---: | ---: | ---: | ---: | | $a$ | $a$ | $\leq a$ | $\leq a$ | | $b$ | $b$ | $b$ | $b$ | | $c$ | $\geq c$ | $\geq c$ | $c$ | - By considering the assertion for $(a, a, c)$ and $(a, c, c)$ we see that one of $f(a, c)$ and $f(c, a)$ is $\geq c$ and the other is $\leq a$. - Hence, by considering $(a, b, c)$ we find that one of $f(a, b)$ and $f(b, c)$ must be $b$, and similarly for $f(b, a)$ and $f(c, b)$. - Now, WLOG $f(b, a)=b$; we prove we get the first case. - By considering $(a, a, b)$ we deduce $f(a, b) \leq a$, so $f(b, c)=b$ and then $f(c, b) \geq c$. - Finally, considering $(c, b, a)$ once again in conjunction with the first bullet, we arrive at the conclusion that $f(a, c) \leq a$; similarly $f(c, a) \geq c$. From this it's easy to obtain that $f(x, y) \equiv x$ or $f(x, y) \equiv y$ are the only solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Find all real-valued functions $f$ defined on pairs of real numbers, having the following property: for all real numbers $a, b, c$, the median of $f(a, b), f(b, c), f(c, a)$ equals the median of $a, b, c$. (The median of three real numbers, not necessarily distinct, is the number that is in the middle when the three numbers are arranged in nondecreasing order.)
|
We prove the following main claim, from which repeated applications can deduce the problem. Claim - Let $a<b<c$ be arbitrary. On $\{a, b, c\}^{2}, f$ takes one of the following two forms, where the column indicates the $x$-value and the row indicates the $y$-value. | $f$ | $a$ | $b$ | $c$ | | ---: | ---: | ---: | ---: | | $a$ | $a$ | $b$ | $\geq c$ | | $b$ | $\leq a$ | $b$ | $\geq c$ | | $c$ | $\leq a$ | $b$ | $c$ | or | $f$ | $a$ | $b$ | $c$ | | ---: | ---: | ---: | ---: | | $a$ | $a$ | $\leq a$ | $\leq a$ | | $b$ | $b$ | $b$ | $b$ | | $c$ | $\geq c$ | $\geq c$ | $c$ | - By considering the assertion for $(a, a, c)$ and $(a, c, c)$ we see that one of $f(a, c)$ and $f(c, a)$ is $\geq c$ and the other is $\leq a$. - Hence, by considering $(a, b, c)$ we find that one of $f(a, b)$ and $f(b, c)$ must be $b$, and similarly for $f(b, a)$ and $f(c, b)$. - Now, WLOG $f(b, a)=b$; we prove we get the first case. - By considering $(a, a, b)$ we deduce $f(a, b) \leq a$, so $f(b, c)=b$ and then $f(c, b) \geq c$. - Finally, considering $(c, b, a)$ once again in conjunction with the first bullet, we arrive at the conclusion that $f(a, c) \leq a$; similarly $f(c, a) \geq c$. From this it's easy to obtain that $f(x, y) \equiv x$ or $f(x, y) \equiv y$ are the only solutions.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2011.jsonl",
"problem_match": null,
"solution_match": null
}
|
26b1aead-ea9b-5abc-8aa1-b2b2fdd6caa9
| 604,523 |
Two circles $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. Line $\ell$ is tangent to $\omega_{1}$ at $P$ and to $\omega_{2}$ at $Q$ so that $A$ is closer to $\ell$ than $B$. Let $X$ and $Y$ be points on major $\operatorname{arcs} \widehat{P A}\left(\right.$ on $\left.\omega_{1}\right)$ and $\overparen{A Q}$ (on $\left.\omega_{2}\right)$, respectively, such that $A X / P X=A Y / Q Y=c$. Extend segments $P A$ and $Q A$ through $A$ to $R$ and $S$, respectively, such that $A R=A S=c \cdot P Q$. Given that the circumcenter of triangle $A R S$ lies on line $X Y$, prove that $\angle X P A=\angle A Q Y$.
|
We begin as follows: Claim - There is a spiral similarity centered at $X$ mapping $A R$ to $P Q$. Similarly there is a spiral similarity centered at $Y$ mapping $S A$ to $P Q$. Now the composition of the two spiral similarities $$ A R \stackrel{X}{\mapsto} P Q \stackrel{Y}{\mapsto} S A $$ must be a rotation, since $A R=A S$. The center of this rotation must coincide with the circumcenter $O$ of $\triangle A R S$, which is known to lie on line $X Y$.  As $O$ is a fixed-point of the composed map above, we may let $O^{\prime}$ be the image of $O$ under the rotation at $X$, so that $$ \triangle X P A \AA \triangle X O^{\prime} O, \quad \triangle Y Q A \AA \triangle Y O^{\prime} O . $$ Because $$ \frac{X O}{X O^{\prime}}=\frac{X A}{X P}=c \frac{Y Q}{Y A}=\frac{Y O}{Y O^{\prime}} $$ it follows $\overline{O^{\prime} O}$ bisects $\angle X O^{\prime} Y$. Finally, we have $$ \measuredangle X P A=\measuredangle X O^{\prime} O=\measuredangle O O^{\prime} Y=\measuredangle A Q Y $$ Remark. Indeed, this also shows $\overline{X P} \| \overline{Y Q}$; so the positive homothety from $\omega_{1}$ to $\omega_{2}$ maps $P$ to $Q$ and $X$ to $Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. Line $\ell$ is tangent to $\omega_{1}$ at $P$ and to $\omega_{2}$ at $Q$ so that $A$ is closer to $\ell$ than $B$. Let $X$ and $Y$ be points on major $\operatorname{arcs} \widehat{P A}\left(\right.$ on $\left.\omega_{1}\right)$ and $\overparen{A Q}$ (on $\left.\omega_{2}\right)$, respectively, such that $A X / P X=A Y / Q Y=c$. Extend segments $P A$ and $Q A$ through $A$ to $R$ and $S$, respectively, such that $A R=A S=c \cdot P Q$. Given that the circumcenter of triangle $A R S$ lies on line $X Y$, prove that $\angle X P A=\angle A Q Y$.
|
We begin as follows: Claim - There is a spiral similarity centered at $X$ mapping $A R$ to $P Q$. Similarly there is a spiral similarity centered at $Y$ mapping $S A$ to $P Q$. Now the composition of the two spiral similarities $$ A R \stackrel{X}{\mapsto} P Q \stackrel{Y}{\mapsto} S A $$ must be a rotation, since $A R=A S$. The center of this rotation must coincide with the circumcenter $O$ of $\triangle A R S$, which is known to lie on line $X Y$.  As $O$ is a fixed-point of the composed map above, we may let $O^{\prime}$ be the image of $O$ under the rotation at $X$, so that $$ \triangle X P A \AA \triangle X O^{\prime} O, \quad \triangle Y Q A \AA \triangle Y O^{\prime} O . $$ Because $$ \frac{X O}{X O^{\prime}}=\frac{X A}{X P}=c \frac{Y Q}{Y A}=\frac{Y O}{Y O^{\prime}} $$ it follows $\overline{O^{\prime} O}$ bisects $\angle X O^{\prime} Y$. Finally, we have $$ \measuredangle X P A=\measuredangle X O^{\prime} O=\measuredangle O O^{\prime} Y=\measuredangle A Q Y $$ Remark. Indeed, this also shows $\overline{X P} \| \overline{Y Q}$; so the positive homothety from $\omega_{1}$ to $\omega_{2}$ maps $P$ to $Q$ and $X$ to $Y$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2011.jsonl",
"problem_match": null,
"solution_match": null
}
|
9fa87277-93b2-53c1-a7ec-8f3e6f2b24be
| 604,533 |
Acute triangle $A B C$ is inscribed in circle $\omega$. Let $H$ and $O$ denote its orthocenter and circumcenter, respectively. Let $M$ and $N$ be the midpoints of sides $A B$ and $A C$, respectively. Rays $M H$ and $N H$ meet $\omega$ at $P$ and $Q$, respectively. Lines $M N$ and $P Q$ meet at $R$. Prove that $\overline{O A} \perp \overline{R A}$.
|
Let $M H$ and $N H$ meet the nine-point circle again at $P^{\prime}$ and $Q^{\prime}$, respectively. Recall that $H$ is the center of the homothety between the circumcircle and the nine-point circle. From this we can see that $P$ and $Q$ are the images of this homothety, meaning that $$ H Q=2 H Q^{\prime} \quad \text { and } \quad H P=2 H P^{\prime} $$ Since $M, P^{\prime}, Q^{\prime}, N$ are cyclic, Power of a Point gives us $$ M H \cdot H P^{\prime}=H N \cdot H Q^{\prime} $$ Multiplying both sides by two, we thus derive $$ H M \cdot H P=H N \cdot H Q $$ It follows that the points $M, N, P, Q$ are concyclic.  Let $\omega_{1}, \omega_{2}, \omega_{3}$ denote the circumcircles of $M N P Q, A M N$, and $A B C$, respectively. The radical axis of $\omega_{1}$ and $\omega_{2}$ is line $M N$, while the radical axis of $\omega_{1}$ and $\omega_{3}$ is line $P Q$. Hence the line $R$ lies on the radical axis of $\omega_{2}$ and $\omega_{3}$. But we claim that $\omega_{2}$ and $\omega_{3}$ are internally tangent at $A$. This follows by noting the homothety at $A$ with ratio 2 sends $M$ to $B$ and $N$ to $C$. Hence the radical axis of $\omega_{2}$ and $\omega_{3}$ is a line tangent to both circles at $A$. Hence $\overline{R A}$ is tangent to $\omega_{3}$. Therefore, $\overline{R A} \perp \overline{O A}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Acute triangle $A B C$ is inscribed in circle $\omega$. Let $H$ and $O$ denote its orthocenter and circumcenter, respectively. Let $M$ and $N$ be the midpoints of sides $A B$ and $A C$, respectively. Rays $M H$ and $N H$ meet $\omega$ at $P$ and $Q$, respectively. Lines $M N$ and $P Q$ meet at $R$. Prove that $\overline{O A} \perp \overline{R A}$.
|
Let $M H$ and $N H$ meet the nine-point circle again at $P^{\prime}$ and $Q^{\prime}$, respectively. Recall that $H$ is the center of the homothety between the circumcircle and the nine-point circle. From this we can see that $P$ and $Q$ are the images of this homothety, meaning that $$ H Q=2 H Q^{\prime} \quad \text { and } \quad H P=2 H P^{\prime} $$ Since $M, P^{\prime}, Q^{\prime}, N$ are cyclic, Power of a Point gives us $$ M H \cdot H P^{\prime}=H N \cdot H Q^{\prime} $$ Multiplying both sides by two, we thus derive $$ H M \cdot H P=H N \cdot H Q $$ It follows that the points $M, N, P, Q$ are concyclic.  Let $\omega_{1}, \omega_{2}, \omega_{3}$ denote the circumcircles of $M N P Q, A M N$, and $A B C$, respectively. The radical axis of $\omega_{1}$ and $\omega_{2}$ is line $M N$, while the radical axis of $\omega_{1}$ and $\omega_{3}$ is line $P Q$. Hence the line $R$ lies on the radical axis of $\omega_{2}$ and $\omega_{3}$. But we claim that $\omega_{2}$ and $\omega_{3}$ are internally tangent at $A$. This follows by noting the homothety at $A$ with ratio 2 sends $M$ to $B$ and $N$ to $C$. Hence the radical axis of $\omega_{2}$ and $\omega_{3}$ is a line tangent to both circles at $A$. Hence $\overline{R A}$ is tangent to $\omega_{3}$. Therefore, $\overline{R A} \perp \overline{O A}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2011.jsonl",
"problem_match": null,
"solution_match": null
}
|
723e424e-665b-5c6e-ac22-fe82323857c7
| 246,871 |
At a certain orphanage, every pair of orphans are either friends or enemies. For every three of an orphan's friends, an even number of pairs of them are enemies. Prove that it's possible to assign each orphan two parents such that every pair of friends shares exactly one parent, but no pair of enemies does, and no three parents are in a love triangle (where each pair of them has a child).
|
Of course, we consider the graph with vertices as children and edges as friendships. Consider all the maximal cliques in the graph (i.e. repeatedly remove maximal cliques until no edges remain; thus all edges are in some clique). Claim - Every vertex is in at most two maximal cliques. Now, for every maximal clique we assign a particular parent to all vertices in that clique, adding in additional distinct parents if there are any deficient children. This satisfies the friendship/enemy condition. Moreover, one can readily check that there are no love triangles: given children $a, b, c$ such that $a$ and $b$ share a parent while $a$ and $c$ share another parent, according to the claim $b$ and $c$ can't share a third parent. This completes the problem. Ironically, the condition that there be no love triangle actually makes the problem easier, because it tells us exactly what to do!
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
At a certain orphanage, every pair of orphans are either friends or enemies. For every three of an orphan's friends, an even number of pairs of them are enemies. Prove that it's possible to assign each orphan two parents such that every pair of friends shares exactly one parent, but no pair of enemies does, and no three parents are in a love triangle (where each pair of them has a child).
|
Of course, we consider the graph with vertices as children and edges as friendships. Consider all the maximal cliques in the graph (i.e. repeatedly remove maximal cliques until no edges remain; thus all edges are in some clique). Claim - Every vertex is in at most two maximal cliques. Now, for every maximal clique we assign a particular parent to all vertices in that clique, adding in additional distinct parents if there are any deficient children. This satisfies the friendship/enemy condition. Moreover, one can readily check that there are no love triangles: given children $a, b, c$ such that $a$ and $b$ share a parent while $a$ and $c$ share another parent, according to the claim $b$ and $c$ can't share a third parent. This completes the problem. Ironically, the condition that there be no love triangle actually makes the problem easier, because it tells us exactly what to do!
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2011.jsonl",
"problem_match": null,
"solution_match": null
}
|
cfd069c1-4b41-5d1f-b07c-6e94b91d1eab
| 30,126 |
Let $a, b, c$ be real numbers in the interval $[0,1]$ with $a+b, b+c, c+a \geq 1$. Prove that $$ 1 \leq(1-a)^{2}+(1-b)^{2}+(1-c)^{2}+\frac{2 \sqrt{2} a b c}{\sqrt{a^{2}+b^{2}+c^{2}}} $$
|
We will prove the inequality for any $a, b, c$ the sides of a possibly degenerate triangle (which is implied by the condition), ignoring the particular constant 1. Homogenizing, we instead prove the problem in the following form: Claim - We have $$ k^{2} \leq(k-a)^{2}+(k-b)^{2}+(k-c)^{2}+\frac{2 \sqrt{2} a b c}{\sqrt{a^{2}+b^{2}+c^{2}}} $$ for any $a, b, c, k$ with $(a, b, c)$ the sides of a possibly degenerate triangle. Letting $x=\frac{1}{2}(b+c-a)$ as is usual, the problem rearranges to In that case, the problem amounts to $$ (x+y+z)^{2} \leq x^{2}+y^{2}+z^{2}+\frac{2(x+y)(y+z)(z+x)}{\sqrt{x^{2}+y^{2}+z^{2}+x y+y z+z x}} $$ or equivalently $$ x^{2}+y^{2}+z^{2}+x y+y z+z x \leq\left(\frac{(x+y)(y+z)(z+x)}{x y+y z+z x}\right)^{2} . $$ To show this, one may let $t=x y+y z+z x$, then using $(x+y)(x+z)=x^{2}+B$ this becomes $$ t^{2}\left(x^{2}+y^{2}+z^{2}+t\right) \leq\left(x^{2}+t\right)\left(y^{2}+t\right)\left(z^{2}+t\right) $$ which is obvious upon expansion. Remark. The inequality holds actually for all real numbers $a, b$, $c$, with very disgusting proofs.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers in the interval $[0,1]$ with $a+b, b+c, c+a \geq 1$. Prove that $$ 1 \leq(1-a)^{2}+(1-b)^{2}+(1-c)^{2}+\frac{2 \sqrt{2} a b c}{\sqrt{a^{2}+b^{2}+c^{2}}} $$
|
We will prove the inequality for any $a, b, c$ the sides of a possibly degenerate triangle (which is implied by the condition), ignoring the particular constant 1. Homogenizing, we instead prove the problem in the following form: Claim - We have $$ k^{2} \leq(k-a)^{2}+(k-b)^{2}+(k-c)^{2}+\frac{2 \sqrt{2} a b c}{\sqrt{a^{2}+b^{2}+c^{2}}} $$ for any $a, b, c, k$ with $(a, b, c)$ the sides of a possibly degenerate triangle. Letting $x=\frac{1}{2}(b+c-a)$ as is usual, the problem rearranges to In that case, the problem amounts to $$ (x+y+z)^{2} \leq x^{2}+y^{2}+z^{2}+\frac{2(x+y)(y+z)(z+x)}{\sqrt{x^{2}+y^{2}+z^{2}+x y+y z+z x}} $$ or equivalently $$ x^{2}+y^{2}+z^{2}+x y+y z+z x \leq\left(\frac{(x+y)(y+z)(z+x)}{x y+y z+z x}\right)^{2} . $$ To show this, one may let $t=x y+y z+z x$, then using $(x+y)(x+z)=x^{2}+B$ this becomes $$ t^{2}\left(x^{2}+y^{2}+z^{2}+t\right) \leq\left(x^{2}+t\right)\left(y^{2}+t\right)\left(z^{2}+t\right) $$ which is obvious upon expansion. Remark. The inequality holds actually for all real numbers $a, b$, $c$, with very disgusting proofs.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2011.jsonl",
"problem_match": null,
"solution_match": null
}
|
264ed071-e4c8-56f1-a77e-15e23c6205fa
| 604,597 |
Let $A B C$ be a triangle. Its excircles touch sides $B C, C A, A B$ at $D, E, F$. Prove that the perimeter of triangle $A B C$ is at most twice that of triangle $D E F$.
|
$$ \begin{aligned} -s+\sum_{\mathrm{cyc}} E F & \geq-s+\sum_{\mathrm{cyc}}[a-(s-a)(\cos B+\cos C)] \\ & =s-\sum_{\mathrm{cyc}} a \cos A=\sum_{\mathrm{cyc}} a\left(\frac{1}{2}-\cos A\right) \\ & =R \sum_{\mathrm{cyc}} \sin A(1-2 \cos A) \\ & =R \sum_{\mathrm{cyc}}(\sin A-\sin 2 A) \end{aligned} $$ Thus we're done upon noting that $$ \frac{\sin 2 B+\sin 2 C}{2}=\sin (B+C) \cos (B-C)=\sin A \cos (B-C) \leq \sin A $$ (Alternatively, one can avoid trigonometry by substituting $\cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$ and doing some routine but long calculation.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Its excircles touch sides $B C, C A, A B$ at $D, E, F$. Prove that the perimeter of triangle $A B C$ is at most twice that of triangle $D E F$.
|
$$ \begin{aligned} -s+\sum_{\mathrm{cyc}} E F & \geq-s+\sum_{\mathrm{cyc}}[a-(s-a)(\cos B+\cos C)] \\ & =s-\sum_{\mathrm{cyc}} a \cos A=\sum_{\mathrm{cyc}} a\left(\frac{1}{2}-\cos A\right) \\ & =R \sum_{\mathrm{cyc}} \sin A(1-2 \cos A) \\ & =R \sum_{\mathrm{cyc}}(\sin A-\sin 2 A) \end{aligned} $$ Thus we're done upon noting that $$ \frac{\sin 2 B+\sin 2 C}{2}=\sin (B+C) \cos (B-C)=\sin A \cos (B-C) \leq \sin A $$ (Alternatively, one can avoid trigonometry by substituting $\cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$ and doing some routine but long calculation.)
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2011.jsonl",
"problem_match": null,
"solution_match": null
}
|
70bbcc9d-ed01-56f4-9053-6e9c10c6ba2e
| 246,906 |
Let $x_{0}, x_{1}, \ldots, x_{n_{0}-1}$ be integers, and let $d_{1}, d_{2}, \ldots, d_{k}$ be positive integers with $n_{0}=d_{1}>d_{2}>\cdots>d_{k}$ and $\operatorname{gcd}\left(d_{1}, d_{2}, \ldots, d_{k}\right)=1$. For every integer $n \geq n_{0}$, define $$ x_{n}=\left\lfloor\frac{x_{n-d_{1}}+x_{n-d_{2}}+\cdots+x_{n-d_{k}}}{k}\right\rfloor . $$ Show that the sequence $\left(x_{n}\right)$ is eventually constant.
|
Note that if the initial terms are contained in some interval $[A, B]$ then they will remain in that interval. Thus the sequence is eventually periodic. Discard initial terms and let the period be $T$; we will consider all indices modulo $T$ from now on. Let $M$ be the maximal term in the sequence (which makes sense since the sequence is periodic). Note that if $x_{n}=M$, we must have $x_{n-d_{i}}=M$ for all $i$ as well. By taking a linear combination $\sum c_{i} d_{i} \equiv 1(\bmod T)($ possibly be Bezout's theorem, since $\operatorname{gcd}_{i}\left(d_{i}\right)=1$ ), we conclude $x_{n-1}=M$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $x_{0}, x_{1}, \ldots, x_{n_{0}-1}$ be integers, and let $d_{1}, d_{2}, \ldots, d_{k}$ be positive integers with $n_{0}=d_{1}>d_{2}>\cdots>d_{k}$ and $\operatorname{gcd}\left(d_{1}, d_{2}, \ldots, d_{k}\right)=1$. For every integer $n \geq n_{0}$, define $$ x_{n}=\left\lfloor\frac{x_{n-d_{1}}+x_{n-d_{2}}+\cdots+x_{n-d_{k}}}{k}\right\rfloor . $$ Show that the sequence $\left(x_{n}\right)$ is eventually constant.
|
Note that if the initial terms are contained in some interval $[A, B]$ then they will remain in that interval. Thus the sequence is eventually periodic. Discard initial terms and let the period be $T$; we will consider all indices modulo $T$ from now on. Let $M$ be the maximal term in the sequence (which makes sense since the sequence is periodic). Note that if $x_{n}=M$, we must have $x_{n-d_{i}}=M$ for all $i$ as well. By taking a linear combination $\sum c_{i} d_{i} \equiv 1(\bmod T)($ possibly be Bezout's theorem, since $\operatorname{gcd}_{i}\left(d_{i}\right)=1$ ), we conclude $x_{n-1}=M$, as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2011.jsonl",
"problem_match": null,
"solution_match": null
}
|
ab138e5e-3a61-518b-a7bf-2cd10225fb97
| 604,635 |
Let $A B C D$ be a quadrilateral with $A C=B D$. Diagonals $A C$ and $B D$ meet at $P$. Let $\omega_{1}$ and $O_{1}$ denote the circumcircle and circumcenter of triangle $A B P$. Let $\omega_{2}$ and $O_{2}$ denote the circumcircle and circumcenter of triangle $C D P$. Segment $B C$ meets $\omega_{1}$ and $\omega_{2}$ again at $S$ and $T$ (other than $B$ and $C$ ), respectively. Let $M$ and $N$ be the midpoints of minor arcs $\widehat{S P}$ (not including $B$ ) and $\overparen{T P}$ (not including $C$ ). Prove that $\overline{M N} \| \overline{O_{1} O_{2}}$.
|
Let $Q$ be the second intersection point of $\omega_{1}, \omega_{2}$. Suffice to show $\overline{Q P} \perp \overline{M N}$. Now $Q$ is the center of a spiral congruence which sends $\overline{A C} \mapsto \overline{B D}$. So $\triangle Q A B$ and $\triangle Q C D$ are similar isosceles. Now, $$ \measuredangle Q P A=\measuredangle Q B A=\measuredangle D C Q=\measuredangle D P Q $$ and so $\overline{Q P}$ is bisects $\angle B P C$.  Now, let $I=\overline{B M} \cap \overline{C N} \cap \overline{P Q}$ be the incenter of $\triangle P B C$. Then $I M \cdot I B=I P \cdot I Q=$ $I N \cdot I C$, so $B M N C$ is cyclic, meaning $\overline{M N}$ is antiparallel to $\overline{B C}$ through $\angle B I C$. Since $\overline{Q P I}$ passes through the circumcenter of $\triangle B I C$, it follows now $\overline{Q P I} \perp \overline{M N}$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral with $A C=B D$. Diagonals $A C$ and $B D$ meet at $P$. Let $\omega_{1}$ and $O_{1}$ denote the circumcircle and circumcenter of triangle $A B P$. Let $\omega_{2}$ and $O_{2}$ denote the circumcircle and circumcenter of triangle $C D P$. Segment $B C$ meets $\omega_{1}$ and $\omega_{2}$ again at $S$ and $T$ (other than $B$ and $C$ ), respectively. Let $M$ and $N$ be the midpoints of minor arcs $\widehat{S P}$ (not including $B$ ) and $\overparen{T P}$ (not including $C$ ). Prove that $\overline{M N} \| \overline{O_{1} O_{2}}$.
|
Let $Q$ be the second intersection point of $\omega_{1}, \omega_{2}$. Suffice to show $\overline{Q P} \perp \overline{M N}$. Now $Q$ is the center of a spiral congruence which sends $\overline{A C} \mapsto \overline{B D}$. So $\triangle Q A B$ and $\triangle Q C D$ are similar isosceles. Now, $$ \measuredangle Q P A=\measuredangle Q B A=\measuredangle D C Q=\measuredangle D P Q $$ and so $\overline{Q P}$ is bisects $\angle B P C$.  Now, let $I=\overline{B M} \cap \overline{C N} \cap \overline{P Q}$ be the incenter of $\triangle P B C$. Then $I M \cdot I B=I P \cdot I Q=$ $I N \cdot I C$, so $B M N C$ is cyclic, meaning $\overline{M N}$ is antiparallel to $\overline{B C}$ through $\angle B I C$. Since $\overline{Q P I}$ passes through the circumcenter of $\triangle B I C$, it follows now $\overline{Q P I} \perp \overline{M N}$ as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2012.jsonl",
"problem_match": null,
"solution_match": null
}
|
62775ef9-c524-508f-9cce-9a4e3a2f54d6
| 604,672 |
Let $\mathbb{N}$ be the set of positive integers. Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function satisfying the following two conditions: (a) $f(m)$ and $f(n)$ are relatively prime whenever $m$ and $n$ are relatively prime. (b) $n \leq f(n) \leq n+2012$ for all $n$. Prove that for any natural number $n$ and any prime $p$, if $p$ divides $f(n)$ then $p$ divides $n$.
|
【 First short solution, by Jeffrey Kwan. Let $p_{0}, p_{1}, p_{2}, \ldots$ denote the sequence of all prime numbers, in any order. Pick any primes $q_{i}$ such that $$ q_{0}\left|f\left(p_{0}\right), \quad q_{1}\right| f\left(p_{1}\right), \quad q_{2} \mid f\left(p_{2}\right), \text { etc. } $$ This is possible since each $f$ value above exceeds 1 . Also, since by hypothesis the $f\left(p_{i}\right)$ are pairwise coprime, the primes $q_{i}$ are all pairwise distinct. Claim - We must have $q_{i}=p_{i}$ for each $i$. (Therefore, $f\left(p_{i}\right)$ is a power of $p_{i}$ for each $i$.) $$ \begin{array}{rr} m+i & \equiv 0 \\ m & \left(\bmod q_{i}\right) \\ m & \equiv{ }^{\prime} \\ \left(\bmod p_{i}\right) \end{array} $$ for $0 \leq i \leq 2012$. But now $f(m)$ should be coprime to all $f\left(p_{i}\right)$, ergo coprime to $q_{0} q_{1} \ldots q_{2012}$, violating $m \leq f(m) \leq m+2012$. All that is left to do is note that whenever $p \nmid n$, we have $\operatorname{gcd}(f(p), f(n))=1$, hence $p \nmid f(n)$. This is the contrapositive of the problem statement.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathbb{N}$ be the set of positive integers. Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function satisfying the following two conditions: (a) $f(m)$ and $f(n)$ are relatively prime whenever $m$ and $n$ are relatively prime. (b) $n \leq f(n) \leq n+2012$ for all $n$. Prove that for any natural number $n$ and any prime $p$, if $p$ divides $f(n)$ then $p$ divides $n$.
|
【 First short solution, by Jeffrey Kwan. Let $p_{0}, p_{1}, p_{2}, \ldots$ denote the sequence of all prime numbers, in any order. Pick any primes $q_{i}$ such that $$ q_{0}\left|f\left(p_{0}\right), \quad q_{1}\right| f\left(p_{1}\right), \quad q_{2} \mid f\left(p_{2}\right), \text { etc. } $$ This is possible since each $f$ value above exceeds 1 . Also, since by hypothesis the $f\left(p_{i}\right)$ are pairwise coprime, the primes $q_{i}$ are all pairwise distinct. Claim - We must have $q_{i}=p_{i}$ for each $i$. (Therefore, $f\left(p_{i}\right)$ is a power of $p_{i}$ for each $i$.) $$ \begin{array}{rr} m+i & \equiv 0 \\ m & \left(\bmod q_{i}\right) \\ m & \equiv{ }^{\prime} \\ \left(\bmod p_{i}\right) \end{array} $$ for $0 \leq i \leq 2012$. But now $f(m)$ should be coprime to all $f\left(p_{i}\right)$, ergo coprime to $q_{0} q_{1} \ldots q_{2012}$, violating $m \leq f(m) \leq m+2012$. All that is left to do is note that whenever $p \nmid n$, we have $\operatorname{gcd}(f(p), f(n))=1$, hence $p \nmid f(n)$. This is the contrapositive of the problem statement.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2012.jsonl",
"problem_match": null,
"solution_match": null
}
|
87070055-1307-5ce2-9d9c-4f119db118a5
| 604,681 |
Let $\mathbb{N}$ be the set of positive integers. Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function satisfying the following two conditions: (a) $f(m)$ and $f(n)$ are relatively prime whenever $m$ and $n$ are relatively prime. (b) $n \leq f(n) \leq n+2012$ for all $n$. Prove that for any natural number $n$ and any prime $p$, if $p$ divides $f(n)$ then $p$ divides $n$.
|
【 Second solution with a grid. Fix $n$ and $p$, and assume for contradiction $p \nmid n$. Claim - There exists a large integer $N$ with $f(N)=N$, that also satisfies $N \equiv 1$ $(\bmod n)$ and $N \equiv 0(\bmod p)$. it to fill in the following table: | | $N+1$ | $N+2$ | $\ldots$ | $N+2012$ | | :---: | :---: | :---: | :---: | :---: | | $M$ | $q_{0,1}$ | $q_{0,2}$ | $\ldots$ | $q_{0,2012}$ | | $M+1$ | $q_{1,1}$ | $q_{1,2}$ | $\ldots$ | $q_{1,2012}$ | | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ | | $M+2012$ | $q_{2012,1}$ | $q_{2012,2}$ | $\ldots$ | $q_{2012,2012}$ |. By the Chinese Remainder Theorem, we can construct $N$ such that $N+1 \equiv 0\left(\bmod q_{i, 1}\right)$ for every $i$, and similarly for $N+2$, and so on. Moreover, we can also tack on the extra conditions $N \equiv 0(\bmod p)$ and $N \equiv 1(\bmod n)$ we wanted. Notice that $N$ cannot be divisible by any of the $q_{i, j}$ 's, since the $q_{i, j}$ 's are greater than 2012. After we've chosen $N$, we can pick $M$ such that $M \equiv 0\left(\bmod q_{0, j}\right)$ for every $j$, and similarly $M+1 \equiv 0\left(\bmod q_{1, j}\right)$, et cetera. Moreover, we can tack on the condition $M \equiv 1$ $(\bmod N)$, which ensures $\operatorname{gcd}(M, N)=1$. What does this do? We claim that $f(N)=N$ now. Indeed $f(M)$ and $f(N)$ are relatively prime; but look at the table! The table tells us that $f(M)$ must have a common factor with each of $N+1, \ldots, N+2012$. So the only possibility is that $f(N)=N$. Now we're basically done. Since $N \equiv 1(\bmod n)$, we have $\operatorname{gcd}(N, n)=1$ and hence $1=\operatorname{gcd}(f(N), f(n))=\operatorname{gcd}(N, f(n))$. But $p \mid N$ and $p \mid f(n)$, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathbb{N}$ be the set of positive integers. Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function satisfying the following two conditions: (a) $f(m)$ and $f(n)$ are relatively prime whenever $m$ and $n$ are relatively prime. (b) $n \leq f(n) \leq n+2012$ for all $n$. Prove that for any natural number $n$ and any prime $p$, if $p$ divides $f(n)$ then $p$ divides $n$.
|
【 Second solution with a grid. Fix $n$ and $p$, and assume for contradiction $p \nmid n$. Claim - There exists a large integer $N$ with $f(N)=N$, that also satisfies $N \equiv 1$ $(\bmod n)$ and $N \equiv 0(\bmod p)$. it to fill in the following table: | | $N+1$ | $N+2$ | $\ldots$ | $N+2012$ | | :---: | :---: | :---: | :---: | :---: | | $M$ | $q_{0,1}$ | $q_{0,2}$ | $\ldots$ | $q_{0,2012}$ | | $M+1$ | $q_{1,1}$ | $q_{1,2}$ | $\ldots$ | $q_{1,2012}$ | | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ | | $M+2012$ | $q_{2012,1}$ | $q_{2012,2}$ | $\ldots$ | $q_{2012,2012}$ |. By the Chinese Remainder Theorem, we can construct $N$ such that $N+1 \equiv 0\left(\bmod q_{i, 1}\right)$ for every $i$, and similarly for $N+2$, and so on. Moreover, we can also tack on the extra conditions $N \equiv 0(\bmod p)$ and $N \equiv 1(\bmod n)$ we wanted. Notice that $N$ cannot be divisible by any of the $q_{i, j}$ 's, since the $q_{i, j}$ 's are greater than 2012. After we've chosen $N$, we can pick $M$ such that $M \equiv 0\left(\bmod q_{0, j}\right)$ for every $j$, and similarly $M+1 \equiv 0\left(\bmod q_{1, j}\right)$, et cetera. Moreover, we can tack on the condition $M \equiv 1$ $(\bmod N)$, which ensures $\operatorname{gcd}(M, N)=1$. What does this do? We claim that $f(N)=N$ now. Indeed $f(M)$ and $f(N)$ are relatively prime; but look at the table! The table tells us that $f(M)$ must have a common factor with each of $N+1, \ldots, N+2012$. So the only possibility is that $f(N)=N$. Now we're basically done. Since $N \equiv 1(\bmod n)$, we have $\operatorname{gcd}(N, n)=1$ and hence $1=\operatorname{gcd}(f(N), f(n))=\operatorname{gcd}(N, f(n))$. But $p \mid N$ and $p \mid f(n)$, contradiction.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2012.jsonl",
"problem_match": null,
"solution_match": null
}
|
87070055-1307-5ce2-9d9c-4f119db118a5
| 604,681 |
In scalene triangle $A B C$, let the feet of the perpendiculars from $A$ to $\overline{B C}, B$ to $\overline{C A}$, $C$ to $\overline{A B}$ be $A_{1}, B_{1}, C_{1}$, respectively. Denote by $A_{2}$ the intersection of lines $B C$ and $B_{1} C_{1}$. Define $B_{2}$ and $C_{2}$ analogously. Let $D, E, F$ be the respective midpoints of sides $\overline{B C}, \overline{C A}, \overline{A B}$. Show that the perpendiculars from $D$ to $\overline{A A_{2}}, E$ to $\overline{B B_{2}}$ and $F$ to $\overline{C C_{2}}$ are concurrent.
|
We claim that they pass through the orthocenter $H$. Indeed, consider the circle with diameter $\overline{B C}$, which circumscribes quadrilateral $B C B_{1} C_{1}$ and has center $D$. Then by Brokard theorem, $\overline{A A_{2}}$ is the polar of line $H$. Thus $\overline{D H} \perp \overline{A A_{2}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In scalene triangle $A B C$, let the feet of the perpendiculars from $A$ to $\overline{B C}, B$ to $\overline{C A}$, $C$ to $\overline{A B}$ be $A_{1}, B_{1}, C_{1}$, respectively. Denote by $A_{2}$ the intersection of lines $B C$ and $B_{1} C_{1}$. Define $B_{2}$ and $C_{2}$ analogously. Let $D, E, F$ be the respective midpoints of sides $\overline{B C}, \overline{C A}, \overline{A B}$. Show that the perpendiculars from $D$ to $\overline{A A_{2}}, E$ to $\overline{B B_{2}}$ and $F$ to $\overline{C C_{2}}$ are concurrent.
|
We claim that they pass through the orthocenter $H$. Indeed, consider the circle with diameter $\overline{B C}$, which circumscribes quadrilateral $B C B_{1} C_{1}$ and has center $D$. Then by Brokard theorem, $\overline{A A_{2}}$ is the polar of line $H$. Thus $\overline{D H} \perp \overline{A A_{2}}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2012.jsonl",
"problem_match": null,
"solution_match": null
}
|
70b8acc3-0ecf-52f5-a77d-182d420fe849
| 604,705 |
A rational number $x$ is given. Prove that there exists a sequence $x_{0}, x_{1}, x_{2}, \ldots$ of rational numbers with the following properties: (a) $x_{0}=x$; (b) for every $n \geq 1$, either $x_{n}=2 x_{n-1}$ or $x_{n}=2 x_{n-1}+\frac{1}{n}$; (c) $x_{n}$ is an integer for some $n$.
|
Think of the sequence as a process over time. We'll show that: Claim - At any given time $t$, if the denominator of $x_{t}$ has some odd prime power $q=p^{e}$, then we can delete a factor of $p$ from the denominator, while only adding powers of two to the denominator. (Thus we can just delete off all the odd primes one by one and then double appropriately many times.) Indeed, let $n$ be large, and suppose $t<2^{r+1} q<2^{r+2} q<\cdots<2^{r+m} q<n$. For some binary variables $\varepsilon_{i} \in\{0,1\}$ we can have $$ x_{n}=2^{n-t} x_{t}+c_{1} \cdot \frac{\varepsilon_{1}}{q}+c_{2} \cdot \frac{\varepsilon_{2}}{q} \cdots+c_{s} \cdot \frac{\varepsilon_{m}}{q} $$ where $c_{i}$ is some power of 2 (to be exact, $c_{i}=\frac{2^{n-2^{r+i} q}}{2^{r+1}}$, but the exact value doesn't matter). If $m$ is large enough the set $\left\{0, c_{1}\right\}+\left\{0, c_{2}\right\}+\cdots+\left\{0, c_{m}\right\}$ spans everything modulo p. (Actually, Cauchy-Davenport implies $m=p$ is enough, but one can also just use Pigeonhole to notice some residue appears more than $p$ times, for $m=O\left(p^{2}\right)$.) Thus we can eliminate one factor of $p$ from the denominator, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A rational number $x$ is given. Prove that there exists a sequence $x_{0}, x_{1}, x_{2}, \ldots$ of rational numbers with the following properties: (a) $x_{0}=x$; (b) for every $n \geq 1$, either $x_{n}=2 x_{n-1}$ or $x_{n}=2 x_{n-1}+\frac{1}{n}$; (c) $x_{n}$ is an integer for some $n$.
|
Think of the sequence as a process over time. We'll show that: Claim - At any given time $t$, if the denominator of $x_{t}$ has some odd prime power $q=p^{e}$, then we can delete a factor of $p$ from the denominator, while only adding powers of two to the denominator. (Thus we can just delete off all the odd primes one by one and then double appropriately many times.) Indeed, let $n$ be large, and suppose $t<2^{r+1} q<2^{r+2} q<\cdots<2^{r+m} q<n$. For some binary variables $\varepsilon_{i} \in\{0,1\}$ we can have $$ x_{n}=2^{n-t} x_{t}+c_{1} \cdot \frac{\varepsilon_{1}}{q}+c_{2} \cdot \frac{\varepsilon_{2}}{q} \cdots+c_{s} \cdot \frac{\varepsilon_{m}}{q} $$ where $c_{i}$ is some power of 2 (to be exact, $c_{i}=\frac{2^{n-2^{r+i} q}}{2^{r+1}}$, but the exact value doesn't matter). If $m$ is large enough the set $\left\{0, c_{1}\right\}+\left\{0, c_{2}\right\}+\cdots+\left\{0, c_{m}\right\}$ spans everything modulo p. (Actually, Cauchy-Davenport implies $m=p$ is enough, but one can also just use Pigeonhole to notice some residue appears more than $p$ times, for $m=O\left(p^{2}\right)$.) Thus we can eliminate one factor of $p$ from the denominator, as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2012.jsonl",
"problem_match": null,
"solution_match": null
}
|
3047892a-d390-5297-9fac-1ae20c851da2
| 604,718 |
Positive real numbers $x, y, z$ satisfy $x y z+x y+y z+z x=x+y+z+1$. Prove that $$ \frac{1}{3}\left(\sqrt{\frac{1+x^{2}}{1+x}}+\sqrt{\frac{1+y^{2}}{1+y}}+\sqrt{\frac{1+z^{2}}{1+z}}\right) \leq\left(\frac{x+y+z}{3}\right)^{5 / 8} . $$
|
The key is the identity $$ \begin{aligned} \frac{x^{2}+1}{x+1} & =\frac{\left(x^{2}+1\right)(y+1)(z+1)}{(x+1)(y+1)(z+1)} \\ & =\frac{x(x y z+x y+x z)+x^{2}+y z+y+z+1}{2(1+x+y+z)} \\ & =\frac{x(x+y+z+1-y z)+x^{2}+y z+y+z+1}{2(1+x+y+z)} \\ & =\frac{(x+y)(x+z)+x^{2}+(x-x y z+y+z+1)}{2(1+x+y+z)} \\ & =\frac{2(x+y)(x+z)}{2(1+x+y+z)} \\ & =\frac{(x+y)(x+z)}{1+x+y+z} . \end{aligned} $$ Remark. The "trick" can be rephrased as $\left(x^{2}+1\right)(y+1)(z+1)=2(x+y)(x+z)$. After this, straight Cauchy in the obvious way will do it (reducing everything to an inequality in $s=x+y+z$ ). One writes $$ \begin{aligned} \left(\sum_{\mathrm{cyc}} \frac{\sqrt{(x+y)(x+z)}}{\sqrt{1+s}}\right)^{2} & \leq \frac{\left(\sum_{\mathrm{cyc}} x+y\right)\left(\sum_{\mathrm{cyc}} x+z\right)}{1+s} \\ & =\frac{4 s^{2}}{1+s} \end{aligned} $$ and so it suffices to check that $\frac{4 s^{2}}{1+s} \leq 9(s / 3)^{5 / 4}$, which is true because $$ (s / 3)^{5} \cdot 9^{4} \cdot(1+s)^{4}-\left(4 s^{2}\right)^{4}=s^{5}(s-3)^{2}\left(27 s^{2}+14 s+3\right) \geq 0 $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Positive real numbers $x, y, z$ satisfy $x y z+x y+y z+z x=x+y+z+1$. Prove that $$ \frac{1}{3}\left(\sqrt{\frac{1+x^{2}}{1+x}}+\sqrt{\frac{1+y^{2}}{1+y}}+\sqrt{\frac{1+z^{2}}{1+z}}\right) \leq\left(\frac{x+y+z}{3}\right)^{5 / 8} . $$
|
The key is the identity $$ \begin{aligned} \frac{x^{2}+1}{x+1} & =\frac{\left(x^{2}+1\right)(y+1)(z+1)}{(x+1)(y+1)(z+1)} \\ & =\frac{x(x y z+x y+x z)+x^{2}+y z+y+z+1}{2(1+x+y+z)} \\ & =\frac{x(x+y+z+1-y z)+x^{2}+y z+y+z+1}{2(1+x+y+z)} \\ & =\frac{(x+y)(x+z)+x^{2}+(x-x y z+y+z+1)}{2(1+x+y+z)} \\ & =\frac{2(x+y)(x+z)}{2(1+x+y+z)} \\ & =\frac{(x+y)(x+z)}{1+x+y+z} . \end{aligned} $$ Remark. The "trick" can be rephrased as $\left(x^{2}+1\right)(y+1)(z+1)=2(x+y)(x+z)$. After this, straight Cauchy in the obvious way will do it (reducing everything to an inequality in $s=x+y+z$ ). One writes $$ \begin{aligned} \left(\sum_{\mathrm{cyc}} \frac{\sqrt{(x+y)(x+z)}}{\sqrt{1+s}}\right)^{2} & \leq \frac{\left(\sum_{\mathrm{cyc}} x+y\right)\left(\sum_{\mathrm{cyc}} x+z\right)}{1+s} \\ & =\frac{4 s^{2}}{1+s} \end{aligned} $$ and so it suffices to check that $\frac{4 s^{2}}{1+s} \leq 9(s / 3)^{5 / 4}$, which is true because $$ (s / 3)^{5} \cdot 9^{4} \cdot(1+s)^{4}-\left(4 s^{2}\right)^{4}=s^{5}(s-3)^{2}\left(27 s^{2}+14 s+3\right) \geq 0 $$
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2012.jsonl",
"problem_match": null,
"solution_match": null
}
|
d19b6c03-611d-583a-8f30-356b0098ecd7
| 604,729 |
Triangle $A B C$ is inscribed in circle $\Omega$. The interior angle bisector of angle $A$ intersects side $B C$ and $\Omega$ at $D$ and $L$ (other than $A$ ), respectively. Let $M$ be the midpoint of side $B C$. The circumcircle of triangle $A D M$ intersects sides $A B$ and $A C$ again at $Q$ and $P$ (other than $A$ ), respectively. Let $N$ be the midpoint of segment $P Q$, and let $H$ be the foot of the perpendicular from $L$ to line $N D$. Prove that line $M L$ is tangent to the circumcircle of triangle $H M N$.
|
By angle chasing, equivalent to show $\overline{M N} \| \overline{A D}$, so discard the point $H$. We now present a three solutions. 『 Third solution using barycentrics (mine). Once reduced to $\overline{M N} \| \overline{A B}$, straight bary will also work. By power of a point one obtains $$ \begin{aligned} P & =\left(a^{2}: 0: 2 b(b+c)-a^{2}\right) \\ Q & =\left(a^{2}: 2 c(b+c)-a^{2}: 0\right) \\ \Longrightarrow N & =\left(a^{2}(b+c): 2 b c(b+c)-b a^{2}: 2 b c(b+c)-c a^{2}\right) . \end{aligned} $$ Now the point at infinity along $\overline{A D}$ is $(-(b+c): b: c)$ and so we need only verify $$ \operatorname{det}\left[\begin{array}{ccc} a^{2}(b+c) & 2 b c(b+c)-b a^{2} & 2 b c(b+c)-c a^{2} \\ 0 & 1 & 1 \\ -(b+c) & b & c \end{array}\right]=0 $$ which follows since the first row is $-a^{2}$ times the third row plus $2 b c(b+c)$ times the second row.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangle $A B C$ is inscribed in circle $\Omega$. The interior angle bisector of angle $A$ intersects side $B C$ and $\Omega$ at $D$ and $L$ (other than $A$ ), respectively. Let $M$ be the midpoint of side $B C$. The circumcircle of triangle $A D M$ intersects sides $A B$ and $A C$ again at $Q$ and $P$ (other than $A$ ), respectively. Let $N$ be the midpoint of segment $P Q$, and let $H$ be the foot of the perpendicular from $L$ to line $N D$. Prove that line $M L$ is tangent to the circumcircle of triangle $H M N$.
|
By angle chasing, equivalent to show $\overline{M N} \| \overline{A D}$, so discard the point $H$. We now present a three solutions. 『 Third solution using barycentrics (mine). Once reduced to $\overline{M N} \| \overline{A B}$, straight bary will also work. By power of a point one obtains $$ \begin{aligned} P & =\left(a^{2}: 0: 2 b(b+c)-a^{2}\right) \\ Q & =\left(a^{2}: 2 c(b+c)-a^{2}: 0\right) \\ \Longrightarrow N & =\left(a^{2}(b+c): 2 b c(b+c)-b a^{2}: 2 b c(b+c)-c a^{2}\right) . \end{aligned} $$ Now the point at infinity along $\overline{A D}$ is $(-(b+c): b: c)$ and so we need only verify $$ \operatorname{det}\left[\begin{array}{ccc} a^{2}(b+c) & 2 b c(b+c)-b a^{2} & 2 b c(b+c)-c a^{2} \\ 0 & 1 & 1 \\ -(b+c) & b & c \end{array}\right]=0 $$ which follows since the first row is $-a^{2}$ times the third row plus $2 b c(b+c)$ times the second row.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2012.jsonl",
"problem_match": null,
"solution_match": null
}
|
b1efdfe8-c5b1-51ea-b52d-592e31c268da
| 246,994 |
Let $A B C$ be a triangle and $D, E, F$ be the midpoints of $\operatorname{arcs} B C, C A, A B$ on the circumcircle. Line $\ell_{a}$ passes through the feet of the perpendiculars from $A$ to $\overline{D B}$ and $\overline{D C}$. Line $m_{a}$ passes through the feet of the perpendiculars from $D$ to $\overline{A B}$ and $\overline{A C}$. Let $A_{1}$ denote the intersection of lines $\ell_{a}$ and $m_{a}$. Define points $B_{1}$ and $C_{1}$ similarly. Prove that triangles $D E F$ and $A_{1} B_{1} C_{1}$ are similar to each other.
|
In fact, it is true for any points $D, E, F$ on the circumcircle. More strongly we contend: Claim - Point $A_{1}$ is the midpoint of $\overline{H D}$.  Hence $A_{1} B_{1} C_{1}$ is similar to $D E F$ through a homothety at $H$ with ratio $\frac{1}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and $D, E, F$ be the midpoints of $\operatorname{arcs} B C, C A, A B$ on the circumcircle. Line $\ell_{a}$ passes through the feet of the perpendiculars from $A$ to $\overline{D B}$ and $\overline{D C}$. Line $m_{a}$ passes through the feet of the perpendiculars from $D$ to $\overline{A B}$ and $\overline{A C}$. Let $A_{1}$ denote the intersection of lines $\ell_{a}$ and $m_{a}$. Define points $B_{1}$ and $C_{1}$ similarly. Prove that triangles $D E F$ and $A_{1} B_{1} C_{1}$ are similar to each other.
|
In fact, it is true for any points $D, E, F$ on the circumcircle. More strongly we contend: Claim - Point $A_{1}$ is the midpoint of $\overline{H D}$.  Hence $A_{1} B_{1} C_{1}$ is similar to $D E F$ through a homothety at $H$ with ratio $\frac{1}{2}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2013.jsonl",
"problem_match": null,
"solution_match": null
}
|
8b6a4ae3-17f2-5de2-af5f-b29a3e34f347
| 604,848 |
Divide the plane into an infinite square grid by drawing all the lines $x=m$ and $y=n$ for $m, n \in \mathbb{Z}$. Next, if a square's upper-right corner has both coordinates even, color it black; otherwise, color it white (in this way, exactly $1 / 4$ of the squares are black and no two black squares are adjacent). Let $r$ and $s$ be odd integers, and let $(x, y)$ be a point in the interior of any white square such that $r x-s y$ is irrational. Shoot a laser out of this point with slope $r / s$; lasers pass through white squares and reflect off black squares. Prove that the path of this laser will from a closed loop.
|
We re-color the white squares as red, blue, or green according as to whether they have a black square directly to the left/right, above/below, or neither, as shown below. Finally, we fix time zero to be a moment just before the laser passes a horizontal (WLOG) lattice line (not necessarily a wall). Shown below is an example for $(r, s)=(3,5)$. 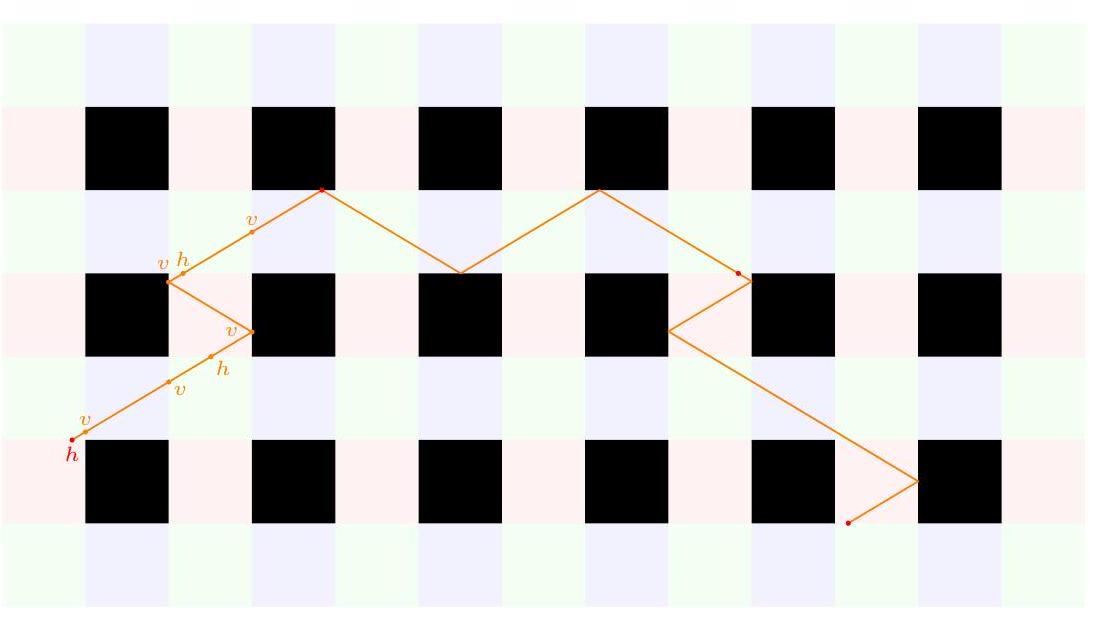 The main idea is to keep track of every time the laser passes a lattice line (again, not necessarily a wall). There are four possible types of events: - A horizontal $h$ event where the laser switches from red to green (or vice-versa); - A horizontal $h$ event where the laser rebounds off a wall, remaining in a blue square, but flips the $x$-component of its velocity; - A vertical $v$ event where the laser switches from blue to green (or vice-versa) - A vertical $v$ event where the laser rebounds off a wall, remaining in a red square, but flips the $y$-component of its velocity. The first key observation is that: Claim - In the first second, the laser will encounter exactly $r$ horizontal events and $s$ vertical events. In every second after that, the same sequence of $r+s$ events occurs. We let the key-word be the sequence $w$ of $r+s$ letters corresponding to the sequence. For example, the picture above denotes an example with keyword $w=h v v h v v h v$; so no matter what, every second, the laser will encounter eight lattice lines, which are horizontal and vertical in that order. Claim - Color is periodic every 3 seconds. Now in a 3 -second period, consider the $3 r$ horizontal events and $3 s$ vertical events (both are odd). In order for the color to remain the same (as the only color changes are $R \leftrightarrow G$ for $h$ and $B \leftrightarrow G$ for $v$ ) there must have been an even number of color swaps for each orientation. Therefore there was an odd number of wall collisions of each orientation. So, the laser is pointing in the opposite direction at the end of 3 seconds. Finally, let $x_{t}$ be the fractional part of the $x$ coordinate after $t$ seconds (the $y$-coordinate is always zero by our setup at these moments). Note that $$ x_{t+1}= \begin{cases}x_{t} & \text { even number of vertical wall collisions } \\ 1-x_{t} & \text { odd numbers of vertical wall collisions }\end{cases} $$ Since over the there seconds there were an odd number of vertical collisions; it follows $x_{3}=1-x_{0}$. Thus at the end of three seconds, the laser is in a symmetric position from the start; and in 6 seconds it will form a closed loop.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Divide the plane into an infinite square grid by drawing all the lines $x=m$ and $y=n$ for $m, n \in \mathbb{Z}$. Next, if a square's upper-right corner has both coordinates even, color it black; otherwise, color it white (in this way, exactly $1 / 4$ of the squares are black and no two black squares are adjacent). Let $r$ and $s$ be odd integers, and let $(x, y)$ be a point in the interior of any white square such that $r x-s y$ is irrational. Shoot a laser out of this point with slope $r / s$; lasers pass through white squares and reflect off black squares. Prove that the path of this laser will from a closed loop.
|
We re-color the white squares as red, blue, or green according as to whether they have a black square directly to the left/right, above/below, or neither, as shown below. Finally, we fix time zero to be a moment just before the laser passes a horizontal (WLOG) lattice line (not necessarily a wall). Shown below is an example for $(r, s)=(3,5)$.  The main idea is to keep track of every time the laser passes a lattice line (again, not necessarily a wall). There are four possible types of events: - A horizontal $h$ event where the laser switches from red to green (or vice-versa); - A horizontal $h$ event where the laser rebounds off a wall, remaining in a blue square, but flips the $x$-component of its velocity; - A vertical $v$ event where the laser switches from blue to green (or vice-versa) - A vertical $v$ event where the laser rebounds off a wall, remaining in a red square, but flips the $y$-component of its velocity. The first key observation is that: Claim - In the first second, the laser will encounter exactly $r$ horizontal events and $s$ vertical events. In every second after that, the same sequence of $r+s$ events occurs. We let the key-word be the sequence $w$ of $r+s$ letters corresponding to the sequence. For example, the picture above denotes an example with keyword $w=h v v h v v h v$; so no matter what, every second, the laser will encounter eight lattice lines, which are horizontal and vertical in that order. Claim - Color is periodic every 3 seconds. Now in a 3 -second period, consider the $3 r$ horizontal events and $3 s$ vertical events (both are odd). In order for the color to remain the same (as the only color changes are $R \leftrightarrow G$ for $h$ and $B \leftrightarrow G$ for $v$ ) there must have been an even number of color swaps for each orientation. Therefore there was an odd number of wall collisions of each orientation. So, the laser is pointing in the opposite direction at the end of 3 seconds. Finally, let $x_{t}$ be the fractional part of the $x$ coordinate after $t$ seconds (the $y$-coordinate is always zero by our setup at these moments). Note that $$ x_{t+1}= \begin{cases}x_{t} & \text { even number of vertical wall collisions } \\ 1-x_{t} & \text { odd numbers of vertical wall collisions }\end{cases} $$ Since over the there seconds there were an odd number of vertical collisions; it follows $x_{3}=1-x_{0}$. Thus at the end of three seconds, the laser is in a symmetric position from the start; and in 6 seconds it will form a closed loop.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2013.jsonl",
"problem_match": null,
"solution_match": null
}
|
35cc0902-361a-5c22-84bc-2ab559edfad8
| 604,874 |
Let $p$ be a prime. Prove that in a complete graph with $1000 p$ vertices whose edges are labelled with integers, one can find a cycle whose sum of labels is divisible by $p$.
|
Select $p-1$ disjoint triangles arbitrarily. If any of these triangles have 0 sum modulo $p$ we are done. Otherwise, we may label the vertices $u_{i}, x_{i}$, and $v_{i}$ (where $1 \leq i \leq p-1$ ) in such a way that $u_{i} x_{i}+x_{i} v_{i} \neq u_{i} v_{i}$. Let $A_{i}=\left\{u_{i} x_{i}+x_{i} v_{i}, u_{i} v_{i}\right\}$. We can show that $\left|A_{1}+A_{2}+\cdots+A_{t}\right| \geq \min \{p, t+1\}$ for each $1 \leq t \leq p-1$, by using induction on $t$ alongside Cauchy-Davenport. So, $A_{1}+A_{2}+\cdots+A_{p-1}$ spans all of $\mathbb{Z}_{p}$. All that's left to do is join the triangles together to form a cycle, and then delete either $u_{i} x_{i}, x_{i} v_{i}$ or $u_{i} v_{i}$ from each triangle in such a way that the final sum is $0 \bmod p$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $p$ be a prime. Prove that in a complete graph with $1000 p$ vertices whose edges are labelled with integers, one can find a cycle whose sum of labels is divisible by $p$.
|
Select $p-1$ disjoint triangles arbitrarily. If any of these triangles have 0 sum modulo $p$ we are done. Otherwise, we may label the vertices $u_{i}, x_{i}$, and $v_{i}$ (where $1 \leq i \leq p-1$ ) in such a way that $u_{i} x_{i}+x_{i} v_{i} \neq u_{i} v_{i}$. Let $A_{i}=\left\{u_{i} x_{i}+x_{i} v_{i}, u_{i} v_{i}\right\}$. We can show that $\left|A_{1}+A_{2}+\cdots+A_{t}\right| \geq \min \{p, t+1\}$ for each $1 \leq t \leq p-1$, by using induction on $t$ alongside Cauchy-Davenport. So, $A_{1}+A_{2}+\cdots+A_{p-1}$ spans all of $\mathbb{Z}_{p}$. All that's left to do is join the triangles together to form a cycle, and then delete either $u_{i} x_{i}, x_{i} v_{i}$ or $u_{i} v_{i}$ from each triangle in such a way that the final sum is $0 \bmod p$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2013.jsonl",
"problem_match": null,
"solution_match": null
}
|
f35197a5-adef-56e1-b1a4-c89a0eccb578
| 247,061 |
A country has $n$ cities, labelled $1,2,3, \ldots, n$. It wants to build exactly $n-1$ roads between certain pairs of cities so that every city is reachable from every other city via some sequence of roads. However, it is not permitted to put roads between pairs of cities that have labels differing by exactly 1 , and it is also not permitted to put a road between cities 1 and $n$. Let $T_{n}$ be the total number of possible ways to build these roads. (a) For all odd $n$, prove that $T_{n}$ is divisible by $n$. (b) For all even $n$, prove that $T_{n}$ is divisible by $n / 2$.
|
You can just spin the tree! Fixing $n$, the group $G=\mathbb{Z} / n \mathbb{Z}$ acts on the set of trees by rotation (where we imagine placing $1,2, \ldots, n$ along a circle). Claim - For odd $n$, all trees have trivial stabilizer.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A country has $n$ cities, labelled $1,2,3, \ldots, n$. It wants to build exactly $n-1$ roads between certain pairs of cities so that every city is reachable from every other city via some sequence of roads. However, it is not permitted to put roads between pairs of cities that have labels differing by exactly 1 , and it is also not permitted to put a road between cities 1 and $n$. Let $T_{n}$ be the total number of possible ways to build these roads. (a) For all odd $n$, prove that $T_{n}$ is divisible by $n$. (b) For all even $n$, prove that $T_{n}$ is divisible by $n / 2$.
|
You can just spin the tree! Fixing $n$, the group $G=\mathbb{Z} / n \mathbb{Z}$ acts on the set of trees by rotation (where we imagine placing $1,2, \ldots, n$ along a circle). Claim - For odd $n$, all trees have trivial stabilizer.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2013.jsonl",
"problem_match": null,
"solution_match": null
}
|
0020b1ef-6825-5a05-adff-d2d518051ec9
| 604,937 |
Define a function $f: \mathbb{N} \rightarrow \mathbb{N}$ by $f(1)=1, f(n+1)=f(n)+2^{f(n)}$ for every positive integer $n$. Prove that $f(1), f(2), \ldots, f\left(3^{2013}\right)$ leave distinct remainders when divided by $3^{2013}$.
|
I'll prove by induction on $k \geq 1$ that any $3^{k}$ consecutive values of $f$ produce distinct residues modulo $3^{k}$. The base case $k=1$ is easily checked ( $f$ is always odd, hence $f$ cycles $1,0,2 \bmod 3)$. For the inductive step, assume it's true up to $k$. Since $2^{\bullet}\left(\bmod 3^{k+1}\right)$ cycles every $2 \cdot 3^{k}$, and $f$ is always odd, it follows that $$ \begin{aligned} f\left(n+3^{k}\right)-f(n) & =2^{f(n)}+2^{f(n+1)}+\cdots+2^{f\left(n+3^{k}-1\right)} \quad\left(\bmod 3^{k+1}\right) \\ & \equiv 2^{1}+2^{3}+\cdots+2^{2 \cdot 3^{k}-1} \quad\left(\bmod 3^{k+1}\right) \\ & =2 \cdot \frac{4^{3^{k}}-1}{4-1} \end{aligned} $$ Hence $$ f\left(n+3^{k}\right)-f(n) \equiv C \quad\left(\bmod 3^{k+1}\right) \quad \text { where } \quad C=2 \cdot \frac{4^{3^{k}}-1}{4-1} $$ noting that $C$ does not depend on $n$. Exponent lifting gives $\nu_{3}(C)=k$ hence $f(n)$, $f\left(n+3^{k}\right), f\left(n+2 \cdot 3^{k}\right)$ differ mod $3^{k+1}$ for all $n$, and the inductive hypothesis now solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Define a function $f: \mathbb{N} \rightarrow \mathbb{N}$ by $f(1)=1, f(n+1)=f(n)+2^{f(n)}$ for every positive integer $n$. Prove that $f(1), f(2), \ldots, f\left(3^{2013}\right)$ leave distinct remainders when divided by $3^{2013}$.
|
I'll prove by induction on $k \geq 1$ that any $3^{k}$ consecutive values of $f$ produce distinct residues modulo $3^{k}$. The base case $k=1$ is easily checked ( $f$ is always odd, hence $f$ cycles $1,0,2 \bmod 3)$. For the inductive step, assume it's true up to $k$. Since $2^{\bullet}\left(\bmod 3^{k+1}\right)$ cycles every $2 \cdot 3^{k}$, and $f$ is always odd, it follows that $$ \begin{aligned} f\left(n+3^{k}\right)-f(n) & =2^{f(n)}+2^{f(n+1)}+\cdots+2^{f\left(n+3^{k}-1\right)} \quad\left(\bmod 3^{k+1}\right) \\ & \equiv 2^{1}+2^{3}+\cdots+2^{2 \cdot 3^{k}-1} \quad\left(\bmod 3^{k+1}\right) \\ & =2 \cdot \frac{4^{3^{k}}-1}{4-1} \end{aligned} $$ Hence $$ f\left(n+3^{k}\right)-f(n) \equiv C \quad\left(\bmod 3^{k+1}\right) \quad \text { where } \quad C=2 \cdot \frac{4^{3^{k}}-1}{4-1} $$ noting that $C$ does not depend on $n$. Exponent lifting gives $\nu_{3}(C)=k$ hence $f(n)$, $f\left(n+3^{k}\right), f\left(n+2 \cdot 3^{k}\right)$ differ mod $3^{k+1}$ for all $n$, and the inductive hypothesis now solves the problem.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2013.jsonl",
"problem_match": null,
"solution_match": null
}
|
a7e6796d-cb34-59d6-a4da-062af781308d
| 247,086 |
Let $\leftarrow$ denote the left arrow key on a standard keyboard. If one opens a text editor and types the keys "ab $\leftarrow \mathrm{cd} \leftarrow \leftarrow \mathrm{e} \leftarrow \leftarrow \mathrm{f}$ ", the result is "faecdb". We say that a string $B$ is reachable from a string $A$ if it is possible to insert some amount of $\leftarrow$ 's in $A$, such that typing the resulting characters produces $B$. So, our example shows that "faecdb" is reachable from "abcdef". Prove that for any two strings $A$ and $B, A$ is reachable from $B$ if and only if $B$ is reachable from $A$.
|
Obviously $A$ and $B$ should have the same multiset of characters, and we focus only on that situation. Claim - If $A=123 \ldots n$ and $B=\sigma(1) \sigma(2) \ldots \sigma(n)$ is a permutation of $A$, then $B$ is reachable if and only if it is $\mathbf{2 1 3}$-avoiding, i.e. there are no indices $i<j<k$ such that $\sigma(j)<\sigma(i)<\sigma(k)$. Claim - A permutation $\sigma$ on $\{1, \ldots, n\}$ is 213 -avoiding if and only if the inverse $\sigma^{-1}$ is. This essentially finishes the problem. Suppose $B$ is reachable from $A$. By using the typing pattern, we get some permutation $\sigma:\{1, \ldots, n\}$ such that the $i$ th character of $A$ is the $\sigma(i)$ th character of $B$, and which is 213 -avoiding by the claim. (The permutation is unique if $A$ has all distinct characters, but there could be multiple if $A$ has repeated ones.) Then $\sigma^{-1}$ is 213 -avoiding too and gives us a way to change $B$ into $A$.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
Let $\leftarrow$ denote the left arrow key on a standard keyboard. If one opens a text editor and types the keys "ab $\leftarrow \mathrm{cd} \leftarrow \leftarrow \mathrm{e} \leftarrow \leftarrow \mathrm{f}$ ", the result is "faecdb". We say that a string $B$ is reachable from a string $A$ if it is possible to insert some amount of $\leftarrow$ 's in $A$, such that typing the resulting characters produces $B$. So, our example shows that "faecdb" is reachable from "abcdef". Prove that for any two strings $A$ and $B, A$ is reachable from $B$ if and only if $B$ is reachable from $A$.
|
Obviously $A$ and $B$ should have the same multiset of characters, and we focus only on that situation. Claim - If $A=123 \ldots n$ and $B=\sigma(1) \sigma(2) \ldots \sigma(n)$ is a permutation of $A$, then $B$ is reachable if and only if it is $\mathbf{2 1 3}$-avoiding, i.e. there are no indices $i<j<k$ such that $\sigma(j)<\sigma(i)<\sigma(k)$. Claim - A permutation $\sigma$ on $\{1, \ldots, n\}$ is 213 -avoiding if and only if the inverse $\sigma^{-1}$ is. This essentially finishes the problem. Suppose $B$ is reachable from $A$. By using the typing pattern, we get some permutation $\sigma:\{1, \ldots, n\}$ such that the $i$ th character of $A$ is the $\sigma(i)$ th character of $B$, and which is 213 -avoiding by the claim. (The permutation is unique if $A$ has all distinct characters, but there could be multiple if $A$ has repeated ones.) Then $\sigma^{-1}$ is 213 -avoiding too and gives us a way to change $B$ into $A$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
90e685bc-fedb-57c6-9479-276d3a106280
| 604,988 |
Consider a convex pentagon circumscribed about a circle. We name the lines that connect vertices of the pentagon with the opposite points of tangency with the circle gergonnians. (a) Prove that if four gergonnians are concurrent, then all five of them are concurrent. (b) Prove that if there is a triple of gergonnians that are concurrent, then there is another triple of gergonnians that are concurrent.
|
This problem is insta-killed by taking a homography sending the concurrency point (in either part) to the center of the circle while fixing the incircle. Alternatively, one may send any four of the tangency points to a rectangle. Here are the details. Let $A B C D E$ be a pentagon with gergonnians $\overline{A V}, \overline{B W}, \overline{C X}$, $\overline{D Y}, \overline{E Z}$. We prove the following lemma, which (up to a suitable permutation of point names) solves both parts (a) and (b). ## Lemma The gergonnians $\overline{A V}, \overline{C X}, \overline{D Y}$ are concurrent if and only if the gergonnians $\overline{A V}$, $\overline{B W}, \overline{E Z}$ are concurrent.  Then $X$ and $Y$ are symmetric around $\overline{A P V}$ by hypothesis. Since $D=\overline{V V} \cap \overline{P Y}$, $C=\overline{V V} \cap \overline{P X}$, it follows that $C$ and $D$, and hence $Z$ and $W$, are also symmetric around $\overline{A P V}$. Consequently $B$ and $E$ are symmetric too. So $\overline{B W}$ and $\overline{E Z}$ meet on $\overline{A V}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a convex pentagon circumscribed about a circle. We name the lines that connect vertices of the pentagon with the opposite points of tangency with the circle gergonnians. (a) Prove that if four gergonnians are concurrent, then all five of them are concurrent. (b) Prove that if there is a triple of gergonnians that are concurrent, then there is another triple of gergonnians that are concurrent.
|
This problem is insta-killed by taking a homography sending the concurrency point (in either part) to the center of the circle while fixing the incircle. Alternatively, one may send any four of the tangency points to a rectangle. Here are the details. Let $A B C D E$ be a pentagon with gergonnians $\overline{A V}, \overline{B W}, \overline{C X}$, $\overline{D Y}, \overline{E Z}$. We prove the following lemma, which (up to a suitable permutation of point names) solves both parts (a) and (b). ## Lemma The gergonnians $\overline{A V}, \overline{C X}, \overline{D Y}$ are concurrent if and only if the gergonnians $\overline{A V}$, $\overline{B W}, \overline{E Z}$ are concurrent.  Then $X$ and $Y$ are symmetric around $\overline{A P V}$ by hypothesis. Since $D=\overline{V V} \cap \overline{P Y}$, $C=\overline{V V} \cap \overline{P X}$, it follows that $C$ and $D$, and hence $Z$ and $W$, are also symmetric around $\overline{A P V}$. Consequently $B$ and $E$ are symmetric too. So $\overline{B W}$ and $\overline{E Z}$ meet on $\overline{A V}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
98534a00-1ed8-5169-9f84-0106af8c2004
| 605,001 |
Let $P(x)$ and $Q(x)$ be arbitrary polynomials with real coefficients, with $P \neq 0$, and let $d=\operatorname{deg} P$. Prove that there exist polynomials $A(x)$ and $B(x)$, not both zero, such that $\max \{\operatorname{deg} A, \operatorname{deg} B\} \leq d / 2$ and $P(x) \mid A(x)+Q(x) \cdot B(x)$.
|
Let $V$ be the vector space of real polynomials with degree at most $d / 2$. Consider maps of linear spaces $$ \begin{aligned} V^{\oplus 2} & \rightarrow \mathbb{R}[x] /(P(x)) \\ \text { by } \quad(A, B) & \mapsto A+Q B \quad(\bmod P) . \end{aligned} $$ The domain has dimension $$ 2(\lfloor d / 2\rfloor+1) $$ while the codomain has dimension $d$. For dimension reasons it has nontrivial kernel.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P(x)$ and $Q(x)$ be arbitrary polynomials with real coefficients, with $P \neq 0$, and let $d=\operatorname{deg} P$. Prove that there exist polynomials $A(x)$ and $B(x)$, not both zero, such that $\max \{\operatorname{deg} A, \operatorname{deg} B\} \leq d / 2$ and $P(x) \mid A(x)+Q(x) \cdot B(x)$.
|
Let $V$ be the vector space of real polynomials with degree at most $d / 2$. Consider maps of linear spaces $$ \begin{aligned} V^{\oplus 2} & \rightarrow \mathbb{R}[x] /(P(x)) \\ \text { by } \quad(A, B) & \mapsto A+Q B \quad(\bmod P) . \end{aligned} $$ The domain has dimension $$ 2(\lfloor d / 2\rfloor+1) $$ while the codomain has dimension $d$. For dimension reasons it has nontrivial kernel.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
3d10f26e-0c2c-52b6-a79b-c33fbaff1b9b
| 247,130 |
Suppose we have distinct positive integers $a, b, c, d$ and an odd prime $p$ not dividing any of them, and an integer $M$ such that if one considers the infinite sequence $$ \begin{gathered} c a-d b \\ c a^{2}-d b^{2} \\ c a^{3}-d b^{3} \\ c a^{4}-d b^{4} \end{gathered} $$ and looks at the highest power of $p$ that divides each of them, these powers are not all zero, and are all at most $M$. Prove that there exists some $T$ (which may depend on $a, b, c, d, p, M)$ such that whenever $p$ divides an element of this sequence, the maximum power of $p$ that divides that element is exactly $p^{T}$.
|
By orders, the indices of terms divisible by $p$ is an arithmetic subsequence of $\mathbb{N}$ : say they are $\kappa, \kappa+\lambda, \kappa+2 \lambda, \ldots$, where $\lambda$ is the order of $a / b$. That means we want $$ \nu_{p}\left(c a^{\kappa+n \lambda}-d b^{\kappa+n \lambda}\right)=\nu_{p}\left(\left(\frac{a^{\lambda}}{b^{\lambda}}\right)^{n}-\frac{d a^{\kappa}}{c b^{\kappa}}\right) $$ to be constant. Thus, we have reduced the problem to the following proposition: ## Proposition Let $p$ be an odd prime. Let $x, y \in \mathbb{Q}_{>0}$ such that $x \equiv y \equiv 1(\bmod p)$. If the sequence $\nu_{p}\left(x^{n}-y\right)$ of positive integers is nonconstant, then it is unbounded. For this it would be sufficient to prove the following claim. Claim - Let $p$ be an odd prime. Let $x, y \in \mathbb{Q}>0$ such that $x \equiv y \equiv 1(\bmod p)$. Suppose $m$ and $n$ are positive integers such that $$ d=\nu_{p}\left(x^{n}-y\right)<\nu_{p}\left(x^{m}-y\right)=e . $$ Then there exists $\ell$ such that $\nu_{p}\left(x^{\ell}-y\right) \geq e+1$. $$ \nu_{p}\left(x^{k}-1\right)=e $$ namely $k=p^{e-d}|m-n|$. (In fact, one could also choose more carefully $k=p^{e-d} \cdot \operatorname{gcd}(m-$ $\left.n, p^{\infty}\right)$, so that $k$ is a power of $p$.) Suppose we set $x^{k}=p^{e} u+1$ and $x^{m}=p^{e} v+y$ where $u, v \in \mathbb{Q}$ aren't divisible by $p$. Now for any integer $1 \leq r \leq p-1$ we consider $$ \begin{aligned} x^{k r+m}-y & =\left(p^{e} u+1\right)^{r} \cdot\left(p^{e} v+y\right)-y \\ & =p^{e}(v+y u \cdot r)+p^{2 e}(\ldots) \end{aligned} $$ By selecting $r$ with $r \equiv-v / u(\bmod p)$, we ensure $p^{e+1} \mid x^{k r+m}-y$, hence $\ell=k r+m$ is as desired. $$ x^{\ell-m} \equiv 1 \quad\left(\bmod p^{e}\right) \text { but } x^{\ell-m} \not \equiv 1 \quad\left(\bmod p^{e+1}\right) $$ In particular, we need $\nu_{p}\left(x^{\ell-m}-1\right)=e$ exactly. So the $k$ in the claim must exist if we are going to succeed. On the other hand, if $k$ is some integer for which $\nu_{p}\left(x^{k}-1\right)=e$, then by choosing $\ell-m$ to be some multiple of $k$ with no extra factors of $p$, we hope that we can get $\nu_{p}\left(x^{\ell}-y\right)=e+1$. That's why we write $\ell=k r+m$ and see what happens when we expand.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Suppose we have distinct positive integers $a, b, c, d$ and an odd prime $p$ not dividing any of them, and an integer $M$ such that if one considers the infinite sequence $$ \begin{gathered} c a-d b \\ c a^{2}-d b^{2} \\ c a^{3}-d b^{3} \\ c a^{4}-d b^{4} \end{gathered} $$ and looks at the highest power of $p$ that divides each of them, these powers are not all zero, and are all at most $M$. Prove that there exists some $T$ (which may depend on $a, b, c, d, p, M)$ such that whenever $p$ divides an element of this sequence, the maximum power of $p$ that divides that element is exactly $p^{T}$.
|
By orders, the indices of terms divisible by $p$ is an arithmetic subsequence of $\mathbb{N}$ : say they are $\kappa, \kappa+\lambda, \kappa+2 \lambda, \ldots$, where $\lambda$ is the order of $a / b$. That means we want $$ \nu_{p}\left(c a^{\kappa+n \lambda}-d b^{\kappa+n \lambda}\right)=\nu_{p}\left(\left(\frac{a^{\lambda}}{b^{\lambda}}\right)^{n}-\frac{d a^{\kappa}}{c b^{\kappa}}\right) $$ to be constant. Thus, we have reduced the problem to the following proposition: ## Proposition Let $p$ be an odd prime. Let $x, y \in \mathbb{Q}_{>0}$ such that $x \equiv y \equiv 1(\bmod p)$. If the sequence $\nu_{p}\left(x^{n}-y\right)$ of positive integers is nonconstant, then it is unbounded. For this it would be sufficient to prove the following claim. Claim - Let $p$ be an odd prime. Let $x, y \in \mathbb{Q}>0$ such that $x \equiv y \equiv 1(\bmod p)$. Suppose $m$ and $n$ are positive integers such that $$ d=\nu_{p}\left(x^{n}-y\right)<\nu_{p}\left(x^{m}-y\right)=e . $$ Then there exists $\ell$ such that $\nu_{p}\left(x^{\ell}-y\right) \geq e+1$. $$ \nu_{p}\left(x^{k}-1\right)=e $$ namely $k=p^{e-d}|m-n|$. (In fact, one could also choose more carefully $k=p^{e-d} \cdot \operatorname{gcd}(m-$ $\left.n, p^{\infty}\right)$, so that $k$ is a power of $p$.) Suppose we set $x^{k}=p^{e} u+1$ and $x^{m}=p^{e} v+y$ where $u, v \in \mathbb{Q}$ aren't divisible by $p$. Now for any integer $1 \leq r \leq p-1$ we consider $$ \begin{aligned} x^{k r+m}-y & =\left(p^{e} u+1\right)^{r} \cdot\left(p^{e} v+y\right)-y \\ & =p^{e}(v+y u \cdot r)+p^{2 e}(\ldots) \end{aligned} $$ By selecting $r$ with $r \equiv-v / u(\bmod p)$, we ensure $p^{e+1} \mid x^{k r+m}-y$, hence $\ell=k r+m$ is as desired. $$ x^{\ell-m} \equiv 1 \quad\left(\bmod p^{e}\right) \text { but } x^{\ell-m} \not \equiv 1 \quad\left(\bmod p^{e+1}\right) $$ In particular, we need $\nu_{p}\left(x^{\ell-m}-1\right)=e$ exactly. So the $k$ in the claim must exist if we are going to succeed. On the other hand, if $k$ is some integer for which $\nu_{p}\left(x^{k}-1\right)=e$, then by choosing $\ell-m$ to be some multiple of $k$ with no extra factors of $p$, we hope that we can get $\nu_{p}\left(x^{\ell}-y\right)=e+1$. That's why we write $\ell=k r+m$ and see what happens when we expand.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
e54d1b92-0d7f-508f-913d-a32c5891dfd2
| 605,067 |
Let $a_{1}, a_{2}, \ldots, a_{n}$ be a sequence of real numbers, and let $m$ be a fixed positive integer less than $n$. We say an index $k$ with $1 \leq k \leq n$ is good if there exists some $\ell$ with $1 \leq \ell \leq m$ such that $$ a_{k}+a_{k+1}+\cdots+a_{k+\ell-1} \geq 0 $$ where the indices are taken modulo $n$. Let $T$ be the set of all good indices. Prove that $$ \sum_{k \in T} a_{k} \geq 0 $$
|
First we prove the result if the indices are not taken modulo $n$. Call a number $\ell$-good if $\ell$ is the smallest number such that $a_{k}+a_{k+1}+\cdots+a_{k+\ell-1} \geq 0$, and $\ell \leq m$. Then if $a_{k}$ is $\ell$-good, the numbers $a_{k+1}, \ldots, a_{k+\ell-1}$ are good as well. Then by greedy from left to right, we can group all the good numbers into blocks with nonnegative sums. Repeatedly take the first good number, if $\ell$-good, group it with the next $\ell$ numbers. An example for $m=3$ : $$ \langle 4\rangle \quad \begin{array}{ccccccccc} -1 & -2 & 6\rangle & -9 & -7 & \langle 3\rangle & \langle-2 & 4\rangle & \langle-1 . \end{array} $$ We can now return to the original problem. Let $N$ be a large integer; applying the algorithm to $N$ copies of the sequence, we deduce that $$ N \sum_{k \in T} a_{k}+c_{N} \geq 0 $$ where $c_{N}$ represents some "error" from left-over terms. As $\left|c_{N}\right| \leq \sum\left|a_{i}\right|$, by taking $N$ large enough we deduce the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be a sequence of real numbers, and let $m$ be a fixed positive integer less than $n$. We say an index $k$ with $1 \leq k \leq n$ is good if there exists some $\ell$ with $1 \leq \ell \leq m$ such that $$ a_{k}+a_{k+1}+\cdots+a_{k+\ell-1} \geq 0 $$ where the indices are taken modulo $n$. Let $T$ be the set of all good indices. Prove that $$ \sum_{k \in T} a_{k} \geq 0 $$
|
First we prove the result if the indices are not taken modulo $n$. Call a number $\ell$-good if $\ell$ is the smallest number such that $a_{k}+a_{k+1}+\cdots+a_{k+\ell-1} \geq 0$, and $\ell \leq m$. Then if $a_{k}$ is $\ell$-good, the numbers $a_{k+1}, \ldots, a_{k+\ell-1}$ are good as well. Then by greedy from left to right, we can group all the good numbers into blocks with nonnegative sums. Repeatedly take the first good number, if $\ell$-good, group it with the next $\ell$ numbers. An example for $m=3$ : $$ \langle 4\rangle \quad \begin{array}{ccccccccc} -1 & -2 & 6\rangle & -9 & -7 & \langle 3\rangle & \langle-2 & 4\rangle & \langle-1 . \end{array} $$ We can now return to the original problem. Let $N$ be a large integer; applying the algorithm to $N$ copies of the sequence, we deduce that $$ N \sum_{k \in T} a_{k}+c_{N} \geq 0 $$ where $c_{N}$ represents some "error" from left-over terms. As $\left|c_{N}\right| \leq \sum\left|a_{i}\right|$, by taking $N$ large enough we deduce the problem.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
00d2f0d6-fe23-5402-ada9-bb9391dddf43
| 605,085 |
Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.
|
The main content of the problem: Claim - $\angle H X_{a} G=90^{\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. First proof by Brokard. To do this, it suffices to show that $M$ has the same power with respect to the circle with diameter $\overline{A H}$ and the circle with diameter $\overline{K L}$. In fact I claim both circles are orthogonal to the circle with diameter $\overline{B C}$ ! The former follows from Brokard's theorem, noting that $A$ is on the polar of $H$, and the latter follows from the harmonic bundle.  Then $\overline{A M}$ is the radical axis, so $X$ lies on both circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.
|
The main content of the problem: Claim - $\angle H X_{a} G=90^{\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. First proof by Brokard. To do this, it suffices to show that $M$ has the same power with respect to the circle with diameter $\overline{A H}$ and the circle with diameter $\overline{K L}$. In fact I claim both circles are orthogonal to the circle with diameter $\overline{B C}$ ! The former follows from Brokard's theorem, noting that $A$ is on the polar of $H$, and the latter follows from the harmonic bundle.  Then $\overline{A M}$ is the radical axis, so $X$ lies on both circles.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
d778b1a2-8833-5ff1-b989-ae75089d6fc8
| 605,093 |
Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.
|
The main content of the problem: Claim - $\angle H X_{a} G=90^{\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. Second proof by orthocenter reflection, Bendit Chan. As before, we know $M X \cdot M A=$ $M K \cdot M L=M B \cdot M C$, but $X$ lies inside segment $A M$. Construct parallelogram $A B A^{\prime} C$. Then $M X \cdot M A^{\prime}=M B \cdot M C$, so $X B A^{\prime} C$ is concyclic. However, it is well-known the circumcircle of $\triangle B A^{\prime} C$ (which is the reflection of $(A B C)$ across $\overline{B C}$ ) passes through $H$ and in fact has diameter $\overline{A^{\prime} H}$. So this gives $\angle H X A^{\prime}=90^{\circ}$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.
|
The main content of the problem: Claim - $\angle H X_{a} G=90^{\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. Second proof by orthocenter reflection, Bendit Chan. As before, we know $M X \cdot M A=$ $M K \cdot M L=M B \cdot M C$, but $X$ lies inside segment $A M$. Construct parallelogram $A B A^{\prime} C$. Then $M X \cdot M A^{\prime}=M B \cdot M C$, so $X B A^{\prime} C$ is concyclic. However, it is well-known the circumcircle of $\triangle B A^{\prime} C$ (which is the reflection of $(A B C)$ across $\overline{B C}$ ) passes through $H$ and in fact has diameter $\overline{A^{\prime} H}$. So this gives $\angle H X A^{\prime}=90^{\circ}$ as needed.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
d778b1a2-8833-5ff1-b989-ae75089d6fc8
| 605,093 |
Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.
|
The main content of the problem: Claim - $\angle H X_{a} G=90^{\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. Third proof by barycentric coordinates. Alternatively we may just compute $X=\left(a^{2}\right.$ : $\left.2 S_{A}: 2 S_{A}\right)$. Let $F=\left(0: S_{C}: S_{B}\right)$ be the foot from $H$. Then we check that $X H F M$ is cyclic, which is power of a point from $A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle. Let $K_{a}, L_{a}$, and $M_{a}$ be the respective intersections with $B C$ of the internal angle bisector, external angle bisector, and the median from $A$. The circumcircle of $A K_{a} L_{a}$ intersects $A M_{a}$ a second time at a point $X_{a}$ different from $A$. Define $X_{b}$ and $X_{c}$ analogously. Prove that the circumcenter of $X_{a} X_{b} X_{c}$ lies on the Euler line of $A B C$.
|
The main content of the problem: Claim - $\angle H X_{a} G=90^{\circ}$. This implies the result, since then the desired circumcenter is the midpoint of $\overline{G H}$. (This is the main difficulty; the Euler line is a red herring.) In what follows, we abbreviate $K_{a} L_{a}, M_{a}, X_{a}$ to $K, L, M, X$. Third proof by barycentric coordinates. Alternatively we may just compute $X=\left(a^{2}\right.$ : $\left.2 S_{A}: 2 S_{A}\right)$. Let $F=\left(0: S_{C}: S_{B}\right)$ be the foot from $H$. Then we check that $X H F M$ is cyclic, which is power of a point from $A$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
d778b1a2-8833-5ff1-b989-ae75089d6fc8
| 605,093 |
Let $P$ be the set of all primes, and let $M$ be a non-empty subset of $P$. Suppose that for any non-empty subset $\left\{p_{1}, p_{2}, \ldots, p_{k}\right\}$ of $M$, all prime factors of $p_{1} p_{2} \ldots p_{k}+1$ are also in $M$. Prove that $M=P$.
|
Obviously $|M|=\infty$. Assume for contradiction $p \notin M$. We say a prime $q \in M$ is sparse if there are only finitely many elements of $M$ which are $q(\bmod p)$ (in particular there are finitely many sparse primes). Now let $C$ be the product of all sparse primes (note $p \nmid C$ ). First, set $a_{0}=1$. For $k \geq 0$, consider then the prime factorization of the number $$ C a_{k}+1 $$ No prime in its factorization is sparse, so consider the number $a_{k+1}$ obtained by replacing each prime in its factorization with some arbitrary representative of that prime's residue class. In this way we select a number $a_{k+1}$ such that - $a_{k+1} \equiv C a_{k}+1(\bmod p)$, and - $a_{k+1}$ is a product of distinct primes in $M$. In particular, $a_{k} \equiv C^{k}+C^{k-1}+\cdots+1(\bmod p)$ But since $C \not \equiv 0(\bmod p)$, we can find a $k$ such that $a_{k} \equiv 0(\bmod p)($ namely, $k=p-1$ if $C \equiv 1$ and $k=p-2$ else) which is clearly impossible since $a_{k}$ is a product of primes in $M$ !
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $P$ be the set of all primes, and let $M$ be a non-empty subset of $P$. Suppose that for any non-empty subset $\left\{p_{1}, p_{2}, \ldots, p_{k}\right\}$ of $M$, all prime factors of $p_{1} p_{2} \ldots p_{k}+1$ are also in $M$. Prove that $M=P$.
|
Obviously $|M|=\infty$. Assume for contradiction $p \notin M$. We say a prime $q \in M$ is sparse if there are only finitely many elements of $M$ which are $q(\bmod p)$ (in particular there are finitely many sparse primes). Now let $C$ be the product of all sparse primes (note $p \nmid C$ ). First, set $a_{0}=1$. For $k \geq 0$, consider then the prime factorization of the number $$ C a_{k}+1 $$ No prime in its factorization is sparse, so consider the number $a_{k+1}$ obtained by replacing each prime in its factorization with some arbitrary representative of that prime's residue class. In this way we select a number $a_{k+1}$ such that - $a_{k+1} \equiv C a_{k}+1(\bmod p)$, and - $a_{k+1}$ is a product of distinct primes in $M$. In particular, $a_{k} \equiv C^{k}+C^{k-1}+\cdots+1(\bmod p)$ But since $C \not \equiv 0(\bmod p)$, we can find a $k$ such that $a_{k} \equiv 0(\bmod p)($ namely, $k=p-1$ if $C \equiv 1$ and $k=p-2$ else) which is clearly impossible since $a_{k}$ is a product of primes in $M$ !
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
70c4b7c9-88b8-5a6b-b00b-d6e35f50327a
| 247,169 |
Let $x, y, z$ be real numbers (not necessarily positive) such that $x^{4}+y^{4}+z^{4}+x y z=4$. Prove that $x \leq 2$ and $$ \sqrt{2-x} \geq \frac{y+z}{2} $$
|
We prove that the condition $x^{4}+y^{4}+z^{4}+x y z=4$ implies $$ \sqrt{2-x} \geq \frac{y+z}{2} $$ We first prove the easy part. Claim - We have $x \leq 2$. $$ \begin{aligned} 5=x^{4}+y^{4}+\left(z^{4}+1\right)+x y z & =\frac{3 x^{4}}{4}+\left(\frac{x^{4}}{4}+y^{4}\right)+\left(z^{4}+1\right)+x y z \\ & \geq \frac{3 x^{4}}{4}+x^{2} y^{2}+2 z^{2}+x y z . \end{aligned} $$ We evidently have that $x^{2} y^{2}+2 z^{2}+x y z \geq 0$ because the quadratic form $a^{2}+a b+2 b^{2}$ is positive definite, so $x^{4} \leq \frac{20}{3} \Longrightarrow x \leq 2$. Now, the desired statement is implied by its square, so it suffices to show that $$ 2-x \geq\left(\frac{y+z}{2}\right)^{2} $$ We are going to proceed by contradiction (it seems that many solutions do this) and assume that $$ 2-x<\left(\frac{y+z}{2}\right)^{2} \Longleftrightarrow 4 x+y^{2}+2 y z+z^{2}>8 $$ By AM-GM, $$ \begin{aligned} x^{4}+3 & \geq 4 x \\ \frac{y^{4}+1}{2} & \geq y^{2} \\ \frac{z^{4}+1}{2} & \geq z^{2} \end{aligned} $$ which yields that $$ x^{4}+\frac{y^{4}+z^{4}}{2}+2 y z+4>8 $$ If we replace $x^{4}=4-\left(y^{4}+z^{4}+x y z\right)$ now, this gives $$ -\frac{y^{4}+z^{4}}{2}+(2-x) y z>0 \Longrightarrow(2-x) y z>\frac{y^{4}+z^{4}}{2} $$ Since $2-x$ and the right-hand side are positive, we have $y z \geq 0$. Now $$ \frac{y^{4}+z^{4}}{2 y z}<2-x<\left(\frac{y+z}{2}\right)^{2} \Longrightarrow 2 y^{4}+2 z^{4}<y z(y+z)^{2}=y^{3} z+2 y^{2} z^{2}+y z^{3} $$ This is clearly false by AM-GM, so we have a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be real numbers (not necessarily positive) such that $x^{4}+y^{4}+z^{4}+x y z=4$. Prove that $x \leq 2$ and $$ \sqrt{2-x} \geq \frac{y+z}{2} $$
|
We prove that the condition $x^{4}+y^{4}+z^{4}+x y z=4$ implies $$ \sqrt{2-x} \geq \frac{y+z}{2} $$ We first prove the easy part. Claim - We have $x \leq 2$. $$ \begin{aligned} 5=x^{4}+y^{4}+\left(z^{4}+1\right)+x y z & =\frac{3 x^{4}}{4}+\left(\frac{x^{4}}{4}+y^{4}\right)+\left(z^{4}+1\right)+x y z \\ & \geq \frac{3 x^{4}}{4}+x^{2} y^{2}+2 z^{2}+x y z . \end{aligned} $$ We evidently have that $x^{2} y^{2}+2 z^{2}+x y z \geq 0$ because the quadratic form $a^{2}+a b+2 b^{2}$ is positive definite, so $x^{4} \leq \frac{20}{3} \Longrightarrow x \leq 2$. Now, the desired statement is implied by its square, so it suffices to show that $$ 2-x \geq\left(\frac{y+z}{2}\right)^{2} $$ We are going to proceed by contradiction (it seems that many solutions do this) and assume that $$ 2-x<\left(\frac{y+z}{2}\right)^{2} \Longleftrightarrow 4 x+y^{2}+2 y z+z^{2}>8 $$ By AM-GM, $$ \begin{aligned} x^{4}+3 & \geq 4 x \\ \frac{y^{4}+1}{2} & \geq y^{2} \\ \frac{z^{4}+1}{2} & \geq z^{2} \end{aligned} $$ which yields that $$ x^{4}+\frac{y^{4}+z^{4}}{2}+2 y z+4>8 $$ If we replace $x^{4}=4-\left(y^{4}+z^{4}+x y z\right)$ now, this gives $$ -\frac{y^{4}+z^{4}}{2}+(2-x) y z>0 \Longrightarrow(2-x) y z>\frac{y^{4}+z^{4}}{2} $$ Since $2-x$ and the right-hand side are positive, we have $y z \geq 0$. Now $$ \frac{y^{4}+z^{4}}{2 y z}<2-x<\left(\frac{y+z}{2}\right)^{2} \Longrightarrow 2 y^{4}+2 z^{4}<y z(y+z)^{2}=y^{3} z+2 y^{2} z^{2}+y z^{3} $$ This is clearly false by AM-GM, so we have a contradiction.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
72ca44d8-86af-543b-8f27-1d59477563c0
| 605,149 |
Let $\varphi(n)$ denote the number of positive integers less than $n$ that are relatively prime to $n$. Prove that there exists a positive integer $m$ for which the equation $\varphi(n)=m$ has at least 2015 solutions in $n$.
|
『 First solution with ad-hoc subsets, by Evan Chen. I consider the following eleven prime numbers: $$ S=\{11,13,17,19,29,31,37,41,43,61,71\} $$ This has the property that for any $p \in S$, all prime factors of $p-1$ are one digit. Let $N=(210)^{\text {billion }}$, and consider $M=\varphi(N)$. For any subset $T \subset S$, we have $$ M=\varphi\left(\frac{N}{\prod_{p \in T}(p-1)} \prod_{p \in T} p\right) $$ Since $2^{|S|}>2015$ we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\varphi(n)$ denote the number of positive integers less than $n$ that are relatively prime to $n$. Prove that there exists a positive integer $m$ for which the equation $\varphi(n)=m$ has at least 2015 solutions in $n$.
|
『 First solution with ad-hoc subsets, by Evan Chen. I consider the following eleven prime numbers: $$ S=\{11,13,17,19,29,31,37,41,43,61,71\} $$ This has the property that for any $p \in S$, all prime factors of $p-1$ are one digit. Let $N=(210)^{\text {billion }}$, and consider $M=\varphi(N)$. For any subset $T \subset S$, we have $$ M=\varphi\left(\frac{N}{\prod_{p \in T}(p-1)} \prod_{p \in T} p\right) $$ Since $2^{|S|}>2015$ we're done.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
4fed42ef-ea79-5f3f-ab14-085900664295
| 247,185 |
Let $\varphi(n)$ denote the number of positive integers less than $n$ that are relatively prime to $n$. Prove that there exists a positive integer $m$ for which the equation $\varphi(n)=m$ has at least 2015 solutions in $n$.
|
【 Second solution with smallest primes, by Yang Liu. Let $2=p_{1}<p_{2}<\cdots<p_{2015}$ be the smallest 2015 primes. Then the 2015 numbers $$ \begin{aligned} n_{1} & =\left(p_{1}-1\right) p_{2} \ldots p_{2015} \\ n_{2} & =p_{1}\left(p_{2}-1\right) \ldots p_{2015} \\ & \vdots \\ n_{2015} & =p_{1} p_{2} \ldots\left(p_{2015}-1\right) \end{aligned} $$ all have the same phi value, namely $$ \varphi\left(p_{1} p_{2} \ldots p_{2015}\right)=\prod_{i=1}^{2015}\left(p_{i}-1\right) $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\varphi(n)$ denote the number of positive integers less than $n$ that are relatively prime to $n$. Prove that there exists a positive integer $m$ for which the equation $\varphi(n)=m$ has at least 2015 solutions in $n$.
|
【 Second solution with smallest primes, by Yang Liu. Let $2=p_{1}<p_{2}<\cdots<p_{2015}$ be the smallest 2015 primes. Then the 2015 numbers $$ \begin{aligned} n_{1} & =\left(p_{1}-1\right) p_{2} \ldots p_{2015} \\ n_{2} & =p_{1}\left(p_{2}-1\right) \ldots p_{2015} \\ & \vdots \\ n_{2015} & =p_{1} p_{2} \ldots\left(p_{2015}-1\right) \end{aligned} $$ all have the same phi value, namely $$ \varphi\left(p_{1} p_{2} \ldots p_{2015}\right)=\prod_{i=1}^{2015}\left(p_{i}-1\right) $$
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
4fed42ef-ea79-5f3f-ab14-085900664295
| 247,185 |
A Nim-style game is defined as follows. Two positive integers $k$ and $n$ are specified, along with a finite set $S$ of $k$-tuples of integers (not necessarily positive). At the start of the game, the $k$-tuple $(~ n, 0,0, \ldots, 0)$ is written on the blackboard. A legal move consists of erasing the tuple $\left(a_{1}, a_{2}, \ldots, a_{k}\right)$ which is written on the blackboard and replacing it with $\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{k}+b_{k}\right)$, where $\left(b_{1}, b_{2}, \ldots, b_{k}\right)$ is an element of the set $S$. Two players take turns making legal moves, and the first to write a negative integer loses. In the event that neither player is ever forced to write a negative integer, the game is a draw. Prove that there is a choice of $k$ and $S$ with the following property: the first player has a winning strategy if $n$ is a power of 2 , and otherwise the second player has a winning strategy.
|
 Now, the "game" is played as follows. The mechanics are controlled by the turn counters $A$ and $B$. Observe the game starts with Alice playing Init. Thereafter, we say that the game is - In the main part if $A+B=1$, and no one has played Init a second time. - In the death part otherwise. Observe that in the main state, on Alice's turn we always have $(A, B)=(1,0)$ and on Bob's turn we always have $(A, B)=(0,1)$. Claim - A player who plays Init a second time must lose. In particular, a player who makes a move when $A=B=0$ must lose. - Suppose the offending player is in a situation where $A=B=0$. Then he/she must play Init. At this point, the opposing player can respond by playing Kill. Then the offending player must play Init again. The opposing player now responds with Kill'. This iteration continues until $X$ reaches a negative number and the offending player loses. - Suppose Alice has $(A, B)=(1,0)$ but plays Init again anyways. Then Bob responds with PunB to punish her; he then wins as in the first case. - Suppose Bob has $(A, B)=(0,1)$ but plays Init again anyways. Alice responds with PunA in the same way. Thus we may assume that players avoid the death part at all costs. Hence the second moves consist of Bob playing Sleep, and then Alice playing Begin (thus restoring the value of $n$ in $X$ ), then Bob playing Sleep. Now we return to analysis of the main part. We say the game is in state $S$ for $S \in$ $\left\{S_{X}^{0}, S_{X}, S_{X}^{\prime}, S_{Y}^{0}, S_{Y}, S_{Y}^{\prime}, \mathrm{Cl}\right\}$ if $S=1$ and all other variables are zero. By construction, this is always the case. From then on the main part is divided into several phases: - An $X$-phase: this begins with Alice at $S_{X}^{0}$, and ends when the game is in a state other than $S_{X}$ and $S_{X}^{\prime}$. (She can never return to $S_{X}^{0}$ during an $X$-phase.) - A $Y$-phase: this begins with Alice at $S_{Y}^{0}$, and ends when the game is in a state other than $S_{Y}$ and $S_{Y}^{\prime}$. (She can never return to $S_{Y}^{0}$ during a $Y$-phase.) Claim - Consider an $X$-phase in which $(X, Y)=(x, 0), x>1$. Then Alice can complete the phase without losing if and only if $x$ is even; if so she begins a $Y$-phase with $(X, Y)=(0, x / 2)$. Now note that unless $X=0$, Bob now has a winning move WrongX. Conversely he may only play Sleep if $X=0$. We have an analogous claim for $Y$-phases. Thus if $n$ is not a power of 2 , we see that Alice eventually loses. Now suppose $n=2^{k}$; then Alice reaches $(X, Y)=\left(0,2^{k-1}\right),\left(2^{k-2}, 0\right), \ldots$ until either reaching $(1,0)$ or $(0,1)$. At this point she can play ClaimX or ClaimY, respectively; the game is now in state Cl. Bob cannot play either FakeX or FakeY, so he must play Sleep, and then Alice wins by playing Win. Thus Alice has a winning strategy when $n=2^{k}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A Nim-style game is defined as follows. Two positive integers $k$ and $n$ are specified, along with a finite set $S$ of $k$-tuples of integers (not necessarily positive). At the start of the game, the $k$-tuple $(~ n, 0,0, \ldots, 0)$ is written on the blackboard. A legal move consists of erasing the tuple $\left(a_{1}, a_{2}, \ldots, a_{k}\right)$ which is written on the blackboard and replacing it with $\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{k}+b_{k}\right)$, where $\left(b_{1}, b_{2}, \ldots, b_{k}\right)$ is an element of the set $S$. Two players take turns making legal moves, and the first to write a negative integer loses. In the event that neither player is ever forced to write a negative integer, the game is a draw. Prove that there is a choice of $k$ and $S$ with the following property: the first player has a winning strategy if $n$ is a power of 2 , and otherwise the second player has a winning strategy.
|
 Now, the "game" is played as follows. The mechanics are controlled by the turn counters $A$ and $B$. Observe the game starts with Alice playing Init. Thereafter, we say that the game is - In the main part if $A+B=1$, and no one has played Init a second time. - In the death part otherwise. Observe that in the main state, on Alice's turn we always have $(A, B)=(1,0)$ and on Bob's turn we always have $(A, B)=(0,1)$. Claim - A player who plays Init a second time must lose. In particular, a player who makes a move when $A=B=0$ must lose. - Suppose the offending player is in a situation where $A=B=0$. Then he/she must play Init. At this point, the opposing player can respond by playing Kill. Then the offending player must play Init again. The opposing player now responds with Kill'. This iteration continues until $X$ reaches a negative number and the offending player loses. - Suppose Alice has $(A, B)=(1,0)$ but plays Init again anyways. Then Bob responds with PunB to punish her; he then wins as in the first case. - Suppose Bob has $(A, B)=(0,1)$ but plays Init again anyways. Alice responds with PunA in the same way. Thus we may assume that players avoid the death part at all costs. Hence the second moves consist of Bob playing Sleep, and then Alice playing Begin (thus restoring the value of $n$ in $X$ ), then Bob playing Sleep. Now we return to analysis of the main part. We say the game is in state $S$ for $S \in$ $\left\{S_{X}^{0}, S_{X}, S_{X}^{\prime}, S_{Y}^{0}, S_{Y}, S_{Y}^{\prime}, \mathrm{Cl}\right\}$ if $S=1$ and all other variables are zero. By construction, this is always the case. From then on the main part is divided into several phases: - An $X$-phase: this begins with Alice at $S_{X}^{0}$, and ends when the game is in a state other than $S_{X}$ and $S_{X}^{\prime}$. (She can never return to $S_{X}^{0}$ during an $X$-phase.) - A $Y$-phase: this begins with Alice at $S_{Y}^{0}$, and ends when the game is in a state other than $S_{Y}$ and $S_{Y}^{\prime}$. (She can never return to $S_{Y}^{0}$ during a $Y$-phase.) Claim - Consider an $X$-phase in which $(X, Y)=(x, 0), x>1$. Then Alice can complete the phase without losing if and only if $x$ is even; if so she begins a $Y$-phase with $(X, Y)=(0, x / 2)$. Now note that unless $X=0$, Bob now has a winning move WrongX. Conversely he may only play Sleep if $X=0$. We have an analogous claim for $Y$-phases. Thus if $n$ is not a power of 2 , we see that Alice eventually loses. Now suppose $n=2^{k}$; then Alice reaches $(X, Y)=\left(0,2^{k-1}\right),\left(2^{k-2}, 0\right), \ldots$ until either reaching $(1,0)$ or $(0,1)$. At this point she can play ClaimX or ClaimY, respectively; the game is now in state Cl. Bob cannot play either FakeX or FakeY, so he must play Sleep, and then Alice wins by playing Win. Thus Alice has a winning strategy when $n=2^{k}$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
1c6e51e7-3739-593b-95a1-e4436102ed70
| 605,195 |
Let $A=A(x, y)$ and $B=B(x, y)$ be two-variable polynomials with real coefficients. Suppose that $A(x, y) / B(x, y)$ is a polynomial in $x$ for infinitely many values of $y$, and a polynomial in $y$ for infinitely many values of $x$. Prove that $B$ divides $A$, meaning there exists a third polynomial $C$ with real coefficients such that $A=B \cdot C$.
|
This is essentially an application of the division algorithm, but the details require significant care. First, we claim that $A / B$ can be written as a polynomial in $x$ whose coefficients are rational functions in $y$. To see this, use the division algorithm to get $$ A=Q \cdot B+R \quad Q, R \in(\mathbb{R}(y))[x] $$ where $Q$ and $R$ are polynomials in $x$ whose coefficients are rational functions in $y$, and moreover $\operatorname{deg}_{x} B>\operatorname{deg}_{x} R$. Now, we claim that $R \equiv 0$. Indeed, we have by hypothesis that for infinitely many values of $y_{0}$ that $B\left(x, y_{0}\right)$ divides $A\left(x, y_{0}\right)$, which means $B\left(x, y_{0}\right) \mid R\left(x, y_{0}\right)$ as polynomials in $\mathbb{R}[x]$. Now, we have $\operatorname{deg}_{x} B\left(x, y_{0}\right)>\operatorname{deg}_{x} R\left(x, y_{0}\right)$ outside of finitely many values of $y_{0}$ (but not all of them!); this means for infinitely many $y_{0}$ we have $R\left(x, y_{0}\right) \equiv 0$. So each coefficient of $x^{i}$ (in $\left.\mathbb{R}(y)\right)$ has infinitely many roots, hence is a zero polynomial. Consequently, we are able to write $A / B=F(x, y) / M(y)$ where $F \in \mathbb{R}[x, y]$ and $M \in \mathbb{R}[y]$ are each polynomials. Repeating the same argument now gives $$ \frac{A}{B}=\frac{F(x, y)}{M(y)}=\frac{G(x, y)}{N(x)} $$ Now, by unique factorization of polynomials in $\mathbb{R}[x, y]$, we can discuss GCD's. So, we tacitly assume $\operatorname{gcd}(F, M)=\operatorname{gcd}(G, N)=(1)$. Also, we obviously have $\operatorname{gcd}(M, N)=(1)$. But $F \cdot N=G \cdot M$, so $M \mid F \cdot N$, thus we conclude $M$ is the constant polynomial. This implies the result. Remark. This fact does not generalize to arbitrary functions that are separately polynomial: see e.g. http://aops.com/community/c6h523650p2978180.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $A=A(x, y)$ and $B=B(x, y)$ be two-variable polynomials with real coefficients. Suppose that $A(x, y) / B(x, y)$ is a polynomial in $x$ for infinitely many values of $y$, and a polynomial in $y$ for infinitely many values of $x$. Prove that $B$ divides $A$, meaning there exists a third polynomial $C$ with real coefficients such that $A=B \cdot C$.
|
This is essentially an application of the division algorithm, but the details require significant care. First, we claim that $A / B$ can be written as a polynomial in $x$ whose coefficients are rational functions in $y$. To see this, use the division algorithm to get $$ A=Q \cdot B+R \quad Q, R \in(\mathbb{R}(y))[x] $$ where $Q$ and $R$ are polynomials in $x$ whose coefficients are rational functions in $y$, and moreover $\operatorname{deg}_{x} B>\operatorname{deg}_{x} R$. Now, we claim that $R \equiv 0$. Indeed, we have by hypothesis that for infinitely many values of $y_{0}$ that $B\left(x, y_{0}\right)$ divides $A\left(x, y_{0}\right)$, which means $B\left(x, y_{0}\right) \mid R\left(x, y_{0}\right)$ as polynomials in $\mathbb{R}[x]$. Now, we have $\operatorname{deg}_{x} B\left(x, y_{0}\right)>\operatorname{deg}_{x} R\left(x, y_{0}\right)$ outside of finitely many values of $y_{0}$ (but not all of them!); this means for infinitely many $y_{0}$ we have $R\left(x, y_{0}\right) \equiv 0$. So each coefficient of $x^{i}$ (in $\left.\mathbb{R}(y)\right)$ has infinitely many roots, hence is a zero polynomial. Consequently, we are able to write $A / B=F(x, y) / M(y)$ where $F \in \mathbb{R}[x, y]$ and $M \in \mathbb{R}[y]$ are each polynomials. Repeating the same argument now gives $$ \frac{A}{B}=\frac{F(x, y)}{M(y)}=\frac{G(x, y)}{N(x)} $$ Now, by unique factorization of polynomials in $\mathbb{R}[x, y]$, we can discuss GCD's. So, we tacitly assume $\operatorname{gcd}(F, M)=\operatorname{gcd}(G, N)=(1)$. Also, we obviously have $\operatorname{gcd}(M, N)=(1)$. But $F \cdot N=G \cdot M$, so $M \mid F \cdot N$, thus we conclude $M$ is the constant polynomial. This implies the result. Remark. This fact does not generalize to arbitrary functions that are separately polynomial: see e.g. http://aops.com/community/c6h523650p2978180.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
3ed94480-7f7e-5200-ac83-4e61dd79a0fa
| 247,203 |
Let $A B C$ be a scalene triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose the circle $\gamma$ with diameter $\overline{A H}$ meets the circumcircle of $A B C$ at $G \neq A$, and meets line $\overline{A N}$ at $Q \neq A$. The tangent to $\gamma$ at $G$ meets line $O M$ at $P$. Show that the circumcircles of $\triangle G N Q$ and $\triangle M B C$ intersect on $\overline{P N}$.
|
【 First solution (found by contestants). Denote by $\triangle D E F$ the orthic triangle. Observe $\overline{P A}$ and $\overline{P G}$ are tangents to $\gamma$, since $\overline{O M}$ is the perpendicular bisector of $\overline{A G}$. Also note that $\overline{A G}, \overline{E F}, \overline{B C}$ are concurrent at some point $R$ by radical axis on $(A B C), \gamma$, (BFEC). Now, consider circles (PAGM), (MFDNE), and (MBC). We already saw the point $R$ satisfies $$ R A \cdot R G=R E \cdot R F=R B \cdot R C $$ and hence has equal powers to all three circles; but since the circles at $M$ already, they must actually be coaxial. Assume they meet again at $T \in \overline{R M}$, say. Then $\angle P T M$ and $\angle M T N$ are both right angles, hence $T$ lies on $\overline{P N}$. Finally $H$ is the orthocenter of $\triangle A R N$, and thus the circle with diameter $\overline{R N}$ passes through $G, Q, N$. 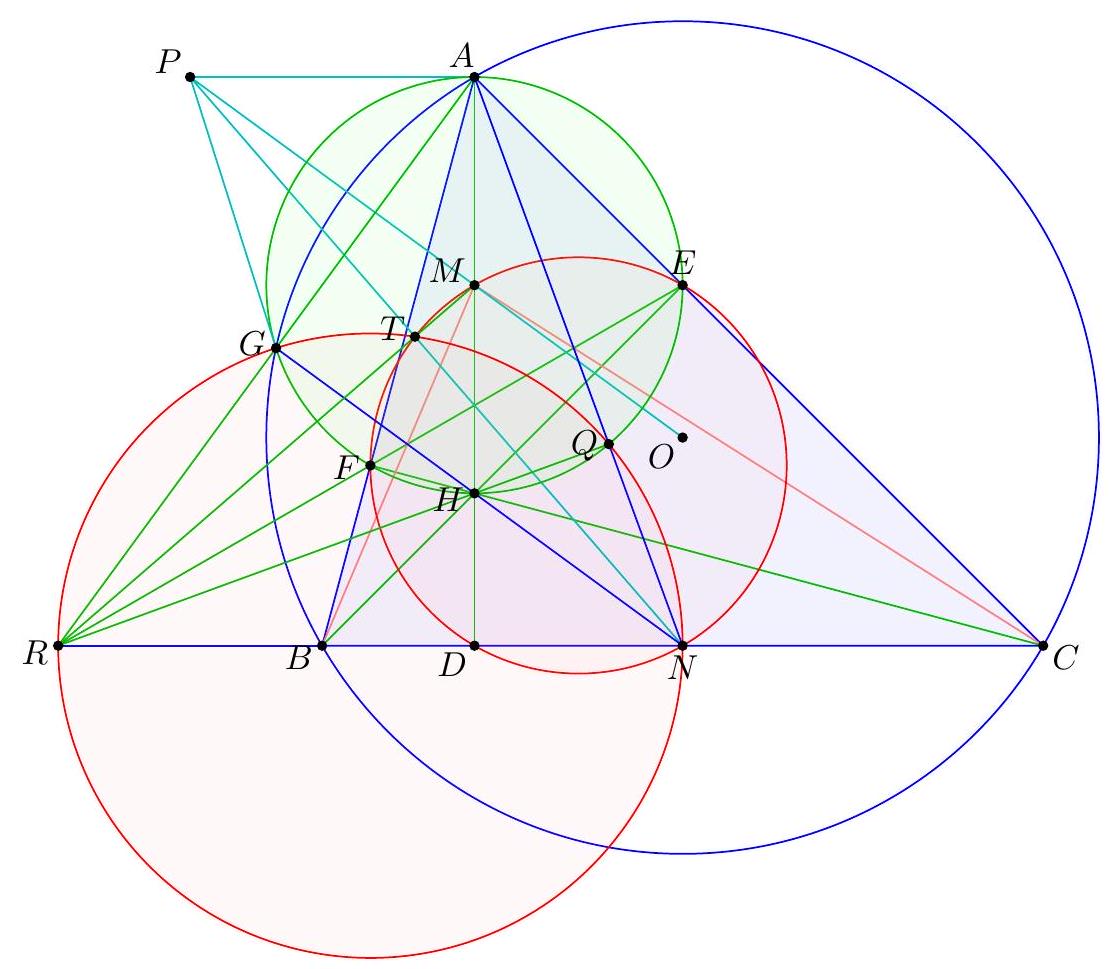
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose the circle $\gamma$ with diameter $\overline{A H}$ meets the circumcircle of $A B C$ at $G \neq A$, and meets line $\overline{A N}$ at $Q \neq A$. The tangent to $\gamma$ at $G$ meets line $O M$ at $P$. Show that the circumcircles of $\triangle G N Q$ and $\triangle M B C$ intersect on $\overline{P N}$.
|
【 First solution (found by contestants). Denote by $\triangle D E F$ the orthic triangle. Observe $\overline{P A}$ and $\overline{P G}$ are tangents to $\gamma$, since $\overline{O M}$ is the perpendicular bisector of $\overline{A G}$. Also note that $\overline{A G}, \overline{E F}, \overline{B C}$ are concurrent at some point $R$ by radical axis on $(A B C), \gamma$, (BFEC). Now, consider circles (PAGM), (MFDNE), and (MBC). We already saw the point $R$ satisfies $$ R A \cdot R G=R E \cdot R F=R B \cdot R C $$ and hence has equal powers to all three circles; but since the circles at $M$ already, they must actually be coaxial. Assume they meet again at $T \in \overline{R M}$, say. Then $\angle P T M$ and $\angle M T N$ are both right angles, hence $T$ lies on $\overline{P N}$. Finally $H$ is the orthocenter of $\triangle A R N$, and thus the circle with diameter $\overline{R N}$ passes through $G, Q, N$. 
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
0b2da215-a965-5452-acd0-899fee8c8474
| 247,210 |
Let $A B C$ be a scalene triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose the circle $\gamma$ with diameter $\overline{A H}$ meets the circumcircle of $A B C$ at $G \neq A$, and meets line $\overline{A N}$ at $Q \neq A$. The tangent to $\gamma$ at $G$ meets line $O M$ at $P$. Show that the circumcircles of $\triangle G N Q$ and $\triangle M B C$ intersect on $\overline{P N}$.
|
『 Alternate solution (by proposer). Let $L$ be diametrically opposite $A$ on the circumcircle. Denote by $\triangle D E F$ the orthic triangle. Let $X=\overline{A H} \cap \overline{E F}$. Finally, let $T$ be the second intersection of (MFDNE) and (MBC). 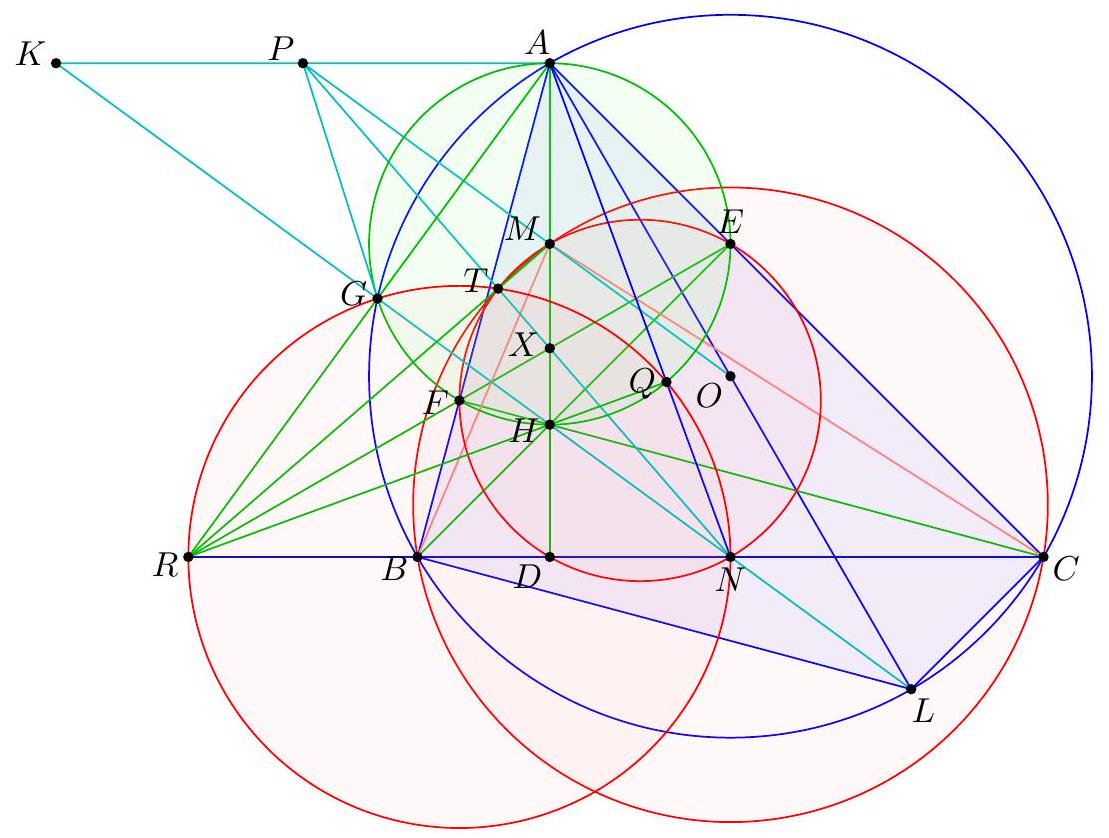 We begin with a few easy observations. First, points $H, G, N, L$ are collinear and $\angle A G L=90^{\circ}$. Also, $Q$ is the foot from $H$ to $\overline{A N}$. Consequently, lines $A G, E F, H Q$, $B C, T M$ concur at a point $R$ (radical axis). Moreover, we already know $\angle M T N=90^{\circ}$. This implies $T$ lies on the circle with diameter $\overline{R N}$, which is exactly the circumcircle of $\triangle G Q N$. Note by Brokard's Theorem on $A F H E$, the point $X$ is the orthocenter of $\triangle M B C$. But $\angle M T N=90^{\circ}$ already, and $N$ is the midpoint of $\overline{B C}$. Consequently, points $T, X$, $N$ are collinear. Finally, we claim $P, X, N$ are collinear, which solves the problem. Note $P=\overline{G G} \cap \overline{A A}$. Set $K=\overline{H N L} \cap \overline{A P}$. Then by noting $$ -1=(D, X ; A, H) \stackrel{N}{=}(\infty, \overline{N X} \cap \overline{A K} ; A, K) $$ we see that $\overline{N X}$ bisects segment $\overline{A K}$, as desired. (A more projective finish is to show that $\overline{P X N}$ is the polar of $R$ to $\gamma$ ). Remark. The original problem proposal reads as follows: Let $A B C$ be a triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose ray $O M$ meets the line parallel to $\overline{B C}$ through $A$ at $P$. Prove that the line through the circumcenter of $\triangle M B C$ and the midpoint of $\overline{O H}$ is parallel to $\overline{N P}$. The points $G$ and $Q$ were added to the picture later to prevent the problem from being immediate by coordinates.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose the circle $\gamma$ with diameter $\overline{A H}$ meets the circumcircle of $A B C$ at $G \neq A$, and meets line $\overline{A N}$ at $Q \neq A$. The tangent to $\gamma$ at $G$ meets line $O M$ at $P$. Show that the circumcircles of $\triangle G N Q$ and $\triangle M B C$ intersect on $\overline{P N}$.
|
『 Alternate solution (by proposer). Let $L$ be diametrically opposite $A$ on the circumcircle. Denote by $\triangle D E F$ the orthic triangle. Let $X=\overline{A H} \cap \overline{E F}$. Finally, let $T$ be the second intersection of (MFDNE) and (MBC).  We begin with a few easy observations. First, points $H, G, N, L$ are collinear and $\angle A G L=90^{\circ}$. Also, $Q$ is the foot from $H$ to $\overline{A N}$. Consequently, lines $A G, E F, H Q$, $B C, T M$ concur at a point $R$ (radical axis). Moreover, we already know $\angle M T N=90^{\circ}$. This implies $T$ lies on the circle with diameter $\overline{R N}$, which is exactly the circumcircle of $\triangle G Q N$. Note by Brokard's Theorem on $A F H E$, the point $X$ is the orthocenter of $\triangle M B C$. But $\angle M T N=90^{\circ}$ already, and $N$ is the midpoint of $\overline{B C}$. Consequently, points $T, X$, $N$ are collinear. Finally, we claim $P, X, N$ are collinear, which solves the problem. Note $P=\overline{G G} \cap \overline{A A}$. Set $K=\overline{H N L} \cap \overline{A P}$. Then by noting $$ -1=(D, X ; A, H) \stackrel{N}{=}(\infty, \overline{N X} \cap \overline{A K} ; A, K) $$ we see that $\overline{N X}$ bisects segment $\overline{A K}$, as desired. (A more projective finish is to show that $\overline{P X N}$ is the polar of $R$ to $\gamma$ ). Remark. The original problem proposal reads as follows: Let $A B C$ be a triangle with orthocenter $H$ and circumcenter $O$ and denote by $M, N$ the midpoints of $\overline{A H}, \overline{B C}$. Suppose ray $O M$ meets the line parallel to $\overline{B C}$ through $A$ at $P$. Prove that the line through the circumcenter of $\triangle M B C$ and the midpoint of $\overline{O H}$ is parallel to $\overline{N P}$. The points $G$ and $Q$ were added to the picture later to prevent the problem from being immediate by coordinates.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
0b2da215-a965-5452-acd0-899fee8c8474
| 247,210 |
Decide whether or not there exists a nonconstant polynomial $Q(x)$ with integer coefficients with the following property: for every positive integer $n>2$, the numbers $$ Q(0), Q(1), Q(2), \ldots, Q(n-1) $$ produce at most $0.499 n$ distinct residues when taken modulo $n$.
|
We claim that $$ Q(x)=420\left(x^{2}-1\right)^{2} $$ works. Clearly, it suffices to prove the result when $n=4$ and when $n$ is an odd prime $p$. The case $n=4$ is trivial, so assume now $n=p$ is an odd prime. First, we prove the following easy claim. Claim - For any odd prime $p$, there are at least $\frac{1}{2}(p-3)$ values of $a$ for which $\left(\frac{1-a^{2}}{p}\right)=+1$. Remark. The above identity comes from starting with the equation $1-a^{2}=b^{2}$, and writing it as $\left(\frac{1}{b}\right)^{2}-\left(\frac{a}{b}\right)^{2}=1$. Then solve $\frac{1}{b}-\frac{a}{b}=k$ and $\frac{1}{b}+\frac{a}{b}=1 / k$ for $a$. Let $F(x)=\left(x^{2}-1\right)^{2}$. The range of $F$ modulo $p$ is contained within the $\frac{1}{2}(p+1)$ quadratic residues modulo $p$. On the other hand, if for some $t$ neither of $1 \pm t$ is a quadratic residue, then $t^{2}$ is omitted from the range of $F$ as well. Call such a value of $t$ useful, and let $N$ be the number of useful residues. We aim to show $N \geq \frac{1}{4} p-2$. We compute a lower bound on the number $N$ of useful $t$ by writing $$ \begin{aligned} N & =\frac{1}{4}\left(\sum_{t}\left[\left(1-\left(\frac{1-t}{p}\right)\right)\left(1-\left(\frac{1+t}{p}\right)\right)\right]-\left(1-\left(\frac{2}{p}\right)\right)-\left(1-\left(\frac{-2}{p}\right)\right)\right) \\ & \geq \frac{1}{4} \sum_{t}\left[\left(1-\left(\frac{1-t}{p}\right)\right)\left(1-\left(\frac{1+t}{p}\right)\right)\right]-1 \\ & =\frac{1}{4}\left(p+\sum_{t}\left(\frac{1-t^{2}}{p}\right)\right)-1 \\ & \geq \frac{1}{4}\left(p+(+1) \cdot \frac{1}{2}(p-3)+0 \cdot 2+(-1) \cdot\left((p-2)-\frac{1}{2}(p-3)\right)\right)-1 \\ & \geq \frac{1}{4}(p-5) . \end{aligned} $$ Thus, the range of $F$ has size at most $$ \frac{1}{2}(p+1)-\frac{1}{2} N \leq \frac{3}{8}(p+3) . $$ This is less than $0.499 p$ for any $p \geq 11$. Remark. In fact, the computation above is essentially an equality. There are only two points where terms are dropped: one, when $p \equiv 3(\bmod 4)$ there are no $k^{2}=-1$ in the lemma, and secondly, the terms $1-(2 / p)$ and $1-(-2 / p)$ are dropped in the initial estimate for $N$. With suitable modifications, one can show that in fact, the range of $F$ is exactly equal to $$ \frac{1}{2}(p+1)-\frac{1}{2} N=\left\{\begin{array}{lll} \frac{1}{8}(3 p+5) & p \equiv 1 & (\bmod 8) \\ \frac{1}{8}(3 p+7) & p \equiv 3 & (\bmod 8) \\ \frac{1}{8}(3 p+9) & p \equiv 5 & (\bmod 8) \\ \frac{1}{8}(3 p+3) & p \equiv 7 & (\bmod 8) \end{array}\right. $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Decide whether or not there exists a nonconstant polynomial $Q(x)$ with integer coefficients with the following property: for every positive integer $n>2$, the numbers $$ Q(0), Q(1), Q(2), \ldots, Q(n-1) $$ produce at most $0.499 n$ distinct residues when taken modulo $n$.
|
We claim that $$ Q(x)=420\left(x^{2}-1\right)^{2} $$ works. Clearly, it suffices to prove the result when $n=4$ and when $n$ is an odd prime $p$. The case $n=4$ is trivial, so assume now $n=p$ is an odd prime. First, we prove the following easy claim. Claim - For any odd prime $p$, there are at least $\frac{1}{2}(p-3)$ values of $a$ for which $\left(\frac{1-a^{2}}{p}\right)=+1$. Remark. The above identity comes from starting with the equation $1-a^{2}=b^{2}$, and writing it as $\left(\frac{1}{b}\right)^{2}-\left(\frac{a}{b}\right)^{2}=1$. Then solve $\frac{1}{b}-\frac{a}{b}=k$ and $\frac{1}{b}+\frac{a}{b}=1 / k$ for $a$. Let $F(x)=\left(x^{2}-1\right)^{2}$. The range of $F$ modulo $p$ is contained within the $\frac{1}{2}(p+1)$ quadratic residues modulo $p$. On the other hand, if for some $t$ neither of $1 \pm t$ is a quadratic residue, then $t^{2}$ is omitted from the range of $F$ as well. Call such a value of $t$ useful, and let $N$ be the number of useful residues. We aim to show $N \geq \frac{1}{4} p-2$. We compute a lower bound on the number $N$ of useful $t$ by writing $$ \begin{aligned} N & =\frac{1}{4}\left(\sum_{t}\left[\left(1-\left(\frac{1-t}{p}\right)\right)\left(1-\left(\frac{1+t}{p}\right)\right)\right]-\left(1-\left(\frac{2}{p}\right)\right)-\left(1-\left(\frac{-2}{p}\right)\right)\right) \\ & \geq \frac{1}{4} \sum_{t}\left[\left(1-\left(\frac{1-t}{p}\right)\right)\left(1-\left(\frac{1+t}{p}\right)\right)\right]-1 \\ & =\frac{1}{4}\left(p+\sum_{t}\left(\frac{1-t^{2}}{p}\right)\right)-1 \\ & \geq \frac{1}{4}\left(p+(+1) \cdot \frac{1}{2}(p-3)+0 \cdot 2+(-1) \cdot\left((p-2)-\frac{1}{2}(p-3)\right)\right)-1 \\ & \geq \frac{1}{4}(p-5) . \end{aligned} $$ Thus, the range of $F$ has size at most $$ \frac{1}{2}(p+1)-\frac{1}{2} N \leq \frac{3}{8}(p+3) . $$ This is less than $0.499 p$ for any $p \geq 11$. Remark. In fact, the computation above is essentially an equality. There are only two points where terms are dropped: one, when $p \equiv 3(\bmod 4)$ there are no $k^{2}=-1$ in the lemma, and secondly, the terms $1-(2 / p)$ and $1-(-2 / p)$ are dropped in the initial estimate for $N$. With suitable modifications, one can show that in fact, the range of $F$ is exactly equal to $$ \frac{1}{2}(p+1)-\frac{1}{2} N=\left\{\begin{array}{lll} \frac{1}{8}(3 p+5) & p \equiv 1 & (\bmod 8) \\ \frac{1}{8}(3 p+7) & p \equiv 3 & (\bmod 8) \\ \frac{1}{8}(3 p+9) & p \equiv 5 & (\bmod 8) \\ \frac{1}{8}(3 p+3) & p \equiv 7 & (\bmod 8) \end{array}\right. $$
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
f98b4f70-b990-5c2b-905c-9c9fbf3ba797
| 605,262 |
Prove that if $n$ and $k$ are positive integers satisfying $\varphi^{k}(n)=1$, then $n \leq 3^{k}$. (Here $\varphi^{k}$ denotes $k$ applications of the Euler phi function.)
|
The main observation is that the exponent of 2 decreases by at most 1 with each application of $\varphi$. This will give us the desired estimate. Define the weight function $w$ on positive integers as follows: it satisfies $$ \begin{aligned} w(a b) & =w(a)+w(b) \\ w(2) & =1 ; \quad \text { and } \\ w(p) & =w(p-1) \quad \text { for any prime } p>2 \end{aligned} $$ By induction, we see that $w(n)$ counts the powers of 2 that are produced as $\varphi$ is repeatedly applied to $n$. In particular, $k \geq w(n)$. From $w(2)=1$, it suffices to prove that $w(p) \geq \log _{3} p$ for every $p>2$. We use strong induction and note that $$ w(p)=w(2)+w\left(\frac{p-1}{2}\right) \geq 1+\log _{3}(p-1)-\log _{3} 2 \geq \log _{3} p $$ for any $p>2$. This solves the problem. Moreover, the stronger bound $$ n \leq 2 \cdot 3^{k-1} $$ is true and best possible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that if $n$ and $k$ are positive integers satisfying $\varphi^{k}(n)=1$, then $n \leq 3^{k}$. (Here $\varphi^{k}$ denotes $k$ applications of the Euler phi function.)
|
The main observation is that the exponent of 2 decreases by at most 1 with each application of $\varphi$. This will give us the desired estimate. Define the weight function $w$ on positive integers as follows: it satisfies $$ \begin{aligned} w(a b) & =w(a)+w(b) \\ w(2) & =1 ; \quad \text { and } \\ w(p) & =w(p-1) \quad \text { for any prime } p>2 \end{aligned} $$ By induction, we see that $w(n)$ counts the powers of 2 that are produced as $\varphi$ is repeatedly applied to $n$. In particular, $k \geq w(n)$. From $w(2)=1$, it suffices to prove that $w(p) \geq \log _{3} p$ for every $p>2$. We use strong induction and note that $$ w(p)=w(2)+w\left(\frac{p-1}{2}\right) \geq 1+\log _{3}(p-1)-\log _{3} 2 \geq \log _{3} p $$ for any $p>2$. This solves the problem. Moreover, the stronger bound $$ n \leq 2 \cdot 3^{k-1} $$ is true and best possible.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
74d8577d-8dde-51cf-9c53-b756bc6569dd
| 247,228 |
In the coordinate plane are finitely many walls, which are disjoint line segments, none of which are parallel to either axis. A bulldozer starts at an arbitrary point and moves in the $+x$ direction. Every time it hits a wall, it turns at a right angle to its path, away from the wall, and continues moving. (Thus the bulldozer always moves parallel to the axes.) Prove that it is impossible for the bulldozer to hit both sides of every wall.
|
We say a wall $v$ is above another wall $w$ if some point on $v$ is directly above a point on $w$. (This relation is anti-symmetric, as walls do not intersect). The critical claim is as follows: Claim - There exists a lowest wall, i.e. a wall not above any other walls. Now consider the leftmost vertical segment $\overline{Q_{i} P_{i+1}}$ and the rightmost vertical segment $\overline{Q_{j} P_{j+1}}$. The broken line gives a path from $P_{i+1}$ to $Q_{j}$, as well as a path from $P_{j+1}$ to $Q_{i}$. These clearly must intersect, contradiction. Remark. This claim is Iran TST 2010. Thus if the bulldozer eventually moves upwards indefinitely, it may never hit the bottom side of the lowest wall. Similarly, if the bulldozer eventually moves downwards indefinitely, it may never hit the upper side of the highest wall.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the coordinate plane are finitely many walls, which are disjoint line segments, none of which are parallel to either axis. A bulldozer starts at an arbitrary point and moves in the $+x$ direction. Every time it hits a wall, it turns at a right angle to its path, away from the wall, and continues moving. (Thus the bulldozer always moves parallel to the axes.) Prove that it is impossible for the bulldozer to hit both sides of every wall.
|
We say a wall $v$ is above another wall $w$ if some point on $v$ is directly above a point on $w$. (This relation is anti-symmetric, as walls do not intersect). The critical claim is as follows: Claim - There exists a lowest wall, i.e. a wall not above any other walls. Now consider the leftmost vertical segment $\overline{Q_{i} P_{i+1}}$ and the rightmost vertical segment $\overline{Q_{j} P_{j+1}}$. The broken line gives a path from $P_{i+1}$ to $Q_{j}$, as well as a path from $P_{j+1}$ to $Q_{i}$. These clearly must intersect, contradiction. Remark. This claim is Iran TST 2010. Thus if the bulldozer eventually moves upwards indefinitely, it may never hit the bottom side of the lowest wall. Similarly, if the bulldozer eventually moves downwards indefinitely, it may never hit the upper side of the highest wall.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
abc7e923-abab-532a-9956-70fd0bbf9d52
| 605,295 |
Let $A B C$ be a triangle with incenter $I$, and whose incircle is tangent to $\overline{B C}, \overline{C A}$, $\overline{A B}$ at $D, E, F$, respectively. Let $K$ be the foot of the altitude from $D$ to $\overline{E F}$. Suppose that the circumcircle of $\triangle A I B$ meets the incircle at two distinct points $C_{1}$ and $C_{2}$, while the circumcircle of $\triangle A I C$ meets the incircle at two distinct points $B_{1}$ and $B_{2}$. Prove that the radical axis of the circumcircles of $\triangle B B_{1} B_{2}$ and $\triangle C C_{1} C_{2}$ passes through the midpoint $M$ of $\overline{D K}$.
|
\I First solution (Allen Liu). Let $X, Y, Z$ be midpoints of $E F, F D, D E$, and let $G$ be the Gergonne point. By radical axis on $(A E I F),(D E F),(A I C)$ we see that $B_{1}$, $X, B_{2}$ are collinear. Likewise, $B_{1}, Z, B_{2}$ are collinear, so lines $B_{1} B_{2}$ and $X Z$ coincide. Similarly, lines $C_{1} C_{2}$ and $X Y$ coincide. In particular lines $B_{1} B_{2}$ and $C_{1} C_{2}$ meet at $X$. 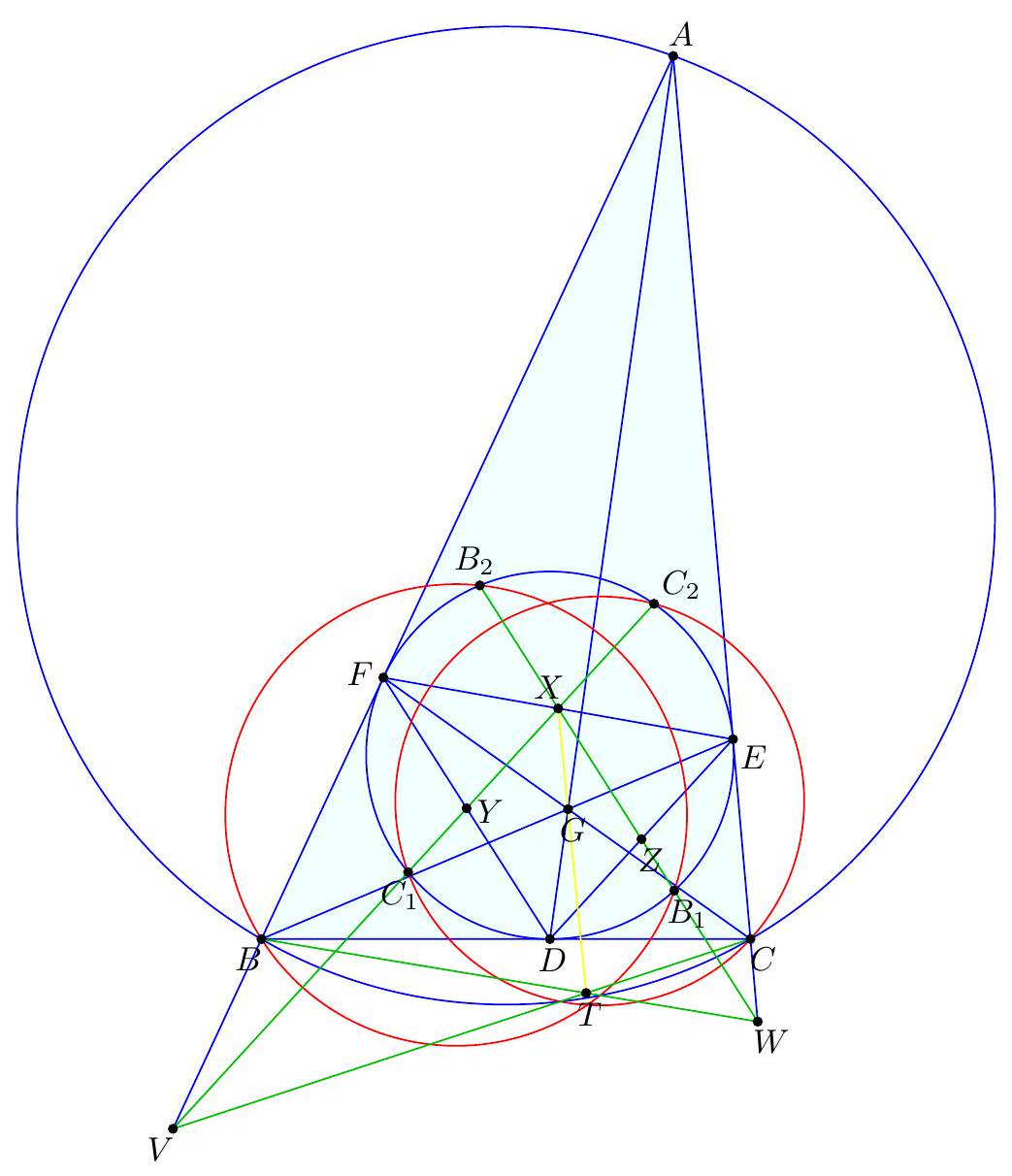 Note $G$ is the symmedian point of $D E F$, so it is well-known that $X G$ passes through the midpoint of $D K$. So we just have to prove $G$ lies on the radical axis. First, note that $\triangle D E F$ is the cevian triangle of the Gergonne point $G$. Set $V=$ $\overline{X Y} \cap \overline{A B}, W=\overline{X Z} \cap \overline{A C}$, and $T=\overline{B W} \cap \overline{C V}$. We begin with the following completely projective claim. Claim - The points $X, G, T$ are collinear. - By Cevian Nest on $\triangle A B C$, it follows that $\overline{A X}, \overline{B Y}, \overline{C Z}$ are concurrent. - Hence $\triangle B Y V$ and $\triangle C Z W$ are perspective. - Hence $\triangle B Z W$ and $\triangle C Y V$ are perspective too. - Hence we deduce by Desargues theorem that $T, X$, and $\overline{B Z} \cap \overline{C Y}$ are collinear. - Finally, the Cevian Nest theorem applied on $\triangle G B C$ (which has cevian triangles $\triangle D F E, \triangle X Z Y$ ) we deduce $G, X$, and $\overline{B Z} \cap \overline{C Y}$, proving the claim. One could also proceed by using barycentric coordinates on $\triangle D E F$. Remark (Eric Shen). The first four bullets can be replaced by non-projective means: one can check that $\overline{B Z} \cap \overline{C Y}$ is the radical center of $(B I C),\left(B B_{1} B_{2}\right),\left(C C_{1} C_{2}\right)$ and therefore it lies on line $\overline{X T}$. Now, we contend point $V$ is the radical center $\left(C C_{1} C_{2}\right),(A B C)$ and $(D E F)$. To see this, let $V^{\prime}=\overline{E D} \cap \overline{A B}$; then $\left(F V^{\prime} ; A B\right)$ is harmonic, and $V$ is the midpoint of $\overline{F V^{\prime}}$, and thus $V A \cdot V B=V F^{2}=V C_{1} \cdot V C_{2}$. So in fact $\overline{C V}$ is the radical axis of $(A B C)$ and $\left(C C_{1} C_{2}\right)$. Similarly, $\overline{B W}$ is the radical axis of $(A B C)$ and $\left(B B_{1} B_{2}\right)$. Thus $T$ is the radical center of $(A B C),\left(B B_{1} B_{2}\right),\left(C C_{1} C_{2}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$, and whose incircle is tangent to $\overline{B C}, \overline{C A}$, $\overline{A B}$ at $D, E, F$, respectively. Let $K$ be the foot of the altitude from $D$ to $\overline{E F}$. Suppose that the circumcircle of $\triangle A I B$ meets the incircle at two distinct points $C_{1}$ and $C_{2}$, while the circumcircle of $\triangle A I C$ meets the incircle at two distinct points $B_{1}$ and $B_{2}$. Prove that the radical axis of the circumcircles of $\triangle B B_{1} B_{2}$ and $\triangle C C_{1} C_{2}$ passes through the midpoint $M$ of $\overline{D K}$.
|
\I First solution (Allen Liu). Let $X, Y, Z$ be midpoints of $E F, F D, D E$, and let $G$ be the Gergonne point. By radical axis on $(A E I F),(D E F),(A I C)$ we see that $B_{1}$, $X, B_{2}$ are collinear. Likewise, $B_{1}, Z, B_{2}$ are collinear, so lines $B_{1} B_{2}$ and $X Z$ coincide. Similarly, lines $C_{1} C_{2}$ and $X Y$ coincide. In particular lines $B_{1} B_{2}$ and $C_{1} C_{2}$ meet at $X$.  Note $G$ is the symmedian point of $D E F$, so it is well-known that $X G$ passes through the midpoint of $D K$. So we just have to prove $G$ lies on the radical axis. First, note that $\triangle D E F$ is the cevian triangle of the Gergonne point $G$. Set $V=$ $\overline{X Y} \cap \overline{A B}, W=\overline{X Z} \cap \overline{A C}$, and $T=\overline{B W} \cap \overline{C V}$. We begin with the following completely projective claim. Claim - The points $X, G, T$ are collinear. - By Cevian Nest on $\triangle A B C$, it follows that $\overline{A X}, \overline{B Y}, \overline{C Z}$ are concurrent. - Hence $\triangle B Y V$ and $\triangle C Z W$ are perspective. - Hence $\triangle B Z W$ and $\triangle C Y V$ are perspective too. - Hence we deduce by Desargues theorem that $T, X$, and $\overline{B Z} \cap \overline{C Y}$ are collinear. - Finally, the Cevian Nest theorem applied on $\triangle G B C$ (which has cevian triangles $\triangle D F E, \triangle X Z Y$ ) we deduce $G, X$, and $\overline{B Z} \cap \overline{C Y}$, proving the claim. One could also proceed by using barycentric coordinates on $\triangle D E F$. Remark (Eric Shen). The first four bullets can be replaced by non-projective means: one can check that $\overline{B Z} \cap \overline{C Y}$ is the radical center of $(B I C),\left(B B_{1} B_{2}\right),\left(C C_{1} C_{2}\right)$ and therefore it lies on line $\overline{X T}$. Now, we contend point $V$ is the radical center $\left(C C_{1} C_{2}\right),(A B C)$ and $(D E F)$. To see this, let $V^{\prime}=\overline{E D} \cap \overline{A B}$; then $\left(F V^{\prime} ; A B\right)$ is harmonic, and $V$ is the midpoint of $\overline{F V^{\prime}}$, and thus $V A \cdot V B=V F^{2}=V C_{1} \cdot V C_{2}$. So in fact $\overline{C V}$ is the radical axis of $(A B C)$ and $\left(C C_{1} C_{2}\right)$. Similarly, $\overline{B W}$ is the radical axis of $(A B C)$ and $\left(B B_{1} B_{2}\right)$. Thus $T$ is the radical center of $(A B C),\left(B B_{1} B_{2}\right),\left(C C_{1} C_{2}\right)$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2016.jsonl",
"problem_match": null,
"solution_match": null
}
|
1965f734-a65e-55f1-ad1d-bc54710433bc
| 247,247 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.