problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
The circle inscribed in $\triangle A B C$ has its center at point $I$ and touches side $B C$ at point $D$. Points $P$ and $Q$ are chosen on segments $B I$ and $C I$, respectively, such that $\varangle B A C=2 \varangle P A Q$. Prove: $\varangle P D Q=90^{\circ} . \quad$ (Dušan Đukić)
|
Let $E$ and $F$ be the feet of the perpendiculars from $P$ and $Q$ to the line $BC$, and let $M$ be the midpoint of the segment $PQ$.
Consider a point $X$ on the side $BC$ such that $\angle BAX = 2 \angle BAP$. Then, $\angle CAX = \angle BAC - 2 \angle BAP = 2 \angle CAQ$, so $P$ and $Q$ are the centers of the inscribed circles of triangles $BAX$ and $CAX$, respectively. It follows that $XP$ and $XQ$ are the angle bisectors of $\angle BXA$ and $\angle CXA$, so $\angle PXQ = 90^\circ$. The condition $\angle PDQ = 90^\circ$ is equivalent to $MD = MP = MQ = $
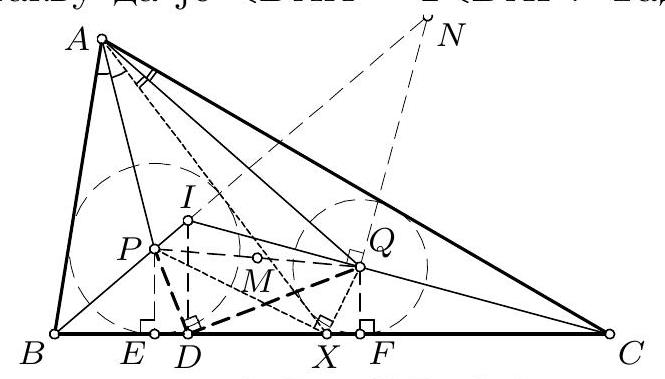
$MX$, and since $ME = MF$, it suffices to prove that $DE = XF$. Both lengths can be easily calculated based on the "main problem": $DE = BD - BE = \frac{AB + BC - AC}{2} - \frac{AB + BX - AX}{2} = \frac{CX - AC + AX}{2} = XF$.
Second solution. Let the line $BI$ intersect the circumcircle of $\triangle APQ$ again at point $N$. We have $\angle AIN = 180^\circ - \angle BIA = 90^\circ - \frac{\gamma}{2} = \angle DIQ$. Also, since $\angle INQ = \angle PAQ = \frac{\alpha}{2}$ and $\angle IQN = \angle BIC - \angle INQ = \left(90^\circ + \frac{\alpha}{2}\right) - \frac{\alpha}{2} = 90^\circ$, we have $\frac{IQ}{IN} = \sin \frac{\alpha}{2} = \frac{IA}{ID}$, so $\frac{IA}{IN} = \frac{ID}{IQ}$. It follows that triangles $DIQ$ and $AIN$ are similar, so $\angle IDQ = \angle IAN = 180^\circ - \angle AIN - \angle ANI = 180^\circ - \left(90^\circ - \frac{\gamma}{2}\right) - \angle ANP = 90^\circ + \frac{\gamma}{2} - \angle AQP$. Similarly, $\angle IDP = 90^\circ + \frac{\beta}{2} - \angle APQ$, so by adding we get $\angle PDQ = 180^\circ + \frac{\beta + \gamma}{2} - (180^\circ - \angle PAQ) = 90^\circ$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Кружница уписана у $\triangle A B C$ има центар у тачки $I$ и додирује страницу $B C$ у тачки $D$. На дужима $B I$ и $C I$ одабране су тачке $P$ и $Q$, редом, такве да важи $\varangle B A C=2 \varangle P A Q$. Доказати: $\varangle P D Q=90^{\circ} . \quad$ (Дуиан Ђукић)
|
Означимо са $E$ и $F$ редом подножја нормала из $P$ и $Q$ на праву $B C$, а са $M$ средиште дужи $P Q$.
Посматрајмо тачку $X$ на страници $B C$ такву да је $\varangle B A X=2 \varangle B A P$. Тада је такође $\varangle C A X=\varangle B A C-2 \varangle B A P=$ $2 \varangle C A Q$, па су $P$ и $Q$ редом центри уписаних кругова троуглова $B A X$ и $C A X$. Следи да су $X P$ и $X Q$ симетрале углова $B X A$ и $C X A$, па је $\varangle P X Q=90^{\circ}$. Услов $\varangle P D Q=90^{\circ}$ је еквивалентан са $M D=M P=M Q=$

$M X$, а како је $M E=M F$, довољно је доказати да је $D E=X F$. Обе дужине се једноставно рачунају на основу "великог задатка": $D E=B D-B E=$ $\frac{A B+B C-A C}{2}-\frac{A B+B X-A X}{2}=\frac{C X-A C+A X}{2}=X F$.
Друго решење. Нека права $B I$ поново сече описани круг $\triangle A P Q$ у тачки $N$. $\overline{\text { Имамо } \varangle A I N}=180^{\circ}-\varangle B I A=90^{\circ}-\frac{\gamma}{2}=\varangle D I Q$. Такође, како је $\varangle I N Q=$ $\varangle P A Q=\frac{\alpha}{2}$ и $\varangle I Q N=\varangle B I C-\varangle I N Q=\left(90^{\circ}+\frac{\alpha}{2}\right)-\frac{\alpha}{2}=90^{\circ}$, имамо $\frac{I Q}{I N}=$ $\sin \frac{\alpha}{2}=\frac{I A}{I D}$, одакле је $\frac{I A}{I N}=\frac{I D}{I Q}$. Следи да су троуглови $D I Q$ и $A I N$ слични, па је $\varangle I D Q=\varangle I A N=180^{\circ}-\varangle A I N-\varangle A N I=180^{\circ}-\left(90^{\circ}-\frac{\gamma}{2}\right)-\varangle A N P=$ $90^{\circ}+\frac{\gamma}{2}-\varangle A Q P$. Аналогно је $\varangle I D P=90^{\circ}+\frac{\beta}{2}-\varangle A P Q$, па сабирањем добијамо $\varangle P D Q=180^{\circ}+\frac{\beta+\gamma}{2}-\left(180^{\circ}-\varangle P A Q\right)=90^{\circ}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
71c515e0-959c-5fc7-a499-d68734c41f77
| 608,114
|
Given are $n$ lines, no two of which are parallel and no three of which intersect at the same point. By intersection points, we consider all points where some two of these lines intersect.
(a) Prove that among the given lines, there is one such that on each side of it there are at least
$$
\left\lfloor\frac{(n-1)(n-2)}{10}\right\rfloor
$$
intersection points (points on that line are not counted).
(b) For which values of $n$ can the estimate from part (a) not be improved?
(Dušan Đukić)
## Ministry of Education, Science and Technological Development Mathematical Society of Serbia <br> 12th SERBIAN MATHEMATICAL OLYMPIAD FOR HIGH SCHOOL STUDENTS
## Second Day
|
For each of the given lines, outside of it, there are
$$
m=\frac{(n-1)(n-2)}{2}
$$
intersection points. Assume that for each line, on one side of it, there are no more than $k$ intersection points, where $k \leqslant \frac{n}{2}$. Let's count the triples $(p, A, B)$, where $A$ and $B$ are intersection points on different sides of the line $p$, in two ways. By the assumption, for each line $p$, there are no more than $k(m-k)$ such triples, so the total number of such triples $N \leqslant n k(m-k)$.
Now consider two types of such triples: type 1, when points $A$ and $B$ are on the same given line, and type 2, when they are not.
Each quadruple of the given lines, together with the intersection points they determine, determines exactly 4 triples of type 1, and each triple is determined by exactly one quadruple of lines. Therefore, there are $4\binom{n}{4}$ triples of type 1. Also, each quintuple of the given lines, together with the intersection points they determine, determines at least 5 triples of type 2, so there are at least $5\binom{n}{5}$ triples of type 2. This can be verified directly: there are six different arrangements of five lines in general position, as shown in the figure.
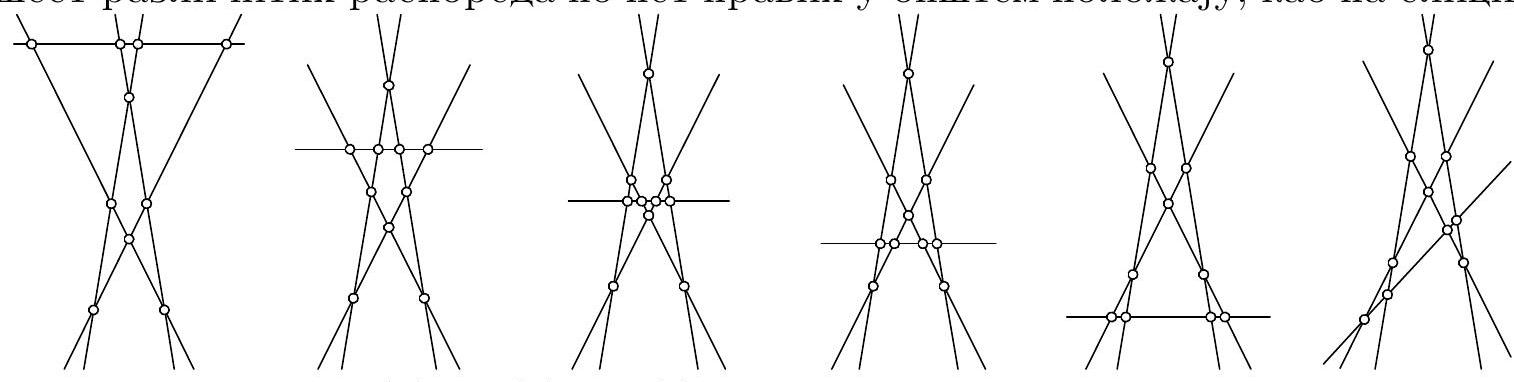
Therefore, $N \geqslant 4\binom{n}{4}+5\binom{n}{5}=n\binom{n}{4}$.
It follows that $k(m-k) \geqslant\binom{n}{4}=\frac{m(m-1)}{6}$. From this, we get
$$
k \geqslant k_{0}=\frac{1}{2}\left(m-\sqrt{\frac{m^{2}+2 m}{3}}\right)
$$
The inequality $k_{0}>\frac{m}{5}=\frac{(n-1)(n-2)}{10}$ reduces to $m>25$, which holds for $n \geqslant 9$, while for $n=8$ we have $k_{0}>\left[\frac{m}{5}\right]=4$, so we need to examine the cases $n \leqslant 7$.
For $n \leqslant 4$, the statement is trivial, as is the achievement of equality, since then $k_{0}=\left[\frac{m}{5}\right]=0$. For $n=5,6,7$, we have $\left\lceil k_{0}\right\rceil=\left[\frac{m}{5}\right]=1,2,3$, respectively, so the statement of the problem holds in these cases as well, and equality is achieved in the cases shown in the figure.
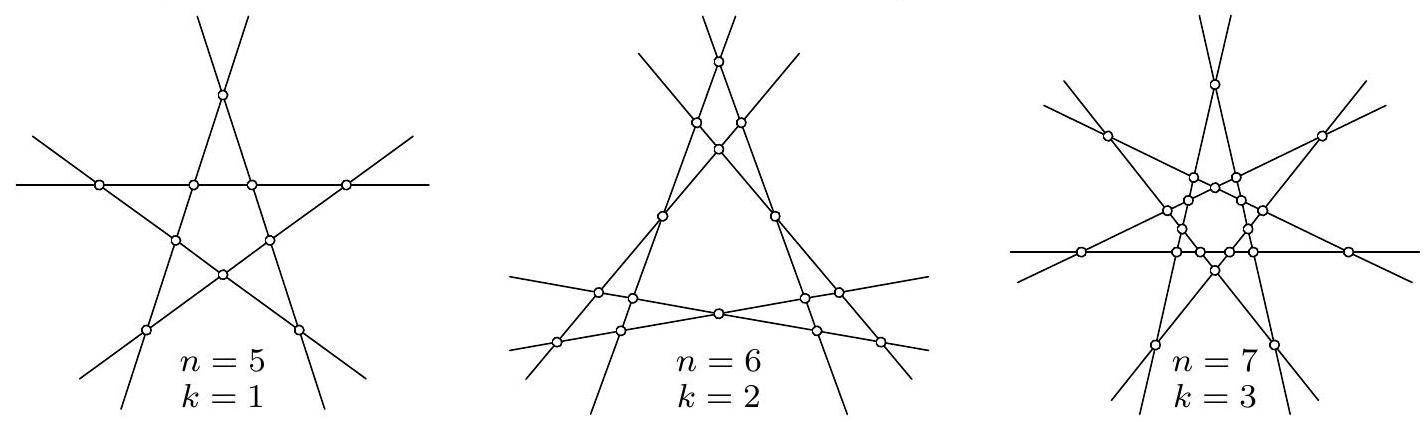
Note. On the other hand, each quintuple determines at most 7 triples $(p, A, B)$ of type 2. This can be used to show that there is always a line on one side of which there are fewer than $\left(\frac{1}{2}-\frac{1}{2 \sqrt{15}}\right) m$ points.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
У равни је дато $n$ правих међу којима никоје две нису паралелне и никоје три се не секу у једној тачки. Под пресечним тачкама сматрамо све тачке у којима се секу неке две од ових правих.
(a) Доказати да међу датим правим постоји једна са чије се сваке стране налази бар по
$$
\left\lfloor\frac{(n-1)(n-2)}{10}\right\rfloor
$$
пресечних тачака (тачке на тој правој се не рачунају).
(б) За које вредности $n$ се оцена из дела под (а) не може побољшати?
(Душан Ђукић)
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 12. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
## Други дан
|
За сваку од датих правих, пресечних тачака ван ње има
$$
m=\frac{(n-1)(n-2)}{2}
$$
Претпоставимо да, за сваку праву, с једне њене стране има не више од $k$ пресечних тачака, где је $k \leqslant \frac{n}{2}$. Пребројмо на два начина тројке $(p, A, B)$, где су $A$ и $B$ пресечне тачке са различитих страна праве $p$. По претпоставци, за сваку праву $p$ има не више од $k(m-k)$ оваквих тројки, па је њихов укупан број $N \leqslant n k(m-k)$.
Размотримо сада два типа оваквих тројки: mun 1 , када су тачке $A$ и $B$ на истој од датих правих, и mun 2 , када нису.
Свака четворка датих правих, заједно са њима одређеним пресечним тачкама, одређује тачно 4 тројке типа 1 , а свака тројка је одређена тачно једном четворком правих. Следи да има $4\binom{n}{4}$ тројки типа 1. Такође, свака петорка датих правих са њима одређеним пресечним тачкама одређује бар 5 тројки типа 2 , те тројки типа 2 има бар $5\binom{n}{5}$. Ово се директно проверава: постоји шест различитих распореда по пет правих у општем положају, као на слици.

Према томе, $N \geqslant 4\binom{n}{4}+5\binom{n}{5}=n\binom{n}{4}$.
Следи да је $k(m-k) \geqslant\binom{ n}{4}=\frac{m(m-1)}{6}$. Одавде се добија
$$
k \geqslant k_{0}=\frac{1}{2}\left(m-\sqrt{\frac{m^{2}+2 m}{3}}\right)
$$
Како се неједнакост $k_{0}>\frac{m}{5}=\frac{(n-1)(n-2)}{10}$ своди на $m>25$, што важи за $n \geqslant 9$, док за $n=8$ имамо $k_{0}>\left[\frac{m}{5}\right]=4$, остаје да испитамо случајеве $n \leqslant 7$.
За $n \leqslant 4$ је тврђење тривијално, као и достизање једнакости, јер је тада $k_{0}=\left[\frac{m}{5}\right]=0$. За $n=5,6,7$ је редом $\left\lceil k_{0}\right\rceil=\left[\frac{m}{5}\right]=1,2,3$, па тврђење задатка и тада важи, а достижу се и једнакости у случајевима на слици.

Напомена. С друге стране, свака петорка одређује највише 7 тројки $(p, A, B)$ типа 2. Овако се може показати да увек постоји права са чије се једне стране налази мање од $\left(\frac{1}{2}-\frac{1}{2 \sqrt{15}}\right) m$ тачака.
|
{
"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
d158c412-f7e0-58ff-8c36-f646042b7cdc
| 608,116
|
Prove that there exists exactly one polynomial $P(x)$ with real coefficients for which the polynomial
$$
(x+y)^{1000}-P(x)-P(y)
$$
is divisible by the polynomial $x y-x-y$.
(Dusan Dukic)
|
Let $n=1000$. By substituting $x=u+1$ and $y=v+1$, we obtain that the polynomial $u v-1$ divides the polynomial $P(u+1)+P(v+1)-(u+v+2)^{n}$. An equivalent condition is that $P(u+1)+P(v+1)-(u+v+2)^{n}=0$ whenever $u v-1=0$ (see the note). Thus, for $u \neq 0$ and $v=\frac{1}{u}$, we have $P(u+1)+P\left(\frac{1}{u}+1\right)=\left(u+\frac{1}{u}+2\right)^{n}=\frac{(u+1)^{2 n}}{u^{n}}$. The polynomial $Q(x)=P(x+1)=\sum_{i=0}^{n} a_{i} x^{i}$ satisfies
$2 a_{0}+\sum_{i=1}^{n} a_{i}\left(u^{i}+u^{-i}\right)=Q(u)+Q\left(\frac{1}{u}\right)=\frac{(u+1)^{2 n}}{u^{n}}=\binom{2 n}{n}+\sum_{i=1}^{n}\binom{2 n}{n-i}\left(u^{i}+u^{-i}\right)$, from which it immediately follows that $a_{0}=\frac{1}{2}\binom{2 n}{n}$ and $a_{i}=\binom{2 n}{n-i}$ for $1 \leqslant i \leqslant n$. Therefore,
$$
P(x)=\frac{1}{2}\binom{2 n}{n}+\sum_{i=1}^{n}\binom{2 n}{n-i}(x-1)^{i}
$$
Second solution. We seek polynomials $P(x)=\sum_{i=0}^{n} p_{i} x^{i}$ and $Q(x, y)=\sum_{i, j} a_{i, j} x^{i} y^{j}$ such that
$$
A(x, y)=(x y-x-y) Q(x, y)=(x+y)^{1000}-P(x)-P(y)
$$
Note that $\operatorname{deg} Q \leqslant 998$. Indeed, if $a_{i, j} x^{i} y^{j}$ is the monomial of the highest degree in $Q(x, y)$, then the coefficient of $x^{i+1} y^{j+1}$ in $A(x, y)$ is $a_{i, j} \neq 0$, so $i+j+2 \leqslant 1000$. It follows that $\operatorname{deg} A \leqslant 1000$, and thus $\operatorname{deg} P \leqslant 1000$.
Equating the coefficients of $x^{i} y^{j}$ in (*) gives the equations $a_{i-1, j-1}=\binom{1000}{i}$ for $i+j=998(i, j>0), a_{i-1, j-1}=a_{i-1, j}+a_{i, j-1}$ for $i+j<998(i, j>0)$ and $a_{i-1,0}=$ $a_{0, i-1}=p_{i}$, from which we find by simple induction that $a_{i-1, j-1}=\binom{2000-i-j}{1000-i}$ for $i+j \leqslant 1000(i, j>0)$ and $p_{i}=\binom{1999-i}{999}$, i.e.,
$$
P(x)=x^{1000}+\binom{1000}{999} x^{999}+\binom{1001}{999} x^{998}+\cdots+\binom{1998}{999} x
$$
It follows from the construction that this polynomial satisfies the conditions of the problem.
Third solution. There do not exist two different polynomials with the desired property. Indeed, if $P_{1}(x) \not \equiv P_{2}(x)$ have this property, then $x y-x-y$ divides the difference $P_{1}(x)+P_{1}(y)-P_{2}(x)-P_{2}(y)=(x y-x-y) U(x, y)$. However, if $c x^{i} y^{j}$ is the monomial of the highest degree in $U(x, y)$, then the coefficient of $x^{i+1} y^{j+1}$ on the left side of this equality is $c \neq 0$, which is impossible.
We now prove that for every symmetric polynomial $Q(x, y)$ there exists a polynomial $P(t)$ such that $x y-x-y \mid Q(x, y)-P(x)-P(y)$. It suffices to prove that for polynomials $Q$ of the form $x^{i} y^{j}+x^{j} y^{i}(0 \leqslant i \leqslant j)$ there exists the desired polynomial $P_{i, j}(t)$. The statement is trivial for $i=0$. For $i>0$ we prove it by induction on $i+j$. Namely, $x^{i} y^{j}+x^{j} y^{i} \equiv(x+y)\left(x^{i-1} y^{j-1}+x^{j-1} y^{i-1}\right)=\left(x^{i} y^{j-1}+x^{j-1} y^{i}\right)+$ $\left(x^{i-1} y^{j}+x^{j} y^{i-1}\right)(\bmod x y-x-y)$, so we can take $P_{i, j}(t)=P_{i, j-1}(t)+P_{i-1, j}(t)$.
Note. If $P(x, y)$ is an irreducible polynomial and $Q(x, y)$ is a polynomial such that $\overline{Q(x, y)=0}$ whenever $P(x, y)=0$, then the polynomial $Q$ is divisible by the polynomial $P$. This is not entirely trivial. In the polynomial ring $\mathbb{R}[y][x]$, the Euclidean algorithm can be used to find polynomials $A(x, y), B(x, y)$ and $C(y)$ such that $\operatorname{deg}_{x} B<\operatorname{deg}_{x} P$ and $A \cdot P-B \cdot Q=C(y)$. Thus, whenever $Q(x, y)=0$, we have $C(y)=0$, so $C$ has infinitely many zeros, hence $C \equiv 0$ and $P \mid B \cdot Q$. Due to the irreducibility of the polynomial $P$ and the uniqueness of factorization in the ring $\mathbb{R}[y][x]$, it follows that $P \mid Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Доказати да постоји тачно један полином $P(x)$ с реалним коефицијентима за који је полином
$$
(x+y)^{1000}-P(x)-P(y)
$$
дељив полиномом $x y-x-y$.
(Душан Ђукић)
|
Означимо $n=1000$. Сменом $x=u+1$ и $y=v+1$ добијамо да полином $u v-1$ дели полином $P(u+1)+P(v+1)-(u+v+2)^{n}$. Еквивалентан услов је да је $P(u+1)+P(v+1)-(u+v+2)^{n}=0$ кад год је $u v-1=0$ (видети напомену). Тако за $u \neq 0$ и $v=\frac{1}{u}$ имамо $P(u+1)+P\left(\frac{1}{u}+1\right)=\left(u+\frac{1}{u}+2\right)^{n}=\frac{(u+1)^{2 n}}{u^{n}}$. Полином $Q(x)=P(x+1)=\sum_{i=0}^{n} a_{i} x^{i}$ задовољава
$2 a_{0}+\sum_{i=1}^{n} a_{i}\left(u^{i}+u^{-i}\right)=Q(u)+Q\left(\frac{1}{u}\right)=\frac{(u+1)^{2 n}}{u^{n}}=\binom{2 n}{n}+\sum_{i=1}^{n}\binom{2 n}{n-i}\left(u^{i}+u^{-i}\right)$, одакле одмах следи да је $a_{0}=\frac{1}{2}\binom{2 n}{n}$ и $a_{i}=\binom{2 n}{n-i}$ за $1 \leqslant i \leqslant n$. Дакле,
$$
P(x)=\frac{1}{2}\binom{2 n}{n}+\sum_{i=1}^{n}\binom{2 n}{n-i}(x-1)^{i}
$$
Друго решење. Тражимо полиноме $P(x)=\sum_{i=0}^{n} p_{i} x^{i}$ и $Q(x, y)=\sum_{i, j} a_{i, j} x^{i} y^{j}$ такве да је
$$
A(x, y)=(x y-x-y) Q(x, y)=(x+y)^{1000}-P(x)-P(y)
$$
Приметимо да је $\operatorname{deg} Q \leqslant 998$. Заиста, ако је $a_{i, j} x^{i} y^{j}$ моном највећег степена у $Q(x, y)$, онда је коефицијент уз $x^{i+1} y^{j+1}$ у $A(x, y)$ једнак $a_{i, j} \neq 0$, па је $i+j+2 \leqslant 1000$. Следи да је $\operatorname{deg} A \leqslant 1000$, па је и $\operatorname{deg} P \leqslant 1000$.
Изједначавање коефицијената уз $x^{i} y^{j}$ у (*) даје једнакости $a_{i-1, j-1}=\binom{1000}{i}$ за $i+j=998(i, j>0), a_{i-1, j-1}=a_{i-1, j}+a_{i, j-1}$ за $i+j<998(i, j>0)$ и $a_{i-1,0}=$ $a_{0, i-1}=p_{i}$, одакле једноставном индукцијом налазимо $a_{i-1, j-1}=\binom{2000-i-j}{1000-i}$ за $i+j \leqslant 1000(i, j>0)$ и $p_{i}=\binom{1999-i}{999}$, тј.
$$
P(x)=x^{1000}+\binom{1000}{999} x^{999}+\binom{1001}{999} x^{998}+\cdots+\binom{1998}{999} x
$$
Из конструкције следи да овај полином задовољава услове задатка.
Tреће решење. Не постоје два различита полинома са жељеним својством. Заиста, ако $P_{1}(x) \not \equiv P_{2}(x)$ имају то својство, онда $x y-x-y$ дели разлику $P_{1}(x)+P_{1}(y)-P_{2}(x)-P_{2}(y)=(x y-x-y) U(x, y)$. Међутим, ако је $c x^{i} y^{j}$ моном највећег степена у $U(x, y)$, онда је коефицијент уз $x^{i+1} y^{j+1}$ на левој страни ове једнакости једнак $c \neq 0$, што је немогуће.
Докажимо сада да за сваки симетричан полином $Q(x, y)$ постоји полином $P(t)$ такав да $x y-x-y \mid Q(x, y)-P(x)-P(y)$. Довољно је доказати да за полиноме $Q$ облика $x^{i} y^{j}+x^{j} y^{i}(0 \leqslant i \leqslant j)$ постоји тражени полином $P_{i, j}(t)$. Тврђење је тривијално за $i=0$. За $i>0$ доказ спроводимо индукцијом по $i+j$. Наиме, $x^{i} y^{j}+x^{j} y^{i} \equiv(x+y)\left(x^{i-1} y^{j-1}+x^{j-1} y^{i-1}\right)=\left(x^{i} y^{j-1}+x^{j-1} y^{i}\right)+$ $\left(x^{i-1} y^{j}+x^{j} y^{i-1}\right)(\bmod x y-x-y)$, па можемо узети $P_{i, j}(t)=P_{i, j-1}(t)+P_{i-1, j}(t)$.
Напомена. Ако је $P(x, y)$ нерастављив полином и $Q(x, y)$ полином такав да је $\overline{Q(x, y)=0}$ кад год је $P(x, y)=0$, онда је полином $Q$ дељив полиномом $P$. Ово није потпуно тривијално. У прстену полинома $\mathbb{R}[y][x]$ Еуклидовим алгоритмом могу се наћи полиноми $A(x, y), B(x, y)$ и $C(y)$ такви да је $\operatorname{deg}_{x} B<\operatorname{deg}_{x} P$ и $A \cdot P-B \cdot Q=C(y)$. Дакле, кад год је $Q(x, y)=0$, важи $C(y)=0$, па $C$ има
бесконачно много нула, одакле је $C \equiv 0$ и $P \mid B \cdot Q$. Због нерастављивости полинома $P$ и јединствености факторизације у прстену $\mathbb{R}[y][x]$ следи $P \mid Q$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
f4e952db-9772-548f-bd81-4e575435e434
| 608,117
|
For a given natural number $k$, let $n_{k}$ be the smallest natural number such that there exists a finite set $A$ of integers with the following properties:
- for every $a \in A$ there exist $x, y \in A$ (not necessarily distinct) such that
$$
n_{k} \mid a-x-y
$$
- there is no subset $B$ of the set $A$ for which $|B| \leqslant k$ and $n_{k} \mid \sum_{b \in B} b$.
Prove that for all $k, k \geqslant 3$, we have
$$
n_{k}<\left(\frac{13}{8}\right)^{k+2}
$$
(Bojan Baić)
Time for work 270 minutes.
Solutions to the problems should be explained in detail.
Each problem is worth 7 points.
## SOLUTIONS
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
Let $F_{i}$ denote the Fibonacci numbers: $F_{1}=F_{2}=1, F_{i+1}=F_{i}+F_{i-1}$. Consider the set $A=\left\{a_{1}, a_{2}, \ldots, a_{k+1}\right\}$ with $n=F_{k+2}+3$, where
$$
a_{i}=(-1)^{k-1-i} F_{i+1} \text { for } i=1,2, \ldots, k-1, \quad a_{k}=F_{k}+1 \quad \text { and } \quad a_{k+1}=F_{k}+2
$$
In the case of even $k$, we see that $a_{i}=a_{i+1}+a_{i+2}(1 \leqslant i \leqslant k-3), a_{k-2} \equiv a_{k}+a_{k+1}$ $(\bmod n), a_{k-1}=a_{k+1}+a_{2}, a_{k}=a_{k-1}+a_{1}$ and $a_{k+1}=a_{k}+a_{1}$, so the set $A$ satisfies the first condition of the problem. This condition is similarly verified for odd $k$.
We prove by induction on $k$ (the base case $k=3$ can be directly verified) that the second condition is also satisfied, i.e., there is no subset $B \subsetneq A$ such that $n \mid \sum_{b \in B} b$. Since the sum of the elements of the set $A$ is zero, we can assume without loss of generality (by replacing $B$ with $A \backslash B$ if necessary) that $B$ contains at most one of the elements $F_{k}, F_{k}+1, F_{k}+2$. Then
$1-F_{k}=-\left(F_{k-1}+F_{k-3}+\cdots\right) \leqslant \sum_{b \in B} b \leqslant\left(F_{k}+2\right)+F_{k-2}+F_{k-4}+\cdots=F_{k+1}+1$,
so it must be $\sum_{b \in B} b=0$. Based on the inductive hypothesis for $k-1$, the set $B$ cannot be a subset of the set $\left\{a_{1}, a_{2}, \ldots, a_{k-2}\right\}$, i.e., it must be $a_{k-1}=F_{k} \in B$. However, then $\sum_{b \in B} b \geqslant F_{k}-F_{k-1}-F_{k-3}-\cdots=1$, which is a contradiction. The proof is complete.
Therefore, $n_{k} \leqslant F_{k+2}+3<\phi^{k-3}\left(F_{5}+3\right)<\phi^{k+2}<\left(\frac{13}{8}\right)^{k+2}$, where $\phi=\frac{1+\sqrt{5}}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
За задат природан број $k$, нека је $n_{k}$ најмањи природан број такав да постоји коначан скуп $A$ целих бројева са следећим особинама:
- за свако $a \in A$ постоје $x, y \in A$ (не обавезно различити) такви да
$$
n_{k} \mid a-x-y
$$
- не постоји подскуп $B$ скупа $A$ за који важи $|B| \leqslant k$ и $n_{k} \mid \sum_{b \in B} b$.
Доказати да за све $k, k \geqslant 3$, важи
$$
n_{k}<\left(\frac{13}{8}\right)^{k+2}
$$
(Бојан Bаиић)
Време за рад 270 минута.
Решења задатака детаљно образложити.
Сваки задатак вреди 7 бодова.
## РЕШЕЊА
|
Са $F_{i}$ означавамо Фибоначијеве бројеве: $F_{1}=F_{2}=1, F_{i+1}=F_{i}+F_{i-1}$. Посматрајмо скуп $A=\left\{a_{1}, a_{2}, \ldots, a_{k+1}\right\}$ са $n=F_{k+2}+3$, где су
$$
a_{i}=(-1)^{k-1-i} F_{i+1} \text { за } i=1,2, \ldots, k-1, \quad a_{k}=F_{k}+1 \quad \text { и } \quad a_{k+1}=F_{k}+2
$$
У случају парног $k$ видимо да је $a_{i}=a_{i+1}+a_{i+2}(1 \leqslant i \leqslant k-3), a_{k-2} \equiv a_{k}+a_{k+1}$ $(\bmod n), a_{k-1}=a_{k+1}+a_{2}, a_{k}=a_{k-1}+a_{1}$ и $a_{k+1}=a_{k}+a_{1}$, па скуп $A$ задовољава први услов задатка. Овај услов се слично проверава и за непарно $k$.
Докажимо индукцијом по $k$ (база $k=3$ се директно проверава) да је задовољен и други услов, тј. да не постоји подскуп $B \subsetneq A$ такав да $n \mid \sum_{b \in B} b$. Како је збир елемената скупа $A$ једнак нули, можемо да сматрамо без смањења општости (заменом $B$ са $A \backslash B$ по потреби) да $B$ садржи највише један од елемената $F_{k}, F_{k}+1, F_{k}+2$. Тада је
$1-F_{k}=-\left(F_{k-1}+F_{k-3}+\cdots\right) \leqslant \sum_{b \in B} b \leqslant\left(F_{k}+2\right)+F_{k-2}+F_{k-4}+\cdots=F_{k+1}+1$,
па мора бити $\sum_{b \in B} b=0$. На основу индуктивне претпоставке за $k-1$, скуп $B$ не може бити подскуп скупа $\left\{a_{1}, a_{2}, \ldots, a_{k-2}\right\}$, тј. мора бити $a_{k-1}=F_{k} \in B$. Међутим, тада је $\sum_{b \in B} b \geqslant F_{k}-F_{k-1}-F_{k-3}-\cdots=1$, што је контрадикција. Доказ је завршен.
Према томе, $n_{k} \leqslant F_{k+2}+3<\phi^{k-3}\left(F_{5}+3\right)<\phi^{k+2}<\left(\frac{13}{8}\right)^{k+2}$, где је $\phi=\frac{1+\sqrt{5}}{2}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2018_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
3b39165b-9b1f-5ca9-804d-60e9f1d52471
| 608,119
|
For a sequence of non-negative real numbers $a_{1}, a_{2}, \ldots, a_{k}$, we say it is embeddable in the interval $[b, c]$ if there exist numbers $x_{0}, x_{1}, \ldots, x_{k}$ in the interval $[b, c]$ such that $\left|x_{i}-x_{i-1}\right|=a_{i}$ for $i=1,2, \ldots, k$. A sequence is normalized if all its elements are not greater than 1. For a given natural number $n$, prove:
(a) every normalized sequence of length $2 n+1$ is embeddable in the interval $\left[0,2-\frac{1}{2^{n}}\right]$;
(b) there exists a normalized sequence of length $4 n+3$ that is not embeddable in $\left[0,2-\frac{1}{2^{n}}\right]$.
(Dušan Đukić)
|
(a) It is sufficient to prove that every normalized sequence $a_{1}, a_{2}, \ldots, a_{2 n+1}$ can be embedded in some interval of length $2-\frac{1}{2^{n}}$. We prove the statement by induction on $n$. It is true for $n=0$; let $n \geqslant 1$. By the induction hypothesis, there exists a sequence $x_{0}, x_{1}, \ldots, x_{2 n-1} \in\left[0,2-\frac{1}{2^{n-1}}\right]$ such that $\left|x_{i}-x_{i-1}\right|=a_{i}$ for $i=1, \ldots, 2 n-1$. Without loss of generality, we assume that $x_{2 n-1} \leqslant 1-\frac{1}{2^{n}}$.
(10) If $a_{2 n} \geqslant \frac{1}{2^{n}}$, we can take $x_{2 n}=x_{2 n-1}+a_{2 n} \in\left[1,2-\frac{1}{2^{n}}\right]$ and $x_{2 n+1}=$ $x_{2 n}-a_{2 n+1} \in\left[0,2-\frac{1}{2^{n}}\right]$, thus the sequence is embedded in the interval $\left[0,2-\frac{1}{2^{n}}\right]$.
$\left(2^{\circ}\right)$ If $a_{2 n}<\frac{1}{2^{n}}$, we take $x_{2 n}=x_{2 n-1}-a_{2 n} \in\left[-\frac{1}{2^{n}}, 1-\frac{1}{2^{n}}\right]$ and $x_{2 n+1}=x_{2 n}+$ $a_{2 n+1}$, thus the sequence is embedded in one of the intervals $\left[0,2-\frac{1}{2^{n}}\right]$ and $\left[-\frac{1}{2^{n}}, 2-\frac{1}{2^{n-1}}\right]$.
(b) Let $N=3 \cdot 2^{n-1}-1$. We will prove that the sequence of length $4 n-1$
$1,1-\frac{1}{N}, 1,1-\frac{2}{N}, 1,1-\frac{2^{2}}{N}, \ldots, 1,1-\frac{2^{n-1}}{N}, 1,1-\frac{2^{n-2}}{N}, 1, \ldots, 1-\frac{2}{N}, 1,1-\frac{1}{N}, 1$ cannot be embedded in the interval $\left(-1+\frac{1}{2 N}, 1-\frac{1}{2 N}\right)$, from which the statement follows.
Assume the contrary. By simple induction, it can be proved that:
(i) $\left|x_{2 i}\right|<1-\frac{2^{i+1}-1}{2 N}$ and $\left|x_{2 i+1}\right|>\frac{2^{i+1}-1}{2 N}$ for $i=0, \ldots, n$;
(ii) $\left|x_{2 i}\right|<\frac{2^{2 n+2-i}-1}{2 N}$ and $\left|x_{2 i+1}\right|>1-\frac{2^{2 n+2-i}-1}{2 N}$ for $i=n+1, \ldots, 2 n+1$.
Thus, for $x_{4 n+3}$ we obtain a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
За низ ненегативних реалних бројева $a_{1}, a_{2}, \ldots, a_{k}$ кажемо да је уложсив у интервал $[b, c]$ ако постоје бројеви $x_{0}, x_{1}, \ldots, x_{k}$ из интервала $[b, c]$ такви да важи $\left|x_{i}-x_{i-1}\right|=a_{i}$ за $i=1,2, \ldots, k$. Низ је нормиран ако су сви његови чланови не већи од 1. За задат природан број $n$, доказати:
(a) сваки нормиран низ дужине $2 n+1$ је уложив у интервал $\left[0,2-\frac{1}{2^{n}}\right]$;
(б) постоји нормиран низ дужине $4 n+3$ који није уложив у $\left[0,2-\frac{1}{2^{n}}\right]$.
(Душан Ђукић)
|
(a) Довољно је доказати да је сваки нормиран низ $a_{1}, a_{2}, \ldots, a_{2 n+1}$ уложив у неки интервал дужине $2-\frac{1}{2^{n}}$. Тврђење доказујемо индукцијом по $n$. Оно је тачно за $n=0$; нека је $n \geqslant 1$. По индуктивној претпоставци постоји низ $x_{0}, x_{1}, \ldots, x_{2 n-1} \in\left[0,2-\frac{1}{2^{n-1}}\right]$ такав да је $\left|x_{i}-x_{i-1}\right|=a_{i}$ за $i=1, \ldots, 2 n-1$. Не умањујући општост, сматраћемо да је $x_{2 n-1} \leqslant 1-\frac{1}{2^{n}}$.
(10) Ако је $a_{2 n} \geqslant \frac{1}{2^{n}}$, можемо узети $x_{2 n}=x_{2 n-1}+a_{2 n} \in\left[1,2-\frac{1}{2^{n}}\right]$ и $x_{2 n+1}=$ $x_{2 n}-a_{2 n+1} \in\left[0,2-\frac{1}{2^{n}}\right]$, чиме је низ уложен у интервал $\left[0,2-\frac{1}{2^{n}}\right]$.
$\left(2^{\circ}\right)$ Ако је $a_{2 n}<\frac{1}{2^{n}}$, узећемо $x_{2 n}=x_{2 n-1}-a_{2 n} \in\left[-\frac{1}{2^{n}}, 1-\frac{1}{2^{n}}\right]$ и $x_{2 n+1}=x_{2 n}+$ $a_{2 n+1}$, чиме је низ уложен у један од интервала $\left[0,2-\frac{1}{2^{n}}\right]$ и $\left[-\frac{1}{2^{n}}, 2-\frac{1}{2^{n-1}}\right]$.
(б) Означимо $N=3 \cdot 2^{n-1}-1$. Доказаћемо да се низ дужине $4 n-1$
$1,1-\frac{1}{N}, 1,1-\frac{2}{N}, 1,1-\frac{2^{2}}{N}, \ldots, 1,1-\frac{2^{n-1}}{N}, 1,1-\frac{2^{n-2}}{N}, 1, \ldots, 1-\frac{2}{N}, 1,1-\frac{1}{N}, 1$ не може уложити у интервал $\left(-1+\frac{1}{2 N}, 1-\frac{1}{2 N}\right)$, одакле следи твр ење.
Претпоставимо супротно. Једноставном индукцијом се доказује да је:
(i) $\left|x_{2 i}\right|<1-\frac{2^{i+1}-1}{2 N}$ и $\left|x_{2 i+1}\right|>\frac{2^{i+1}-1}{2 N}$ за $i=0, \ldots, n$;
(ii) $\left|x_{2 i}\right|<\frac{2^{2 n+2-i}-1}{2 N}$ и $\left|x_{2 i+1}\right|>1-\frac{2^{2 n+2-i}-1}{2 N}$ за $i=n+1, \ldots, 2 n+1$.
Тако за $x_{4 n+3}$ добијамо контрадикцију.
|
{
"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
b9f57707-d4b0-5397-9cee-fac7b724a4db
| 608,121
|
Convex quadrilateral $ABCD$ is circumscribed around a circle $k$. Lines $AD$ and $BC$ intersect at point $P$, and the circumcircles of $\triangle PAB$ and $\triangle PCD$ intersect at point $X$. Prove that the tangents from point $X$ to circle $k$ form equal angles with lines $AX$ and $CX$.
(Dušan Đukić)
# Ministry of Education, Science and Technological Development Mathematical Society of Serbia <br> 13th SERBIAN MATHEMATICAL OLYMPIAD FOR HIGH SCHOOL STUDENTS
## Second day
|
Since $\varangle X A D = \varangle X B C$ and $\varangle X D P = \varangle X C P$, it follows that $\triangle X A D \sim \triangle X B C$.
Let the angle bisector $s_{X}$ of $\angle A X C$ intersect the circles $P A B$ and $P C D$ at points $K$ and $R$, and the angle bisector $s_{P}$ of $\angle A P C$ intersect the circles $P A B$ and $P C D$ at points $L$ and $S$. The line $s_{P}$ passes through the center $I$ of the circle $k$ and it holds that $L A = L B = L I$ and $S C = S D = S I$.
Since $\varangle I L K = \varangle P X K = \varangle P X R = \varangle I S R$, it follows that $K L \parallel R S$. Further, we have $\varangle R X S = \varangle R X C - \varangle S P C = \frac{1}{2}(\varangle A X C - \varangle A P C) = \frac{1}{2} \varangle B X C$ and, similarly, $\varangle L X K = \frac{1}{2} \varangle B X C$. It follows that the chords $K L$ and $R S$ in the circles $P A B$ and $P C D$, as well as the chords $L B$ and $S D$, subtend equal peripheral angles, so $\frac{K L}{R S} = \frac{L B}{S D} = \frac{L I}{S I}$. It follows that $\triangle I K L \sim \triangle I R S$, so point $I$ lies on the line $K R$, which is the angle bisector of $\angle A X C$. The statement of the problem immediately follows.
Second solution. Let $U$ and $V$ be the intersections of the angle bisectors of $\angle A X D$ and $\angle B X C$ with $A D$ and $B C$, respectively. As in the first solution, $\triangle X A D \sim \triangle X B C$, so $\varangle X U P = \varangle X V P$, and points $X, P, U$, and $V$ lie on the same circle $\gamma$. We will
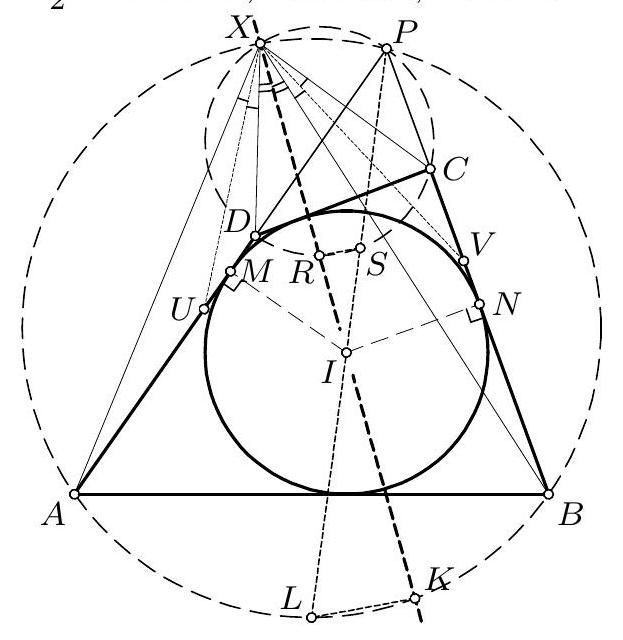
prove that point $I$ is also on this circle and that $I U = I V$. It follows that $I$ lies on the angle bisector of $\angle U X V$, which is also the angle bisector of $\angle A X C$.
Let $M$ and $N$ be the points of tangency of the circle $k$ with sides $A D$ and $B C$, respectively. Denote $A M = a, B N = b, C N = c$, and $D M = d$. Then $A B = a + b, C D = c + d$ and $A U : U D = (a + b) : (c + d)$, from which we find $A U = \frac{a + b}{a + b + c + d} \cdot A D = \frac{(a + b)(a + d)}{a + b + c + d}$; similarly, we have $B V = \frac{(b + a)(b + c)}{a + b + c + d}$. It follows that $A M - A U = B V - B N = \frac{a c - b d}{a + b + c + d}$, so $M U = N V$ and triangles $I M U$ and $I N V$ are congruent and similarly oriented. Therefore, $I U = I V$ and $\varangle U I V = \varangle M I N = 180^{\circ} - \varangle V P U$, i.e., $I$ is the midpoint of the arc $U V$ of the circle $P X U V$.
Third solution. The following statement from projective geometry is well-known.
- Desargues' Involution Theorem. A conic $\gamma$ is circumscribed around a quadrilateral $\overline{A B C D}$. A line $\ell$ intersects $A B, C D, B C, D A, A C, B D$ at points $X_{1}$, $X_{2}, Y_{1}, Y_{2}, Z_{1}, Z_{2}$, respectively, and intersects the conic $\gamma$ at $W_{1}$ and $W_{2}$. Then there exists an involution on the line $\ell$ that maps $X_{1} \leftrightarrow X_{2}, Y_{1} \leftrightarrow Y_{2}, Z_{1} \leftrightarrow Z_{2}$, and $W_{1} \leftrightarrow W_{2}$.
The dual statement (obtained by polar transformation with respect to $\gamma$) is as follows:
- A conic $\gamma$ is inscribed in a quadrilateral $A B C D$ where $A D \cap B C = \{P\}$ and $A B \cap C D = \{Q\}$. The lines $X U$ and $X V$ are tangents from an arbitrary point $X$ to $\gamma$. Then there exists an involution on the pencil of lines through $X$ that maps $X A \leftrightarrow X C, X B \leftrightarrow X D, X P \leftrightarrow X Q$, and $X U \leftrightarrow X V$.
In our case, the angles $\angle A X C, \angle B X D$, and $\angle P X Q$ have a common bisector $s$, so the mentioned involution is precisely the reflection with respect to $s$. It follows that the two tangents from $X$ to the circle (conic) $k$ are symmetric with respect to $s$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Конвексан четвороугао $A B C D$ је описан око кружнице $k$. Праве $A D$ и $B C$ се секу у тачки $P$, а кружнице описане око $\triangle P A B$ и $\triangle P C D$ се секу у тачки $X$. Доказати да тангенте из тачке $X$ на кружницу $k$ граде једнаке углове са правима $A X$ и $C X$.
(Дуиан Ђукић)
# Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 13. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
## Други дан
|
Пошто је $\varangle X A D=\varangle X B C$ и $\varangle X D P=\varangle X C P$, важи $\triangle X A D \sim \triangle X B C$.
Нека симетрала $s_{X}$ угла $A X C$ сече кругове $P A B$ и $P C D$ у тачкама $K$ и $R$, а симетрала $s_{P}$ угла $A P C$ сече кругове $P A B$ и $P C D$ у тачкама $L$ и $S$. Права $s_{P}$ пролази кроз центар $I$ круга $k$ и важи $L A=L B=L I$ и $S C=S D=S I$.
Како је $\varangle I L K=\varangle P X K=\varangle P X R=\varangle I S R$, важи $K L \| R S$. Даље, имамо $\varangle R X S=\varangle R X C-\varangle S P C=\frac{1}{2}(\varangle A X C-\varangle A P C)=\frac{1}{2} \varangle B X C$ и, слично, $\varangle L X K=$ $\frac{1}{2} \varangle B X C$. Следи да тетивама $K L$ и $R S$ у круговима $P A B$ и $P C D$, као и тетивама $L B$ и $S D$, одговарају једнаки периферијски углови, па је $\frac{K L}{R S}=\frac{L B}{S D}=\frac{L I}{S I}$. Следи да је $\triangle I K L \sim \triangle I R S$, па тачка $I$ лежи на правој $K R$, што је симетрала угла $A X C$. Тврђење задатка одмах следи.
Друго решење. Означимо са $U$ и $V$ редом пресеке симетрала углова $A X D$ и $B X C$ са $A D$ и $B C$. Као и у првом решењу, $\triangle X A D \sim$ $\triangle X B C$, одакле је $\varangle X U P=\varangle X V P$, па тачке $X, P, U$ и $V$ леже на истом кругу $\gamma$. Дока-

заћемо да је и тачка $I$ на овом кругу и да је $I U=I V$. Следиће да $I$ припада симетрали угла $U X V$, што је уједно и симетрала угла $A X C$.
Нека су $M$ и $N$ редом тачке додира круга $k$ са страницама $A D$ и $B C$. Означимо $A M=a, B N=b, C N=c$ и $D M=d$. Тада је $A B=a+b, C D=c+d$ и $A U: U D=(a+b):(c+d)$, одакле налазимо $A U=\frac{a+b}{a+b+c+d} \cdot A D=\frac{(a+b)(a+d)}{a+b+c+d}$; слично имамо $B V=\frac{(b+a)(b+c)}{a+b+c+d}$. Следи да је $A M-A U=B V-B N=\frac{a c-b d}{a+b+c+d}$, па је $M U=N V$ и троуглови $I M U$ и $I N V$ су подударни и исто оријентисани. Према томе, $I U=I V$ и $\varangle U I V=\varangle M I N=180^{\circ}-\varangle V P U$, тј. $I$ је средиште лука $U V$ круга $P X U V$.
Tреће решеъе. Познато је следеће тврђење из пројективне геометрије.
- Дезаргова теорема о инволуиији. Коника $\gamma$ је описана око четвороугла $\overline{A B C D}$. Права $\ell$ сече $A B, C D, B C, D A, A C, B D$ редом у тачкама $X_{1}$, $X_{2}, Y_{1}, Y_{2}, Z_{1}, Z_{2}$, и сече конику $\gamma$ у $W_{1}$ и $W_{2}$. Тада постоји инволуција на правој $\ell$ која слика $X_{1} \leftrightarrow X_{2}, Y_{1} \leftrightarrow Y_{2}, Z_{1} \leftrightarrow Z_{2}$ и $W_{1} \leftrightarrow W_{2}$.
Дуално тврђење (добијено поларним пресликавањем у односу на $\gamma$ ) гласи овако:
- Коника $\gamma$ је уписана у четвороугао $A B C D$ у коме је $A D \cap B C=\{P\}$ и $A B \cap C D=\{Q\}$. Праве $X U$ и $X V$ су тангенте из произвољне тачке $X$ на $\gamma$. Тада постоји инволуција на прамену правих кроз $X$ која слика $X A \leftrightarrow X C, X B \leftrightarrow X D, X P \leftrightarrow X Q$ и $X U \leftrightarrow X V$.
У нашем случају углови $A X C, B X D$ и $P X Q$ имају заједничку симетралу $s$, па је поменута инволуција управо осна симетрија у односу на $s$. Следи да су две тангенте из $X$ на круг (конику) $k$ симетричне у односу на $s$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
fdfc7a3c-cc42-58d9-a9d0-58614ae1ecec
| 608,122
|
Given is $\triangle ABC$. Let $A_1$ be the centrally symmetric image of the intersection point of the angle bisector of $\measuredangle BAC$ and side $BC$, where the center of symmetry is the midpoint of side $BC$. Similarly, we define points $B_1$ (on side $CA$) and $C_1$ (on side $AB$). The intersection of the circumcircle of $\triangle A_1 B_1 C_1$ with line $AB$ is the set $\{Z, C_1\}$, with line $BC$ is the set $\{X, A_1\}$, and with line $CA$ is the set $\{Y, B_1\}$. If the normals from points $X, Y$, and $Z$ to $BC, CA$, and $AB$, respectively, intersect at one point, prove that $\triangle ABC$ is isosceles.
(Miloš Milosavljević)
|
Let us recall that points $P$ and $Q$ inside $\triangle ABC$ are called isogonal conjugates if $\varangle PAB = \varangle QAC$ and $\varangle PBC = \varangle QBA$. Then it also holds that $\varangle PCA = \varangle QCB$.
Lemma. The feet of the perpendiculars from points $P$ and $Q$ to the lines $BC$, $CA$, and $AB$ lie on the same circle.
Proof. Let $P_a$ and $Q_a$ be the feet of the perpendiculars from $P$ and $Q$ to $BC$; similarly, denote $P_b, Q_b, P_c, Q_c$. From $\varangle AP_bP_c = \varangle APP_c = \varangle AQQ_b = \varangle AQ_cQ_b$ it follows that $\triangle AP_bP_c \sim \triangle AQ_cQ_b$, so the points $P_b, P_c, Q_b, Q_c$ lie on the same circle $k$, and its center is the intersection of the perpendicular bisectors of segments $P_bQ_b$ and $P_cQ_c$, which is precisely the midpoint $U$ of segment $PQ$. Similarly, the points $P_c, P_a, Q_c, Q_a$ are equidistant from point $U$, so $P_a$ and $Q_a$ also lie on circle $k$.
Assume that the perpendiculars from $X, Y$, and $Z$ to $BC$, $CA$, and $AB$ respectively intersect at point $P$. If point $Q$ is the isogonal conjugate of point $P$ in $\triangle ABC$, the feet of the perpendiculars from $Q$ to $BC$, $CA$, and $AB$ are, by the Lemma, precisely the points $A_1, B_1$, and $C_1$.
Let $A_0, B_0$, and $C_0$ be the intersections of the internal angle bisectors of angles at $A, B$, and $C$ with the opposite sides, respectively. As usual, let $BC = a$, $CA = b$, and $AB = c$. From the ratio $BA_0 : A_0C = c : b$ we find $BA_1 = A_0C = \frac{ab}{b+c}$ and, similarly, $A_1C = \frac{ac}{b+c}$, $CB_1 = \frac{bc}{c+a}$, $B_1A = \frac{ba}{c+a}$, $AC_1 = \frac{ca}{a+b}$, and $C_1B = \frac{cb}{a+b}$. Now we have
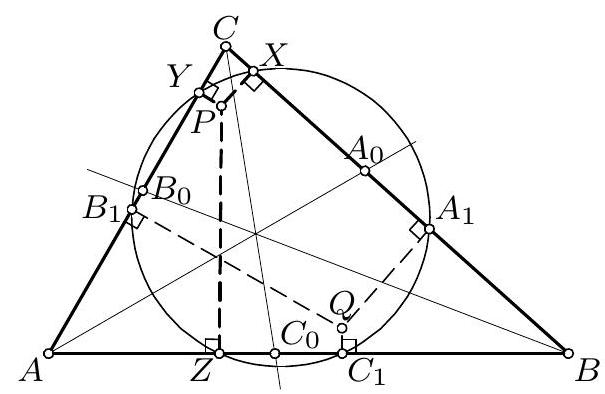
\[
\begin{aligned}
0 & = \left(BA_1^2 - A_1C^2\right) + \left(CB_1^2 - B_1A^2\right) + \left(AC_1^2 - C_1B^2\right) \\
& = \frac{a^2(b-c)}{b+c} + \frac{b^2(c-a)}{c+a} + \frac{c^2(a-b)}{a+b} \\
& = \frac{a^4(b-c) + b^4(c-a) + c^4(a-b) - (b-c)(c-a)(a-b)(ab + bc + ca)}{(b+c)(c+a)(a+b)} \\
& = -\frac{(b-c)(c-a)(a-b)(a+b+c)^2}{(b+c)(c+a)(a+b)}
\end{aligned}
\]
from which it follows that $a = b$ or $a = c$ or $b = c$.
Second Solution. As in the first solution, $BA_1 = A_0C = \frac{ab}{b+c}$, $A_1C = \frac{ac}{b+c}$, $CB_1 = \frac{bc}{c+a}$, $\overline{B_1A = \frac{ba}{c+a}}$, $AC_1 = \frac{ca}{a+b}$, and $C_1B = \frac{cb}{a+b}$. Let $BX = x$, $CY = y$, and $AZ = z$. The power of point $A$ gives $AB_1 \cdot AY = AC_1 \cdot AZ$, i.e., $\frac{by}{c+a} + \frac{cz}{a+b} = \frac{b^2}{c+a}$. Similarly, we get $\frac{cz}{a+b} + \frac{ax}{b+c} = \frac{c^2}{a+b}$ and $\frac{ax}{b+c} + \frac{by}{c+a} = \frac{a^2}{b+c}$. From this, it follows that $\frac{2ax}{b+c} = \frac{a^2}{b+c} + \frac{c^2}{a+b} - \frac{b^2}{c+a}$, which simplifies to $x = \frac{1}{2}a - \frac{(b+c)(b-c)(b^2 + c^2 + ab + ac + bc)}{2a(a+b)(a+c)}$, and so on. The condition that the three perpendiculars are concurrent is
\[
\begin{aligned}
0 & = (a+b)(a+c)(b+c)\left[x^2 - (a-x)^2 + y^2 - (b-y)^2 + z^2 - (c-z)^2\right] \\
& = (b+c)^2(c-b)\left(T - a^2\right) + (c+a)^2(a-c)\left(T - b^2\right) + (a+b)^2(b-a)\left(T - c^2\right) \\
& = a^2(b+c)^2(b-c) + b^2(c+a)^2(c-a) + c^2(a+b)^2(a-b) - (a-b)(b-c)(c-a)T \\
& = -(a-b)(b-c)(c-a)(a+b+c)^2
\end{aligned}
\]
where $T = a^2 + b^2 + c^2 + ab + bc + ca$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Дат је $\triangle A B C$. Нека је $A_{1}$ централносиметрична слика пресечне тачке симетрале $\measuredangle B A C$ и странице $B C$, где је центар симетрије средина странице $B C$. Аналогно дефинишемо тачке $B_{1}$ (на страници $C A$ ) и $C_{1}$ (на страници $A B)$. Пресек кружнице описане око $\triangle A_{1} B_{1} C_{1}$ с правом $A B$ је скуп $\left\{Z, C_{1}\right\}$, с правом $B C$ је скуп $\left\{X, A_{1}\right\}$, а с правом $C A$ је скуп $\left\{Y, B_{1}\right\}$. Ако се нормале из тачака $X, Y$ и $Z$ на $B C, C A$ и $A B$, редом, секу у једној тачки, доказати да је $\triangle A B C$ једнакокрак.
(Милош Милосављевић)
|
Подсетимо се да тачке $P$ и $Q$ унутар $\triangle A B C$ зовемо изогонално спрегнутим ако је $\varangle P A B=\varangle Q A C$ и $\varangle P B C=\varangle Q B A$. Тада такође важи $\varangle P C A=\varangle Q C B$.
Лема. Подножја нормала из тачака $P$ и $Q$ на праве $B C, C A$ и $A B$ леже на истом кругу.
Доказ. Нека су $P_{a}$ и $Q_{a}$ редом подножја нормала из $P$ и $Q$ на $B C$; аналогно означавамо $P_{b}, Q_{b}, P_{c}, Q_{c}$. Из $\varangle A P_{b} P_{c}=\varangle A P P_{c}=\varangle A Q Q_{b}=\varangle A Q_{c} Q_{b}$ следи $\triangle A P_{b} P_{c} \sim \triangle A Q_{c} Q_{b}$, па су тачке $P_{b}, P_{c}, Q_{b}, Q_{c}$ на истом кругу $k$, а његов центар је пресек симетрала дужи $P_{b} Q_{b}$ и $P_{c} Q_{c}$, што је управо средиште $U$ дужи $P Q$. Аналогно, и тачке $P_{c}, P_{a}, Q_{c}, Q_{a}$ су једнако удаљене од тачке $U$, па и $P_{a}$ и $Q_{a}$ леже на кругу $k$.
Претпоставимо да се нормале из $X, Y$ и $Z$ редом на $B C, C A$ и $A B$ секу у тачки $P$. Ако је тачка $Q$ изогонално спрегнута тачки $P$ у $\triangle A B C$, подножја нормала из $Q$ на $B C, C A$ и $A B$ су по Леми управо тачке $A_{1}, B_{1}$ и $C_{1}$.
Означимо са $A_{0}, B_{0}$ и $C_{0}$ редом пресеке унутрашњих симетрала углова код $A, B$ и $C$ с наспрамним страницама. Уобичајено, $B C=a, C A=b$ и $A B=c$. Из односа $B A_{0}$ : $A_{0} C=c: b$ налазимо $B A_{1}=A_{0} C=\frac{a b}{b+c}$ и, слично, $A_{1} C=\frac{a c}{b+c}, C B_{1}=\frac{b c}{c+a}, B_{1} A=\frac{b a}{c+a}$, $A C_{1}=\frac{c a}{a+b}$ и $C_{1} B=\frac{c b}{a+b}$. Сада имамо

$$
\begin{aligned}
0 & =\left(B A_{1}^{2}-A_{1} C^{2}\right)+\left(C B_{1}^{2}-B_{1} A^{2}\right)+\left(A C_{1}^{2}-C_{1} B^{2}\right) \\
& =\frac{a^{2}(b-c)}{b+c}+\frac{b^{2}(c-a)}{c+a}+\frac{c^{2}(a-b)}{a+b} \\
& =\frac{a^{4}(b-c)+b^{4}(c-a)+c^{4}(a-b)-(b-c)(c-a)(a-b)(a b+b c+c a)}{(b+c)(c+a)(a+b)} \\
& =-\frac{(b-c)(c-a)(a-b)(a+b+c)^{2}}{(b+c)(c+a)(a+b)}
\end{aligned}
$$
одакле следи $a=b$ или $a=c$ или $b=c$.
Друго решење. Као у првом решењу, $B A_{1}=A_{0} C=\frac{a b}{b+c}, A_{1} C=\frac{a c}{b+c}, C B_{1}=\frac{b c}{c+a}$, $\overline{B_{1} A=\frac{b a}{c+a}, A} C_{1}=\frac{c a}{a+b}$ и $C_{1} B=\frac{c b}{a+b}$. Означимо $B X=x, C Y=y$ и $A Z=z$. Потенција тачке $A$ даје $A B_{1} \cdot A Y=A C_{1} \cdot A Z$, тј. $\frac{b y}{c+a}+\frac{c z}{a+b}=\frac{b^{2}}{c+a}$. Слично добијамо $\frac{c z}{a+b}+\frac{a x}{b+c}=\frac{c^{2}}{a+b}$ и $\frac{a x}{b+c}+\frac{b y}{c+a}=\frac{a^{2}}{b+c}$. Одавде следи $\frac{2 a x}{b+c}=\frac{a^{2}}{b+c}+\frac{c^{2}}{a+b}-\frac{b^{2}}{c+a}$ што се своди на $x=\frac{1}{2} a-\frac{(b+c)(b-c)\left(b^{2}+c^{2}+a b+a c+b c\right)}{2 a(a+b)(a+c)}$, итд. Услов да су три нормале конкурентне је
$$
\begin{aligned}
0 & =(a+b)(a+c)(b+c)\left[x^{2}-(a-x)^{2}+y^{2}-(b-y)^{2}+z^{2}-(c-z)^{2}\right] \\
& =(b+c)^{2}(c-b)\left(T-a^{2}\right)+(c+a)^{2}(a-c)\left(T-b^{2}\right)+(a+b)^{2}(b-a)\left(T-c^{2}\right) \\
& =a^{2}(b+c)^{2}(b-c)+b^{2}(c+a)^{2}(c-a)+c^{2}(a+b)^{2}(a-b)-(a-b)(b-c)(c-a) T \\
& =-(a-b)(b-c)(c-a)(a+b+c)^{2}
\end{aligned}
$$
где је $T=a^{2}+b^{2}+c^{2}+a b+b c+c a$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
013c54f1-36e6-56c1-a5a7-11ce133b1653
| 608,123
|
Sequences $\left(a_{n}\right)_{n=0}^{\infty}$ and $\left(b_{n}\right)_{n=0}^{\infty}$ are defined by the recurrence relations
$$
a_{0}=0, \quad a_{1}=1, \quad a_{n+1}=\frac{2018}{n} a_{n}+a_{n-1} \quad \text { for } n \geqslant 1
$$
and
$$
b_{0}=0, \quad b_{1}=1, \quad b_{n+1}=\frac{2020}{n} b_{n}+b_{n-1} \quad \text { for } n \geqslant 1
$$
Prove:
$$
\frac{a_{1010}}{1010}=\frac{b_{1009}}{1009}
$$
(Dushan Dukic)
Time for work 270 minutes.
Solutions to the problems should be explained in detail.
Each problem is worth 7 points.
## SOLUTIONS
|
Define the sequence $\left(c_{m, n}\right)\left(m, n \in \mathbb{N}_{0}\right)$ by the conditions
$$
c_{m, 0}=0, \quad c_{m, 1}=1, \quad c_{m, n+1}=\frac{2 m}{n} c_{m, n}+c_{m, n-1} \quad \text { for } n \geqslant 1
$$
Then $a_{n}=c_{1010, n}$ and $b_{n}=c_{1009, n}$.
We observe that, for example, $c_{1, n}=n, c_{2, n}=n^{2}$ and $c_{3, n}=\frac{2 n^{3}+n}{3}$. We claim that for every $m \in \mathbb{N}$ there exists a monic polynomial $P_{m}(x)$ such that
$$
P_{m}(x+1)=\frac{2 m}{x} P_{m}(x)+P_{m}(x-1)
$$
since it is clear that $P_{m}(0)=0$, by induction it will follow that $c_{m, n}=P_{m}(n) / P_{m}(1)$.
Lemma. Define the sequence of polynomials $P_{k}$ by the conditions $P_{0}(x)=0, P_{1}(x)=x$ and
$$
P_{k+1}(x)=x P_{k}(x)+\frac{k(k-1)}{4} \cdot P_{k-1}(x)
$$
Then the polynomials $P_{k}$ satisfy (1).
Moreover, $P_{k}(x+1)-2 P_{k}(x)+P_{k}(x-1)=\frac{k(k-1)}{x} \cdot P_{k-1}(x)$.
Proof. If we denote
$$
\begin{aligned}
& A_{k}(x)=P_{k+1}(x)-x P_{k}(x)-\frac{k(k-1)}{4} P_{k-1}(x) \equiv 0 \\
& B_{k}(x)=P_{k}(x+1)-2 P_{k}(x)+P_{k}(x-1)-\frac{k(k-1)}{x} P_{k-1}(x) \\
& C_{k}(x)=P_{k}(x+1)-P_{k}(x-1)-\frac{2 k}{x} P_{k}(x)
\end{aligned}
$$
and assume that $B_{i}(x) \equiv C_{i}(x) \equiv 0$ for all $i \leqslant k$, then
$$
\begin{aligned}
& B_{k+1}(x)-x B_{k}(x)-\frac{k(k-1)}{4} B_{k-1}(x)= \\
& C_{k}(x)+A_{k}(x+1)+A_{k}(x-1)-2 A_{k}(x)-\frac{k(k-1)}{x} A_{k-1}(x)=0
\end{aligned}
$$
so $B_{k+1} \equiv 0$. On the other hand,
$$
\begin{aligned}
& C_{k+1}(x)-x C_{k}(x)-\frac{k(k-1)}{4} C_{k-1}(x)= \\
& B_{k}(x)+A_{k}(x+1)-A_{k}(x-1)-\frac{2(k+1)}{x} A_{k}(x)=0
\end{aligned}
$$
so $C_{k+1} \equiv 0$.
From (2) it follows that the polynomials $Q_{0}(x)=0$ and $Q_{k}(x)=\frac{2^{k-1}}{(k-1)!} P_{k}(x)$ satisfy the relation $Q_{k+1}(x)=\frac{2 x}{k} Q_{k}(x)+Q_{k-1}(x)$, so by induction we get $Q_{k}(x)=x c_{x, k}$ for all $x \in \mathbb{N}$. Hence $P_{k}(x)=\frac{(k-1)!}{2^{k-1}} \cdot x c_{x, k}$ and
$$
\frac{c_{m, n}}{n}=\frac{1}{n} \cdot \frac{P_{m}(n)}{P_{m}(1)}=\frac{c_{n, m}}{c_{1, m}}=\frac{c_{n, m}}{m}
$$
The statement of the problem is obtained for $m=1010$ and $n=1009$.
Second solution. For a given $m \geqslant 0$ consider the generating function of the sequence $c_{m, n}$ given by the conditions $(*)$ :
$$
f_{m}(x)=\frac{1}{2 m}+\sum_{n=1}^{\infty} \frac{c_{m, n}}{n} x^{n}
$$
From the recurrence relation $(*)$ it follows that the function $f_{m}$ satisfies the differential equation $\left(1-x^{2}\right) f_{m}^{\prime}(x)=2 m \cdot f_{m}(x)$. This equation is easily solved: if we write it as $\frac{f_{m}^{\prime}(x)}{f_{m}(x)}=\frac{2 m}{1-x^{2}}$, integration with respect to $x$ gives $\ln \left|f_{m}(x)\right|=\int \frac{2 m}{1-x^{2}} d x=$
$m \ln \frac{1+x}{1-x}+$ const, i.e., $f_{m}(x)=C \cdot\left(\frac{1+x}{1-x}\right)^{m}$. The condition $f_{m}(0)=\frac{1}{2 m}$ finally gives $C=1$, so
$$
\begin{aligned}
f_{m}(x) & =\frac{1}{2 m}\left(\frac{1+x}{1-x}\right)^{m}=\frac{1}{2 m}(1+x)^{m}(1-x)^{-m}= \\
& =\frac{1}{2 m} \sum_{i=0}^{m}\binom{m}{i} x^{i} \cdot \sum_{j=1}^{\infty}\binom{m-1+j}{m-1} x^{j}
\end{aligned}
$$
The coefficient of $x^{n}$ is
$$
\frac{c_{m, n}}{n}=\frac{1}{2 m} \sum_{i=0}^{m}\binom{m}{i}\binom{m+n-1-i}{m-1}=\frac{1}{2} \sum_{i} \frac{(m+n-1-i)!}{i!(m-i)!(n-i)!}
$$
This expression is symmetric in $m$ and $n$, so $\frac{c_{m, n}}{n}=\frac{c_{n, m}}{m}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Низови $\left(a_{n}\right)_{n=0}^{\infty}$ и $\left(b_{n}\right)_{n=0}^{\infty}$ дефинисани су рекурентним релацијама
$$
a_{0}=0, \quad a_{1}=1, \quad a_{n+1}=\frac{2018}{n} a_{n}+a_{n-1} \quad \text { за } n \geqslant 1
$$
и
$$
b_{0}=0, \quad b_{1}=1, \quad b_{n+1}=\frac{2020}{n} b_{n}+b_{n-1} \quad \text { за } n \geqslant 1
$$
Доказати:
$$
\frac{a_{1010}}{1010}=\frac{b_{1009}}{1009}
$$
(Душан Ђукић)
Време за рад 270 минута.
Решења задатака детаљно образложити.
Сваки задатак вреди 7 бодова.
## РЕШЕЊА
|
Дефинишимо низ $\left(c_{m, n}\right)\left(m, n \in \mathbb{N}_{0}\right)$ условима
$$
c_{m, 0}=0, \quad c_{m, 1}=1, \quad c_{m, n+1}=\frac{2 m}{n} c_{m, n}+c_{m, n-1} \quad \text { за } n \geqslant 1
$$
Тада је $a_{n}=c_{1010, n}$ и $b_{n}=c_{1009, n}$.
Видимо да је нпр. $c_{1, n}=n, c_{2, n}=n^{2}$ и $c_{3, n}=\frac{2 n^{3}+n}{3}$. Тврдимо да за свако $m \in \mathbb{N}$ постоји моничан полином $P_{m}(x)$ такав да је
$$
P_{m}(x+1)=\frac{2 m}{x} P_{m}(x)+P_{m}(x-1)
$$
пошто је очигледно $P_{m}(0)=0$, индукцијом ће следити $c_{m, n}=P_{m}(n) / P_{m}(1)$.
Лема. Дефинишимо низ полинома $P_{k}$ условима $P_{0}(x)=0, P_{1}(x)=x$ и
$$
P_{k+1}(x)=x P_{k}(x)+\frac{k(k-1)}{4} \cdot P_{k-1}(x)
$$
Тада полиноми $P_{k}$ задовољавају (1).
Шта више, важи $P_{k}(x+1)-2 P_{k}(x)+P_{k}(x-1)=\frac{k(k-1)}{x} \cdot P_{k-1}(x)$.
Доказ. Ако означимо
$$
\begin{aligned}
& A_{k}(x)=P_{k+1}(x)-x P_{k}(x)-\frac{k(k-1)}{4} P_{k-1}(x) \equiv 0 \\
& B_{k}(x)=P_{k}(x+1)-2 P_{k}(x)+P_{k}(x-1)-\frac{k(k-1)}{x} P_{k-1}(x) \\
& C_{k}(x)=P_{k}(x+1)-P_{k}(x-1)-\frac{2 k}{x} P_{k}(x)
\end{aligned}
$$
и претпоставимо да је $B_{i}(x) \equiv C_{i}(x) \equiv 0$ за све $i \leqslant k$, тада је
$$
\begin{aligned}
& B_{k+1}(x)-x B_{k}(x)-\frac{k(k-1)}{4} B_{k-1}(x)= \\
& C_{k}(x)+A_{k}(x+1)+A_{k}(x-1)-2 A_{k}(x)-\frac{k(k-1)}{x} A_{k-1}(x)=0
\end{aligned}
$$
па је $B_{k+1} \equiv 0$. С друге стране,
$$
\begin{aligned}
& C_{k+1}(x)-x C_{k}(x)-\frac{k(k-1)}{4} C_{k-1}(x)= \\
& B_{k}(x)+A_{k}(x+1)-A_{k}(x-1)-\frac{2(k+1)}{x} A_{k}(x)=0
\end{aligned}
$$
па је и $C_{k+1} \equiv 0$.
Из (2) следи да полиноми $Q_{0}(x)=0$ и $Q_{k}(x)=\frac{2^{k-1}}{(k-1)!} P_{k}(x)$ задовољавају везу $Q_{k+1}(x)=\frac{2 x}{k} Q_{k}(x)+Q_{k-1}(x)$, па индукцијом добијамо $Q_{k}(x)=x c_{x, k}$ за све $x \in \mathbb{N}$. Одавде је $P_{k}(x)=\frac{(k-1)!}{2^{k-1}} \cdot x c_{x, k}$ и
$$
\frac{c_{m, n}}{n}=\frac{1}{n} \cdot \frac{P_{m}(n)}{P_{m}(1)}=\frac{c_{n, m}}{c_{1, m}}=\frac{c_{n, m}}{m}
$$
Тврђење задатка се добија за $m=1010$ и $n=1009$.
Друго решење. За дато $m \geqslant 0$ посматрајмо генераторску функцију низа $c_{m, n}$ датог условима $(*)$ :
$$
f_{m}(x)=\frac{1}{2 m}+\sum_{n=1}^{\infty} \frac{c_{m, n}}{n} x^{n}
$$
Из рекурентне везе $(*)$ следи да функција $f_{m}$ задовољава диференцијалну једначину $\left(1-x^{2}\right) f_{m}^{\prime}(x)=2 m \cdot f_{m}(x)$. Ова једначина се лако решава: ако је запишемо као $\frac{f_{m}^{\prime}(x)}{f_{m}(x)}=\frac{2 m}{1-x^{2}}$, интеграција по $x$ даје $\ln \left|f_{m}(x)\right|=\int \frac{2 m}{1-x^{2}} d x=$
$m \ln \frac{1+x}{1-x}+$ const, тј. $f_{m}(x)=C \cdot\left(\frac{1+x}{1-x}\right)^{m}$. Услов $f_{m}(0)=\frac{1}{2 m}$ најзад даје $C=1$, те је
$$
\begin{aligned}
f_{m}(x) & =\frac{1}{2 m}\left(\frac{1+x}{1-x}\right)^{m}=\frac{1}{2 m}(1+x)^{m}(1-x)^{-m}= \\
& =\frac{1}{2 m} \sum_{i=0}^{m}\binom{m}{i} x^{i} \cdot \sum_{j=1}^{\infty}\binom{m-1+j}{m-1} x^{j}
\end{aligned}
$$
Коефицијент уз $x^{n}$ је
$$
\frac{c_{m, n}}{n}=\frac{1}{2 m} \sum_{i=0}^{m}\binom{m}{i}\binom{m+n-1-i}{m-1}=\frac{1}{2} \sum_{i} \frac{(m+n-1-i)!}{i!(m-i)!(n-i)!}
$$
Овај израз је симетричан по $m$ и $n$, па је $\frac{c_{m, n}}{n}=\frac{c_{n, m}}{m}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2019_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
c79ca003-a393-58a3-a754-d1e66ac1df55
| 608,125
|
There is a convex polyhedron with at least 5 vertices, in each of which exactly three edges meet. Prove that it is possible to assign a rational number to each vertex of this polyhedron so that the following conditions are satisfied:
(i) at least one of the assigned numbers is equal to 2020;
(ii) for each face of the polyhedron, the product of the numbers at all vertices of that face is equal to 1.
(Bojan Bajic with collaborators)
|
Let $c=$ 2020. First, consider the case when there is a face $\mathcal{F}$ with an even number of vertices. Then it is sufficient to assign the numbers $c$ and $\frac{1}{c}$ alternately to the vertices of the face $\mathcal{F}$, and the number 1 to all other vertices of the polyhedron. Indeed, the product of the numbers on the face $\mathcal{F}$ is equal to 1, and every other face either shares an edge with the face $\mathcal{F}$ (where the product is 1) or has no
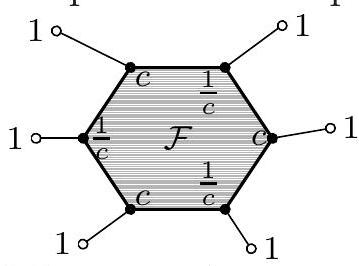
common vertex with $\mathcal{F}$ (then all numbers on it are ones).
Next, we assume that all faces have an odd number of vertices. Consider two disjoint faces of the polyhedron $\mathcal{F}_{A}$ and $\mathcal{F}_{B}$ and vertices $A$ and $B$ on them, respectively, such that $A B$ is an edge of the polyhedron. We will assign the numbers $c$ and $\frac{1}{c}$ alternately to the vertices of these two faces, except for $A$ and $B$, as shown in the figure, and the number 1 to all other vertices of the polyhedron. In this case, it is easy to see that the condition of the problem is satisfied.
Finally, let us ensure that such faces $\mathcal{F}_{A}$ and $\mathcal{F}_{B}$ can always be found. There is a face $\mathcal{F}$ that is not a triangle (otherwise, the given polyhedron would be a tetrahedron). Consider four
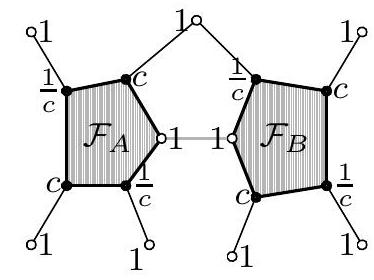
consecutive adjacent faces $\mathcal{F}_{1}, \mathcal{F}_{2}, \mathcal{F}_{3}$, and $\mathcal{F}_{4}$. If the faces $\mathcal{F}_{1}$ and $\mathcal{F}_{3}$ are disjoint, take them, and if they are not, then they share an entire edge, and the three faces $\mathcal{F}_{1}, \mathcal{F}_{3}$, and $\mathcal{F}$ form a belt that separates $\mathcal{F}_{2}$ from $\mathcal{F}_{4}$, so in this case, we can take $\mathcal{F}_{2}$ and $\mathcal{F}_{4}$.
It seems reasonable to set up a system of linear equations in the logarithms of the assigned numbers, as it has more equations than unknowns, which guarantees the existence of a non-trivial integer solution. However, for the assigned numbers to be rational, one of the variables in this solution must be equal to $\pm 1$, which is not clear why it can be achieved.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Дат је конвексан полиедар са бар 5 темена у чијем се сваком темену састају тачно по три ивице. Доказати да је могуће доделити сваком темену тог полиедра неки рационалан број тако да буду задовољени следећи услови:
(i) бар један од додељених бројева је једнак 2020;
(ii) за сваку страну полиедра, производ бројева у свим теменима те стране је једнак 1 .
(Бојан Баиић са сараднииима)
|
Означимо $c=$ 2020. Прво размотримо случај када постоји страна $\mathcal{F}$ са парним бројем темена. Тада је довољно доделити теменима стране $\mathcal{F}$ наизменично бројеве $c$ и $\frac{1}{c}$, а свим осталим теменима полиедра број 1. Заиста, производ бројева на страни $\mathcal{F}$ је једнак 1 , а свака друга страна или дели ивицу са страном $\mathcal{F}$ (а на њој је производ 1) или нема

ниједно заједничко теме са $\mathcal{F}$ (тада су сви бројеви на њој јединице).
Надаље сматрамо да све стране имају непаран број темена. Посматрајмо две дисјунктне стране полиедра $\mathcal{F}_{A}$ и $\mathcal{F}_{B}$ и темена $A$ и $B$ на њима, редом, тако да је $A B$ ивица полиедра. Теменима ових двеју страна, изузев $A$ и $B$, доделићемо наизменично бројеве $c$ и $\frac{1}{c}$ као на слици, а свим осталим теменима полиедра број 1. И у овом случају се лако види да је услов задатка испуњен.
Најзад, уверимо се да се овакве стране $\mathcal{F}_{A}$ и $\mathcal{F}_{B}$ увек могу наћи. Постоји страна $\mathcal{F}$ која није троугао (иначе би дати полиедар био тетраедар). Посматрајмо чети-

ри узастопне њој суседне стране $\mathcal{F}_{1}, \mathcal{F}_{2}, \mathcal{F}_{3}$ и $\mathcal{F}_{4}$. Ако су стране $\mathcal{F}_{1}$ и $\mathcal{F}_{3}$ дисјунктне, узмимо њих, а ако нису, онда оне имају заједничку целу ивицу, па три стране $\mathcal{F}_{1}, \mathcal{F}_{3}$ и $\mathcal{F}$ чине појас који раздваја $\mathcal{F}_{2}$ од $\mathcal{F}_{4}$, те у том случају можемо узети $\mathcal{F}_{2}$ и $\mathcal{F}_{4}$.
Найомена. Делује примамљиво поставити систем линеарних једначина по логаритмима уписаних бројева, јер он има више једначина него непознатих, што гарантује постојање нетривијалног целобројног решења. Ипак, да би уписани бројеви били рационални, једна од променљивих у том решењу мора бити једнака $\pm 1$, што није јасно зашто се може постићи.
|
{
"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
fd9093c8-dbd7-533e-a112-6a246b080454
| 608,127
|
In the trapezoid $ABCD$ whose interior angles are not right angles, the diagonals $AC$ and $BD$ intersect at point $E$. Let $P$ and $Q$ be the feet of the perpendiculars from vertex $A$ and $B$ to the lines $BC$ and $AD$, respectively. The circumcircles of triangles $CEQ$ and $DEP$ intersect at point $F \neq E$. Prove that the lines $AP$, $BQ$, and $EF$ either intersect at one point or are parallel.
(Dusan Dukic)
|
The case when $A D \| B C$ is simple. Indeed, then $E$ is the midpoint of the diagonal $A C$, so $E A=E C=E P$, and similarly $E B=E D=E Q$. From this it follows that the circles $C E Q$ and $D E P$ are symmetric with respect to the perpendicular bisector of segments $C P$ and $D Q$, so $E F \perp C P$, i.e., $E F\|A P\| B Q$.
Let $O$ be the intersection point of the lines $A D$ and $B C$. Triangles $O A P$ and $O B Q$ are similar, so $\frac{O P}{O Q}=\frac{O A}{O B}=\frac{O D}{O C}$, i.e., $O C \cdot O P=O D \cdot O Q$, from which it follows that the points $C, D, P$ and $Q$ lie on some circle $\gamma$.
Let the lines $A P$ and $B Q$ intersect at point $H$, and the lines $D P$ and $C Q$ at point $G$. Since $G C \cdot G Q=G D \cdot G P$, point $G$ has equal power with respect to the circles $C E Q$ and $D E P$, so it lies on their radical axis $E F$. On the other hand, points $E, G$ and $H$ are collinear on
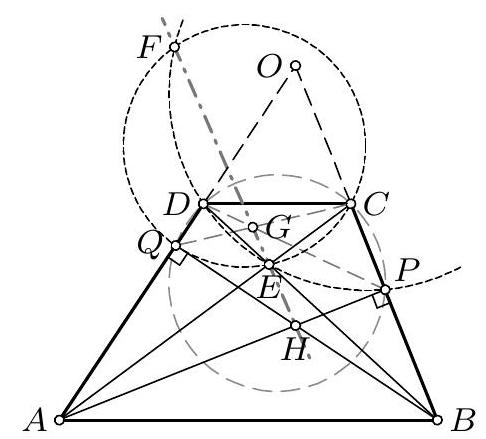
the basis of Pappus's theorem for the sets of points $B, C, P$ and $A, D, Q$. It follows that all four points $H, E, G$ and $F$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
У трапезу $A B C D$ чији унутрашњи углови нису прави, дијагонале $A C$ и $B D$ секу се у тачки $E$. Нека су $P$ и $Q$ редом подножја нормала из темена $A$ и $B$ на праве $B C$ и $A D$. Описане кружнице троуглова $C E Q$ и $D E P$ секу се у тачки $F \neq E$. Доказати да се праве $A P, B Q$ и $E F$ секу у једној тачки или су паралелне.
(Душан Ђукић)
|
Случај када је $A D \| B C$ је једноставан. Наиме, тада је $E$ средиште дијагонале $A C$, те је $E A=E C=E P$, а слично важи и $E B=E D=E Q$. Одатле следи да су кругови $C E Q$ и $D E P$ симетрични у односу на симетралу дужи $C P$ и $D Q$, те је $E F \perp C P$, тј. $E F\|A P\| B Q$.
Означимо са $O$ тачку пресека правих $A D$ и $B C$. Троуглови $O A P$ и $O B Q$ су
слични, па је $\frac{O P}{O Q}=\frac{O A}{O B}=\frac{O D}{O C}$, тј. $O C \cdot O P=O D \cdot O Q$, одакле следи да тачке $C, D, P$ и $Q$ леже на неком кругу $\gamma$.
Нека се праве $A P$ и $B Q$ секу у тачки $H$, а праве $D P$ и $C Q$ у тачки $G$. Како је $G C \cdot G Q=G D \cdot G P$, тачка $G$ има једнаку потенцију у односу на кругове $C E Q$ и $D E P$, па она лежи на њиховој радикалној оси $E F$. С друге стране, тачке $E, G$ и $H$ су колинеарне на

основу Папосове теореме за тројке тачака $B, C, P$ и $A, D, Q$. Следи да су све четири тачке $H, E, G$ и $F$ колинеарне.
|
{
"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
1a2cc065-6ae5-5f2d-b66a-67bc1d6b6c38
| 608,129
|
For a natural number $n$, we denote by $v_{2}(n)$ the largest integer $k \geqslant 0$ such that $2^{k} \mid n$. Suppose the function $f: \mathbb{N} \rightarrow \mathbb{N}$ satisfies the conditions:
(i) $f(x) \leqslant 3 x$ for all $x \in \mathbb{N}$;
(ii) $v_{2}(f(x)+f(y))=v_{2}(x+y)$ for all $x, y \in \mathbb{N}$.
Prove that for every natural number $a$ there exists a unique natural number $x$ such that $f(x)=3 a$.
(Dušan Đukić)
|
By setting $x=y$ we get $v_{2}(f(x))=v_{2}(x)$. If $v_{2}(a)=k>0$, by considering the function $g(x)=f\left(2^{k} x\right) / 2^{k}$, the statement reduces to the case of odd $a$. Therefore, we further assume that $2 \nmid a$.
Notice that if $x \not \equiv y\left(\bmod 2^{k}\right)$, then $f(x) \not \equiv f(y)\left(\bmod 2^{k}\right)$. Indeed, if $z \equiv-x\left(\bmod 2^{k}\right)$, then $2^{k} \nmid z+y$, so $f(y) \not \equiv-f(z) \equiv f(x)\left(\bmod 2^{k}\right)$. From this, it also follows that the function $f$ is injective.
Let $2^{k-1}<3 a<2^{k}$, where $k \in \mathbb{N}$. Since $f(1), f(3), \ldots, f\left(2^{k}-1\right)$ are distinct modulo $2^{k}$, there exists an odd number $x<2^{k}$ such that $f(x) \equiv 3 a$ $\left(\bmod 2^{k}\right)$. Assume that $f(x) \neq 3 a$. Then $f(x)>2^{k}$, so from $f(x)+$ $f\left(2^{k}-x\right) \equiv 2^{k}\left(\bmod 2^{k+1}\right)$ it follows that $f(x)+f\left(2^{k}-x\right) \geqslant 3 \cdot 2^{k}$. On the other hand, $f(x)+f\left(2^{k}-x\right) \leqslant 3\left(x+\left(2^{k}-x\right)\right)=3 \cdot 2^{k}$, so this is possible only if $f(x)=3 x$. Hence, $x \equiv a\left(\bmod 2^{k}\right)$, so $x=a$, i.e., $f(x)=3 a$ again.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
За природан број $n$, са $v_{2}(n)$ означавамо највећи цео број $k \geqslant 0$ такав да $2^{k} \mid n$. Претпоставимо да функција $f: \mathbb{N} \rightarrow \mathbb{N}$ задовољава услове:
(i) $f(x) \leqslant 3 x$ за све $x \in \mathbb{N}$;
(ii) $v_{2}(f(x)+f(y))=v_{2}(x+y)$ за све $x, y \in \mathbb{N}$.
Доказати да за сваки природан број $a$ постоји тачно један природан број $x$ такав да је $f(x)=3 a$.
(Душан Ђукић)
|
Заменом $x=y$ добијамо $v_{2}(f(x))=v_{2}(x)$. Ако је $v_{2}(a)=k>0$, посматрањем функције $g(x)=f\left(2^{k} x\right) / 2^{k}$ тврђење сводимо на случај непарног $a$. Зато надаље сматрамо да $2 \nmid a$.
Приметимо да, ако је $x \not \equiv y\left(\bmod 2^{k}\right)$, онда је $f(x) \not \equiv f(y)\left(\bmod 2^{k}\right)$. Заиста, ако је $z \equiv-x\left(\bmod 2^{k}\right)$, онда $2^{k} \nmid z+y$, па је $f(y) \not \equiv-f(z) \equiv f(x)\left(\bmod 2^{k}\right)$. Одавде такође следи да је функција $f$ инјективна.
Нека је $2^{k-1}<3 a<2^{k}$, где је $k \in \mathbb{N}$. Како су $f(1), f(3), \ldots, f\left(2^{k}-1\right)$ међусобно различити по модулу $2^{k}$, постоји непаран број $x<2^{k}$ такав да је $f(x) \equiv 3 a$ $\left(\bmod 2^{k}\right)$. Претпоставимо да је $f(x) \neq 3 a$. Тада је $f(x)>2^{k}$, па из $f(x)+$ $f\left(2^{k}-x\right) \equiv 2^{k}\left(\bmod 2^{k+1}\right)$ следи да је $f(x)+f\left(2^{k}-x\right) \geqslant 3 \cdot 2^{k}$. Међутим, с друге стране је $f(x)+f\left(2^{k}-x\right) \leqslant 3\left(x+\left(2^{k}-x\right)\right)=3 \cdot 2^{k}$, па је то могуће једино ако је $f(x)=3 x$. Одавде је $x \equiv a\left(\bmod 2^{k}\right)$, па је $x=a$, тј. опет је $f(x)=3 a$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2020_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
71ae7ada-967f-53c2-b310-b6b50ad4dc56
| 608,130
|
Let $A X Y Z B$ be a convex pentagon inscribed in a semicircle of diameter $A B$. Denote by $P, Q, R, S$ the feet of the perpendiculars from $Y$ onto lines $A X, B X$, $A Z, B Z$, respectively. Prove that the acute angle formed by lines $P Q$ and $R S$ is half the size of $\angle X O Z$, where $O$ is the midpoint of segment $A B$.
|
【 First approach using angle chasing. Define $T=\overline{P Q} \cap \overline{R S}$. Also, let $2 \alpha, 2 \beta, 2 \gamma, 2 \delta$ denote the measures of arcs $\overparen{A X}, \widehat{X Y}, \widehat{Y Z}, \widehat{Z B}$, respectively, so that $\alpha+\beta+\gamma+\delta=90^{\circ}$. 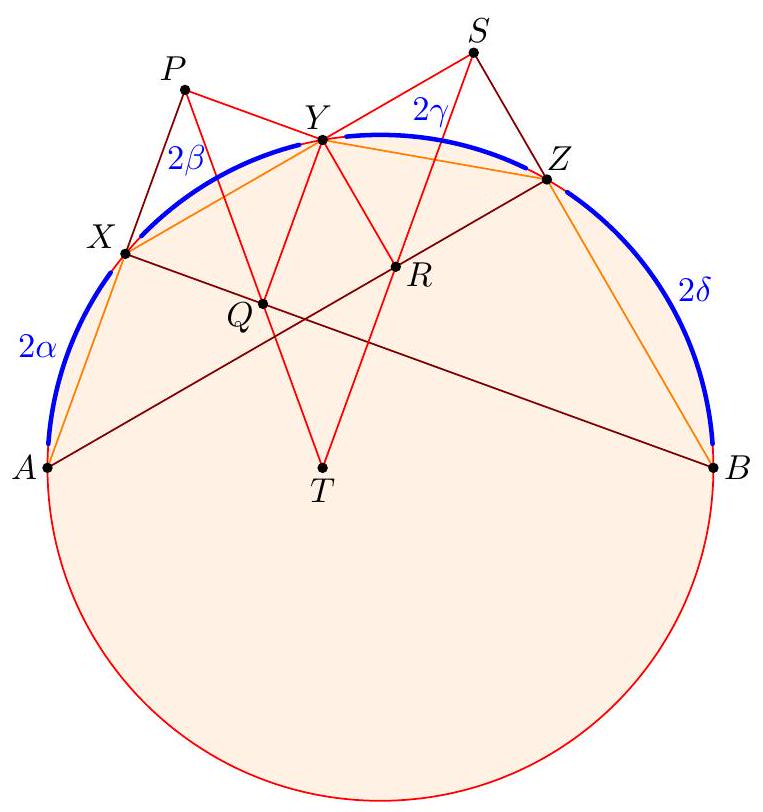 We now compute the following angles: $$ \begin{aligned} & \angle S R Y=\angle S Z Y=90^{\circ}-\angle Y Z A=90^{\circ}-(\alpha+\beta) \\ & \angle Y Q P=\angle Y X P=90^{\circ}-\angle B X Y=90^{\circ}-(\gamma+\delta) \\ & \angle Q Y R=180^{\circ}-\angle(\overline{Z R}, \overline{Q X})=180^{\circ}-\frac{2 \beta+2 \gamma+180^{\circ}}{2}=90^{\circ}-(\beta+\gamma) \end{aligned} $$ Hence, we can then compute $$ \begin{aligned} \angle R T Q & =360^{\circ}-\left(\angle Q Y R+\left(180^{\circ}-\angle S R Y\right)+\left(180^{\circ}-\angle Y Q P\right)\right) \\ & =\angle S R Y+\angle Y Q P-\angle Q Y R \\ & =\left(90^{\circ}-(\alpha+\beta)\right)+\left(90^{\circ}-(\gamma+\delta)\right)-\left(90^{\circ}-(\beta+\gamma)\right) \end{aligned} $$ $$ \begin{aligned} & =90^{\circ}-(\alpha+\delta) \\ & =\beta+\gamma \end{aligned} $$ Since $\angle X O Z=\frac{2 \beta+2 \gamma}{2}=\beta+\gamma$, the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A X Y Z B$ be a convex pentagon inscribed in a semicircle of diameter $A B$. Denote by $P, Q, R, S$ the feet of the perpendiculars from $Y$ onto lines $A X, B X$, $A Z, B Z$, respectively. Prove that the acute angle formed by lines $P Q$ and $R S$ is half the size of $\angle X O Z$, where $O$ is the midpoint of segment $A B$.
|
【 First approach using angle chasing. Define $T=\overline{P Q} \cap \overline{R S}$. Also, let $2 \alpha, 2 \beta, 2 \gamma, 2 \delta$ denote the measures of arcs $\overparen{A X}, \widehat{X Y}, \widehat{Y Z}, \widehat{Z B}$, respectively, so that $\alpha+\beta+\gamma+\delta=90^{\circ}$.  We now compute the following angles: $$ \begin{aligned} & \angle S R Y=\angle S Z Y=90^{\circ}-\angle Y Z A=90^{\circ}-(\alpha+\beta) \\ & \angle Y Q P=\angle Y X P=90^{\circ}-\angle B X Y=90^{\circ}-(\gamma+\delta) \\ & \angle Q Y R=180^{\circ}-\angle(\overline{Z R}, \overline{Q X})=180^{\circ}-\frac{2 \beta+2 \gamma+180^{\circ}}{2}=90^{\circ}-(\beta+\gamma) \end{aligned} $$ Hence, we can then compute $$ \begin{aligned} \angle R T Q & =360^{\circ}-\left(\angle Q Y R+\left(180^{\circ}-\angle S R Y\right)+\left(180^{\circ}-\angle Y Q P\right)\right) \\ & =\angle S R Y+\angle Y Q P-\angle Q Y R \\ & =\left(90^{\circ}-(\alpha+\beta)\right)+\left(90^{\circ}-(\gamma+\delta)\right)-\left(90^{\circ}-(\beta+\gamma)\right) \end{aligned} $$ $$ \begin{aligned} & =90^{\circ}-(\alpha+\delta) \\ & =\beta+\gamma \end{aligned} $$ Since $\angle X O Z=\frac{2 \beta+2 \gamma}{2}=\beta+\gamma$, the proof is complete.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d69d980d-bcac-5f57-9853-fb19401e1981
| 604,227
|
Let $A X Y Z B$ be a convex pentagon inscribed in a semicircle of diameter $A B$. Denote by $P, Q, R, S$ the feet of the perpendiculars from $Y$ onto lines $A X, B X$, $A Z, B Z$, respectively. Prove that the acute angle formed by lines $P Q$ and $R S$ is half the size of $\angle X O Z$, where $O$ is the midpoint of segment $A B$.
|
【 Second approach using Simson lines, ignoring the diameter condition. In this solution, we will ignore the condition that $\overline{A B}$ is a diameter; the solution works equally well without it, as long as $O$ is redefined as the center of $(A X Y Z B)$ instead. We will again show the angle formed by lines $P Q$ and $R S$ is half the measure of $\widehat{X Z}$. 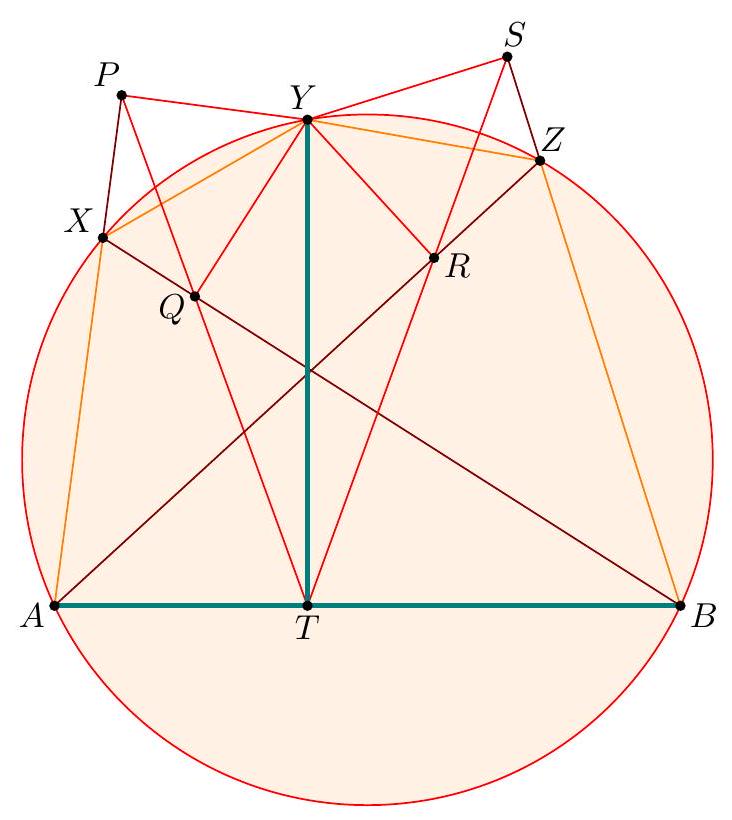 Now it's straightforward to see $A P Y R T$ is cyclic (in the circle with diameter $\overline{A Y}$ ), and therefore $$ \angle R T Y=\angle R A Y=\angle Z A Y $$ Similarly, $$ \angle Y T Q=\angle Y B Q=\angle Y B X $$ Summing these gives $\angle R T Q$ is equal to half the measure of arc $\widehat{X Z}$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A X Y Z B$ be a convex pentagon inscribed in a semicircle of diameter $A B$. Denote by $P, Q, R, S$ the feet of the perpendiculars from $Y$ onto lines $A X, B X$, $A Z, B Z$, respectively. Prove that the acute angle formed by lines $P Q$ and $R S$ is half the size of $\angle X O Z$, where $O$ is the midpoint of segment $A B$.
|
【 Second approach using Simson lines, ignoring the diameter condition. In this solution, we will ignore the condition that $\overline{A B}$ is a diameter; the solution works equally well without it, as long as $O$ is redefined as the center of $(A X Y Z B)$ instead. We will again show the angle formed by lines $P Q$ and $R S$ is half the measure of $\widehat{X Z}$.  Now it's straightforward to see $A P Y R T$ is cyclic (in the circle with diameter $\overline{A Y}$ ), and therefore $$ \angle R T Y=\angle R A Y=\angle Z A Y $$ Similarly, $$ \angle Y T Q=\angle Y B Q=\angle Y B X $$ Summing these gives $\angle R T Q$ is equal to half the measure of arc $\widehat{X Z}$ as needed.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d69d980d-bcac-5f57-9853-fb19401e1981
| 604,227
|
A triangle is called a parabolic triangle if its vertices lie on a parabola $y=x^{2}$. Prove that for every nonnegative integer $n$, there is an odd number $m$ and a parabolic triangle with vertices at three distinct points with integer coordinates with area $\left(2^{n} m\right)^{2}$ 。
|
A triangle is called a parabolic triangle if its vertices lie on a parabola $y=x^{2}$. Prove that for every nonnegative integer $n$, there is an odd number $m$ and a parabolic triangle with vertices at three distinct points with integer coordinates with area $\left(2^{n} m\right)^{2}$. For $n=0$, take instead $(a, b)=(1,0)$. For $n>0$, consider a triangle with vertices at $\left(a, a^{2}\right),\left(-a, a^{2}\right)$ and $\left(b, b^{2}\right)$. Then the area of this triangle was equal to $$ \frac{1}{2}(2 a)\left(b^{2}-a^{2}\right)=a\left(b^{2}-a^{2}\right) . $$ To make this equal $2^{2 n} m^{2}$, simply pick $a=2^{2 n}$, and then pick $b$ such that $b^{2}-m^{2}=2^{4 n}$, for example $m=2^{4 n-2}-1$ and $b=2^{4 n-2}+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A triangle is called a parabolic triangle if its vertices lie on a parabola $y=x^{2}$. Prove that for every nonnegative integer $n$, there is an odd number $m$ and a parabolic triangle with vertices at three distinct points with integer coordinates with area $\left(2^{n} m\right)^{2}$ 。
|
A triangle is called a parabolic triangle if its vertices lie on a parabola $y=x^{2}$. Prove that for every nonnegative integer $n$, there is an odd number $m$ and a parabolic triangle with vertices at three distinct points with integer coordinates with area $\left(2^{n} m\right)^{2}$. For $n=0$, take instead $(a, b)=(1,0)$. For $n>0$, consider a triangle with vertices at $\left(a, a^{2}\right),\left(-a, a^{2}\right)$ and $\left(b, b^{2}\right)$. Then the area of this triangle was equal to $$ \frac{1}{2}(2 a)\left(b^{2}-a^{2}\right)=a\left(b^{2}-a^{2}\right) . $$ To make this equal $2^{2 n} m^{2}$, simply pick $a=2^{2 n}$, and then pick $b$ such that $b^{2}-m^{2}=2^{4 n}$, for example $m=2^{4 n-2}-1$ and $b=2^{4 n-2}+1$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
2cd606e3-0045-54be-bd71-2f451c042970
| 245,576
|
Two permutations $a_{1}, a_{2}, \ldots, a_{2010}$ and $b_{1}, b_{2}, \ldots, b_{2010}$ of the numbers $1,2, \ldots, 2010$ are said to intersect if $a_{k}=b_{k}$ for some value of $k$ in the range $1 \leq k \leq 2010$. Show that there exist 1006 permutations of the numbers $1,2, \ldots, 2010$ such that any other such permutation is guaranteed to intersect at least one of these 1006 permutations.
|
A valid choice is the following 1006 permutations: | 1 | 2 | 3 | $\cdots$ | 1004 | 1005 | 1006 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 2 | 3 | 4 | $\cdots$ | 1005 | 1006 | 1 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | 3 | 4 | 5 | $\cdots$ | 1006 | 1 | 2 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | | 1004 | 1005 | 1006 | $\cdots$ | 1001 | 1002 | 1003 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | 1005 | 1006 | 1 | $\cdots$ | 1002 | 1003 | 1004 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | 1006 | 1 | 2 | $\cdots$ | 1003 | 1004 | 1005 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | This works. Indeed, any permutation should have one of $\{1,2, \ldots, 1006\}$ somewhere in the first 1006 positions, so one will get an intersection. Remark. In fact, the last 1004 entries do not matter with this construction, and we chose to leave them as $1007,1008, \ldots, 2010$ only for concreteness. Remark. Using Hall's marriage lemma one may prove that the result becomes false with 1006 replaced by 1005 .
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Two permutations $a_{1}, a_{2}, \ldots, a_{2010}$ and $b_{1}, b_{2}, \ldots, b_{2010}$ of the numbers $1,2, \ldots, 2010$ are said to intersect if $a_{k}=b_{k}$ for some value of $k$ in the range $1 \leq k \leq 2010$. Show that there exist 1006 permutations of the numbers $1,2, \ldots, 2010$ such that any other such permutation is guaranteed to intersect at least one of these 1006 permutations.
|
A valid choice is the following 1006 permutations: | 1 | 2 | 3 | $\cdots$ | 1004 | 1005 | 1006 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 2 | 3 | 4 | $\cdots$ | 1005 | 1006 | 1 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | 3 | 4 | 5 | $\cdots$ | 1006 | 1 | 2 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | | 1004 | 1005 | 1006 | $\cdots$ | 1001 | 1002 | 1003 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | 1005 | 1006 | 1 | $\cdots$ | 1002 | 1003 | 1004 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | | 1006 | 1 | 2 | $\cdots$ | 1003 | 1004 | 1005 | 1007 | 1008 | $\cdots$ | 2009 | 2010 | This works. Indeed, any permutation should have one of $\{1,2, \ldots, 1006\}$ somewhere in the first 1006 positions, so one will get an intersection. Remark. In fact, the last 1004 entries do not matter with this construction, and we chose to leave them as $1007,1008, \ldots, 2010$ only for concreteness. Remark. Using Hall's marriage lemma one may prove that the result becomes false with 1006 replaced by 1005 .
|
{
"resource_path": "USAJMO/segmented/en-JMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
eecd3366-ba52-53f1-9d29-549c3d51858c
| 245,585
|
Let $a, b, c$ be positive real numbers such that $a^{2}+b^{2}+c^{2}+(a+b+c)^{2} \leq 4$. Prove that $$ \frac{a b+1}{(a+b)^{2}}+\frac{b c+1}{(b+c)^{2}}+\frac{c a+1}{(c+a)^{2}} \geq 3 $$
|
The condition becomes $2 \geq a^{2}+b^{2}+c^{2}+a b+b c+c a$. Therefore, $$ \begin{aligned} \sum_{\text {cyc }} \frac{2 a b+2}{(a+b)^{2}} & \geq \sum_{\text {cyc }} \frac{2 a b+\left(a^{2}+b^{2}+c^{2}+a b+b c+c a\right)}{(a+b)^{2}} \\ & =\sum_{\text {cyc }} \frac{(a+b)^{2}+(c+a)(c+b)}{(a+b)^{2}} \\ & =3+\sum_{\text {cyc }} \frac{(c+a)(c+b)}{(a+b)^{2}} \\ & \geq 3+3 \sqrt[3]{\prod_{\text {cyc }} \frac{(c+a)(c+b)}{(a+b)^{2}}}=3+3=6 \end{aligned} $$ with the last line by AM-GM. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a^{2}+b^{2}+c^{2}+(a+b+c)^{2} \leq 4$. Prove that $$ \frac{a b+1}{(a+b)^{2}}+\frac{b c+1}{(b+c)^{2}}+\frac{c a+1}{(c+a)^{2}} \geq 3 $$
|
The condition becomes $2 \geq a^{2}+b^{2}+c^{2}+a b+b c+c a$. Therefore, $$ \begin{aligned} \sum_{\text {cyc }} \frac{2 a b+2}{(a+b)^{2}} & \geq \sum_{\text {cyc }} \frac{2 a b+\left(a^{2}+b^{2}+c^{2}+a b+b c+c a\right)}{(a+b)^{2}} \\ & =\sum_{\text {cyc }} \frac{(a+b)^{2}+(c+a)(c+b)}{(a+b)^{2}} \\ & =3+\sum_{\text {cyc }} \frac{(c+a)(c+b)}{(a+b)^{2}} \\ & \geq 3+3 \sqrt[3]{\prod_{\text {cyc }} \frac{(c+a)(c+b)}{(a+b)^{2}}}=3+3=6 \end{aligned} $$ with the last line by AM-GM. This completes the proof.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2011-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
069d5dbb-deab-5cbd-980e-a28d7b5ab3fb
| 604,332
|
A word is defined as any finite string of letters. A word is a palindrome if it reads the same backwards and forwards. Let a sequence of words $W_{0}, W_{1}, W_{2}, \ldots$ be defined as follows: $W_{0}=a, W_{1}=b$, and for $n \geq 2, W_{n}$ is the word formed by writing $W_{n-2}$ followed by $W_{n-1}$. Prove that for any $n \geq 1$, the word formed by writing $W_{1}, W_{2}, W_{3}, \ldots, W_{n}$ in succession is a palindrome.
|
$$ \begin{aligned} & W_{0}=a \\ & W_{1}=b \\ & W_{2}=a b \\ & W_{3}=b a b \\ & W_{4}=a b b a b \\ & W_{5}=b a b a b b a b \\ & W_{6}=a b b a b b a b a b b a b \\ & W_{7}=b a b a b b a b a b b a b b a b a b b a b \end{aligned} $$ We prove that $W_{1} W_{2} \ldots W_{n}$ is a palindrome by induction on $n$. The base cases $n=$ $1,2,3,4$ can be verified by hand. For the inductive step, we let $\bar{X}$ denote the word $X$ written backwards. Then $$ \begin{aligned} W_{1} W_{2} \ldots W_{n-3} W_{n-2} W_{n-1} W_{n} & \stackrel{\mathrm{IH}}{=}\left(\overline{W_{n-1} W_{n-2} W_{n-3}} \ldots \overline{W_{2} W_{1}}\right) W_{n} \\ & =\left(\overline{W_{n-1} W_{n-2} W_{n-3}} \ldots \overline{W_{2} W_{1}}\right) W_{n-2} W_{n-1} \\ & =\overline{W_{n-1} W_{n-2}}\left(\overline{W_{n-3}} \ldots \overline{W_{2} W_{1}}\right) W_{n-2} W_{n-1} \end{aligned} $$ with the first equality being by the induction hypothesis. By induction hypothesis again the inner parenthesized term is also a palindrome, and so this completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A word is defined as any finite string of letters. A word is a palindrome if it reads the same backwards and forwards. Let a sequence of words $W_{0}, W_{1}, W_{2}, \ldots$ be defined as follows: $W_{0}=a, W_{1}=b$, and for $n \geq 2, W_{n}$ is the word formed by writing $W_{n-2}$ followed by $W_{n-1}$. Prove that for any $n \geq 1$, the word formed by writing $W_{1}, W_{2}, W_{3}, \ldots, W_{n}$ in succession is a palindrome.
|
$$ \begin{aligned} & W_{0}=a \\ & W_{1}=b \\ & W_{2}=a b \\ & W_{3}=b a b \\ & W_{4}=a b b a b \\ & W_{5}=b a b a b b a b \\ & W_{6}=a b b a b b a b a b b a b \\ & W_{7}=b a b a b b a b a b b a b b a b a b b a b \end{aligned} $$ We prove that $W_{1} W_{2} \ldots W_{n}$ is a palindrome by induction on $n$. The base cases $n=$ $1,2,3,4$ can be verified by hand. For the inductive step, we let $\bar{X}$ denote the word $X$ written backwards. Then $$ \begin{aligned} W_{1} W_{2} \ldots W_{n-3} W_{n-2} W_{n-1} W_{n} & \stackrel{\mathrm{IH}}{=}\left(\overline{W_{n-1} W_{n-2} W_{n-3}} \ldots \overline{W_{2} W_{1}}\right) W_{n} \\ & =\left(\overline{W_{n-1} W_{n-2} W_{n-3}} \ldots \overline{W_{2} W_{1}}\right) W_{n-2} W_{n-1} \\ & =\overline{W_{n-1} W_{n-2}}\left(\overline{W_{n-3}} \ldots \overline{W_{2} W_{1}}\right) W_{n-2} W_{n-1} \end{aligned} $$ with the first equality being by the induction hypothesis. By induction hypothesis again the inner parenthesized term is also a palindrome, and so this completes the proof.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2011-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
20845013-db4a-573d-b476-f736ee0e41f2
| 604,359
|
Points $A, B, C, D, E$ lie on a circle $\omega$ and point $P$ lies outside the circle. The given points are such that (i) lines $P B$ and $P D$ are tangent to $\omega$, (ii) $P, A, C$ are collinear, and (iii) $\overline{D E} \| \overline{A C}$. Prove that $\overline{B E}$ bisects $\overline{A C}$.
|
【 First solution using harmonic bundles. Let $M=\overline{B E} \cap \overline{A C}$ and let $\infty$ be the point at infinity along $\overline{D E} \| \overline{A C}$.  Note that $A B C D$ is harmonic, so $$ -1=(A C ; B D) \stackrel{E}{=}(A C ; M \infty) $$ implying $M$ is the midpoint of $\overline{A C}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $A, B, C, D, E$ lie on a circle $\omega$ and point $P$ lies outside the circle. The given points are such that (i) lines $P B$ and $P D$ are tangent to $\omega$, (ii) $P, A, C$ are collinear, and (iii) $\overline{D E} \| \overline{A C}$. Prove that $\overline{B E}$ bisects $\overline{A C}$.
|
【 First solution using harmonic bundles. Let $M=\overline{B E} \cap \overline{A C}$ and let $\infty$ be the point at infinity along $\overline{D E} \| \overline{A C}$.  Note that $A B C D$ is harmonic, so $$ -1=(A C ; B D) \stackrel{E}{=}(A C ; M \infty) $$ implying $M$ is the midpoint of $\overline{A C}$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2011-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
1c3e332e-38c9-5782-a8b8-61dab59c4f00
| 245,639
|
Points $A, B, C, D, E$ lie on a circle $\omega$ and point $P$ lies outside the circle. The given points are such that (i) lines $P B$ and $P D$ are tangent to $\omega$, (ii) $P, A, C$ are collinear, and (iii) $\overline{D E} \| \overline{A C}$. Prove that $\overline{B E}$ bisects $\overline{A C}$.
|
I Second solution using complex numbers (Cynthia Du). Suppose we let $b, d, e$ be free on unit circle, so $p=\frac{2 b d}{b+d}$. Then $d / c=a / e$, and $a+c=p+a c \bar{p}$. Consequently, $$ \begin{aligned} a c & =d e \\ \frac{1}{2}(a+c) & =\frac{b d}{b+d}+d e \cdot \frac{1}{b+d}=\frac{d(b+e)}{b+d} \\ \frac{a+c}{2 a c} & =\frac{(b+e)}{e(b+d)} \end{aligned} $$ From here it's easy to see $$ \frac{a+c}{2}+\frac{a+c}{2 a c} \cdot b e=b+e $$ which is what we wanted to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $A, B, C, D, E$ lie on a circle $\omega$ and point $P$ lies outside the circle. The given points are such that (i) lines $P B$ and $P D$ are tangent to $\omega$, (ii) $P, A, C$ are collinear, and (iii) $\overline{D E} \| \overline{A C}$. Prove that $\overline{B E}$ bisects $\overline{A C}$.
|
I Second solution using complex numbers (Cynthia Du). Suppose we let $b, d, e$ be free on unit circle, so $p=\frac{2 b d}{b+d}$. Then $d / c=a / e$, and $a+c=p+a c \bar{p}$. Consequently, $$ \begin{aligned} a c & =d e \\ \frac{1}{2}(a+c) & =\frac{b d}{b+d}+d e \cdot \frac{1}{b+d}=\frac{d(b+e)}{b+d} \\ \frac{a+c}{2 a c} & =\frac{(b+e)}{e(b+d)} \end{aligned} $$ From here it's easy to see $$ \frac{a+c}{2}+\frac{a+c}{2 a c} \cdot b e=b+e $$ which is what we wanted to prove.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2011-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
1c3e332e-38c9-5782-a8b8-61dab59c4f00
| 245,639
|
Given a triangle $A B C$, let $P$ and $Q$ be points on segments $\overline{A B}$ and $\overline{A C}$, respectively, such that $A P=A Q$. Let $S$ and $R$ be distinct points on segment $\overline{B C}$ such that $S$ lies between $B$ and $R, \angle B P S=\angle P R S$, and $\angle C Q R=\angle Q S R$. Prove that $P, Q$, $R, S$ are concyclic.
|
Assume for contradiction that $(P R S)$ and $(Q R S)$ are distinct. Then $\overline{R S}$ is the radical axis of these two circles. However, $\overline{A P}$ is tangent to $(P R S)$ and $\overline{A Q}$ is tangent to $(Q R S)$, so point $A$ has equal power to both circles, which is impossible since $A$ does not lie on line $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $P$ and $Q$ be points on segments $\overline{A B}$ and $\overline{A C}$, respectively, such that $A P=A Q$. Let $S$ and $R$ be distinct points on segment $\overline{B C}$ such that $S$ lies between $B$ and $R, \angle B P S=\angle P R S$, and $\angle C Q R=\angle Q S R$. Prove that $P, Q$, $R, S$ are concyclic.
|
Assume for contradiction that $(P R S)$ and $(Q R S)$ are distinct. Then $\overline{R S}$ is the radical axis of these two circles. However, $\overline{A P}$ is tangent to $(P R S)$ and $\overline{A Q}$ is tangent to $(Q R S)$, so point $A$ has equal power to both circles, which is impossible since $A$ does not lie on line $B C$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
bf7a848f-f837-50d8-9fd2-638c322575ee
| 604,417
|
For $a, b, c>0$ prove that $$ \frac{a^{3}+3 b^{3}}{5 a+b}+\frac{b^{3}+3 c^{3}}{5 b+c}+\frac{c^{3}+3 a^{3}}{5 c+a} \geq \frac{2}{3}\left(a^{2}+b^{2}+c^{2}\right) $$
|
Cauchy-Schwarz approach. Apply Titu lemma to get $$ \sum_{\mathrm{cyc}} \frac{a^{3}}{5 a+b}=\sum_{\mathrm{cyc}} \frac{a^{4}}{5 a^{2}+a b} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{2}}{\sum_{\mathrm{cyc}}\left(5 a^{2}+a b\right)} \geq \frac{a^{2}+b^{2}+c^{2}}{6} $$ where the last step follows from the identity $\sum_{\text {cyc }}\left(5 a^{2}+a b\right) \leq 6\left(a^{2}+b^{2}+c^{2}\right)$. Similarly, $$ \sum_{\text {cyc }} \frac{b^{3}}{5 a+b}=\sum_{\mathrm{cyc}} \frac{b^{4}}{5 a b+b^{2}} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{2}}{\sum_{\mathrm{cyc}}\left(5 a b+b^{2}\right)} \geq \frac{a^{2}+b^{2}+c^{2}}{6} $$ using the fact that $\sum_{\text {cyc }} 5 a b+b^{2} \leq 6\left(a^{2}+b^{2}+c^{2}\right)$. Therefore, adding the first display to three times the second display implies the result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
For $a, b, c>0$ prove that $$ \frac{a^{3}+3 b^{3}}{5 a+b}+\frac{b^{3}+3 c^{3}}{5 b+c}+\frac{c^{3}+3 a^{3}}{5 c+a} \geq \frac{2}{3}\left(a^{2}+b^{2}+c^{2}\right) $$
|
Cauchy-Schwarz approach. Apply Titu lemma to get $$ \sum_{\mathrm{cyc}} \frac{a^{3}}{5 a+b}=\sum_{\mathrm{cyc}} \frac{a^{4}}{5 a^{2}+a b} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{2}}{\sum_{\mathrm{cyc}}\left(5 a^{2}+a b\right)} \geq \frac{a^{2}+b^{2}+c^{2}}{6} $$ where the last step follows from the identity $\sum_{\text {cyc }}\left(5 a^{2}+a b\right) \leq 6\left(a^{2}+b^{2}+c^{2}\right)$. Similarly, $$ \sum_{\text {cyc }} \frac{b^{3}}{5 a+b}=\sum_{\mathrm{cyc}} \frac{b^{4}}{5 a b+b^{2}} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{2}}{\sum_{\mathrm{cyc}}\left(5 a b+b^{2}\right)} \geq \frac{a^{2}+b^{2}+c^{2}}{6} $$ using the fact that $\sum_{\text {cyc }} 5 a b+b^{2} \leq 6\left(a^{2}+b^{2}+c^{2}\right)$. Therefore, adding the first display to three times the second display implies the result.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
788af525-af5c-5d1d-bb57-88fb0dc4d9f8
| 604,441
|
For $a, b, c>0$ prove that $$ \frac{a^{3}+3 b^{3}}{5 a+b}+\frac{b^{3}+3 c^{3}}{5 b+c}+\frac{c^{3}+3 a^{3}}{5 c+a} \geq \frac{2}{3}\left(a^{2}+b^{2}+c^{2}\right) $$
|
đ Cauchy-Schwarz approach. The main magical claim is: Claim - We have $$ \frac{a^{3}+3 b^{3}}{5 a+b} \geq \frac{25}{36} b^{2}-\frac{1}{36} a^{2} $$ $$ \frac{x^{3}+3}{5 x+1} \geq \frac{25-x^{2}}{36} $$ However, $$ \begin{aligned} 36\left(x^{3}+3\right)-(5 x+1)\left(25-x^{2}\right) & =41 x^{3}+x^{2}-125 x+83 \\ & =(x-1)^{2}(41 x+83) \geq 0 \end{aligned} $$ Sum the claim cyclically to finish. Remark (Derivation of the main claim). The overall strategy is to hope for a constant $k$ such that $$ \frac{a^{3}+3 b^{3}}{5 a+b} \geq k a^{2}+\left(\frac{2}{3}-k\right) b^{2} $$ is true. Letting $x=a / b$ as above and expanding, we need a value $k$ such that the cubic polynomial $P(x):=\left(x^{3}+3\right)-(5 x+1)\left(k x^{2}+\left(\frac{2}{3}-k\right)\right)=(1-5 k) x^{3}-k x^{2}+\left(5 k-\frac{10}{3}\right) x+\left(k+\frac{7}{3}\right)$ is nonnegative everywhere. Since $P(1)=0$ necessarily, in order for $P(1-\varepsilon)$ and $P(1+\varepsilon)$ to both be nonnegative (for small $\varepsilon$ ), the polynomial $P$ must have a double root at 1 , meaning the first derivative $P^{\prime}(1)=0$ needs to vanish. In other words, we need $$ 3(1-5 k)-2 k+\left(5 k-\frac{10}{3}\right)=0 $$ Solving gives $k=-1 / 36$. One then factors out the repeated root $(x-1)^{2}$ from the resulting $P$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
For $a, b, c>0$ prove that $$ \frac{a^{3}+3 b^{3}}{5 a+b}+\frac{b^{3}+3 c^{3}}{5 b+c}+\frac{c^{3}+3 a^{3}}{5 c+a} \geq \frac{2}{3}\left(a^{2}+b^{2}+c^{2}\right) $$
|
đ Cauchy-Schwarz approach. The main magical claim is: Claim - We have $$ \frac{a^{3}+3 b^{3}}{5 a+b} \geq \frac{25}{36} b^{2}-\frac{1}{36} a^{2} $$ $$ \frac{x^{3}+3}{5 x+1} \geq \frac{25-x^{2}}{36} $$ However, $$ \begin{aligned} 36\left(x^{3}+3\right)-(5 x+1)\left(25-x^{2}\right) & =41 x^{3}+x^{2}-125 x+83 \\ & =(x-1)^{2}(41 x+83) \geq 0 \end{aligned} $$ Sum the claim cyclically to finish. Remark (Derivation of the main claim). The overall strategy is to hope for a constant $k$ such that $$ \frac{a^{3}+3 b^{3}}{5 a+b} \geq k a^{2}+\left(\frac{2}{3}-k\right) b^{2} $$ is true. Letting $x=a / b$ as above and expanding, we need a value $k$ such that the cubic polynomial $P(x):=\left(x^{3}+3\right)-(5 x+1)\left(k x^{2}+\left(\frac{2}{3}-k\right)\right)=(1-5 k) x^{3}-k x^{2}+\left(5 k-\frac{10}{3}\right) x+\left(k+\frac{7}{3}\right)$ is nonnegative everywhere. Since $P(1)=0$ necessarily, in order for $P(1-\varepsilon)$ and $P(1+\varepsilon)$ to both be nonnegative (for small $\varepsilon$ ), the polynomial $P$ must have a double root at 1 , meaning the first derivative $P^{\prime}(1)=0$ needs to vanish. In other words, we need $$ 3(1-5 k)-2 k+\left(5 k-\frac{10}{3}\right)=0 $$ Solving gives $k=-1 / 36$. One then factors out the repeated root $(x-1)^{2}$ from the resulting $P$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
788af525-af5c-5d1d-bb57-88fb0dc4d9f8
| 604,441
|
Let $\alpha$ be an irrational number with $0<\alpha<1$, and draw a circle in the plane whose circumference has length 1 . Given any integer $n \geq 3$, define a sequence of points $P_{1}, P_{2}, \ldots, P_{n}$ as follows. First select any point $P_{1}$ on the circle, and for $2 \leq k \leq n$ define $P_{k}$ as the point on the circle for which the length of $\operatorname{arc} P_{k-1} P_{k}$ is $\alpha$, when travelling counterclockwise around the circle from $P_{k-1}$ to $P_{k}$. Suppose that $P_{a}$ and $P_{b}$ are the nearest adjacent points on either side of $P_{n}$. Prove that $a+b \leq n$.
|
No points coincide since $\alpha$ is irrational. Assume for contradiction that $n<a+b<2 n$. Then it follows that $$ \overline{P_{n} P_{a+b-n}} \| \overline{P_{a} P_{b}} $$ as shown below.  This is an obvious contradiction since then $P_{a+b-n}$ is contained in the arc $\widehat{P_{a} P_{b}}$ of the circle through $P_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\alpha$ be an irrational number with $0<\alpha<1$, and draw a circle in the plane whose circumference has length 1 . Given any integer $n \geq 3$, define a sequence of points $P_{1}, P_{2}, \ldots, P_{n}$ as follows. First select any point $P_{1}$ on the circle, and for $2 \leq k \leq n$ define $P_{k}$ as the point on the circle for which the length of $\operatorname{arc} P_{k-1} P_{k}$ is $\alpha$, when travelling counterclockwise around the circle from $P_{k-1}$ to $P_{k}$. Suppose that $P_{a}$ and $P_{b}$ are the nearest adjacent points on either side of $P_{n}$. Prove that $a+b \leq n$.
|
No points coincide since $\alpha$ is irrational. Assume for contradiction that $n<a+b<2 n$. Then it follows that $$ \overline{P_{n} P_{a+b-n}} \| \overline{P_{a} P_{b}} $$ as shown below.  This is an obvious contradiction since then $P_{a+b-n}$ is contained in the arc $\widehat{P_{a} P_{b}}$ of the circle through $P_{n}$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
cd08c5fb-5151-50ca-8bd9-1f707817abfc
| 604,463
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
【 First solution (complex numbers). Let $p=0$ and set $\gamma$ as the real line. Then $A^{\prime}$ is the intersection of $b c$ and $p \bar{a}$. So, we get $$ a^{\prime}=\frac{\bar{a}(\bar{b} c-b \bar{c})}{(\bar{b}-\bar{c}) \bar{a}-(b-c) a} . $$ 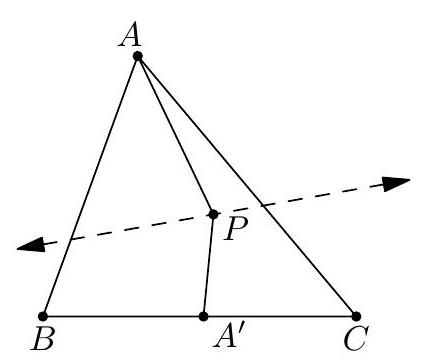 Note that $$ \bar{a}^{\prime}=\frac{a(b \bar{c}-\bar{b} c)}{(b-c) a-(\bar{b}-\bar{c}) \bar{a}} . $$ Thus it suffices to prove This is equivalent to $$ 0=\operatorname{det}\left[\begin{array}{lll} \bar{a}(\bar{b} c-b \bar{c}) & a(\bar{b} c-b \bar{c}) & (\bar{b}-\bar{c}) \bar{a}-(b-c) a \\ \bar{b}(\bar{c} a-c \bar{a}) & b(\bar{c} a-c \bar{a}) & (\bar{c}-\bar{a}) \bar{b}-(c-a) b \\ \bar{c}(\bar{a} b-a \bar{b}) & c(\bar{a} b-a \bar{b}) & (\bar{a}-\bar{b}) \bar{c}-(a-b) c \end{array}\right] . $$ This determinant has the property that the rows sum to zero, and we're done. Remark. Alternatively, if you don't notice that you could just blindly expand: $$ \begin{aligned} & \sum_{\mathrm{cyc}}((\bar{b}-\bar{c}) \bar{a}-(b-c) a) \cdot-\operatorname{det}\left[\begin{array}{ll} b & \bar{b} \\ c & \bar{c} \end{array}\right](\bar{c} a-c \bar{a})(\bar{a} b-a \bar{b}) \\ = & (\bar{b} c-c \bar{b})(\bar{c} a-c \bar{a})(\bar{a} b-a \bar{b}) \sum_{\mathrm{cyc}}(a b-a c+\overline{c a}-\bar{b} \bar{a})=0 \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
【 First solution (complex numbers). Let $p=0$ and set $\gamma$ as the real line. Then $A^{\prime}$ is the intersection of $b c$ and $p \bar{a}$. So, we get $$ a^{\prime}=\frac{\bar{a}(\bar{b} c-b \bar{c})}{(\bar{b}-\bar{c}) \bar{a}-(b-c) a} . $$  Note that $$ \bar{a}^{\prime}=\frac{a(b \bar{c}-\bar{b} c)}{(b-c) a-(\bar{b}-\bar{c}) \bar{a}} . $$ Thus it suffices to prove This is equivalent to $$ 0=\operatorname{det}\left[\begin{array}{lll} \bar{a}(\bar{b} c-b \bar{c}) & a(\bar{b} c-b \bar{c}) & (\bar{b}-\bar{c}) \bar{a}-(b-c) a \\ \bar{b}(\bar{c} a-c \bar{a}) & b(\bar{c} a-c \bar{a}) & (\bar{c}-\bar{a}) \bar{b}-(c-a) b \\ \bar{c}(\bar{a} b-a \bar{b}) & c(\bar{a} b-a \bar{b}) & (\bar{a}-\bar{b}) \bar{c}-(a-b) c \end{array}\right] . $$ This determinant has the property that the rows sum to zero, and we're done. Remark. Alternatively, if you don't notice that you could just blindly expand: $$ \begin{aligned} & \sum_{\mathrm{cyc}}((\bar{b}-\bar{c}) \bar{a}-(b-c) a) \cdot-\operatorname{det}\left[\begin{array}{ll} b & \bar{b} \\ c & \bar{c} \end{array}\right](\bar{c} a-c \bar{a})(\bar{a} b-a \bar{b}) \\ = & (\bar{b} c-c \bar{b})(\bar{c} a-c \bar{a})(\bar{a} b-a \bar{b}) \sum_{\mathrm{cyc}}(a b-a c+\overline{c a}-\bar{b} \bar{a})=0 \end{aligned} $$
|
{
"resource_path": "USAJMO/segmented/en-JMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4669eaf-0b27-5264-9ada-e6d4788114f3
| 245,707
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
\I Second solution (Desargues involution). We let $C^{\prime \prime}=\overline{A^{\prime} B^{\prime}} \cap \overline{A B}$. Consider complete quadrilateral $A B C A^{\prime} B^{\prime} C^{\prime \prime} C$. We see that there is an involutive pairing $\tau$ at $P$ swapping $\left(P A, P A^{\prime}\right),\left(P B, P B^{\prime}\right),\left(P C, P C^{\prime \prime}\right)$. From the first two, we see $\tau$ coincides with reflection about $\ell$, hence conclude $C^{\prime \prime}=C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
\I Second solution (Desargues involution). We let $C^{\prime \prime}=\overline{A^{\prime} B^{\prime}} \cap \overline{A B}$. Consider complete quadrilateral $A B C A^{\prime} B^{\prime} C^{\prime \prime} C$. We see that there is an involutive pairing $\tau$ at $P$ swapping $\left(P A, P A^{\prime}\right),\left(P B, P B^{\prime}\right),\left(P C, P C^{\prime \prime}\right)$. From the first two, we see $\tau$ coincides with reflection about $\ell$, hence conclude $C^{\prime \prime}=C$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4669eaf-0b27-5264-9ada-e6d4788114f3
| 245,707
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
ब Third solution (barycentric), by Catherine $\mathbf{X u}$. We will perform barycentric coordinates on the triangle $P C C^{\prime}$, with $P=(1,0,0), C^{\prime}=(0,1,0)$, and $C=(0,0,1)$. Set $a=C C^{\prime}, b=C P, c=C^{\prime} P$ as usual. Since $A, B, C^{\prime}$ are collinear, we will define $A=(p: k: q)$ and $B=(p: \ell: q)$. Claim - Line $\gamma$ is the angle bisector of $\angle A P A^{\prime}, \angle B P B^{\prime}$, and $\angle C P C^{\prime}$. Thus $B^{\prime}$ is the intersection of the isogonal of $B$ with respect to $\angle P$ with the line $C A$; that is, $$ B^{\prime}=\left(\frac{p}{k} \frac{b^{2}}{\ell}: \frac{b^{2}}{\ell}: \frac{c^{2}}{q}\right) $$ Analogously, $A^{\prime}$ is the intersection of the isogonal of $A$ with respect to $\angle P$ with the line $C B$; that is, $$ A^{\prime}=\left(\frac{p}{\ell} \frac{b^{2}}{k}: \frac{b^{2}}{k}: \frac{c^{2}}{q}\right) $$ The ratio of the first to third coordinate in these two points is both $b^{2} p q: c^{2} k \ell$, so it follows $A^{\prime}, B^{\prime}$, and $C^{\prime}$ are collinear. Remark (Problem reference). The converse of this problem appears as problem 1052 attributed S. V. Markelov in the book Geometriya: 9-11 Klassy: Ot Uchebnoy Zadachi k Tvorcheskoy, 1996, by I. F. Sharygin.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
ब Third solution (barycentric), by Catherine $\mathbf{X u}$. We will perform barycentric coordinates on the triangle $P C C^{\prime}$, with $P=(1,0,0), C^{\prime}=(0,1,0)$, and $C=(0,0,1)$. Set $a=C C^{\prime}, b=C P, c=C^{\prime} P$ as usual. Since $A, B, C^{\prime}$ are collinear, we will define $A=(p: k: q)$ and $B=(p: \ell: q)$. Claim - Line $\gamma$ is the angle bisector of $\angle A P A^{\prime}, \angle B P B^{\prime}$, and $\angle C P C^{\prime}$. Thus $B^{\prime}$ is the intersection of the isogonal of $B$ with respect to $\angle P$ with the line $C A$; that is, $$ B^{\prime}=\left(\frac{p}{k} \frac{b^{2}}{\ell}: \frac{b^{2}}{\ell}: \frac{c^{2}}{q}\right) $$ Analogously, $A^{\prime}$ is the intersection of the isogonal of $A$ with respect to $\angle P$ with the line $C B$; that is, $$ A^{\prime}=\left(\frac{p}{\ell} \frac{b^{2}}{k}: \frac{b^{2}}{k}: \frac{c^{2}}{q}\right) $$ The ratio of the first to third coordinate in these two points is both $b^{2} p q: c^{2} k \ell$, so it follows $A^{\prime}, B^{\prime}$, and $C^{\prime}$ are collinear. Remark (Problem reference). The converse of this problem appears as problem 1052 attributed S. V. Markelov in the book Geometriya: 9-11 Klassy: Ot Uchebnoy Zadachi k Tvorcheskoy, 1996, by I. F. Sharygin.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4669eaf-0b27-5264-9ada-e6d4788114f3
| 245,707
|
In triangle $A B C$, points $P, Q, R$ lie on sides $B C, C A, A B$, respectively. Let $\omega_{A}$, $\omega_{B}, \omega_{C}$ denote the circumcircles of triangles $A Q R, B R P, C P Q$, respectively. Given the fact that segment $A P$ intersects $\omega_{A}, \omega_{B}, \omega_{C}$ again at $X, Y, Z$ respectively, prove that $Y X / X Z=B P / P C$.
|
Let $M$ be the concurrence point of $\omega_{A}, \omega_{B}, \omega_{C}$ (by Miquel's theorem).  Then $M$ is the center of a spiral similarity sending $\overline{Y Z}$ to $\overline{B C}$. So it suffices to show that this spiral similarity also sends $X$ to $P$, but $$ \measuredangle M X Y=\measuredangle M X A=\measuredangle M R A=\measuredangle M R B=\measuredangle M P B $$ so this follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, points $P, Q, R$ lie on sides $B C, C A, A B$, respectively. Let $\omega_{A}$, $\omega_{B}, \omega_{C}$ denote the circumcircles of triangles $A Q R, B R P, C P Q$, respectively. Given the fact that segment $A P$ intersects $\omega_{A}, \omega_{B}, \omega_{C}$ again at $X, Y, Z$ respectively, prove that $Y X / X Z=B P / P C$.
|
Let $M$ be the concurrence point of $\omega_{A}, \omega_{B}, \omega_{C}$ (by Miquel's theorem).  Then $M$ is the center of a spiral similarity sending $\overline{Y Z}$ to $\overline{B C}$. So it suffices to show that this spiral similarity also sends $X$ to $P$, but $$ \measuredangle M X Y=\measuredangle M X A=\measuredangle M R A=\measuredangle M R B=\measuredangle M P B $$ so this follows.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2013-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
73edf22f-bdf8-5e92-ad71-2a1817d4f13a
| 604,581
|
Quadrilateral $X A B Y$ is inscribed in the semicircle $\omega$ with diameter $\overline{X Y}$. Segments $A Y$ and $B X$ meet at $P$. Point $Z$ is the foot of the perpendicular from $P$ to line $\overline{X Y}$. Point $C$ lies on $\omega$ such that line $X C$ is perpendicular to line $A Z$. Let $Q$ be the intersection of segments $A Y$ and $X C$. Prove that $$ \frac{B Y}{X P}+\frac{C Y}{X Q}=\frac{A Y}{A X} $$
|
Let $\beta=\angle Y X P$ and $\alpha=\angle P Y X$ and set $X Y=1$. We do not direct angles in the following solution.  Observe that $$ \angle A Z X=\angle A P X=\alpha+\beta $$ since $A P Z X$ is cyclic. In particular, $\angle C X Y=90^{\circ}-(\alpha+\beta)$. It is immediate that $$ B Y=\sin \beta, \quad C Y=\cos (\alpha+\beta), \quad A Y=\cos \alpha, \quad A X=\sin \alpha $$ The Law of Sines on $\triangle X P Y$ gives $X P=X Y \frac{\sin \alpha}{\sin (\alpha+\beta)}$, and on $\triangle X Q Y$ gives $X Q=$ $X Y \frac{\sin \alpha}{\sin (90+\beta)}=\frac{\sin \alpha}{\cos \beta}$. So, the given is equivalent to $$ \frac{\sin \beta}{\frac{\sin \alpha}{\sin (\alpha+\beta)}}+\frac{\cos (\alpha+\beta)}{\frac{\sin \alpha}{\cos \beta}}=\frac{\cos \alpha}{\sin \alpha} $$ which is equivalent to $\cos \alpha=\cos \beta \cos (\alpha+\beta)+\sin \beta \sin (\alpha+\beta)$. This is obvious, because the right-hand side is just $\cos ((\alpha+\beta)-\beta)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Quadrilateral $X A B Y$ is inscribed in the semicircle $\omega$ with diameter $\overline{X Y}$. Segments $A Y$ and $B X$ meet at $P$. Point $Z$ is the foot of the perpendicular from $P$ to line $\overline{X Y}$. Point $C$ lies on $\omega$ such that line $X C$ is perpendicular to line $A Z$. Let $Q$ be the intersection of segments $A Y$ and $X C$. Prove that $$ \frac{B Y}{X P}+\frac{C Y}{X Q}=\frac{A Y}{A X} $$
|
Let $\beta=\angle Y X P$ and $\alpha=\angle P Y X$ and set $X Y=1$. We do not direct angles in the following solution.  Observe that $$ \angle A Z X=\angle A P X=\alpha+\beta $$ since $A P Z X$ is cyclic. In particular, $\angle C X Y=90^{\circ}-(\alpha+\beta)$. It is immediate that $$ B Y=\sin \beta, \quad C Y=\cos (\alpha+\beta), \quad A Y=\cos \alpha, \quad A X=\sin \alpha $$ The Law of Sines on $\triangle X P Y$ gives $X P=X Y \frac{\sin \alpha}{\sin (\alpha+\beta)}$, and on $\triangle X Q Y$ gives $X Q=$ $X Y \frac{\sin \alpha}{\sin (90+\beta)}=\frac{\sin \alpha}{\cos \beta}$. So, the given is equivalent to $$ \frac{\sin \beta}{\frac{\sin \alpha}{\sin (\alpha+\beta)}}+\frac{\cos (\alpha+\beta)}{\frac{\sin \alpha}{\cos \beta}}=\frac{\cos \alpha}{\sin \alpha} $$ which is equivalent to $\cos \alpha=\cos \beta \cos (\alpha+\beta)+\sin \beta \sin (\alpha+\beta)$. This is obvious, because the right-hand side is just $\cos ((\alpha+\beta)-\beta)$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2013-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5355a867-a8f0-5ed5-a0cd-6fca8cfb1d4f
| 604,606
|
Let $a, b, c$ be real numbers greater than or equal to 1 . Prove that $$ \min \left(\frac{10 a^{2}-5 a+1}{b^{2}-5 b+10}, \frac{10 b^{2}-5 b+1}{c^{2}-5 c+10}, \frac{10 c^{2}-5 c+1}{a^{2}-5 a+10}\right) \leq a b c $$
|
Notice that $$ \frac{10 a^{2}-5 a+1}{a^{2}-5 a+10} \leq a^{3} $$ since it rearranges to $(a-1)^{5} \geq 0$. Cyclically multiply to get $$ \prod_{\mathrm{cyc}}\left(\frac{10 a^{2}-5 a+1}{b^{2}-5 b+10}\right) \leq(a b c)^{3} $$ and the minimum is at most the geometric mean.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers greater than or equal to 1 . Prove that $$ \min \left(\frac{10 a^{2}-5 a+1}{b^{2}-5 b+10}, \frac{10 b^{2}-5 b+1}{c^{2}-5 c+10}, \frac{10 c^{2}-5 c+1}{a^{2}-5 a+10}\right) \leq a b c $$
|
Notice that $$ \frac{10 a^{2}-5 a+1}{a^{2}-5 a+10} \leq a^{3} $$ since it rearranges to $(a-1)^{5} \geq 0$. Cyclically multiply to get $$ \prod_{\mathrm{cyc}}\left(\frac{10 a^{2}-5 a+1}{b^{2}-5 b+10}\right) \leq(a b c)^{3} $$ and the minimum is at most the geometric mean.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2014-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
02f8b7ea-d27e-5339-aed5-3a17c89492f0
| 604,632
|
Let $b \geq 2$ be a fixed integer, and let $s_{b}(n)$ denote the sum of the base- $b$ digits of $n$. Show that there are infinitely many positive integers that cannot be represented in the from $n+s_{b}(n)$ where $n$ is a positive integer.
|
For brevity let $f(n)=n+s_{b}(n)$. Select any integer $M$. Observe that $f(x) \geq b^{2 M}$ for any $x \geq b^{2 M}$, but also $f\left(b^{2 M}-k\right) \geq b^{2 M}$ for $k=1,2, \ldots, M$, since the base- $b$ expansion of $b^{2 M}-k$ will start out with at least $M$ digits $b-1$. Thus $f$ omits at least $M$ values in $\left[1, b^{2 M}\right]$ for any $M$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $b \geq 2$ be a fixed integer, and let $s_{b}(n)$ denote the sum of the base- $b$ digits of $n$. Show that there are infinitely many positive integers that cannot be represented in the from $n+s_{b}(n)$ where $n$ is a positive integer.
|
For brevity let $f(n)=n+s_{b}(n)$. Select any integer $M$. Observe that $f(x) \geq b^{2 M}$ for any $x \geq b^{2 M}$, but also $f\left(b^{2 M}-k\right) \geq b^{2 M}$ for $k=1,2, \ldots, M$, since the base- $b$ expansion of $b^{2 M}-k$ will start out with at least $M$ digits $b-1$. Thus $f$ omits at least $M$ values in $\left[1, b^{2 M}\right]$ for any $M$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2014-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
54de7089-b41e-588c-95ae-dbb1f20fde3d
| 604,670
|
Let $A B C$ be a triangle with incenter $I$, incircle $\gamma$ and circumcircle $\Gamma$. Let $M, N, P$ be the midpoints of $\overline{B C}, \overline{C A}, \overline{A B}$ and let $E, F$ be the tangency points of $\gamma$ with $\overline{C A}$ and $\overline{A B}$, respectively. Let $U, V$ be the intersections of line $E F$ with line $M N$ and line $M P$, respectively, and let $X$ be the midpoint of $\operatorname{arc} B A C$ of $\Gamma$. (a) Prove that $I$ lies on ray $C V$. (b) Prove that line $X I$ bisects $\overline{U V}$.
|
The fact that $I=\overline{B U} \cap \overline{C V}$ and is Lemma 1.45 from EGMO. As for (b), we note: Claim - Line $I X$ is a symmedian of $\triangle I B C$. Since $B V U C$ is cyclic with diagonals intersecting at $I$, and $I X$ is symmedian of $\triangle I B C$, it is median of $\triangle I U V$, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$, incircle $\gamma$ and circumcircle $\Gamma$. Let $M, N, P$ be the midpoints of $\overline{B C}, \overline{C A}, \overline{A B}$ and let $E, F$ be the tangency points of $\gamma$ with $\overline{C A}$ and $\overline{A B}$, respectively. Let $U, V$ be the intersections of line $E F$ with line $M N$ and line $M P$, respectively, and let $X$ be the midpoint of $\operatorname{arc} B A C$ of $\Gamma$. (a) Prove that $I$ lies on ray $C V$. (b) Prove that line $X I$ bisects $\overline{U V}$.
|
The fact that $I=\overline{B U} \cap \overline{C V}$ and is Lemma 1.45 from EGMO. As for (b), we note: Claim - Line $I X$ is a symmedian of $\triangle I B C$. Since $B V U C$ is cyclic with diagonals intersecting at $I$, and $I X$ is symmedian of $\triangle I B C$, it is median of $\triangle I U V$, as needed.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2014-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d563008c-b0fe-575f-bf62-c6e14f70b59e
| 604,701
|
Given a sequence of real numbers, a move consists of choosing two terms and replacing each with their arithmetic mean. Show that there exists a sequence of 2015 distinct real numbers such that after one initial move is applied to the sequence - no matter what move - there is always a way to continue with a finite sequence of moves so as to obtain in the end a constant sequence.
|
One valid example of a sequence is $0,1, \ldots, 2014$. We will show how to achieve the all-1007 sequence based on the first move. Say two numbers are opposites if their average is 1007 . We consider 1007 as its own opposite. We consider two cases: - First, suppose the first initial move did not involve the number 1007. Suppose the two numbers changed were $a$ and $b$, replaced by $c=\frac{1}{2}(a+b)$ twice. - If $a$ and $b$ are opposites, we simply operate on all the other pairs of opposites. - Otherwise let $a^{\prime}$ and $b^{\prime}$ be the opposites of $a$ and $b$, so all four of $a, b, a^{\prime}, b^{\prime}$ are distinct. Then operate on $a^{\prime}$ and $b^{\prime}$ to get $c^{\prime}=2014-c$. We work with only these four numbers ande replace them as follows: $$ \begin{array}{cccc} \frac{1}{2}(a+b) & \frac{1}{2}(a+b) & a^{\prime} & b^{\prime} \\ \frac{1}{2}(a+b) & \frac{1}{2}(a+b) & \frac{1}{2}\left(a^{\prime}+b^{\prime}\right) & \frac{1}{2}\left(a^{\prime}+b^{\prime}\right) \\ 1007 & \frac{1}{2}(a+b) & 1007 & \frac{1}{2}\left(a^{\prime}+b^{\prime}\right) \\ 1007 & 1007 & 1007 & 1007 \end{array} $$ Finally, we operate on the remaining 1005 pairs of opposites. - Now suppose the first initial move involved the number 1007 and some $a$. Let $k$ be any number other than $a$ or its opposite, and let $a^{\prime}, k^{\prime}$ be the opposites of $a$ and $k$. We work with only these five numbers: and replace them in the following way: $$ \begin{array}{ccccc} \frac{1}{2}(a+1007) & \frac{1}{2}(a+1007) & a^{\prime} & k & k^{\prime} \\ \frac{1}{2}(a+1007) & \frac{1}{2}(a+1007) & a^{\prime} & 1007 & 1007 \\ \frac{1}{2}(a+1007) & \frac{1}{2}(a+1007) & \frac{1}{2}\left(a^{\prime}+1007\right) & \frac{1}{2}\left(a^{\prime}+1007\right) & 1007 \\ 1007 & \frac{1}{2}(a+1007) & 1007 & \frac{1}{2}\left(a^{\prime}+1007\right) & 1007 \\ 1007 & 1007 & 1007 & 1007 & 1007 \end{array} $$ Finally, we operate on the remaining 1005 pairs of opposites. However for "most" sequences one expects the result to not be possible. As a simple example, the goal is impossible for $(0,1, \ldots, 2013,2015)$ since the average of the terms is $1007+\frac{1}{2015}$, but in the process the only denominators ever generated are powers of 2 . This narrows the search somewhat.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a sequence of real numbers, a move consists of choosing two terms and replacing each with their arithmetic mean. Show that there exists a sequence of 2015 distinct real numbers such that after one initial move is applied to the sequence - no matter what move - there is always a way to continue with a finite sequence of moves so as to obtain in the end a constant sequence.
|
One valid example of a sequence is $0,1, \ldots, 2014$. We will show how to achieve the all-1007 sequence based on the first move. Say two numbers are opposites if their average is 1007 . We consider 1007 as its own opposite. We consider two cases: - First, suppose the first initial move did not involve the number 1007. Suppose the two numbers changed were $a$ and $b$, replaced by $c=\frac{1}{2}(a+b)$ twice. - If $a$ and $b$ are opposites, we simply operate on all the other pairs of opposites. - Otherwise let $a^{\prime}$ and $b^{\prime}$ be the opposites of $a$ and $b$, so all four of $a, b, a^{\prime}, b^{\prime}$ are distinct. Then operate on $a^{\prime}$ and $b^{\prime}$ to get $c^{\prime}=2014-c$. We work with only these four numbers ande replace them as follows: $$ \begin{array}{cccc} \frac{1}{2}(a+b) & \frac{1}{2}(a+b) & a^{\prime} & b^{\prime} \\ \frac{1}{2}(a+b) & \frac{1}{2}(a+b) & \frac{1}{2}\left(a^{\prime}+b^{\prime}\right) & \frac{1}{2}\left(a^{\prime}+b^{\prime}\right) \\ 1007 & \frac{1}{2}(a+b) & 1007 & \frac{1}{2}\left(a^{\prime}+b^{\prime}\right) \\ 1007 & 1007 & 1007 & 1007 \end{array} $$ Finally, we operate on the remaining 1005 pairs of opposites. - Now suppose the first initial move involved the number 1007 and some $a$. Let $k$ be any number other than $a$ or its opposite, and let $a^{\prime}, k^{\prime}$ be the opposites of $a$ and $k$. We work with only these five numbers: and replace them in the following way: $$ \begin{array}{ccccc} \frac{1}{2}(a+1007) & \frac{1}{2}(a+1007) & a^{\prime} & k & k^{\prime} \\ \frac{1}{2}(a+1007) & \frac{1}{2}(a+1007) & a^{\prime} & 1007 & 1007 \\ \frac{1}{2}(a+1007) & \frac{1}{2}(a+1007) & \frac{1}{2}\left(a^{\prime}+1007\right) & \frac{1}{2}\left(a^{\prime}+1007\right) & 1007 \\ 1007 & \frac{1}{2}(a+1007) & 1007 & \frac{1}{2}\left(a^{\prime}+1007\right) & 1007 \\ 1007 & 1007 & 1007 & 1007 & 1007 \end{array} $$ Finally, we operate on the remaining 1005 pairs of opposites. However for "most" sequences one expects the result to not be possible. As a simple example, the goal is impossible for $(0,1, \ldots, 2013,2015)$ since the average of the terms is $1007+\frac{1}{2015}$, but in the process the only denominators ever generated are powers of 2 . This narrows the search somewhat.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2015-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
63fa8bf7-99e2-5442-92c9-9b6f655f29b8
| 245,838
|
Quadrilateral $A P B Q$ is inscribed in circle $\omega$ with $\angle P=\angle Q=90^{\circ}$ and $A P=$ $A Q<B P$. Let $X$ be a variable point on segment $\overline{P Q}$. Line $A X$ meets $\omega$ again at $S$ (other than $A$ ). Point $T$ lies on arc $A Q B$ of $\omega$ such that $\overline{X T}$ is perpendicular to $\overline{A X}$. Let $M$ denote the midpoint of chord $\overline{S T}$. As $X$ varies on segment $\overline{P Q}$, show that $M$ moves along a circle.
|
- $X$ at the midpoint of $\overline{P Q}$ (giving the midpoint of $\overline{B Q}$ ) which determines the circle; this circle then passes through $P$ by symmetry and we can find the center by taking the intersection of two perpendicular bisectors (which two?). 【 Complex solution (Evan Chen). Toss on the complex unit circle with $a=-1, b=1$, $z=-\frac{1}{2}$. Let $s$ and $t$ be on the unit circle. We claim $Z$ is the center. It follows from standard formulas that $$ x=\frac{1}{2}(s+t-1+s / t) $$ thus $$ 4 \operatorname{Re} x+2=s+t+\frac{1}{s}+\frac{1}{t}+\frac{s}{t}+\frac{t}{s} $$ which depends only on $P$ and $Q$, and not on $X$. Thus $$ 4\left|z-\frac{s+t}{2}\right|^{2}=|s+t+1|^{2}=3+(4 \operatorname{Re} x+2) $$ does not depend on $X$, done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Quadrilateral $A P B Q$ is inscribed in circle $\omega$ with $\angle P=\angle Q=90^{\circ}$ and $A P=$ $A Q<B P$. Let $X$ be a variable point on segment $\overline{P Q}$. Line $A X$ meets $\omega$ again at $S$ (other than $A$ ). Point $T$ lies on arc $A Q B$ of $\omega$ such that $\overline{X T}$ is perpendicular to $\overline{A X}$. Let $M$ denote the midpoint of chord $\overline{S T}$. As $X$ varies on segment $\overline{P Q}$, show that $M$ moves along a circle.
|
- $X$ at the midpoint of $\overline{P Q}$ (giving the midpoint of $\overline{B Q}$ ) which determines the circle; this circle then passes through $P$ by symmetry and we can find the center by taking the intersection of two perpendicular bisectors (which two?). 【 Complex solution (Evan Chen). Toss on the complex unit circle with $a=-1, b=1$, $z=-\frac{1}{2}$. Let $s$ and $t$ be on the unit circle. We claim $Z$ is the center. It follows from standard formulas that $$ x=\frac{1}{2}(s+t-1+s / t) $$ thus $$ 4 \operatorname{Re} x+2=s+t+\frac{1}{s}+\frac{1}{t}+\frac{s}{t}+\frac{t}{s} $$ which depends only on $P$ and $Q$, and not on $X$. Thus $$ 4\left|z-\frac{s+t}{2}\right|^{2}=|s+t+1|^{2}=3+(4 \operatorname{Re} x+2) $$ does not depend on $X$, done.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2015-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
19e652a1-5f12-538e-956c-8a943291f946
| 604,751
|
Quadrilateral $A P B Q$ is inscribed in circle $\omega$ with $\angle P=\angle Q=90^{\circ}$ and $A P=$ $A Q<B P$. Let $X$ be a variable point on segment $\overline{P Q}$. Line $A X$ meets $\omega$ again at $S$ (other than $A$ ). Point $T$ lies on arc $A Q B$ of $\omega$ such that $\overline{X T}$ is perpendicular to $\overline{A X}$. Let $M$ denote the midpoint of chord $\overline{S T}$. As $X$ varies on segment $\overline{P Q}$, show that $M$ moves along a circle.
|
- $X$ at the midpoint of $\overline{P Q}$ (giving the midpoint of $\overline{B Q}$ ) which determines the circle; this circle then passes through $P$ by symmetry and we can find the center by taking the intersection of two perpendicular bisectors (which two?). 【 Homothety solution (Alex Whatley). Let $G, N, O$ denote the centroid, nine-point center, and circumcenter of triangle $A S T$, respectively. Let $Y$ denote the midpoint of $\overline{A S}$. Then the three points $X, Y, M$ lie on the nine-point circle of triangle $A S T$, which is centered at $N$ and has radius $\frac{1}{2} A O$.  Let $R$ denote the radius of $\omega$. Note that the nine-point circle of $\triangle A S T$ has radius equal to $\frac{1}{2} R$, and hence is independent of $S$ and $T$. Then the power of $A$ with respect to the nine-point circle equals $$ A N^{2}-\left(\frac{1}{2} R\right)^{2}=A X \cdot A Y=\frac{1}{2} A X \cdot A S=\frac{1}{2} A Q^{2} $$ and hence $$ A N^{2}=\left(\frac{1}{2} R\right)^{2}+\frac{1}{2} A Q^{2} $$ which does not depend on the choice of $X$. So $N$ moves along a circle centered at $A$. Since the points $O, G, N$ are collinear on the Euler line of $\triangle A S T$ with $$ G O=\frac{2}{3} N O $$ it follows by homothety that $G$ moves along a circle as well, whose center is situated one-third of the way from $A$ to $O$. Finally, since $A, G, M$ are collinear with $$ A M=\frac{3}{2} A G $$ it follows that $M$ moves along a circle centered at the midpoint of $\overline{A O}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Quadrilateral $A P B Q$ is inscribed in circle $\omega$ with $\angle P=\angle Q=90^{\circ}$ and $A P=$ $A Q<B P$. Let $X$ be a variable point on segment $\overline{P Q}$. Line $A X$ meets $\omega$ again at $S$ (other than $A$ ). Point $T$ lies on arc $A Q B$ of $\omega$ such that $\overline{X T}$ is perpendicular to $\overline{A X}$. Let $M$ denote the midpoint of chord $\overline{S T}$. As $X$ varies on segment $\overline{P Q}$, show that $M$ moves along a circle.
|
- $X$ at the midpoint of $\overline{P Q}$ (giving the midpoint of $\overline{B Q}$ ) which determines the circle; this circle then passes through $P$ by symmetry and we can find the center by taking the intersection of two perpendicular bisectors (which two?). 【 Homothety solution (Alex Whatley). Let $G, N, O$ denote the centroid, nine-point center, and circumcenter of triangle $A S T$, respectively. Let $Y$ denote the midpoint of $\overline{A S}$. Then the three points $X, Y, M$ lie on the nine-point circle of triangle $A S T$, which is centered at $N$ and has radius $\frac{1}{2} A O$.  Let $R$ denote the radius of $\omega$. Note that the nine-point circle of $\triangle A S T$ has radius equal to $\frac{1}{2} R$, and hence is independent of $S$ and $T$. Then the power of $A$ with respect to the nine-point circle equals $$ A N^{2}-\left(\frac{1}{2} R\right)^{2}=A X \cdot A Y=\frac{1}{2} A X \cdot A S=\frac{1}{2} A Q^{2} $$ and hence $$ A N^{2}=\left(\frac{1}{2} R\right)^{2}+\frac{1}{2} A Q^{2} $$ which does not depend on the choice of $X$. So $N$ moves along a circle centered at $A$. Since the points $O, G, N$ are collinear on the Euler line of $\triangle A S T$ with $$ G O=\frac{2}{3} N O $$ it follows by homothety that $G$ moves along a circle as well, whose center is situated one-third of the way from $A$ to $O$. Finally, since $A, G, M$ are collinear with $$ A M=\frac{3}{2} A G $$ it follows that $M$ moves along a circle centered at the midpoint of $\overline{A O}$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2015-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
19e652a1-5f12-538e-956c-8a943291f946
| 604,751
|
Quadrilateral $A P B Q$ is inscribed in circle $\omega$ with $\angle P=\angle Q=90^{\circ}$ and $A P=$ $A Q<B P$. Let $X$ be a variable point on segment $\overline{P Q}$. Line $A X$ meets $\omega$ again at $S$ (other than $A$ ). Point $T$ lies on arc $A Q B$ of $\omega$ such that $\overline{X T}$ is perpendicular to $\overline{A X}$. Let $M$ denote the midpoint of chord $\overline{S T}$. As $X$ varies on segment $\overline{P Q}$, show that $M$ moves along a circle.
|
- $X$ at the midpoint of $\overline{P Q}$ (giving the midpoint of $\overline{B Q}$ ) which determines the circle; this circle then passes through $P$ by symmetry and we can find the center by taking the intersection of two perpendicular bisectors (which two?). 【 Power of a point solution (Zuming Feng, official solution). We complete the picture by letting $\triangle K Y X$ be the orthic triangle of $\triangle A S T$; in that case line $X Y$ meets the $\omega$ again at $P$ and $Q$. 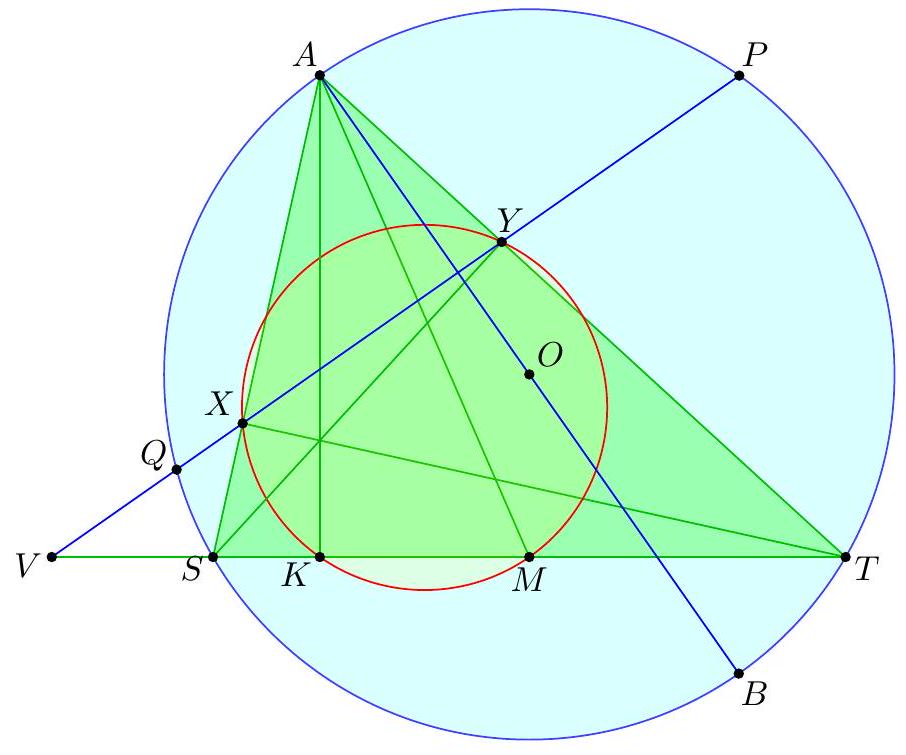 The main claim is: Claim - Quadrilateral $P Q K M$ is cyclic. $$ V Q \cdot V P=V S \cdot V T=V X \cdot V Y=V K \cdot V M $$ using the nine-point circle, and the circle with diameter $\overline{S T}$. But the circumcenter of $P Q K M$, is the midpoint of $\overline{A O}$, since it lies on the perpendicular bisectors of $\overline{K M}$ and $\overline{P Q}$. So it is fixed, the end.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Quadrilateral $A P B Q$ is inscribed in circle $\omega$ with $\angle P=\angle Q=90^{\circ}$ and $A P=$ $A Q<B P$. Let $X$ be a variable point on segment $\overline{P Q}$. Line $A X$ meets $\omega$ again at $S$ (other than $A$ ). Point $T$ lies on arc $A Q B$ of $\omega$ such that $\overline{X T}$ is perpendicular to $\overline{A X}$. Let $M$ denote the midpoint of chord $\overline{S T}$. As $X$ varies on segment $\overline{P Q}$, show that $M$ moves along a circle.
|
- $X$ at the midpoint of $\overline{P Q}$ (giving the midpoint of $\overline{B Q}$ ) which determines the circle; this circle then passes through $P$ by symmetry and we can find the center by taking the intersection of two perpendicular bisectors (which two?). 【 Power of a point solution (Zuming Feng, official solution). We complete the picture by letting $\triangle K Y X$ be the orthic triangle of $\triangle A S T$; in that case line $X Y$ meets the $\omega$ again at $P$ and $Q$.  The main claim is: Claim - Quadrilateral $P Q K M$ is cyclic. $$ V Q \cdot V P=V S \cdot V T=V X \cdot V Y=V K \cdot V M $$ using the nine-point circle, and the circle with diameter $\overline{S T}$. But the circumcenter of $P Q K M$, is the midpoint of $\overline{A O}$, since it lies on the perpendicular bisectors of $\overline{K M}$ and $\overline{P Q}$. So it is fixed, the end.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2015-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
19e652a1-5f12-538e-956c-8a943291f946
| 604,751
|
The isosceles triangle $\triangle A B C$, with $A B=A C$, is inscribed in the circle $\omega$. Let $P$ be a variable point on the arc $B C$ that does not contain $A$, and let $I_{B}$ and $I_{C}$ denote the incenters of triangles $\triangle A B P$ and $\triangle A C P$, respectively. Prove that as $P$ varies, the circumcircle of triangle $\triangle P I_{B} I_{C}$ passes through a fixed point.
|
Let $M$ be the midpoint of arc $B C$ not containing $A$. We claim $M$ is the desired fixed point.  Let $M_{B}, M_{C}$ be the second intersections of $P I_{B}$ and $P I_{C}$ with circumcircle. Claim - We have $\triangle I_{B} M_{B} M \cong \triangle I_{C} M_{C} M$. $$ \begin{aligned} M_{B} I_{B} & =M_{B} B=M_{C} C=M_{C} I_{C} \\ M M_{B} & =M M_{C} \\ \angle I_{B} M_{B} M & =\frac{1}{2} \widehat{P M}=\angle I_{C} M_{C} M \end{aligned} $$ This implies the desired congruence. Since $\angle M P A=90^{\circ}$ and ray $P A$ bisects $\angle I_{B} P I_{C}$, the conclusion $M I_{B}=M I_{C}$ finishes the problem. Remark 1.1. Complex in the obvious way DOES NOT WORK, because the usual claim ("the fixed point is arc midpoint") is FALSE if the hypothesis that $P$ lies in the interior of the arc is dropped. See figure below.  Fun story, I pointed this out to Zuming during grading; I was the only one that realized the subtlety.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The isosceles triangle $\triangle A B C$, with $A B=A C$, is inscribed in the circle $\omega$. Let $P$ be a variable point on the arc $B C$ that does not contain $A$, and let $I_{B}$ and $I_{C}$ denote the incenters of triangles $\triangle A B P$ and $\triangle A C P$, respectively. Prove that as $P$ varies, the circumcircle of triangle $\triangle P I_{B} I_{C}$ passes through a fixed point.
|
Let $M$ be the midpoint of arc $B C$ not containing $A$. We claim $M$ is the desired fixed point.  Let $M_{B}, M_{C}$ be the second intersections of $P I_{B}$ and $P I_{C}$ with circumcircle. Claim - We have $\triangle I_{B} M_{B} M \cong \triangle I_{C} M_{C} M$. $$ \begin{aligned} M_{B} I_{B} & =M_{B} B=M_{C} C=M_{C} I_{C} \\ M M_{B} & =M M_{C} \\ \angle I_{B} M_{B} M & =\frac{1}{2} \widehat{P M}=\angle I_{C} M_{C} M \end{aligned} $$ This implies the desired congruence. Since $\angle M P A=90^{\circ}$ and ray $P A$ bisects $\angle I_{B} P I_{C}$, the conclusion $M I_{B}=M I_{C}$ finishes the problem. Remark 1.1. Complex in the obvious way DOES NOT WORK, because the usual claim ("the fixed point is arc midpoint") is FALSE if the hypothesis that $P$ lies in the interior of the arc is dropped. See figure below.  Fun story, I pointed this out to Zuming during grading; I was the only one that realized the subtlety.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
665eb3fe-700d-5462-9dee-e9fd634b4918
| 245,897
|
Prove that there exists a positive integer $n<10^{6}$ such that $5^{n}$ has six consecutive zeros in its decimal representation.
|
We will prove that $n=20+2^{19}=524308$ fits the bill. First, we claim that $$ 5^{n} \equiv 5^{20} \quad\left(\bmod 5^{20}\right) \quad \text { and } \quad 5^{n} \equiv 5^{20} \quad\left(\bmod 2^{20}\right) $$ Indeed, the first equality holds since both sides are $0\left(\bmod 5^{20}\right)$, and the second by $\varphi\left(2^{20}\right)=2^{19}$ and Euler's theorem. Hence $$ 5^{n} \equiv 5^{20} \quad\left(\bmod 10^{20}\right) $$ In other words, the last 20 digits of $5^{n}$ will match the decimal representation of $5^{20}$, with leading zeros. However, we have $$ 5^{20}=\frac{1}{2^{20}} \cdot 10^{20}<\frac{1}{1000^{2}} \cdot 10^{20}=10^{-6} \cdot 10^{20} $$ and hence those first six of those 20 digits will all be zero. This completes the proof! (To be concrete, it turns out that $5^{20}=95367431640625$ and so the last 20 digits of $5^{n}$ will be 00000095367431640625.$)$ Remark. Many of the first posts in the JMO 2016 discussion thread (see https://aops. com/community/c5h1230514) claimed that the problem was "super easy". In fact, the problem was solved by only about $10 \%$ of contestants. ब Authorship comments. This problem was inspired by the observation $5^{8} \equiv 5^{4}$ $\left(\bmod 10^{4}\right)$, i.e. that $5^{8}$ ended with 0625. I noticed this one day back in November, when I was lying on my bed after a long afternoon and was mindlessly computing powers of 5 in my head because I was too tired to do much else. When I reached $5^{8}$ I noticed for the first time that the ending 0625 was actually induced by $5^{4}$. (Given how much MathCounts I did, I really should have known this earlier!) Thinking about this for a few more seconds, I realized one could obtain arbitrarily long strings of 0 's by using a similar trick modulo larger powers of 10 . This surprised me, because I would have thought that if this was true, then I would have learned about it back in my contest days. However, I could not find any references, and I thought the result was quite nice, so I submitted it as a proposal for the JMO, where I thought it might be appreciated. The joke about six consecutive zeros is due to Zuming Feng.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exists a positive integer $n<10^{6}$ such that $5^{n}$ has six consecutive zeros in its decimal representation.
|
We will prove that $n=20+2^{19}=524308$ fits the bill. First, we claim that $$ 5^{n} \equiv 5^{20} \quad\left(\bmod 5^{20}\right) \quad \text { and } \quad 5^{n} \equiv 5^{20} \quad\left(\bmod 2^{20}\right) $$ Indeed, the first equality holds since both sides are $0\left(\bmod 5^{20}\right)$, and the second by $\varphi\left(2^{20}\right)=2^{19}$ and Euler's theorem. Hence $$ 5^{n} \equiv 5^{20} \quad\left(\bmod 10^{20}\right) $$ In other words, the last 20 digits of $5^{n}$ will match the decimal representation of $5^{20}$, with leading zeros. However, we have $$ 5^{20}=\frac{1}{2^{20}} \cdot 10^{20}<\frac{1}{1000^{2}} \cdot 10^{20}=10^{-6} \cdot 10^{20} $$ and hence those first six of those 20 digits will all be zero. This completes the proof! (To be concrete, it turns out that $5^{20}=95367431640625$ and so the last 20 digits of $5^{n}$ will be 00000095367431640625.$)$ Remark. Many of the first posts in the JMO 2016 discussion thread (see https://aops. com/community/c5h1230514) claimed that the problem was "super easy". In fact, the problem was solved by only about $10 \%$ of contestants. ब Authorship comments. This problem was inspired by the observation $5^{8} \equiv 5^{4}$ $\left(\bmod 10^{4}\right)$, i.e. that $5^{8}$ ended with 0625. I noticed this one day back in November, when I was lying on my bed after a long afternoon and was mindlessly computing powers of 5 in my head because I was too tired to do much else. When I reached $5^{8}$ I noticed for the first time that the ending 0625 was actually induced by $5^{4}$. (Given how much MathCounts I did, I really should have known this earlier!) Thinking about this for a few more seconds, I realized one could obtain arbitrarily long strings of 0 's by using a similar trick modulo larger powers of 10 . This surprised me, because I would have thought that if this was true, then I would have learned about it back in my contest days. However, I could not find any references, and I thought the result was quite nice, so I submitted it as a proposal for the JMO, where I thought it might be appreciated. The joke about six consecutive zeros is due to Zuming Feng.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
4a1a2905-7cda-5045-aac9-22971b25d3b5
| 245,908
|
Let $\triangle A B C$ be an acute triangle, with $O$ as its circumcenter. Point $H$ is the foot of the perpendicular from $A$ to line $B C$, and points $P$ and $Q$ are the feet of the perpendiculars from $H$ to the lines $A B$ and $A C$, respectively. Given that $$ A H^{2}=2 A O^{2} $$ prove that the points $O, P$, and $Q$ are collinear.
|
【 First approach (synthetic). First, since $A P \cdot A B=A H^{2}=A Q \cdot A C$, it follows that $P Q C B$ is cyclic. Consequently, we have $A O \perp P Q$.  Let $K$ be the foot of $A$ onto $P Q$, and let $D$ be the point diametrically opposite $A$. Thus $A, K, O, D$ are collinear. Since quadrilateral $K Q C D$ is cyclic $\left(~ \angle Q K D=\angle Q C D=90^{\circ}\right)$, we have $$ A K \cdot A D=A Q \cdot A C=A H^{2} \Longrightarrow A K=\frac{A H^{2}}{A D}=\frac{A H^{2}}{2 A O}=A O $$ so $K=O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute triangle, with $O$ as its circumcenter. Point $H$ is the foot of the perpendicular from $A$ to line $B C$, and points $P$ and $Q$ are the feet of the perpendiculars from $H$ to the lines $A B$ and $A C$, respectively. Given that $$ A H^{2}=2 A O^{2} $$ prove that the points $O, P$, and $Q$ are collinear.
|
【 First approach (synthetic). First, since $A P \cdot A B=A H^{2}=A Q \cdot A C$, it follows that $P Q C B$ is cyclic. Consequently, we have $A O \perp P Q$.  Let $K$ be the foot of $A$ onto $P Q$, and let $D$ be the point diametrically opposite $A$. Thus $A, K, O, D$ are collinear. Since quadrilateral $K Q C D$ is cyclic $\left(~ \angle Q K D=\angle Q C D=90^{\circ}\right)$, we have $$ A K \cdot A D=A Q \cdot A C=A H^{2} \Longrightarrow A K=\frac{A H^{2}}{A D}=\frac{A H^{2}}{2 A O}=A O $$ so $K=O$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
2100831c-cad4-5705-a63a-5d8c36095914
| 604,928
|
Let $\triangle A B C$ be an acute triangle, with $O$ as its circumcenter. Point $H$ is the foot of the perpendicular from $A$ to line $B C$, and points $P$ and $Q$ are the feet of the perpendiculars from $H$ to the lines $A B$ and $A C$, respectively. Given that $$ A H^{2}=2 A O^{2} $$ prove that the points $O, P$, and $Q$ are collinear.
|
ब Second approach (coordinates), with Joshua Hsieh. We impose coordinates with $H$ at the origin and $A=(0, a), B=(-b, 0), C=(c, 0)$, for $a, b, c>0$. Claim - The circumcenter has coordinates $\left(\frac{c-b}{2}, \frac{a}{2}-\frac{b c}{2 a}\right)$. - By power of a point, the second intersection of line $A H$ with the circumcircle is $\left(0,-\frac{b c}{a}\right)$. - Since the orthocenter is the reflection of this point across line $B C$, the orthocenter is given exactly by $\left(0, \frac{b c}{a}\right)$. - The centroid is is $\frac{\vec{A}+\vec{B}+\vec{C}}{3}=\left(\frac{c-b}{3}, \frac{a}{3}\right)$. - Since $\vec{H}-\vec{O}=3(\vec{G}-\vec{O})$ according to the Euler line, we have $\vec{O}=\frac{3}{2} \vec{G}-\frac{1}{2} \vec{H}$. This gives the desired formula. Note that $H Q=\frac{H A \cdot H C}{A C}=\frac{a c}{\sqrt{a^{2}+c^{2}}}$. If we let $T$ be the foot from $Q$ to $B C$, then $\triangle H Q T \tilde{+} \triangle A H C$ and so the $x$-coordinate of $Q$ is given by $H Q \cdot \frac{A H}{A C}=\frac{a^{2} c}{a^{2}+c^{2}}$. Repeating the analogous calculation for $Q$ and $P$ gives $$ \begin{aligned} Q & =\left(\frac{a^{2} c}{a^{2}+c^{2}}, \frac{a c^{2}}{a^{2}+c^{2}}\right) \\ P & =\left(-\frac{a^{2} b}{a^{2}+b^{2}}, \frac{a b^{2}}{a^{2}+b^{2}}\right) . \end{aligned} $$ Then, $O, P, Q$ are collinear if and only if the following shoelace determinant vanishes (with denominators cleared out): $$ \begin{aligned} 0 & =\operatorname{det}\left[\begin{array}{ccc} -a^{2} b & a b^{2} & a^{2}+b^{2} \\ a^{2} c & a c^{2} & a^{2}+c^{2} \\ a(c-b) & a^{2}-b c & 2 a \end{array}\right]=a \operatorname{det}\left[\begin{array}{ccc} -a b & a b^{2} & a^{2}+b^{2} \\ a c & a c^{2} & a^{2}+c^{2} \\ c-b & a^{2}-b c & 2 a \end{array}\right] \\ & =a \operatorname{det}\left[\begin{array}{ccc} -a(b+c) & a\left(b^{2}-c^{2}\right) & b^{2}-c^{2} \\ a c & a c^{2} & a^{2}+c^{2} \\ c-b & a^{2}-b c & 2 a \end{array}\right]=a(b+c) \operatorname{det}\left[\begin{array}{ccc} -a & a(b-c) & b-c \\ a c & a c^{2} & a^{2}+c^{2} \\ c-b & a^{2}-b c & 2 a \end{array}\right] \\ & =a(b+c) \cdot\left[-a\left(a^{2} c^{2}-a^{4}+b c\left(a^{2}+c^{2}\right)\right)+a c(b-c)\left(-a^{2}-b c\right)-(b-c)^{2} \cdot a^{3}\right] \\ & =a^{2}(b+c)\left(a^{4}-a^{2} b^{2}-b^{2} c^{2}-c^{2} a^{2}\right) . \end{aligned} $$ On the other hand, $$ \begin{aligned} A H^{2} & =a^{2} \\ 2 A O^{2} & =2\left[\left(\frac{c-b}{2}\right)^{2}+\left(-\frac{a}{2}-\frac{b c}{2 a}\right)^{2}\right]=\frac{a^{2}+b^{2}+c^{2}+\frac{b^{2} c^{2}}{a^{2}}}{2} \\ \Longrightarrow A H^{2}-2 A O^{2} & =\frac{1}{2}\left(a^{2}-b^{2}-c^{2}-\frac{b^{2} c^{2}}{a^{2}}\right) . \end{aligned} $$ So the conditions are equivalent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute triangle, with $O$ as its circumcenter. Point $H$ is the foot of the perpendicular from $A$ to line $B C$, and points $P$ and $Q$ are the feet of the perpendiculars from $H$ to the lines $A B$ and $A C$, respectively. Given that $$ A H^{2}=2 A O^{2} $$ prove that the points $O, P$, and $Q$ are collinear.
|
ब Second approach (coordinates), with Joshua Hsieh. We impose coordinates with $H$ at the origin and $A=(0, a), B=(-b, 0), C=(c, 0)$, for $a, b, c>0$. Claim - The circumcenter has coordinates $\left(\frac{c-b}{2}, \frac{a}{2}-\frac{b c}{2 a}\right)$. - By power of a point, the second intersection of line $A H$ with the circumcircle is $\left(0,-\frac{b c}{a}\right)$. - Since the orthocenter is the reflection of this point across line $B C$, the orthocenter is given exactly by $\left(0, \frac{b c}{a}\right)$. - The centroid is is $\frac{\vec{A}+\vec{B}+\vec{C}}{3}=\left(\frac{c-b}{3}, \frac{a}{3}\right)$. - Since $\vec{H}-\vec{O}=3(\vec{G}-\vec{O})$ according to the Euler line, we have $\vec{O}=\frac{3}{2} \vec{G}-\frac{1}{2} \vec{H}$. This gives the desired formula. Note that $H Q=\frac{H A \cdot H C}{A C}=\frac{a c}{\sqrt{a^{2}+c^{2}}}$. If we let $T$ be the foot from $Q$ to $B C$, then $\triangle H Q T \tilde{+} \triangle A H C$ and so the $x$-coordinate of $Q$ is given by $H Q \cdot \frac{A H}{A C}=\frac{a^{2} c}{a^{2}+c^{2}}$. Repeating the analogous calculation for $Q$ and $P$ gives $$ \begin{aligned} Q & =\left(\frac{a^{2} c}{a^{2}+c^{2}}, \frac{a c^{2}}{a^{2}+c^{2}}\right) \\ P & =\left(-\frac{a^{2} b}{a^{2}+b^{2}}, \frac{a b^{2}}{a^{2}+b^{2}}\right) . \end{aligned} $$ Then, $O, P, Q$ are collinear if and only if the following shoelace determinant vanishes (with denominators cleared out): $$ \begin{aligned} 0 & =\operatorname{det}\left[\begin{array}{ccc} -a^{2} b & a b^{2} & a^{2}+b^{2} \\ a^{2} c & a c^{2} & a^{2}+c^{2} \\ a(c-b) & a^{2}-b c & 2 a \end{array}\right]=a \operatorname{det}\left[\begin{array}{ccc} -a b & a b^{2} & a^{2}+b^{2} \\ a c & a c^{2} & a^{2}+c^{2} \\ c-b & a^{2}-b c & 2 a \end{array}\right] \\ & =a \operatorname{det}\left[\begin{array}{ccc} -a(b+c) & a\left(b^{2}-c^{2}\right) & b^{2}-c^{2} \\ a c & a c^{2} & a^{2}+c^{2} \\ c-b & a^{2}-b c & 2 a \end{array}\right]=a(b+c) \operatorname{det}\left[\begin{array}{ccc} -a & a(b-c) & b-c \\ a c & a c^{2} & a^{2}+c^{2} \\ c-b & a^{2}-b c & 2 a \end{array}\right] \\ & =a(b+c) \cdot\left[-a\left(a^{2} c^{2}-a^{4}+b c\left(a^{2}+c^{2}\right)\right)+a c(b-c)\left(-a^{2}-b c\right)-(b-c)^{2} \cdot a^{3}\right] \\ & =a^{2}(b+c)\left(a^{4}-a^{2} b^{2}-b^{2} c^{2}-c^{2} a^{2}\right) . \end{aligned} $$ On the other hand, $$ \begin{aligned} A H^{2} & =a^{2} \\ 2 A O^{2} & =2\left[\left(\frac{c-b}{2}\right)^{2}+\left(-\frac{a}{2}-\frac{b c}{2 a}\right)^{2}\right]=\frac{a^{2}+b^{2}+c^{2}+\frac{b^{2} c^{2}}{a^{2}}}{2} \\ \Longrightarrow A H^{2}-2 A O^{2} & =\frac{1}{2}\left(a^{2}-b^{2}-c^{2}-\frac{b^{2} c^{2}}{a^{2}}\right) . \end{aligned} $$ So the conditions are equivalent.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
2100831c-cad4-5705-a63a-5d8c36095914
| 604,928
|
Prove that there exist infinitely many pairs of relatively prime positive integers $a, b>1$ for which $a+b$ divides $a^{b}+b^{a}$.
|
One construction: let $d \equiv 1(\bmod 4), d>1$. Let $x=\frac{d^{d}+2^{d}}{d+2}$. Then set $$ a=\frac{x+d}{2}, \quad b=\frac{x-d}{2} $$ To see this works, first check that $b$ is odd and $a$ is even. Let $d=a-b$ be odd. Then: $$ \begin{aligned} a+b \mid a^{b}+b^{a} & \Longleftrightarrow(-b)^{b}+b^{a} \equiv 0 \quad(\bmod a+b) \\ & \Longleftrightarrow b^{a-b} \equiv 1 \quad(\bmod a+b) \\ & \Longleftrightarrow b^{d} \equiv 1 \quad(\bmod d+2 b) \\ & \Longleftrightarrow(-2)^{d} \equiv d^{d} \quad(\bmod d+2 b) \\ & \Longleftrightarrow d+2 b \mid d^{d}+2^{d} . \end{aligned} $$ So it would be enough that $$ d+2 b=\frac{d^{d}+2^{d}}{d+2} \Longrightarrow b=\frac{1}{2}\left(\frac{d^{d}+2^{d}}{d+2}-d\right) $$ which is what we constructed. Also, since $\operatorname{gcd}(x, d)=1$ it follows $\operatorname{gcd}(a, b)=\operatorname{gcd}(d, b)=$ 1. Remark. Ryan Kim points out that in fact, $(a, b)=(2 n-1,2 n+1)$ is always a solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exist infinitely many pairs of relatively prime positive integers $a, b>1$ for which $a+b$ divides $a^{b}+b^{a}$.
|
One construction: let $d \equiv 1(\bmod 4), d>1$. Let $x=\frac{d^{d}+2^{d}}{d+2}$. Then set $$ a=\frac{x+d}{2}, \quad b=\frac{x-d}{2} $$ To see this works, first check that $b$ is odd and $a$ is even. Let $d=a-b$ be odd. Then: $$ \begin{aligned} a+b \mid a^{b}+b^{a} & \Longleftrightarrow(-b)^{b}+b^{a} \equiv 0 \quad(\bmod a+b) \\ & \Longleftrightarrow b^{a-b} \equiv 1 \quad(\bmod a+b) \\ & \Longleftrightarrow b^{d} \equiv 1 \quad(\bmod d+2 b) \\ & \Longleftrightarrow(-2)^{d} \equiv d^{d} \quad(\bmod d+2 b) \\ & \Longleftrightarrow d+2 b \mid d^{d}+2^{d} . \end{aligned} $$ So it would be enough that $$ d+2 b=\frac{d^{d}+2^{d}}{d+2} \Longrightarrow b=\frac{1}{2}\left(\frac{d^{d}+2^{d}}{d+2}-d\right) $$ which is what we constructed. Also, since $\operatorname{gcd}(x, d)=1$ it follows $\operatorname{gcd}(a, b)=\operatorname{gcd}(d, b)=$ 1. Remark. Ryan Kim points out that in fact, $(a, b)=(2 n-1,2 n+1)$ is always a solution.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8c485124-df45-5d2d-9924-c24895e9a9dd
| 245,952
|
Let $A B C$ be an equilateral triangle and $P$ a point on its circumcircle. Set $D=$ $\overline{P A} \cap \overline{B C}, E=\overline{P B} \cap \overline{C A}, F=\overline{P C} \cap \overline{A B}$. Prove that the area of triangle $D E F$ is twice the area of triangle $A B C$.
|
\ First solution (barycentric). We invoke barycentric coordinates on $A B C$. Let $P=(u: v: w)$, with $u v+v w+w u=0$ (circumcircle equation with $a=b=c$ ). Then $D=(0: v: w), E=(u: 0: w), F=(u: v: 0)$. Hence $$ \begin{aligned} \frac{[D E F]}{[A B C]} & =\frac{1}{(u+v)(v+w)(w+u)} \operatorname{det}\left[\begin{array}{lll} 0 & v & w \\ u & 0 & w \\ u & v & 0 \end{array}\right] \\ & =\frac{2 u v w}{(u+v)(v+w)(w+u)} \\ & =\frac{2 u v w}{(u+v+w)(u v+v w+w u)-u v w} \\ & =\frac{2 u v w}{-u v w}=-2 \end{aligned} $$ as desired (areas signed).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an equilateral triangle and $P$ a point on its circumcircle. Set $D=$ $\overline{P A} \cap \overline{B C}, E=\overline{P B} \cap \overline{C A}, F=\overline{P C} \cap \overline{A B}$. Prove that the area of triangle $D E F$ is twice the area of triangle $A B C$.
|
\ First solution (barycentric). We invoke barycentric coordinates on $A B C$. Let $P=(u: v: w)$, with $u v+v w+w u=0$ (circumcircle equation with $a=b=c$ ). Then $D=(0: v: w), E=(u: 0: w), F=(u: v: 0)$. Hence $$ \begin{aligned} \frac{[D E F]}{[A B C]} & =\frac{1}{(u+v)(v+w)(w+u)} \operatorname{det}\left[\begin{array}{lll} 0 & v & w \\ u & 0 & w \\ u & v & 0 \end{array}\right] \\ & =\frac{2 u v w}{(u+v)(v+w)(w+u)} \\ & =\frac{2 u v w}{(u+v+w)(u v+v w+w u)-u v w} \\ & =\frac{2 u v w}{-u v w}=-2 \end{aligned} $$ as desired (areas signed).
|
{
"resource_path": "USAJMO/segmented/en-JMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
721270c6-a678-51e8-b1ee-c66a9e8b8bf3
| 245,966
|
Let $O$ and $H$ be the circumcenter and the orthocenter of an acute triangle $A B C$. Points $M$ and $D$ lie on side $B C$ such that $B M=C M$ and $\angle B A D=\angle C A D$. Ray $M O$ intersects the circumcircle of triangle $B H C$ in point $N$. Prove that $\angle A D O=\angle H A N$.
|
Let $P$ and $Q$ be the arc midpoints of $\widehat{B C}$, so that $A D M Q$ is cyclic (as $\measuredangle Q A D=$ $\measuredangle Q M D=90^{\circ}$ ). Since it's known that $(B H C)$ and $(A B C)$ are reflections across line $B C$, it follows $N$ is the reflection of the arc midpoint $P$ across $M$. Claim - Quadrilateral $A D N O$ is cyclic.  To finish, note that $\measuredangle H A N=\measuredangle O N A=\measuredangle O D A$. Remark. The orthocenter $H$ is superficial and can be deleted basically immediately. One can reverse-engineer the fact that $A D N O$ is cyclic from the truth of the problem statement. Remark. One can also show $A D N O$ concyclic by just computing $\measuredangle D A O=\measuredangle P A O$ and $\measuredangle D N O=\measuredangle D P N=\measuredangle A P Q$ in terms of the angles of the triangle, or even more directly just because $$ \measuredangle D N O=\measuredangle D N P=\measuredangle N P D=\measuredangle O P D=\measuredangle O N A=\measuredangle H A N $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ and $H$ be the circumcenter and the orthocenter of an acute triangle $A B C$. Points $M$ and $D$ lie on side $B C$ such that $B M=C M$ and $\angle B A D=\angle C A D$. Ray $M O$ intersects the circumcircle of triangle $B H C$ in point $N$. Prove that $\angle A D O=\angle H A N$.
|
Let $P$ and $Q$ be the arc midpoints of $\widehat{B C}$, so that $A D M Q$ is cyclic (as $\measuredangle Q A D=$ $\measuredangle Q M D=90^{\circ}$ ). Since it's known that $(B H C)$ and $(A B C)$ are reflections across line $B C$, it follows $N$ is the reflection of the arc midpoint $P$ across $M$. Claim - Quadrilateral $A D N O$ is cyclic.  To finish, note that $\measuredangle H A N=\measuredangle O N A=\measuredangle O D A$. Remark. The orthocenter $H$ is superficial and can be deleted basically immediately. One can reverse-engineer the fact that $A D N O$ is cyclic from the truth of the problem statement. Remark. One can also show $A D N O$ concyclic by just computing $\measuredangle D A O=\measuredangle P A O$ and $\measuredangle D N O=\measuredangle D P N=\measuredangle A P Q$ in terms of the angles of the triangle, or even more directly just because $$ \measuredangle D N O=\measuredangle D N P=\measuredangle N P D=\measuredangle O P D=\measuredangle O N A=\measuredangle H A N $$
|
{
"resource_path": "USAJMO/segmented/en-JMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
a827710d-83e5-5b8f-820c-0c3ce42fe761
| 245,981
|
Let $P_{1}, P_{2}, \ldots, P_{2 n}$ be $2 n$ distinct points on the unit circle $x^{2}+y^{2}=1$, other than $(1,0)$. Each point is colored either red or blue, with exactly $n$ red points and $n$ blue points. Let $R_{1}, R_{2}, \ldots, R_{n}$ be any ordering of the red points. Let $B_{1}$ be the nearest blue point to $R_{1}$ traveling counterclockwise around the circle starting from $R_{1}$. Then let $B_{2}$ be the nearest of the remaining blue points to $R_{2}$ travelling counterclockwise around the circle from $R_{2}$, and so on, until we have labeled all of the blue points $B_{1}, \ldots, B_{n}$. Show that the number of counterclockwise arcs of the form $R_{i} \rightarrow B_{i}$ that contain the point $(1,0)$ is independent of the way we chose the ordering $R_{1}, \ldots, R_{n}$ of the red points.
|
\ First "local" solution by swapping two points. Let $1 \leq i<n$ be any index and consider the two red points $R_{i}$ and $R_{i+1}$. There are two blue points $B_{i}$ and $B_{i+1}$ associated with them. Claim - If we swap the locations of points $R_{i}$ and $R_{i+1}$ then the new $\operatorname{arcs} R_{i} \rightarrow B_{i}$ and $R_{i+1} \rightarrow B_{i+1}$ will cover the same points. The two blue points can then be located in three possible ways: either 0,1 , or 2 of them lie on the arc $R_{i} \rightarrow R_{i+1}$. For each of the cases below, we illustrate on the left the locations of $B_{i}$ and $B_{i+1}$ and the corresponding arcs in green; then on the right we show the modified picture where $R_{i}$ and $R_{i+1}$ have swapped. (Note that by hypothesis there are no other blue points in the green arcs). Case 1  Case 2  Case $3 R_{i+1}{ }^{\prime}$  Observe that in all cases, the number of arcs covering any given point on the circumference is not changed. Consequently, this proves the claim. Finally, it is enough to recall that any permutation of the red points can be achieved by swapping consecutive points (put another way: $(i i+1)$ generates the permutation group $S_{n}$ ). This solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $P_{1}, P_{2}, \ldots, P_{2 n}$ be $2 n$ distinct points on the unit circle $x^{2}+y^{2}=1$, other than $(1,0)$. Each point is colored either red or blue, with exactly $n$ red points and $n$ blue points. Let $R_{1}, R_{2}, \ldots, R_{n}$ be any ordering of the red points. Let $B_{1}$ be the nearest blue point to $R_{1}$ traveling counterclockwise around the circle starting from $R_{1}$. Then let $B_{2}$ be the nearest of the remaining blue points to $R_{2}$ travelling counterclockwise around the circle from $R_{2}$, and so on, until we have labeled all of the blue points $B_{1}, \ldots, B_{n}$. Show that the number of counterclockwise arcs of the form $R_{i} \rightarrow B_{i}$ that contain the point $(1,0)$ is independent of the way we chose the ordering $R_{1}, \ldots, R_{n}$ of the red points.
|
\ First "local" solution by swapping two points. Let $1 \leq i<n$ be any index and consider the two red points $R_{i}$ and $R_{i+1}$. There are two blue points $B_{i}$ and $B_{i+1}$ associated with them. Claim - If we swap the locations of points $R_{i}$ and $R_{i+1}$ then the new $\operatorname{arcs} R_{i} \rightarrow B_{i}$ and $R_{i+1} \rightarrow B_{i+1}$ will cover the same points. The two blue points can then be located in three possible ways: either 0,1 , or 2 of them lie on the arc $R_{i} \rightarrow R_{i+1}$. For each of the cases below, we illustrate on the left the locations of $B_{i}$ and $B_{i+1}$ and the corresponding arcs in green; then on the right we show the modified picture where $R_{i}$ and $R_{i+1}$ have swapped. (Note that by hypothesis there are no other blue points in the green arcs). Case 1  Case 2  Case $3 R_{i+1}{ }^{\prime}$  Observe that in all cases, the number of arcs covering any given point on the circumference is not changed. Consequently, this proves the claim. Finally, it is enough to recall that any permutation of the red points can be achieved by swapping consecutive points (put another way: $(i i+1)$ generates the permutation group $S_{n}$ ). This solves the problem.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6cc8af89-f27f-5806-a452-9eabb5f60f3d
| 605,074
|
Let $P_{1}, P_{2}, \ldots, P_{2 n}$ be $2 n$ distinct points on the unit circle $x^{2}+y^{2}=1$, other than $(1,0)$. Each point is colored either red or blue, with exactly $n$ red points and $n$ blue points. Let $R_{1}, R_{2}, \ldots, R_{n}$ be any ordering of the red points. Let $B_{1}$ be the nearest blue point to $R_{1}$ traveling counterclockwise around the circle starting from $R_{1}$. Then let $B_{2}$ be the nearest of the remaining blue points to $R_{2}$ travelling counterclockwise around the circle from $R_{2}$, and so on, until we have labeled all of the blue points $B_{1}, \ldots, B_{n}$. Show that the number of counterclockwise arcs of the form $R_{i} \rightarrow B_{i}$ that contain the point $(1,0)$ is independent of the way we chose the ordering $R_{1}, \ldots, R_{n}$ of the red points.
|
II Second longer solution using an invariant. Visually, if we draw all the segments $R_{i} \rightarrow B_{i}$ then we obtain a set of $n$ chords. Say a chord is inverted if satisfies the problem condition, and stable otherwise. The problem contends that the number of stable/inverted chords depends only on the layout of the points and not on the choice of chords.  In fact we'll describe the number of inverted chords explicitly. Starting from $(1,0)$ we keep a running tally of $R-B$; in other words we start the counter at 0 and decrement by 1 at each blue point and increment by 1 at each red point. Let $x \leq 0$ be the lowest number ever recorded. Then: Claim - The number of inverted chords is $-x$ (and hence independent of the choice of chords). This is by induction on $n$. I think the easiest thing is to delete chord $R_{1} B_{1}$; note that the arc cut out by this chord contains no blue points. So if the chord was stable certainly no change to $x$. On the other hand, if the chord is inverted, then in particular the last point before $(1,0)$ was red, and so $x<0$. In this situation one sees that deleting the chord changes $x$ to $x+1$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $P_{1}, P_{2}, \ldots, P_{2 n}$ be $2 n$ distinct points on the unit circle $x^{2}+y^{2}=1$, other than $(1,0)$. Each point is colored either red or blue, with exactly $n$ red points and $n$ blue points. Let $R_{1}, R_{2}, \ldots, R_{n}$ be any ordering of the red points. Let $B_{1}$ be the nearest blue point to $R_{1}$ traveling counterclockwise around the circle starting from $R_{1}$. Then let $B_{2}$ be the nearest of the remaining blue points to $R_{2}$ travelling counterclockwise around the circle from $R_{2}$, and so on, until we have labeled all of the blue points $B_{1}, \ldots, B_{n}$. Show that the number of counterclockwise arcs of the form $R_{i} \rightarrow B_{i}$ that contain the point $(1,0)$ is independent of the way we chose the ordering $R_{1}, \ldots, R_{n}$ of the red points.
|
II Second longer solution using an invariant. Visually, if we draw all the segments $R_{i} \rightarrow B_{i}$ then we obtain a set of $n$ chords. Say a chord is inverted if satisfies the problem condition, and stable otherwise. The problem contends that the number of stable/inverted chords depends only on the layout of the points and not on the choice of chords.  In fact we'll describe the number of inverted chords explicitly. Starting from $(1,0)$ we keep a running tally of $R-B$; in other words we start the counter at 0 and decrement by 1 at each blue point and increment by 1 at each red point. Let $x \leq 0$ be the lowest number ever recorded. Then: Claim - The number of inverted chords is $-x$ (and hence independent of the choice of chords). This is by induction on $n$. I think the easiest thing is to delete chord $R_{1} B_{1}$; note that the arc cut out by this chord contains no blue points. So if the chord was stable certainly no change to $x$. On the other hand, if the chord is inverted, then in particular the last point before $(1,0)$ was red, and so $x<0$. In this situation one sees that deleting the chord changes $x$ to $x+1$, as desired.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6cc8af89-f27f-5806-a452-9eabb5f60f3d
| 605,074
|
Let $a, b, c$ be positive real numbers such that $a+b+c=4 \sqrt[3]{a b c}$. Prove that $$ 2(a b+b c+c a)+4 \min \left(a^{2}, b^{2}, c^{2}\right) \geq a^{2}+b^{2}+c^{2} $$
|
WLOG let $c=\min (a, b, c)=1$ by scaling. The given inequality becomes equivalent to $$ 4 a b+2 a+2 b+3 \geq(a+b)^{2} \quad \forall a+b=4(a b)^{1 / 3}-1 $$ Now, let $t=(a b)^{1 / 3}$ and eliminate $a+b$ using the condition, to get $$ 4 t^{3}+2(4 t-1)+3 \geq(4 t-1)^{2} \Longleftrightarrow 0 \leq 4 t^{3}-16 t^{2}+16 t=4 t(t-2)^{2} $$ which solves the problem. Equality occurs only if $t=2$, meaning $a b=8$ and $a+b=7$, which gives $$ \{a, b\}=\left\{\frac{7 \pm \sqrt{17}}{2}\right\} $$ with the assumption $c=1$. Scaling gives the curve of equality cases.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a+b+c=4 \sqrt[3]{a b c}$. Prove that $$ 2(a b+b c+c a)+4 \min \left(a^{2}, b^{2}, c^{2}\right) \geq a^{2}+b^{2}+c^{2} $$
|
WLOG let $c=\min (a, b, c)=1$ by scaling. The given inequality becomes equivalent to $$ 4 a b+2 a+2 b+3 \geq(a+b)^{2} \quad \forall a+b=4(a b)^{1 / 3}-1 $$ Now, let $t=(a b)^{1 / 3}$ and eliminate $a+b$ using the condition, to get $$ 4 t^{3}+2(4 t-1)+3 \geq(4 t-1)^{2} \Longleftrightarrow 0 \leq 4 t^{3}-16 t^{2}+16 t=4 t(t-2)^{2} $$ which solves the problem. Equality occurs only if $t=2$, meaning $a b=8$ and $a+b=7$, which gives $$ \{a, b\}=\left\{\frac{7 \pm \sqrt{17}}{2}\right\} $$ with the assumption $c=1$. Scaling gives the curve of equality cases.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e342a18e-6407-52ef-b019-302cfa311d1c
| 605,118
|
Let $A B C D$ be a quadrilateral inscribed in circle $\omega$ with $\overline{A C} \perp \overline{B D}$. Let $E$ and $F$ be the reflections of $D$ over $\overline{B A}$ and $\overline{B C}$, respectively, and let $P$ be the intersection of $\overline{B D}$ and $\overline{E F}$. Suppose that the circumcircles of $E P D$ and $F P D$ meet $\omega$ at $Q$ and $R$ different from $D$. Show that $E Q=F R$.
|
Most of this problem is about realizing where the points $P, Q, R$ are. 【I Second solution (Danielle Wang). Here is a solution which does not identify the point $P$ at all. We know that $B E=B D=B F$, by construction.  Claim - The points $B, Q, E$ are collinear. Similarly the points $B, R, F$ are collinear. Observe that $B E=B D=B F$, so $B$ is the circumcenter of $\triangle D E F$. Thus, $\measuredangle D E P=$ $\measuredangle D E F=90^{\circ}-\beta$. Then $$ \begin{aligned} \measuredangle D P E & =\measuredangle D E P+\measuredangle P D E=\left(90^{\circ}-\beta\right)+\alpha \\ & =\alpha-\beta+90^{\circ} \\ \measuredangle D Q^{\prime} B & =\measuredangle D C B=\measuredangle D C A+\measuredangle A C B \\ & =\measuredangle D B A-\left(90^{\circ}-\measuredangle D B C\right)=-\left(90^{\circ}-\alpha\right)-\left(90^{\circ}-\left(90^{\circ}-\beta\right)\right) \\ & =\alpha-\beta+90^{\circ} . \end{aligned} $$ Thus $Q^{\prime}$ lies on the desired circle, so $Q^{\prime}=Q$. Now, by power of a point we have $B Q \cdot B E=B P \cdot B D=B R \cdot B F$, so $B Q=B P=B R$. Hence $E Q=P D=F R$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in circle $\omega$ with $\overline{A C} \perp \overline{B D}$. Let $E$ and $F$ be the reflections of $D$ over $\overline{B A}$ and $\overline{B C}$, respectively, and let $P$ be the intersection of $\overline{B D}$ and $\overline{E F}$. Suppose that the circumcircles of $E P D$ and $F P D$ meet $\omega$ at $Q$ and $R$ different from $D$. Show that $E Q=F R$.
|
Most of this problem is about realizing where the points $P, Q, R$ are. 【I Second solution (Danielle Wang). Here is a solution which does not identify the point $P$ at all. We know that $B E=B D=B F$, by construction.  Claim - The points $B, Q, E$ are collinear. Similarly the points $B, R, F$ are collinear. Observe that $B E=B D=B F$, so $B$ is the circumcenter of $\triangle D E F$. Thus, $\measuredangle D E P=$ $\measuredangle D E F=90^{\circ}-\beta$. Then $$ \begin{aligned} \measuredangle D P E & =\measuredangle D E P+\measuredangle P D E=\left(90^{\circ}-\beta\right)+\alpha \\ & =\alpha-\beta+90^{\circ} \\ \measuredangle D Q^{\prime} B & =\measuredangle D C B=\measuredangle D C A+\measuredangle A C B \\ & =\measuredangle D B A-\left(90^{\circ}-\measuredangle D B C\right)=-\left(90^{\circ}-\alpha\right)-\left(90^{\circ}-\left(90^{\circ}-\beta\right)\right) \\ & =\alpha-\beta+90^{\circ} . \end{aligned} $$ Thus $Q^{\prime}$ lies on the desired circle, so $Q^{\prime}=Q$. Now, by power of a point we have $B Q \cdot B E=B P \cdot B D=B R \cdot B F$, so $B Q=B P=B R$. Hence $E Q=P D=F R$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
3626de4d-1073-5e04-94d9-46dcafbda4da
| 246,014
|
Let $p$ be a prime, and let $a_{1}, \ldots, a_{p}$ be integers. Show that there exists an integer $k$ such that the numbers $$ a_{1}+k, a_{2}+2 k, \ldots, a_{p}+p k $$ produce at least $\frac{1}{2} p$ distinct remainders upon division by $p$.
|
For each $k=0, \ldots, p-1$ let $G_{k}$ be the graph on $\{1, \ldots, p\}$ where we join $\{i, j\}$ if and only if $$ a_{i}+i k \equiv a_{j}+j k \quad(\bmod p) \Longleftrightarrow k \equiv-\frac{a_{i}-a_{j}}{i-j} \quad(\bmod p) $$ So we want a graph $G_{k}$ with at least $\frac{1}{2} p$ connected components. However, each $\{i, j\}$ appears in exactly one graph $G_{k}$, so some graph has at most $\frac{1}{p}\binom{p}{2}=\frac{1}{2}(p-1)$ edges (by "pigeonhole"). This graph has at least $\frac{1}{2}(p+1)$ connected components, as desired. Remark. Here is an example for $p=5$ showing equality can occur: $$ \left[\begin{array}{lllll} 0 & 0 & 3 & 4 & 3 \\ 0 & 1 & 0 & 2 & 2 \\ 0 & 2 & 2 & 0 & 1 \\ 0 & 3 & 4 & 3 & 0 \\ 0 & 4 & 1 & 1 & 4 \end{array}\right] . $$ Ankan Bhattacharya points out more generally that $a_{i}=i^{2}$ is sharp in general.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime, and let $a_{1}, \ldots, a_{p}$ be integers. Show that there exists an integer $k$ such that the numbers $$ a_{1}+k, a_{2}+2 k, \ldots, a_{p}+p k $$ produce at least $\frac{1}{2} p$ distinct remainders upon division by $p$.
|
For each $k=0, \ldots, p-1$ let $G_{k}$ be the graph on $\{1, \ldots, p\}$ where we join $\{i, j\}$ if and only if $$ a_{i}+i k \equiv a_{j}+j k \quad(\bmod p) \Longleftrightarrow k \equiv-\frac{a_{i}-a_{j}}{i-j} \quad(\bmod p) $$ So we want a graph $G_{k}$ with at least $\frac{1}{2} p$ connected components. However, each $\{i, j\}$ appears in exactly one graph $G_{k}$, so some graph has at most $\frac{1}{p}\binom{p}{2}=\frac{1}{2}(p-1)$ edges (by "pigeonhole"). This graph has at least $\frac{1}{2}(p+1)$ connected components, as desired. Remark. Here is an example for $p=5$ showing equality can occur: $$ \left[\begin{array}{lllll} 0 & 0 & 3 & 4 & 3 \\ 0 & 1 & 0 & 2 & 2 \\ 0 & 2 & 2 & 0 & 1 \\ 0 & 3 & 4 & 3 & 0 \\ 0 & 4 & 1 & 1 & 4 \end{array}\right] . $$ Ankan Bhattacharya points out more generally that $a_{i}=i^{2}$ is sharp in general.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5e8ad2de-f676-5f29-ad1a-10f63aff5c25
| 605,168
|
Karl starts with $n$ cards labeled $1,2, \ldots, n$ lined up in random order on his desk. He calls a pair $(a, b)$ of cards swapped if $a>b$ and the card labeled $a$ is to the left of the card labeled $b$. Karl picks up the card labeled 1 and inserts it back into the sequence in the opposite position: if the card labeled 1 had $i$ cards to its left, then it now has $i$ cards to its right. He then picks up the card labeled 2 and reinserts it in the same manner, and so on, until he has picked up and put back each of the cards $1, \ldots, n$ exactly once in that order. For example, if $n=4$, then one example of a process is $$ 3142 \longrightarrow 3412 \longrightarrow 2341 \longrightarrow 2431 \longrightarrow 2341 $$ which has three swapped pairs both before and after. Show that, no matter what lineup of cards Karl started with, his final lineup has the same number of swapped pairs as the starting lineup.
|
We define a new process $P^{\prime}$ where, when re-inserting card $i$, we additionally change its label from $i$ to $n+i$. An example of $P^{\prime}$ also starting with 3142 is: $$ 3142 \longrightarrow 3452 \longrightarrow 6345 \longrightarrow 6475 \longrightarrow 6785 . $$ Note that now, each step of $P^{\prime}$ preserves the number of inversions. Moreover, the final configuration of $P^{\prime}$ is the same as the final configuration of $P$ with all cards incremented by $n$, and of course thus has the same number of inversions. Boom.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Karl starts with $n$ cards labeled $1,2, \ldots, n$ lined up in random order on his desk. He calls a pair $(a, b)$ of cards swapped if $a>b$ and the card labeled $a$ is to the left of the card labeled $b$. Karl picks up the card labeled 1 and inserts it back into the sequence in the opposite position: if the card labeled 1 had $i$ cards to its left, then it now has $i$ cards to its right. He then picks up the card labeled 2 and reinserts it in the same manner, and so on, until he has picked up and put back each of the cards $1, \ldots, n$ exactly once in that order. For example, if $n=4$, then one example of a process is $$ 3142 \longrightarrow 3412 \longrightarrow 2341 \longrightarrow 2431 \longrightarrow 2341 $$ which has three swapped pairs both before and after. Show that, no matter what lineup of cards Karl started with, his final lineup has the same number of swapped pairs as the starting lineup.
|
We define a new process $P^{\prime}$ where, when re-inserting card $i$, we additionally change its label from $i$ to $n+i$. An example of $P^{\prime}$ also starting with 3142 is: $$ 3142 \longrightarrow 3452 \longrightarrow 6345 \longrightarrow 6475 \longrightarrow 6785 . $$ Note that now, each step of $P^{\prime}$ preserves the number of inversions. Moreover, the final configuration of $P^{\prime}$ is the same as the final configuration of $P$ with all cards incremented by $n$, and of course thus has the same number of inversions. Boom.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
7ef691c2-04e6-5b50-9afc-f3d726bb293e
| 605,180
|
There are $a+b$ bowls arranged in a row, numbered 1 through $a+b$, where $a$ and $b$ are given positive integers. Initially, each of the first $a$ bowls contains an apple, and each of the last $b$ bowls contains a pear. A legal move consists of moving an apple from bowl $i$ to bowl $i+1$ and a pear from bowl $j$ to bowl $j-1$, provided that the difference $i-j$ is even. We permit multiple fruits in the same bowl at the same time. The goal is to end up with the first $b$ bowls each containing a pear and the last $a$ bowls each containing an apple. Show that this is possible if and only if the product $a b$ is even.
|
First we show that if $a b$ is even then the goal is possible. We prove the result by induction on $a+b$. - If $\min (a, b)=0$ there is nothing to check. - If $\min (a, b)=1$, say $a=1$, then $b$ is even, and we can swap the (only) leftmost apple with the rightmost pear by working only with those fruits. - Now assume $\min (a, b) \geq 2$ and $a+b$ is odd. Then we can swap the leftmost apple with rightmost pear by working only with those fruits, reducing to the situation of $(a-1, b-1)$ which is possible by induction (at least one of them is even). - Finally assume $\min (a, b) \geq 2$ and $a+b$ is even (i.e. $a$ and $b$ are both even). Then we can swap the apple in position 1 with the pear in position $a+b-1$, and the apple in position 2 with the pear in position $a+b$. This reduces to the situation of $(a-2, b-2)$ which is also possible by induction. Now we show that the result is impossible if $a b$ is odd. Define $$ \begin{aligned} & X=\text { number apples in odd-numbered bowls } \\ & Y=\text { number pears in odd-numbered bowls. } \end{aligned} $$ Note that $X-Y$ does not change under this operation. However, if $a$ and $b$ are odd, then we initially have $X=\frac{1}{2}(a+1)$ and $Y=\frac{1}{2}(b-1)$, while the target position has $X=\frac{1}{2}(a-1)$ and $Y=\frac{1}{2}(b+1)$. So when $a b$ is odd this is not possible. First, note that apples only move right and pears only move left, a successful operation must take exactly $a b$ moves. So it is enough to prove that the number of moves made must be even. However, the number of fruits in odd-numbered bowls either increases by +2 or -2 in each move (according to whether $i$ and $j$ are both even or both odd), and since it ends up being the same at the end, the number of moves must be even. Alternatively, as pointed out in the official solutions, one can consider the sums of squares of positions of fruits. The quantity changes by $$ \left[(i+1)^{2}+(j-1)^{2}\right]-\left(i^{2}+j^{2}\right)=2(i-j)+2 \equiv 2(\bmod 4) $$ at each step, and eventually the sums of squares returns to zero, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are $a+b$ bowls arranged in a row, numbered 1 through $a+b$, where $a$ and $b$ are given positive integers. Initially, each of the first $a$ bowls contains an apple, and each of the last $b$ bowls contains a pear. A legal move consists of moving an apple from bowl $i$ to bowl $i+1$ and a pear from bowl $j$ to bowl $j-1$, provided that the difference $i-j$ is even. We permit multiple fruits in the same bowl at the same time. The goal is to end up with the first $b$ bowls each containing a pear and the last $a$ bowls each containing an apple. Show that this is possible if and only if the product $a b$ is even.
|
First we show that if $a b$ is even then the goal is possible. We prove the result by induction on $a+b$. - If $\min (a, b)=0$ there is nothing to check. - If $\min (a, b)=1$, say $a=1$, then $b$ is even, and we can swap the (only) leftmost apple with the rightmost pear by working only with those fruits. - Now assume $\min (a, b) \geq 2$ and $a+b$ is odd. Then we can swap the leftmost apple with rightmost pear by working only with those fruits, reducing to the situation of $(a-1, b-1)$ which is possible by induction (at least one of them is even). - Finally assume $\min (a, b) \geq 2$ and $a+b$ is even (i.e. $a$ and $b$ are both even). Then we can swap the apple in position 1 with the pear in position $a+b-1$, and the apple in position 2 with the pear in position $a+b$. This reduces to the situation of $(a-2, b-2)$ which is also possible by induction. Now we show that the result is impossible if $a b$ is odd. Define $$ \begin{aligned} & X=\text { number apples in odd-numbered bowls } \\ & Y=\text { number pears in odd-numbered bowls. } \end{aligned} $$ Note that $X-Y$ does not change under this operation. However, if $a$ and $b$ are odd, then we initially have $X=\frac{1}{2}(a+1)$ and $Y=\frac{1}{2}(b-1)$, while the target position has $X=\frac{1}{2}(a-1)$ and $Y=\frac{1}{2}(b+1)$. So when $a b$ is odd this is not possible. First, note that apples only move right and pears only move left, a successful operation must take exactly $a b$ moves. So it is enough to prove that the number of moves made must be even. However, the number of fruits in odd-numbered bowls either increases by +2 or -2 in each move (according to whether $i$ and $j$ are both even or both odd), and since it ends up being the same at the end, the number of moves must be even. Alternatively, as pointed out in the official solutions, one can consider the sums of squares of positions of fruits. The quantity changes by $$ \left[(i+1)^{2}+(j-1)^{2}\right]-\left(i^{2}+j^{2}\right)=2(i-j)+2 \equiv 2(\bmod 4) $$ at each step, and eventually the sums of squares returns to zero, as needed.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8b8f29fe-1882-5e94-8934-02bbfbbbeadb
| 246,047
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 First solution using symmedians. We define point $P$ to obey $$ \frac{A P}{B P}=\frac{A D^{2}}{B C^{2}}=\frac{A E^{2}}{B E^{2}} $$ so that $\overline{P E}$ is the $E$-symmedian of $\triangle E A B$, therefore the $E$-median of $\triangle E C D$. Now, note that $$ A D^{2}=A P \cdot A B \quad \text { and } \quad B C^{2}=B P \cdot B A $$ This implies $\triangle A P D \sim \triangle A D B$ and $\triangle B P C \sim \triangle B C A$. Thus $$ \measuredangle D P A=\measuredangle A D B=\measuredangle A C B=\measuredangle B C P $$ and so $P$ satisfies the condition as in the statement (and is the unique point to do so), as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 First solution using symmedians. We define point $P$ to obey $$ \frac{A P}{B P}=\frac{A D^{2}}{B C^{2}}=\frac{A E^{2}}{B E^{2}} $$ so that $\overline{P E}$ is the $E$-symmedian of $\triangle E A B$, therefore the $E$-median of $\triangle E C D$. Now, note that $$ A D^{2}=A P \cdot A B \quad \text { and } \quad B C^{2}=B P \cdot B A $$ This implies $\triangle A P D \sim \triangle A D B$ and $\triangle B P C \sim \triangle B C A$. Thus $$ \measuredangle D P A=\measuredangle A D B=\measuredangle A C B=\measuredangle B C P $$ and so $P$ satisfies the condition as in the statement (and is the unique point to do so), as needed.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
85c5cf58-8840-5ff6-8403-0cbcb9387b65
| 246,066
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 Second solution using only angle chasing (by proposer). We again re-define $P$ to obey $A D^{2}=A P \cdot A B$ and $B C^{2}=B P \cdot B A$. As before, this gives $\triangle A P D \sim \triangle A B D$ and $\triangle B P C \sim \triangle B D P$ and so we let $$ \theta:=\measuredangle D P A=\measuredangle A D B=\measuredangle A C B=\measuredangle B C P . $$ Our goal is to now show $\overline{P E}$ bisects $\overline{C D}$. Let $K=\overline{A C} \cap \overline{P D}$ and $L=\overline{A D} \cap \overline{P C}$. Since $\measuredangle K P A=\theta=\measuredangle A C B$, quadrilateral $B P K C$ is cyclic. Similarly, so is $A P L D$.  Finally $A K L B$ is cyclic since $$ \measuredangle B K A=\measuredangle B K C=\measuredangle B P C=\theta=\measuredangle D P A=\measuredangle D L A=\measuredangle B L A . $$ This implies $\measuredangle C K L=\measuredangle L B A=\measuredangle D C K$, so $\overline{K L} \| \overline{B C}$. Then $P E$ bisects $\overline{B C}$ by Ceva's theorem on $\triangle P C D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 Second solution using only angle chasing (by proposer). We again re-define $P$ to obey $A D^{2}=A P \cdot A B$ and $B C^{2}=B P \cdot B A$. As before, this gives $\triangle A P D \sim \triangle A B D$ and $\triangle B P C \sim \triangle B D P$ and so we let $$ \theta:=\measuredangle D P A=\measuredangle A D B=\measuredangle A C B=\measuredangle B C P . $$ Our goal is to now show $\overline{P E}$ bisects $\overline{C D}$. Let $K=\overline{A C} \cap \overline{P D}$ and $L=\overline{A D} \cap \overline{P C}$. Since $\measuredangle K P A=\theta=\measuredangle A C B$, quadrilateral $B P K C$ is cyclic. Similarly, so is $A P L D$.  Finally $A K L B$ is cyclic since $$ \measuredangle B K A=\measuredangle B K C=\measuredangle B P C=\theta=\measuredangle D P A=\measuredangle D L A=\measuredangle B L A . $$ This implies $\measuredangle C K L=\measuredangle L B A=\measuredangle D C K$, so $\overline{K L} \| \overline{B C}$. Then $P E$ bisects $\overline{B C}$ by Ceva's theorem on $\triangle P C D$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
85c5cf58-8840-5ff6-8403-0cbcb9387b65
| 246,066
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 Third solution (using inversion). By hypothesis, the circle $\omega_{a}$ centered at $A$ with radius $A D$ is orthogonal to the circle $\omega_{b}$ centered at $B$ with radius $B C$. For brevity, we let $\mathbf{I}_{a}$ and $\mathbf{I}_{b}$ denote inversion with respect to $\omega_{a}$ and $\omega_{b}$. We let $P$ denote the intersection of $\overline{A B}$ with the radical axis of $\omega_{a}$ and $\omega_{b}$; hence $P=\mathbf{I}_{a}(B)=\mathbf{I}_{b}(A)$. This already implies that $$ \measuredangle D P A \stackrel{\mathbf{I}_{a}}{=} \measuredangle A D B=\measuredangle A C B \stackrel{\mathbf{I}_{b}}{=} \measuredangle B P C $$ so $P$ satisfies the angle condition.  Claim - The point $K=\mathbf{I}_{a}(C)$ lies on $\omega_{b}$ and $\overline{D P}$. Similarly $L=\mathbf{I}_{b}(D)$ lies on $\omega_{a}$ and $\overline{C P}$. Finally, since $C, L, P$ are collinear, we get $A$ is concyclic with $K=\mathbf{I}_{a}(C), L=\mathbf{I}_{a}(L)$, $B=\mathbf{I}_{a}(P)$, i.e. that $A K L B$ is cyclic. So $\overline{K L} \| \overline{C D}$ by Reim's theorem, and hence $\overline{P E}$ bisects $\overline{C D}$ by Ceva's theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 Third solution (using inversion). By hypothesis, the circle $\omega_{a}$ centered at $A$ with radius $A D$ is orthogonal to the circle $\omega_{b}$ centered at $B$ with radius $B C$. For brevity, we let $\mathbf{I}_{a}$ and $\mathbf{I}_{b}$ denote inversion with respect to $\omega_{a}$ and $\omega_{b}$. We let $P$ denote the intersection of $\overline{A B}$ with the radical axis of $\omega_{a}$ and $\omega_{b}$; hence $P=\mathbf{I}_{a}(B)=\mathbf{I}_{b}(A)$. This already implies that $$ \measuredangle D P A \stackrel{\mathbf{I}_{a}}{=} \measuredangle A D B=\measuredangle A C B \stackrel{\mathbf{I}_{b}}{=} \measuredangle B P C $$ so $P$ satisfies the angle condition.  Claim - The point $K=\mathbf{I}_{a}(C)$ lies on $\omega_{b}$ and $\overline{D P}$. Similarly $L=\mathbf{I}_{b}(D)$ lies on $\omega_{a}$ and $\overline{C P}$. Finally, since $C, L, P$ are collinear, we get $A$ is concyclic with $K=\mathbf{I}_{a}(C), L=\mathbf{I}_{a}(L)$, $B=\mathbf{I}_{a}(P)$, i.e. that $A K L B$ is cyclic. So $\overline{K L} \| \overline{C D}$ by Reim's theorem, and hence $\overline{P E}$ bisects $\overline{C D}$ by Ceva's theorem.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
85c5cf58-8840-5ff6-8403-0cbcb9387b65
| 246,066
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 First solution by similarity. Note that $\triangle A E F$ is similar to $\triangle A B C$ (and oppositely oriented). However, since they have the same $A$-exradius, it follows they are congruent. 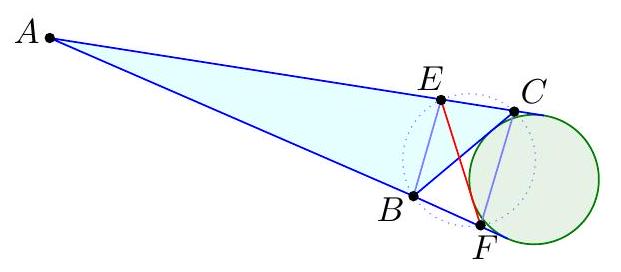 Consequently we get $E F=B C$. But this implies $B F C E$ is a rectangle, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 First solution by similarity. Note that $\triangle A E F$ is similar to $\triangle A B C$ (and oppositely oriented). However, since they have the same $A$-exradius, it follows they are congruent.  Consequently we get $E F=B C$. But this implies $B F C E$ is a rectangle, contradiction.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4395dec-2413-5656-82e2-8ca8061f7932
| 246,077
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 Second length solution by tangent lengths. By $t(\bullet)$ we mean the length of the tangent from $P$ to the $A$-excircle. It is a classical fact for example that $t(A)=s$. The main idea is to use the fact that $$ a \cos A=E F=t(E)+t(F) . $$ Here $E F=a \cos A$ follows from the extended law of sines applied to the circle with diameter $\overline{B C}$, since there we have $E F=B C \sin \angle E C F=a \sin \angle A C F=a \cos A$. We may now compute $$ \begin{aligned} & t(E)=t(A)-A E=s-c \cos A \\ & t(F)=t(A)-A F=s-b \cos A \end{aligned} $$ Therefore, $$ \begin{aligned} a \cos A=2 s-(b+c) \cos A \Longrightarrow \quad(a+b+c) \cos A & =2 s \\ \Longrightarrow \cos A & =1 . \end{aligned} $$ This is an obvious contradiction. Remark. On the other hand, there really is an equality case with $A$ being some point at infinity (meaning $\cos A=1$ ). So, this problem is "sharper" than one might expect; the answer is not "obviously no".
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 Second length solution by tangent lengths. By $t(\bullet)$ we mean the length of the tangent from $P$ to the $A$-excircle. It is a classical fact for example that $t(A)=s$. The main idea is to use the fact that $$ a \cos A=E F=t(E)+t(F) . $$ Here $E F=a \cos A$ follows from the extended law of sines applied to the circle with diameter $\overline{B C}$, since there we have $E F=B C \sin \angle E C F=a \sin \angle A C F=a \cos A$. We may now compute $$ \begin{aligned} & t(E)=t(A)-A E=s-c \cos A \\ & t(F)=t(A)-A F=s-b \cos A \end{aligned} $$ Therefore, $$ \begin{aligned} a \cos A=2 s-(b+c) \cos A \Longrightarrow \quad(a+b+c) \cos A & =2 s \\ \Longrightarrow \cos A & =1 . \end{aligned} $$ This is an obvious contradiction. Remark. On the other hand, there really is an equality case with $A$ being some point at infinity (meaning $\cos A=1$ ). So, this problem is "sharper" than one might expect; the answer is not "obviously no".
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4395dec-2413-5656-82e2-8ca8061f7932
| 246,077
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. I Third solution by Pitot and trigonometry. In fact, the $t(\bullet)$ notation from the previous solution gives us a classical theorem once we note the $A$-excircle is tangent to all four lines $E F, B C, B F$ and $C E$ : Claim (Pitot theorem) - We have $B F+E F=B C+C E$. $$ \begin{array}{ll} B F=t(B)-t(F) & E F=t(E)+t(F) \\ B C=t(B)+t(C) & C E=t(E)-t(C) \end{array} $$ and summing gives the result.  We now calculate all the lengths using trigonometry: $$ \begin{aligned} & B C=a \\ & B F=a \cos \left(180^{\circ}-B\right)=a \cos (A+C) \\ & C E=a \cos C \\ & E F=B C \sin \angle E C F=a \sin \angle A C F=a \cos A \end{aligned} $$ Thus, we apparently have $$ \cos (A+C)+\cos A=1+\cos C $$ but this is impossible since $\cos (A+C)<\cos C$ (since $A+C=180-B<90^{\circ}$ ) and $\cos A<1$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. I Third solution by Pitot and trigonometry. In fact, the $t(\bullet)$ notation from the previous solution gives us a classical theorem once we note the $A$-excircle is tangent to all four lines $E F, B C, B F$ and $C E$ : Claim (Pitot theorem) - We have $B F+E F=B C+C E$. $$ \begin{array}{ll} B F=t(B)-t(F) & E F=t(E)+t(F) \\ B C=t(B)+t(C) & C E=t(E)-t(C) \end{array} $$ and summing gives the result.  We now calculate all the lengths using trigonometry: $$ \begin{aligned} & B C=a \\ & B F=a \cos \left(180^{\circ}-B\right)=a \cos (A+C) \\ & C E=a \cos C \\ & E F=B C \sin \angle E C F=a \sin \angle A C F=a \cos A \end{aligned} $$ Thus, we apparently have $$ \cos (A+C)+\cos A=1+\cos C $$ but this is impossible since $\cos (A+C)<\cos C$ (since $A+C=180-B<90^{\circ}$ ) and $\cos A<1$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4395dec-2413-5656-82e2-8ca8061f7932
| 246,077
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 Fourth solution by Pitot and Ptolemy (Evan Chen). We give a trig-free way to finish from Pitot's theorem $$ B F+E F=B C+C E . $$ Assume that $x=B F, y=C E$, and $B C=1$; then the above relation becomes $$ 1+y-x=B C+C E-B F=E F=E F \cdot 1=x y+\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)} $$ with the last step by Ptolemy's theorem. This rearranges to give $$ (1+y)(1-x)=\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)} \Longrightarrow \frac{1+y}{1-y}=\frac{1+x}{1-x} \Longrightarrow x=y $$ but that means $B E C F$ is a rectangle: contradicting the fact that lines $B E$ and $C F$ meet at a point $A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 Fourth solution by Pitot and Ptolemy (Evan Chen). We give a trig-free way to finish from Pitot's theorem $$ B F+E F=B C+C E . $$ Assume that $x=B F, y=C E$, and $B C=1$; then the above relation becomes $$ 1+y-x=B C+C E-B F=E F=E F \cdot 1=x y+\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)} $$ with the last step by Ptolemy's theorem. This rearranges to give $$ (1+y)(1-x)=\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)} \Longrightarrow \frac{1+y}{1-y}=\frac{1+x}{1-x} \Longrightarrow x=y $$ but that means $B E C F$ is a rectangle: contradicting the fact that lines $B E$ and $C F$ meet at a point $A$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4395dec-2413-5656-82e2-8ca8061f7932
| 246,077
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 『 Fifth solution, by angle chasing only! Let $J$ denote the $A$-excenter. Then $J$ should be the intersection of the internal bisectors of $\angle F E C$ and $\angle F B C$, so it is the midpoint of arc $\widehat{F C}$ on the circle with diameter $\overline{B C}$.  But now we get $\angle B J C=90^{\circ}$ from $J$ lying on this circle. Yet $\angle B J C=90^{\circ}-\frac{1}{2} \angle A$ in general, so $\angle A=0^{\circ}$ which is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 『 Fifth solution, by angle chasing only! Let $J$ denote the $A$-excenter. Then $J$ should be the intersection of the internal bisectors of $\angle F E C$ and $\angle F B C$, so it is the midpoint of arc $\widehat{F C}$ on the circle with diameter $\overline{B C}$.  But now we get $\angle B J C=90^{\circ}$ from $J$ lying on this circle. Yet $\angle B J C=90^{\circ}-\frac{1}{2} \angle A$ in general, so $\angle A=0^{\circ}$ which is impossible.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4395dec-2413-5656-82e2-8ca8061f7932
| 246,077
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 Sixth solution (Zuming Feng). This is similar to the preceding solution, but phrased using contradiction and inequalities. We let $X$ and $Y$ denote the tangency points of the $A$-excircle on lines $A B$ and $A C$. Moreover, let $J$ denote the $A$-excenter.  Note that $A B>A E$ and $A X=A Y$, therefore $B X<E Y$. By considering the right triangles $X B J$ and $Y E J$ (which both have $J X=J Y$ ), we conclude $\tan \angle X B J>$ $\tan \angle Y E J$, thus $$ \angle X B J>\angle Y E J $$ However, if line $E F$ was actually tangent to the $A$-excircle, we would have $$ 2 \angle X B J=\angle X B C=\angle F B C=\angle F E C=\angle F E Y=2 \angle J E Y $$ which is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 Sixth solution (Zuming Feng). This is similar to the preceding solution, but phrased using contradiction and inequalities. We let $X$ and $Y$ denote the tangency points of the $A$-excircle on lines $A B$ and $A C$. Moreover, let $J$ denote the $A$-excenter.  Note that $A B>A E$ and $A X=A Y$, therefore $B X<E Y$. By considering the right triangles $X B J$ and $Y E J$ (which both have $J X=J Y$ ), we conclude $\tan \angle X B J>$ $\tan \angle Y E J$, thus $$ \angle X B J>\angle Y E J $$ However, if line $E F$ was actually tangent to the $A$-excircle, we would have $$ 2 \angle X B J=\angle X B C=\angle F B C=\angle F E C=\angle F E Y=2 \angle J E Y $$ which is a contradiction.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4395dec-2413-5656-82e2-8ca8061f7932
| 246,077
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 Seventh solution, by complex numbers, for comedic effect (Evan Chen). Let us denote the tangency points of the $A$-excircle with sides $B C, C A, A B$ as $x, y, z$. Assume moreover that line $E F$ is tangent to the $A$-excircle at a point $P$. Also, for brevity let $s=x y+y z+z x$. Then, we have $$ \begin{aligned} & E=\frac{2 p y}{p+y}=\frac{1}{2}\left(b+y+y-y^{2} \bar{b}\right)=\frac{z x}{z+x}+y-\frac{y^{2}}{z+x} \\ & \Longrightarrow \frac{2}{\frac{1}{p}+\frac{1}{y}}=\frac{x y+x z+z x-y^{2}}{z+x} \Longrightarrow \frac{\frac{1}{p}+\frac{1}{y}}{2}=\frac{x+z}{s-y^{2}} \end{aligned} $$ Similarly by considering the point $F$, $$ \frac{\frac{1}{p}+\frac{1}{z}}{2}=\frac{x+y}{s-z^{2}} $$ Thus we can eliminate $P$ and obtain $$ \begin{aligned} \Longrightarrow \frac{\frac{1}{y}-\frac{1}{z}}{2} & =\frac{x+z}{s-y^{2}}-\frac{x+y}{s-z^{2}}=\frac{-s(y-z)+x\left(y^{2}-z^{2}\right)+\left(y^{3}-z^{3}\right)}{\left(s-y^{2}\right)\left(s-z^{2}\right)} \\ \Longleftrightarrow \frac{1}{2 y z} & =\frac{s-x(y+z)-\left(y^{2}+y z+z^{2}\right)}{\left(s-y^{2}\right)\left(s-z^{2}\right)}=\frac{-\left(y^{2}+z^{2}\right)}{\left(s-y^{2}\right)\left(s-z^{2}\right)} \\ \Longleftrightarrow 0 & =\left(s-y^{2}\right)\left(s-z^{2}\right)+2 y z\left(y^{2}+z^{2}\right) \\ & =[x(y+z)+y(z-y)][x(y+z)+z(y-z)]+2 y z\left(y^{2}+z^{2}\right) \\ & =x^{2}(y+z)^{2}-(y-z)^{2} \cdot x(y+z)+y z\left(2 y^{2}+2 z^{2}-(y-z)^{2}\right) \\ & =x^{2}(y+z)^{2}-(y-z)^{2} \cdot x(y+z)+y z(y+z)^{2} \\ & =x y z(y+z)\left[\frac{x}{y}+\frac{x}{z}-\frac{y}{z}-\frac{z}{y}+2+\frac{y}{x}+\frac{z}{x}\right] \end{aligned} $$ However, $\triangle X Y Z$ is obtuse with $\angle X>90^{\circ}$, we have $y+z \neq 0$. Note that $$ \begin{aligned} & \frac{x}{y}+\frac{y}{x}=2 \operatorname{Re} \frac{x}{y}=2 \cos (2 \angle X Z Y) \\ & \frac{x}{z}+\frac{z}{x}=2 \operatorname{Re} \frac{x}{z}=2 \cos (2 \angle X Y Z) \\ & \frac{y}{z}+\frac{z}{y}=2 \operatorname{Re} \frac{y}{z}<2 \end{aligned} $$ and since $\cos (2 \angle X Z Y)+\cos (2 \angle X Y Z)>0$ (say by sum-to-product), we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>90^{\circ}$ and let $E$ and $F$ be the feet of the altitudes from $B$ and $C$. Can line $E F$ be tangent to the $A$-excircle?
|
We show it is not possible, by contradiction (assuming $E F$ is indeed tangent). Thus $B E C F$ is a convex cyclic quadrilateral inscribed in a circle with diameter $\overline{B C}$. Note also that the $A$-excircle lies on the opposite side from $A$ as line $E F$, since $A, E, C$ are collinear in that order. 【 Seventh solution, by complex numbers, for comedic effect (Evan Chen). Let us denote the tangency points of the $A$-excircle with sides $B C, C A, A B$ as $x, y, z$. Assume moreover that line $E F$ is tangent to the $A$-excircle at a point $P$. Also, for brevity let $s=x y+y z+z x$. Then, we have $$ \begin{aligned} & E=\frac{2 p y}{p+y}=\frac{1}{2}\left(b+y+y-y^{2} \bar{b}\right)=\frac{z x}{z+x}+y-\frac{y^{2}}{z+x} \\ & \Longrightarrow \frac{2}{\frac{1}{p}+\frac{1}{y}}=\frac{x y+x z+z x-y^{2}}{z+x} \Longrightarrow \frac{\frac{1}{p}+\frac{1}{y}}{2}=\frac{x+z}{s-y^{2}} \end{aligned} $$ Similarly by considering the point $F$, $$ \frac{\frac{1}{p}+\frac{1}{z}}{2}=\frac{x+y}{s-z^{2}} $$ Thus we can eliminate $P$ and obtain $$ \begin{aligned} \Longrightarrow \frac{\frac{1}{y}-\frac{1}{z}}{2} & =\frac{x+z}{s-y^{2}}-\frac{x+y}{s-z^{2}}=\frac{-s(y-z)+x\left(y^{2}-z^{2}\right)+\left(y^{3}-z^{3}\right)}{\left(s-y^{2}\right)\left(s-z^{2}\right)} \\ \Longleftrightarrow \frac{1}{2 y z} & =\frac{s-x(y+z)-\left(y^{2}+y z+z^{2}\right)}{\left(s-y^{2}\right)\left(s-z^{2}\right)}=\frac{-\left(y^{2}+z^{2}\right)}{\left(s-y^{2}\right)\left(s-z^{2}\right)} \\ \Longleftrightarrow 0 & =\left(s-y^{2}\right)\left(s-z^{2}\right)+2 y z\left(y^{2}+z^{2}\right) \\ & =[x(y+z)+y(z-y)][x(y+z)+z(y-z)]+2 y z\left(y^{2}+z^{2}\right) \\ & =x^{2}(y+z)^{2}-(y-z)^{2} \cdot x(y+z)+y z\left(2 y^{2}+2 z^{2}-(y-z)^{2}\right) \\ & =x^{2}(y+z)^{2}-(y-z)^{2} \cdot x(y+z)+y z(y+z)^{2} \\ & =x y z(y+z)\left[\frac{x}{y}+\frac{x}{z}-\frac{y}{z}-\frac{z}{y}+2+\frac{y}{x}+\frac{z}{x}\right] \end{aligned} $$ However, $\triangle X Y Z$ is obtuse with $\angle X>90^{\circ}$, we have $y+z \neq 0$. Note that $$ \begin{aligned} & \frac{x}{y}+\frac{y}{x}=2 \operatorname{Re} \frac{x}{y}=2 \cos (2 \angle X Z Y) \\ & \frac{x}{z}+\frac{z}{x}=2 \operatorname{Re} \frac{x}{z}=2 \cos (2 \angle X Y Z) \\ & \frac{y}{z}+\frac{z}{y}=2 \operatorname{Re} \frac{y}{z}<2 \end{aligned} $$ and since $\cos (2 \angle X Z Y)+\cos (2 \angle X Y Z)>0$ (say by sum-to-product), we are done.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4395dec-2413-5656-82e2-8ca8061f7932
| 246,077
|
Let $n \geq 2$ be an integer. Carl has $n$ books arranged on a bookshelf. Each book has a height and a width. No two books have the same height, and no two books have the same width. Initially, the books are arranged in increasing order of height from left to right. In a move, Carl picks any two adjacent books where the left book is wider and shorter than the right book, and swaps their locations. Carl does this repeatedly until no further moves are possible. Prove that regardless of how Carl makes his moves, he must stop after a finite number of moves, and when he does stop, the books are sorted in increasing order of width from left to right.
|
We say that a pair of books $(A, B)$ is height-inverted if $A$ is to the left of $B$ and taller than $A$. Similarly define width-inverted pairs. Note that every operation decreases the number of width-inverted pairs. This proves the procedure terminates, since the number of width-inverted pairs starts at $\binom{n}{2}$ and cannot increase indefinitely. Now consider a situation where no more moves are possible. Assume for contradiction two consecutive books $(A, B)$ are still width-inverted. Since the operation isn't possible anymore, they are also height-inverted. In particular, the operation could never have swapped $A$ and $B$. But this contradicts the assumption there were no height-inverted pairs initially.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 2$ be an integer. Carl has $n$ books arranged on a bookshelf. Each book has a height and a width. No two books have the same height, and no two books have the same width. Initially, the books are arranged in increasing order of height from left to right. In a move, Carl picks any two adjacent books where the left book is wider and shorter than the right book, and swaps their locations. Carl does this repeatedly until no further moves are possible. Prove that regardless of how Carl makes his moves, he must stop after a finite number of moves, and when he does stop, the books are sorted in increasing order of width from left to right.
|
We say that a pair of books $(A, B)$ is height-inverted if $A$ is to the left of $B$ and taller than $A$. Similarly define width-inverted pairs. Note that every operation decreases the number of width-inverted pairs. This proves the procedure terminates, since the number of width-inverted pairs starts at $\binom{n}{2}$ and cannot increase indefinitely. Now consider a situation where no more moves are possible. Assume for contradiction two consecutive books $(A, B)$ are still width-inverted. Since the operation isn't possible anymore, they are also height-inverted. In particular, the operation could never have swapped $A$ and $B$. But this contradicts the assumption there were no height-inverted pairs initially.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
a8927b95-cf5e-5e24-b9d8-d040878eb1b7
| 605,382
|
Let $A B C D$ be a convex quadrilateral inscribed in a circle and satisfying $$ D A<A B=B C<C D $$ Points $E$ and $F$ are chosen on sides $C D$ and $A B$ such that $\overline{B E} \perp \overline{A C}$ and $\overline{E F} \| \overline{B C}$. Prove that $F B=F D$.
|
【 First solution by inscribed angle theorem. Since $\overline{E F} \| \overline{B C}$ we may set $\theta=\angle F E B=$ $\angle C B E=\angle E B F$. This already implies $F E=F B$, so we will in fact prove that $F$ is the circumcenter of $\triangle B E D$. 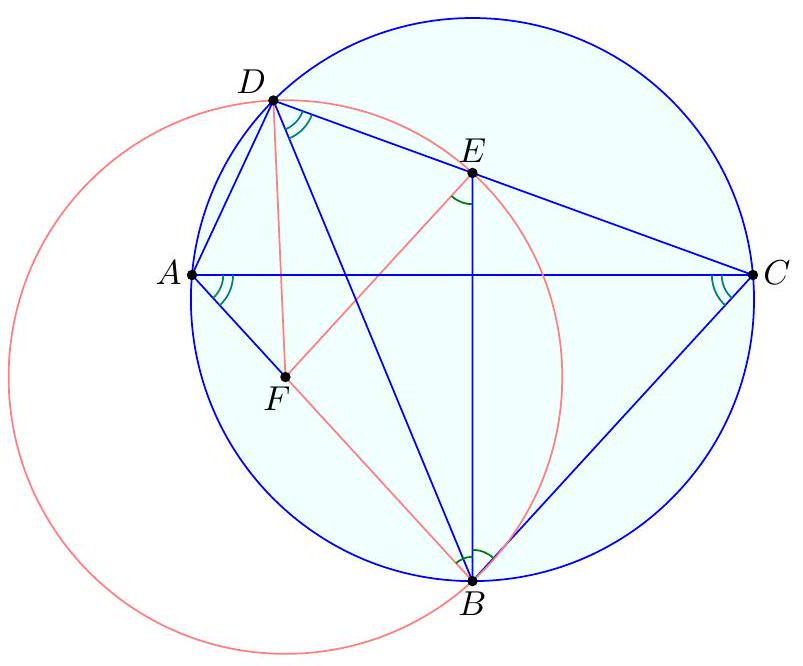 Note that $\angle B D C=\angle B A C=90^{\circ}-\theta$. However, $\angle B F E=180^{\circ}-2 \theta$. So by the inscribed angle theorem, $D$ lies on the circle centered at $F$ with radius $F E=F B$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral inscribed in a circle and satisfying $$ D A<A B=B C<C D $$ Points $E$ and $F$ are chosen on sides $C D$ and $A B$ such that $\overline{B E} \perp \overline{A C}$ and $\overline{E F} \| \overline{B C}$. Prove that $F B=F D$.
|
【 First solution by inscribed angle theorem. Since $\overline{E F} \| \overline{B C}$ we may set $\theta=\angle F E B=$ $\angle C B E=\angle E B F$. This already implies $F E=F B$, so we will in fact prove that $F$ is the circumcenter of $\triangle B E D$.  Note that $\angle B D C=\angle B A C=90^{\circ}-\theta$. However, $\angle B F E=180^{\circ}-2 \theta$. So by the inscribed angle theorem, $D$ lies on the circle centered at $F$ with radius $F E=F B$, as desired.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5cb0198-dcef-5584-832a-adfcfe560780
| 605,422
|
Let $A B C D$ be a convex quadrilateral inscribed in a circle and satisfying $$ D A<A B=B C<C D $$ Points $E$ and $F$ are chosen on sides $C D$ and $A B$ such that $\overline{B E} \perp \overline{A C}$ and $\overline{E F} \| \overline{B C}$. Prove that $F B=F D$.
|
đ Second general solution by angle chasing. By Reim's theorem, $A F E D$ is cyclic. 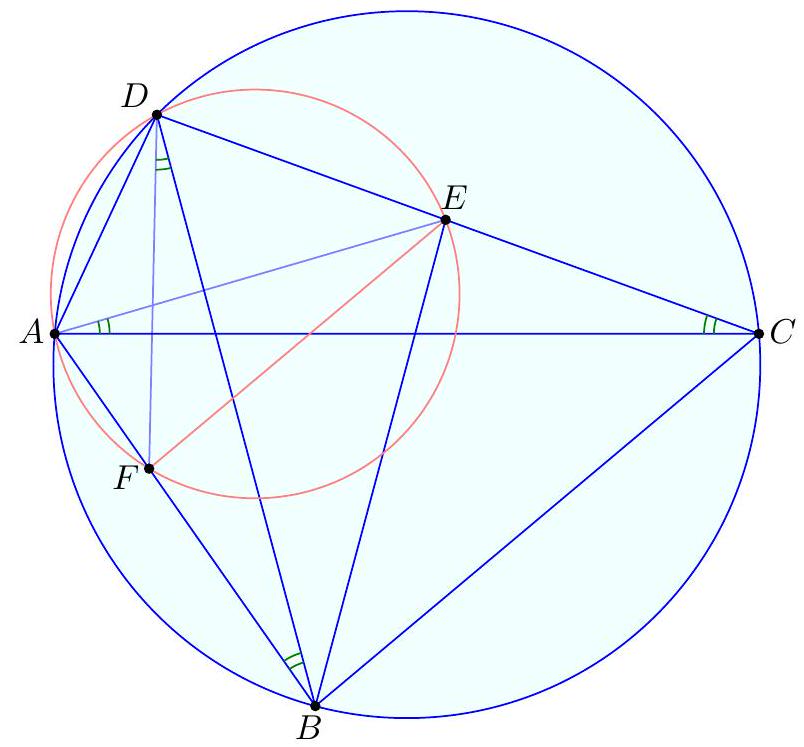 Hence $$ \begin{aligned} \measuredangle F D B & =\measuredangle F D C-\measuredangle B D C=\measuredangle F A E-\measuredangle F A C \\ & =\measuredangle C A E=\measuredangle E C A=\measuredangle D C A=\measuredangle D B A=\measuredangle D B F \end{aligned} $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral inscribed in a circle and satisfying $$ D A<A B=B C<C D $$ Points $E$ and $F$ are chosen on sides $C D$ and $A B$ such that $\overline{B E} \perp \overline{A C}$ and $\overline{E F} \| \overline{B C}$. Prove that $F B=F D$.
|
đ Second general solution by angle chasing. By Reim's theorem, $A F E D$ is cyclic.  Hence $$ \begin{aligned} \measuredangle F D B & =\measuredangle F D C-\measuredangle B D C=\measuredangle F A E-\measuredangle F A C \\ & =\measuredangle C A E=\measuredangle E C A=\measuredangle D C A=\measuredangle D B A=\measuredangle D B F \end{aligned} $$ as desired.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5cb0198-dcef-5584-832a-adfcfe560780
| 605,422
|
Let $A B C D$ be a convex quadrilateral inscribed in a circle and satisfying $$ D A<A B=B C<C D $$ Points $E$ and $F$ are chosen on sides $C D$ and $A B$ such that $\overline{B E} \perp \overline{A C}$ and $\overline{E F} \| \overline{B C}$. Prove that $F B=F D$.
|
\ Third general solution by Pascal. Extend rays $A E$ and $D F$ to meet the circumcircle again at $G$ and $H$. By Pascal's theorem on $H D C B A G$, it follows that $E, F$, and $G H \cap B C$ are collinear, which means that $\overline{E F}\|\overline{G H}\| \overline{B C}$.  Since $E A=E C$, it follows $D A G C$ in isosceles trapezoid. But also $G H B C$ is an isosceles trapezoid. Thus $\mathrm{m} \widehat{D A}=\mathrm{m} \widehat{G C}=\mathrm{m} \widehat{B H}$, so $D A H B$ is an isosceles trapezoid. Thus $F D=F B$. Remark. Addicts of projective geometry can use Pascal on $D B C A H G$ to finish rather than noting the equal arcs.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral inscribed in a circle and satisfying $$ D A<A B=B C<C D $$ Points $E$ and $F$ are chosen on sides $C D$ and $A B$ such that $\overline{B E} \perp \overline{A C}$ and $\overline{E F} \| \overline{B C}$. Prove that $F B=F D$.
|
\ Third general solution by Pascal. Extend rays $A E$ and $D F$ to meet the circumcircle again at $G$ and $H$. By Pascal's theorem on $H D C B A G$, it follows that $E, F$, and $G H \cap B C$ are collinear, which means that $\overline{E F}\|\overline{G H}\| \overline{B C}$.  Since $E A=E C$, it follows $D A G C$ in isosceles trapezoid. But also $G H B C$ is an isosceles trapezoid. Thus $\mathrm{m} \widehat{D A}=\mathrm{m} \widehat{G C}=\mathrm{m} \widehat{B H}$, so $D A H B$ is an isosceles trapezoid. Thus $F D=F B$. Remark. Addicts of projective geometry can use Pascal on $D B C A H G$ to finish rather than noting the equal arcs.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5cb0198-dcef-5584-832a-adfcfe560780
| 605,422
|
Let $n \geq 2$ be an integer. Let $P\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ be a nonconstant $n$-variable polynomial with real coefficients. Assuming that $P$ vanishes whenever two of its arguments are equal, prove that $P$ has at least $n$ ! terms.
|
『 First solution using induction (by Ankan). Begin with the following observation: Claim - Let $1 \leq i<j \leq n$. There is no term of $P$ which omits both $x_{i}$ and $x_{j}$. Remark (Technical warning for experts). The fact we used is not true if $\mathbb{R}$ is replaced by a field with finitely many elements, such as $\mathbb{F}_{p}$, even with one variable. For example the one-variable polynomial $X^{p}-X$ vanishes on every element of $\mathbb{F}_{p}$, by Fermat's little theorem. We proceed by induction on $n \geq 2$ with the base case $n=2$ being clear. Assume WLOG $P$ is not divisible by any of $x_{1}, \ldots, x_{n}$, since otherwise we may simply divide out this factor. Now for the inductive step, note that - The polynomial $P\left(0, x_{2}, x_{3}, \ldots, x_{n}\right)$ obviously satisfies the inductive hypothesis and is not identically zero since $x_{1} \nmid P$, so it has at least ( $n-1$ )! terms. - Similarly, $P\left(x_{1}, 0, x_{3}, \ldots, x_{n}\right)$ also has at least $(n-1)$ ! terms. - Similarly, $P\left(x_{1}, x_{2}, 0, \ldots, x_{n}\right)$ also has at least $(n-1)$ ! terms. - . . .and so on. By the claim, all the terms obtained in this way came from different terms of the original polynomial $P$. Therefore, $P$ itself has at least $n \cdot(n-1)!=n!$ terms. Remark. Equality is achieved by the Vandermonde polynomial $P=\prod_{1 \leq i<j \leq n}\left(x_{i}-x_{j}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n \geq 2$ be an integer. Let $P\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ be a nonconstant $n$-variable polynomial with real coefficients. Assuming that $P$ vanishes whenever two of its arguments are equal, prove that $P$ has at least $n$ ! terms.
|
『 First solution using induction (by Ankan). Begin with the following observation: Claim - Let $1 \leq i<j \leq n$. There is no term of $P$ which omits both $x_{i}$ and $x_{j}$. Remark (Technical warning for experts). The fact we used is not true if $\mathbb{R}$ is replaced by a field with finitely many elements, such as $\mathbb{F}_{p}$, even with one variable. For example the one-variable polynomial $X^{p}-X$ vanishes on every element of $\mathbb{F}_{p}$, by Fermat's little theorem. We proceed by induction on $n \geq 2$ with the base case $n=2$ being clear. Assume WLOG $P$ is not divisible by any of $x_{1}, \ldots, x_{n}$, since otherwise we may simply divide out this factor. Now for the inductive step, note that - The polynomial $P\left(0, x_{2}, x_{3}, \ldots, x_{n}\right)$ obviously satisfies the inductive hypothesis and is not identically zero since $x_{1} \nmid P$, so it has at least ( $n-1$ )! terms. - Similarly, $P\left(x_{1}, 0, x_{3}, \ldots, x_{n}\right)$ also has at least $(n-1)$ ! terms. - Similarly, $P\left(x_{1}, x_{2}, 0, \ldots, x_{n}\right)$ also has at least $(n-1)$ ! terms. - . . .and so on. By the claim, all the terms obtained in this way came from different terms of the original polynomial $P$. Therefore, $P$ itself has at least $n \cdot(n-1)!=n!$ terms. Remark. Equality is achieved by the Vandermonde polynomial $P=\prod_{1 \leq i<j \leq n}\left(x_{i}-x_{j}\right)$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
bf5e94d6-1a9a-51a0-9a40-3e7bfb4b115c
| 246,148
|
Let $n \geq 2$ be an integer. Let $P\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ be a nonconstant $n$-variable polynomial with real coefficients. Assuming that $P$ vanishes whenever two of its arguments are equal, prove that $P$ has at least $n$ ! terms.
|
【 Second solution using Vandermonde polynomial (by Yang Liu). Since $x_{i}-x_{j}$ divides $P$ for any $i \neq j$, it follows that $P$ should be divisible by the Vandermonde polynomial $$ V=\prod_{i<j}\left(x_{j}-x_{i}\right)=\sum_{\sigma} \operatorname{sgn}(\sigma) x_{1}^{\sigma(0)} x_{2}^{\sigma(1)} \ldots x_{n}^{\sigma(n-1)} $$ where the sum runs over all permutations $\sigma$ on $\{0, \ldots, n-1\}$. Consequently, we may write $$ P=\sum_{\sigma} \operatorname{sgn}(\sigma) x_{1}^{\sigma(0)} x_{2}^{\sigma(1)} \ldots x_{n}^{\sigma(n-1)} Q $$ The main idea is that each of the $n$ ! terms of the above sum has a monomial not appearing in any of the other terms. As an example, consider $x_{1}^{n-1} x_{2}^{n-2} \ldots x_{n-1}^{1} x_{n}^{0}$. Among all monomial in $Q$, consider the monomial $x_{1}^{e_{1}} x_{2}^{e_{2}} \ldots x_{n}^{e_{n}}$ with the largest $e_{1}$, then largest $e_{2}, \ldots$. (In other words, take the lexicographically largest $\left(e_{1}, \ldots, e_{n}\right)$.) This term $$ x_{1}^{e_{1}+(n-1)} x_{2}^{e_{2}+(n-2)} \ldots x_{n}^{e_{n}} $$ can't appear anywhere else because it is strictly lexicographically larger than any other term appearing in any other expansion. Repeating this argument with every $\sigma$ gives the conclusion.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n \geq 2$ be an integer. Let $P\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ be a nonconstant $n$-variable polynomial with real coefficients. Assuming that $P$ vanishes whenever two of its arguments are equal, prove that $P$ has at least $n$ ! terms.
|
【 Second solution using Vandermonde polynomial (by Yang Liu). Since $x_{i}-x_{j}$ divides $P$ for any $i \neq j$, it follows that $P$ should be divisible by the Vandermonde polynomial $$ V=\prod_{i<j}\left(x_{j}-x_{i}\right)=\sum_{\sigma} \operatorname{sgn}(\sigma) x_{1}^{\sigma(0)} x_{2}^{\sigma(1)} \ldots x_{n}^{\sigma(n-1)} $$ where the sum runs over all permutations $\sigma$ on $\{0, \ldots, n-1\}$. Consequently, we may write $$ P=\sum_{\sigma} \operatorname{sgn}(\sigma) x_{1}^{\sigma(0)} x_{2}^{\sigma(1)} \ldots x_{n}^{\sigma(n-1)} Q $$ The main idea is that each of the $n$ ! terms of the above sum has a monomial not appearing in any of the other terms. As an example, consider $x_{1}^{n-1} x_{2}^{n-2} \ldots x_{n-1}^{1} x_{n}^{0}$. Among all monomial in $Q$, consider the monomial $x_{1}^{e_{1}} x_{2}^{e_{2}} \ldots x_{n}^{e_{n}}$ with the largest $e_{1}$, then largest $e_{2}, \ldots$. (In other words, take the lexicographically largest $\left(e_{1}, \ldots, e_{n}\right)$.) This term $$ x_{1}^{e_{1}+(n-1)} x_{2}^{e_{2}+(n-2)} \ldots x_{n}^{e_{n}} $$ can't appear anywhere else because it is strictly lexicographically larger than any other term appearing in any other expansion. Repeating this argument with every $\sigma$ gives the conclusion.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
bf5e94d6-1a9a-51a0-9a40-3e7bfb4b115c
| 246,148
|
Rectangles $B C C_{1} B_{2}, C A A_{1} C_{2}$, and $A B B_{1} A_{2}$ are erected outside an acute triangle $A B C$. Suppose that $$ \angle B C_{1} C+\angle C A_{1} A+\angle A B_{1} B=180^{\circ} . $$ Prove that lines $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent.
|
The angle condition implies the circumcircles of the three rectangles concur at a single point $P$.  Then $\measuredangle C P B_{2}=\measuredangle C P A_{1}=90^{\circ}$, hence $P$ lies on $A_{1} B_{2}$ etc., so we're done. Remark. As one might guess from the two-sentence solution, the entire difficulty of the problem is getting the characterization of the concurrence point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Rectangles $B C C_{1} B_{2}, C A A_{1} C_{2}$, and $A B B_{1} A_{2}$ are erected outside an acute triangle $A B C$. Suppose that $$ \angle B C_{1} C+\angle C A_{1} A+\angle A B_{1} B=180^{\circ} . $$ Prove that lines $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent.
|
The angle condition implies the circumcircles of the three rectangles concur at a single point $P$.  Then $\measuredangle C P B_{2}=\measuredangle C P A_{1}=90^{\circ}$, hence $P$ lies on $A_{1} B_{2}$ etc., so we're done. Remark. As one might guess from the two-sentence solution, the entire difficulty of the problem is getting the characterization of the concurrence point.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2021-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6c28363b-d4e8-5b95-82b2-04909136f6df
| 605,504
|
An equilateral triangle $\Delta$ of side length $L>0$ is given. Suppose that $n$ equilateral triangles with side length 1 and with non-overlapping interiors are drawn inside $\Delta$, such that each unit equilateral triangle has sides parallel to $\Delta$, but with opposite orientation. Prove that $$ n \leq \frac{2}{3} L^{2} . $$
|
 Claim - All the hexagons are disjoint and lie inside $\Delta$. Since each hexagon has area $\frac{3 \sqrt{3}}{8}$ and lies inside $\Delta$, we conclude $$ \frac{3 \sqrt{3}}{8} \cdot n \leq \frac{\sqrt{3}}{4} L^{2} \Longrightarrow n \leq \frac{2}{3} L^{2} $$ Remark. The constant $\frac{2}{3}$ is sharp and cannot be improved. The following tessellation shows how to achieve the $\frac{2}{3}$ density. In the figure on the left, one of the green hexagons is drawn in for illustration. The version on the right has all the hexagons. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
An equilateral triangle $\Delta$ of side length $L>0$ is given. Suppose that $n$ equilateral triangles with side length 1 and with non-overlapping interiors are drawn inside $\Delta$, such that each unit equilateral triangle has sides parallel to $\Delta$, but with opposite orientation. Prove that $$ n \leq \frac{2}{3} L^{2} . $$
|
 Claim - All the hexagons are disjoint and lie inside $\Delta$. Since each hexagon has area $\frac{3 \sqrt{3}}{8}$ and lies inside $\Delta$, we conclude $$ \frac{3 \sqrt{3}}{8} \cdot n \leq \frac{\sqrt{3}}{4} L^{2} \Longrightarrow n \leq \frac{2}{3} L^{2} $$ Remark. The constant $\frac{2}{3}$ is sharp and cannot be improved. The following tessellation shows how to achieve the $\frac{2}{3}$ density. In the figure on the left, one of the green hexagons is drawn in for illustration. The version on the right has all the hexagons. 
|
{
"resource_path": "USAJMO/segmented/en-JMO-2021-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d8d96dab-95e9-5b16-9bfb-1998245eb361
| 605,514
|
Let $a$ and $b$ be positive integers. Every cell of an $(a+b+1) \times(a+b+1)$ grid is colored either amber or bronze such that there are at least $a^{2}+a b-b$ amber cells and at least $b^{2}+a b-a$ bronze cells. Prove that it is possible to choose $a$ amber cells and $b$ bronze cells such that no two of the $a+b$ chosen cells lie in the same row or column.
|
Claim - There exists a transversal $T_{a}$ with at least $a$ amber cells. Analogously, there exists a transversal $T_{b}$ with at least $b$ bronze cells. $$ \frac{a^{2}+a b-b}{a+b+1}=(a-1)+\frac{1}{a+b+1}>a-1 $$ Now imagine we transform $T_{a}$ to $T_{b}$ in some number of steps, by repeatedly choosing cells $c$ and $c^{\prime}$ and swapping them with the two other corners of the rectangle formed by their row/column, as shown in the figure.  By "discrete intermediate value theorem", the number of amber cells will be either $a$ or $a+1$ at some point during this transformation. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $a$ and $b$ be positive integers. Every cell of an $(a+b+1) \times(a+b+1)$ grid is colored either amber or bronze such that there are at least $a^{2}+a b-b$ amber cells and at least $b^{2}+a b-a$ bronze cells. Prove that it is possible to choose $a$ amber cells and $b$ bronze cells such that no two of the $a+b$ chosen cells lie in the same row or column.
|
Claim - There exists a transversal $T_{a}$ with at least $a$ amber cells. Analogously, there exists a transversal $T_{b}$ with at least $b$ bronze cells. $$ \frac{a^{2}+a b-b}{a+b+1}=(a-1)+\frac{1}{a+b+1}>a-1 $$ Now imagine we transform $T_{a}$ to $T_{b}$ in some number of steps, by repeatedly choosing cells $c$ and $c^{\prime}$ and swapping them with the two other corners of the rectangle formed by their row/column, as shown in the figure.  By "discrete intermediate value theorem", the number of amber cells will be either $a$ or $a+1$ at some point during this transformation. This completes the proof.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2022-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8c4f1aab-d759-5c44-9a36-84792c78c27b
| 246,226
|
Let $b \geq 2$ and $w \geq 2$ be fixed integers, and $n=b+w$. Given are $2 b$ identical black rods and $2 w$ identical white rods, each of side length 1. We assemble a regular $2 n$-gon using these rods so that parallel sides are the same color. Then, a convex $2 b$-gon $B$ is formed by translating the black rods, and a convex $2 w$-gon $W$ is formed by translating the white rods. An example of one way of doing the assembly when $b=3$ and $w=2$ is shown below, as well as the resulting polygons $B$ and $W$.  Prove that the difference of the areas of $B$ and $W$ depends only on the numbers $b$ and $w$, and not on how the $2 n$-gon was assembled.
|
We are going to prove that one may swap a black rod with an adjacent white rod (as well as the rods parallel to them) without affecting the difference in the areas of $B-W$. Let $\vec{u}$ and $\vec{v}$ denote the originally black and white vectors that were adjacent on the $2 n$-gon and are now going to be swapped. Let $\vec{x}$ denote the sum of all the other black vectors between $\vec{u}$ and $-\vec{u}$, and define $\vec{y}$ similarly. See the diagram below, where $B_{0}$ and $W_{0}$ are the polygons before the swap, and $B_{1}$ and $W_{1}$ are the resulting changed polygons.  Observe that the only change in $B$ and $W$ is in the parallelograms shown above in each diagram. Letting $\wedge$ denote the wedge product, we need to show that $$ \vec{u} \wedge \vec{x}-\vec{v} \wedge \vec{y}=\vec{v} \wedge \vec{x}-\vec{u} \wedge \vec{y} $$ which can be rewritten as $$ (\vec{u}-\vec{v}) \wedge(\vec{x}+\vec{y})=0 $$ In other words, it would suffice to show $\vec{u}-\vec{v}$ and $\vec{x}+\vec{y}$ are parallel. (Students not familiar with wedge products can replace every $\wedge$ with the cross product $\times$ instead.) Claim - Both $\vec{u}-\vec{v}$ and $\vec{x}+\vec{y}$ are perpendicular to vector $\vec{u}+\vec{v}$. For the other perpendicularity, note that $\vec{u}+\vec{v}+\vec{x}+\vec{y}$ traces out a diameter of the circumcircle of the original $2 n$-gon; call this diameter $A B$, so $$ A+\vec{u}+\vec{v}+\vec{x}+\vec{y}=B $$ Now point $A+\vec{u}+\vec{v}$ is a point on this semicircle, which means (by the inscribed angle theorem) the angle between $\vec{u}+\vec{v}$ and $\vec{x}+\vec{y}$ is $90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $b \geq 2$ and $w \geq 2$ be fixed integers, and $n=b+w$. Given are $2 b$ identical black rods and $2 w$ identical white rods, each of side length 1. We assemble a regular $2 n$-gon using these rods so that parallel sides are the same color. Then, a convex $2 b$-gon $B$ is formed by translating the black rods, and a convex $2 w$-gon $W$ is formed by translating the white rods. An example of one way of doing the assembly when $b=3$ and $w=2$ is shown below, as well as the resulting polygons $B$ and $W$.  Prove that the difference of the areas of $B$ and $W$ depends only on the numbers $b$ and $w$, and not on how the $2 n$-gon was assembled.
|
We are going to prove that one may swap a black rod with an adjacent white rod (as well as the rods parallel to them) without affecting the difference in the areas of $B-W$. Let $\vec{u}$ and $\vec{v}$ denote the originally black and white vectors that were adjacent on the $2 n$-gon and are now going to be swapped. Let $\vec{x}$ denote the sum of all the other black vectors between $\vec{u}$ and $-\vec{u}$, and define $\vec{y}$ similarly. See the diagram below, where $B_{0}$ and $W_{0}$ are the polygons before the swap, and $B_{1}$ and $W_{1}$ are the resulting changed polygons.  Observe that the only change in $B$ and $W$ is in the parallelograms shown above in each diagram. Letting $\wedge$ denote the wedge product, we need to show that $$ \vec{u} \wedge \vec{x}-\vec{v} \wedge \vec{y}=\vec{v} \wedge \vec{x}-\vec{u} \wedge \vec{y} $$ which can be rewritten as $$ (\vec{u}-\vec{v}) \wedge(\vec{x}+\vec{y})=0 $$ In other words, it would suffice to show $\vec{u}-\vec{v}$ and $\vec{x}+\vec{y}$ are parallel. (Students not familiar with wedge products can replace every $\wedge$ with the cross product $\times$ instead.) Claim - Both $\vec{u}-\vec{v}$ and $\vec{x}+\vec{y}$ are perpendicular to vector $\vec{u}+\vec{v}$. For the other perpendicularity, note that $\vec{u}+\vec{v}+\vec{x}+\vec{y}$ traces out a diameter of the circumcircle of the original $2 n$-gon; call this diameter $A B$, so $$ A+\vec{u}+\vec{v}+\vec{x}+\vec{y}=B $$ Now point $A+\vec{u}+\vec{v}$ is a point on this semicircle, which means (by the inscribed angle theorem) the angle between $\vec{u}+\vec{v}$ and $\vec{x}+\vec{y}$ is $90^{\circ}$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2022-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
282b92ea-bdce-53f9-95f2-d51604d9cd2b
| 605,613
|
Let $A B C D$ be a rhombus, and let $K$ and $L$ be points such that $K$ lies inside the rhombus, $L$ lies outside the rhombus, and $K A=K B=L C=L D$. Prove that there exist points $X$ and $Y$ on lines $A C$ and $B D$ such that $K X L Y$ is also a rhombus.
|
To start, notice that $\triangle A K B \cong \triangle D L C$ by SSS. Then by the condition $K$ lies inside the rhombus while $L$ lies outside it, we find that the two congruent triangles are just translations of each other (i.e. they have the same orientation). 『 First solution. Let $M$ be the midpoint of $\overline{K L}$ and is $O$ the center of the rhombus. $$ \text { Claim }-\overline{M O} \perp \overline{A B} . $$ We choose $X$ and $Y$ to be the intersections of the perpendicular bisector of $\overline{K L}$ with $\overline{A C}$ and $\overline{B D}$.  Claim - The midpoint of $\overline{X Y}$ coincides with the midpoint of $\overline{K L}$. $$ \begin{aligned} & \overline{X Y} \perp \overline{K L} \| \overline{B C} \\ & \overline{M O} \perp \overline{A B} \\ & \overline{B D} \perp \overline{A C} \end{aligned} $$ it follows that $\triangle M O Y$, which was determined by the three lines $\overline{X Y}, \overline{M O}, \overline{B D}$, is similar to $\triangle A B C$. In particular, it is isosceles with $M Y=M O$. Analogously, $M X=M O$. Remark. It is also possible to simply use coordinates to prove both claims.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a rhombus, and let $K$ and $L$ be points such that $K$ lies inside the rhombus, $L$ lies outside the rhombus, and $K A=K B=L C=L D$. Prove that there exist points $X$ and $Y$ on lines $A C$ and $B D$ such that $K X L Y$ is also a rhombus.
|
To start, notice that $\triangle A K B \cong \triangle D L C$ by SSS. Then by the condition $K$ lies inside the rhombus while $L$ lies outside it, we find that the two congruent triangles are just translations of each other (i.e. they have the same orientation). 『 First solution. Let $M$ be the midpoint of $\overline{K L}$ and is $O$ the center of the rhombus. $$ \text { Claim }-\overline{M O} \perp \overline{A B} . $$ We choose $X$ and $Y$ to be the intersections of the perpendicular bisector of $\overline{K L}$ with $\overline{A C}$ and $\overline{B D}$.  Claim - The midpoint of $\overline{X Y}$ coincides with the midpoint of $\overline{K L}$. $$ \begin{aligned} & \overline{X Y} \perp \overline{K L} \| \overline{B C} \\ & \overline{M O} \perp \overline{A B} \\ & \overline{B D} \perp \overline{A C} \end{aligned} $$ it follows that $\triangle M O Y$, which was determined by the three lines $\overline{X Y}, \overline{M O}, \overline{B D}$, is similar to $\triangle A B C$. In particular, it is isosceles with $M Y=M O$. Analogously, $M X=M O$. Remark. It is also possible to simply use coordinates to prove both claims.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2022-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
70f23366-034d-567c-8225-f7c980135b3c
| 246,243
|
Let $A B C D$ be a rhombus, and let $K$ and $L$ be points such that $K$ lies inside the rhombus, $L$ lies outside the rhombus, and $K A=K B=L C=L D$. Prove that there exist points $X$ and $Y$ on lines $A C$ and $B D$ such that $K X L Y$ is also a rhombus.
|
To start, notice that $\triangle A K B \cong \triangle D L C$ by SSS. Then by the condition $K$ lies inside the rhombus while $L$ lies outside it, we find that the two congruent triangles are just translations of each other (i.e. they have the same orientation). 【 Second solution (author's solution). In this solution, we instead define $X$ and $Y$ as the intersections of the circles centered at $K$ and $L$ of equal radii $K A$, which will be denoted $\omega_{K}$ and $\omega_{L}$. It is clear that $K X L Y$ is a rhombus under this construction, so it suffices to show that $X$ and $Y$ lie on $A C$ and $B D$ (in some order).  To see this, let $\overline{A C}$ meet $\omega_{K}$ again at $X^{\prime}$. We have $$ \measuredangle C X^{\prime} D=\measuredangle B X^{\prime} C=\measuredangle B X^{\prime} A=\frac{1}{2} \mathrm{~m} \overparen{A B}=\mathrm{m} \overparen{C D} $$ where the arcs are directed modulo $360^{\circ}$; here $\overparen{A B}$ is the arc of $\omega_{K}$ cut out by $\measuredangle A X B$, and $\overparen{D C}$ is the analogous arc of $\omega_{L}$. This implies $X^{\prime}$ lies on $\omega_{L}$ by the inscribed angle theorem. Hence $X=X^{\prime}$, and it follows $X$ lies on $\overline{A C}$. Analogously $Y$ lies on $B D$. Remark. The angle calculation above can also be replaced with a length calculation, as follows. Let $M$ and $N$ be the projections of $K$ and $L$ onto $\overline{A C}$, respectively. Then $X^{\prime}$ is the reflection of $A$ across $M$; analogously, the second intersection $X^{\prime \prime}$ with $\overline{A C}$ should be the reflection of $C$ across $N$. So to get $X=X^{\prime}=X^{\prime \prime}$, we would need to show $A C=2 M N$. However, note that $A K L D$ is a parallelogram. As $M N$ was the projection of $\overline{K L}$ onto $\overline{A C}$, its length should be the same as the projection of $\overline{A D}$ onto $\overline{A C}$, which is obviously $\frac{1}{2} A C$ because the projection of $D$ onto $\overline{A C}$ is exactly the midpoint of $\overline{A C}$ (i.e. the center of the rhombus).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a rhombus, and let $K$ and $L$ be points such that $K$ lies inside the rhombus, $L$ lies outside the rhombus, and $K A=K B=L C=L D$. Prove that there exist points $X$ and $Y$ on lines $A C$ and $B D$ such that $K X L Y$ is also a rhombus.
|
To start, notice that $\triangle A K B \cong \triangle D L C$ by SSS. Then by the condition $K$ lies inside the rhombus while $L$ lies outside it, we find that the two congruent triangles are just translations of each other (i.e. they have the same orientation). 【 Second solution (author's solution). In this solution, we instead define $X$ and $Y$ as the intersections of the circles centered at $K$ and $L$ of equal radii $K A$, which will be denoted $\omega_{K}$ and $\omega_{L}$. It is clear that $K X L Y$ is a rhombus under this construction, so it suffices to show that $X$ and $Y$ lie on $A C$ and $B D$ (in some order).  To see this, let $\overline{A C}$ meet $\omega_{K}$ again at $X^{\prime}$. We have $$ \measuredangle C X^{\prime} D=\measuredangle B X^{\prime} C=\measuredangle B X^{\prime} A=\frac{1}{2} \mathrm{~m} \overparen{A B}=\mathrm{m} \overparen{C D} $$ where the arcs are directed modulo $360^{\circ}$; here $\overparen{A B}$ is the arc of $\omega_{K}$ cut out by $\measuredangle A X B$, and $\overparen{D C}$ is the analogous arc of $\omega_{L}$. This implies $X^{\prime}$ lies on $\omega_{L}$ by the inscribed angle theorem. Hence $X=X^{\prime}$, and it follows $X$ lies on $\overline{A C}$. Analogously $Y$ lies on $B D$. Remark. The angle calculation above can also be replaced with a length calculation, as follows. Let $M$ and $N$ be the projections of $K$ and $L$ onto $\overline{A C}$, respectively. Then $X^{\prime}$ is the reflection of $A$ across $M$; analogously, the second intersection $X^{\prime \prime}$ with $\overline{A C}$ should be the reflection of $C$ across $N$. So to get $X=X^{\prime}=X^{\prime \prime}$, we would need to show $A C=2 M N$. However, note that $A K L D$ is a parallelogram. As $M N$ was the projection of $\overline{K L}$ onto $\overline{A C}$, its length should be the same as the projection of $\overline{A D}$ onto $\overline{A C}$, which is obviously $\frac{1}{2} A C$ because the projection of $D$ onto $\overline{A C}$ is exactly the midpoint of $\overline{A C}$ (i.e. the center of the rhombus).
|
{
"resource_path": "USAJMO/segmented/en-JMO-2022-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
70f23366-034d-567c-8225-f7c980135b3c
| 246,243
|
Let $a_{0}, b_{0}, c_{0}$ be complex numbers, and define $$ \begin{aligned} a_{n+1} & =a_{n}^{2}+2 b_{n} c_{n} \\ b_{n+1} & =b_{n}^{2}+2 c_{n} a_{n} \\ c_{n+1} & =c_{n}^{2}+2 a_{n} b_{n} \end{aligned} $$ for all nonnegative integers $n$. Suppose that $\max \left\{\left|a_{n}\right|,\left|b_{n}\right|,\left|c_{n}\right|\right\} \leq 2022$ for all $n \geq 0$. Prove that $$ \left|a_{0}\right|^{2}+\left|b_{0}\right|^{2}+\left|c_{0}\right|^{2} \leq 1 $$
|
For brevity, set $s_{n}:=\left|a_{n}\right|^{2}+\left|b_{n}\right|^{2}+\left|c_{n}\right|^{2}$. Note that the $s_{n}$ are real numbers. Claim (Key miraculous identity) - We have $$ s_{n+1}-s_{n}^{2}=2\left|a_{n} \overline{b_{n}}+b_{n} \overline{c_{n}}+c_{n} \overline{a_{n}}\right|^{2} $$ $$ \begin{aligned} s_{n+1} & =\left|a_{n}^{2}+2 b_{n} c_{n}\right|^{2}+\left|b_{n}^{2}+2 c_{n} a_{n}\right|^{2}+\left|c_{n}^{2}+2 a_{n} b_{n}\right|^{2} \\ & =\sum_{\text {cyc }}\left|a_{n}^{2}+2 b_{n} c_{n}\right|^{2} \\ & =\sum_{\text {cyc }}\left(a_{n}^{2}+2 b_{n} c_{n}\right)\left({\overline{a_{n}}}^{2}+2 \overline{b_{n}} \overline{c_{n}}\right) \\ & =\sum_{\text {cyc }}\left(\left|a_{n}\right|^{4}+2{\overline{a_{n}}}^{2} b_{n} c_{n}+2 a_{n}^{2} \overline{b_{n}} \overline{c_{n}}+4\left|b_{n}\right|^{2}\left|c_{n}\right|^{2}\right) \\ & =s_{n}^{2}+2 \sum_{\text {cyc }}\left({\overline{a_{n}}}^{2} b_{n} c_{n}+a_{n}^{2} \overline{b_{n}} \overline{c_{n}}+\left|b_{n}\right|^{2}\left|c_{n}\right|^{2}\right) \end{aligned} $$ Meanwhile, $$ \begin{aligned} &\left|a_{n} \overline{b_{n}}+b_{n} \overline{c_{n}}+c_{n} \overline{a_{n}}\right|^{2}=\left(a_{n} \overline{b_{n}}+b_{n} \overline{c_{n}}+c_{n} \overline{a_{n}}\right)\left(\overline{a_{n}} b_{n}+\overline{b_{n}} c_{n}+\overline{c_{n}} a_{n}\right) \\ &=\left|a_{n}\right|^{2}\left|b_{n}^{2}\right|+a_{n}{\overline{b_{n}}}^{2} c_{n}+a_{n}^{2} \overline{b_{n}} \overline{c_{n}} \\ &+\overline{a_{n}} b_{n}^{2} \overline{c_{n}}+\left|b_{n}\right|^{2}\left|c_{n}\right|^{2}+a_{n} b_{n} \bar{c}^{2} \\ &+{\overline{a_{n}}}^{2} b_{n} c_{n}+\overline{a_{n}} \overline{b_{n}} c_{n}^{2}+\left|a_{n}\right|^{2}\left|c_{n}\right|^{2} \end{aligned} $$ which exactly matches the earlier sum, term for term. In particular, $s_{n+1} \geq s_{n}^{2}$, so applying repeatedly, $$ s_{n} \geq s_{0}^{2^{n}} $$ Hence if $s_{0}>1$, it follows $s_{n}$ is unbounded, contradicting $\max \left\{\left|a_{n}\right|,\left|b_{n}\right|,\left|c_{n}\right|\right\} \leq 2022$. $$ \begin{aligned} a_{n+1} & =a_{n}^{2}+2 b_{n} c_{n} \\ c_{n+1} & =b_{n}^{2}+2 c_{n} a_{n} \\ b_{n+1} & =c_{n}^{2}+2 a_{n} b_{n} \end{aligned} $$ which is OK because we are just rearranging the terms in each triple. Then if $\omega$ is any complex number with $\omega^{3}=1$, and we define $$ z_{n}:=a_{n}+b_{n} \omega+c_{n} \omega^{2}, $$ the recursion amounts to saying that $z_{n+1}=z_{n}^{2}$. This allows us to analyze $\left|z_{n}\right|$ in a similar way as above, as now $\left|z_{n}\right|=\left|z_{0}\right|^{2^{n}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a_{0}, b_{0}, c_{0}$ be complex numbers, and define $$ \begin{aligned} a_{n+1} & =a_{n}^{2}+2 b_{n} c_{n} \\ b_{n+1} & =b_{n}^{2}+2 c_{n} a_{n} \\ c_{n+1} & =c_{n}^{2}+2 a_{n} b_{n} \end{aligned} $$ for all nonnegative integers $n$. Suppose that $\max \left\{\left|a_{n}\right|,\left|b_{n}\right|,\left|c_{n}\right|\right\} \leq 2022$ for all $n \geq 0$. Prove that $$ \left|a_{0}\right|^{2}+\left|b_{0}\right|^{2}+\left|c_{0}\right|^{2} \leq 1 $$
|
For brevity, set $s_{n}:=\left|a_{n}\right|^{2}+\left|b_{n}\right|^{2}+\left|c_{n}\right|^{2}$. Note that the $s_{n}$ are real numbers. Claim (Key miraculous identity) - We have $$ s_{n+1}-s_{n}^{2}=2\left|a_{n} \overline{b_{n}}+b_{n} \overline{c_{n}}+c_{n} \overline{a_{n}}\right|^{2} $$ $$ \begin{aligned} s_{n+1} & =\left|a_{n}^{2}+2 b_{n} c_{n}\right|^{2}+\left|b_{n}^{2}+2 c_{n} a_{n}\right|^{2}+\left|c_{n}^{2}+2 a_{n} b_{n}\right|^{2} \\ & =\sum_{\text {cyc }}\left|a_{n}^{2}+2 b_{n} c_{n}\right|^{2} \\ & =\sum_{\text {cyc }}\left(a_{n}^{2}+2 b_{n} c_{n}\right)\left({\overline{a_{n}}}^{2}+2 \overline{b_{n}} \overline{c_{n}}\right) \\ & =\sum_{\text {cyc }}\left(\left|a_{n}\right|^{4}+2{\overline{a_{n}}}^{2} b_{n} c_{n}+2 a_{n}^{2} \overline{b_{n}} \overline{c_{n}}+4\left|b_{n}\right|^{2}\left|c_{n}\right|^{2}\right) \\ & =s_{n}^{2}+2 \sum_{\text {cyc }}\left({\overline{a_{n}}}^{2} b_{n} c_{n}+a_{n}^{2} \overline{b_{n}} \overline{c_{n}}+\left|b_{n}\right|^{2}\left|c_{n}\right|^{2}\right) \end{aligned} $$ Meanwhile, $$ \begin{aligned} &\left|a_{n} \overline{b_{n}}+b_{n} \overline{c_{n}}+c_{n} \overline{a_{n}}\right|^{2}=\left(a_{n} \overline{b_{n}}+b_{n} \overline{c_{n}}+c_{n} \overline{a_{n}}\right)\left(\overline{a_{n}} b_{n}+\overline{b_{n}} c_{n}+\overline{c_{n}} a_{n}\right) \\ &=\left|a_{n}\right|^{2}\left|b_{n}^{2}\right|+a_{n}{\overline{b_{n}}}^{2} c_{n}+a_{n}^{2} \overline{b_{n}} \overline{c_{n}} \\ &+\overline{a_{n}} b_{n}^{2} \overline{c_{n}}+\left|b_{n}\right|^{2}\left|c_{n}\right|^{2}+a_{n} b_{n} \bar{c}^{2} \\ &+{\overline{a_{n}}}^{2} b_{n} c_{n}+\overline{a_{n}} \overline{b_{n}} c_{n}^{2}+\left|a_{n}\right|^{2}\left|c_{n}\right|^{2} \end{aligned} $$ which exactly matches the earlier sum, term for term. In particular, $s_{n+1} \geq s_{n}^{2}$, so applying repeatedly, $$ s_{n} \geq s_{0}^{2^{n}} $$ Hence if $s_{0}>1$, it follows $s_{n}$ is unbounded, contradicting $\max \left\{\left|a_{n}\right|,\left|b_{n}\right|,\left|c_{n}\right|\right\} \leq 2022$. $$ \begin{aligned} a_{n+1} & =a_{n}^{2}+2 b_{n} c_{n} \\ c_{n+1} & =b_{n}^{2}+2 c_{n} a_{n} \\ b_{n+1} & =c_{n}^{2}+2 a_{n} b_{n} \end{aligned} $$ which is OK because we are just rearranging the terms in each triple. Then if $\omega$ is any complex number with $\omega^{3}=1$, and we define $$ z_{n}:=a_{n}+b_{n} \omega+c_{n} \omega^{2}, $$ the recursion amounts to saying that $z_{n+1}=z_{n}^{2}$. This allows us to analyze $\left|z_{n}\right|$ in a similar way as above, as now $\left|z_{n}\right|=\left|z_{0}\right|^{2^{n}}$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2022-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5051f81f-a3f7-5848-b52e-8aef0facd4bf
| 605,675
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Most common synthetic approach. The solution hinges on the following claim: Claim - $Q$ coincides with the reflection of $D$ across $M$. $$ M B \cdot M Q=M A \cdot M P=M C \cdot M D . $$ Since $M B=M C$, the claim follows. It follows that $\overline{M N} \| \overline{A D}$, as $M$ and $N$ are respectively the midpoints of $\overline{A Q}$ and $\overline{D Q}$. Thus $\overline{M N} \perp \overline{B C}$, and so $N$ lies on the perpendicular bisector of $\overline{B C}$, as needed. Remark (David Lin). One can prove the main claim without power of a point as well, as follows: Let $R$ be the foot from $B$ to $\overline{A M}$, so $B R C P$ is a parallelogram. Note that $A B D R$ is cyclic, and hence $$ \measuredangle D R M=\measuredangle D B A=Q B A=\measuredangle Q P A=\measuredangle Q P M $$ Thus, $\overline{D R} \| \overline{P Q}$, so $D R Q P$ is also a parallelogram.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Most common synthetic approach. The solution hinges on the following claim: Claim - $Q$ coincides with the reflection of $D$ across $M$. $$ M B \cdot M Q=M A \cdot M P=M C \cdot M D . $$ Since $M B=M C$, the claim follows. It follows that $\overline{M N} \| \overline{A D}$, as $M$ and $N$ are respectively the midpoints of $\overline{A Q}$ and $\overline{D Q}$. Thus $\overline{M N} \perp \overline{B C}$, and so $N$ lies on the perpendicular bisector of $\overline{B C}$, as needed. Remark (David Lin). One can prove the main claim without power of a point as well, as follows: Let $R$ be the foot from $B$ to $\overline{A M}$, so $B R C P$ is a parallelogram. Note that $A B D R$ is cyclic, and hence $$ \measuredangle D R M=\measuredangle D B A=Q B A=\measuredangle Q P A=\measuredangle Q P M $$ Thus, $\overline{D R} \| \overline{P Q}$, so $D R Q P$ is also a parallelogram.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 ## \ Synthetic approach with no additional points at all. Claim - $\triangle B P C \sim \triangle A N M$ (oppositely oriented). $$ \frac{B M}{B P}=\frac{A M}{A Q} \Longrightarrow \frac{2 B M}{B P}=\frac{A M}{A Q / 2} \Longrightarrow \frac{B C}{B P}=\frac{A M}{A N} $$ implying the similarity (since $\measuredangle M A Q=\measuredangle B P M$ ). This similarity gives us the equality of directed angles $$ \measuredangle(B C, M N)=-\measuredangle(P C, A M)=90^{\circ} $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 ## \ Synthetic approach with no additional points at all. Claim - $\triangle B P C \sim \triangle A N M$ (oppositely oriented). $$ \frac{B M}{B P}=\frac{A M}{A Q} \Longrightarrow \frac{2 B M}{B P}=\frac{A M}{A Q / 2} \Longrightarrow \frac{B C}{B P}=\frac{A M}{A N} $$ implying the similarity (since $\measuredangle M A Q=\measuredangle B P M$ ). This similarity gives us the equality of directed angles $$ \measuredangle(B C, M N)=-\measuredangle(P C, A M)=90^{\circ} $$ as desired.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 \ Synthetic approach using only the point $R$. Again let $R$ be the foot from $B$ to $\overline{A M}$, so $B R C P$ is a parallelogram. Claim - $A R Q C$ is cyclic; equivalently, $\triangle M A Q \sim \triangle M C R$. Note that in $\triangle M C R$, the $M$-median is parallel to $\overline{C P}$ and hence perpendicular to $\overline{R M}$. The same should be true in $\triangle M A Q$ by the similarity, so $\overline{M N} \perp \overline{M Q}$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 \ Synthetic approach using only the point $R$. Again let $R$ be the foot from $B$ to $\overline{A M}$, so $B R C P$ is a parallelogram. Claim - $A R Q C$ is cyclic; equivalently, $\triangle M A Q \sim \triangle M C R$. Note that in $\triangle M C R$, the $M$-median is parallel to $\overline{C P}$ and hence perpendicular to $\overline{R M}$. The same should be true in $\triangle M A Q$ by the similarity, so $\overline{M N} \perp \overline{M Q}$ as needed.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Cartesian coordinates approach with power of a point. Suppose we set $B=(-1,0)$, $M=(0,0), C=(1,0)$, and $A=(a, b)$. One may compute: $$ \begin{aligned} \overleftrightarrow{A M}: 0 & =b x-a y \Longleftrightarrow y=\frac{b}{a} x \\ \overleftrightarrow{C P}: 0 & =a(x-1)+b y \Longleftrightarrow y=-\frac{a}{b}(x-1)=-\frac{a}{b} x+\frac{a}{b} \\ P & =\left(\frac{a^{2}}{a^{2}+b^{2}}, \frac{a b}{a^{2}+b^{2}}\right) \end{aligned} $$ Now note that $$ A M=\sqrt{a^{2}+b^{2}}, \quad P M=\frac{a}{\sqrt{a^{2}+b^{2}}} $$ together with power of a point $$ A M \cdot P M=B M \cdot Q M $$ to immediately deduce that $Q=(a, 0)$. Hence $N=(0, b / 2)$ and we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Cartesian coordinates approach with power of a point. Suppose we set $B=(-1,0)$, $M=(0,0), C=(1,0)$, and $A=(a, b)$. One may compute: $$ \begin{aligned} \overleftrightarrow{A M}: 0 & =b x-a y \Longleftrightarrow y=\frac{b}{a} x \\ \overleftrightarrow{C P}: 0 & =a(x-1)+b y \Longleftrightarrow y=-\frac{a}{b}(x-1)=-\frac{a}{b} x+\frac{a}{b} \\ P & =\left(\frac{a^{2}}{a^{2}+b^{2}}, \frac{a b}{a^{2}+b^{2}}\right) \end{aligned} $$ Now note that $$ A M=\sqrt{a^{2}+b^{2}}, \quad P M=\frac{a}{\sqrt{a^{2}+b^{2}}} $$ together with power of a point $$ A M \cdot P M=B M \cdot Q M $$ to immediately deduce that $Q=(a, 0)$. Hence $N=(0, b / 2)$ and we're done.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Cartesian coordinates approach without power of a point (outline). After computing $A$ and $P$ as above, one could also directly calculate $$ \begin{aligned} & \text { Perpendicular bisector of } \overline{A B}: y=-\frac{a+1}{b} x+\frac{a^{2}+b^{2}-1}{2 b} \\ & \text { Perpendicular bisector of } \overline{P B}: y=-\left(\frac{2 a}{b}+\frac{b}{a}\right) x-\frac{b}{2 a} \\ & \text { Perpendicular bisector of } \overline{P A}: y=-\frac{a}{b} x+\frac{a+a^{2}+b^{2}}{2 b} \\ & \text { Circumcenter of } \triangle P A B=\left(-\frac{a+1}{2}, \frac{2 a^{2}+2 a+b^{2}}{2 b}\right) \end{aligned} $$ This is enough to extract the coordinates of $Q=(\bullet, 0)$, because $B=(-1,0)$ is given, and the $x$-coordinate of the circumcenter should be the average of the $x$-coordinates of $B$ and $Q$. In other words, $Q=(-a, 0)$. Hence, $N=\left(0, \frac{b}{2}\right)$, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 【 Cartesian coordinates approach without power of a point (outline). After computing $A$ and $P$ as above, one could also directly calculate $$ \begin{aligned} & \text { Perpendicular bisector of } \overline{A B}: y=-\frac{a+1}{b} x+\frac{a^{2}+b^{2}-1}{2 b} \\ & \text { Perpendicular bisector of } \overline{P B}: y=-\left(\frac{2 a}{b}+\frac{b}{a}\right) x-\frac{b}{2 a} \\ & \text { Perpendicular bisector of } \overline{P A}: y=-\frac{a}{b} x+\frac{a+a^{2}+b^{2}}{2 b} \\ & \text { Circumcenter of } \triangle P A B=\left(-\frac{a+1}{2}, \frac{2 a^{2}+2 a+b^{2}}{2 b}\right) \end{aligned} $$ This is enough to extract the coordinates of $Q=(\bullet, 0)$, because $B=(-1,0)$ is given, and the $x$-coordinate of the circumcenter should be the average of the $x$-coordinates of $B$ and $Q$. In other words, $Q=(-a, 0)$. Hence, $N=\left(0, \frac{b}{2}\right)$, as needed.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 \I III-advised barycentric approach (outline). Use reference triangle $A B C$. The $A$ median is parametrized by $(t: 1: 1)$ for $t \in \mathbb{R}$. So because of $\overline{C P} \perp \overline{A M}$, we are looking for $t$ such that $$ \left(\frac{t \vec{A}+\vec{B}+\vec{C}}{t+2}-\vec{C}\right) \perp\left(A-\frac{\vec{B}+\vec{C}}{2}\right) $$ This is equivalent to $$ (t \vec{A}+\vec{B}-(t+1) \vec{C}) \perp(2 \vec{A}-\vec{B}-\vec{C}) $$ By the perpendicularity formula for barycentric coordinates (EGMO 7.16), this is equivalent to $$ \begin{aligned} 0 & =a^{2} t-b^{2} \cdot(3 t+2)+c^{2} \cdot(2-t) \\ & =\left(a^{2}-3 b^{2}-c^{2}\right) t-2\left(b^{2}-c^{2}\right) \\ \Longrightarrow t & =\frac{2\left(b^{2}-c^{2}\right)}{a^{2}-3 b^{2}-c^{2}} \end{aligned} $$ In other words, $$ P=\left(2\left(b^{2}-c^{2}\right): a^{2}-3 b^{2}-c^{2}: a^{2}-3 b^{2}-c^{2}\right) . $$ A long calculation gives $a^{2} y_{P} z_{P}+b^{2} z_{P} x_{P}+c^{2} x_{P} y_{P}=\left(a^{2}-3 b^{2}-c^{2}\right)\left(a^{2}-b^{2}+c^{2}\right)\left(a^{2}-\right.$ $\left.2 b^{2}-2 c^{2}\right)$. Together with $x_{P}+y_{P}+z_{P}=2 a^{2}-4 b^{2}-4 c^{2}$, this makes the equation of $(A B P)$ as $$ 0=-a^{2} y z-b^{2} z x-c^{2} x y+\frac{a^{2}-b^{2}+c^{2}}{2} z(x+y+z) $$ To solve for $Q$, set $x=0$ to get to get $$ a^{2} y z=\frac{a^{2}-b^{2}+c^{2}}{2} z(y+z) \Longrightarrow \frac{y}{z}=\frac{a^{2}-b^{2}+c^{2}}{a^{2}+b^{2}-c^{2}} $$ In other words, $$ Q=\left(0: a^{2}-b^{2}+c^{2}: a^{2}+b^{2}-c^{2}\right) $$ Taking the average with $A=(1,0,0)$ then gives $$ N=\left(2 a^{2}: a^{2}-b^{2}+c^{2}: a^{2}+b^{2}-c^{2}\right) . $$ The equation for the perpendicular bisector of $\overline{B C}$ is given by (see EGMO 7.19) $$ 0=a^{2}(z-y)+x\left(c^{2}-b^{2}\right) $$ which contains $N$, as needed. $$ p=\frac{(a-m) \bar{c}+(\bar{a}-\bar{m}) c+\bar{a} m-a \bar{m}}{2(\bar{a}-\bar{m})}=\frac{a^{2} b-a^{2} c-a b^{2}-2 a b c-a c^{2}+b^{2} c+3 b c^{2}}{4 b c-2 a(b+c)} $$ Meanwhile, an extremely ugly calculation will eventually yield $$ q=\frac{\frac{b c}{a}+b+c-a}{2} $$ SO $$ n=\frac{a+q}{2}=\frac{a+b+c+\frac{b c}{a}}{4}=\frac{(a+b)(a+c)}{2 a} $$ There are a few ways to then verify $N B=N C$. The simplest seems to be to verify that $$ \frac{n-\frac{b+c}{2}}{b-c}=\frac{a-b-c+\frac{b c}{a}}{4(b-c)}=\frac{(a-b)(a-c)}{2 a(b-c)} $$ is pure imaginary, which is clear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$, let $M$ be the midpoint of $\overline{B C}$. Let $P$ be the foot of the perpendicular from $C$ to $A M$. Suppose that the circumcircle of triangle $A B P$ intersects line $B C$ at two distinct points $B$ and $Q$. Let $N$ be the midpoint of $\overline{A Q}$. Prove that $N B=N C$.
|
 \I III-advised barycentric approach (outline). Use reference triangle $A B C$. The $A$ median is parametrized by $(t: 1: 1)$ for $t \in \mathbb{R}$. So because of $\overline{C P} \perp \overline{A M}$, we are looking for $t$ such that $$ \left(\frac{t \vec{A}+\vec{B}+\vec{C}}{t+2}-\vec{C}\right) \perp\left(A-\frac{\vec{B}+\vec{C}}{2}\right) $$ This is equivalent to $$ (t \vec{A}+\vec{B}-(t+1) \vec{C}) \perp(2 \vec{A}-\vec{B}-\vec{C}) $$ By the perpendicularity formula for barycentric coordinates (EGMO 7.16), this is equivalent to $$ \begin{aligned} 0 & =a^{2} t-b^{2} \cdot(3 t+2)+c^{2} \cdot(2-t) \\ & =\left(a^{2}-3 b^{2}-c^{2}\right) t-2\left(b^{2}-c^{2}\right) \\ \Longrightarrow t & =\frac{2\left(b^{2}-c^{2}\right)}{a^{2}-3 b^{2}-c^{2}} \end{aligned} $$ In other words, $$ P=\left(2\left(b^{2}-c^{2}\right): a^{2}-3 b^{2}-c^{2}: a^{2}-3 b^{2}-c^{2}\right) . $$ A long calculation gives $a^{2} y_{P} z_{P}+b^{2} z_{P} x_{P}+c^{2} x_{P} y_{P}=\left(a^{2}-3 b^{2}-c^{2}\right)\left(a^{2}-b^{2}+c^{2}\right)\left(a^{2}-\right.$ $\left.2 b^{2}-2 c^{2}\right)$. Together with $x_{P}+y_{P}+z_{P}=2 a^{2}-4 b^{2}-4 c^{2}$, this makes the equation of $(A B P)$ as $$ 0=-a^{2} y z-b^{2} z x-c^{2} x y+\frac{a^{2}-b^{2}+c^{2}}{2} z(x+y+z) $$ To solve for $Q$, set $x=0$ to get to get $$ a^{2} y z=\frac{a^{2}-b^{2}+c^{2}}{2} z(y+z) \Longrightarrow \frac{y}{z}=\frac{a^{2}-b^{2}+c^{2}}{a^{2}+b^{2}-c^{2}} $$ In other words, $$ Q=\left(0: a^{2}-b^{2}+c^{2}: a^{2}+b^{2}-c^{2}\right) $$ Taking the average with $A=(1,0,0)$ then gives $$ N=\left(2 a^{2}: a^{2}-b^{2}+c^{2}: a^{2}+b^{2}-c^{2}\right) . $$ The equation for the perpendicular bisector of $\overline{B C}$ is given by (see EGMO 7.19) $$ 0=a^{2}(z-y)+x\left(c^{2}-b^{2}\right) $$ which contains $N$, as needed. $$ p=\frac{(a-m) \bar{c}+(\bar{a}-\bar{m}) c+\bar{a} m-a \bar{m}}{2(\bar{a}-\bar{m})}=\frac{a^{2} b-a^{2} c-a b^{2}-2 a b c-a c^{2}+b^{2} c+3 b c^{2}}{4 b c-2 a(b+c)} $$ Meanwhile, an extremely ugly calculation will eventually yield $$ q=\frac{\frac{b c}{a}+b+c-a}{2} $$ SO $$ n=\frac{a+q}{2}=\frac{a+b+c+\frac{b c}{a}}{4}=\frac{(a+b)(a+c)}{2 a} $$ There are a few ways to then verify $N B=N C$. The simplest seems to be to verify that $$ \frac{n-\frac{b+c}{2}}{b-c}=\frac{a-b-c+\frac{b c}{a}}{4(b-c)}=\frac{(a-b)(a-c)}{2 a(b-c)} $$ is pure imaginary, which is clear.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
28631499-bf56-5d95-934f-0e89c0d24220
| 246,281
|
Positive integers $a$ and $N$ are fixed, and $N$ positive integers are written on a blackboard. Alice and Bob play the following game. On Alice's turn, she must replace some integer $n$ on the board with $n+a$, and on Bob's turn he must replace some even integer $n$ on the board with $n / 2$. Alice goes first and they alternate turns. If on his turn Bob has no valid moves, the game ends. After analyzing the $N$ integers on the board, Bob realizes that, regardless of what moves Alice makes, he will be able to force the game to end eventually. Show that, in fact, for this value of $a$ and these $N$ integers on the board, the game is guaranteed to end regardless of Alice's or Bob's moves.
|
For $N=1$, there is nothing to prove. We address $N \geq 2$ only henceforth. Let $S$ denote the numbers on the board. Claim - When $N \geq 2$, if $\nu_{2}(x)<\nu_{2}(a)$ for all $x \in S$, the game must terminate no matter what either player does. Hence, in fact the game will always terminate in exactly $\sum_{x \in S} \nu_{2}(x)$ moves in this case, regardless of what either player does. Claim - When $N \geq 2$, if there exists a number $x$ on the board such that $\nu_{2}(x) \geq$ $\nu_{2}(a)$, then Alice can cause the game to go on forever. - Operate on the first entry if $\nu_{2}(x)=\nu_{2}(a)$ (the new entry thus has $\nu_{2}(x+a)>\nu_{2}(a)$ ); - Operate on any other entry besides the first one, otherwise. A double induction then shows that - Just before each of Bob's turns, $\nu_{2}(x)>\nu_{2}(a)$ always holds; and - After each of Bob's turns, $\nu_{2}(x) \geq \nu_{2}(a)$ always holds. In particular Bob will never run out of legal moves, since halving $x$ is always legal.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Positive integers $a$ and $N$ are fixed, and $N$ positive integers are written on a blackboard. Alice and Bob play the following game. On Alice's turn, she must replace some integer $n$ on the board with $n+a$, and on Bob's turn he must replace some even integer $n$ on the board with $n / 2$. Alice goes first and they alternate turns. If on his turn Bob has no valid moves, the game ends. After analyzing the $N$ integers on the board, Bob realizes that, regardless of what moves Alice makes, he will be able to force the game to end eventually. Show that, in fact, for this value of $a$ and these $N$ integers on the board, the game is guaranteed to end regardless of Alice's or Bob's moves.
|
For $N=1$, there is nothing to prove. We address $N \geq 2$ only henceforth. Let $S$ denote the numbers on the board. Claim - When $N \geq 2$, if $\nu_{2}(x)<\nu_{2}(a)$ for all $x \in S$, the game must terminate no matter what either player does. Hence, in fact the game will always terminate in exactly $\sum_{x \in S} \nu_{2}(x)$ moves in this case, regardless of what either player does. Claim - When $N \geq 2$, if there exists a number $x$ on the board such that $\nu_{2}(x) \geq$ $\nu_{2}(a)$, then Alice can cause the game to go on forever. - Operate on the first entry if $\nu_{2}(x)=\nu_{2}(a)$ (the new entry thus has $\nu_{2}(x+a)>\nu_{2}(a)$ ); - Operate on any other entry besides the first one, otherwise. A double induction then shows that - Just before each of Bob's turns, $\nu_{2}(x)>\nu_{2}(a)$ always holds; and - After each of Bob's turns, $\nu_{2}(x) \geq \nu_{2}(a)$ always holds. In particular Bob will never run out of legal moves, since halving $x$ is always legal.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5a0c2e05-3fc5-5fdf-b1b1-dd37f92d4e76
| 605,776
|
Isosceles triangle $A B C$, with $A B=A C$, is inscribed in circle $\omega$. Let $D$ be an arbitrary point inside $B C$ such that $B D \neq D C$. Ray $A D$ intersects $\omega$ again at $E$ (other than $A$ ). Point $F$ (other than $E$ ) is chosen on $\omega$ such that $\angle D F E=90^{\circ}$. Line $F E$ intersects rays $A B$ and $A C$ at points $X$ and $Y$, respectively. Prove that $\angle X D E=\angle E D Y$.
|
【 Angle chasing solution. Note that $(B D A)$ and $(C D A)$ are congruent, since $B A=C A$ and $\angle B D A+\angle C D A=180^{\circ}$. So these two circles are reflections around line $E D$. Moreover, $(D E F)$ is obviously also symmetric around line $E D$.  Hence, the radical axis of $(B D A)$ and $(D E F)$, and the radical axis of $(C D A)$ and $(D E F)$, should be symmetric about line $D E$. But these radical axii are exactly lines $X D$ and $Y D$, so we're done. Remark (Motivation). The main idea is that you can replace $D X$ and $D Y$ with the radical axii, letting $X^{\prime}$ and $Y^{\prime}$ be the second intersections of the blue circles. Then for the problem to be true, you'd need $X^{\prime}$ and $Y^{\prime}$ to be reflections. That's equivalent to $(B D A)$ and $(C D A)$ being congruent; you check it and it's indeed true.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Isosceles triangle $A B C$, with $A B=A C$, is inscribed in circle $\omega$. Let $D$ be an arbitrary point inside $B C$ such that $B D \neq D C$. Ray $A D$ intersects $\omega$ again at $E$ (other than $A$ ). Point $F$ (other than $E$ ) is chosen on $\omega$ such that $\angle D F E=90^{\circ}$. Line $F E$ intersects rays $A B$ and $A C$ at points $X$ and $Y$, respectively. Prove that $\angle X D E=\angle E D Y$.
|
【 Angle chasing solution. Note that $(B D A)$ and $(C D A)$ are congruent, since $B A=C A$ and $\angle B D A+\angle C D A=180^{\circ}$. So these two circles are reflections around line $E D$. Moreover, $(D E F)$ is obviously also symmetric around line $E D$.  Hence, the radical axis of $(B D A)$ and $(D E F)$, and the radical axis of $(C D A)$ and $(D E F)$, should be symmetric about line $D E$. But these radical axii are exactly lines $X D$ and $Y D$, so we're done. Remark (Motivation). The main idea is that you can replace $D X$ and $D Y$ with the radical axii, letting $X^{\prime}$ and $Y^{\prime}$ be the second intersections of the blue circles. Then for the problem to be true, you'd need $X^{\prime}$ and $Y^{\prime}$ to be reflections. That's equivalent to $(B D A)$ and $(C D A)$ being congruent; you check it and it's indeed true.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4008818-65bf-5365-944e-c9dfc70bb804
| 605,786
|
Isosceles triangle $A B C$, with $A B=A C$, is inscribed in circle $\omega$. Let $D$ be an arbitrary point inside $B C$ such that $B D \neq D C$. Ray $A D$ intersects $\omega$ again at $E$ (other than $A$ ). Point $F$ (other than $E$ ) is chosen on $\omega$ such that $\angle D F E=90^{\circ}$. Line $F E$ intersects rays $A B$ and $A C$ at points $X$ and $Y$, respectively. Prove that $\angle X D E=\angle E D Y$.
|
【 Harmonic solution (mine). Let $T$ be the point on line $\overline{X F E Y}$ such that $\angle E D T=90^{\circ}$, and let $\overline{A T}$ meet $\omega$ again at $K$. Then $$ T D^{2}=T F \cdot T E=T K \cdot T A \Longrightarrow \angle D K T=90^{\circ} $$ so line $D K$ passes through the antipode $M$ of $A$.  Thus, $$ -1=(A M ; C B)_{\omega} \stackrel{D}{=}(E K ; B C)_{\omega} \stackrel{A}{=}(T E ; X Y) $$ and since $\angle E D T=90^{\circ}$ we're done. Remark (Motivation). The idea is to kill the points $X$ and $Y$ by reinterpreting the desired condition as $(T D ; X Y)=-1$ and then projecting through $A$ onto $\omega$. This eliminates points $X$ and $Y$ altogether and reduces the problem to showing that $\overline{T A}$ passes through the harmonic conjugate of $E$ with respect to $B C$ on $\omega$. The labels on the diagram are slightly misleading in that $\triangle E B C$ should probably be thought of as the "reference" triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Isosceles triangle $A B C$, with $A B=A C$, is inscribed in circle $\omega$. Let $D$ be an arbitrary point inside $B C$ such that $B D \neq D C$. Ray $A D$ intersects $\omega$ again at $E$ (other than $A$ ). Point $F$ (other than $E$ ) is chosen on $\omega$ such that $\angle D F E=90^{\circ}$. Line $F E$ intersects rays $A B$ and $A C$ at points $X$ and $Y$, respectively. Prove that $\angle X D E=\angle E D Y$.
|
【 Harmonic solution (mine). Let $T$ be the point on line $\overline{X F E Y}$ such that $\angle E D T=90^{\circ}$, and let $\overline{A T}$ meet $\omega$ again at $K$. Then $$ T D^{2}=T F \cdot T E=T K \cdot T A \Longrightarrow \angle D K T=90^{\circ} $$ so line $D K$ passes through the antipode $M$ of $A$.  Thus, $$ -1=(A M ; C B)_{\omega} \stackrel{D}{=}(E K ; B C)_{\omega} \stackrel{A}{=}(T E ; X Y) $$ and since $\angle E D T=90^{\circ}$ we're done. Remark (Motivation). The idea is to kill the points $X$ and $Y$ by reinterpreting the desired condition as $(T D ; X Y)=-1$ and then projecting through $A$ onto $\omega$. This eliminates points $X$ and $Y$ altogether and reduces the problem to showing that $\overline{T A}$ passes through the harmonic conjugate of $E$ with respect to $B C$ on $\omega$. The labels on the diagram are slightly misleading in that $\triangle E B C$ should probably be thought of as the "reference" triangle.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4008818-65bf-5365-944e-c9dfc70bb804
| 605,786
|
Isosceles triangle $A B C$, with $A B=A C$, is inscribed in circle $\omega$. Let $D$ be an arbitrary point inside $B C$ such that $B D \neq D C$. Ray $A D$ intersects $\omega$ again at $E$ (other than $A$ ). Point $F$ (other than $E$ ) is chosen on $\omega$ such that $\angle D F E=90^{\circ}$. Line $F E$ intersects rays $A B$ and $A C$ at points $X$ and $Y$, respectively. Prove that $\angle X D E=\angle E D Y$.
|
【 Pascal solution (Zuming Feng). Extend ray $F D$ to the antipode $T$ of $E$ on $\omega$. Then, - By Pascal's theorem on $E F T A B C$, the points $X, D$, and $P:=\overline{E C} \cap \overline{A T}$ are collinear. - Similarly by Pascal's theorem on $E F T A C B$, the points the points $Y, D$, and $Q:=\overline{E B} \cap \overline{A T}$ are collinear.  Now it suffices to prove $\overline{E D}$ bisects $\angle Q D P$. However, $\overline{E D}$ is the angle bisector of $\angle Q E P=\angle B E C$, but also $\overline{E A} \perp \overline{Q P}$. Thus triangle $Q E P$ is isosceles with $Q E=P E$, and $\overline{E A}$ cuts it in half. Since $D$ is on $\overline{E A}$, the result follows now.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Isosceles triangle $A B C$, with $A B=A C$, is inscribed in circle $\omega$. Let $D$ be an arbitrary point inside $B C$ such that $B D \neq D C$. Ray $A D$ intersects $\omega$ again at $E$ (other than $A$ ). Point $F$ (other than $E$ ) is chosen on $\omega$ such that $\angle D F E=90^{\circ}$. Line $F E$ intersects rays $A B$ and $A C$ at points $X$ and $Y$, respectively. Prove that $\angle X D E=\angle E D Y$.
|
【 Pascal solution (Zuming Feng). Extend ray $F D$ to the antipode $T$ of $E$ on $\omega$. Then, - By Pascal's theorem on $E F T A B C$, the points $X, D$, and $P:=\overline{E C} \cap \overline{A T}$ are collinear. - Similarly by Pascal's theorem on $E F T A C B$, the points the points $Y, D$, and $Q:=\overline{E B} \cap \overline{A T}$ are collinear.  Now it suffices to prove $\overline{E D}$ bisects $\angle Q D P$. However, $\overline{E D}$ is the angle bisector of $\angle Q E P=\angle B E C$, but also $\overline{E A} \perp \overline{Q P}$. Thus triangle $Q E P$ is isosceles with $Q E=P E$, and $\overline{E A}$ cuts it in half. Since $D$ is on $\overline{E A}$, the result follows now.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4008818-65bf-5365-944e-c9dfc70bb804
| 605,786
|
Let $A B C D$ be a cyclic quadrilateral with $A B=7$ and $C D=8$. Points $P$ and $Q$ are selected on line segment $A B$ so that $A P=B Q=3$. Points $R$ and $S$ are selected on line segment $C D$ so that $C R=D S=2$. Prove that $P Q R S$ is a cyclic quadrilateral.
|
\l The one-liner. The four points $P, Q, R, S$ have equal power -12 with respect to $(A B C D)$. So in fact they're on a circle concentric with $(A B C D)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral with $A B=7$ and $C D=8$. Points $P$ and $Q$ are selected on line segment $A B$ so that $A P=B Q=3$. Points $R$ and $S$ are selected on line segment $C D$ so that $C R=D S=2$. Prove that $P Q R S$ is a cyclic quadrilateral.
|
\l The one-liner. The four points $P, Q, R, S$ have equal power -12 with respect to $(A B C D)$. So in fact they're on a circle concentric with $(A B C D)$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
894ef183-ab35-5d91-bdff-aaeb6b064930
| 246,325
|
Let $A B C D$ be a cyclic quadrilateral with $A B=7$ and $C D=8$. Points $P$ and $Q$ are selected on line segment $A B$ so that $A P=B Q=3$. Points $R$ and $S$ are selected on line segment $C D$ so that $C R=D S=2$. Prove that $P Q R S$ is a cyclic quadrilateral.
|
\ The external power solution. We distinguish between two cases. Case where $A B$ and $C D$ are not parallel. We let lines $A B$ and $C D$ meet at $T$. Without loss of generality, $A$ lies between $B$ and $T$ and $D$ lies between $C$ and $T$. Let $x=T A$ and $y=T D$, as shown below.  By power of a point, $$ \begin{aligned} A B C D \text { cyclic } \Longleftrightarrow x(x+7) & =y(y+8) \\ P Q R S \text { cyclic } \Longleftrightarrow(x+3)(x+4) & =(y+2)(y+6) . \end{aligned} $$ However, the latter equation is just the former with 12 added to both sides. (That is, $(x+3)(x+4)=x(x+7)+12$ while $(y+2)(y+6)=y(y+8)+12$.$) So the conclusion is$ immediate. Case where $A B$ and $C D$ are parallel. In that case $A B C D$ is an isosceles trapezoid. Then the entire picture is symmetric around the common perpendicular bisector of the lines $A B$ and $C D$. Now $P Q R S$ is also an isosceles trapezoid, so it's cyclic too. 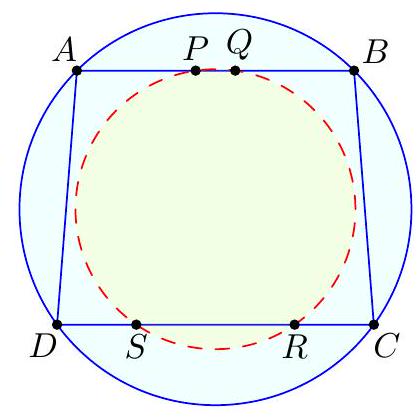
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral with $A B=7$ and $C D=8$. Points $P$ and $Q$ are selected on line segment $A B$ so that $A P=B Q=3$. Points $R$ and $S$ are selected on line segment $C D$ so that $C R=D S=2$. Prove that $P Q R S$ is a cyclic quadrilateral.
|
\ The external power solution. We distinguish between two cases. Case where $A B$ and $C D$ are not parallel. We let lines $A B$ and $C D$ meet at $T$. Without loss of generality, $A$ lies between $B$ and $T$ and $D$ lies between $C$ and $T$. Let $x=T A$ and $y=T D$, as shown below.  By power of a point, $$ \begin{aligned} A B C D \text { cyclic } \Longleftrightarrow x(x+7) & =y(y+8) \\ P Q R S \text { cyclic } \Longleftrightarrow(x+3)(x+4) & =(y+2)(y+6) . \end{aligned} $$ However, the latter equation is just the former with 12 added to both sides. (That is, $(x+3)(x+4)=x(x+7)+12$ while $(y+2)(y+6)=y(y+8)+12$.$) So the conclusion is$ immediate. Case where $A B$ and $C D$ are parallel. In that case $A B C D$ is an isosceles trapezoid. Then the entire picture is symmetric around the common perpendicular bisector of the lines $A B$ and $C D$. Now $P Q R S$ is also an isosceles trapezoid, so it's cyclic too. 
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
894ef183-ab35-5d91-bdff-aaeb6b064930
| 246,325
|
Let $m$ and $n$ be positive integers. Let $S$ be the set of lattice points $(x, y)$ with $1 \leq x \leq 2 m$ and $1 \leq y \leq 2 n$. A configuration of $m n$ rectangles is called happy if each point of $S$ is the vertex of exactly one rectangle. Prove that the number of happy configurations is odd.
|
I Original proposer's solution. To this end, let's denote by $f(2 m, 2 n)$ the number of happy configurations for a $2 m \times 2 n$ grid of lattice points (not necessarily equally spaced - this doesn't change the count). We already have the following easy case. Claim - We have $f(2,2 n)=(2 n-1)!!=(2 n-1) \cdot(2 n-3) \cdots \cdots 3 \cdot 1$. We will prove that: Claim - Assume $m, n \geq 1$. When $f(2 m, 2 n) \equiv f(2 m-2,2 n)(\bmod 2)$. Now configurations fixed by $\tau$ can be described readily: this occurs if and only if the last two columns are self-contained, meaning every rectangle with a vertex in these columns is completely contained in these two columns.  Hence it follows that $$ f(2 m, 2 n)=2(\text { number of pairs })+f(2 m-2,2 n) \cdot f(2,2 n) $$ Taking modulo 2 gives the result. By the same token $f(2 m, 2 n) \equiv f(2 m, 2 n-2)(\bmod 2)$. So all $f$-values have the same parity, and from $f(2,2)=1$ we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $m$ and $n$ be positive integers. Let $S$ be the set of lattice points $(x, y)$ with $1 \leq x \leq 2 m$ and $1 \leq y \leq 2 n$. A configuration of $m n$ rectangles is called happy if each point of $S$ is the vertex of exactly one rectangle. Prove that the number of happy configurations is odd.
|
I Original proposer's solution. To this end, let's denote by $f(2 m, 2 n)$ the number of happy configurations for a $2 m \times 2 n$ grid of lattice points (not necessarily equally spaced - this doesn't change the count). We already have the following easy case. Claim - We have $f(2,2 n)=(2 n-1)!!=(2 n-1) \cdot(2 n-3) \cdots \cdots 3 \cdot 1$. We will prove that: Claim - Assume $m, n \geq 1$. When $f(2 m, 2 n) \equiv f(2 m-2,2 n)(\bmod 2)$. Now configurations fixed by $\tau$ can be described readily: this occurs if and only if the last two columns are self-contained, meaning every rectangle with a vertex in these columns is completely contained in these two columns.  Hence it follows that $$ f(2 m, 2 n)=2(\text { number of pairs })+f(2 m-2,2 n) \cdot f(2,2 n) $$ Taking modulo 2 gives the result. By the same token $f(2 m, 2 n) \equiv f(2 m, 2 n-2)(\bmod 2)$. So all $f$-values have the same parity, and from $f(2,2)=1$ we're done.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
095333c0-e79f-5415-a86c-5878035b113c
| 246,334
|
Let $m$ and $n$ be positive integers. Let $S$ be the set of lattice points $(x, y)$ with $1 \leq x \leq 2 m$ and $1 \leq y \leq 2 n$. A configuration of $m n$ rectangles is called happy if each point of $S$ is the vertex of exactly one rectangle. Prove that the number of happy configurations is odd.
|
\l Evan's permutation-based solution. Retain the notation $f(2 m, 2 n)$ from before. Given a happy configuration, consider all the rectangles whose left edge is in the first column. Highlight every column containing the right edge of such a rectangle. For example, in the figure below, there are two highlighted columns. (The rectangles are drawn crooked so one can tell them apart.)  We organize happy configurations based on the set of highlighted columns. Specifically, define the relation $\sim$ on configurations by saying that $\mathcal{C} \sim \mathcal{C}^{\prime}$ if they differ by any permutation of the highlighted columns. This is an equivalence relation. And in general, if there are $k$ highlighted columns, its equivalence class under $\sim$ has $k$ ! elements. Then Claim - $f(2 m, 2 n)$ has the same parity as the number of happy configurations with exactly one highlighted column. There are $2 m-1$ ways to pick a single highlighted column, and then $f(2,2 n)=(2 n-1)!!$ ways to use the left column and highlighted column. So the count in the claim is exactly given by $$ (2 m-1) \cdot(2 n-1)!!f(2 m-2,2 n) $$ This implies $f(2 m, 2 n) \equiv f(2 m-2,2 n)(\bmod 2)$ and proceeding by induction as before solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $m$ and $n$ be positive integers. Let $S$ be the set of lattice points $(x, y)$ with $1 \leq x \leq 2 m$ and $1 \leq y \leq 2 n$. A configuration of $m n$ rectangles is called happy if each point of $S$ is the vertex of exactly one rectangle. Prove that the number of happy configurations is odd.
|
\l Evan's permutation-based solution. Retain the notation $f(2 m, 2 n)$ from before. Given a happy configuration, consider all the rectangles whose left edge is in the first column. Highlight every column containing the right edge of such a rectangle. For example, in the figure below, there are two highlighted columns. (The rectangles are drawn crooked so one can tell them apart.)  We organize happy configurations based on the set of highlighted columns. Specifically, define the relation $\sim$ on configurations by saying that $\mathcal{C} \sim \mathcal{C}^{\prime}$ if they differ by any permutation of the highlighted columns. This is an equivalence relation. And in general, if there are $k$ highlighted columns, its equivalence class under $\sim$ has $k$ ! elements. Then Claim - $f(2 m, 2 n)$ has the same parity as the number of happy configurations with exactly one highlighted column. There are $2 m-1$ ways to pick a single highlighted column, and then $f(2,2 n)=(2 n-1)!!$ ways to use the left column and highlighted column. So the count in the claim is exactly given by $$ (2 m-1) \cdot(2 n-1)!!f(2 m-2,2 n) $$ This implies $f(2 m, 2 n) \equiv f(2 m-2,2 n)(\bmod 2)$ and proceeding by induction as before solves the problem.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
095333c0-e79f-5415-a86c-5878035b113c
| 246,334
|
A sequence $a_{1}, a_{2}, \ldots$ of positive integers is defined recursively by $a_{1}=2$ and $$ a_{n+1}=a_{n}^{n+1}-1 \quad \text { for } n \geq 1 $$ Prove that for every odd prime $p$ and integer $k$, some term of the sequence is divisible by $p^{k}$.
|
We start with the following. Claim - Assume $n$ is a positive integer divisible by $p-1$. Then either $a_{n-1} \equiv 0$ $(\bmod p)$ or $a_{n} \equiv 0(\bmod p)$. $$ a_{n}=a_{n-1}^{n}-1 \equiv x^{p-1}-1 \equiv 0 \quad(\bmod p) $$ where $x:=a_{n-1}^{\frac{n}{p-1}}$ is an integer not divisible by $p$. Claim - If $n \geq 2$ is even, then $$ a_{n}^{n+1} \mid a_{n+2} $$ By considering multiples $n$ of $p-1$ which are larger than $k$, we see that if $a_{n} \equiv 0$ $(\bmod p)$ ever happens, we are done by combining the two previous claims. So the difficult case of the problem is the bad situation where $a_{n-1} \equiv 0(\bmod p)$ occurs for almost all $n \equiv 0(\bmod p-1)$. To resolve the difficult case and finish the problem, we zoom in on specific $n$ that will let us use lifting the exponent on $a_{n-1}$. Claim - Suppose $n$ is an (even) integer satisfying $$ \begin{aligned} & n \equiv 0 \quad(\bmod p-1) \\ & n \equiv 1 \quad\left(\bmod p^{k-1}\right) \end{aligned} $$ If $a_{n-1} \equiv 0(\bmod p)$, then in fact $p^{k} \mid a_{n-1}$. $$ 0 \equiv \frac{1}{a_{n-2}}-1 \quad(\bmod p) \Longrightarrow a_{n-2} \equiv 1 \quad(\bmod p) $$ Hence lifting the exponent applies and we get $$ \nu_{p}\left(a_{n-1}\right) \equiv \nu_{p}\left(a_{n-2}^{n-1}-1\right)=\nu_{p}\left(a_{n-2}-1\right)+\nu_{p}(n-1) \geq 1+(k-1)=k $$ as desired. Remark. The first few terms are $a_{1}=2, a_{2}=3, a_{3}=26, a_{4}=456975$, and $a_{5}=$ 19927930852449199486318359374, ... No element of the sequence is divisible by 4: the residues modulo 4 alternate between 2 and 3 . Remark. The second claim is important for the solution to work once $k \geq 2$. One could imagine a variation of the first claim that states if $n$ is divisible by $\varphi\left(p^{k}\right)=p^{k-1}(p-1)$, then either $a_{n-1} \equiv 0(\bmod p)$ or $a_{n} \equiv 0\left(\bmod p^{k}\right)$. However this gives an obstruction (for $k \geq 2)$ where we are guaranteed to have $n-1 \not \equiv 0(\bmod p)$ now, so lifting the exponent will never give additional factors of $p$ we want.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A sequence $a_{1}, a_{2}, \ldots$ of positive integers is defined recursively by $a_{1}=2$ and $$ a_{n+1}=a_{n}^{n+1}-1 \quad \text { for } n \geq 1 $$ Prove that for every odd prime $p$ and integer $k$, some term of the sequence is divisible by $p^{k}$.
|
We start with the following. Claim - Assume $n$ is a positive integer divisible by $p-1$. Then either $a_{n-1} \equiv 0$ $(\bmod p)$ or $a_{n} \equiv 0(\bmod p)$. $$ a_{n}=a_{n-1}^{n}-1 \equiv x^{p-1}-1 \equiv 0 \quad(\bmod p) $$ where $x:=a_{n-1}^{\frac{n}{p-1}}$ is an integer not divisible by $p$. Claim - If $n \geq 2$ is even, then $$ a_{n}^{n+1} \mid a_{n+2} $$ By considering multiples $n$ of $p-1$ which are larger than $k$, we see that if $a_{n} \equiv 0$ $(\bmod p)$ ever happens, we are done by combining the two previous claims. So the difficult case of the problem is the bad situation where $a_{n-1} \equiv 0(\bmod p)$ occurs for almost all $n \equiv 0(\bmod p-1)$. To resolve the difficult case and finish the problem, we zoom in on specific $n$ that will let us use lifting the exponent on $a_{n-1}$. Claim - Suppose $n$ is an (even) integer satisfying $$ \begin{aligned} & n \equiv 0 \quad(\bmod p-1) \\ & n \equiv 1 \quad\left(\bmod p^{k-1}\right) \end{aligned} $$ If $a_{n-1} \equiv 0(\bmod p)$, then in fact $p^{k} \mid a_{n-1}$. $$ 0 \equiv \frac{1}{a_{n-2}}-1 \quad(\bmod p) \Longrightarrow a_{n-2} \equiv 1 \quad(\bmod p) $$ Hence lifting the exponent applies and we get $$ \nu_{p}\left(a_{n-1}\right) \equiv \nu_{p}\left(a_{n-2}^{n-1}-1\right)=\nu_{p}\left(a_{n-2}-1\right)+\nu_{p}(n-1) \geq 1+(k-1)=k $$ as desired. Remark. The first few terms are $a_{1}=2, a_{2}=3, a_{3}=26, a_{4}=456975$, and $a_{5}=$ 19927930852449199486318359374, ... No element of the sequence is divisible by 4: the residues modulo 4 alternate between 2 and 3 . Remark. The second claim is important for the solution to work once $k \geq 2$. One could imagine a variation of the first claim that states if $n$ is divisible by $\varphi\left(p^{k}\right)=p^{k-1}(p-1)$, then either $a_{n-1} \equiv 0(\bmod p)$ or $a_{n} \equiv 0\left(\bmod p^{k}\right)$. However this gives an obstruction (for $k \geq 2)$ where we are guaranteed to have $n-1 \not \equiv 0(\bmod p)$ now, so lifting the exponent will never give additional factors of $p$ we want.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
55948696-9e42-57e8-988b-07916f91ee8a
| 605,875
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
ब The author's original solution. Complete isosceles trapezoid $A B Q C$ (so $D \in \overline{A Q}$ ). Reflect $B$ across $E$ to point $F$. 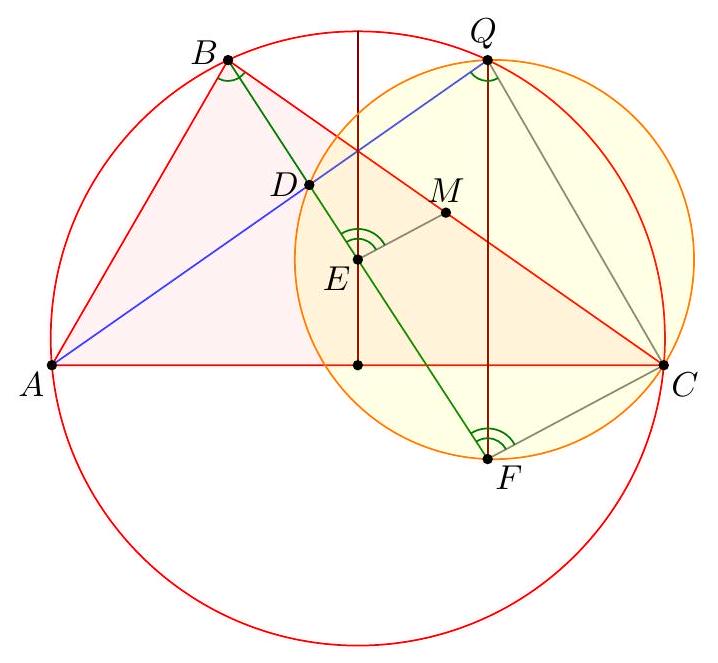 Claim - We have $D Q C F$ is cyclic. $$ \begin{aligned} \measuredangle F D C & =-\measuredangle C D B=180^{\circ}-\left(90^{\circ}+\measuredangle C A B\right)=90^{\circ}-\measuredangle C A B \\ & =90^{\circ}-\measuredangle Q C A=\measuredangle F Q C . \end{aligned} $$ To conclude, note that $$ \measuredangle B E M=\measuredangle B F C=\measuredangle D F C=\measuredangle D Q C=\measuredangle A Q C=\measuredangle A B C=\measuredangle A B M $$ Remark (Motivation). Here is one possible way to come up with the construction of point $F$ (at least this is what led Evan to find it). If one directs all the angles in the obvious way, there are really two points $D$ and $D^{\prime}$ that are possible, although one is outside the triangle; they give corresponding points $E$ and $E^{\prime}$. The circles $B E M$ and $B E^{\prime} M$ must then actually coincide since they are both alleged to be tangent to line $A B$. See the figure below.  One can already prove using angle chasing that $\overline{A B}$ is tangent to $\left(B E E^{\prime}\right)$. So the point of the problem is to show that $M$ lies on this circle too. However, from looking at the diagram, one may realize that in fact it seems $$ \triangle M E E^{\prime} \stackrel{ }{\sim} \triangle C D D^{\prime} $$ is going to be true from just those marked in the figure (and this would certainly imply the desired concyclic conclusion). Since $M$ is a midpoint, it makes sense to dilate $\triangle E M E^{\prime}$ from $B$ by a factor of 2 to get $\triangle F C F^{\prime}$ so that the desired similarity is actually a spiral similarity at $C$. Then the spiral similarity lemma says that the desired similarity is equivalent to requiring $\overline{D D^{\prime}} \cap \overline{F F^{\prime}}=Q$ to lie on both $(C D F)$ and $\left(C D^{\prime} F^{\prime}\right)$. Hence the key construction and claim from the solution are both discovered naturally, and we find the solution above. (The points $D^{\prime}, E^{\prime}, F^{\prime}$ can then be deleted to hide the motivation.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
ब The author's original solution. Complete isosceles trapezoid $A B Q C$ (so $D \in \overline{A Q}$ ). Reflect $B$ across $E$ to point $F$.  Claim - We have $D Q C F$ is cyclic. $$ \begin{aligned} \measuredangle F D C & =-\measuredangle C D B=180^{\circ}-\left(90^{\circ}+\measuredangle C A B\right)=90^{\circ}-\measuredangle C A B \\ & =90^{\circ}-\measuredangle Q C A=\measuredangle F Q C . \end{aligned} $$ To conclude, note that $$ \measuredangle B E M=\measuredangle B F C=\measuredangle D F C=\measuredangle D Q C=\measuredangle A Q C=\measuredangle A B C=\measuredangle A B M $$ Remark (Motivation). Here is one possible way to come up with the construction of point $F$ (at least this is what led Evan to find it). If one directs all the angles in the obvious way, there are really two points $D$ and $D^{\prime}$ that are possible, although one is outside the triangle; they give corresponding points $E$ and $E^{\prime}$. The circles $B E M$ and $B E^{\prime} M$ must then actually coincide since they are both alleged to be tangent to line $A B$. See the figure below.  One can already prove using angle chasing that $\overline{A B}$ is tangent to $\left(B E E^{\prime}\right)$. So the point of the problem is to show that $M$ lies on this circle too. However, from looking at the diagram, one may realize that in fact it seems $$ \triangle M E E^{\prime} \stackrel{ }{\sim} \triangle C D D^{\prime} $$ is going to be true from just those marked in the figure (and this would certainly imply the desired concyclic conclusion). Since $M$ is a midpoint, it makes sense to dilate $\triangle E M E^{\prime}$ from $B$ by a factor of 2 to get $\triangle F C F^{\prime}$ so that the desired similarity is actually a spiral similarity at $C$. Then the spiral similarity lemma says that the desired similarity is equivalent to requiring $\overline{D D^{\prime}} \cap \overline{F F^{\prime}}=Q$ to lie on both $(C D F)$ and $\left(C D^{\prime} F^{\prime}\right)$. Hence the key construction and claim from the solution are both discovered naturally, and we find the solution above. (The points $D^{\prime}, E^{\prime}, F^{\prime}$ can then be deleted to hide the motivation.)
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
0082373f-0732-5cf0-8d49-df0179f668fd
| 605,912
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
Another short solution. Let $Z$ be on line $B D E$ such that $\angle B A Z=90^{\circ}$. This lets us interpret the angle condition as follows: $$ \text { Claim - Points } A, D, Z, C \text { are cyclic. } $$  Define $W$ as the midpoint of $\overline{B Z}$, so $\overline{M W} \| \overline{C Z}$. And let $O$ denote the center of $(A B C)$. Claim - Points $M, E, O, W$ are cyclic. $$ \begin{aligned} \measuredangle M O E & =\measuredangle(\overline{O M}, \overline{B C})+\measuredangle(\overline{B C}, \overline{A C})+\measuredangle(\overline{A C}, \overline{O E}) \\ & =90^{\circ}+\measuredangle B C A+90^{\circ} \\ & =\measuredangle B C A=\measuredangle C A D=\measuredangle C Z D=\measuredangle M W D=\measuredangle M W E . \end{aligned} $$ To finish, note $$ \begin{aligned} \measuredangle M E B & =\measuredangle M E W=\measuredangle M O W \\ & =\measuredangle(\overline{M O}, \overline{B C})+\measuredangle(\overline{B C}, \overline{A B})+\measuredangle(\overline{A B}, \overline{O W}) \\ & =90^{\circ}+\measuredangle C B A+90^{\circ}=\measuredangle C B A=\measuredangle M B A . \end{aligned} $$ This implies the desired tangency.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
Another short solution. Let $Z$ be on line $B D E$ such that $\angle B A Z=90^{\circ}$. This lets us interpret the angle condition as follows: $$ \text { Claim - Points } A, D, Z, C \text { are cyclic. } $$  Define $W$ as the midpoint of $\overline{B Z}$, so $\overline{M W} \| \overline{C Z}$. And let $O$ denote the center of $(A B C)$. Claim - Points $M, E, O, W$ are cyclic. $$ \begin{aligned} \measuredangle M O E & =\measuredangle(\overline{O M}, \overline{B C})+\measuredangle(\overline{B C}, \overline{A C})+\measuredangle(\overline{A C}, \overline{O E}) \\ & =90^{\circ}+\measuredangle B C A+90^{\circ} \\ & =\measuredangle B C A=\measuredangle C A D=\measuredangle C Z D=\measuredangle M W D=\measuredangle M W E . \end{aligned} $$ To finish, note $$ \begin{aligned} \measuredangle M E B & =\measuredangle M E W=\measuredangle M O W \\ & =\measuredangle(\overline{M O}, \overline{B C})+\measuredangle(\overline{B C}, \overline{A B})+\measuredangle(\overline{A B}, \overline{O W}) \\ & =90^{\circ}+\measuredangle C B A+90^{\circ}=\measuredangle C B A=\measuredangle M B A . \end{aligned} $$ This implies the desired tangency.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
0082373f-0732-5cf0-8d49-df0179f668fd
| 605,912
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
I A Menelaus-based approach (Kevin Ren). Let $P$ be on $\overline{B C}$ with $A P=P C$. Let $Y$ be the point on line $A B$ such that $\angle A C Y=90^{\circ}$; as $\angle A Y C=90^{\circ}-A$ it follows $B D Y C$ is cyclic. Let $K=\overline{A P} \cap \overline{C Y}$, so $\triangle A C K$ is a right triangle with $P$ the midpoint of its hypotenuse.  Claim - Triangles BPE and DYK are similar. Claim - Triangles $B E M$ and $Y D C$ are similar. $$ \frac{B P}{B C} \frac{Y C}{Y K} \frac{A K}{A P}=1 $$ Since $A K / A P=2$ (note that $P$ is the midpoint of the hypotenuse of right triangle $A C K)$ and $B C=2 B M$, this simplifies to $$ \frac{B P}{B M}=\frac{Y K}{Y C} $$ To finish, note that $$ \measuredangle D B A=\measuredangle D B Y=\measuredangle D C Y=\measuredangle B M E $$ implying the desired tangency.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
I A Menelaus-based approach (Kevin Ren). Let $P$ be on $\overline{B C}$ with $A P=P C$. Let $Y$ be the point on line $A B$ such that $\angle A C Y=90^{\circ}$; as $\angle A Y C=90^{\circ}-A$ it follows $B D Y C$ is cyclic. Let $K=\overline{A P} \cap \overline{C Y}$, so $\triangle A C K$ is a right triangle with $P$ the midpoint of its hypotenuse.  Claim - Triangles BPE and DYK are similar. Claim - Triangles $B E M$ and $Y D C$ are similar. $$ \frac{B P}{B C} \frac{Y C}{Y K} \frac{A K}{A P}=1 $$ Since $A K / A P=2$ (note that $P$ is the midpoint of the hypotenuse of right triangle $A C K)$ and $B C=2 B M$, this simplifies to $$ \frac{B P}{B M}=\frac{Y K}{Y C} $$ To finish, note that $$ \measuredangle D B A=\measuredangle D B Y=\measuredangle D C Y=\measuredangle B M E $$ implying the desired tangency.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
0082373f-0732-5cf0-8d49-df0179f668fd
| 605,912
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
『 A spiral similarity approach (Hans $\mathbf{Y u}$ ). As in the previous solution, let $Y$ be the point on line $A B$ such that $\angle A C Y=90^{\circ}$; so $B D Y C$ is cyclic. Let $\Gamma$ be the circle through $B$ and $M$ tangent to $\overline{A B}$, and let $\Omega:=(B C Y D)$. We need to show $E \in \Gamma$.  Denote by $S$ the second intersection of $\Gamma$ and $\Omega$. The main idea behind is to consider the spiral similarity $$ \Psi: \Omega \rightarrow \Gamma \quad C \mapsto M \text { and } Y \mapsto B $$ centered at $S$ (due to the spiral similarity lemma), and show that $\Psi(D)=E$. The spiral similarity lemma already promises $\Psi(D)$ lies on line $B D$. Claim - We have $\Psi(A)=O$, the circumcenter of $A B C$. Claim - $\Psi$ maps line $A D$ to line $O P$. $$ \measuredangle(\overline{A D}, \overline{O P})=\measuredangle A P O=\measuredangle O P C=\measuredangle Y C P=\measuredangle(\overline{Y C}, \overline{B M}) $$ As $\Psi$ maps line $Y C$ to line $B M$ and $\Psi(A)=O$, we're done. Hence $\Psi(D)$ should not only lie on $B D$ but also line $O P$. This proves $\Psi(D)=E$, so $E \in \Gamma$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $D$ is selected inside acute triangle $A B C$ so that $\angle D A C=\angle A C B$ and $\angle B D C=90^{\circ}+\angle B A C$. Point $E$ is chosen on ray $B D$ so that $A E=E C$. Let $M$ be the midpoint of $B C$. Show that line $A B$ is tangent to the circumcircle of triangle $B E M$.
|
『 A spiral similarity approach (Hans $\mathbf{Y u}$ ). As in the previous solution, let $Y$ be the point on line $A B$ such that $\angle A C Y=90^{\circ}$; so $B D Y C$ is cyclic. Let $\Gamma$ be the circle through $B$ and $M$ tangent to $\overline{A B}$, and let $\Omega:=(B C Y D)$. We need to show $E \in \Gamma$.  Denote by $S$ the second intersection of $\Gamma$ and $\Omega$. The main idea behind is to consider the spiral similarity $$ \Psi: \Omega \rightarrow \Gamma \quad C \mapsto M \text { and } Y \mapsto B $$ centered at $S$ (due to the spiral similarity lemma), and show that $\Psi(D)=E$. The spiral similarity lemma already promises $\Psi(D)$ lies on line $B D$. Claim - We have $\Psi(A)=O$, the circumcenter of $A B C$. Claim - $\Psi$ maps line $A D$ to line $O P$. $$ \measuredangle(\overline{A D}, \overline{O P})=\measuredangle A P O=\measuredangle O P C=\measuredangle Y C P=\measuredangle(\overline{Y C}, \overline{B M}) $$ As $\Psi$ maps line $Y C$ to line $B M$ and $\Psi(A)=O$, we're done. Hence $\Psi(D)$ should not only lie on $B D$ but also line $O P$. This proves $\Psi(D)=E$, so $E \in \Gamma$ as needed.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
0082373f-0732-5cf0-8d49-df0179f668fd
| 605,912
|
Prove that the average of the numbers $n \sin n^{\circ}$ for $n=2,4,6, \ldots, 180$ is $\cot 1^{\circ}$.
|
Because $$ n \sin n^{\circ}+(180-n) \sin \left(180^{\circ}-n^{\circ}\right)=180 \sin n^{\circ} $$ So enough to show that $$ \sum_{n=0}^{89} \sin (2 n)^{\circ}=\cot 1^{\circ} $$ Let $\zeta=\cos 2^{\circ}+i \sin 2^{\circ}$ be a primitive root. Then $$ \begin{aligned} \sum_{n=0}^{89} \frac{\zeta^{n}-\zeta^{-n}}{2 i} & =\frac{1}{2 i}\left[\frac{\zeta^{90}-1}{\zeta-1}-\frac{\zeta^{-90}-1}{\zeta^{-1}-1}\right] \\ & =\frac{1}{2 i}\left[\frac{-2}{\zeta-1}-\frac{-2}{\zeta^{-1}-1}\right] \\ & =\frac{1}{-i} \frac{\zeta^{-1}-\zeta}{(\zeta-1)\left(\zeta^{-1}-1\right)}=i \cdot \frac{\zeta+1}{\zeta-1} \end{aligned} $$ Also, $$ \begin{aligned} \cot 1^{\circ} & =\frac{\cos 1^{\circ}}{\sin 1^{\circ}}=\frac{\left(\cos 1^{\circ}\right)^{2}}{\cos 1^{\circ} \sin 1^{\circ}} \\ & =\frac{\frac{\cos 2^{\circ}+1}{2}}{\frac{\sin 2^{\circ}}{2}}=\frac{\frac{1}{2}\left(\zeta+\zeta^{-1}\right)+1}{\frac{1}{2 i}\left(\zeta-\zeta^{-1}\right)} \\ & =i \cdot \frac{(\zeta+1)^{2}}{\zeta^{2}-1}=i \cdot \frac{\zeta+1}{\zeta-1} \end{aligned} $$ So we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that the average of the numbers $n \sin n^{\circ}$ for $n=2,4,6, \ldots, 180$ is $\cot 1^{\circ}$.
|
Because $$ n \sin n^{\circ}+(180-n) \sin \left(180^{\circ}-n^{\circ}\right)=180 \sin n^{\circ} $$ So enough to show that $$ \sum_{n=0}^{89} \sin (2 n)^{\circ}=\cot 1^{\circ} $$ Let $\zeta=\cos 2^{\circ}+i \sin 2^{\circ}$ be a primitive root. Then $$ \begin{aligned} \sum_{n=0}^{89} \frac{\zeta^{n}-\zeta^{-n}}{2 i} & =\frac{1}{2 i}\left[\frac{\zeta^{90}-1}{\zeta-1}-\frac{\zeta^{-90}-1}{\zeta^{-1}-1}\right] \\ & =\frac{1}{2 i}\left[\frac{-2}{\zeta-1}-\frac{-2}{\zeta^{-1}-1}\right] \\ & =\frac{1}{-i} \frac{\zeta^{-1}-\zeta}{(\zeta-1)\left(\zeta^{-1}-1\right)}=i \cdot \frac{\zeta+1}{\zeta-1} \end{aligned} $$ Also, $$ \begin{aligned} \cot 1^{\circ} & =\frac{\cos 1^{\circ}}{\sin 1^{\circ}}=\frac{\left(\cos 1^{\circ}\right)^{2}}{\cos 1^{\circ} \sin 1^{\circ}} \\ & =\frac{\frac{\cos 2^{\circ}+1}{2}}{\frac{\sin 2^{\circ}}{2}}=\frac{\frac{1}{2}\left(\zeta+\zeta^{-1}\right)+1}{\frac{1}{2 i}\left(\zeta-\zeta^{-1}\right)} \\ & =i \cdot \frac{(\zeta+1)^{2}}{\zeta^{2}-1}=i \cdot \frac{\zeta+1}{\zeta-1} \end{aligned} $$ So we're done.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1996-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e90ff08a-e5f2-5a86-ba8f-15314ddc2297
| 247,787
|
For any nonempty set $S$ of real numbers, let $\sigma(S)$ denote the sum of the elements of $S$. Given a set $A$ of $n$ positive integers, consider the collection of all distinct sums $\sigma(S)$ as $S$ ranges over the nonempty subsets of $A$. Prove that this collection of sums can be partitioned into $n$ classes so that in each class, the ratio of the largest sum to the smallest sum does not exceed 2 .
|
By induction on $n$ with $n=1$ being easy. For the inductive step, assume $$ A=\left\{a_{1}>a_{2}>\cdots>a_{n}\right\} $$ Fix any index $k$ with the property that $$ a_{k}>\frac{\sigma(A)}{2^{k}} $$ (which must exist since $\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{2^{k}}<1$ ). Then - We make $k$ classes for the sums between $\frac{\sigma(A)}{2^{k}}$ and $\sigma(A)$; this handles every set which has any element in $\left\{a_{1}, \ldots, a_{k}\right\}$. - We make $n-k$ classes via induction hypothesis on $\left\{a_{k+1}, \ldots, a_{n}\right\}$. This solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For any nonempty set $S$ of real numbers, let $\sigma(S)$ denote the sum of the elements of $S$. Given a set $A$ of $n$ positive integers, consider the collection of all distinct sums $\sigma(S)$ as $S$ ranges over the nonempty subsets of $A$. Prove that this collection of sums can be partitioned into $n$ classes so that in each class, the ratio of the largest sum to the smallest sum does not exceed 2 .
|
By induction on $n$ with $n=1$ being easy. For the inductive step, assume $$ A=\left\{a_{1}>a_{2}>\cdots>a_{n}\right\} $$ Fix any index $k$ with the property that $$ a_{k}>\frac{\sigma(A)}{2^{k}} $$ (which must exist since $\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{2^{k}}<1$ ). Then - We make $k$ classes for the sums between $\frac{\sigma(A)}{2^{k}}$ and $\sigma(A)$; this handles every set which has any element in $\left\{a_{1}, \ldots, a_{k}\right\}$. - We make $n-k$ classes via induction hypothesis on $\left\{a_{k+1}, \ldots, a_{n}\right\}$. This solves the problem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1996-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
50f2626a-4df1-52a3-bc11-71499dacfb8d
| 605,963
|
Let $A B C$ be a triangle. Prove that there is a line $\ell$ (in the plane of triangle $A B C$ ) such that the intersection of the interior of triangle $A B C$ and the interior of its reflection $A^{\prime} B^{\prime} C^{\prime}$ in $\ell$ has area more than $\frac{2}{3}$ the area of triangle $A B C$.
|
All that's needed is: Claim - If $A B C$ is a triangle where $\frac{1}{2}<\frac{A B}{A C}<1$, then the $\angle A$ bisector works. $$ \frac{[A B D]}{[A B C]}=\frac{B D}{B C}=\frac{A B}{A B+A C} $$ by angle bisector theorem. In general, suppose $x<y<z$ are sides of a triangle. Then $\frac{1}{2}<\frac{y}{z}<1$ by triangle inequality as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Prove that there is a line $\ell$ (in the plane of triangle $A B C$ ) such that the intersection of the interior of triangle $A B C$ and the interior of its reflection $A^{\prime} B^{\prime} C^{\prime}$ in $\ell$ has area more than $\frac{2}{3}$ the area of triangle $A B C$.
|
All that's needed is: Claim - If $A B C$ is a triangle where $\frac{1}{2}<\frac{A B}{A C}<1$, then the $\angle A$ bisector works. $$ \frac{[A B D]}{[A B C]}=\frac{B D}{B C}=\frac{A B}{A B+A C} $$ by angle bisector theorem. In general, suppose $x<y<z$ are sides of a triangle. Then $\frac{1}{2}<\frac{y}{z}<1$ by triangle inequality as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1996-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
14c5d17b-1423-568b-becb-e7fa55513f26
| 247,805
|
An $n$-term sequence $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ in which each term is either 0 or 1 is called a binary sequence of length $n$. Let $a_{n}$ be the number of binary sequences of length $n$ containing no three consecutive terms equal to $0,1,0$ in that order. Let $b_{n}$ be the number of binary sequences of length $n$ that contain no four consecutive terms equal to $0,0,1,1$ or $1,1,0,0$ in that order. Prove that $b_{n+1}=2 a_{n}$ for all positive integers $n$.
|
Consider the map from sequences of the latter form to sequences of the first form by $$ \left(y_{1}, \ldots, y_{n+1}\right) \mapsto\left(y_{1}+y_{2}, y_{2}+y_{3}, \ldots, y_{n}+y_{n+1}\right) . $$ It is 2-to-1. The end.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An $n$-term sequence $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ in which each term is either 0 or 1 is called a binary sequence of length $n$. Let $a_{n}$ be the number of binary sequences of length $n$ containing no three consecutive terms equal to $0,1,0$ in that order. Let $b_{n}$ be the number of binary sequences of length $n$ that contain no four consecutive terms equal to $0,0,1,1$ or $1,1,0,0$ in that order. Prove that $b_{n+1}=2 a_{n}$ for all positive integers $n$.
|
Consider the map from sequences of the latter form to sequences of the first form by $$ \left(y_{1}, \ldots, y_{n+1}\right) \mapsto\left(y_{1}+y_{2}, y_{2}+y_{3}, \ldots, y_{n}+y_{n+1}\right) . $$ It is 2-to-1. The end.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1996-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8adb2fd2-c08b-5937-8609-0e794cef3e2a
| 247,814
|
Let $A B C$ be a triangle, and $M$ an interior point such that $\angle M A B=10^{\circ}, \angle M B A=$ $20^{\circ}, \angle M A C=40^{\circ}$ and $\angle M C A=30^{\circ}$. Prove that the triangle is isosceles.
|
Let $\theta=\angle M B C<80^{\circ}$. By trig Ceva, we get $$ \frac{\sin 10^{\circ}}{\sin 40^{\circ}} \cdot \frac{\sin \theta}{\sin 20^{\circ}} \cdot \frac{\sin 30^{\circ}}{\sin \left(80^{\circ}-\theta\right)}=1 $$ This simplifies to $$ \sin \theta=4 \sin \left(80^{\circ}-\theta\right) \sin 40^{\circ} \cos 10^{\circ} $$ Claim - We have $\theta=60^{\circ}$. $$ \begin{aligned} 4 \sin 20^{\circ} \sin 40^{\circ} \cos 10^{\circ} & =2\left(\cos 20^{\circ}-\cos 60^{\circ}\right) \cos 10^{\circ} \\ & =2 \cos 20^{\circ} \cos 10^{\circ}+\sin 80^{\circ} \\ & =\left(\cos 30^{\circ}-\cos 10^{\circ}\right)+\sin 80^{\circ}=\cos 30^{\circ} \end{aligned} $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle, and $M$ an interior point such that $\angle M A B=10^{\circ}, \angle M B A=$ $20^{\circ}, \angle M A C=40^{\circ}$ and $\angle M C A=30^{\circ}$. Prove that the triangle is isosceles.
|
Let $\theta=\angle M B C<80^{\circ}$. By trig Ceva, we get $$ \frac{\sin 10^{\circ}}{\sin 40^{\circ}} \cdot \frac{\sin \theta}{\sin 20^{\circ}} \cdot \frac{\sin 30^{\circ}}{\sin \left(80^{\circ}-\theta\right)}=1 $$ This simplifies to $$ \sin \theta=4 \sin \left(80^{\circ}-\theta\right) \sin 40^{\circ} \cos 10^{\circ} $$ Claim - We have $\theta=60^{\circ}$. $$ \begin{aligned} 4 \sin 20^{\circ} \sin 40^{\circ} \cos 10^{\circ} & =2\left(\cos 20^{\circ}-\cos 60^{\circ}\right) \cos 10^{\circ} \\ & =2 \cos 20^{\circ} \cos 10^{\circ}+\sin 80^{\circ} \\ & =\left(\cos 30^{\circ}-\cos 10^{\circ}\right)+\sin 80^{\circ}=\cos 30^{\circ} \end{aligned} $$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1996-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
297c9d8f-2f3c-5b3d-bb8f-3f893f1cd10a
| 247,820
|
Determine with proof whether there is a subset $X \subseteq \mathbb{Z}$ with the following property: for any $n \in \mathbb{Z}$, there is exactly one solution to $a+2 b=n$, with $a, b \in X$.
|
The idea is generating functions, but extra care is required since exponents will be in $\mathbb{Z}$ rather than in $\mathbb{Z}_{\geq 0}$. However, consider formally the limit $$ f(x)=\prod_{k \geq 0}\left(1+x^{(-4)^{k}}\right) $$ For size reasons, this indeed converges formally to a power series, in the sense that the coefficient of any $x^{k}$ is eventually zero or one for all partial sums. We claim $X=\left\{n:\left[x^{n}\right] f(x)=1\right\}$ works. For a given $n$, we can truncate the sum at some large $N$ again for size reasons. For convenience assume $N$ is even. Now set $$ f_{N}(x)=\prod_{k=0}^{N}\left(1+x^{(-4)^{k}}\right) $$ Next, we compute $$ f_{N}(x) f_{N}\left(x^{2}\right)=\frac{(1+x)\left(1+x^{2}\right) \ldots\left(1+x^{2^{2 N+1}}\right)}{x^{2+8+\cdots+2^{2 N-1}}}=\cdots+x^{-2}+x^{-1}+1+x+x^{2}+\ldots $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine with proof whether there is a subset $X \subseteq \mathbb{Z}$ with the following property: for any $n \in \mathbb{Z}$, there is exactly one solution to $a+2 b=n$, with $a, b \in X$.
|
The idea is generating functions, but extra care is required since exponents will be in $\mathbb{Z}$ rather than in $\mathbb{Z}_{\geq 0}$. However, consider formally the limit $$ f(x)=\prod_{k \geq 0}\left(1+x^{(-4)^{k}}\right) $$ For size reasons, this indeed converges formally to a power series, in the sense that the coefficient of any $x^{k}$ is eventually zero or one for all partial sums. We claim $X=\left\{n:\left[x^{n}\right] f(x)=1\right\}$ works. For a given $n$, we can truncate the sum at some large $N$ again for size reasons. For convenience assume $N$ is even. Now set $$ f_{N}(x)=\prod_{k=0}^{N}\left(1+x^{(-4)^{k}}\right) $$ Next, we compute $$ f_{N}(x) f_{N}\left(x^{2}\right)=\frac{(1+x)\left(1+x^{2}\right) \ldots\left(1+x^{2^{2 N+1}}\right)}{x^{2+8+\cdots+2^{2 N-1}}}=\cdots+x^{-2}+x^{-1}+1+x+x^{2}+\ldots $$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1996-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
ebf7a25b-d340-57ab-be66-4555f8681921
| 247,829
|
Let $p_{1}, p_{2}, p_{3}, \ldots$ be the prime numbers listed in increasing order, and let $0<x_{0}<1$ be a real number between 0 and 1 . For each positive integer $k$, define $$ x_{k}= \begin{cases}0 & \text { if } x_{k-1}=0 \\ \left\{\frac{p_{k}}{x_{k-1}}\right\} & \text { if } x_{k-1} \neq 0\end{cases} $$ where $\{x\}$ denotes the fractional part of $x$. Find, with proof, all $x_{0}$ satisfying $0<x_{0}<1$ for which the sequence $x_{0}, x_{1}, x_{2}, \ldots$ eventually becomes 0 .
|
## The answer is $x_{0}$ rational. If $x_{0}$ is irrational, then all $x_{i}$ are irrational by induction. So the sequence cannot become zero. If $x_{0}$ is rational, then all are. Now one simply observes that the denominators of $x_{n}$ are strictly decreasing, until we reach $0=\frac{0}{1}$. This concludes the proof. Remark. The sequence $p_{k}$ could have been any sequence of integers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p_{1}, p_{2}, p_{3}, \ldots$ be the prime numbers listed in increasing order, and let $0<x_{0}<1$ be a real number between 0 and 1 . For each positive integer $k$, define $$ x_{k}= \begin{cases}0 & \text { if } x_{k-1}=0 \\ \left\{\frac{p_{k}}{x_{k-1}}\right\} & \text { if } x_{k-1} \neq 0\end{cases} $$ where $\{x\}$ denotes the fractional part of $x$. Find, with proof, all $x_{0}$ satisfying $0<x_{0}<1$ for which the sequence $x_{0}, x_{1}, x_{2}, \ldots$ eventually becomes 0 .
|
## The answer is $x_{0}$ rational. If $x_{0}$ is irrational, then all $x_{i}$ are irrational by induction. So the sequence cannot become zero. If $x_{0}$ is rational, then all are. Now one simply observes that the denominators of $x_{n}$ are strictly decreasing, until we reach $0=\frac{0}{1}$. This concludes the proof. Remark. The sequence $p_{k}$ could have been any sequence of integers.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1997-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
830c237c-3463-5713-85d3-fab5ea46ccc9
| 606,035
|
Prove that for any integer $n$, there exists a unique polynomial $Q$ with coefficients in $\{0,1, \ldots, 9\}$ such that $Q(-2)=Q(-5)=n$.
|
If we let $$ Q(x)=\sum_{k \geq 0} a_{k} x^{k} $$ then $a_{k}$ is uniquely determined by $n\left(\bmod 2^{k}\right)$ and $n\left(\bmod 5^{k}\right)$. Indeed, we can extract the coefficients of $Q$ exactly by the following algorithm: - Define $b_{0}=c_{0}=n$. - For $i \geq 0$, let $a_{i}$ be the unique digit satisfying $a_{i} \equiv b_{i}(\bmod 2), a_{i} \equiv c_{i}(\bmod 5)$. Then, define $$ b_{i+1}=\frac{b_{i}-a_{i}}{-2}, \quad c_{i+1}=\frac{c_{i}-a_{i}}{-5} . $$ In fact, we will prove the following claim: Claim - Suppose $b_{0}$ and $c_{0}$ are any integers such that $$ b_{0} \equiv c_{0} \quad(\bmod 3) . $$ Then defining $b_{i}$ and $c_{i}$ as above, we have $b_{i} \equiv c_{i}(\bmod 3)$ for all $i$, and $b_{N}=c_{N}=0$ for large enough $N$. $$ (b, c) \mapsto\left(\frac{b-a}{-2}, \frac{c-a}{-5}\right) $$ for some $0 \leq a \leq 9$ (a function in $b$ and $c$ ). The $b \equiv c(\bmod 3)$ is clearly preserved. Also, examining the size, - If $|c|>2$, we have $\left|\frac{c-a}{-5}\right| \leq \frac{|c|+9}{5}<|c|$. Thus, we eventually reach a pair with $|c| \leq 2$. - Similarly, if $|b|>9$, we have $\left|\frac{b-a}{-2}\right| \leq \frac{|b|+9}{2}<|b|$, so we eventually reach a pair with $|b| \leq 9$. this leaves us with $5 \cdot 19=95$ ordered pairs to check (though only about one third have $b \equiv c(\bmod 3))$. This can be done by the following code: ``` import functools @functools.lru_cache() def f(x0, yO): if x0 == 0 and y0 == 0: return 0 if x0 % 2 == (y0 % 5) % 2: d = y0 % 5 else: d = (y0 % 5) + 5 x1 = (x0 - d) // (-2) y1 = (y0 - d) // (-5) return 1 + f(x1, y1) for x in range(-9, 10): for y in range(-2, 3): if (x % 3 == y % 3): print(f"({x:2d}, {y:2d}) finished in {f(x,y)} moves") ``` As this gives the output  we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for any integer $n$, there exists a unique polynomial $Q$ with coefficients in $\{0,1, \ldots, 9\}$ such that $Q(-2)=Q(-5)=n$.
|
If we let $$ Q(x)=\sum_{k \geq 0} a_{k} x^{k} $$ then $a_{k}$ is uniquely determined by $n\left(\bmod 2^{k}\right)$ and $n\left(\bmod 5^{k}\right)$. Indeed, we can extract the coefficients of $Q$ exactly by the following algorithm: - Define $b_{0}=c_{0}=n$. - For $i \geq 0$, let $a_{i}$ be the unique digit satisfying $a_{i} \equiv b_{i}(\bmod 2), a_{i} \equiv c_{i}(\bmod 5)$. Then, define $$ b_{i+1}=\frac{b_{i}-a_{i}}{-2}, \quad c_{i+1}=\frac{c_{i}-a_{i}}{-5} . $$ In fact, we will prove the following claim: Claim - Suppose $b_{0}$ and $c_{0}$ are any integers such that $$ b_{0} \equiv c_{0} \quad(\bmod 3) . $$ Then defining $b_{i}$ and $c_{i}$ as above, we have $b_{i} \equiv c_{i}(\bmod 3)$ for all $i$, and $b_{N}=c_{N}=0$ for large enough $N$. $$ (b, c) \mapsto\left(\frac{b-a}{-2}, \frac{c-a}{-5}\right) $$ for some $0 \leq a \leq 9$ (a function in $b$ and $c$ ). The $b \equiv c(\bmod 3)$ is clearly preserved. Also, examining the size, - If $|c|>2$, we have $\left|\frac{c-a}{-5}\right| \leq \frac{|c|+9}{5}<|c|$. Thus, we eventually reach a pair with $|c| \leq 2$. - Similarly, if $|b|>9$, we have $\left|\frac{b-a}{-2}\right| \leq \frac{|b|+9}{2}<|b|$, so we eventually reach a pair with $|b| \leq 9$. this leaves us with $5 \cdot 19=95$ ordered pairs to check (though only about one third have $b \equiv c(\bmod 3))$. This can be done by the following code: ``` import functools @functools.lru_cache() def f(x0, yO): if x0 == 0 and y0 == 0: return 0 if x0 % 2 == (y0 % 5) % 2: d = y0 % 5 else: d = (y0 % 5) + 5 x1 = (x0 - d) // (-2) y1 = (y0 - d) // (-5) return 1 + f(x1, y1) for x in range(-9, 10): for y in range(-2, 3): if (x % 3 == y % 3): print(f"({x:2d}, {y:2d}) finished in {f(x,y)} moves") ``` As this gives the output  we are done.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1997-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
9b401843-9ff3-50fe-a6dc-36758c232a49
| 606,058
|
To clip a convex $n$-gon means to choose a pair of consecutive sides $A B, B C$ and to replace them by the three segments $A M, M N$, and $N C$, where $M$ is the midpoint of $A B$ and $N$ is the midpoint of $B C$. In other words, one cuts off the triangle $M B N$ to obtain a convex $(n+1)$-gon. A regular hexagon $\mathcal{P}_{6}$ of area 1 is clipped to obtain a heptagon $\mathcal{P}_{7}$. Then $\mathcal{P}_{7}$ is clipped (in one of the seven possible ways) to obtain an octagon $\mathcal{P}_{8}$, and so on. Prove that no matter how the clippings are done, the area of $\mathcal{P}_{n}$ is greater than $\frac{1}{3}$, for all $n \geq 6$.
|
Call the original hexagon $A B C D E F$. We show the area common to triangles $A C E$ and $B D F$ is in every $\mathcal{P}_{n}$; this solves the problem since the area is $1 / 3$. For every side of a clipped polygon, we define its foundation recursively as follows: - $A B, B C, C D, D E, E F, F A$ are each their own foundation (we also call these original sides). - When a new clipped edge is added, its foundation is the union of the foundations of the two edges it touches. Hence, any foundations are nonempty subsets of original sides. Claim - All foundations are in fact at most two-element sets of adjacent original sides. Now, if a side has foundation contained in $\{A B, B C\}$, say, then the side should be contained within triangle $A B C$. Hence the side does not touch $A C$. This proves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
To clip a convex $n$-gon means to choose a pair of consecutive sides $A B, B C$ and to replace them by the three segments $A M, M N$, and $N C$, where $M$ is the midpoint of $A B$ and $N$ is the midpoint of $B C$. In other words, one cuts off the triangle $M B N$ to obtain a convex $(n+1)$-gon. A regular hexagon $\mathcal{P}_{6}$ of area 1 is clipped to obtain a heptagon $\mathcal{P}_{7}$. Then $\mathcal{P}_{7}$ is clipped (in one of the seven possible ways) to obtain an octagon $\mathcal{P}_{8}$, and so on. Prove that no matter how the clippings are done, the area of $\mathcal{P}_{n}$ is greater than $\frac{1}{3}$, for all $n \geq 6$.
|
Call the original hexagon $A B C D E F$. We show the area common to triangles $A C E$ and $B D F$ is in every $\mathcal{P}_{n}$; this solves the problem since the area is $1 / 3$. For every side of a clipped polygon, we define its foundation recursively as follows: - $A B, B C, C D, D E, E F, F A$ are each their own foundation (we also call these original sides). - When a new clipped edge is added, its foundation is the union of the foundations of the two edges it touches. Hence, any foundations are nonempty subsets of original sides. Claim - All foundations are in fact at most two-element sets of adjacent original sides. Now, if a side has foundation contained in $\{A B, B C\}$, say, then the side should be contained within triangle $A B C$. Hence the side does not touch $A C$. This proves the problem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1997-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f7e20e09-5fe4-59da-b202-05618b6ad5d7
| 247,863
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.